2. 山西大学 计算智能与中文信息处理重点实验室,山西 太原 030006
2. Key Laboratory of Computational Intelligence and Chinese Information Processing, Shanxi University, Taiyuan 030006, China
支持向量机(support vector machine,SVM)是由Vapnik等[1]提出的基于统计学习理论和结构风险最小化准则的一种学习策略,在小样本多维度的数据分类和回归问题方面表现出了优良的泛化性能,广泛应用于机器学习、模式识别、模式分类、图像处理等领域[2-8]。目前在大规模数据处理方面,SVM仍存在一些不足。主要问题是当样本数n较大时,会消耗大量的内存空间和运算时间,严重降低了SVM的学习效率,限制了SVM在大规模数据集上的应用。
粒度支持向量机的含义最早由Tang等[9]提出,其主要思想是首先构建粒度空间获得一系列信息粒,然后在每个信息粒上进行SVM学习,最后聚合信息粒上的信息获得最终的决策函数。依据粒划分方式的不同,衍生出了基于聚类的GSVM、基于分类的GSVM以及基于关联规则的GSVM等方法[10-19]。GSVM采用粒化的方式压缩数据集的规模,以提高SVM的学习效率,而目前的GSVM大都在静态层级进行划分,即只对信息粒进行有限次的浅层次划分,丢失了大量对分类起关键作用的样本信息,且冗余信息较多,降低了模型的性能。尽管已经提出的动态粒度支持向量机(dynamic granular support vector machine,DGSVM)[20],以及动态支持向量回归机(dynamic granular support vector regression,DGSVR)[21],采用动态的方式对重要信息粒深层次划分,对无关信息粒则进行浅层次划分,但DGSVM随着粒划分过程会使数据规模不断增加,使得SVM的效率有所降低。
为了进一步提升SVM在大规模数据集上的应用能力,本文提出了采用划分融合双向控制的粒度支持向量机方法。在SVM分类过程中,对分类起关键重要的信息分布于超平面附近,称为强信息区,超平面远端的信息对分类影响较小,称为弱信息区,本文提出的方法通过对强信息区的强信息粒进行深度划分,同时融合弱信息区的弱信息粒,使训练数据始终动态保持在较小规模。该方法分为两个阶段,首先通过聚类算法对原始数据集进行初始粒划分,挑选粒中代表信息组成新的训练集训练得到初始分类超平面,然后通过迭代划分融合的方式深度划分强信息粒,同时融合远端弱信息粒。实验表明,该方法能够在保证模型精度的条件下显著提升SVM的学习效率。
1 粒度支持向量机粒度支持向量机引入粒计算的概念,对复杂问题进行抽象和简化,以较低的代价来得到问题的满意近似解。在多种的粒划分方式中,基于聚类的粒度支持向量机(clustering-based granular support vector machine, CGSVM)是当前研究的热点之一[22-25]。CGSVM通过聚类算法将大规模数据集分解成多个小规模数据簇,簇内信息具有高度相似性,而簇间信息相似度较低,挑选出每个簇中具有代表性的样本信息作为新的训练样本,整合所有挑选出的样本训练得到新的模型。
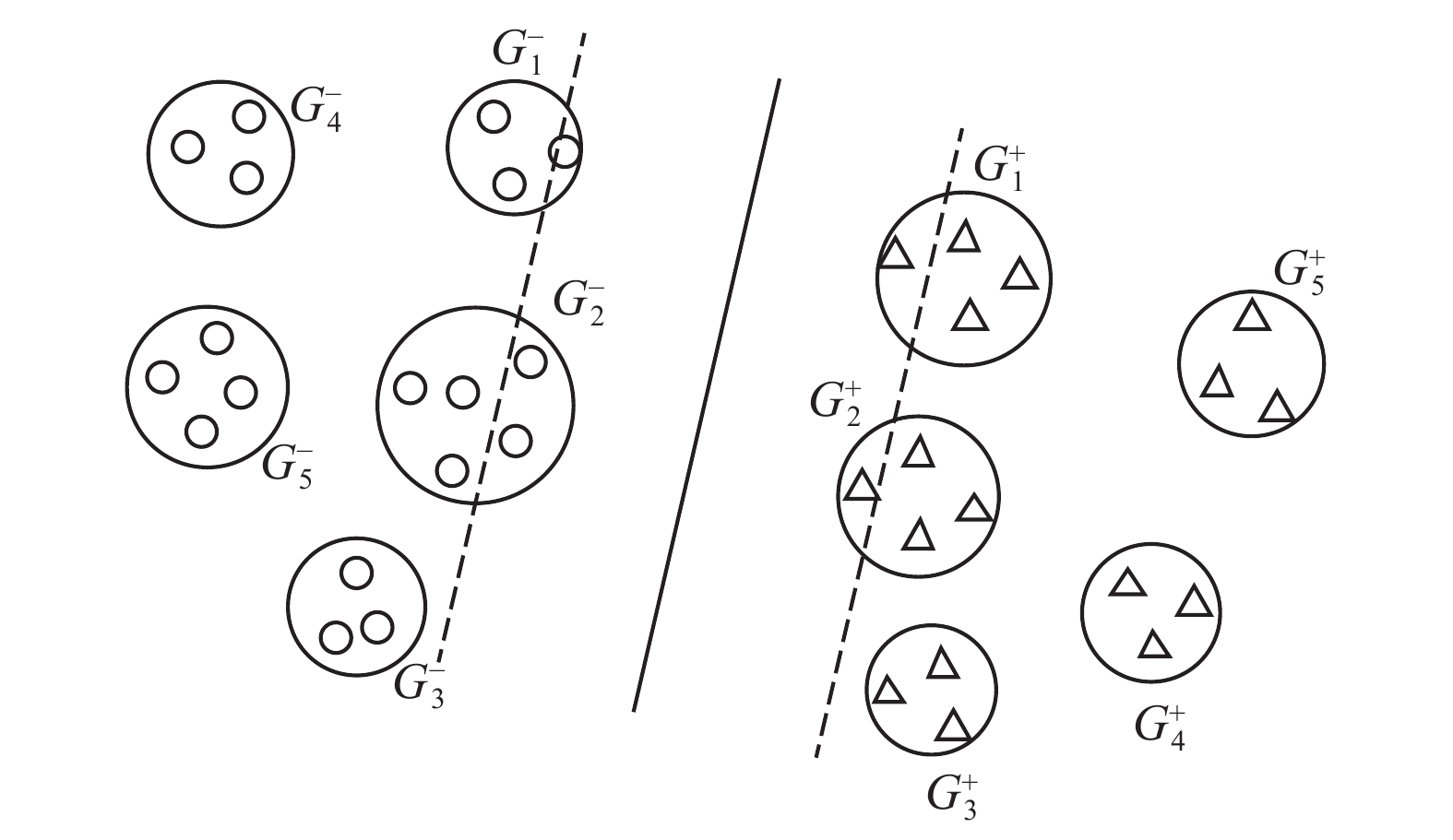
CGSVM只采用了少量代表样本作为训练集,有效地加速了SVM学习过程。但CGSVM本身也存在一些不足,在SVM学习过程中,距离分类超平面较近的信息对分类起关键作用,而距离超平面较远的信息几乎不影响模型训练过程。CGSVM在数据处理过程中没有区分不同信息粒对分类的影响程度,对所有信息粒都进行同等层次的划分,导致对重要信息提取不足且仍存在过多的冗余信息。如图1中,距离超平面较近的
|
Download:
|
| 图 1 CGSVM粒度划分 Fig. 1 CGSVM granular division | |
现阶段CGSVM通过静态的、浅层次的方式,对粒划后的信息粒进行无差别的信息提取,导致对分类起关键作用的信息提取不足且还保留了大量对分类影响较小的冗余信息。本文提出的方法采用多层次的划分策略,由于超平面附近的样本信息有较大概率成为支持向量,距离超平面较远的样本信息对分类几乎没有影响,因此,DFSVM采取动态迭代划分的方式,对超平面附近可能成为支持向量的信息粒深度划分,同时融合距离超平面较远的冗余信息,不断更新超平面以获得更多潜在有效的分类信息,该方法能够将训练集始终固定在一个较小的规模,加速了SVM的训练过程。
2.1 初始粒划分给定原始数据集
| ${D'} = \{ (G_1^ + ,G_2^ + , \cdots, G_k^ + ) \cap (G_1^ - ,G_2^ - , \cdots , G_k^ - )\} $ |
式中:
| $\displaystyle{\mu _i} = \frac{{\displaystyle\sum\limits_{p = 1}^{{n_i}} {\varphi \left( {{x_p}} \right)} }}{{{n_i}}} = \frac{1}{{{n_i}}}\sqrt {\sum\limits_{p = 1}^{{n_i}} {\sum\limits_{q = 1}^{n_i'} {K\left( {{x_p},{x_q}} \right)} } } $ | (1) |
| $ \begin{gathered}\displaystyle {\gamma _i}= \frac{{\max \left( {{x_l}} \right) - \min \left( {{x_s}} \right)}}{2} = \qquad\\\displaystyle \frac{1}{2}\sqrt {\varphi {{\left( {{x_l}} \right)}^2} - 2\varphi \left( {{x_l}} \right)\varphi \left( {{x_m}} \right) + \varphi {{\left( {{x_m}} \right)}^2}} = \\\displaystyle \sqrt {K\left( {{x_l},\left. {{x_l}} \right)} \right. - 2K\left( {{x_l}} \right.,\left. {{x_m}} \right) + K\left( {{x_m},\left. {{x_m}} \right)} \right.} \end{gathered}$ | (2) |
式中:
| $\begin{gathered} {\rm dis}\left( {\varphi \left( {{x_s}} \right),\left. {{\mu _i}} \right)} \right. = \\ \displaystyle\sqrt {\!K\left( {{x_s},\left. {{x_s}} \right)} \right. \!-\! \frac{2}{{{n_i}}}\sum\limits_{j = 1}^{{n_i}} {\!K\left( {{x_s},{x_p}} \right) \!+\! \frac{1}{{{n_i}^2}}\!\sum\limits_{p = 1}^{{n_i}} {\sum\limits_{q = 1}^{n_i'} \!{K\left( {{x_p},{x_q}} \right)} } } } \end{gathered}$ | (3) |
通过初始粒划分将原始数据集划分为
通过初始粒划过程获得超平面
| $\gamma = \frac{2}{{||{ W}||}}$ | (4) |
针对每个划分好的信息粒,选择中心点
| ${D'} = \frac{{{{ W}^{\rm T}} \cdot \varphi + b}}{{||{ W}||}} = \frac{{\displaystyle\sum\limits_{i = 1}^{{n'}} {{\alpha _i}{y_i}k\left( {{x_i},{\mu _i}} \right) + b} }}{{\sqrt {{{\left( {\displaystyle\sum\limits_{i = 1}^{{n'}} {{\alpha _i}{y_i}{x_i}} } \right)}^2}} }}$ | (5) |
动态划分过程通过衡量粒与超平面之间距离来选取候选粒进行深度划分。但由于不同粒的大小、粒内部数据分布等差异,密度较大的粒中信息分布集中、重叠度大,含有更多潜在成为支持向量的信息;密度较小的粒中信息分布稀疏,包含的支持向量信息少。因此,对超平面附近密度较大的信息粒优先选择在当前迭代过程中划分,密度相对较小的信息粒可能成为后续划分过程中的候选粒。为了衡量每个粒的差异程度,给出粒密度的定义:
| ${\rho _i} = \frac{{{n_i}}}{{{\gamma _i}}} = \frac{{{n_i}}}{{\sqrt {K\left( {{x_l},\left. {{x_l}} \right)} \right. - 2K\left( {{x_l},\left. {{x_m}} \right)} \right. + K\left( {{x_m},\left. {{x_m}} \right)} \right.} }}$ | (6) |
式中:
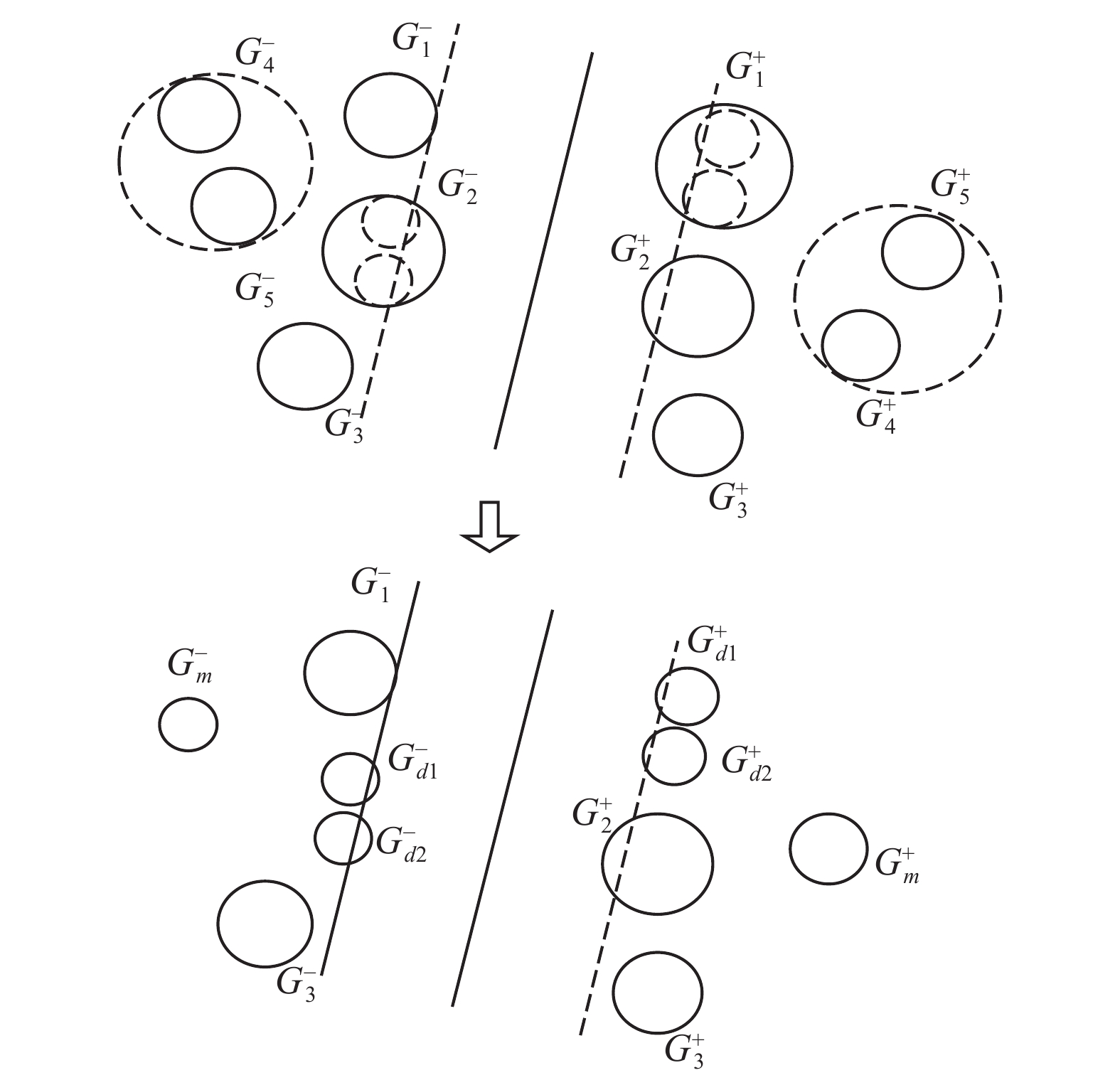
图2表示DFSVM动态粒划过程,其中
DFSVM模型的数据处理过程分为两个阶段:1) 对原始数据进行初始粒划分,然后通过式(1)计算得到每个粒的粒心,将所有粒心作为训练集训练得到初始分类超平面;2)利用动态划分融合的思想,对信息粒不断迭代处理以获得最优分类超平面。首先通过式(4)与参数
|
Download:
|
| 图 2 动态划分融合过程 Fig. 2 Dynamic division and fusion process | |
本文提出的DFSVM针对传统SVM无法高效的处理大规模数据以及CGSVM静态划分的不足进行了改进,探讨的目标是DFSVM是否能够在保证精度损失较少的情况下有效提升SVM的学习效率。本文在不同的参数下做了大量实验,基本算法描述如下:
算法 采用划分融合双向控制的粒度支持向量机
输入 原始数据集
输出 划分融合过程得到的模型测试结果集。
1)用聚类算法将数据集
2)将划分后的每个粒中心加入到训练集中训练得到初始分类超平面
3)通过式(4)和式(6)计算强信息区的信息粒与超平面的距离
4)通过式(4)和式(6)计算弱信息区信息粒、超平面的距离
5)将更新后的信息粒代替原信息加入到训练集并更新分类超平面,同时记录模型测试结果;
6)重复4)~6),直到满足停止条件
7)记录模型结果集,算法结束。
传统SVM模型训练的时间复杂度和空间复杂度分别为
本文实验在多个UCI数据集和标准数据集上进行实验,见表1,SVM选用高斯核函数,在多种参数下进行实验。实验在一台CPU为2.50 GHz,内存8 GB计算机上运行,实验平台为Matlab2016a。
| 表 1 实验数据集 Tab.1 Experimental data sets |
本文提出的采用划分融合双向控制的粒度支持向量机模型,在粒划分过程中逐步提取潜在的支持向量信息,通过信息融合清除掉过多的冗余信息,提升SVM的学习效率。本小节实验验证DFSVM粒划分融合过程中对SVM泛化能力的影响。
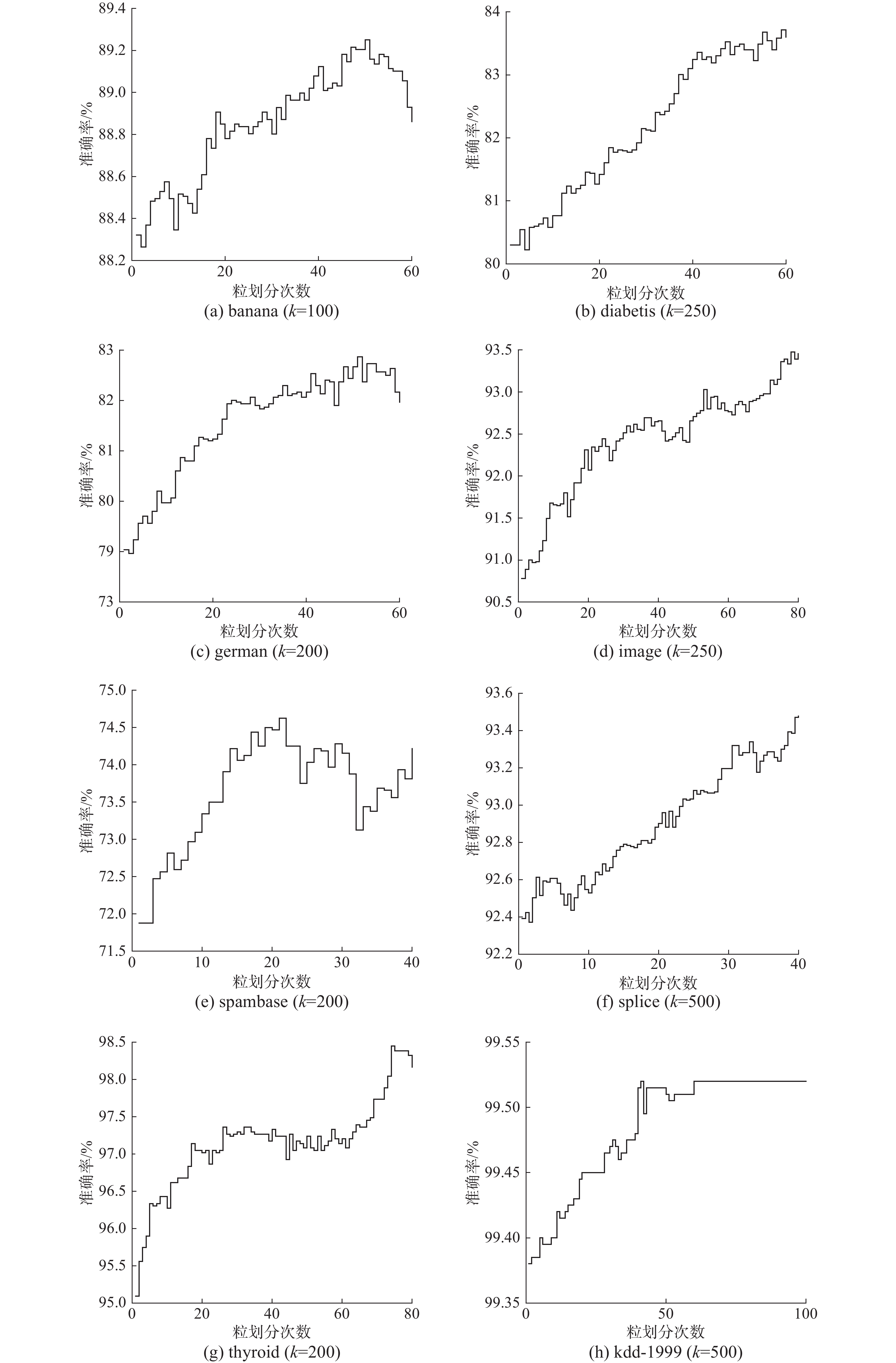
由于初始参数
从图3中可以看出,在对数据集迭代划分融合过程中,SVM的分类准确率逐步提高,但不同数据集的变化情况也存在差异。
|
Download:
|
| 图 3 粒划分过程中精度变化 Fig. 3 Accuracy change during granules division process | |
实验结果表明本文提出的方法能够充分提取数据集中的关键信息,有效地提升了模型的学习效率。在有限次的数据处理过程中,数据分布增强了对SVM的适应性,但随着划分次数增加,数据分布的改变可能导致SVM过拟合化,降低模型性能,如spambase数据显示出迭代次数大于20时,准确率有明显下降趋势。实验表明采用划分融合双向控制的粒度划分方法在一定程度上具有普适性。
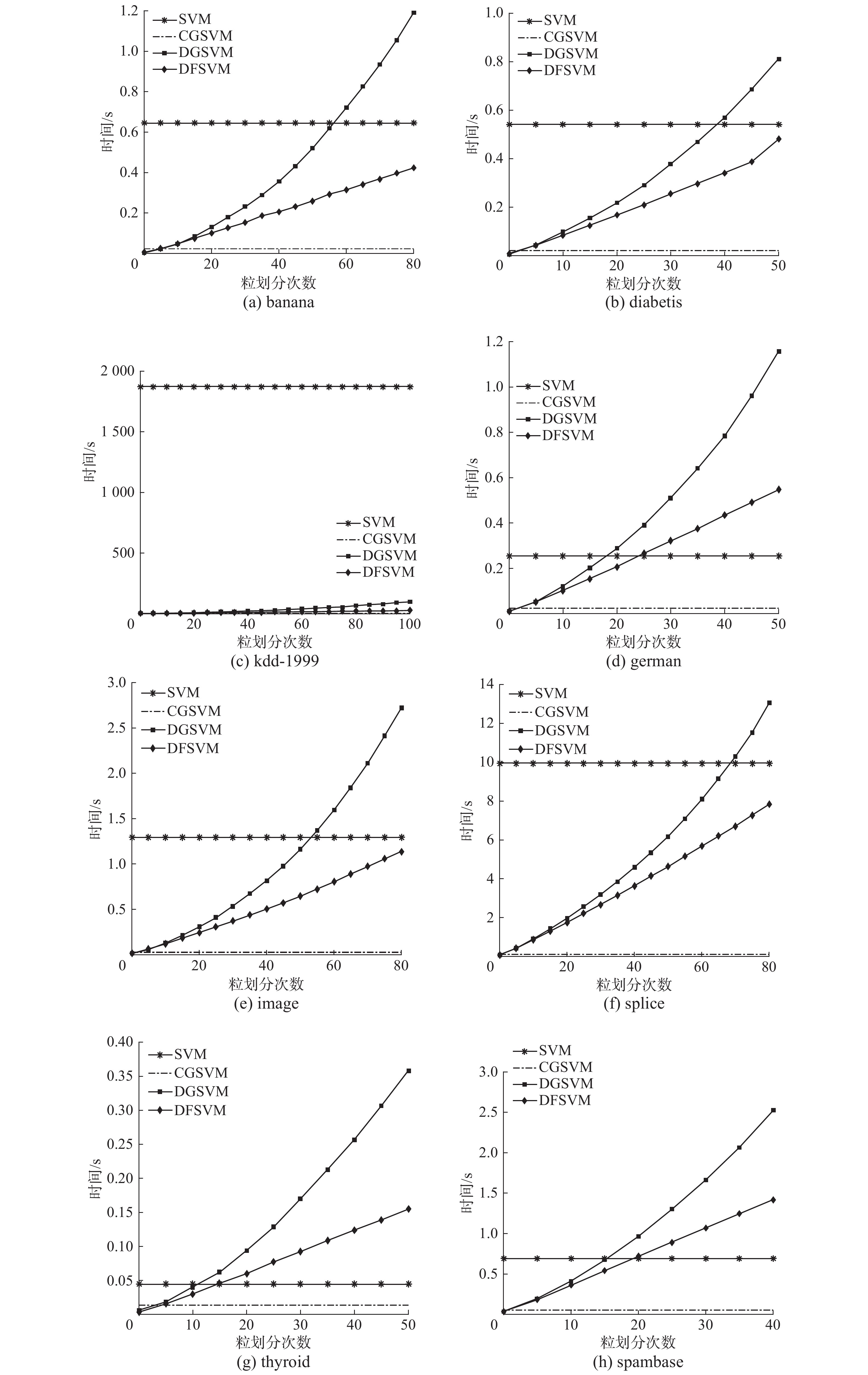
3.3 模型精度与时间结果分析针对在迭代过程中模型预测准确率和时间变化与传统SVM、CGSVM、DGSVM进行对比,参数选取与4.2节中实验相同,DGSVM平均每次划分数据增量为4,图4为时间对比图,图5为准确率对比图。
|
Download:
|
| 图 4 不同方法模型训练时间对比 Fig. 4 Comparison of model training time on different methods | |
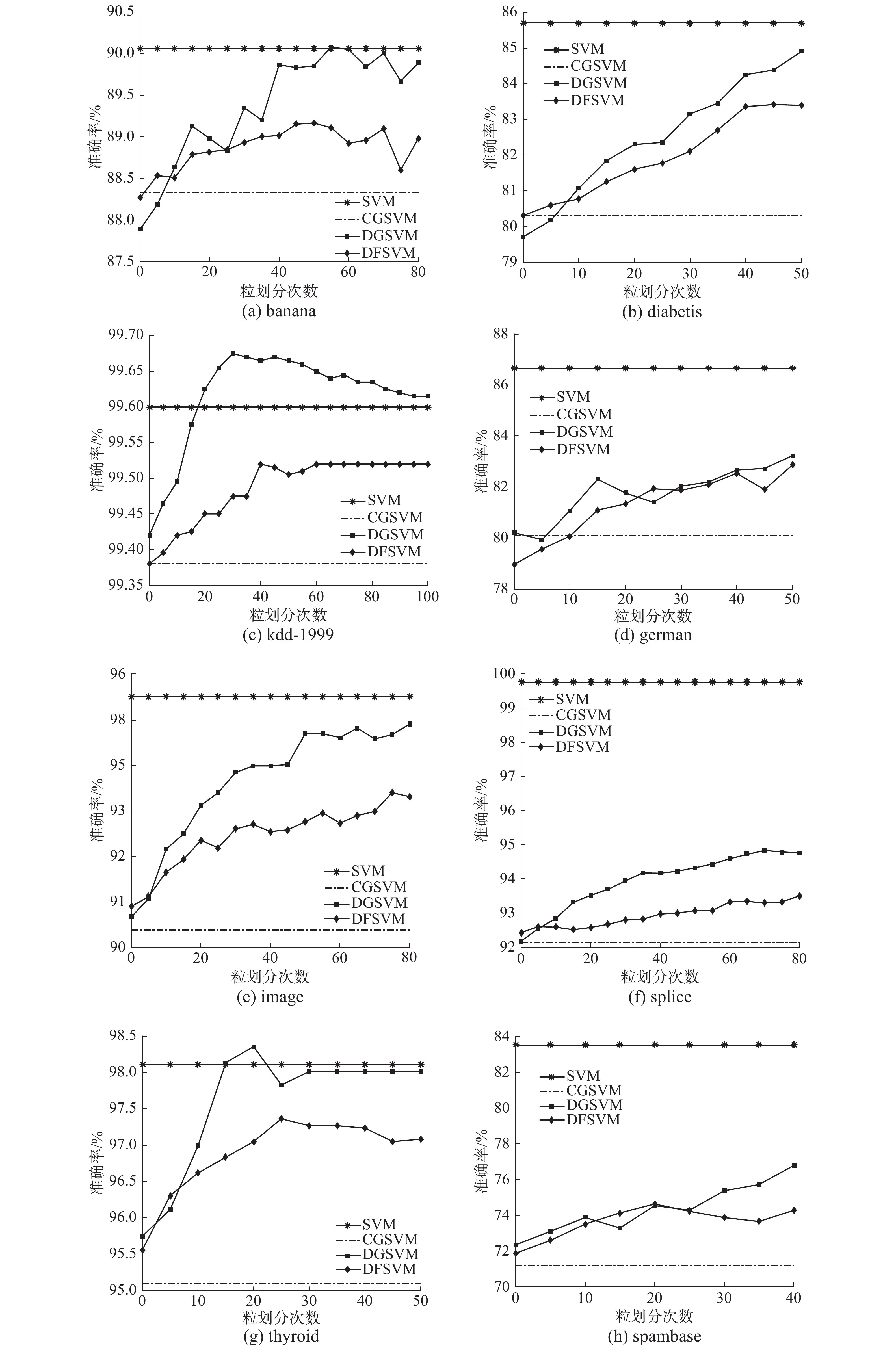
|
Download:
|
| 图 5 不同方法测试精度对比 Fig. 5 Accuracy comparison on different methods | |
图4中的实验结果表明,随着迭代次数的增加,DGSVM的训练时间增加率快于DFSVM。实验在german、thyroid、spambase数据集上的预测准确率没有在有效粒划次数内达到最优,在其他数据集上都达到了最优值。图5中结果表明DGSVM的精度达到的峰值要高于DFSVM,但时间消耗上要接近DFSVM的两倍,且高于传统SVM的训练时间。DGSVM与DFSVM在传统SVM基础上通过数据压缩的方式降低了数据规模,提升了模型效率,而迭代次数会影响DGSVM与DFSVM的学习效率。DFSVM通过划分融合的方式动态保持了数据规模的稳定,而DGSVM的数据规模在划分的过程中不断增大,导致训练时间增加。DFSVM在时间上有明显的提升,与DGSVM相比仍然损失了一些精度。
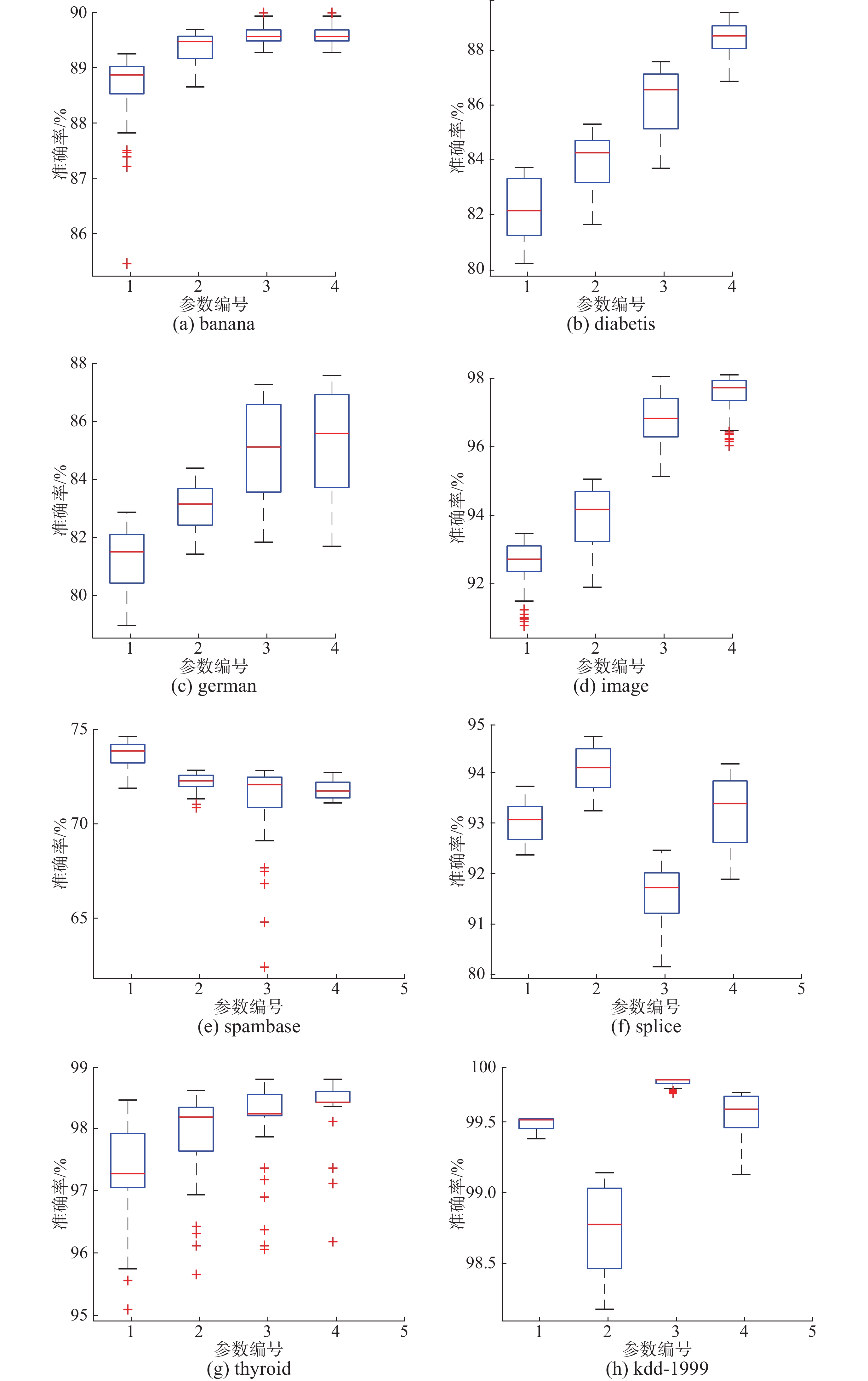
3.4 参数对DFSVM的影响 3.4.1 迭代参数与粒划分参数分析DFSVM迭代过程中参数
| 表 2 迭代参数
|
由表2中数据可以看出,随着参数
本实验中主要调节SVM中参数惩罚因子
|
Download:
|
|
图 6 惩罚因子
|
|
| 表 3 SVM模型参数取值 Tab.3 The value of the SVM model parameters |
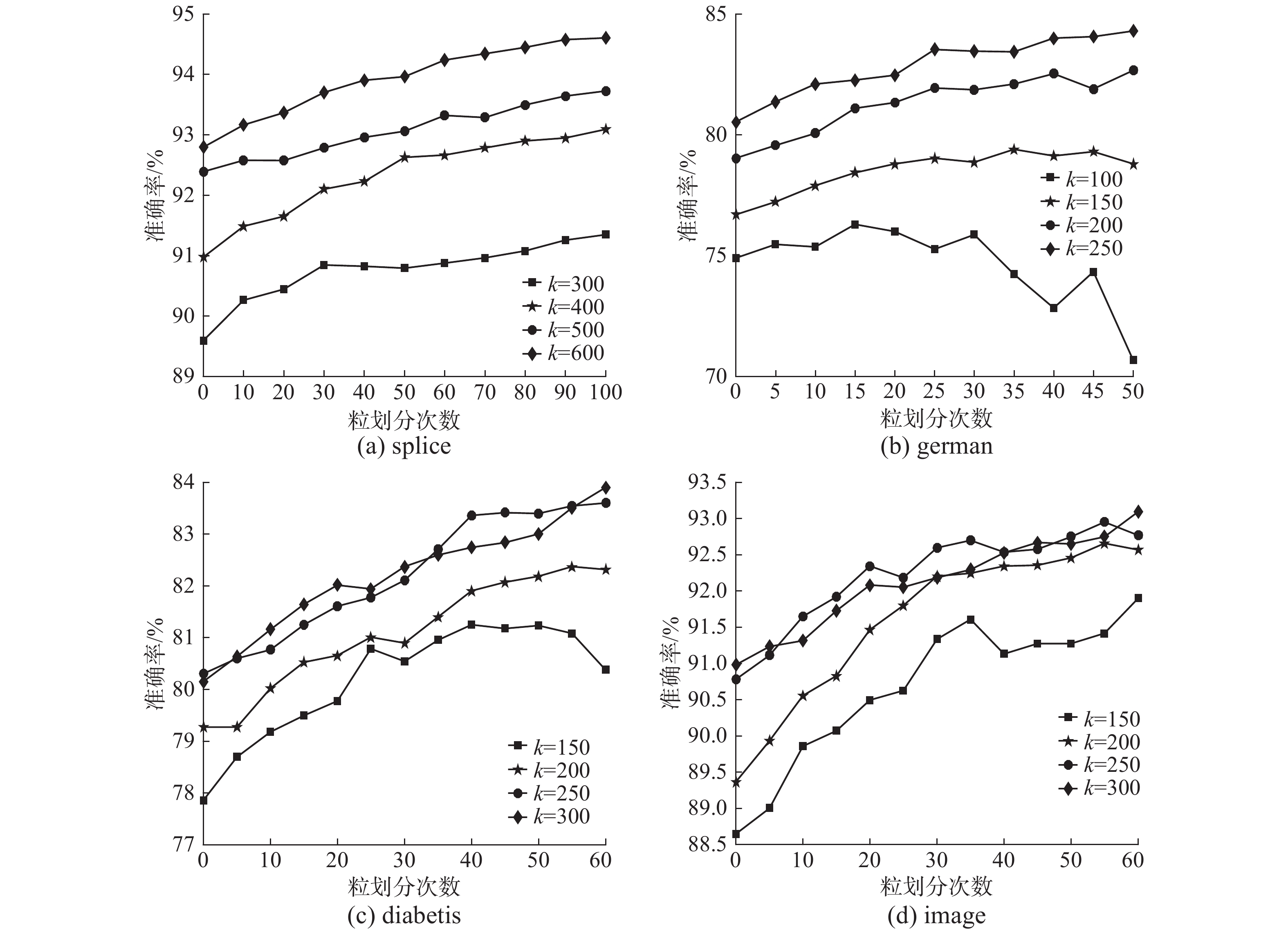
动态划分首先要通过初始聚类参数
|
Download:
|
|
图 7 初始聚类参数
|
|
由于不同数据集规模和分布差异,参数
本文在动态粒度支持向量机的基础上结合划分与融合的思想,扩展了SVM在大规模数据集上应用的能力,通过多种参数共同调节,能够保证在精度损失较小的情况下,提升SVM的学习效率。但在采用划分与融合的思想在数据处理过程中可能会改变数据集的分布,限制了数据迭代划分次数,参数调节也增加了模型的复杂度。在未来的工作中,会继续针对该模型在实际应用问题中进行探讨,在简化模型的同时保证模型的泛化性能。
| [1] |
VAPNIK V. The nature of statistical learning theory[M]. New York: Springer, 1995.
( 0) 0)
|
| [2] |
YUAN Ruixi, LI Zhu, GUAN Xiaohong, et al. An SVM-based machine learning method for accurate internet traffic classification[J]. Information systems frontiers, 2010, 12(2): 149-156. DOI:10.1007/s10796-008-9131-2 ( 0) 0)
|
| [3] |
CHEN G Y, XIE W F. Pattern recognition with SVM and dual-tree complex wavelets[J]. Image and vision computing, 2007, 25(6): 960-966. DOI:10.1016/j.imavis.2006.07.009 ( 0) 0)
|
| [4] |
REYNA R A, ESTEVE D, HOUZET D, et al. Implementation of the SVM neural network generalization function for image processing[C]//Proceedings of the 5th IEEE International Workshop on Computer Architectures for Machine Perception. Padova, Italy, 2000: 147–151.
( 0) 0)
|
| [5] |
LIU Yang, WEN Kaiwen, GAO Quanxue, et al. SVM based multi-label learning with missing labels for image annotation[J]. Pattern recognition, 2018, 78: 307-317. DOI:10.1016/j.patcog.2018.01.022 ( 0) 0)
|
| [6] |
XIONG Xiaoxia, CHEN Long, LIANG Jun. A new framework of vehicle collision prediction by combining SVM and HMM[J]. IEEE transactions on intelligent transportation systems, 2018, 19(3): 699-710. DOI:10.1109/TITS.2017.2699191 ( 0) 0)
|
| [7] |
BISHWAS A K, MANI A, PALADE V. An all-pair quantum SVM approach for big data multiclass classification[J]. Quantum information processing, 2018, 17(10): 282. DOI:10.1007/s11128-018-2046-z ( 0) 0)
|
| [8] |
ZHOU Xueliang, JIANG Pingyu, WANG Xianxiang. Recognition of control chart patterns using fuzzy SVM with a hybrid kernel function[J]. Journal of intelligent manufacturing, 2018, 29(1): 51-67. DOI:10.1007/s10845-015-1089-6 ( 0) 0)
|
| [9] |
TANG Yuchun, JIN Bo, SUN Yi, et al. Granular support vector machines for medical binary classification problems[C]//Proceedings of 2004 IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology. La Jolla, USA, 2004: 73–78.
( 0) 0)
|
| [10] |
YU H, YANG J, HAN Jiawei. Classifying large data sets using SVMs with hierarchical clusters[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington, USA, 2003: 306–315.
( 0) 0)
|
| [11] |
WANG Wenjian, XU Zongben. A heuristic training for support vector regression[J]. Neurocomputing, 2004, 61: 259-275. DOI:10.1016/j.neucom.2003.11.012 ( 0) 0)
|
| [12] |
MAO Xueyu, SARKAR P, CHAKRABARTI D. Overlapping Clustering Models, and One (class) SVM to Bind Them All[J]. arXiv: 1806.06945, 2018.
( 0) 0)
|
| [13] |
DING Shifei, QI Bingjuan. Research of granular support vector machine[J]. Artificial intelligence review, 2012, 38(1): 1-7. DOI:10.1007/s10462-011-9235-9 ( 0) 0)
|
| [14] |
GUO Husheng, WANG Wenjian, MEN Changqian. A novel learning model-Kernel granular support vector machine[C]//Proceedings of 2009 International Conference on Machine Learning and Cybernetics. Hebei, China, 2009: 930–935.
( 0) 0)
|
| [15] |
程凤伟, 王文剑, 郭虎升. 动态粒度SVM学习算法[J]. 模式识别与人工智能, 2014, 27(4): 372-377. CHENG Fengwei, WANG Wenjian, GUO Husheng. Dynamic granular support vector machine learning algorithm[J]. Pattern recognition and artificial intelligence, 2014, 27(4): 372-377. DOI:10.3969/j.issn.1003-6059.2014.04.012 (  0) 0)
|
| [16] |
HASSAN R, OTHMAN R M, SHAH Z A. Granular support vector machine to identify unknown structural classes of protein[J]. International journal of data mining and bioinformatics, 2015, 12(4): 451-467. DOI:10.1504/IJDMB.2015.070065 ( 0) 0)
|
| [17] |
GUO Husheng, WANG Wenjian. Granular support vector machine: a review[J]. Artificial intelligence review, 2019, 51(1): 19-32. DOI:10.1007/s10462-017-9555-5 ( 0) 0)
|
| [18] |
MA Zhixian, LI Weitian, WANG Lei, et al. X-ray astronomical point sources recognition using granular binary-tree SVM[C]//Proceedings of the 13th International Conference on Signal Processing. Chengdu, China, 2017: 1021–1026.
( 0) 0)
|
| [19] |
GUO Husheng, WANG Wenjian. Support vector machine based on hierarchical and dynamical granulation[J]. Neurocomputing, 2016, 211: 22-33. DOI:10.1016/j.neucom.2015.10.136 ( 0) 0)
|
| [20] |
郭虎升, 王文剑. 动态粒度支持向量回归机[J]. 软件学报, 2013, 24(11): 2535-2547. GUO Husheng, WANG Wenjian. Dynamical granular support vector regression machine[J]. Journal of software, 2013, 24(11): 2535-2547. (  0) 0)
|
| [21] |
YAO Y. Perspectives of granular computing[C]//Proceedings of 2005 IEEE International Conference on Granular Computing. Beijing, China, 2005: 85–90.
( 0) 0)
|
| [22] |
TANG Yuchun, JIN Bo, ZHANG Yanqing. Granular support vector machines with association rules mining for protein homology prediction[J]. Artificial intelligence in medicine, 2005, 35(1/2): 121-134. ( 0) 0)
|
| [23] |
LI Boyang, WANG Qiangwei, HU Jinglu. A fast SVM training method for very large datasets[C]//Proceedings of 2009 International Joint Conference on Neural Networks. Atlanta, USA, 2009: 1784–1789.
( 0) 0)
|
| [24] |
LI Xiaoou, YU Wen. Fast support vector machine classification for large data sets[J]. International journal of computational intelligence systems, 2014, 7(2): 197-212. DOI:10.1080/18756891.2013.868148 ( 0) 0)
|
| [25] |
LI Xiaoou, CERVANTES J, YU Wen. A novel SVM classification method for large data sets[C]//Proceedings of 2010 IEEE International Conference on Granular Computing. San Jose, USA, 2010: 297–302.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


