机器学习、数据挖掘等技术在诸如生物特征识别、文本分类和医学诊断等领域得到了广泛应用[1-6]。近年来,随着传感器技术、信息技术等科学技术的迅猛发展,数据获取的途径日益丰富,这给机器学习等技术带来了极大的发展机遇。然而在实践中,通常会因为存储设备损坏、数据采集设备能力有限等多种因素导致数据出现缺失的情况,我们称其为不完整数据问题。此类问题普遍存在于众多领域中,如:微阵列数据[7-8]、移动电话数据[9]、可视化数据[10]、工业数据[11]、软件项目数据[12]等。然而,传统机器学习的方法往往都是针对完整数据而设计的,因此缺失数据给这些方法带来了极大挑战。
目前已有不少学者针对不完整数据提出了一些解决策略,大致可以分为三类,其一为替代法,即用同一数据集内其他样本的完整部分替代缺失值,有时甚至会将众多缺失属性补以统一的固定值。这种策略虽然简单,但众多研究表明,绝大多数原始数据集的样本属性间都不是相互独立的,因此单一的替换策略直接忽略了属性间的关系,并不可取;其二为删除法,例如在许多统计软件如:SPSS、SAS中,默认采用Listwise deletion(LD)策略处理缺失值,直接删除带有缺失项的样本。然而,这种策略是以减少原始数据为代价换取数据完整,在信息获取代价较大时会造成严重的资源浪费和重要信息的损失。因此,解决不完整数据问题的第3种策略,即在多数现有的机器学习算法被应用到实际问题之前,将缺失数据填充完整的策略更为主流一些。
当前的缺失值填充方法大多运用统计学和机器学习领域的相关技术,对不完整数据的剩余部分进行建模和分析,从而产生较为合适的值用以填充。最常用的统计学填充法是均值填充[13],它简单快速,但是无法较好地拟合原始数据,因此通常适用于快速填充或者只有极少数属性缺失的情况;同样基于统计学的回归填充通常基于数据的完整部分来建立回归模型,对于包含缺失值的样本,将已知属性值代入方程来估计未知属性值。除此以外,在过去的十年里,许多机器学习填充方法也被相继提出,在机器学习填充法中,缺失的属性通常被视为一个训练模型的目标输出,剩余其他完整属性是用于训练和测试的输入特性,算法通常根据数据集的完备部分使用一些诸如KNN、决策树(DT)、多层感知器(MLP)、自组织映射(SOM)等机器学习方法来训练相关模型,在模型中对不完整属性进行估计。
当前最常用的机器学习填充方法有K最近邻填充(KNNI)[14]、聚类填充(CKNNI[15])等。其中,K最近邻填充的一个最大的特点在于KNN是一种懒惰式的学习方法,在应用到缺失值填充问题时不需要建立明确的模型(如决策树模型或诸多其他繁琐的填充规则),无论使用何种方法对数据进行分析,总能找到距缺失样本最近的若干个样本用于填充。因此,基于该方法的很多改进方法也被相继提出,如WKNNI[16]等,它们通常使用某种度量指标(如皮尔逊相关系数、距离函数等)来衡量样本间的相似度大小或采用特征提取等手段来对重要属性进行加权后再进行填充,取得了较好的填充效果;聚类填充方法如:CKNNI[15]根据样本间的相似度大小将所有样本聚类得到若干个簇,簇内样本间的相似度较高,再针对缺失样本,利用其所在簇内的其他样本对缺失部分进行填充。虽然这类方法也在一定程度上考虑了样本在空间分布中的信息,但由于聚类是无监督的,因此无法知悉经过聚类操作后会得到怎样的聚类结果,同时聚类算法初始中心个数也很难确定。此外,还有一些其他的机器学习算法被应用于缺失值填充领域,如结合期望最大化方法(EM)用于最大似然估计的方法、基于支持向量机的填充方法等,但是这些方法在时间复杂度方面都非常庞大,收敛速度极慢,对于某些数据集甚至达到了指数级别。
上述所提方法大多为单一填充法(如均值填充、KNN填充等),往往会降低估计量的方差。针对这一缺陷,Rubin在1987年提出了多重填充的思想。单一填充往往针对每个缺失值产生一个可能的值用以填充,而多重填充(如MICE[17]、MILC[18-19])是指在对填充值的预测分布中,通过一组(m>1)合理的值来替代所有缺失值的过程[5, 20]。数据经过多重填充处理后,会得到m个完整的数据集,每一个数据集都可以运用分析完整数据的方法对其分析,然后再融合这些不同数据集的分析结果,给出综合估计,显著缩小了由单一填充所导致的偏差,可获得更好的填充效果。
尽管现有的这些填充方法都具有各自的优势,某些方法能较好地实现对缺失数据的恢复。但是研究表明,目前还没有哪一种填充方法可以在任意给定的数据集和所有场景下都取得最佳的填充效果[21]。此外,现有的绝大多数方法仍缺乏对样本空间分布信息的考虑,忽略了空间邻域信息对数据恢复的影响。因此,本文提出了一种新的框架,可用于诸多现有的填充方法以进一步提升填充效果。框架由3部分组成,分别为预填充、空间邻域信息挖掘和修正填充。首先利用传统的填充方法对数据集进行预填充,得到完整数据;然后构造性的对预填充后的数据集构造覆盖,挖掘样本的空间邻域信息;最后利用邻域内样本的有效信息对预填充的结果进行修正,从而得到最终的完整数据集。
1 相关工作 1.1 缺失机制和缺失模式根据Rubin的总结,共有3种类型的缺失机制会导致一个不完整数据集的产生,分别为完全随机缺失、随机缺失和非随机缺失。
完全随机缺失:样本的某一属性出现缺失的概率和其他样本以及该属性本身的值无关。即当某属性值发生缺失的可能性与其他样本无关且与该样本属性自身也无关时称作完全随机缺失。
随机缺失:当某样本属性缺失的可能性与模型中某些观测样本有关而与该样本自身无关时称其为随机缺失。
非随机缺失:当样本属性中存在缺失值的可能性仅与其自身相关时则称为非随机缺失。
除此之外,还有两种缺失模式,分别为单调缺失和非单调缺失。前者指的是针对同一个记录或者变量的缺失,后者指的是针对任何记录、任何变量的缺失,本文的实验是以非单调缺失模式为前提进行的。
1.2 构造性覆盖算法张铃等[22]提出的基于覆盖的构造性机器学习方法主要是以M-P模型的几何表示为理论基础,针对样本自身的特点来构造神经网络。构造性覆盖算法可以看作一个3层网络分类器。
输入层:共n个神经元,每个神经元对应样本的一维,即样本的特征属性,
隐藏层:共s个神经元。初始时,隐层神经元为0个,每求得一个球形覆盖,增加一个神经元,直到将所有的样本都被覆盖,从而求得一组覆盖:
输出层:共m个神经元,第t个神经元的输入为同类的一组覆盖,输出为该覆盖的类别。
构造性覆盖算法针对样本自身的特点,根据学习样本的特征用超平面切割球面形成“球形领域”作为神经元来构造神经网络,基于超球面上的样本来构造每个类别的覆盖。该算法可以处理海量样本,适用于多分类问题且分类能力强、运算速度快[23]。
2 基于空间邻域信息的修正填充方法 2.1 预填充给定不完整数据集
| ${\rm IND} = \{ (i,j)|x_i^{(j)} = NaN\} $ | (1) |
利用经典的填充算法对DS进行填充,在本文中称为预填充。预填充后得到完整数据集DSc。分别选用以下7种填充方法实现预填充:
1) 均值填充(MEI)[13]
| $ x_i^{(j)} = \mathop \sum \limits_{k \in I({\rm comp})} \frac{{x_k^{(j)}}}{{{n_{|I({\rm comp})|}}}} $ | (2) |
式中:
2) 中值填充(MEDI)[13]
令
| $ x_i^j = \left\{ {\begin{array}{*{20}{c}} {\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\varOmega ^*}_{\left[ {n + 1/2} \right]}},&{n\;od 2 \ne 0}\\ {\left( {{\varOmega ^*}_{\left[ {n/2} \right]} + {\varOmega ^*}_{\left[ {n + 1/2} \right]}} \right)/2},&{n\;od 2 = 0} \end{array}} \right. $ | (3) |
3) KNNI[14]
| $ d_i^t = {\rm dist} \left( {x_i,x_t} \right) = \sqrt {\mathop \sum \limits_{p = 1}^n {{\left( {x_i^p - x_t^p} \right)}^2}} $ | (4) |
| $ x_i^j = \left( {\mathop \sum \limits_{\forall {x_t} \in {N_i}} x_t^j} \right)/\left| {{N_i}} \right|,\;\;\;\;x_t^j \ne {\rm NaN} $ | (5) |
式中:
4) WKNNI[16]
| $x_i^j = \mathop \sum \limits_{\forall {x_t} \in {N_i}} x_t^j{\omega _{t}}\;,\;\;\;\;{\omega _t} = \frac{{1/d_i^t}}{{\mathop \sum \limits_{t = 1}^k 1/d_i^t}}$ | (6) |
式中:Ni表示距离第i个样本最近的k个第j维属性不缺失的样本集合;
5) Soft-impute(SoftI)[24]:通过对SVD分解的迭代软阈值处理来填充不完整数据。
6) Matrix-Factorization-impute(MFI)[25]:将不完整数据用矩阵形式表示并直接将其分解为低秩的U和V,然后对U中的元素采用L1稀疏惩罚,对V中的元素采用L2稀疏惩罚,通过梯度下降法求解。
7) MICE[20]:利用链式方程实现多重填充。
2.2 挖掘空间邻域信息在对不完整数据进行填充的过程中,最关键的问题在于如何通过对数据集中样本的剩余完整信息进行分析。在这一节中,我们利用一种有监督的空间邻域信息挖掘方法,挖掘与缺失样本具有更高相似性的某邻域内样本的有效信息。
1)通过式(2)变换将
| ${\rm{}}T:{\rm DS}{_c} \to {S^{n + 1}},T\left( x \right) = \left( {x,\sqrt {{R^2} - {{\left| x \right|}^2}} } \right)$ | (7) |
式中
2)随机选取一个未被标记的样本
| $ < x_k,x_i > x_{k}^{\left( 1 \right)}x_{i}^{\left( 1 \right)} + \cdots + x_{k}^{\left( {n + 1} \right)}x_{i}^{\left( {n + 1} \right)},\;\;\;i \in \left\{ {1,2, \cdots, m} \right\}$ | (8) |
| $ {d_1} = \mathop {\max }\limits_{y_k{ \ne }y_i} \left\{ {\left\langle {x_k,x_i} \right\rangle } \right\},\;\;\;i \in \left\{ {1,2, \cdots, m} \right\} $ | (9) |
| ${d_2} = \mathop {\min }\limits_{y_k = y{{_i}}} \left\{ {\left\langle {x_k,x_i} \right\rangle {\rm{|}}\left\langle {x_k,x_i} \right\rangle > {d_1}} \right\},\;\;\;i \in \left\{ {1,2, \cdots, m} \right\}$ | (10) |
| $ R = ({d_1} + {d_2})/2 $ | (11) |
式中:
3)构造一个以
经过1)~3)得到的覆盖集合C能够很好地刻画样本空间的空间邻域信息。
2.3 利用空间邻域信息修正预填充结果为方便起见,本文以二分类问题为例,描述如何利用空间邻域信息进行缺失值的填充。
令
| ${C_1} = \left\{ {C_1^1,C_1^2, \cdots ,C_1^{{k_1}}} \right\};{C_2} = \left\{ {C_2^1,C_2^2, \cdots ,C_2^{{k_2}}} \right\}$ | (12) |
式中:k1表示第一类样本的覆盖的个数,k2表示第二类样本的覆盖的个数。
对于
| $ x_i^{\left( j \right)} = \left\{ {\begin{array}{*{20}{l}} {(\mathop \sum \limits_{t = 1}^{\left| \psi \right|} {{(x_s^{\left( j \right)})}_t})/\left| \psi \right|},&{\left| \psi \right| \ne 0}\\ {x_p^{\left( j \right)}},&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{\left| \psi \right| = 0} \end{array}} \right. $ | (13) |
| $ \psi = \left\{ x_{s}^{(j)}| {x_s} \in \left\{ C_{v}^k - x_i \right\} \wedge (s,j) \notin {\rm IND} \right\} $ | (14) |
式中:ψ表示在
在极少数情况下会出现覆盖内除
算法针对所有的缺失属性依次进行判断和修正填充,最终得到修正填充后的完整数据集
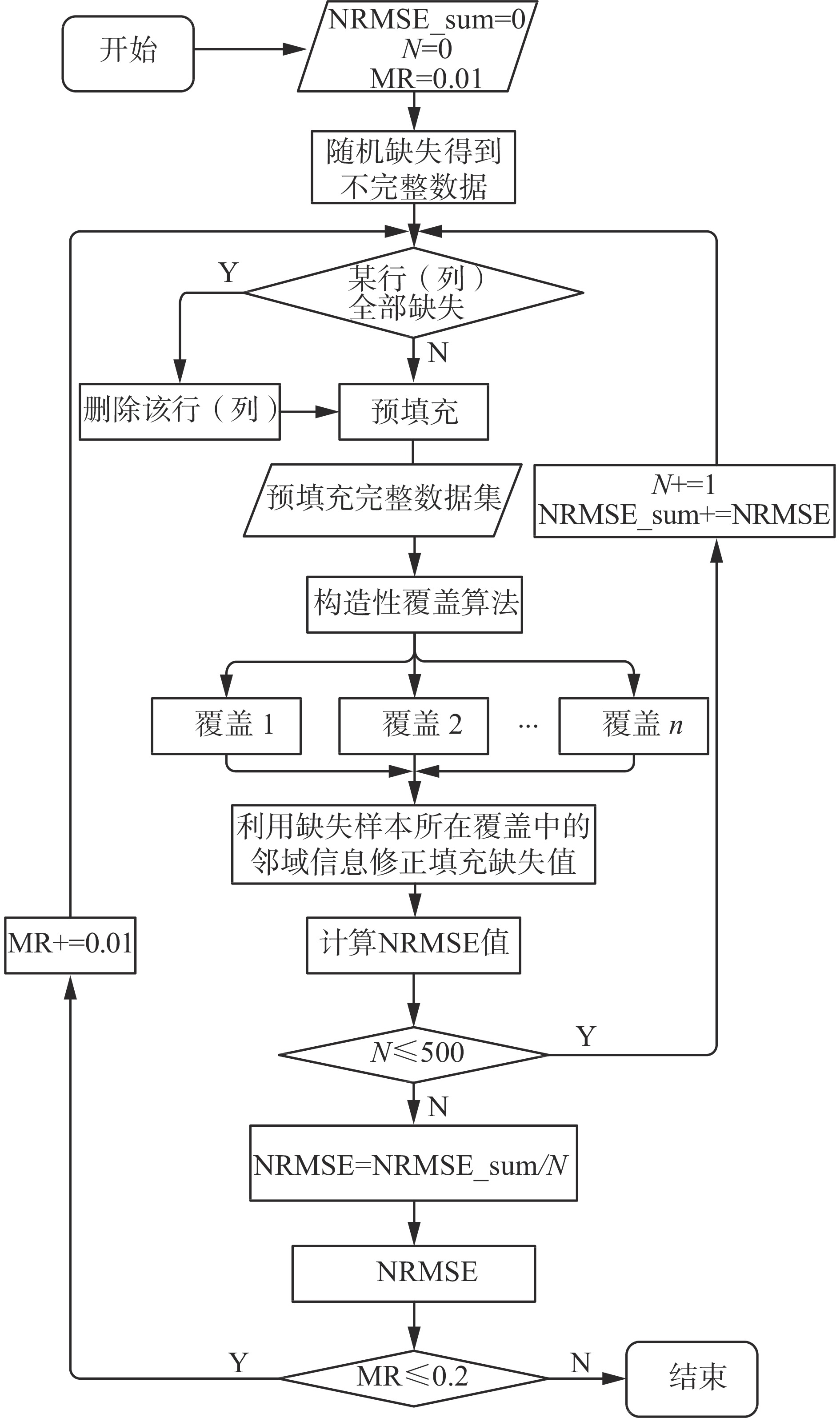
|
Download:
|
| 图 1 算法流程图 Fig. 1 The flow chart of the proposed method | |
本小节中,本文提出的框架分别与2.1节提出的7种当前已有的缺失值填充方法对比。由于本文的方法是对已有填充方法得到的填充结果进一步的修正。因此,这7种经典的方法也是本文预填充阶段所选取的填充方法。另外,本文使用一种常见的度量缺失值填充效果的指标(NRMSE)来量化填充效果,进一步验证方法的有效性。
实验首先在UCI上的完整数据集上,以随机缺失的方式得到不完整数据,缺失率从小到大依次为0.01、0.02、0.03、0.04、0.05、0.10、0.15和0.20;然后用现有的填充方法与本文提出的框架结合后对得到的不完整数据进行处理;最后根据修正填充前的原始数据集和修正填充后得到的最终完整集得出不同缺失率下的NRMSE值及其变化趋势。为了避免因单次填充而导致的误差对实验结果的影响,实验在每种缺失率下均重复随机缺失多次,最终得到的NRMSE值为多次重复缺失后得到的均值。
3.2 实验数据集本文从UCI中选取了8个数据集进行实验的比较和分析,表1给出了8个数据集的基本信息,包括数据集名称、样本个数、属性个数以及类别个数,其中balance-s、BCC、dba和lym分别是balance-scale、Breast Cancer Coimbra、data_banknote_authentication和lymphography数据集的简写。
| 表 1 数据集简介 Tab.1 The introduction of the datasets |
本文采用的评价不完整数据填充性能的指标是归一化均方根误差,定义如下:
| $ {\rm{NRMSE}} = \frac{{\sqrt {{\rm mean}{{({x_{\rm guess}} - {x_{\rm ori}})}^2}} }}{{{\rm std}\left( {{x_{\rm ori}}} \right)}} $ | (15) |
式中:
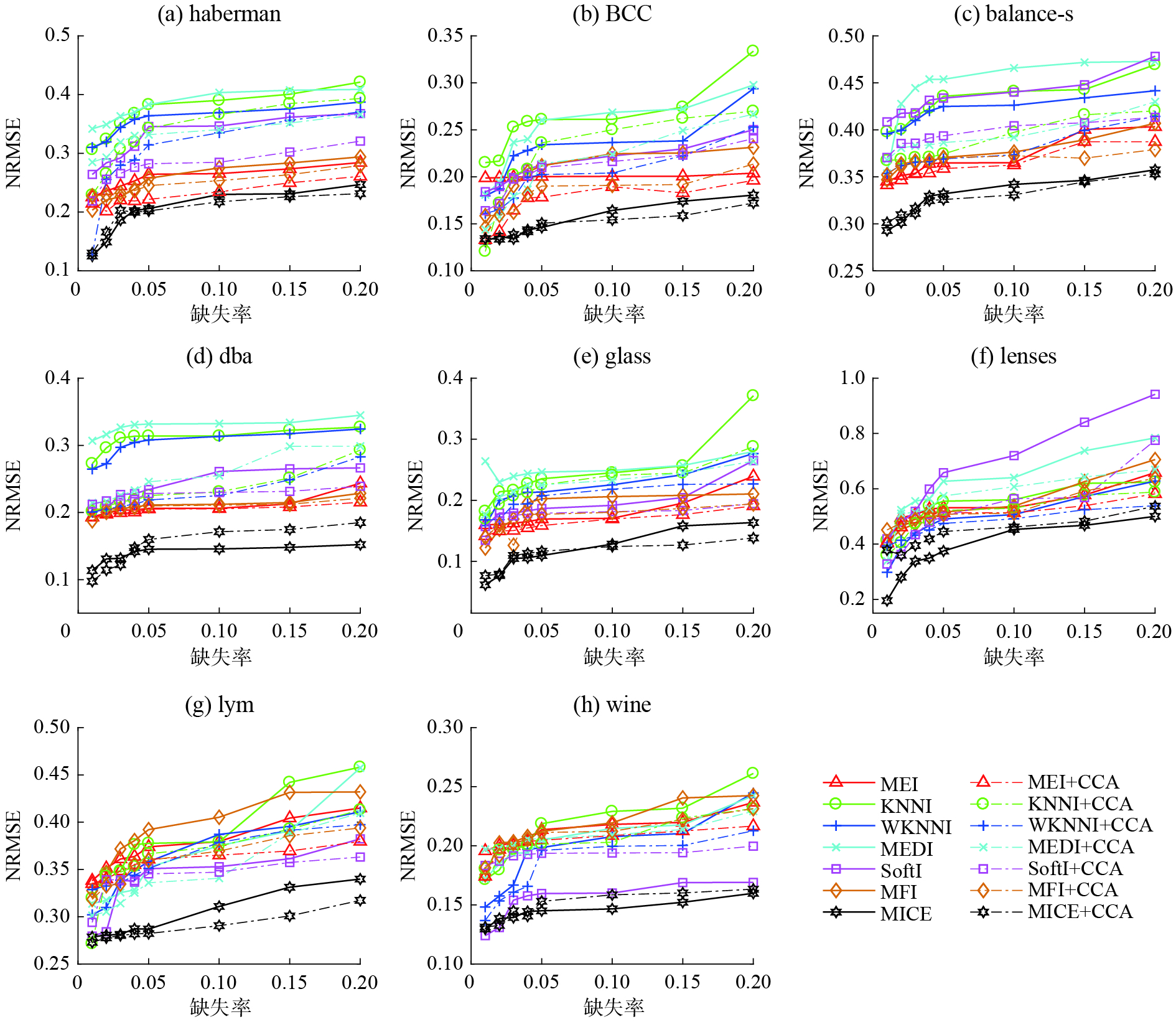
本小节中,通过NRMSE度量指标对本文所提框架与当前已有的缺失值填充方法所产生的结果进行对比和分析,研究在不同的缺失率下,框架对于现有填充方法的提升效果呈现出何种趋势。图2分别展示了7组填充方法在不同数据集上以及不同缺失率下对应的NRMSE值的变化趋势。
|
Download:
|
| 图 2 7组填充方法在8个数据集上以及在不同缺失率下对应的NRMSE值 Fig. 2 The NRMSE values corresponding to 7 groups of imputation methods on 8 datasets and at different missing rates | |
除此之外,图3更为直观地展示了7种现有填充方法分别在与本文所提框架结合后填充效果的提升。其中,MR表示的是缺失率。从实验结果中不难发现,由于数据的随机缺失导致缺失值的分布具有一定的随机性,同时因缺失场景的不同和缺失数据本身的特点共同决定了没有任何一种现有的填充方法可以在所有数据集上都能取得最好的填充效果。但是本文所提框架应用于多数现有填充方法和数据集上所呈现出来的填充效果均优于对比算法,如haberman、BCC等数据集。从总体上来看,针对一些特征(维)数较少而样本数较多的数据集而言,当缺失率较小时,对应的NRMSE值也较小,当缺失率达到最小时,NRMSE值往往也达到最小,意味着填充效果最好,但是随着缺失率的不断增大,对应的NRMSE逐渐呈现出增长的趋势。这是因为缺失率越小,出现缺失的属性数就越少,而当样本数远大特征(维)数时,例如dba数据集的特征(维)数是5,但却拥有1 372个样本,当缺失率为1%时,出现缺失的属性数是13,而该数据本身具有1 372个样本,故可用于填充的剩余完整样本数还有很多,这对于数据的恢复十分有利。随着缺失率的增长,剩余完整样本逐渐变少,对应的NRMSE值也呈现出上升的趋势。当然,也会出现极少数的特殊情况,如:MEI方法在haberman数据集上当缺失率为2%时,对应的NRMSE值略小于缺失率等于1%时对应的值,即随着缺失率的增大,NRMSE值却在减小,类似的情况还有MEDI方法在glass数据集上以及SoftI方法在balance-s数据集上等。这种情况出现的原因是实验所得的不完整数据是通过随机缺失的方式得到的,且在挖掘空间邻域信息的过程中也采用了多次覆盖,因此具有一定的随机性,尽管重复随机缺失了很多次,最后取多次实验所得的NRMSE度量值的均值为最终结果,但也只能在一定程度上较为稳定地反映出NRMSE值的总体变化趋势,此外,针对一些数据样本较少的数据集而言,当缺失率较小时,对应缺失率下的缺失属性的数量也十分接近,在这种情况下,可能会出现缺失率略大反而填充效果略好的情况,但从经过多次重复实验的结果来看可知NRMSE指标的总体变化呈上升趋势。
从BCC和balance-s数据集上的实验结果中可以看出,尽管有少数对比算法在缺失率较小的时候呈现出的填充效果要优于本文的方法,但是,随着缺失率的不断增长,本文方法所展现出来的优势逐渐明显。如MICE+CCA在balance-s数据集上,当缺失率达到5%以及在glass数据集上达到10%以后,填充效果开始逐渐优于对比算法。此外,我们发现一些现有的单一填充方法在用本文框架修正填充后,填充效果更加逼近效果较好的多元填充方法,如:WKNNI+CCA在lenses数据集上当缺失率达到20%时,几乎取得了等同于MICE的填充效果。这表明了通过和本文所提框架结合后可以更加有效地提升现有填充方法所产生的效果。
当然,也有方法与框架结合后的提升效果不佳,如:MICE+CCA在dba和wine数据集上的填充效果较对比方法差。这是因为MICE本身就运用了多重填充的思想,已经在一定程度上规避了因单一填充而引入的误差,因此,在通常情况下都会取得十分不错的填充效果。但是,MICE+CCA在BCC、glass、haberman和lym等数据集上随着缺失率的不断增大,对于MICE方法的提升效果逐渐明显。此外,同样是在dba和wine数据集上,本文所提出的用于修正填充其他现有方法的效果相对于对比算法的效果而言仍具有较大优势,如:KNNI+CCA、MFI+CCA等。
从lenses数据集和lym数据集上的实验结果来看,一方面,除了MICE方法在lenses上的填充效果比MICE+ CCA好以外,其他几组对比算法的效果均没有本文提出的方法好,尤其是SoftI+CCA在lenses数据集上以及KNNI+CCA、MFI+CCA等方法在lym数据集上的填充效果均显著优于对比算法;另一方面,尽管MICE在lenses上的效果更好一些,但是与本文提出的MICE+CCA的效果相比较,差距并不是很大,而后者表现出的算法稳定性更高。

|
Download:
|
| 图 3 7组现有填充方法经修正后的填充效果提升图 Fig. 3 The improvement of the imputation effect by using proposed method | |
针对当前已有的大多数填充方法忽视了样本空间分布信息对数据恢复的影响,本文提出了一种可广泛应用于现有填充方法的框架,旨在对利用现有方法得到的填充结果进行修正,从而提升填充效果。该框架由预填充、空间邻域信息挖掘和修正填充3部分构成,首先利用现有填充方法对样本进行预填充;再通过引入一种空间邻域信息挖掘方法来找到与待填样本具有更高相似度的若干个空间邻域;最后利用待填样本的空间邻域内的有效信息对现有填充方法产生的填充结果进行修正。
实验选取了7种经典的填充方法(包括单一填充和多重填充),在8个UCI数据集上进行了对比。结果表明,本文提出的框架确实能够在大多数数据集上有效提升现有填充方法的填充效果。尽管在少数数据集上的提升效果不佳,但是从实验所得的不同缺失率下的NRMSE度量值的变化趋势来看,多数与框架结合后的填充方法通常呈现出较为平稳的填充趋势,不会随着缺失率的不断增长而出现较大波动,而且在某些数据集上呈现出一个重要规律,即随着缺失率的不断增大,框架对于现有填充方法的提升效果逐渐明显。除此之外,本文所提框架还可以将一些效果较差的单一填充方法的填充效果提升至更好的多重填充方法所取得的效果。
| [1] |
LARRAÑAGA P, CALVO B, SANTANA R, et al. Machine learning in bioinformatics[J]. Briefings in bioinformatics, 2006, 7(1): 86-112. DOI:10.1093/bib/bbk007 ( 0) 0)
|
| [2] |
HARPER P R. A review and comparison of classification algorithms for medical decision making[J]. Health policy, 2005, 71(3): 315-331. DOI:10.1016/j.healthpol.2004.05.002 ( 0) 0)
|
| [3] |
SEBASTIANI F. Machine learning in automated text categorization[J]. ACM computing surveys, 2002, 34(1): 1-47. DOI:10.1145/505282.505283 ( 0) 0)
|
| [4] |
KONG S G, HEO J, ABIDI B R, et al. Recent advances in visual and infrared face recognition—a review[J]. Computer vision and image understanding, 2005, 97(1): 103-135. DOI:10.1016/j.cviu.2004.04.001 ( 0) 0)
|
| [5] |
FU Xiao, REN Yinzi, YANG Guiqiu, et al. A computational model for heart failure stratification[C]//Proceedings of 2011 IEEE Computing in Cardiology. Hangzhou, China, 2011: 385–388.
( 0) 0)
|
| [6] |
FIALHO A S, KAYMAK U, ALMEIDA R J, et al. Probabilistic fuzzy prediction of mortality in intensive care units[C]//Proceedings of 2012 IEEE International Conference on Fuzzy Systems. Brisbane, Australia, 2012: 1–8.
( 0) 0)
|
| [7] |
AITTOKALLIO T. Dealing with missing values in large-scale studies: microarray data imputation and beyond[J]. Briefings in bioinformatics, 2010, 11(2): 253-264. DOI:10.1093/bib/bbp059 ( 0) 0)
|
| [8] |
DE SOUTO M C P, JASKOWIAK P A, COSTA I G. Impact of missing data imputation methods on gene expression clustering and classification[J]. BMC bioinformatics, 2015, 16: 64. DOI:10.1186/s12859-015-0494-3 ( 0) 0)
|
| [9] |
LIU Siyuan, CHEN Lei, NI L M. Anomaly detection from incomplete data[J]. ACM transactions on knowledge discovery from data, 2014, 9(2): 11. ( 0) 0)
|
| [10] |
LIU Ji, MUSIALSKI P, WONKA P, et al. Tensor completion for estimating missing values in visual data[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(1): 208-220. DOI:10.1109/TPAMI.2012.39 ( 0) 0)
|
| [11] |
LAKSHMINARAYAN K, HARP S A, SAMAD T. Imputation of missing data in industrial databases[J]. Applied intelligence, 1999, 11(3): 259-275. DOI:10.1023/A:1008334909089 ( 0) 0)
|
| [12] |
SONG Qinhao, SHEPPERD M, CHEN Xiangru, et al. Can k-NN imputation improve the performance of C4.5 with small software project data sets? A comparative evaluation[J]. Journal of systems and software, 2008, 81(12): 2361-2370. DOI:10.1016/j.jss.2008.05.008 ( 0) 0)
|
| [13] |
DONDERS A R T, VAN DER HEIJDEN G J M G, STIJNEN T, et al. Review: a gentle introduction to imputation of missing values[J]. Journal of clinical epidemiology, 2006, 59(10): 1087-1091. DOI:10.1016/j.jclinepi.2006.01.014 ( 0) 0)
|
| [14] |
TROYANSKAYA O, CANTOR M, SHERLOCK G, et al. Missing value estimation methods for DNA microarrays[J]. Bioinformatics, 2001, 17(6): 520-525. DOI:10.1093/bioinformatics/17.6.520 ( 0) 0)
|
| [15] |
KEERIN P, KURUTACH W, BOONGOEN T. Cluster-based KNN missing value imputation for DNA microarray data[C]//Proceedings of 2012 IEEE International Conference on Systems, Man, and Cybernetics. Seoul, South Korea, 2012: 445-450.
( 0) 0)
|
| [16] |
VAN BUUREN S, GROOTHUIS-OUDSHOORN K. Mice: Multivariate imputation by chained equations in R[J]. Journal of statistical software, 2011, 45(3): 75765. ( 0) 0)
|
| [17] |
GEBREGZIABHER M, DESANTIS S M. Latent class based multiple imputation approach for missing categorical data[J]. Journal of statistical planning and inference, 2010, 140(11): 3252-3262. DOI:10.1016/j.jspi.2010.04.020 ( 0) 0)
|
| [18] |
VERMUNT J K, VAN GINKEL J R, VAN DER ARK L A, et al. 9. Multiple imputation of incomplete categorical data using latent class analysis[J]. Sociological methodology, 2008, 38(1): 369-397. DOI:10.1111/j.1467-9531.2008.00202.x ( 0) 0)
|
| [19] |
TOUTENBURG H. Rubin, D.B.: multiple imputation for nonresponse in surveys[J]. Statistical papers, 1990, 31(1): 180. DOI:10.1007/BF02924688 ( 0) 0)
|
| [20] |
SIM J M, KWON O, LEE K C. Adaptive pairing of classifier and imputation methods based on the characteristics of missing values in data sets[J]. Expert systems with applications, 2016, 46: 485-493. DOI:10.1016/j.eswa.2015.11.004 ( 0) 0)
|
| [21] |
张铃, 张钹. M-P神经元模型的几何意义及其应用[J]. 软件学报, 1998, 9(5): 334-338. ZHANG Ling, ZHANG Bo. A geometrical representation of M-P neural model and its applications[J]. Journal of software, 1998, 9(5): 334-338. (  0) 0)
|
| [22] |
张燕平, 张铃. 机器学习理论与算法[M]. 北京: 科学出版社, 2012: 56–66.
( 0) 0)
|
| [23] |
JÖRNSTEN R, WANG Huiyu, WELSH W J, et al. DNA microarray data imputation and significance analysis of differential expression[J]. Bioinformatics, 2005, 21(22): 4155-4161. DOI:10.1093/bioinformatics/bti638 ( 0) 0)
|
| [24] |
MAZUMDER R, HASTIE T, TIBSHIRANI R. Spectral regularization algorithms for learning large incomplete matrices[J]. The journal of machine learning research, 2010, 11: 2287-2322. ( 0) 0)
|
| [25] |
RANJBAR M, MORADI P, AZAMI M, et al. An imputation-based matrix factorization method for improving accuracy of collaborative filtering systems[J]. Engineering applications of artificial intelligence, 2015, 46: 58-66. DOI:10.1016/j.engappai.2015.08.010 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


