有效的数据低维表示不仅能够发现数据集中的潜在信息，还能去除原始数据中的冗余特征，快速处理高维数据，其中最具代表性的方法包括主成分分析^[1]、线性判别分析^[2]及非负矩阵分解^[3]。然而PCA和LDA得到的数据低维表示中可能会包含负值元素，这在实际的应用中缺少合理的解释；而NMF是一种非负约束下的矩阵分解方法，仅允许原始数据的加法而非减法组合，因此它有利于稀疏的且基于部分的表示，比非稀疏的全局表示更稳健。

经典的NMF是一种无监督学习算法，不能充分利用原始数据的类别信息。为了提高NMF的判别能力，Wang等^[4]提出了Fisher-NMF(FNMF)，而Zafeiriou等^[5]和Kotsia等^[6]在NMF的目标函数中增加了散度差项，建立起判别子空间法。由于LDA^[2]中Fisher准则的比值形式很难处理，集成在NMF模型中会出现“小样本问题”。为此，可考虑最大间距准则(max margin criterion，MMC)^[7-8]，该准则是以类中心及类散度为度量依据，使得降维后不同类样本之间距离越远而同类样本之间距离越近，在充分使用原始数据类别信息的基础上使得改进后的NMF(如NDMF^[9])具有良好的判别性质。

另外，为了揭示和利用数据的内在几何结构，出现了许多基于流形特征的NMF，例如GNMF^[10]、GDNMF^[11]、LCGNMF^[12]和NLMF^[13]等，这些方法通过添加图拉普拉斯正则化项达到了提高图像聚类或分类性能的目的。Shang等^[14]同时考虑数据流形和特征流形，提出了图对偶正则化NMF(DNMF)。而Meng等^[15]则在图对偶模型中加入了稀疏性(DSNMF)和正交性的约束^[16]，有效地简化了高维计算，揭示数据和特征之间的双流形结构。

由于NDMF^[9]具有良好的判别性质，而NLMF^[13]又利用了数据的图结构来提升其分类性能，故本文将两种方法结合起来提出一种基于图正则化的稀疏判别非负矩阵分解算法(GSDNMF-L_2,1)，在充分利用数据的类别信息的同时，不仅保持了数据样本之间的局部流形结构，而且能提取稀疏的特征，进而提升了其分类性能。若干图像数据集上的实验结果表明，该方法在特征提取与分类性能等方面优于其他各对比算法。

1 相关工作 1.1 非负矩阵分解(NMF)

假设由 $n$ 个非负样本数据 ${{{x}}_{{i}}} \in {{\rm{R}}^m}\left( {i = 1, 2,\cdots ,n} \right)$ 组成的非负数据矩阵 ${{X}} = \left[ {{{{x}}_{{1}}}\;{{{x}}_{{2}}}\; \cdots \,{{{x}}_{{n}}}} \right] \in {{\rm{R}}_ + }^{m \times n}$ ，非负矩阵分解^[3]的目标是将非负数据矩阵 ${{X}}$ 分解为基矩阵 ${{W}} = \left[ {{{{w}}_{{1}}}\;{{{w}}_{{2}}}\; \cdots \;{{{w}}_{{r}}}} \right] \in {{\rm{R}}_ + }^{m \times r}$ 和系数矩阵 ${{H}} = $ $[{{{h}}_{{1}}}\;{{{h}}_{{2}}}\; \cdots \;{{{h}}_{{n}}}] \in {{\rm{R}}_ + }^{r \times n}$ 的乘积，即 ${{X}} \approx {{WH}}$ ，当 $r \leqslant \min$ (m,n)时，矩阵 ${{X}}$ 就达到了有效压缩。NMF可表示为以下最小化问题：

$\begin{array}{l} \mathop {\min }\limits_{{\bf{W}},{\bf{H}}} \begin{array}{*{20}{c}} {} \end{array}\left\| {{{X}} - {{WH}}} \right\|_F^2 \\ {\rm{s.t.}}\begin{array}{*{20}{c}} {} \end{array}{{W}} \geqslant 0,{{H}} \geqslant 0 \\ \end{array} $

(1)

其中 $\left\| \cdot \right\|_F$ 表示Frobenius范数。该问题的求解采用以下乘性迭代规则：

$\begin{gathered} {{{W}}_{{{ik}}}} \leftarrow {{{W}}_{{{ik}}}}\dfrac{{{{\left( {{{X}}{{{H}}^{\rm{T}}}} \right)}_{{{ik}}}}}}{{{{\left( {{{WH}}{{{H}}^{\rm{T}}}} \right)}_{{{ik}}}}}},{{{H}}_{{{kj}}}} \leftarrow {{{H}}_{{{kj}}}}\dfrac{{{{\left( {{{{W}}^{\rm{T}}}{{X}}} \right)}_{{{kj}}}}}}{{{{\left( {{{{W}}^{\rm{T}}}{{WH}}} \right)}_{{{kj}}}}}}\\ \left( {i = 1,2, \cdots ,m{\text{；}}k = 1,2, \cdots ,r{\text{；}}j = 1,2, \cdots ,n} \right) \end{gathered}$

(2)

1.2 图正则化非负矩阵分解(GNMF)

图正则化非负矩阵分解(graph regularized non-negative matrix factorization，GNMF)^[9]考虑了数据样本之间的流形结构，希望数据样本在低维空间中尽可能多地保持其近邻结构，从而寻找数据在低维空间中的紧致嵌入。该问题可用以下优化模型表示：

$\begin{array}{l} \mathop {\min}\limits_{{W},{{H}}} \begin{array}{*{20}{c}} {} \end{array}\left\| {{{X}} - {{WH}}} \right\|_F^2 +{\textit{λ}}{\rm{tr}}\left( {{{HL}}{{{H}}^{\rm{T}}}} \right)\\ {\rm{s.t.}}\begin{array}{*{20}{c}} {} \end{array}{{W}} \geqslant {{0}},{{H}} \geqslant {{0}} \end{array}$

(3)

其中 ${{L}} = {{D}} - {{S}}$ 为拉普拉斯矩阵， ${{S}}$ 是权矩阵， ${{D}}$ 为对角矩阵， ${{{D}}_{{{ii}}}} = \displaystyle\sum\limits_j {{{{S}}_{_{{{ij}}}}}} $ 。

求解该问题的乘性迭代规则为

$\begin{gathered} {{{W}}_{{{ik}}}} \leftarrow {{{W}}_{{{ik}}}}\dfrac{{{{\left( {{{X}}{{{H}}^{\rm{T}}}} \right)}_{{{ik}}}}}}{{{{\left( {{{WH}}{{{H}}^{\rm{T}}}} \right)}_{{{ik}}}}}},{{{H}}_{{{kj}}}} \leftarrow {{{H}}_{{{kj}}}}\dfrac{{{{\left( {{{{W}}^{\rm{T}}}{{X}} + \lambda {{H}}{{{S}}_{{H}}}} \right)}_{{{kj}}}}}}{{{{\left( {{{{W}}^{\rm{T}}}{{WH}} + \lambda {{H}}{{{D}}_{{H}}}} \right)}_{{{kj}}}}}}\\ \left( {i = 1,2, \cdots ,m{\text{；}}k = 1,2, \cdots ,r{\text{；}}j = 1,2, \cdots ,n} \right) \end{gathered} $

(4)

1.3 最大间距准则(MMC)

设有 $C$ 类样本，最大间距准则的主要思想是寻找一个投影矩阵 ${{P}}$ 使得投影后同类样本之间的散度最小而不同类样本之间的散度最大，达到保持原始数据判别信息的目的，它可表示为以下优化问题：

$\max {\rm{tr}}\left( {{{{P}}^{\rm{T}}}({{{S}}_{{b}}} - {{{S}}_{{w}}}){{P}}} \right)$

(5)

式中： ${{{S}}_{{b}}} = \displaystyle\sum\limits_{c = 1}^C {(\bar {{x}} - {{\bar {{x}}}_{{c}}})(\bar {{x}} - {{\bar {{x}}}_{{c}}}){)^{\rm{T}}}} $ 为类间散度矩阵； ${{{S}}_{{w}}} = $ $\displaystyle\sum\limits_{c = 1}^C {\displaystyle\sum\limits_{j = 1}^{{n_c}} {({{x}}_{{j}}^{{c}} - \overline {{{{x}}_{{c}}}} ){{({{x}}_{{j}}^{{c}} - \overline {{{{x}}_{{c}}}} )}^{\rm{T}}}} } $ 为类内散度矩阵； $\overline {{x}} $ 表示所有样本的均值，而 $ {{\overline{{x}}_{{c}}}} $ 为 $c$ 类样本的均值， ${{{n}}_{{c}}}$ 为 $c$ 类样本数。

2 本文算法

根据流形学习的图嵌入思想^[17-19]，数据在高维空间中的局部邻域关系在低维样本空间中应得到保持，同时也希望原始数据集的散度关系得到保持，因此在NMF的目标函数中通过添加图正则化约束和判别约束可达到提高算法分类性能的目的。

2.1 构建权重矩阵

基于图嵌入的流形学习法其前提是构建相应的邻接图及权矩阵。传统的流形学习方法通常是利用k-近邻法或ε-邻域法来构建图和权矩阵，但此类方法的性能依赖于参数k或ε。本文利用基于同类样本的稀疏表示方法选择邻域样本，该方法是自适应且与参数无关的，对噪声数据具有鲁棒性。

图1比较了两种方法选择的邻域样本。其中，k-近邻法选择的邻域样本包含了数据集中不同类别的人脸，人脸角度变化与标注图像一致。相比而言，本文方法所选的样本不仅和标注人脸具有相似角度，而且最接近其正面的人脸图像，且相应的稀疏表示系数越大，越接近标注样本。所以，基于同类样本的稀疏表示方法构建的权重矩阵不仅包含了样本的类别信息，而且还包含了样本间的局部邻域结构，从而具有良好的判别性质。

对于某一类数据样本 ${{x}}_{{i}}^{{c}}$ ，将它表示为所有同类的其他样本的稀疏线性组合，这可以用以下优化模型来表示：

$\begin{array}{l} \min \begin{array}{*{20}{c}} {} \end{array}{\left\| {{{s}}_{{i}}^{{c}}} \right\|_1}\\ {\rm{s.t.}}\begin{array}{*{20}{c}} {} \end{array}{{{x}}_{{i}}} = {{{X}}_{{c}}}{{s}}_{{i}}^{{c}},c\left( {{{{x}}_{{i}}}} \right) = c \end{array}$

(6)

式中： ${{{X}}_{{c}}}$ 为第c类所有样本组成的矩阵，表示系数向量 ${{s}}_{{i}}^{{c}}$ 中的每一个分量描述了与 ${{x}}_{{i}}^{{c}}$ 同类的其他相应样本在表示 ${{x}}_{{i}}^{{c}}$ 时的贡献大小，从而可以用来表示样本之间的相似性。 $c({{{x}}_{{i}}})$ 表示样本 ${{x}}_{{i}}^{{c}}$ 的类标签， ${n_c}$ 表示第c类样本的数量，且n = $ \displaystyle\sum\limits_{c = 1}^C {{n_c}} $ 。从而，有以下基于稀疏表示的样本权矩阵：

${{{S}}_{{H}}} = {\left( {{{{S}}_{{ij}}}} \right)_{n \times n}} = {\rm diag}\left\{ {{{{S}}^{{1}}},{{{S}}^{{2}}}, \cdots ,{{{S}}^{{C}}}} \right\}$

(7)

其中：子矩阵 ${{{S}}^{{C}}} \in {R^{n{}_c \times {n_c}}}$ 是由第c类中每个训练样本 ${{x}}_{{i}}^{{c}}$ 的稀疏表示系数 ${{s}}_{{i}}^{{c}}$ 所组成的分块矩阵。

2.2 正则化约束

图正则化是基于邻域保持嵌入的，它将训练样本之间的局部邻域关系通过权矩阵S在由NMF的系数矩阵H的列向量h_j所张成的子空间中得到保持，因此得到以下图正则化约束项：

$ \begin{split} \frac{1}{2}\sum\limits_{i,j = 1}^n {\left\| {{{{h}}_{{i}}} - {{{h}}_{{j}}}} \right\|_2^2{{{S}}_{{{ij}}}}} = & {\rm{tr}}\left( {{{H}}{{{D}}_{{H}}}{{{H}}^{\rm{T}}}} \right) - {\rm{tr}}\left( {{{H}}{{{S}}_{{H}}}{{{H}}^{\rm{T}}}} \right) =\\ & {\rm{tr}}\left( {{{H}}{{{L}}_{{H}}}{{{H}}^{\rm{T}}}} \right) \end{split}$

(8)

式中： ${{{S}}_{{H}}}$ 为权矩阵； ${{{L}}_{{H}}} = {{{D}}_{{H}}} - {{{S}}_{{H}}}$ 为拉普拉斯矩阵；D_H为对角矩阵且对角元素为 ${{{D}}_{{Hii}}} = \displaystyle\sum\limits_{{j}} {{{{S}}_{{Hij}}}} $ 。

以NMF中的基矩阵W为投影矩阵，使得投影后同类样本之间的散度最小而不同类样本之间的散度最大^[19]，以保留训练样本的判别特征，从而有以下基于MMC准则的判别约束项：

${\rm{tr}}\left( {{{{W}}^{\rm{T}}}\left( {{{{S}}_{{B}}} - {{{S}}_{{W}}}} \right){{W}}} \right)$

(9)

为满足NMF的非负约束的要求，式(9)可改写为

${\rm{tr}}\left( {{{{W}}^{\rm{T}}}\left( {\left( {{{S}}_{{B}}^ + - {{S}}_{\left| {{B}} \right|}^ - } \right) - \left( {{{S}}_{{W}}^ + - {{S}}_{\left| {{W}} \right|}^ - } \right)} \right){{W}}} \right)$

(10)

式中： ${{{S}}_{{B}}}$ 表示由所有训练样本的类间散度矩阵； ${{S}}_{{B}}^ + $ 和 ${{S}}_{\left| {{B}} \right|}^ - $ 分别表示 ${{{S}}_{{B}}}$ 的正元素和非正元素的绝对值构成的矩阵； ${{{S}}_{{W}}}$ 表示类内散度矩阵； ${{S}}_{{W}}^ + $ 和 ${{S}}_{\left| {{W}} \right|}^ - $ 分别表示 ${{{S}}_{{W}}}$ 的正元素和非正元素的绝对值构成的矩阵。

对于图像数据，其特征维度和冗余程度都很高，基于稀疏编码的思想^[20]，将样本 ${{{x}}_{{i}}}$ 表示为基图像的稀疏线性表示，可以减少高维样本的计算量，得到更具鲁棒性的特征：

${{{x}}_{{i}}} \approx {{{w}}_{{1}}}{{{h}}_{{{1,i}}}} + {{{w}}_{{2}}}{{h}}{}_{{{2,i}}} + \cdots + {{{w}}_{{r}}}{{{h}}_{{{r,i}}}}$

(11)

通常使用 ${L_0}$ 范数对系数矩阵进行稀疏性约束，但 ${L_0}$ 范数的求解属于NP难问题，常用 ${L_1}$ 范数作为其凸近似进行近似求解：

${\left\| {{H}} \right\|_1} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^n {\left| {{{{h}}_{{{ij}}}}} \right|} } $

(12)

系数矩阵 ${{H}}$ 的每一列可看作原始数据 ${{X}}$ 在子空间中的低维表示， ${L_1}$ 范数使得系数矩阵 ${{H}}$ 整体保持稀疏，本文使用 ${L_{2,1}}$ 范数对系数矩阵 ${{H}}$ 进行列稀疏约束，使得每一个低维表示 ${{{h}}_{{j}}}$ 保持稀疏，能够在特征空间中用尽可能少的特征重构原始数据：

$\left\| {{{{H}}^{\bf{T}}}} \right\|_{2,1}^{} = \sum\limits_{j = 1}^n {{{\left\| {{{{h}}_{{j}}}} \right\|}_2} = } \sum\limits_{j = 1}^n {\sqrt {\sum\limits_{{\rm{i}} = 1}^r {{{h}}_{{{ij}}}^2} } } $

(13)

其中 ${{{h}}_{{j}}}$ 为矩阵 ${{H}}$ 的第 $j$ 列向量。

2.3 优化模型与求解

由以上分析，利用图正则化约束来保持样本之间的邻域结构；以最大间距准则保持数据集的判别性；以 ${L_{2,1}}$ 范数进行稀疏性约束^[21]，建立优化模型：

$\begin{split} & min \begin{array}{*{20}{c}} {} \end{array}\left\| {{{X}} - {{WH}}} \right\|_F^2 + \lambda {\rm{tr}}\left( {{{H}}{{{L}}_{{H}}}{{{H}}^{\rm{T}}}} \right) + \\ & \beta {\rm{tr}}\left( {{{{W}}^{\rm{T}}}\left( {\left( {{{S}}_{{W}}^ + - {{S}}_{\left| {{W}} \right|}^ - } \right) - \left( {{{S}}_{{B}}^ + - {{S}}_{\left| {{B}} \right|}^ - } \right)} \right){{W}}} \right) + \mu \left\| {{{{H}}^{\rm{T}}}} \right\|_{2,1}^{} \\& {\rm{s.t.}}\begin{array}{*{20}{c}} {} \end{array}{{W}} \geqslant 0,{{H}} \geqslant 0 \end{split} $

(14)

令 ${\varPhi _{ik}}$ 与 ${\varPsi _{kj}}$ 为拉格朗日乘子，构造拉格朗日函数：

$\begin{gathered} L = \left\| {{{X}} - {{WH}}} \right\|_F^2 +{\textit{λ}} {\rm{tr}}\left( {{{H}}{{{L}}_{{H}}}{{{H}}^{\rm{T}}}} \right) + \\ \beta {\rm{tr}}\left( {{{{W}}^{\rm{T}}}\left( {\left( {{{S}}_{{W}}^ + - {{S}}_{\left| {{W}} \right|}^ - } \right) - \left( {{{S}}_{{B}}^ + - {{S}}_{\left| {{B}} \right|}^ - } \right)} \right){{W}}} \right) + \\ \mu {\rm{tr}}\left( {{{{H}}^{\rm{T}}}{{QH}}} \right) - {\rm{tr}}\left( {\varPhi {{{W}}^{\rm{T}}}} \right) - {\rm{tr}}\left( {\varPsi {{H}}} \right) \end{gathered} $

(15)

式中： ${{Q}}$ 为对角矩阵，且 ${{{Q}}_{{{ii}}}} = \dfrac{1}{{{\rm{2}}{{\left\| {{{H}}_{{i}}^{\bf{T}}} \right\|}_2}}}$ ， ${{H}}_{{i}}^{\rm T}$ 为系数矩阵 ${{H}}$ 的转置的第 $i$ 列。

使用交替迭代方法求解。先固定 ${{H}}$ ，更新 ${{W}}$ ；然后固定 ${{W}}$ ，更新 ${{H}}$ 。式(15)对 ${{W}}$ 求偏导并令导数等于0，得：

$\begin{gathered} \frac{{\partial L}}{{\partial {{W}}}} = - 2{{X}}{{{H}}^{\rm{T}}} + 2{{WH}}{{{H}}^{\rm{T}}} + \\ 2\beta \left( {\left( {{{S}}_{{W}}^ + - {{S}}_{\left| {{W}} \right|}^ - } \right) - \left( {{{S}}_{{B}}^ + - {{S}}_{\left| {{B}} \right|}^ + } \right)} \right){{W}} - {{\varPhi }} = 0 \end{gathered} $

(16)

由互补松驰条件 ${\varPhi _{ik}}{W_{ik}} = 0$ ，得：

${\left( { - {{X}}{{{H}}^{\rm{T}}} + {{WH}}{{{H}}^{\rm{T}}} + \beta \left( {\left( {{{S}}_{{W}}^ + - {{S}}_{\left| {{W}} \right|}^ - } \right) - \left( {{{S}}_{{B}}^ + - {{S}}_{\left| {{B}} \right|}^ - } \right)} \right){{W}}} \right)_{ik}}{{{W}}_{{{ik}}}} = 0$

(17)

于是，有以下关于 ${{W}}$ 的更新规则：

${{W}}_{{{ik}}}^{t + 1} \leftarrow {{W}}_{{{ik}}}^t\frac{{{{\left( {{{X}}{{{H}}^{\rm{T}}} + \beta \left( {{{S}}_{\left| {{W}} \right|}^ - + {{S}}_{{B}}^ + } \right)} \right)}_{ik}}}}{{{{\left( {{{WH}}{{{H}}^{\rm{T}}} + \beta \left( {{{S}}_{{W}}^ + + {{S}}_{\left| {{B}} \right|}^ - } \right)} \right)}_{ik}}}}$

(18)

同理，得到关于 ${{H}}$ 的更新规则：

$ \begin{gathered} {{H}}_{{{kj}}}^{t + 1} \leftarrow \\ {{H}}_{{{kj}}}^t\frac{{{{\left( {{{{W}}^{\rm{T}}}{{X}} +{\textit{λ}} {{H}}{{{S}}_{{H}}} + \beta {\nabla _{{H}}}{\rm{tr}}\left( {{{W}}\left( {{{S}}_{\left| {{W}} \right|}^ - + {{S}}_{{B}}^ + } \right){{{W}}^{\rm{T}}}} \right)} \right)}_{kj}}}}{{{{\left( {{{{W}}^{\rm{T}}}{{WH}} + {\textit{λ}} {{H}}{{{D}}_{{H}}} + \beta {\nabla _{{H}}}{\rm{tr}}\left( {{{W}}\left( {{{S}}_{{W}}^ + + {{S}}_{\left| {{B}} \right|}^ - } \right){{{W}}^{\rm{T}}}} \right) + \mu {{HQ}}} \right)}_{kj}}}} \end{gathered}$

(19)

在每次迭代得到基图像矩阵 ${{W}}$ 后，对其每一列进行归一化处理，使非负矩阵分解得到的结果保持缩放不变性。设置最大迭代次数 ${T_0}$ ，使算法在最大迭代次数下收敛。

综合以上讨论，得到图正则化稀疏判别非负矩阵分解法：

算法1　图正则化稀疏判别非负矩阵分解算法(GSDNMF-L_2,1)

输入　训练样本 ${{X}} \in {\rm R}_ + ^{m \times n}$ ，样本类别 ${{Y}}$ ，特征数 $r$ ，正则化参数λ、β、μ，最大迭代次数 ${T_0}$ 。

1)利用式(6)和式(7)计算权重矩阵 ${{{S}}_{{H}}}$ ；

2)利用式(9)计算类内散度 ${{{S}}_{{W}}}$ 和类间散度 ${{{S}}_{{B}}}$ ；

3)随机初始化 ${{{W}}_{{0}}}{\rm{ }} \in {\rm{R}}_{\rm{ + }}^{{\rm{m}} \times {\rm{k}}}$ ， ${{{H}}_{{0}}} \in {\rm{R}}_{\rm{ + }}^{{\rm{k}} \times {\rm{n}}}$ ；

4)

Fort= 1: ${T_0}$

利用式(18)得到更新后的 ${{W}}$ ，并对 ${{W}}$ 的每一列进行归一化处理，利用公式(19)得到更新后的 ${{H}}$ ；

End

输出　基矩阵 ${{W}}$ 和系数矩阵 ${{H}}$ 。

2.4 算法复杂度

设 $m$ 为样本维度， $n$ 为样本个数， $k$ 为特征数。算法GSDNMF-L_2,1主要由1)、2)和4)组成，其中步骤1)是构建数据图的权矩阵，其复杂度为 $O\left( {{n^2}m} \right)$ ；步骤2)则是计算类内散度 ${{{S}}_{{W}}}$ 和类间散度 ${{{S}}_{{B}}}$ ，其复杂度为 $O\left( {{m^2}} \right)$ ；对步骤4)，一次迭代计算 ${{W}}$ 和 $ H$ 的复杂度 $O\left( {mnk} \right)$ ，假设算法在 ${T_0}$ 次迭代后收敛，则整个步骤4)的复杂度为 $O\left( {{T_0}mnk} \right)$ 。综上可知，GSDNMF-L_2,1算法的总体时间复杂度为O $\left( {{T_0}mnk + {n^2}m + {m^2}} \right)$ 。

3 实验分析

为了说明GSDNMF-L_2,1算法在图像特征提取中的有效性，分别在ORL和AR人脸数据集和COIL20实物数据集上进行实验，并将之与NMF^[3]、GNMF^[10]、NDMF^[9]等算法进行比较，同时比较利用L₁范数进行稀疏约束的模型(GSDNMF-L₁)。将数据集按0.5的比例随机划分为训练集和测试集，利用训练集进行特征提取，获得基矩阵 ${{W}}$ 。利用测试集计算分类精度：测试样本 ${{x}} \in {{\rm R}^m}$ 在低维子空间中的表示为 ${{y}} \approx {{{W}}^ + }{{x}} \in {{\rm R}^r}$ ，其中 ${{{W}}^ + } = $ $ {({{{W}}^{\rm{T}}}{{W}})^{ - 1}}{{{W}}^{\rm{T}}}$ 为矩阵 ${{W}}$ 的Pseudo逆，使用传统的k-近邻分类器(k-NN)预测类标签。每次实验独立随机，重复20次取平均识别率和方差作为最后实验结果。

3.1 数据集

ORL人脸数据库包含了40个人的人脸图像，每个人有10张，图像具有不同面部表情(睁/闭眼，笑/不笑)、面部细节(眼镜/无眼镜)及不同光照条件。

AR数据集包含了120个人的人脸图像，每个人有26张图像，图像具有不同的面部表情、照明条件和遮挡(太阳眼镜/围巾)。

COIL20数据集包含了20个不同的物体(玩具小鸭、招财猫、杯子等)，其中，每个物体在水平面上每隔5°拍摄一张图片，因此每个物体一共有72幅图片，整个数据集共计l 440幅图片。

实验中，所有图像均压缩成32×32大小的灰度图，将其每列相连构成大小为1 024维的向量，并做归一化处理。如图2所示。

3.2 参数选择

GSDNMF-L_2,1算法包含了图正则化约束参数λ、判别约束参数 $\beta $ 和稀疏参数 $\mu $ 等3个关键参数。为说明3个参数对识别率的影响，分别在两个数据集上采取固定两个参数来确定另一个参数的方法进行讨论，设参数的取值范围为[0,1]，取数据集的类别数作为基图数(ORL取40，AR取120，COIL20取20)，最大迭代次数为300次，实验所得的平均识别率与正则化参数的关系如图3所示。

3.3 实验结果及分析

由图3可知，图正则化参数λ对识别率的影响较大，在[0,0.01]的范围内，识别率随参数的增大而增大，在[0.01,1]的范围内，识别率随参数的增大而减少。判别约束参数和稀疏参数对识别率的影响较小，在[0,1]范围内一直保持较高识别率。经过多次实验，最终确定算法的最优参数组合为λ=0.005，β=1，μ=0.5。

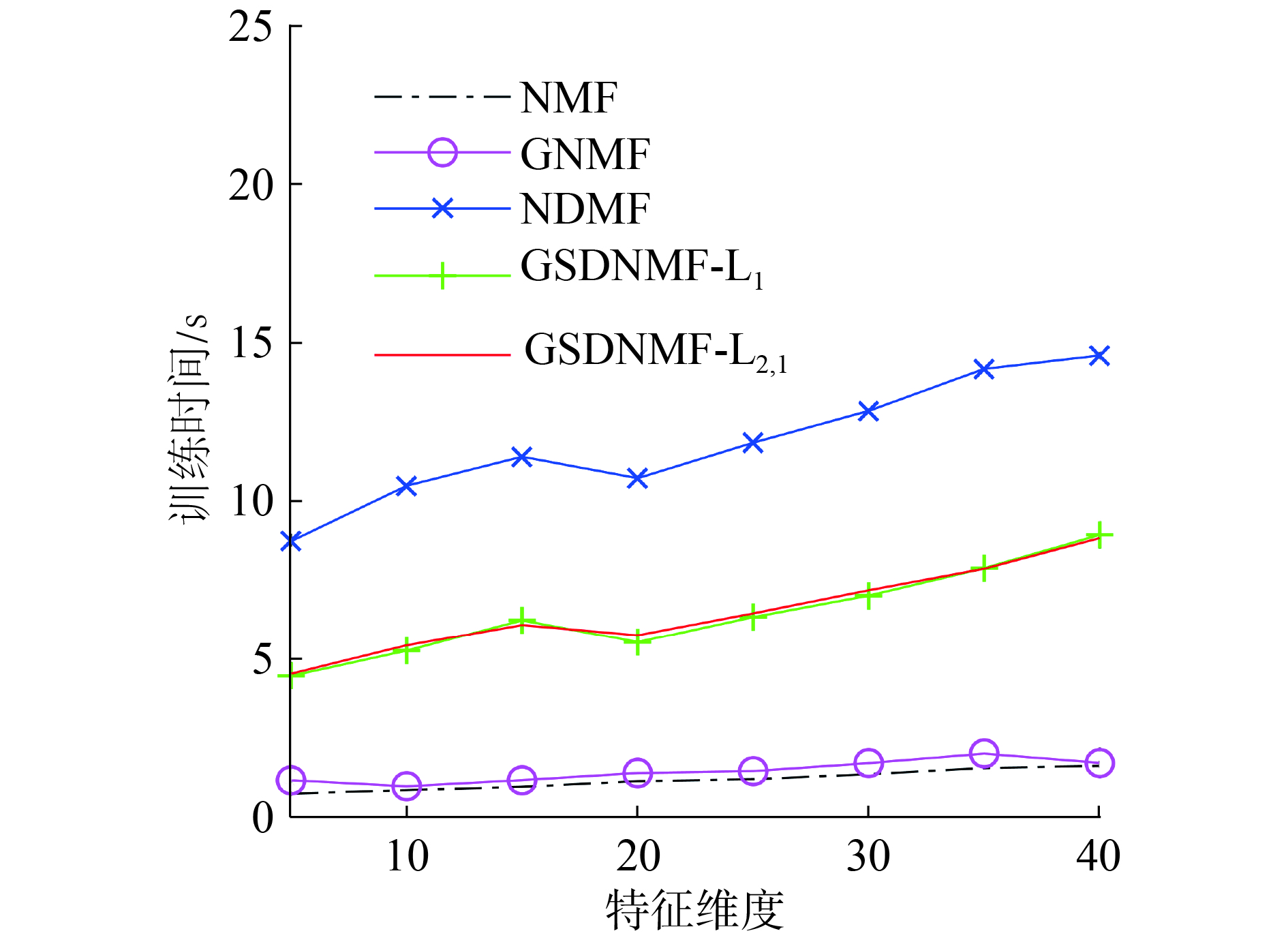
取基图数分别为3、4、5、6、7、8的平方，在3种数据集上独立随机地进行20次实验，计算平均识别率及方差。表1~3给出了5种算法在3种数据集上的平均识别率随基图像个数的增加而变化的情况。在大多数情况下，GSDNMF-L_2,1的识别率要优于其他几种算法，且方差更小，说明在NMF的目标函数中结合图正则化约束和判别约束能够有效提高图像特征提取的准确率和稳定性。图4比较了在ORL数据集上5种算法的训练时间(取类别数40作为基图数目)，可以发现NMF和GNMF的训练时间较短，NDMF训练时间最长，GSDNMF-L_2,1和GSDNMF-L₁比NDMF时间短。可知，利用稀疏编码的思想对系数矩阵H添加稀疏性约束，在每一迭代更新的过程中能够尽可能少地选择基图像重构训练样本，提高了运算速度。

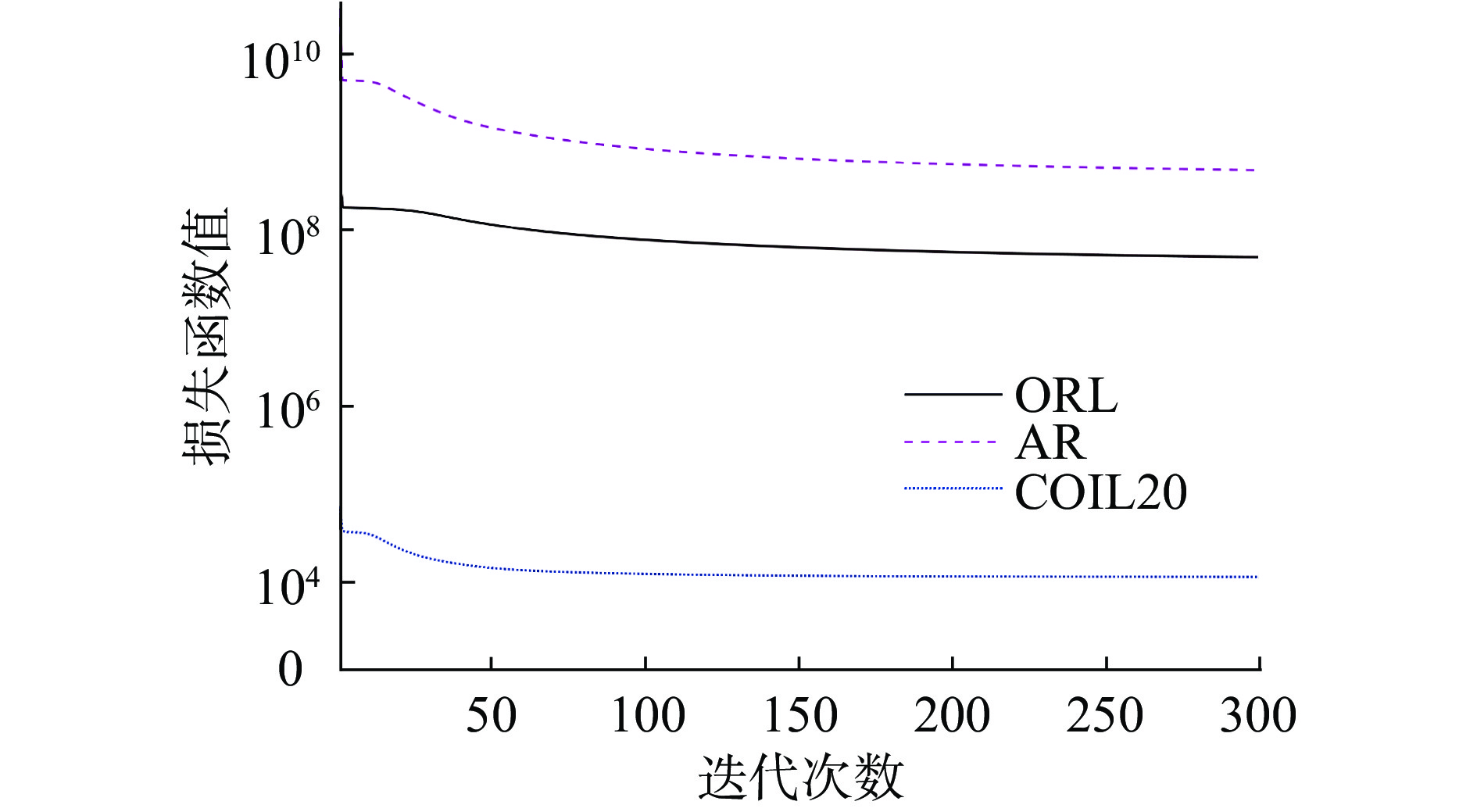
图5给出了GSDNMF-L_2,1算法在3种数据集上的收敛情况，当迭代次数小于10次时损失函数值迅速下降；而当迭代次数大于100时，随着迭代次数的增加其损失函数值的下降趋于平缓，并收敛于一个固定值。本文所有实验均设置最大迭代次数为300次，以保证算法收敛。

为了刻画和评价基图像矩阵的特点，Hoyer^[20]提出采用向量的 ${\rm L_1}$ 范数和 ${\rm L_2}$ 范数的差异来度量向量的稀疏度，其计算方式为

$s(x) = \frac{{\sqrt n - \left( {\displaystyle\sum\limits_i {{{{x}}_{{i}}}} /\sqrt {\displaystyle\sum\limits_i {{{x}}_{{i}}^2} } } \right)}}{{\sqrt n - 1}}$

(16)

其中向量 ${{{x}}_{{i}}}$ 是其第i个分量。稀疏度值域是[0,1]，值越大，说明向量越稀疏。表4比较了5种算法在3种数据集上迭代300次后生成的基图的平均稀疏度(基矩阵的每一列表示一个基图)。图6比较了3种具有判别性质的NMF算法：NDMF^[9]、GSDNMF-L₁和GSDNMF-L_2,1得到的基图。对比发现，3种算法都能得到的图像的局部化表示，且都包含了每类物体的判别信息，但GSDNMF-L_2,1和GSDNMF-L₁得到的基图比NDMF^[9]得到的基图更稀疏。由实验结果可知，本文提出的算法，能够在保证稀疏性的条件下，保持良好分类水平，说明算法分解得到了更有效的基图特征。

4 结束语

本文给出了一种新的图正则化稀疏判别NMF算法(GSDNMF-L_2,1)。该方法在对图像进行特征提取时，充分利用了数据集的标签信息来构造权重矩阵和判别约束项。与已有的图正则化方法不同的是，GSDNMF-L_2,1算法用同类样本的稀疏线性组合来构建权重矩阵，很好地保持了样本内的相似性和样本间的差异性，在最大间距准则下使得类内离散性最小而类间分离性最大，从而获得很强的判别能力。另外，GSDNMF-L_2,1在稀疏性约束条件下得到了稀疏系数矩阵，从而提高了矩阵分解的速度。下一步研究的方向是如何处理新样本，及自动选择最佳特征数量，使算法更加完善。