近年来，随着互联网的快速发展，人们获取数据以及存储数据的能力都迅速提高。不论在科学技术还是在日常生活的各个领域都累积了大量数据。怎样才能快速有效地对这些数据进行分析处理并发掘其中蕴含的有效信息引起人们的关注。大部分机器学习都能够通过矩阵的形式表示，但是在现实生活中经常会使用到数以百万记的样本，通过对矩阵进行处理的机器学习技术的复杂度会随着应用规模的增加呈二次方增长，这会使很多问题无法解决。

目前通常通过低秩矩阵分解、核方法和聚类等方法来解决矩阵分解的问题^[1]。聚类是将输入数据按照某种相似性规则划分为若干类。低秩矩阵分解是将数据矩阵分解成噪声和稀疏低秩两部分。在众多方法之中，通过核方法近似低秩分块矩阵由于其模型合理直观、实施简单、效果显著而受到关注。

本文考虑结构受限下的矩阵分解问题^[2]，其中结构受限主要是低秩结构受限和分块结构受限。本文通过消除噪声并最小化块外对角线来增强类与类之间数据表示的不相关性，从而实现分块约束^[3]；同时通过增强训练样本的自表达属性并缩小样本之间的差距来增强类内数据表示的相关性，从而实现低秩约束^[4]，最后迭代优化求解一系列子问题来实现矩阵分解的目的。随后设计了一个低秩分块矩阵的核近似算法(low-rank block kernel approximation, LBKA)。LBKA不仅能够显著提高算法速度，而且由于低秩分块约束极大的消除了噪声的影响，使得算法近似精度也有了提高。

相较于传统的矩阵分解问题，本文设计了低秩分块矩阵的核近似算法。本文的特点和贡献如下：

1)引入了一种低秩分块矩阵的框架，通过核方法将非线性问题转化为高维空间中的线性问题来解决，这样不仅可以提高算法的精度，还可以通过低秩约束来降低算法复杂度，提高了计算的收敛速度与计算精度。

2)设计了一种低秩分块矩阵的核近似算法。该算法基于增广拉格朗日乘子法和交替方向乘子法构造迭代公式，依次更新系数矩阵Z和辅助变量J、Q、S，直到收敛到稳定的特征矩阵。

3)在人脸识别数据集和字符识别数据集上进行了实验验证。实验结果表明，相较于传统的识别算法，LBKA在收敛速度和近似精度上有所提高。同时通过核矩阵近似处理，极大地降低了噪声对实验的影响。

1 相关工作

本文主要在低秩、稀疏、对角矩阵的分解领域探讨有关低秩分块矩阵的近似问题。

随着非负矩阵分解^[4]等矩阵分解算法的提出，给数据处理领域带来了新的思路。低秩可以看作稀疏的特殊形式，低秩就是特征值稀疏；块对角也是，块对角矩阵自身就具有低秩和稀疏的特性。

现阶段，稀疏表示被广泛应用于信号处理^[3]、机器学习和计算机视觉^[5]等方面。随着基于稀疏表示的分类(SRC)^[6]在人脸识别中的成功应用，已经提出了许多基于SRC的优化算法。例如，Nie等人通过对损失函数和正则化项进行l₂₁范数约束，提出了一种有效的特征选择方法^[7]。

然而稀疏约束只能实现局部约束，而低秩约束却能够实现全局约束。鲁棒主成分分析(robust principal component analysis, RPCA)是最典型的低秩方法，最初是用来将损坏的观测数据恢复为具有低秩结构的数据。后来发现RPCA可以将一个子空间的数据分解成低秩和稀疏噪声两部分。但RPCA无法处理多个子空间的并集。为此提出了潜在的低秩表示(LatLRR)^[8]，通过利用子空间分割的低秩表示的方法解决多个子空间问题。

本节主要介绍一些基本符号并简单说明了两种典型的基于低秩表示的方法：鲁棒主成分分析(RPCA)^[9]和低秩表示(LRR)^[10]。

1.1 基本符号

本文使用粗体大写字母表示矩阵，例如A。用粗体小写字母表示矢量，例如a。对于A，其第i行被表示为行向量[A]_i，其第j列被表示为列向量[A]_:,j。将a_ij或A_ij表示为A的第 $(i,j)$ 项。将Diag(A)作为对角矩阵，其对角线上的第i项是a_i。将单位矩阵表示为I。如果A中的所有项都是非负的，则表示为 ${{A}} \geqslant 0$ 。文中将使用一些范数，包括l₀范数 $||{{A}}|{|_0}$ ，l₁范数 $\displaystyle||{{A}}|{|_1}={\sum _{ij}}|{{{a}}_{ij}}|$ ，Frobenius范数 $\displaystyle||{{A}}|{|_F}=\sqrt {{\sum _{ij}}{{a}}_{ij}^2} $ ，l₂₁范数 $\displaystyle||{{A}}|{|_{21}}={\sum _j}||{[{{A}}]_{ ; , j}}||$ 和核范数 $||{{A}}|{|_*}$ 。

1.2 低秩分块矩阵相关定义

定义1　假设矩阵 ${{A}}=\left[ {{{{a}}_1},{{{a}}_2}, \cdots ,{{{a}}_n}} \right] \in {{\bf{{R}}}^{{ m \times n}}}$ 是一个包含n个数据点的列矩阵。其核矩阵定义为： ${{{B}}_{ij}}={{b}}\left( {{{{a}}_i},{{{a}}_j}} \right)=\left\langle {\phi \left( {{{{a}}_i}} \right),\phi \left( {{{{a}}_j}} \right)} \right\rangle $ ， $\forall i,j=1,2, \cdots n$ ，其中 $\phi :\left. a \right| \to \phi \left( a \right)$ 是内核诱导的特征图。n个映射数据点的所有成对內积存储在核矩阵 ${{K}} \in {{\bf{R}}^{n \times n}}$ 中。

由于核矩阵的内存为O(n²)，所以在实际应用中是使用数据数量的二次方来计算和存储的。例如核主成分分析算法需要计算特征值分解(SVD)，它的复杂度为O(n³)，并且要多次访问核矩阵K。因此要想计算大规模的数据，必须考虑复杂度的影响。

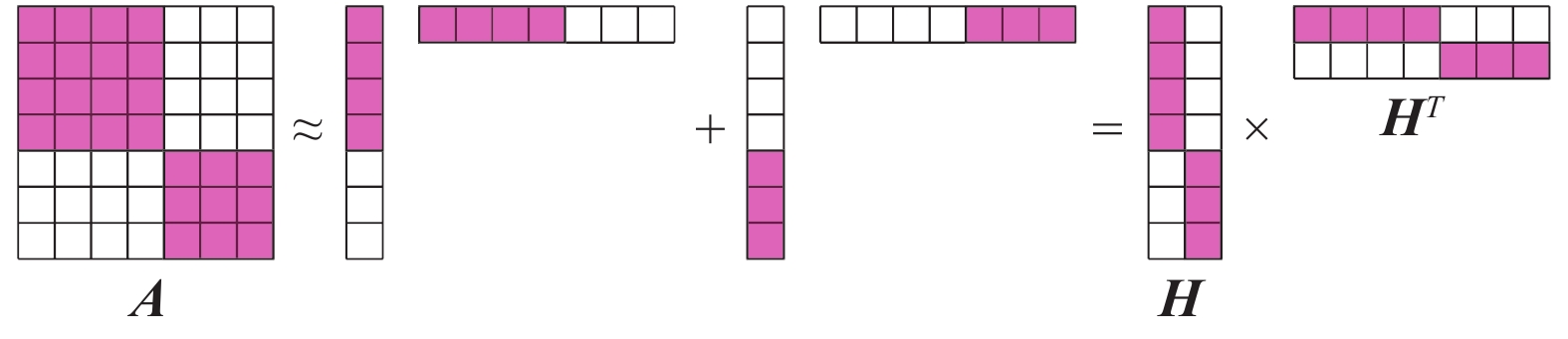
图1是低秩矩阵分块的一个示例，对于任意一个矩阵 ${{A}} \in {{\bf{R}}^{m \times n}}$ ，有

${{A}}={{H}}{{{H}}^{\rm{T}}}$

为了用低秩分块矩阵逼近该相似度矩阵并同时得到聚类结构，可以分别近似这些对角块，每个对角块表示一个聚类。

通过求矩阵秩的最小化来求解低秩矩阵。然而这很难，可以用核近似方法将核范数最小化为

${{{X}}^*}=\mathop {\arg \min }\limits_X f({{X}}) + \varGamma {\left\| {{X}} \right\|_*}$

式中： ${{X}} \in {{\bf{R}}^{m \times n}}$ ， $\varGamma>0$ 是正则化参数。

定义2 (奇异值阈值(SVT))　要想求解核范数最小化问题(NNM)，例如：

${{{X}}^*}=\mathop {\arg \min }\limits_{{X}} \varGamma {\left\| {{X}} \right\|_*} + \frac{1}{2}\left\| {{{X}} - {{A}}} \right\|_F^2$

需要使用奇异值阈值处理算子 ${S_{\varGamma} }( \cdot )$ 给出的闭式解：

${{{X}}^*}={S_{\varGamma} }({{A}})={{{U}}_{{A}}}{S_{\varGamma} }({\Sigma _{{A}}}){{V}}_{{A}}^{\rm{T}}$

式中： ${S_{\varGamma} }({ x})={\rm sgn}({x}) \cdot {\rm max}(\left| x \right| - \varGamma ,0)$ 是软收缩算子； ${{{U}}_{{A}}}{\Sigma _{{A}}}V_{{A}}^{\rm{T}}$ 是A的SVD分解^[11]。

1.2.1 鲁棒的主成分分析(RPCA)

假设 ${{X}}=[{{{x}}_1}, {{{x}}_2},\cdots ,{{{x}}_n}] \in {{{{\bf{R}}}}^{d \times n}}$ 是由n个样本组成的数据矩阵，RPCA的目标是从损坏的矩阵X中确定低秩矩阵X₀，同时消除稀疏噪声E，即 ${{X}}={{{X}}_0} + {{E}}$ 。因此，RPCA的目标函数为

$\begin{array}{l} \mathop {\min }\limits_{{{{X}}_0},{{E}}} {\rm{rank}}({{{X}}_0}) +\textit{λ} {\left\| {{E}} \right\|_0} \\ {\rm{s.t.}} \; {{X}}={{{X}}_0} + {{E}} \\ \end{array} $

(1)

式中 ${\textit{λ}} $ 是平衡参数； $|| \cdot |{|_0}$ 表示l₀范数。由于低秩函数的离散性质和最小化l₀范数十分困难，目前通常分别使用核范数和l₁范数正则化代替低秩约束和l₀范数正则化。因此，式(1)可以重新表述为

$\begin{array}{l} \mathop {\min }\limits_{{{{X}}_0},{{E}}} {\left\| {{{{X}}_0}} \right\|_*} + {\textit{λ}} {\left\| {{E}} \right\|_1} \\ {\rm{s.t.}}\; {{X}}={{{X}}_0} + {{E}} \\ \end{array} $

(2)

其中 $|| \cdot |{|_*}$ 和 $|| \cdot |{|_1}$ 表示核范数和l₁范数。式(2)可以使用增广拉格朗日乘子法(ALM)^[12]来计算。

1.2.2 低秩表示(LRR)

RPCA是基于先验假设，即数据大多是从低秩子空间中提取的，可以用单个子空间来描述。然而真实数据集很难用单个子空间来描述。为此，LRR假设每个数据可以由多个线性低秩子空间的并集近似表示。由此可以得到LRR的目标函数为

$\begin{gathered} \mathop {\min }\limits_{{{Z}},{{E}}} {\rm{rank}}({{Z}}) +{\textit{λ}} {\left\| {{E}} \right\|_1} \\ {\rm{s.t.}}\; {{X}}=D{{Z}} + {{E}} \\ \end{gathered} $

(3)

其中D和 ${\textit{λ}} $ 分别是字典和平衡参数。 $|| \cdot |{|_1}$ 表示不同范数的约束。与RPCA类似，式(3)可以重新表述为

$\begin{array}{l} \mathop {\min }\limits_{{{Z}},{{E}}} {\left\| {{Z}} \right\|_*} +{\textit{λ}}{\left\| {{E}} \right\|_1} \\ {\rm{s.t.}} \; {{X}}=D{{Z}} + {{E}} \\ \end{array} $

(4)

1.3 块对角矩阵的核近似

定义3 (自表达属性)　来自多个子空间的并集的每个数据实例可以通过其他数据实例的线性组合来表示，这种性质被称为自表达属性^[13]。即

${{X}}={{XZ}}$

在存在自表达属性的情况下，数据集中的每个数据点可以由来自其子空间的几个点的线性组合来表示^[14]。所以，自表达属性应该是块对角的。

本文令类与类之间块对角线分量尽可能小，同时提高相关的类内表示，将其结构化形式表示为

$\begin{gathered} \mathop {\min }\limits_{{Z}} {{\textit{λ}}_1}\left\| {{{A}} \odot {{Z}}} \right\|_F^2 + {{\textit{λ}}_2}{\left\| {{{D}} \odot {{Z}}} \right\|_0} \\ {\rm{s.t.}}\; {{X}}={{XZ}} \\ \end{gathered} $

(5)

其中 ${{\textit{λ}} _1}$ 和 ${{\textit{λ}} _2}$ 是用于衡量相应的项的正数， $ \odot $ 表示Hadamard乘积，并且 ${{X}} \in {{\bf{R}}^{d \times n}}$ 。具体地说，第1项是为了最小化类与类之间块对角线分量，并且 ${{A}}={1_n}1_n^{\rm{T}} - {{Y}}$ 。第2项是构造的子空间度量，以提高相关的类内表示。d_ij是度量x_i和x_j之间的距离。本文将两个样本之间的距离定义为欧几里德距离的平方，即 ${\rm{||}}{x_i} - {x_j}{\rm{||}}_2^2$ 。由于l₀范数最小化问题是NP难问题，所以第2项可以被放宽表示为 ${\rm{||}}{{D}} \odot {{Z}}{\rm{|}}{{\rm{|}}_1}$ 。因此，式(5)可以重新表述为

$\begin{gathered} \mathop {\min }\limits_{{Z}} {\textit{λ} _1}\left\| {{{A}} \odot {{Z}}} \right\|_F^2 + {\textit{λ} _2}{\left\| {{{D}} \odot {{Z}}} \right\|_1} \\ {\rm{s.t.}}\; {{X}}={{XZ}} \\ \end{gathered} $

(6)

通过整合公式(4)和(6),可以得到：

$\begin{gathered} \mathop {\min }\limits_{{Z}} {\left\| {{Z}} \right\|_*} + {\textit{λ} _1}\left\| {{\tilde{ A}} \odot {{Z}}} \right\|_F^2 + {\textit{λ} _2}{\left\| {{{D}} \odot {{Z}}} \right\|_1} + {\textit{λ} _3}{\left\| {{E}} \right\|_{21}} \\ {\rm{s.t.}}\; {{X}}={{XZ}} + {{E}} \\ \end{gathered} $

(7)

其中 ${\textit{λ} _1}$ 、 ${\textit{λ} _2}$ 和 ${\textit{λ} _3}$ 为式(7)的相应项加权。

下面本文对式(7)进行核化。

设 $\phi :{{{\bf{R}}}^d} \to H$ 是从输入空间到Hilbert空间的映射， ${{K}} \in {{{\bf{R}}}^{n \times n}}$ 为半正定核矩阵：

${{{K}}_{ij}}={(\phi {({{X}})^{\rm T}}\phi ({{X}}))_{ij}}=\phi {({{ x}_i})^{\rm T}}\phi ({{ x}_j})={\rm ker}({{ x}_i},{{ x}_j})$

其中ker： ${{{\bf{R}}}^d} \times {{{\bf{R}}}^d} \to {{\bf{R}}}$ 是核函数。式(7)中的E可以表示为 ${{E}}={{X}} - {{XZ}}$ ,所以有

$ \mathop {\min }\limits_{{Z}} {\left\| {{Z}} \right\|_*} + {{\textit{λ}} _1}\left\| {{\tilde{ A}} \odot {{Z}}} \right\|_F^2 + {\textit{λ} _2}{\left\| {{{D}} \odot {{Z}}} \right\|_1} + {{\textit{λ}} _3}{\left\| {{{X}} - {{XZ}}} \right\|_{21}} $

(8)

然后定义一个变量 ${{S}}={{I}} - {{Z}} \in {{{\bf{R}}}^{n \times n}}$ ，可以得到 ${\rm{||}}{{X}} - {{XZ}}{\rm{|}}{{\rm{|}}_{21}}={\rm{||}}{{XS}}{\rm{|}}{{\rm{|}}_{21}}={\displaystyle\sum\limits _{i=1}^n}{\rm{||}}{{X}}{s_i}{\rm{||}}=$ ${\displaystyle\sum\limits_{i=1}^n}{({{\rm s}_i}'{{X}}'{{X}}{{\rm s}_i})^{1/2}}$ ,其中 ${{S}}=\left[ {{s_1},{s_2}, \cdots ,{{\rm s}_n}} \right],{s_i} \in {{{\bf{R}}}^n}$ 表示S的第i列。将其中的X替换为 $\phi ({{X}})$ ，可以得到

$\begin{gathered} \mathop {\min }\limits_{{Z}} {\left\| {{Z}} \right\|_*} + {\textit{λ} _1}\left\| {{\tilde{ A}} \odot {{Z}}} \right\|_F^2 + \\ {\textit{λ} _2}{\left\| {{{D}} \odot {{Z}}} \right\|_1} + {\textit{λ} _3}{\displaystyle\sum\limits _{i=1}^n}\sqrt {{s_i}'\phi ({{X}})'\phi ({{X}}){s_i}} \\ {\rm{s}}{\rm{.t}}{\rm{.}} \; {{S}}={{I}} - {{Z}} \\ \end{gathered} $

(9)

因为 ${{K}}=\phi ({\rm x})'\phi ({\rm x})$ ,所以可以通过将函数g(S)定义为 $g({{S}}) \triangleq $ $\displaystyle\sum\limits _{i=1}^n\sqrt {{{\rm s}_i}'{{K}}{{\rm s}_i}} $ ，将式(9)重写为以下问题：

$\begin{gathered} \mathop {\min }\limits_{{Z}} {\left\| {{Z}} \right\|_*} + {\textit{λ} _1}\left\| {{\tilde{ A}} \odot {{Z}}} \right\|_F^2 + {\textit{λ} _2}{\left\| {{{D}} \odot {{Z}}} \right\|_1} + {\textit{λ} _3}g({{S}}) \\ {\rm{s}}{\rm{.t}}{\rm{.}}\; {{S}}={{I}} - {{Z}} \\ \end{gathered} $

(10)

其中核矩阵K包含在g(S)中。

定义4 (拉格朗日乘子法、增广拉格朗日乘子法、交替方向乘子法)

1)假定要求解f(X)的最优化问题，满足 $h({{X}})=0$ ，其中 $f({{X}}):{{{\bf{R}}}^n} \to {{\bf{R}}}$ ， $h({{X}}):{{{\bf{R}}}^n} \to {{{\bf{R}}}^m}$ 。基于拉格朗日乘子法^[13]可以得到以下目标函数：

${L_c}(x,\textit{λ} )=f({{X}}) + \mu h({{X}})$

2)在计算等式约束问题时，使用增广拉格朗日乘子法(ALM)，ALM增加了二次惩罚项，基于ALM可以得到以下目标函数：

${L_c}(x,\textit{λ} )=f({{X}}) + \mu h({{X}}) + \frac{c}{2}{\left\| {h({{X}})} \right\|^2}$

3)要求解f(X)+g(Z)的最优化问题，满足约束条件AX+BZ=C。这类问题需要用到交替方向乘子法(ADMM)^[13]，ADMM是ALM的进一步推广，它将对偶上升法的可分解性与ALM的收敛性相结合，基于ADMM方法可以得到以下目标函数：

$\begin{gathered} {L_c}({ {x,z}},{{\textit{λ}}} )=f({{X}}) + g({{Z}}) + {{{\textit{λ}}} ^{\rm T}}(A{{X}} + B{{Z}} - C) + \\ \displaystyle \frac{c}{2}{\left\| {Ax + Bz - C} \right\|^2} \\ \end{gathered} $

2 低秩分块矩阵的核近似算法

算法1　低秩分块矩阵的核近似算法

输入　特征矩阵X；参数 ${\textit{λ} _1}$ ， ${\textit{λ} _2}$ ， ${\textit{λ} _3}$ ；距离测量矩阵D；

输出　系数矩阵Z。

初始化：J=0, Z=0, Q=0, S=0, ${\textit{λ} _1}$ ， ${\textit{λ} _2}$ ， ${\textit{λ} _3}$ >0,

C₁=0, C₂=0, C₃=0,

while

$\begin{array}{l} \max ({\left\| {{{I}} - {{{Z}}^{t + 1}} - {{{S}}^{t + 1}}} \right\|_\infty },{\left\| {{{{J}}^{t + 1}} - {{{Z}}^{t + 1}}} \right\|_\infty }, \\ {\left\| {{{{Q}}^{t + 1}} - {{{Z}}^{t + 1}}} \right\|_\infty })>{\rm tol} \\ \end{array} $

do

1) 通过式(14)更新系数矩阵Z；

2) 通过式(15)更新辅助变量J；

3) 通过式(17)更新辅助变量Q；

4) 通过式(18)更新辅助变量S；

5) 更新拉格朗日乘子C₁，C₂和C₃；

$\left\{ \begin{array}{l} {{C}}_1^{t + 1}={{C}}_1^t + {\mu ^t}({{I}} - {{{Z}}^{t + 1}} - {{{S}}^{t + 1}}) \\ {{C}}_2^{t + 1}={{C}}_2^t + {\mu ^t}({{{J}}^{t + 1}} - {{{Z}}^{t + 1}}) \\ {{C}}_3^{t + 1}={{C}}_3^t + {\mu ^t}({{{Q}}^{t + 1}} - {{{Z}}^{t + 1}}) \\ \end{array} \right.$

6) 更新 $\mu $

${\mu ^{t + 1}}=\min ({\mu _{\max }},\rho {\mu ^t})$

end

为了优化式(10)，首先引入两个辅助变量J和Q来使问题可分离，将式(10)重写为

$\begin{gathered} \mathop {\min }\limits_{{{J}},{{Z}},{{Q}},{{S}}} {\left\| {{J}} \right\|_*} + \dfrac{{{\textit{λ} _1}}}{2}\left\| {{\tilde{ A}} \odot {{Z}}} \right\|_F^2 + {\textit{λ} _2}{\left\| {{{D}} \odot {{Q}}} \right\|_1} + {\textit{λ} _3}g({{S}}) \\ {\rm{s}}{\rm{.t}}{\rm{.}} {{S}}={{I}} - {{Z}},{{J}}={{Z}},{{Q}}={{Z}},{{Z}} \geqslant 0 \\ \end{gathered} $

(11)

然后，可以通过ALM得到式(11)的增广拉格朗日函数

$\begin{gathered} {L}({{J}},{{Z}},{{Q}},{{S}},{{{C}}_1},{{{C}}_2},{{{C}}_3}){\rm{=}} \\ {\left\| {{J}} \right\|_*} + \dfrac{{{\lambda _1}}}{2}\left\| {{\tilde{ A}} \odot {{Z}}} \right\|_F^2 + {\lambda _2}{\left\| {{{D}} \odot {{Q}}} \right\|_1} + {\lambda _3}g({{S}}) +\\ \left\langle {{{{C}}_1},{{I}} - {{Z}} - {{S}}} \right\rangle + \left\langle {{{{C}}_2},{{J}} - {{Z}}} \right\rangle + \left\langle {{{{C}}_3},{{Q}} - {{Z}}} \right\rangle + \\ \dfrac{\mu }{2}(\left\| {{{J}} - {{Z}}} \right\|_F^2 + \left\| {{{I}} - {{Z}} - {{S}}} \right\|_F^2 + \left\| {{{Q}} - {{Z}}} \right\|_F^2) \\ \end{gathered} $

(12)

其中 $\left\langle {{{J}},{{Q}}} \right\rangle ={\rm tr}({{{J}}^{\rm T}}{{Q}})$ 。C₁、C₂和C₃是拉格朗日乘子， $\mu>0$ 是惩罚参数。下面介绍详细迭代步骤：

更新Z 　固定其他变量并通过下述步骤更新Z

$\begin{gathered} L=\mathop {\min }\limits_{{Z}} \dfrac{{{\textit{λ} _1}}}{2}\left\| {{\tilde{ A}} \odot {{Z}}} \right\|_F^2 + \left\langle {{{C}}_1^t,{{I}} - {{Z}} - {{{S}}^t}} \right\rangle + \\ \;\;\;\;\; \left\langle {{{C}}_2^t,{{{J}}^{t + 1}} - {{Z}}} \right\rangle + \left\langle {{{C}}_3^t,{{{Q}}^t} - {{Z}}} \right\rangle + \dfrac{{{\mu ^t}}}{2}(\left\| {{{{J}}^{t + 1}} - {{Z}}} \right\|_F^2 + \\ \;\;\;\;\; \left\| {{{I}} - {{Z}} - {{{S}}^t}} \right\|_F^2 + \left\| {{{{Q}}^t} - {{Z}}} \right\|_F^2) \\ \end{gathered} $

这相当于

$\begin{gathered} L=\mathop {\min }\limits_{{Z}} \dfrac{{{\textit{λ} _1}}}{2}\left\| {{{Z}} - {{R}}} \right\|_F^2 + \dfrac{{{\mu ^t}}}{2}(\left\| {{{I}} - {{Z}} - {{{S}}^t} + \dfrac{{{{C}}_1^t}}{{{\mu ^t}}}} \right\|_F^2 + \\ \left\| {{{{J}}^{t + 1}} - {{Z}} + \dfrac{{{{C}}_2^t}}{{{\mu ^t}}}} \right\|_F^2 + \left\| {{{{Q}}^t} - {{Z}} + \dfrac{{{{C}}_3^t}}{{{\mu ^t}}}} \right\|_F^2) \\ \end{gathered} $

(13)

其中 ${{R}}=[{{Y}},{0_{n(N - n)}}] \odot {{{Z}}^t}$ 。通过推导 $\partial {{L}}$ $/\partial {{Z}}=0$ ，可以得到Z的最优解，式(13)的闭式解为

$ {{{Z}}^{t + 1}}={[(2 + \dfrac{{{\lambda _1}}}{{{\mu ^t}}}){{I}} + {{K}}]^{( - 1)}} (\dfrac{{{\textit{λ} _1}}}{{{\mu ^t}}}{{R}} + {{{U}}_1} + {{{U}}_2} + {{{U}}_3}) $

(14)

其中 ${{{U}}_1}={{I}} - {{{S}}^t} + \dfrac{{{{C}}_1^t}}{{{\mu ^t}}}$ ， ${{{U}}_2}={{{J}}^{t + 1}} + \dfrac{{{{C}}_2^t}}{{{\mu ^t}}}$ ， ${{{U}}_3}={{{Q}}^t} + \dfrac{{{{C}}_3^t}}{{{\mu ^t}}}$ 。

更新J 　当固定其他变量时，式(12)的目标函数可以表示为J的函数，即

$\begin{gathered} {{{J}}^{t + 1}}=\mathop {\arg \min }\limits_{{J}} {\left\| {{J}} \right\|_*} + \left\langle {{{C}}_2^t,{{J}} - {{{Z}}^t}} \right\rangle + \dfrac{{{\mu ^t}}}{2}\left\| {{{J}} - {{{Z}}^t}} \right\|_F^2 = \\ {\left\| {{J}} \right\|_*} + \dfrac{{{\mu ^t}}}{2}\left\| {{{J}} - \left({{{Z}}^t} - \dfrac{{{{C}}_2^t}}{{{\mu ^t}}}\right)} \right\|_F^2 \\ \end{gathered} $

通过使用奇异值阈值算子(见定义3)，可以得到一个封闭形式的解决方案，即

${{{J}}^{t + 1}}={\varGamma _{1/{\mu ^t}}}({{{Z}}^t} - \frac{{{{C}}_2^t}}{{{\mu ^t}}})={{U}}{S_{1/{\mu ^t}}}(\varSigma ){{{V}}^{\rm T}}$

(15)

式中： ${{U}}\Sigma {{{V}}^{\rm T}}$ 是 $({{{Z}}^t} - \dfrac{{{{C}}_2^t}}{{{\mu ^t}}})$ 的奇异值分解； ${S_{1/{\mu ^t}}}( \cdot )$ 是软阈值算子^[7]，定义为

$ {S_\lambda }(x) = \left\{ {\begin{array}{*{20}{l}} {x - \lambda }&{ {,} \; \; x > \textit{λ} }\\ {x + \lambda }&{ {,} \; \; x < \textit{λ} }\\ {0 }&{{,} \; \; - \textit{λ} < x < \textit{λ} } \end{array}} \right. $

更新Q 　当固定其他变量时，式(12)的目标函数可以表示为Q的函数，即

$ L=\mathop {\min }\limits_{{Q}} {\lambda _2}{\left\| {{{D}} \odot {{Q}}} \right\|_1} + \dfrac{{{\mu ^t}}}{2}\left\| {{{Q}} - \left({{{Z}}^{t + 1}} - \dfrac{{{{C}}_3^t}}{{{\mu ^t}}}\right)} \right\|_F^2 \\ $

(16)

可以通过逐元素的方法进行更新。显然，式(16)可以等效为解决 $n \times N$ 个子问题。对于第i行第j列元素K_ij，式(16)的最优解是

$ {{Q}}_{ij}^{t + 1}=\mathop {\arg \min }\limits_{{{{Q}}_{ij}}} {\textit{λ}_2}{{{D}}_{ij}}\left| {{{{Q}}_{ij}}} \right| + \dfrac{{{\mu ^t}}}{2}{({{{Q}}_{ij}} - {M_{ij}})^2} = {S_{\frac{{{\textit{λ} _2}{{{D}}_{ij}}}}{{{\mu ^t}}}}}({{{M}}_{ij}}) $

(17)

更新S　当固定其他变量时，式(12)的目标函数可以表示为S的函数，即

$L=\mathop {\min }\limits_{{S}} {\textit{λ} _3}g({{S}}) + + \frac{{{\mu ^t}}}{2}\left\| {{{S}} - \left({{I}} - {{{Z}}^{t + 1}} - \frac{{{{C}}_1^t}}{{{\mu ^t}}}\right)} \right\|_F^2$

然后令 $\varGamma ={{I}} - {{{Z}}^{t + 1}} - \dfrac{{{{C}}_1^t}}{{{\mu ^t}}}$ ，则S^t+1的第i行为

$ {S^{t + 1}}(i,;) = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{\left\| {{\varGamma ^i}} \right\|}_2} - \frac{{{\textit{λ} _3}}}{{{\mu ^t}}}}}{{{{\left\| {{\varGamma ^i}} \right\|}_2}}}{\varGamma ^i}}&{ {\rm if} \; {{\left\| {{\varGamma ^i}} \right\|}_2} > \dfrac{{{\textit{λ} _3}}}{{{\mu ^t}}}}\\ 0&{{\rm if} \; {{\left\| {{\varGamma ^i}} \right\|}_2} \leqslant \dfrac{{{\textit{λ} _3}}}{{{\mu ^t}}}} \end{array}} \right. $

(18)

其中 ${\varGamma ^i}$ 是矩阵 ${{\textit{Γ}}} $ 的第i行。

在优化变量J、Z、Q和S之后，ADMM算法还需要更新拉格朗日乘子C₁、C₂、C₃以及参数 $\mu $ ，以便更快地收敛。

最后，本文通过谱聚类算法进行聚类，即先通过构造亲和矩阵来找到数据的低维嵌入，然后使用k均值聚类来实现最后的聚类。

3 算法的性质分析 3.1 算法的收敛性分析

为了解决目标函数，即式(10)，本文使用了迭代更新ADMM算法，如第2章所示。下面证明LBKA的收敛性。

定理1　LBKA是收敛的。

证明　经典的ADMM算法主要解决下述问题：

$\begin{gathered} \mathop {\min }\limits_{{{z}} \in {{{\bf{R}}}^n},{{w}} \in {{{\bf{R}}}^m}} f({{z}}) + h({{w}}) \\ {\rm{s}}{\rm{.t}}{\rm{.}}\; {{Rz}} + {{Tw}}=\mu \\ \end{gathered} $

(19)

其中 ${{R}} \in {{{\bf{R}}}^{p \times n}},{{T}} \in {{{\bf{R}}}^{p \times m}},\mu \in {{{\bf{R}}}^p}$ ，f和h是凸函数。

可以看出，式(11)是式(19)的一种特殊情况。经变换，式(12)可以被转换为式(19)。然后，就可以使用ADMM算法以交替方式更新两个原始变量，并迭代地解决式(19)：

$\begin{gathered} {{{Z}}^{t + 1}}=\mathop {\arg \min }\limits_{{{Z}} \in {{{\bf{R}}}^{n \times N}}} {L_\mu }({{Z}},{{{W}}^t},{{{C}}^t}) \\ {{{W}}^{t + 1}}=\mathop {\arg \min }\limits_{{{W}} \in {{{\bf{R}}}^{m \times N}}} {L_\mu }({{{Z}}^{t + 1}},{{W}},{{{C}}^t}) \\ {{{C}}^{t + 1}}={{{C}}^t} + \mu ({{{RZ}}^{t + 1}} + {{TW}}{^{t + 1}} - {{U}}) \\ \end{gathered} $

(20)

它与第2章中的算法1有相同的更新步骤。因此，式(11)是经典ADMM问题的一个特殊情况。算法1中所提出的优化算法相当于两块ADMM，它的收敛性在理论上得以证明。

3.2 算法的复杂度分析

定理2　根据第2章可以看出LBKA的总时间复杂度为 ${O_k}(2{n^2}N + {n^2}d + nN)$ ，其中n为训练样本数，N为样本总数，d为样本维数，k为迭代次数。

证明　算法1的主要过程在第二节算法迭代的前3步给出，因为需要进行奇异值分解(SVD)和矩阵运算。因此，当训练样本数n和样本总数N非常大时，LBKA的时间复杂度会很高。特别是计算矩阵 ${{J}} \in {{\bf{R}}^{n \times N}}$ 的SVD分解需要 $O({n^2}N)(N>n)$ 的复杂度。在这里需要注意的是，由于要计算矩阵的逆，迭代更新Z时需要 $O({n^2}N + {n^2}d)$ 时间，其中d是样本维数。步骤3的时间复杂度是 $O(nN)$ 。因此，LBKA的总时间复杂度为 ${O_k}(2{n^2}N + {n^2}d + nN)$ ，其中k是迭代次数。

相比之下，基于稀疏表示的分类方法(如SRC和LatLRR)的时间复杂度是 $O({n^2}(N - n)d)$ ，这要比LBKA慢很多。LRLR^[15]和LRRR^[16]等回归方法的计算复杂度为 $O(nd + {n^2}d)$ ，比LBKA快一点，但计算精度比LBKA低。基于低秩和稀疏表示的方法(如RPCA)需要同时计算特征矩阵的SVD并求解软阈值问题。LBKA的总体时间复杂度与低秩稀疏表示方法的总时间大致相同。

4 实验结果与分析 4.1 实验环境

本文在两个数据集上分别测试了人脸识别和字符识别两个识别任务，然后与一些最先进的识别方法进行比较，包括基于稀疏表示的方法，如LRC^[17]，基于低秩标准的方法，如RPCA，和传统的分类方法，如支持向量机(SVM)^[18]，以及块对角低秩表示方法(block-diagonal low-rank representation, BDLRR)^[5]。

为了保证LBKA和对比算法在实验中的参数相同，本文使用交叉验证方法重新实现了所有算法。因此，本文使用的所有算法都是在相同条件下进行测试的，所以实验结果是真实可靠的。

4.2 评估标准

本文使用2个常用的度量指标对实验结果进行评估，分别是准确度(Accuracy)和兰德指数(Rand index)：

1)Accuracy(Acc):

${\rm Acc}=\mathop {\max }\limits_\pi \frac{1}{n}{\Sigma _{ij}}{{X}}_{\pi (i)j}^t{{{X}}_{ij}}$

其中 $\pi $ 是n个组的排列，X^t和X分别是分类准确的样本和所有测试样本，如果点j属于簇i则它们的第i个条目等于1，否则为0。

2)Rand index(RI):

$\rm {RI=\frac{{TP + TN}}{{TP + TN + FP + FN}}}$

其中，TN表示不同类样本的被分到不同个集合，FN表示同一类样本的被分到不同个集合。

4.3 人脸识别

在本节中，本文使用扩展YaleB^[5]面部图像数据集进行实验。

扩展的YaleB数据库：由38个人的2 414个人脸图像组成，每个人有59~64个亮度不同的图像。在实验过程中，随机选择其中的20、25、30、35个图像作为训练集，其余的作为测试集进行实验。

图2为LBKA获得的扩展YaleB数据库的数据表示，从中可以看出获得的矩阵为对角分块结构。表1和表2分别是扩展的YaleB数据库中不同算法的识别精度和兰德指数。从中可以看出，在使用不同数量的训练集进行实验时，LBKA都能得到最好的识别结果。而且随着样本数量的增加，LBKA的识别精度也随之逐渐提高。

4.4 字符识别

本文选取Char74K场景人物图像数据集^[5]来进行实验。在以往的模式识别任务中，由于场景图像十分复杂，很难将想要识别的文本分离出来，而LBKA中对类内类外的处理有助于对场景中字符进行提取。本文将LBKA与其他先进的字符识别算法进行对比，包括CoHOG^[19]、RTPD^[20]，PHOG^[21]、MLFP^[22]和BDLRR^[5]。

Char74K数据库：该数据库总共包含7万4千幅图像，所以叫Chars74K。本文主要关注其中英语字符和数字的识别。本文在实验中只使用了原数据库的一个小子集Char74K-15，其中包含15个训练样本和15个测试样本。

表3和表4列出了LBKA和其他字符识别方法的识别准确度和兰德指数，从中可以看出，LBKA识别的准确度和兰德指数都是最高的。

4.5 实验分析

首先，与两种数据集上的对比算法相比，LBKA进行模式识别时更加准确。

其次，LBKA比现有的识别算法更准确，这说明扩大了对角块和非对角块之间的差异的同时增强了相关数据表示，能够获得更好的识别效果。

第三，LBKA在识别数量有限的样本时比其它对比算法都好。主要原因是LBKA具有稀疏，低秩和分块三大特性。低秩可以有效地挖掘数据相关的基础结构，并且揭示数据矩阵的全局潜在结构；稀疏能够寻找最近的数据子空间；块对角表示能够发掘数据内在结构并阐明数据点的最近子空间。

随着迭代次数的增加LBKA的相对误差在减小，并且总值在图3所示的60次迭代后基本没有变化，这验证了LBKA具有收敛性。图4表示LBKA关于参数和的性能变化。可以看出，LBKA对和的变化值不敏感。更具体的说，当参数处于一个合理范围内时，LBKA准确度较高，这说明增加类内类外约束是十分有必要的。

5 结束语

本文给出了低秩分块矩阵的相关定义，说明了矩阵分解的应用。分析了核近似的优点，并提出了低秩分块矩阵核近似的方法。最后将该方法在人脸识别和字符识别中进行比较。结果表明，所提出的低秩分块矩阵分解算法在收敛速度和近似精度上都具有一定的优势。未来工作包括：

1)从矩阵的核近似出发，对原有的子空间聚类算法进行改进，提高分块的速度和准确性，从而提升算法找到全局最优解的能力。

2)通过与多种矩阵分解算法的比较，观察提出的低秩分块矩阵的核近似算法的表现，进一步分析算法的可行性。

3)本文通过实验证明了LBKA在人脸识别和字符识别等领域的效果比传统识别算法更好，接下来可以研究其在回归、聚类、排序等方面的应用。