2. 山西大学 计算智能与中文信息处理教育部重点实验室,山西 太原 030006
2. Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education University, Shanxi University, Taiyuan 030006, China
传统的监督学习问题中,数据只有一个类别标记变量,通常称为单标记学习问题[1]。但是,在现实世界当中,每个数据对象可能同时具有多个语义项[2]。例如,一个新闻可以包含经济、体育、股票等几个主题;一个图片可以有蓝天、湖泊、树木、绿地等多个语义标注。因此,对于多标记数据的学习,成为近些年的机器学习领域关注重点之一。
在多标记学习当中,数据的高维性会严重影响多标记分类器的性能,因而降维是解决该问题的重要手段。多标记的特征降维的方法主要有特征提取和特征选择。特征提取是通过转换或者映射的方法,将原始高维特征空间转换到一个新的低维特征空间的过程。
常见的特征提取方法包括线性判别分析(LDA)[3]、特征抽取方法(MDDM)[4]和多标记潜在语义搜索(MLSI)[5]。特征提取方法虽然能够提高多标记分类器的分类性能,但该方法形成的新特征空间失去了原特征的语义。不同于特征提取的方法,特征选择方法是根据一定的评价准则,从原始的特征空间中选择一个(组)最优特征子集的过程。常见的评价准则有依赖性度量[6]、信息度量[7-8]、距离度量[9-12]等。例如,Spolaôr等[12]基于二元关系方法和标签幂集法,提出了基于多标记的特征选择方法(RF-BR、RF-LP、IG-BR、IG-LP);Li等[8]利用最大化信息增益来度量特征和标记的相关性,提出基于信息增益的多标记特征选择算法(IGML)等。
在模糊粗糙集模型中,使用模糊相似关系代替经典粗糙集模型中的等价关系,进而衡量两个对象之间的不可区分性。在模糊粗糙集理论中,模糊区分矩阵概念被提出[13-14],Chen等[15]提出了一种基于区分矩阵中的最小元素集的属性约简方法,提高了属性约简的计算效率。Dai等[16]提出一种基于模糊粗糙集合的最大区分对的属性约简算法。
在多标记学习中,每个样本可能同时隶属于多个标记,标记之间也可能存在着某种关系,因而本文针对多标记学习问题,利用KL散度度量标记间的关系,并定义标记权重。考虑权重情况,定义模糊不一致对,提出一种基于模糊不一致对的多标记属性约简方法(MLAR-FL),并通过实验验证了本文算法的有效性。
1 基本概念给定一个决策表<U,A,D>,其中U={x1,x2,···,xn}为非空有限样本集合,称其为论域,A={a1,a2,···,ap}为非空有限的条件属性集,D为一个决策属性。设B为一个条件属性子集,Ra为由属性a所决定的U上的模糊二元关系,RD为由决策属性D决定的U上的二元关系,uRa(x,y)为由Ra导出的U上的某个二元关系,称为样本x,y在属性a下的模糊不可区分度。N(uRa(x,y))=1−uRa(x,y)表示样本x,y在属性下的模糊可区分度。
定义1[13] 给定一个决策表<U,A,D>,决定一个模糊区分矩阵M′,其中的项定义为
| $M'(x,y) = \{ {a_{N({u_{{R_a}}}(x,y))}}|a \in A,\forall x,y \in U{\rm{\} }}$ |
值得注意的是,上述区分矩阵每个项中的元是一个带有模糊可区分度值的条件属性集。
设B是一个属性子集,相对于决策属性D,样本x和y在B下的满意度(satisfiability)定义为[17]
| $ {\rm{SA}}{{\rm{T}}_{B,D}}(M'(x,y)) = \left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_{a \in B} \{ {u_{{R_a}}}(x,y)\} \; = \mathop {{\rm{max}}}\limits_{a \in B} \{ 1 - {u_{{R_a}}}(x,y)\} , \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;N({u_{{R_D}}}(x,y)) = 1; \\ 0,\;\;N({u_{{R_D}}}(x,y)) = 0 \\ \end{array} \right.\; $ |
总满意度(total satisfiability)定义为
| ${\rm{SAT}}(B) = \frac{{\displaystyle\sum\limits_{x,y \in U,x \ne y} {{\rm{SA}}{{\rm{T}}_{B,D}}(M'(x,y))} }}{{\displaystyle\sum\limits_{x,y \in U,x \ne y} {{\rm{SA}}{{\rm{T}}_{A,D}}(M'(x,y))} }}$ |
性质1[13] 给定一个决策表<U,A,D>,B
1)
2)
则B是决策表<U,A,D>的一个模糊粗糙约简。
为表述方便,在下文中,对a∈A,记
| $\begin{array}{l} {\rm{si}}{{\rm{m}}_a}(x,y) = {u_{{R_a}}}(x,y) \\ {\rm{di}}{{\rm{s}}_a}(x,y) = N({u_{{R_a}}}(x,y)) \\ \end{array} $ |
定义2[15] 给定一个决策表<U,A,D>,模糊区分矩阵中每一项对应于样本对(x,y),则该样本对对应的最大模糊区分属性定义为
| $ {\rm{MD}}{{\rm{A}}_A}D(x,y) = \left\{ \begin{array}{l} \{ a|{\rm{di}}{{\rm{s}}_A}(x,y) = \mathop {\max }\limits_{a \in A} {\rm{di}}{{\rm{s}}_a}(x,y), a \in A\} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{u_{{R_D}}}(x,y) = 0 \\ {\mathit{\Phi}} ,\;\;\;\;\;\;\;\;\;{u_{{R_D}}}(x,y) = 1 \\ \end{array} \right. $ |
对于∀a∈A,其对应的最大模糊区分对定义为
| $ {\rm{MD}}{{\rm{P}}_a}D(U) = \{ (x,y)|a \in {\rm{MD}}{{\rm{A}}_A}D(x,y),(x,y) \in U \times U\} $ |
由于MDAAD(x,y)的对称性,则上式可定义为
| $ \begin{array}{l} {\rm{MDP}}_a^{'}D(U) = \{ ({x_i},{x_j})|a \in {\rm{MD}}{{\rm{A}}_A}D({x_i},{x_j}), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\forall {x_i},{x_j} \in U,i< j\} \\ \end{array} $ |
性质2[16] 给定一个决策表<U,A,D>,若B为一个属性子集,则有
| ${\rm{MDP}}_B^{'}D(U) = \mathop \cup \limits_{\forall a \in B} {\rm{MDP}}_a^{'}D(U)$ |
性质3[16] 给定一个决策表<U,A,D>,若属性子集B满足:
1)
2)
则B为决策表的一个约简。
2 多标记属性约简方法给定一个多标记决策表S=<U,A,L>,其中U={x1,x2,···,xn}为样本集,A={a1,a2,···,ad}为条件属性集,L={l1,l2,···,lq}为标记集。若样本x拥有标记li,则li(x)=1,否则li(x)=0。
定义3[18] KL散度(Kullback-Leibler divergence)。设p和q是概率空间
| ${{{D}}_{{\rm{KL}}}}(p||q) = \sum\limits_{x \in {\mathit{\Omega }}} {p(x)\log \frac{{p(x)}}{{q(x)}}} $ | (1) |
式中DKL(p||q)称为分布p关于分布q的KL散度。
KL散度常被用来度量两个随机变量的差异。其值越小表明用p拟合q差异越小。
给定一个多标记决策表S=<U,A,L>,对于∀li∈L,将其看做{0,1}上的随机变量,对应的概率分布记为Hi,对∀li,lj∈L,则lj相对于li的KL散度定义为
| ${D_{ij}}({H_i}||{H_j}) = \sum\limits_{k \in \left\{ {0,1\} } \right.} {{H_i}(k)\log \frac{{{H_i}(k)}}{{{H_j}(k)}}} $ | (2) |
对一个多标记决策表S=<U,A,L>,标记空间L中的标记的重要性各不相同。为此,可以利用KL散度,定义这些标记的权重。
定义4 给定一个多标记决策表S=<U,A,L>,对∀li∈L,定义其在决策表上的权重为
| $ {w_i} = \left( {1{\rm{ - }}\frac{{\displaystyle\sum\limits_{j = 1}^q {{D_{ij}}({H_i}||{H_j})} }}{{\displaystyle\sum\limits_{i = 1}^q {\displaystyle\sum\limits_{j = 1}^q {{D_{ij}}({H_i}||{H_j})} } }}} \right)\cdot\frac{{\rm{1}}}{{{{q - 1}}}},\;1 < i < q $ | (3) |
由于KL散度可以用来度量标记之间的差异,因而用一个标记去拟合所有的标记,若总差异越小,则总损失越小,说明该标记在整个标记空间越重要,则该标记的权重越大。
例1 表1给定一个多标记模糊决策表<U,A,L>,U={x1,x2,x3,x4,x5},A={a1,a2,a3},L={l1,l2,l3}。
| 表 1 一个多标记决策表 Tab.1 A multi-label decision table |
由表1可得标记变量的概率分布:p1(1)=3/5,p1(0)=2/5;p2(1)=2/5,p2(0)=3/5;p3(1)=1/5,p3(0)=4/5;
根据定义3可得标记之间KL散度为
| $\begin{array}{l} {{{D}}_{{\rm{21}}}} = {p_2}(0)\log \dfrac{{{p_2}(0)}}{{{p_1}(0)}} + {p_2}(1)\log \dfrac{{{p_2}(1)}}{{{p_1}(1)}} \\ {{{D}}_{{\rm{23}}}} = {p_2}(0){\rm{log}}\dfrac{{{p_2}(0)}}{{{p_{\rm{3}}}{\rm{(0)}}}} + {p_2}(1)\log \dfrac{{{p_2}(1)}}{{{p_3}(1)}} \end{array} $ |
同理可得D21、D31、D13、D23;根据定义4,可得标记权重:
| $ \begin{array}{l} {w_1} = \left(1 - \dfrac{{\displaystyle\sum\limits_{j = 1}^3 {{D_{1j}}({H_1}||{H_j})} }}{{\displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {{D_{ij}}({H_i}||{H_j})} } }}\right)\cdot\dfrac{1}{2} = 0.284\;7\\ {w_2} = \left(1 - \dfrac{{\displaystyle\sum\limits_{j = 1}^3 {{D_{1j}}({H_1}||{H_j})} }}{{\displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {{D_{ij}}({H_i}||{H_j})} } }}\right)\cdot\dfrac{1}{2} = 0.413\;6\\ {w_3} = \left(1 - \dfrac{{\displaystyle\sum\limits_{j = 1}^3 {{D_{1j}}({H_1}||{H_j})} }}{{\displaystyle\sum\limits_{i = 1}^3 {\displaystyle\sum\limits_{j = 1}^3 {{D_{ij}}({H_i}||{H_j})} } }}\right)\cdot\dfrac{1}{2} = 0.301\;7 \end{array}$ |
定义5 给定一个多标记决策表S=<U,A,L>,对应的标记权重集W={w1,w2,···,wq},定义决策表上的模糊不一致样本对集合为
| $ {\rm{FI}}{{\rm{P}}_A}D = {\rm{\{ }}(x,y)|\exists {l_k} \in L{\rm{,}}{l_k}{\rm{(}}x) \ne {l_k}(y),x{\rm{,}}y \in U{\rm{\} }} $ | (4) |
模糊一致样本对集合为
| $ {\rm{FC}}{{\rm{P}}_A}D = {\rm{\{ (}}x{\rm{,}}y{\rm{)|}}\forall {l_k} \in L{\rm{,}}{l_k}(x) = {l_k}(y),x{\rm{,}}y \in U{\rm{\} }}\; $ | (5) |
对于每一个模糊不一致样本对,定义
| $ {\rm{LL}}(x,y) = \{ i|{l_i}(x) \ne {l_i}(y),1 \leqslant i \leqslant q,(x,y) \in {\rm{FI}}{{\rm{P}}_A}D\} $ | (6) |
为模糊不一致样本对包含的不一致的标签集合。同时定义:
| $ {\rm{DIS}}(x,y) = \left\{ \begin{array}{l} \displaystyle\sum\limits_{k \in {\rm{LL}}(x,y)} {{w_k}} , \;\quad \; (x,y) \in {\rm{FI}}{{\rm{P}}_A}D\\ 0,\;\;(x,y) \in {\rm{FC}}{{\rm{P}}_A}D \end{array} \right. $ | (7) |
为模糊不一致样本对的模糊度量矩阵,若DIS(x,y)为0,则表示x,y在标签集合上为一致的,若DIS(x,y)不为0,则表示x,y在标签集合上为不一致的,且值越大,则表示样本之间的不一致程度越大。
定义6 给定一个多标记决策表S=<U,A,L>,则对于每一个属于模糊度量矩阵的样本对而言,区分样本的最大模糊不相似属性集定义为
| ${\rm{MD}}{{\rm{A}}_A}D(x,y) = \left\{ \begin{array}{l} \{ a|{\rm{di}}{{\rm{s}}_A}(x,y) = \mathop {{\rm{max}}}\limits_{a \in A} {\rm{di}}{{\rm{s}}_a}(x,y), a \in A\} , \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{DIS}}(x,y) \ne 0 \\ \varphi ,\;\;\;\;\;\;\;\;\;\;\;{\rm{DIS}}(x,y) = 0 \\ \end{array} \right.$ | (8) |
性质4 对于最大模糊不相似属性集有
| ${\rm{MD}}{{\rm{A}}_A}D(x,y) = {\rm{MD}}{{\rm{A}}_A}D(y,x)$ | (9) |
证明 由于模糊区分矩阵具有对称性。根据定义6,性质4可得证。
定义7 给定一个多标记决策表S=<U,A,L>,则对于∀a∈A,可定义在该属性上的最大模糊不相似样本对为
| $ \begin{array}{c} {\rm{MDFI}}{{\rm{P}}_a}D(U) = \{ (x,y)|a \in {\rm{MD}}{{\rm{A}}_A}D(x,y), \\ (x,y) \in {\rm{FI}}{{\rm{P}}_A}D\} \end{array} \!\!\!\!\!$ | (10) |
定义8 给定一个多标记决策表S=<U,A,L>,∀B⊆A,定义:
| ${\rm{MDFI}}{{\rm{P}}_B}D(U) = \bigcup\limits_{\forall a \in B} {{\rm{MDFI}}{{\rm{P}}_a}D(U)} $ | (11) |
性质5 给定一个多标记决策表S=<U,A,L>,对于属性子集B,则
| ${\rm{MDFI}}{{\rm{P}}_B}D(U) \subseteq {\rm{MDFI}}{{\rm{P}}_A}D(U),\forall B \subseteq A$ | (12) |
证明 根据定义8,性质5可得证。
性质6 给定一个多标记决策表S=<U,A,L>,∀B'⊆B⊆A,MDFIPB'D (U)⊆MDFIPBD (U)。
证明 由于B′⊆B,所以假设B′={a1,a2,a3
| $ \begin{array}{c} {\rm{MDFI}}{{\rm{P}}_{B'}}D{\rm{(}}U{\rm{)}} = {\rm{MDFI}}{{\rm{P}}_{{a_1}}}D{\rm{(}}U{\rm{)}}\bigcup \\ {{\rm{MDFI}}{{\rm{P}}_{{a_2}}}D{\rm{(}}U{\rm{)}}} \bigcup {{\rm{MDFI}}{{\rm{P}}_{{a_3}}}D(U)} \\ {\rm{MDFI}}{{\rm{P}}_B}D(U) = {\rm{MDFI}}{{\rm{P}}_{{a_1}}}D(U)\bigcup {{\rm{MDFI}}{{\rm{P}}_{{a_2}}}D(U)} \bigcup \\ {{\rm{MDFI}}{{\rm{P}}_{{a_3}}}D(U)\bigcup {{\rm{MDFI}}{{\rm{P}}_{{a_4}}}D(U)} } = \\ {\rm{MDFI}}{{\rm{P}}_{B'}}D{\rm{(}}U{\rm{)}}\bigcup {{\rm{MDFI}}{{\rm{P}}_{{a_4}}}D(U)} \\ \end{array} $ |
由并运算的性质可得,
由上述性质可得,|MDFIPBD (U)|在属性子集B上,满足单调性。
性质7 给定一个多标记决策表S=<U,A,L>,对于∀B′⊆B,∀a∈C–B′,则
| $ \left| {{\rm{MDFI}}{{\rm{P}}_{B'}}D(U)} \right| \leqslant \left| {{\rm{MDFI}}{{\rm{P}}_B}D(U)} \right| $ | (13) |
| $ \left| {{\rm{MDFIP}}{{\rm{C}}_{B'}}D(U)} \right| \leqslant \left| {{\rm{MDFI}}{{\rm{P}}_{B' \cup \{ a\} }}D(U)} \right| $ | (14) |
性质8 给定一个多标记决策表S=<U,A,L>,MDFIPB'D (U)=MDFIPAD (U),当且仅当|MDFIPB'D (U)|=|MDFIPAD (U)|。
证明 根据性质5中式(12),可得MDFIPB′D(U)=MDFIPAD
(U)
性质9 给定一个多标记决策表S=<U,A,L>,若属性子集B满足条件:
1)
2)
则B为该决策表的一个约简。
证明
| $\begin{array}{c} {\rm{SAT}}(B) = \\ \dfrac{{\displaystyle\sum\limits_{x,y \in U,x \ne y} {{\rm{SA}}{{\rm{T}}_{B,L}}(M'(x,y))} }}{{\displaystyle\sum\limits_{x,y \in U,x \ne y} {{\rm{SA}}{{\rm{T}}_{A,L}}(M'(x,y))} }} = \\ \dfrac{{\displaystyle\sum\limits_{x,y \in U,x \ne y} {\left\{ \begin{array}{l} \mathop {\max}\limits_{a \in B} \{ 1 - {u_{Ra}}(x,y)\} ,\;\;\qquad {\rm{DIS}}(x,y) \ne 0\\ 0,\;\;\;\;\;\;\;\;\;\;\;{\rm{DIS}}(x,y) = 0 \end{array} \right.} }}{{\displaystyle\sum\limits_{x,y \in U,x \ne y} {\left\{ \begin{array}{l} \mathop {\mathop {\max}\limits_{a \in A} \{ 1 - {u_{Ra}}(x,y)\} ,\;\;\qquad {\rm{DIS}}(x,y)}\limits_{} \ne 0\\ 0,\;\;\;\;\;\;\;\;\;\;\;{\rm{DIS}}(x,y) = 0 \end{array} \right.} }}\end{array}$ |
若B为一个约简,则相当于
| $ \begin{array}{c} {\rm{SAT}}(B) = {\rm{SAT}}(A) \Leftrightarrow \\ \displaystyle\sum\limits_{x,y \in U,x \ne y} {\left\{ \begin{array}{l} \mathop {\max}\limits_{a \in B} \{ 1 - {u_{Ra}}(x,y)\} ,\;\;\qquad {\rm{DIS}}(x,y) \ne 0 \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{DIS}}(x,y) = 0 \\ \end{array} \right.} = \\ \displaystyle\sum\limits_{x,y \in U,x \ne y} {\left\{ \begin{array}{l} \mathop {\mathop {\max}\limits_{a \in A} \{ 1 - {u_{Ra}}(x,y)\} ,\;\;\qquad {\rm{DIS}}(x,y)}\limits_{} \ne 0 \\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{DIS}}(x,y) = 0 \\ \end{array} \right.} \Leftrightarrow \\ \displaystyle\sum\limits_{x,y \in U,x \ne y} {{\rm{di}}{{\rm{s}}_a}} (x,y),\forall a \in {\rm{MD}}{{\rm{A}}_B}D = \\ \displaystyle\sum\limits_{x,y \in U,x \ne y} {{\rm{di}}{{\rm{s}}_a}(x,y)} ,\forall a \in {\rm{MD}}{{\rm{A}}_A}D \Leftrightarrow \\ {\rm{MDFI}}{{\rm{P}}_B}D(U) = {\rm{MDFI}}{{\rm{P}}_A}D(U) \\ \end{array} $ |
同理可得:
| $\begin{array}{c} {\rm{SAT}}(B')< {\rm{SAT}}(B) \Leftrightarrow \\ {\rm{MDFI}}{{\rm{P}}_{B'}}D(U) \subset {\rm{MDFI}}{{\rm{P}}_B}D(U) \\ \end{array} $ |
定义9 给定一个多标记决策表S=<U,A,L>,∀a∈A,简化后的最大模糊相似对定义为
| $ \begin{array}{c} {\rm{MDFIP}}_a^{'}D(U) = \{ ({x_i},{x_j})|a \in {\rm{MD}}{{\rm{A}}_A}D({x_i},{x_j}),\\ \forall {x_i},{x_j} \in U,i < j\} \end{array} $ | (15) |
| $ \begin{array}{c} {\rm{MDFIP}}_a^*D({{U}}) = \{ ({x_i},{x_j})|a \in {\rm{MD}}{{\rm{A}}_A}D({x_i},{x_j}),\\ \forall {x_i},{x_j} \in U,i > j\} \end{array} $ | (16) |
定义10 给定一个多标记决策表S=<U,A,L>,对于一个属性子集B⊆A,则其对应的约简后的最大模糊相似对定义为
| $ {\rm{MDFIP}}_B^{'}D(U) = \bigcup\limits_{a \in B} {{\rm{MDFIP}}_a^{'}D(U)} $ | (17) |
| $ {\rm{MDFIP}}_B^*D(U) = \bigcup\limits_{a \in B} {{\rm{MDFIP}}_a^*} D(U) $ | (18) |
性质10 给定一个多标记决策表S=<U,A,L>,∀B'⊆B⊆A,MDFIP'B'D (U)⊆MDFIP'BD (U)。
证明 根据定义10,显然,∀a∈B,MDFIP′BD (U)是由MDFIP′aD (U)组成的,因而可得,MDFIP′B′D (U)⊆MDFIP′BD (U),∀B′⊆B,即证。
性质11 给定一个多标记决策表S=<U,A,L>,MDFIP′BD (U)=MDFIP′AD (U),当且仅当|MDFIP′BD (U)|=|MDFIP′AD (U)|
证明 根据定义10和性质7,性质11可得证。
性质12 给定一个多标记决策表S=<U,A,L>,属性子集B是满足条件:
1)
2)
则B是该决策表的一个约简。
证明 根据定义10和性质7,性质12可得证。
定义11 给定一个多标记决策表S=<U,A,L>,B⊆A,∀a∈A−B,在条件属性子集B的基础上,属性a相对于标签集L的重要度定义为
| $ {\rm{sig}}(a,B,L) = \sum\limits_{x,y \in U,x \ne y} {{\rm{DIS}}(x,y),(x,y) \in {\rm{MDFIP}}_a^{'}D(U)} $ | (19) |
根据前文所述,本文所设计的基于模糊不一致对的属性约简算法如下所示。
算法1 基于模糊不一致对的属性约简算法(MLAR-FL)
输入 决策表<U,A,L>;
输出 约简后的属性子集。
1) red=Ø;R=A;z=1;
2) for l∈L
3)根据式(3)计算标记的权重;
4) end for
5)初始化:DIS,MDFIPA′D(U)
6) while z=1
7) B=red;
8) for ∀a∈R
9)根据式(19)计算属性的重要性;
10) end for
11)取最大属性重要性的的属性值yk,对应属性为k;
12) if yk>0
13) red=red+k;R=R−k;
14) DIS(x,y)=0,(x,y)∈MDFIPk′ D(U);
15) else
16) z=0;
17) end if
18) end while
在实验中,对于数值型数据的属性a,样本x,y之间的模糊二元关系的度量为
| $\begin{array}{l} {u_{{R_a}}}(x,y) = \max (\min (\dfrac{{f(a,y) - f(a,x) + {\sigma _a}}}{{{\sigma _a}}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\dfrac{{f(a,x) + {\sigma _a} - f(a,y)}}{{{\sigma _a}}}),0) \\ \end{array} $ |
对于符号型数据的属性a,样本x,y之间的模糊二元关系的度量为
| ${u_{{R_a}}}(x,y) = \left\{ \begin{array}{l} 0,\;\qquad\;f(a,y) \ne f(a,x) \\ 1,\;\qquad\;f(a,y) = f(a,x) \\ \end{array} \right.$ |
采用8个Mulan数据集进行实验,数据集描述如表2所示。
| 表 2 数据集描述 Tab.2 Description of datasets |
本文采用十折交叉验证,将提出的方法基于模糊不一致对的属性约简算法(MLAR-FL)与下列算法进行对比实验。基于标记关系的模糊粗糙模型提出的属性约简算法(FRMFS)[18];基于模糊粗糙集的多标签属性约简算法(MLFRS)[19],MLFRS算法对标记不同的样本进行抽样,重新定义上下近似,从而得到新的特征选择的模型;基于标记权重的多标签属性约简算法(LWMF)[20];基于ReliefF的多标签属性约简算法(RF-ML)[21],其利用分类间隔赋予特征权重,再利用特征对于标记的区分行进行特征选择。将5种属性约简方法在多标签分类的评价指标上进行比较。由于LWMF算法和RF-ML算法为排序算法,最后分类器选择特征的个数由MLFRS最后得到的特征个数决定。
3.2 评价指标在多标签分类当中,我们常使用6种指标来评价分类学习算法的好坏,即Average Precision(AP)、Ranking Loss(RL)、Hamming Loss(HL)、Coverage(CV)、One-error(OE)、Micro-F1(F1)[19]。
令测试集为
Average Precision(AP):用于考察所有样本的预测标记排序中位置排在该样本标记前面的标记仍属于该样本标记的概率的平均,数值越大,说明算法的性能越好,定义为
| $\begin{array}{c} {\rm{avgPre}}(f) = \\ \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\dfrac{1}{{\left| {{R_i}} \right|}}} \displaystyle\sum\limits_{l \in {R_i}} {\dfrac{{\{ k|{\rm{ran}}{k_f}({x_i},k) \leqslant {\rm{ran}}{k_f}({x_i},l),k \in {R_i}\} }}{{{\rm{ran}}{k_f}({x_i},l)}}} \\ \end{array} $ |
Ranking Loss(RL):用来考察所有样本的不相关标记的排序在相关标记前面的概率的平均,数值越小,说明算法的性能越好,定义为
| $ \begin{array}{c} {\rm{rLoss}}(f) = \dfrac{1}{n}\displaystyle\sum\limits_{i = 1}^n {\dfrac{1}{{\left| {{R_i}} \right|\left| {\mathop {{R_i}}\limits^ - } \right|}}} \cdot \\ {\rm{|}}\{ (l,k)|{\rm{ran}}{k_f}({x_i},l) \geqslant {\rm{ran}}{k_f}({x_i},k),(l,k) \in {R_i} \times \mathop {{{\rm{R}}_{\rm{i}}}}\limits^ - \} {\rm{|}} \\ \end{array} $ |
Hamming Loss(HL):用于度量样本在单个标记上的误分类的情况,数值越小,说明算法的性能越好,定义为
| ${\rm{hLoss}}(h) = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{1}{L}} \sum\limits_{l = 1}^L {\left[ {{h_l}({x_i}) \ne {Y_{il}}} \right]} $ |
Coverage(CV):用于度量样本遍历所有与其相关的类别标记平均所需要的步数,数值越小,说明算法的性能越好,定义为
| ${\rm{coverage}}(f) = \frac{1}{n}\sum\limits_{i = 1}^n {\mathop {\max }\limits_{l \in {R_i}} } ({\rm{ran}}{k_f}({x_i},l)) - 1$ |
One-error(OE):用于表示排名靠前的标签不在正确的标签集中的样本比例,数值越小,说明算法的性能越好,定义为
| ${\rm{OE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left[ { { {(\arg {{\max }_{{y_i} \in L}}f({x_i},{y_i}))} \notin Y_i^{'}} } \right]} $ |
Micro-F1(F1):用于衡量在不同标签下的预测情况,数值越大,说明算法的性能越好,定义为
| ${\rm{F1}} = \frac{{2 \times \displaystyle\sum\limits_{i = 1}^n {\mathop {\left\| {Y_i^{'} \cap {y_i}} \right\|}\nolimits_1 } }}{{\displaystyle\sum\limits_{i = 1}^n {\mathop {\left\| {{y_i}} \right\|}\nolimits_1 + \displaystyle\sum\limits_{i = 1}^n {\mathop {\left\| {Y_i^{'}} \right\|}\nolimits_1 } } }}$ |
本文采用MLKNN[22]分类器进行实验,设置K取10,平滑系数取1。
表3~8列出了在8个数据集上,MLAR-FL算法与其余4种算法在6种评价指标上面的实验结果。对于给定的评价指标,符号“↓”表示该评价指标的取值越小,分类性能越优;符号“↑”表示该评价指标的取值越大,分类性能越优。当中,最优结果使用加粗表示。
| 表 3 AP评价指标下各算法的性能比较(↑) Tab.3 Performance comparison of algorithms under AP evaluation index |
| 表 4 RL评价指标下各算法的性能比较(↓) Tab.4 Performance comparison of algorithms under RL evaluation index |
| 表 5 HL评价指标下各算法的性能比较(↓) Tab.5 Performance comparison of algorithms under HL evaluation index |
| 表 6 CV评价指标下各算法的性能比较(↓) Tab.6 Performance comparison of algorithms under CV evaluation index |
| 表 7 OE评价指标下各算法的性能比较(↓) Tab.7 Performance comparison of algorithms under OE evaluation index |
| 表 8 F1评价指标下各算法的性能比较(↑) Tab.8 Performance comparison of algorithms under F1 evaluation index |
1)对于AP、RL、HL、CV、OE指标上MLAR-FL算法在8个数据集合上得到的分类精度都高于其余4种算法;对于F1指标,computer、health、reference数据集上,MALR-FL算法低于其余算法。因而,对于6个评价指标而言,MLAR-FL在前5个评价指标上的表现很好,在F1指标上,得到的结果并非最好。
2)从统计的8个数据集合,6个评价指标,总共48个对比结果可以看出,MLAR-FL的胜率为93.75%,总体而言,MLAR-FL的分类情况较好。
总之,在8个数据集上,MLAR-FL的分类性能比其余4种算法的分类性能好。但是即使得到的特征子集的分类性能好,也不能从整体上了解算法的分类性能在特征数目变化时的变化情况。
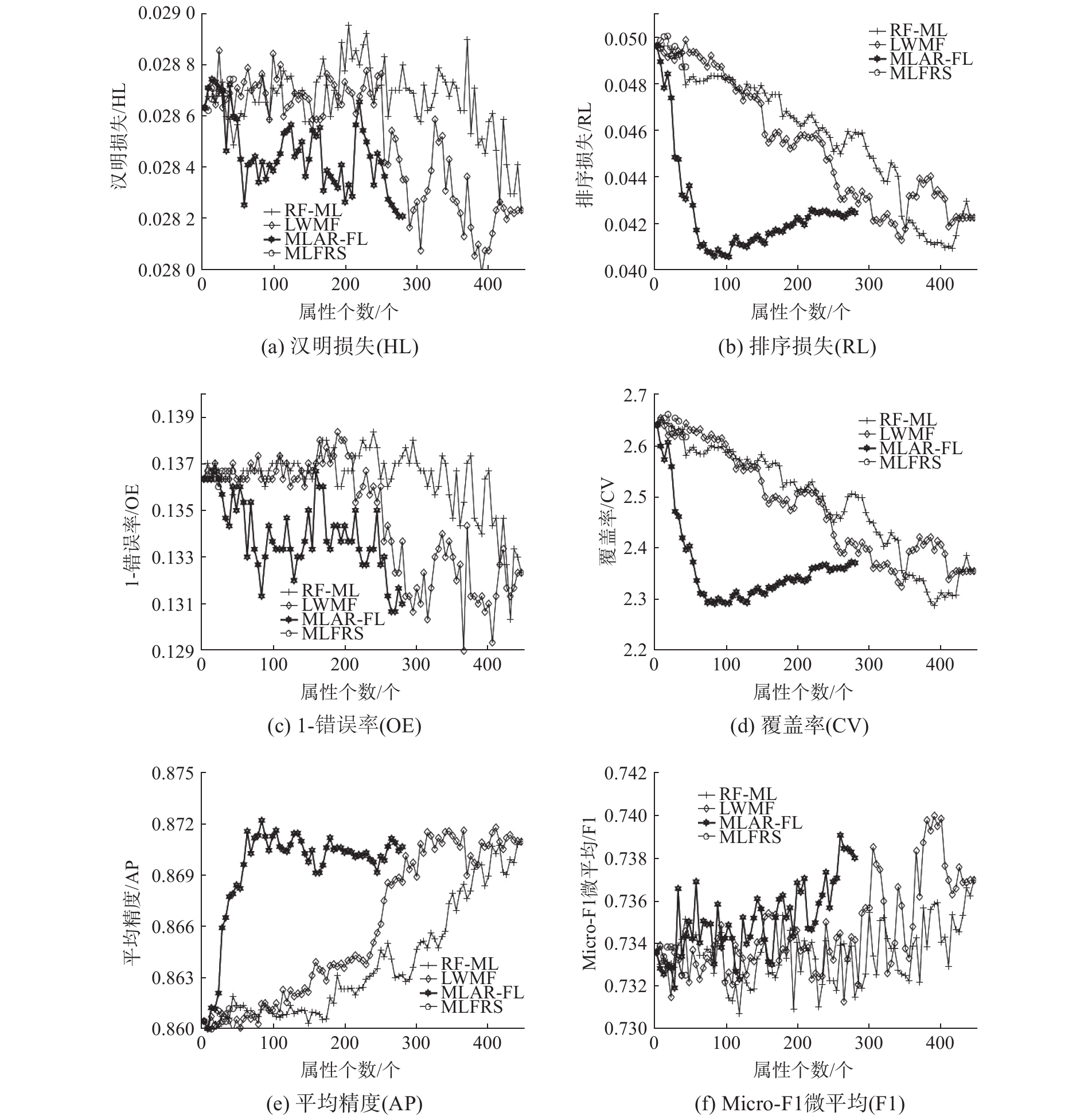
为了能够从整体上直观地对比各个算法的分类性能随着特征数目的变化情况,图1~3分别给出了在数据集business、reference、science上面6种性能评价指标AP、HL、RL、OE、CV、F1下,分类性能随着特征数目的变化趋势。由于FRMFS约简时得到的属性子集数目较少,因而比较分类特征随属性数目的变化趋势时,只考虑MLFRS、LWMF、RF-ML、MLAR-FL 4种算法。
|
Download:
|
| 图 1 数据集business上6种评价指标下各算法的分类性能的变化情况 Fig. 1 Changes in classification performance of each algorithm under six evaluation indicators on the business data set | |

|
Download:
|
| 图 2 数据集reference上6种评价指标下各算法的分类性能的变化情况 Fig. 2 Changes in classification performance of each algorithm under six evaluation indicators on the reference data set | |

|
Download:
|
| 图 3 science数据集上6种评价指标下各算法的分类性能的变化情况 Fig. 3 Changes in classification performance of each algorithm under six evaluation indicators on the science data set | |
1)在science数据集上,对于6种评价指标而言,MLAR-FL的分类性能比其余3种算法的分类性能好,并且在很大程度上优于其余算法;在business数据集上,MLAR-FL的分类性能在AP、RL、CV 3种评价指标上,在小于225个属性个数的情况下,分类情况较大程度上优于其余3种算法,在OE、HL、F1 3种评价指标上,分类性能存在波动,但是仍然在小于225个属性个数的情况下,优于其余3种算法;在reference数据集合上,对于AP、CV、OE、RL、HL 5种评价指标而言,MLAR-HL的分类性能很明显地优于RF-ML算法,与LWMF和MLFRS算法的分类性能比较接近,但仍在很小程度上优于这两种算法,对于F1评价指标而言,LWMF的分类性能与MLAR-FL的分类性能比较接近,且在小于300个属性个数的情况下,LWMF的分类性能优于这两种算法。
2)对于不同的数据集,得到的约简的属性个数不同,但是可以发现,在小于250个属性个数的情况下,MLARF-FL的分类性能普遍优于其余3种算法,同时,随着属性个数的增加,分类性能越来越优,而在达到最高值后,会趋于平稳或者变差,因为越来越多的属性加入到特征空间当中,可能会与原先的属性之间存在一定的影响,影响样本相关性的判断,从而影响分类结果。
以上结果表明,融合标记关系定义模糊不一致对的MLAR-FL算法的分类性能优于其余4种算法,得到的属性子集在一定程度上提高了多标记分类的分类性能。
4 结束语针对多标记数据属性约简算法中为考虑标记关系的问题,本文提出了基于模糊不一致对的多标签属性约简算法,利用KL散度定义标记权重,结合标记权重定义模糊不一致对,使用最大区分对方法进行属性约简。在8个数据集,使用6个评价指标的实验验证了本文所提算法MLAR-FL的有效性,本文不仅使用新的方式度量标记关系,也证明融合该种标记关系在多标记属性约简算法中可以更好地提高约简结果的效能。同时,实验发现基于样本对的属性约简算法普遍存在时间及空间开销过大问题,因而如何提升此类算法的效率将是下一步需要研究的工作。
| [1] |
李华, 李德玉, 王素格, 等. 基于粗糙集的多标记专属特征学习算法[J]. 小型微型计算机系统, 2015, 36(23): 2730-2734. LI Hua, LI Deyu, WANG Suge, et al. Multi-label learning with label-specific features based on rough sets[J]. Journal of Chinese computer systems, 2015, 36(23): 2730-2734. (  0) 0)
|
| [2] |
ZHANG Minling, ZHOU Zhihua. A review on multi-label learning algorithms[J]. IEEE transactions on knowledge and data engineering, 2014, 26(8): 1819-1837. DOI:10.1109/TKDE.2013.39 ( 0) 0)
|
| [3] |
HOTELLING H. Relations between two sets of variates[J]. Biometrika, 1936, 28(3/4): 321-377. DOI:10.2307/2333955 ( 0) 0)
|
| [4] |
SUN Liang, JI Shuiwang, YE Jieping, et al. Multi-label dimensionality reduction[M]. Florida: CRC Press, 2013: 20–22.
( 0) 0)
|
| [5] |
YU Kai, YU Shipeng, TRESP V. Multi-label informed latent semantic indexing[C]//Proceedings of the 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. New York, USA, 2005: 258–265.
( 0) 0)
|
| [6] |
ZHANG Lingjun, HU Qinghua, DUAN Jie, et al. Multi-label feature selection with fuzzy rough sets[C]//Proceedings of 9th International Conference on Rough Sets and Knowledge Technology. Shanghai, China, 2014: 121–128.
( 0) 0)
|
| [7] |
LIN Yaojin, HU Qinghua, LIU Jinghua, et al. Multi-label feature selection based on neighborhood mutual information[J]. Applied soft computing, 2016, 38: 244-256. DOI:10.1016/j.asoc.2015.10.009 ( 0) 0)
|
| [8] |
LI Ling, LIU Huawen, MA Zongjie, et al. Multi-label feature selection via information gain[C]//Proceedings of the 10th International Conference on Advanced Data Mining and Applications. Guilin, China, 2014: 345–355.
( 0) 0)
|
| [9] |
LI Yuwen, LIN Yaojin, LIU Jinghua, et al. Feature selection for multi-label learning based on kernelized fuzzy rough sets[J]. Neurocomputing, 2018, 318: 271-286. DOI:10.1016/j.neucom.2018.08.065 ( 0) 0)
|
| [10] |
李京政, 杨习贝, 王平心, 等. 模糊粗糙集的稳定约简方法[J]. 南京理工大学学报, 2018, 42(1): 68-75. LI Jingzheng, YANG Xibei, WANG Pingxin, et al. Stable attribute reduction approach for fuzzy rough set[J]. Journal of Nanjing University of Science and Technology, 2018, 42(1): 68-75. (  0) 0)
|
| [11] |
SPOOLAÔR N, CHERMAN E A, MONARD M C, et al. Filter approach feature selection methods to support multi-label learning based on ReliefF and information gain[C]//Proceedings of 21th Brazilian Symposium on Artificial Intelligence on Advances in Artificial Intelligence. Curitiba, Brazil, 2012: 72–81.
( 0) 0)
|
| [12] |
ESCALERA S, RADEVA P, PUJOL O. Complex salient regions for computer vision problems[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, USA, 2007: 18–23.
( 0) 0)
|
| [13] |
JENSEN R, SHEN Qiang. New approaches to fuzzy-rough feature selection[J]. IEEE transactions on fuzzy systems, 2009, 17(4): 824-838. DOI:10.1109/TFUZZ.2008.924209 ( 0) 0)
|
| [14] |
JENSEN R, SHEN Qiang. Fuzzy-rough sets assisted attribute selection[J]. IEEE transactions on fuzzy systems, 2007, 15(1): 73-89. DOI:10.1109/TFUZZ.2006.889761 ( 0) 0)
|
| [15] |
CHEN Degang, ZHANG L, ZHAO Suyun, et al. A novel algorithm for finding reducts with fuzzy rough sets[J]. IEEE transactions on fuzzy systems, 2012, 20(2): 385-389. DOI:10.1109/TFUZZ.2011.2173695 ( 0) 0)
|
| [16] |
DAI Jianhua, HU Hu, WU Weizhi, et al. Maximal-discernibility-pair-based approach to attribute reduction in fuzzy rough sets[J]. IEEE transactions on fuzzy systems, 2018, 26(4): 2174-2187. DOI:10.1109/TFUZZ.2017.2768044 ( 0) 0)
|
| [17] |
郭荣超, 李德玉, 王素格. 基于标记关系的模糊粗糙集模型[J]. 模式识别与人工智能, 2017, 30(10): 952-960. GUO Rongchao, LI Deyu, WANG Suge. Fuzzy rough set model based on label relations[J]. Pattern recognition and artificial intelligence, 2017, 30(10): 952-960. (  0) 0)
|
| [18] |
李晓艳, 张子刚, 张逸石, 等. 一种基于KL散度和类分离策略的特征选择算法[J]. 计算机科学, 2012, 39(12): 224-227. LI Xiaoyan, ZHANG Zigang, ZHANG Yishi, et al. KL-divergence based feature selection algorithm with the separate-class strategy[J]. Computer science, 2012, 39(12): 224-227. DOI:10.3969/j.issn.1002-137X.2012.12.053 (  0) 0)
|
| [19] |
LIN Yaojin, LI Yuwen, WANG Chenxi, et al. Attribute reduction for multi-label learning with fuzzy rough set[J]. Knowledge-based systems, 2018, 152: 54-61. ( 0) 0)
|
| [20] |
林梦雷, 刘景华, 王晨曦, 等. 基于标记权重的多标记特征选择算法[J]. 计算机科学, 2017, 44(10): 289-295, 317. LIN Menglei, LIU Jinghua, WANG Chenxi, et al. Multi-label feature selection algorithm based on label weighting[J]. Computer science, 2017, 44(10): 289-295, 317. DOI:10.11896/j.issn.1002-137X.2017.10.052 (  0) 0)
|
| [21] |
SPOLAÔR N, CHERMAN E A, MONARD M C, et al. ReliefF for multi-label feature selection[C]//Proceedings of 2013 Brazilian Conference on Intelligent Systems. Fortaleza, Brazil, 2013: 6–11.
( 0) 0)
|
| [22] |
ZHANG Minling, ZHOU Zhihua. ML-KNN: a lazy learning approach to multi-label learning[J]. Pattern recognition, 2007, 40(7): 2038-2048. DOI:10.1016/j.patcog.2006.12.019 ( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


