油田运输管线属于油田的生命线，地下管线错综复杂，容易存在渗漏等情况对环境造成污染。近年来许多学者对管线污油泄漏问题进行了相关研究，王翔宇^[1]提出长距管线无人机总体设计方案，详细论述了无人机巡线高效、灵活、不受地形限制等优势，能够有效解决人为盗油案件。张彪等^[2]提出基于物联网技术的油田管线智能巡检系统，此系统论述了物联网技术在油田管线中使用智能巡检，并且阐述了油田管线巡检的必要性以及应用价值。目前管线巡检应用无人机、物联网等技术能够提高管线巡检效率，但是对污油区域的识别精度不高，无法真正地实现自动识别污油^[3]。从上面的分析中不难看出利用无人机平台对地面管线进行巡检是监测石油泄漏和污染的有效手段，但无人机在每执行一次巡检任务时会随机采集几千张图像，由人工进行筛选污油区域会增加人工成本以及搜索时间，所以对无人机采集的图片进行自动阈值分割就显得十分重要和迫切，这项工作能够使污油区域更直观地显现出来，及时发现污油区域，处理污油渗漏情况，保护环境。

二维Renyi熵分割方法无法根据图像的改变进行变量调整，导致对部分图像进行分割时未能达到最优分割效果，并且计算时间长。针对上述问题，许多学者利用智能优化算法对二维熵中的变量进行全局寻优，本文则通过改进的萤火虫寻优实现对复杂图像的分割。马英辉等^[4]利用混沌布谷鸟算法优化二维Renyi灰度熵的阈值选取，从而降低Renyi熵算法的计算法复杂度。陈超等^[5]利用狼群算法对二维最大熵进行优化，可以快速准确地对图像中感性目标进行分割。2008年，Yang xin-she^[6]提出了一种多模式的萤火虫优化算法，通过在预期的优化空间中使用点来模拟自然界中的萤火虫个体。萤火虫具有趋光性，模仿此特性，使算法具备全局搜索能力。算法本身的改进主要针对萤火虫的位移、亮度参数和运动策略。对于萤火虫算法，算法的收敛速度和最终得到的最优解的精度直接由萤火虫的飞行步长决定。因此，许多学者对萤火虫步长的更新进行了相关的改进研究。刘家昆等^[7]提出了具有最大和最小荧光值的萤火虫算法，限制荧光素变化的范围，以避免算法后期收敛速度和局部最小值等问题。Coelho L D S等^[8]在萤火虫算法中应用了混沌思想，将混沌序列映射到参数a和r，便于产生局部最优解。通过以上分析，萤火虫算法具有鲁棒性强、整体结构简单、易于实现、全局寻优能力强等优点^[9-11]，为解决污油图像分割问题提供有效可行的寻优策略。

鉴于萤火虫算法的快速全局搜索能力和二维Renyi熵阈值分割方法的较好分割效果，本文采用萤火虫算法对二维Renyi熵函数中的变量进行优化。并利用混沌非周期性、遍历性、随机性的特点优化初始值，用Kent混沌初始化二维Renyi熵中变量，使得变量能够更加接近真实状态。在混沌中细搜索优秀的萤火虫，随机再生相对较差的萤火虫，因此在一定程度上保持了多样性，更好地寻找最优解，即污油图像的分割阈值，快速、高效及精准地对污油图像进行分割，获得清晰的污油区域，从而更好地解决管线渗漏等工程问题。

1 改进的萤火虫优化算法 1.1 萤火虫算法

萤火虫算法利用萤火虫的向光的特性，通过寻找具有最大亮度的萤火虫^[12]来求解问题的目标函数。通过迭代和位置更新，找到亮度最强的萤火虫个体，从而进行全局优化。

1)萤火虫相对亮度为

$I = {I_0} \times {{\rm e}^{ - \gamma {r_{ij}}}}$

式中： ${I_0}$ 为最大的荧光亮度；γ为吸光能力系数； ${r_{ij}}$ 为两个萤火虫之间的空间距离。

2)萤火虫的吸引度为

$\beta = {\beta _0} \times {{\rm e}^{ - \gamma {r_{ij}}}}$

式中 $\;{\beta _0}$ 为萤火虫间的最大的相互吸引的强度。

3)萤火虫i向萤火虫j移动的位置更新公式为

${x_i} = {x_j} + \beta ({x_i} - {x_j}) + {\alpha _1} \times ({\rm rand} - 0.5)$

式中： ${x_i}$ ， ${x_j}$ 为萤火虫位置； ${\alpha _1}$ 为步长因子； ${\rm rand}$ 为 $[0,1]$ 上服从均匀分布的随机因子； ${\alpha _1} \times ({\rm rand} - 0.5)$ 为扰动项，避免算法过早进入最优。

1.2 混沌优化策略

本文采用Kent混沌映射^[13]，该映射在区间(0，1)服从均匀分布，具有更加均匀的搜索效果，其数学表达式为

${x_{n + 1}} = \left\{ {\begin{aligned} & {\frac{{{x_n}}}{\beta },0 < {x_n} < \beta } \\ & {\frac{{(1 - {x_n})}}{{(1 - \beta )}},\beta < {x_n} < 1} \end{aligned}} \right.$

(1)

其中，控制参数 $\beta \in (0,1)$ ，Kent映射的Lyapunov指数大于0，映射在区间 $(0,1)$ 中分布较为均匀，有很好的遍历性。由于受到计算机有限字长和有限精度的影响，参数 $\;\beta = 0.4$ ，并且数值计算采用浮点双精度。

在混沌空间 $(0,1)$ 中映射出优化值，代入式(1)得到混沌序列，然后根据比例变换将混沌序列恢复到解空间，求得适应度函数的值，并将最优值更新原始值。利用式(2)采用动态收缩搜索区域能够有效地加强搜索的速度。

$\left\{ {\begin{array}{*{20}{c}} {{x_{\min ,j}} = \max \{ {x_{\min ,j}},{x_{g,j}} - \rho ({x_{\max ,j}} - {x_{\min ,j}})\} } \\ {{x_{\max ,j}} = \min \{ {x_{\max ,j}},{x_{g,j}} + \rho ({x_{\max ,j}} - {x_{\min ,j}})\} } \end{array}} \right.$

(2)

在此设定第j维变量的搜索范围为 $[{x_{\min ,j}},{x_{\max ,j}}]$ ，当前的最优值为 ${x_{g,j}}$ ，搜索因子为 $\rho $ 。

1.3 基于改进萤火虫的α选取算法

一般实验中二维Renyi熵的参数α取值0.7α，不适用于一些复杂图像，使得参数熵失去原本具有的优势。本文提出对α使用仿生智能搜索算法在其限定空间寻找最优值，将均匀性测度函数 ${U_I}$ 作为目标度函数对参数α进行评测，自动获得最佳参数α和阈值t。

均匀性测度是通过计算分割结果图像的特征参数来评测分割效果，不需要理想图。设在阈值t处进行图像分割，其均匀性测度可按如式(3)~(5)进行计算：

$\widetilde {{f_k}} = \frac{1}{{{N_k}}}\sum\limits_{i \in {R_k}} {{f_i}} $

(3)

$\sigma _k^2 = \frac{1}{{{N_k}}}\sum\limits_{i \in {R_k}} {{{({f_i} - \widetilde {{f_k}})}^2}} $

(4)

${U_I} = 1 - \dfrac{2}{N}\sum\limits_{{R_k} \in I} {\dfrac{{\displaystyle\sum\limits_{i \in {R_k}} {{{({f_i} - \frac{1}{{{N_k}}}\displaystyle\sum\limits_{i \in {R_k}} {{f_i}} )}^2}} }}{{{{({{\max }_{i \in {R_k}}}{f_i} - {{\min }_{i \in {R_k}}}{f_i})}^2}}}} $

(5)

式中： ${N_k}$ 为区域 ${R_k}$ 的像素总和，i为 ${R_k}$ 中的像素， ${f_i}$ 为像素i的灰度值，j为像素i包含在 ${R_k}$ 中的邻域像素。最优的α取值为

$\widehat \alpha = {\rm Arg}\max {U_I}(t(\alpha )),\alpha > 0$

(6)

以式(6)作为改进萤火虫算法的目标函数，用以复杂图像的分割，通过寻优函数自动获得α的取值，可以快速地获得复杂图像的分割阈值。对于二维Renyi熵而言，参数的位数为D=1。一般来说参数 $\alpha \in (0,1)$ 时分割效果最佳，减少算法寻优限定空间。通过实验验证发现参数α限定空间增加时，影响分割的结果不大，但是增加搜索空间给算法的运算时间增加负担。因此，在 $\alpha \in (0,1)$ 内寻找最优值。

2 基于改进萤火虫算法的二维Renyi熵阈值分割方法

本文算法对图像采用二维Renyi熵方法进行图像分割，二维Renyi熵中α变量的初始化使用了Kent混沌，在实际解的区间里把初始粒子更加均匀更加随机的排布。通过引入萤火虫优化机制，将粒子吸引到最优运动中，在混沌中搜索最优的萤火虫，随机地再生出相对较差的萤火虫。传统的萤火虫算法在滤波的算法复杂度和滤波时间上会受到位置更新时需要各粒子间交互作用的影响。为了解决上述问题，本文以粒子群智能算法的思想进行参考，迭代更新，并替换j和i萤火虫进行信息交互。具体方法如下：

1)萤火虫吸引度修正公式：

$\beta = {\beta _0} \times {{\rm e}^{ - \gamma {r_i}}}$

(7)

式中： ${r_i}$ 是粒子i与全局最优值 ${g_{\rm beatk}}$ 间的欧式距离。

2)萤火虫位置修正公式：

$x_k^i = x_k^i + \beta ({g_{\rm bestk}} - x_k^i) + {\alpha _1} \times ({\rm rand} - 0.5)$

(8)

图像的α阶二维Renyi熵定义为

${{H}}(1) = \frac{1}{{1 - \alpha }}\ln \sum\limits_{i = 0}^s {\sum\limits_{j = 0}^t {{{(\frac{{{P_{ij}}}}{{{P_1}(s,t)}})}^\alpha }} } $

${{H}}(2) = \frac{1}{{1 - \alpha }}\ln \sum\limits_{i = s + 1}^{L - 1} {\sum\limits_{j = s + 1}^{L - 1} {{{(\frac{{{P_{ij}}}}{{{P_2}(s,t)}})}^\alpha }} } $

(9)

式中：L为图像灰度级； ${p_{ij}}$ 表示原始图的像素灰度值i和其邻域平均灰度图像像素灰度值j的联合概率密度； ${p_1}$ 、 ${p_2}$ 分别为背景和目标区域的概率。

阈值 $(s,t)$ 对应图像的二维熵定义为

$H(s,t) = H(1) + H(2)$

(10)

二维熵阈值法的最好的分割阈值向量为

$({s^*},{t^*}) = \mathop {\arg \max }\limits_{1 \leqslant s,t \leqslant L - 1} \{ H(s,t)\} $

算法实现步骤如下：

1)产生一个 $(0,1)$ 之间的随机数，代入式(2)应用混沌优化策略获得初始萤火虫。

2)对每个萤火虫的适应度值进行计算。为了求出图像的最优阈值t，利用式(9)、(10)计算第i个萤火虫的Renyi熵( $\alpha = {x_i}$ )；运用式(5)求出其适应度值。通过以上的方法，经过多次运算，求出全部适应度值。

3)模拟萤火虫优化过程并更新萤火虫的位置。根据式(7)计算所有萤火虫的适应度值与全局最优值之间的吸引度；根据式(8)更新萤火虫位置。

4)具有最初10%亮度的萤火虫被优化为用于混沌搜索的优异粒子，具有最后10%亮度的萤火虫被随机产生的新萤火虫取代。

5)若迭代到终止阈值T或者最大迭代次数M，则停止进行迭代；否则，转入步骤2)。

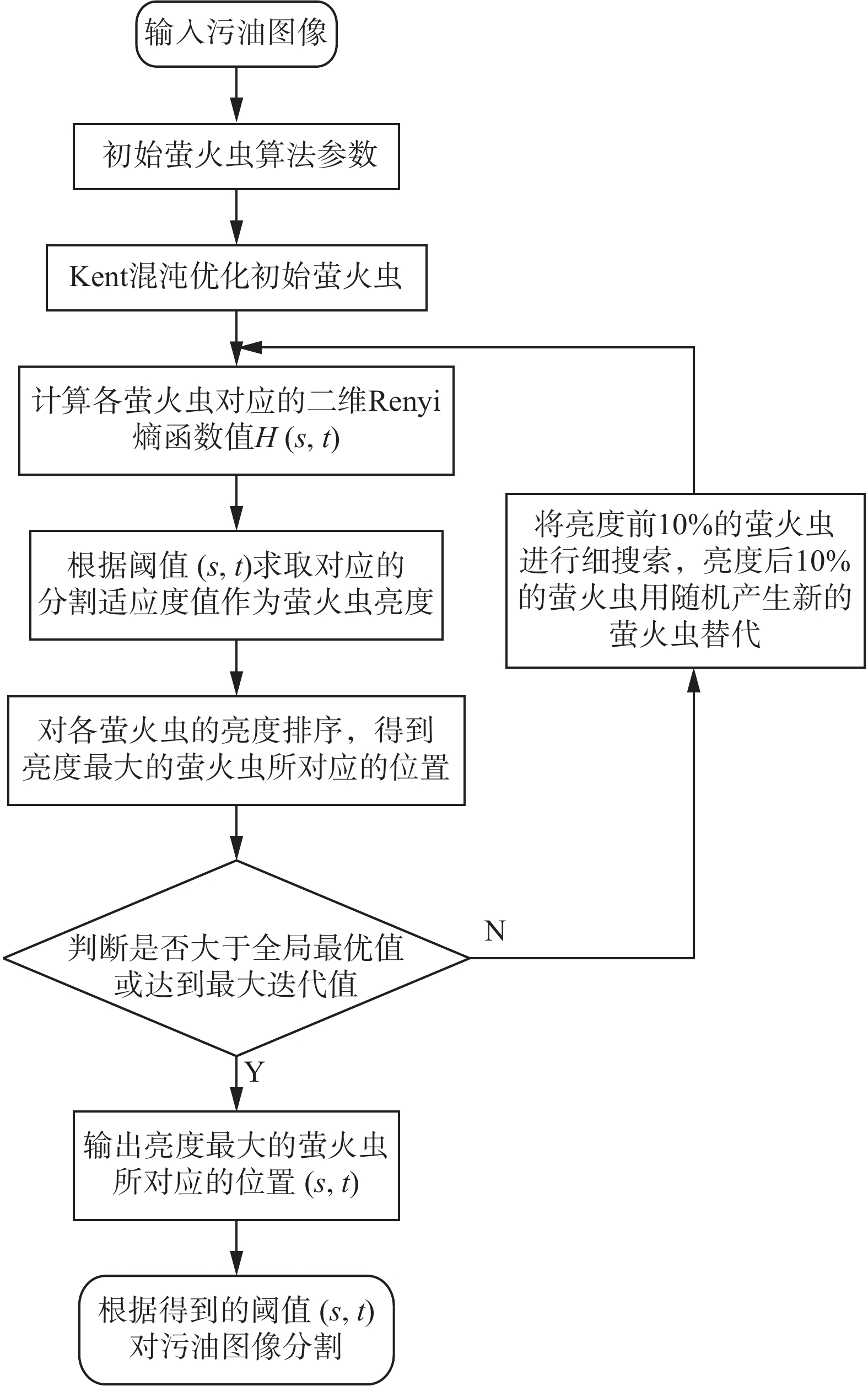
算法实现的整体流程图如图1所示。

3 污油图像分割实验与分析

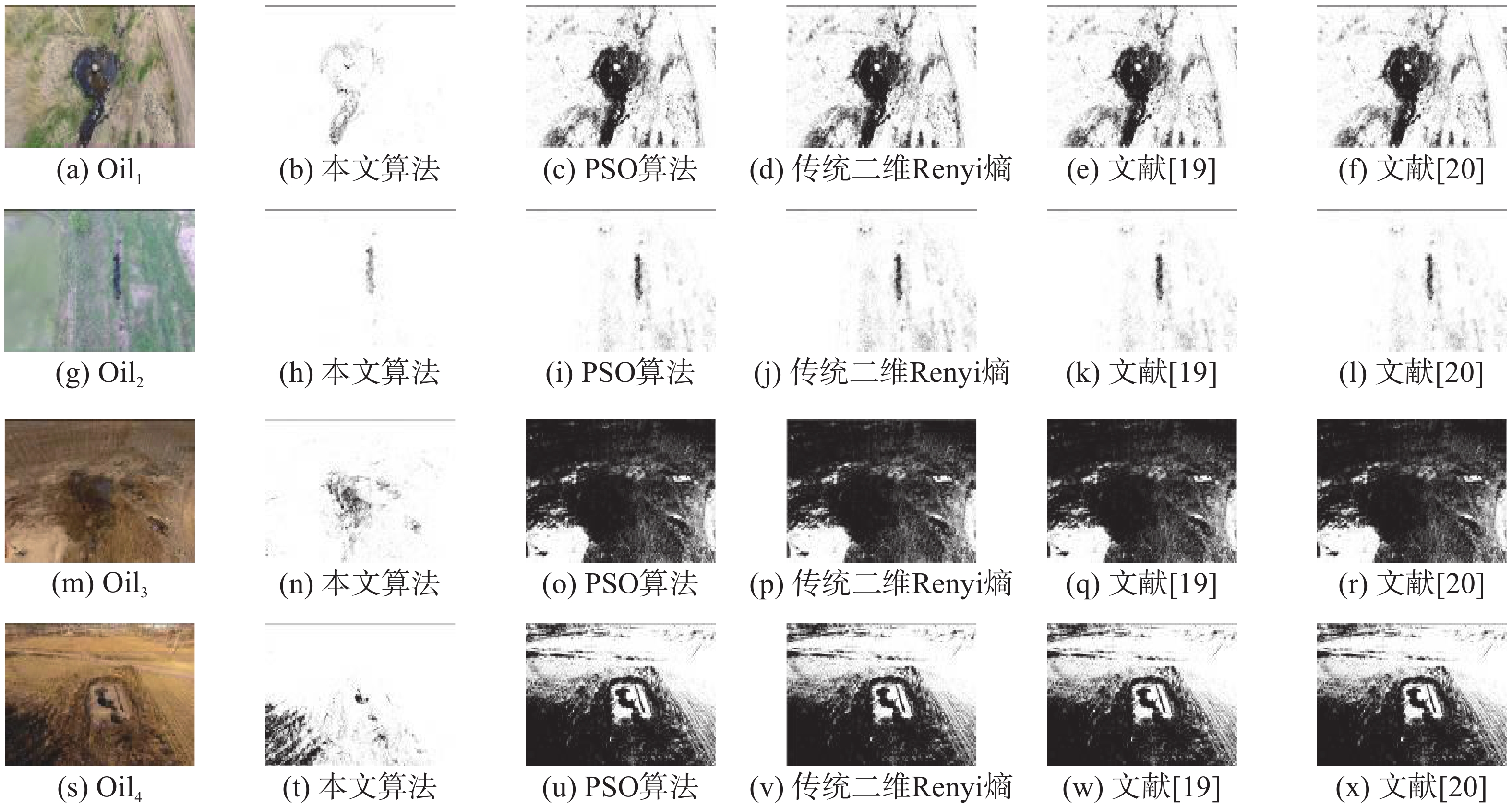
为验证本文算法在实际中的应用效果，将其与二维Renyi熵阈值分割算法、粒子群(PSO)二维Renyi熵分割算法、文献[14-15]进行对比仿真实验，并且给出每种算法的实验结果以及相关数据。为解决污油图像分割的实际问题，选取的污油图像是通过大疆精灵4对大庆油田采油二厂地区进行巡检实地拍摄采集的污油图片，作为本次实验数据样本。首先对采集图像进行预处理，使用自适应霍夫曼方法对可用的图片进行压缩，使图像样本由原来的4 000×2 250压缩到400×225，并且进行归一化处理，对图像采用中值平均滤波的方法进行优化，提高样本的图像质量。实验表明，本方法对不同的污油图像进行分割都十分有效，可以根据不同的图像寻找合适的参数，从而得到满意的分割后的污油图像。限于篇幅，给出4幅典型的污油图像，实验处理结果如图2所示。

粒子群(PSO)Renyi熵分割方法是以PSO为优化函数的二维Renyi熵阈值分割算法。其中，PSO算法用于通过迭代获得最优值，并找到全局最优解，其初始种群 $s = 10$ ；最大迭代次数 $T = 10$ ；学习因子 ${c_1} = 1.499\;5$ ， ${c_2} = 1.499\;5$ ；惯性权重学习因子 $\omega = 1.2$ ；粒子速度学习因子 $v \in (0,1)$ 。

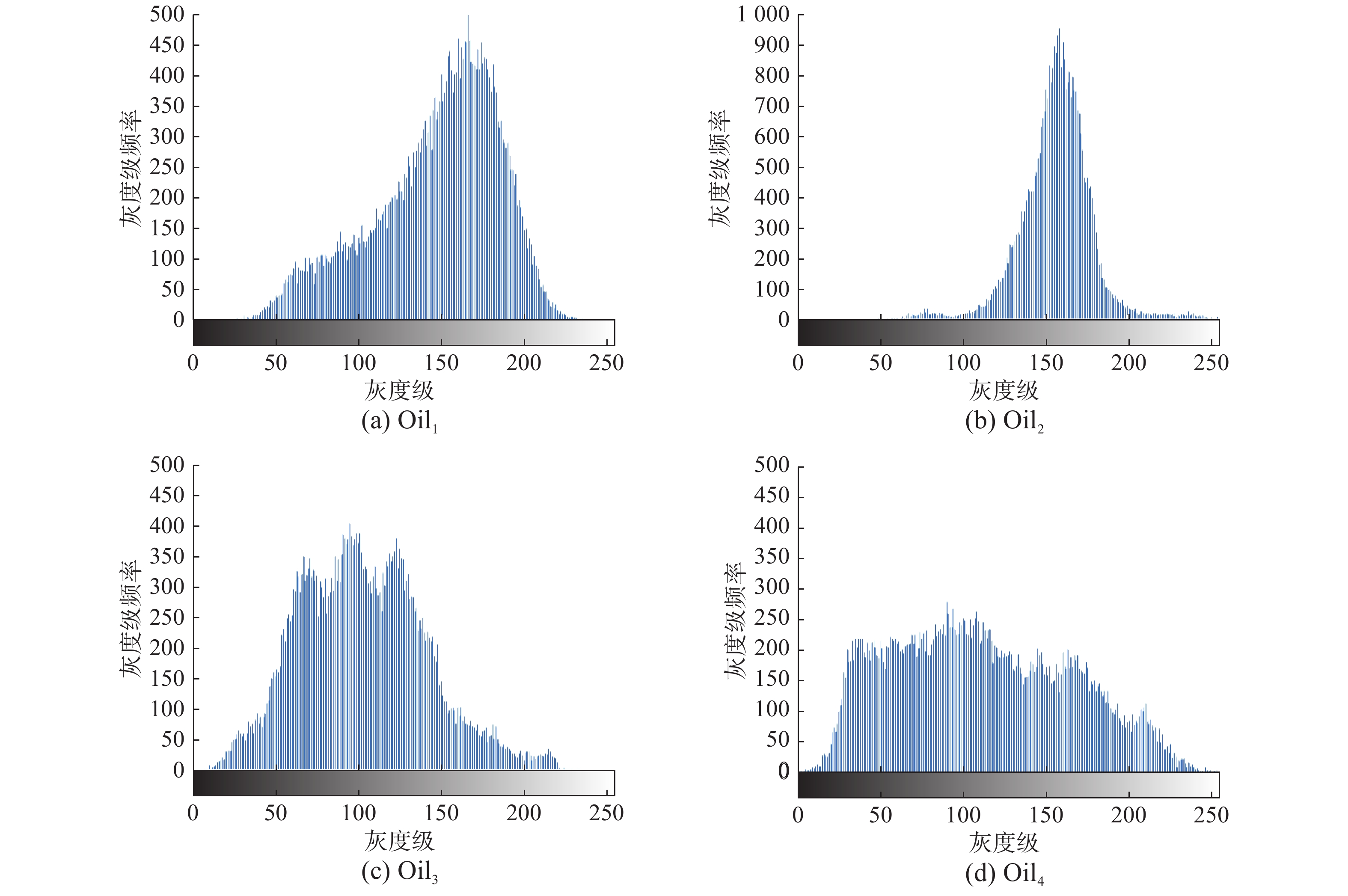
根据图3可以清晰地看到4幅污油图像的灰度直方图，Oil₁和Oil₂两张图片的灰度值对比度较大，常规分割方法可以较好地对图像进行分割；而Oil₃和Oil₄两张图片的灰度值对比度较小，给传统分割算法带来了较大的困难，下面会根据每张图片的分割效果，对3种算法进行详细分析。

从图3所示的Oil₁和Oil₂图像可以看出，污油与其背景具有较大的差异，3种算法对污油区域进行有效的分割。本文算法分割效果最优，文献[14-15]，PSO二维Renyi熵分割方法效果次之，二维Renyi熵分割方法效果最差。后两种方法对2张图像分割后的图像都存在其他不相干区域，分割的精确度不高，可能将错误的区域判别为污油图像，无法解决实际污油图像分割的问题。其中的Oil₃和Oli₄两幅污油图像，由于目标区域与所拍摄背景的对比度较低导致后两种方法无法精确地找到分割阈值，从而造成过分割，无法生成有效地分割图像，不能有效地提高算法的适应性，无法适应拍摄的污油图像的各种情况。而本文提出的方法能够有效地将污油的轮廓区域提取出来，能够适应无人机拍摄的复杂图像，因此本文方法要优于其他两种分割方法。

为了更加直观地对算法进行评价，将PSNR准则作为定量分析算法性能的指标，计算出各算法的运算时间，如表1所示。

PSNR准则的相关表达式为

${\rm PSNR} = 20\log \left(\frac{{255}}{{\rm RMSE}}\right)(\rm dB)$

(11)

${\rm RMSE} = \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^M {\displaystyle\sum\limits_{j = 1}^N {{{(I(i,j) - \hat I(i,j))}^2}} } }}{{MN}}} $

(12)

其中， $I\left( {i,j} \right)$ 是大小为 $M \times N$ 的原图像； $\hat I\left( {i,j} \right)$ 是大小为 $M \times N$ 的分割后的图像。

对4幅污油图像运用了以下几种算法进行分割处理，表1显示了其运算时间及PSNR值。通过对数据的观察分析可知，虽然在时间上本文的方法不比传统Renyi熵分割速度快，但是在优化算法中比PSO算法时间快。本文方法的PSNR值总体比其他两种方法的值高，说明本文方法能够更加精准地进行污油图像分割。同时，为了观察本文改进的萤火虫算法寻优效果，图4给出了该算法每次迭代时最优的适应度函数曲线，发现该算法对4幅污油图片的寻优效果都较快，改进的萤火虫算法能够快速的寻找到全局最优适应度值。

综上所述，基于改进萤火虫算法的二维Renyi熵分割方法较传统的优化算法时间快，能够实现对不同的污油图片有效的区域分割。

4 结束语

本文提出一种改进萤火虫的二维Renyi熵阈值分割算法，该算法在基于二维Renyi熵分割算法的基础上增加了对变量α进行寻优算法，不仅改进优化传统的萤火虫算法，并且对萤火虫的初始种群运用混沌进行初始化。针对实际工况下采集的污油图像进行准确地分割，无需调整算法的参数，也不需要判别图片的分割效果好坏，此算法尤其适用于分割实际环境中采集的复杂图像，能够准确、高效地完成污油区域分割。经过本文改进的算法，其运算时间及分割精度均有所提高，优于PSO优化算法，分割图像的准确度大大提高，即目标与背景区域差别较小的情况下能够有效地进行阈值分割。实验结果表明本文算法可适用于复杂环境中的污油图像分割，能快速处理不同大小、不同噪声等各种情形。