2. 中国空间技术研究院 钱学森空间技术实验室,北京 100094;
3. 鹏城实验室,深圳 518000;
4. 中国航空工业集团公司 沈阳飞机设计研究所,辽宁 沈阳 110035
2. QIAN Xuesen Laboratory of Space Technology, China Academy of Space Technology, Beijing 100094, China;
3. Peng Cheng Laboratory, Shenzhen 518000, China;
4. Shenyang Aircraft Design and Research Institute, Aviation Industry Corporation of China, Shenyang 110035, China
鸟类群体的有组织飞行(organized flight)大致可分为两种方式[1]:线性编队(line formation)和群集编队(cluster formation)。水禽等大型鸟类主要采用线性编队方式飞行,研究此种方式的研究者主要关注线性编队的成因。鸽子、乌鸫等小型鸟类主要采用群集编队方式飞行,研究此种方式的研究者主要关注群集同步的机理[2-5]。
采用群集编队方式飞行的鸟类其单体智能水平并不高,但无论群集规模大小,可实现群体同步且迅速的飞行转向。在大型群集编队方面,Ballerini等[6]通过立体测量和计算机视觉技术重建同一群体中2 600只欧椋鸟(European starlings/Sturnus Vulgaris)的三维位置后发现鸟群个体间交互依赖于拓扑距离(topological distance),而并非大多数理论模型所假设的模式距离(metric distance),即个体与固定数量(6~7只)的邻居进行交互,而非与固定模式距离内的邻居进行交互。在小型群集编队方面,Nagy等[7]通过高精度微型全球定位系统(global positioning system,GPS)跟踪记录10只原鸽(Columba Livia/homing pigeon/domestic pigeon)的飞行,采用统计物理学方法以系列相关函数定义成对交互中的领导关系,进而发现一个清晰的层级制度:鸽群内个体的平均空间位置与其在层级网络中的飞行领导等级(flight leadership rank)密切相关。从进化角度来说,层级交互模式(hierarchical interaction pattern)比之于平等交互模式(egalitarian interaction pattern)信息传递更快,效率更高[8];此外,具有特定社会结构的层级交互模式可补偿个体导航误差,提高群体导航精度[9];需要说明的是,在不考虑领导者切换的条件下,层级网络可简化为双层领导跟随结构,即仅存在唯一领导者,其余跟随者均以特定时延复制领导者运动,该结构可节约个体运动和通信消耗[10]。与仅由攻击和觅食等个体体能特征决定的啄序等级(pecking order rank)不同[11],飞行领导等级是个体不断优化自身利益的结果,亦是领导、学习以及个人能力综合作用的结果[12]。个体速度[13-14]、路径保真度(route fidelity)[15]以及飞行经验[16-17]均可能决定成对领导关系,进而影响个体飞行领导层级:个体受前方邻居的影响往往高于后方邻居,即飞行速度慢的个体需要牺牲方向决策权来跟随快速个体;路径差异越小表示路径保真度越高,单飞时保真度高的个体在成对飞行时较易成为领导者;具有更多飞行经验的鸽子以较大概率可处于在飞行领导层级中较高的层级。
综上所述,以群集编队飞行时,鸟群内部存在平等交互和层级交互两种模式。平等交互模式下,鸟类个体交互范围或为固定半径内的邻居个体,或为最近固定数量的邻居个体,即服从固定邻居范围(fixed neighborhood region,FNR)模型或固定邻居数量(fixed number of neighbors,FNN)模型。层级交互模式下,鸟类个体跟随具有较高飞行领导层级的其他个体进行飞行。为深入研究自由飞行中鸽群两种交互模式的切换关系,Zhang等[18-19]基于Nagy等[7]记录的鸽群自由飞行实验数据,发现鸽群实际上切换采用上述两种交互模式,即当原鸽个体沿平滑轨迹运动时,其飞行方向趋向跟随邻居平均,而当突然转弯或轨迹曲折时,趋向跟随领导者。
至此,可归纳原鸽归巢机制如下。1)双模式决策原则:鸽群在迁徙过程中,群体飞行决策采用平等交互模式或层级交互模式,平等交互模式下,原鸽个体的飞行决策彼此间相互影响,层级交互模式下,存在至少一个原鸽个体,会对其交互范围内的其他原鸽个体的飞行决策产生较大影响。2)模式切换原则:异构原鸽群体的模式切换与鸽群轨迹曲率呈现一定的关联,当鸽群飞行状态不够平稳时,原鸽个体采用层级交互模式,反之采用平等交互模式。3)优势个体原则:异构原鸽群体内存在可能因某些因素导致的某个或某几个优势原鸽个体,当鸽群处于层级交互模式时,非优势原鸽个体会偏重依赖该类优势个体进行飞行决策。
本文在上述原鸽归巢机制分析基础上,建立鸽群交互模式切换模型,模型对应原鸽归巢机制中的双模式决策原则定义了平等交互模式与层级交互模式下的邻居集合与对齐权重,对应模式切换原则定义了由群体轨迹曲率触发的交互模式切换规则,对应优势个体原则将可获知目标位置和速度信息的原鸽个体视为高层级个体。基于LaSalle不变集理论[20]给出鸽群系统可避免碰撞、实现速度渐近同步、相对位置趋于期望并抵达目标的条件。以序参量衡量鸽群同步性,以序参量衡量鸽群同步性,采用蒙特卡罗仿真测试个体数目、高层级个体数目、个体最大速率对鸽群抵达目标时间以及序参量的影响。
1 鸽群交互模式切换模型考虑
| $\left\{ {\begin{array}{*{20}{c}} {{{{{\dot x}}}_i} = {{{v}}_i}} \\ {{{{m}}_i}{{{{\dot v}}}_i} = {{{u}}_i}} \end{array}} \right.,i = 1,2, \cdots ,N$ | (1) |
式中:
定义鸽群中可获知目标
| ${\rm{mod}}{{\rm{e}}_i} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0,}&{{{\bar K}^t} < {K_{{\rm{switch}}}}} \end{array}}\\ {\begin{array}{*{20}{c}} {1,}&{{{\bar K}^t} \geqslant {K_{{\rm{switch}}}}} \end{array}} \end{array}} \right.$ | (2) |
式中
原鸽个体在不同交互模式下,其交互范围并不相同。首先,定义平等交互模式下原鸽个体
| ${\cal N}_i^1\left( {{t_k}} \right){\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\left\{ {j\left| {\left\| {{{{x}}_{ij}}} \right\| \leqslant R_{{\rm{comm}}.}^1 - R_{\lim }^1,j \ne i} \right.} \right\},}&{k = 0} \end{array}} \\ {\begin{array}{*{20}{c}} {\left\{ {j\left| \begin{array}{l} \left\| {{{{x}}_{ij}}} \right\| \leqslant R_{{\rm{comm}}.}^1, \\ j \in {\cal N}_i^1\left( {{t_{k - 1}}} \right),j \ne i \\ or{\rm{ }}\left\| {{{{x}}_{ij}}} \right\| \leqslant R_{{\rm{comm}}.}^1 - R_{\lim }^1, \\ j \notin {\cal N}_i^1\left( {{t_{k - 1}}} \right),j \ne i \\ \end{array} \right.} \right\},}&{k = 1,2, \cdots N } \end{array}} \end{array}} \right.$ | (3) |
式中:
| ${\cal N}_i^2{\rm{ = }}\left\{ {j\left| {\left\| {{{{x}}_{ij}}} \right\| \leqslant R_{{\rm{comm}}.}^2,j \ne i,j = 1,2, \cdots ,N} \right.} \right\}$ | (4) |
式中
| ${{\cal N}_i}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {{\cal N}_i^1,}&{{\rm mod}{{\rm e}_i}{\rm{ = }}0} \\ {{\cal N}_i^2,}&{{\rm mod}{{\rm e}_i}{\rm{ = }}1} \end{array}} \right.$ | (5) |
原鸽个体
| ${{{u}}_i}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {{{{m}}_i}\left( \begin{array}{l} - {K^{\rm{f}}}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} \\ - {K^{\rm{T}}}{\nabla _{{{{x}}_i}}}V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_{\rm{T}}}} \right\|} \right) \\ - {K^{\rm{V}}}w\displaystyle\sum\limits_{j \in {{\cal N}_i}} {{{{v}}_{ij}}} \\ \end{array} \right),}&{i \in {\rm Upper}} \\ {{{{m}}_i}\left( \begin{array}{l} - {K^{\rm{f}}}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} \\ - {K^{\rm{V}}}\left( \begin{array}{l} \displaystyle\sum\limits_{j \in {{\cal N}_i}\backslash {\rm Upper}} {{{{v}}_{ij}}} \\ {\rm{ + }}w\displaystyle\sum\limits_{j \in {{\cal N}_i} \cap {\rm Upper}} {{{{v}}_{ij}}} \\ \end{array} \right) \\ \end{array} \right),}&{i \notin {\rm Upper}} \end{array}} \right.$ | (6) |
式中:
| $w{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {1,}&{{\rm mod}{{\rm e}_i}{\rm{ = }}0} \\ {w',}&{{\rm mod}{{\rm e}_i}{\rm{ = 1}}} \end{array}} \right.$ | (7) |
式中
| $V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{{\left\| {{{{x}}_{ij}}} \right\|}^2} - {{\left( {{R_{{\rm{desire}}}}} \right)}^2}{\rm{Ln}}\left\| {{{{x}}_{ij}}} \right\|,} {0 \leqslant \left\| {{{{x}}_{ij}}} \right\| \leqslant {R_{{\rm{desire}}}}} \\ {\dfrac{1}{2}{{\left( {{R_{{\rm{desire}}}}\left( \begin{array}{l} R_{{\rm{comm}}.}^1 \\ - \left\| {{{{x}}_{ij}}} \right\| \\ \end{array} \right)/\left( {R_{{\rm{comm}}.}^1 - {R_{{\rm{desire}}}}} \right)} \right)}^2}} - \\ { {{\left( {{R_{{\rm{desire}}}}} \right)}^2}{\rm{ln}}\dfrac{{{R_{{\rm{desire}}}}\left( \begin{array}{l} R_{{\rm{comm}}.}^1 \\ - \left\| {{{{x}}_{ij}}} \right\| \\ \end{array} \right)}}{{R_{{\rm{comm}}.}^1 - {R_{{\rm{desire}}}}}},} \\ \qquad{{R_{{\rm{desire}}}} \leqslant \left\| {{{{x}}_{ij}}} \right\| \leqslant R_{{\rm{comm}}.}^1} \end{array}} \right.$ | (8) |
式中
| $V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_{\rm{T}}}} \right\|} \right){\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {\dfrac{{{{\left( \begin{array}{l} \left\| {{{{x}}_i} - {{{x}}_{\rm{T}}}} \right\| \\ - R_{\lim }^2 \\ \end{array} \right)}^2}}}{2},}&{\left\| {{{{x}}_i} - {{{x}}_{\rm{T}}}} \right\| \geqslant R_{\lim }^2} \\ {0,}&{0 \leqslant \left\| {{{{x}}_i} - {{{x}}_{\rm{T}}}} \right\| < R_{\lim }^2} \end{array}} \right.$ | (9) |
式中:
本节旨在从理论分析角度对鸽群交互模式切换模型同步性展开研究。首先定义鸽群平等交互模式下的有向图
| ${l_{ij}} = \left\{ {\begin{array}{*{20}{l}} { - 1,}&{j \in {{\cal N}_i}} \\ 0,&{j \notin {{\cal N}_i},j \ne i} \\ {\left| {{{\cal N}_i}} \right|,}&{j{\rm{ = }}i} \end{array}} \right.$ | (10) |
式中
定义仅保留高层级个体间连接以及高层级个体与低层级个体间连接的鸽群伪拉普拉斯矩阵
| $l_{ij}^{'} = \left\{ {\begin{array}{*{20}{c}} { - 1,}&{\begin{array}{*{20}{c}} {{\rm{if }}\;j \in {{\cal N}_i},i \in {\rm Upper}} \\ {{\rm{or }}\;j \in {{\cal N}_i} \cap {\rm Upper},i \notin {\rm Upper}} \end{array}} \\ 0,&{\begin{array}{*{20}{c}} {{\rm{if }}\;j \notin {{\cal N}_i},i \in {\rm Upper}} \\ {{\rm{or }}\;j \notin {{\cal N}_i} \cap {\rm Upper},i \notin {\rm Upper}} \end{array}} \\ {\left| {{{\cal N}_i} \cap {\rm Upper}} \right|,}&{j{\rm{ = }}i} \end{array}} \right.$ | (11) |
定义鸽群Lyapunov函数
| $H{\rm{ = }}{H_1} + {H_2}$ | (12) |
其中势能函数
| $\begin{array}{l} {H_1}{\rm{ = }}{K^{\rm{f}}}\displaystyle\sum\limits_{i = 1}^N {\left( {\dfrac{1}{2}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} } \right)} {\rm{ + }} \\ {K^{\rm{T}}}\displaystyle\sum\limits_{i \in {\rm Upper}} {\left( {V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_T}} \right\|} \right)} \right)} \\ \end{array} $ | (13) |
动能函数
| ${H_2}{\rm{ = }}\displaystyle\sum\limits_{i = 1}^N {\left( {\dfrac{1}{2}{{v}}_i^{\rm{T}}{{{v}}_i}} \right)} $ | (14) |
假设1 鸽群初始拓扑
假设2
假设3 鸽群初始能量
假设4 鸽群高层级个体集合
引理1[21] 对于一个动态系统
1)存在正常数
2)对于任意的
则对于
定理1 考虑由
证明 当
| $\begin{gathered} \dot H{\rm{ = }}{K^{\rm{f}}}\displaystyle\sum\limits_{i = 1}^N {\left( {\dfrac{1}{2}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {\left( \begin{gathered} {{v}}_i^{\rm{T}}{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right) {\rm{ + }}{{v}}_j^{\rm{T}}{\nabla _{{{{x}}_j}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right) \end{gathered} \right)} } \right)} {\rm{ + }}\\ \begin{gathered} {{K^{\rm{T}}}\displaystyle\sum\limits_{i \in {\rm Upper}} {\left( {{{v}}_i^{\rm{T}}{\nabla _{{{{x}}_i}}}V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_T}} \right\|} \right)} \right)} + \displaystyle\sum\limits_{i = 1}^N {\left( {{{v}}_i^{\rm{T}}{{{{\dot v}}}_i}} \right)} } {\rm{ = }} \end{gathered} \\ {K^{\rm{f}}}\displaystyle\sum\limits_{i = 1}^N {\left( {{{v}}_i^{\rm{T}}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} } \right)} {\rm{ + }} \\ {K^{\rm{T}}}\displaystyle\sum\limits_{i \in {\rm Upper}} {\left( {{{v}}_i^{\rm{T}}{\nabla _{{{{x}}_i}}}V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_T}} \right\|} \right)} \right)} + \displaystyle\sum\limits_{i = 1}^N {\left( {{{v}}_i^{\rm{T}}{{{{\dot v}}}_i}} \right)} \\ \end{gathered} $ | (15) |
将式(1)和式(6)代入式(15),有:
| $\begin{gathered} \dot H{\rm{ = }}{K^{\rm{f}}}\displaystyle\sum\limits_{i = 1}^N {\left( {{{v}}_i^{\rm{T}}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} } \right)}{\rm{ + }} \\ {K^{\rm{T}}}\displaystyle\sum\limits_{i \in {\rm Upper}} {\left( {{{v}}_i^{\rm{T}}{\nabla _{{{{x}}_i}}}V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_T}} \right\|} \right)} \right)} + \displaystyle\sum\limits_{i = 1}^N {\left( {{{v}}_i^{\rm{T}}\dfrac{{{{{u}}_i}}}{{{m_i}}}} \right)}{\rm{ = }} \\ {K^{\rm{f}}}\displaystyle\sum\limits_{i = 1}^N {\left( {{{v}}_i^{\rm{T}}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} } \right)}{\rm{ + }} \\ {K^{\rm{T}}}\displaystyle\sum\limits_{i \in {\rm Upper}} {\left( {{{v}}_i^{\rm{T}}{\nabla _{{{{x}}_i}}}V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_T}} \right\|} \right)} \right)}{\rm{ + }} \\ \displaystyle\sum\limits_{i \in {\rm Upper}} {\left( {{{v}}_i^{\rm{T}}\left( \begin{gathered} - {K^{\rm{f}}}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} \\ - {K^{\rm{T}}}{\nabla _{{{{x}}_i}}}V_i^{\rm{T}}\left( {\left\| {{{{x}}_i} - {{{x}}_{\rm{T}}}} \right\|} \right) - {K^{\rm{V}}}w\displaystyle\sum\limits_{j \in {{\cal N}_i}} {{{{v}}_{ij}}} \\ \end{gathered} \right)} \right)}{\rm{ + }} \\ \displaystyle\sum\limits_{i \notin {\rm Upper}} {\left( {{{v}}_i^{\rm{T}}\left( \begin{gathered} - {K^{\rm{f}}}\displaystyle\sum\limits_{j \in {\cal N}_i^1} {{\nabla _{{{{x}}_i}}}V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right)} \\ - {K^{\rm{V}}}\left( {\displaystyle\sum\limits_{j \in {{\cal N}_i}\backslash {\rm Upper}} {{{{v}}_{ij}}} {\rm{ + }}w\displaystyle\sum\limits_{j \in {{\cal N}_i} \cap {\rm Upper}} {{{{v}}_{ij}}} } \right) \\ \end{gathered} \right)} \right)} {\rm{ = }} \\ -{K^{\rm{V}}}\left( \begin{gathered} \displaystyle\sum\limits_{i = 1}^N {\left( {{{v}}_i^{\rm{T}}\displaystyle\sum\limits_{j \in {{\cal N}_{\rm{i}}}} {{{{v}}_{ij}}} } \right)} \\ + \left( {w - 1} \right)\left( \begin{gathered}{l} \displaystyle\sum\limits_{i \in {\rm Upper}} {{{v}}_i^{\rm{T}}\displaystyle\sum\limits_{j \in {{\cal N}_i}} {{{{v}}_{ij}}} } \\ + \displaystyle\sum\limits_{i \notin {\rm Upper}} {{{v}}_i^{\rm{T}}\displaystyle\sum\limits_{j \in {{\cal N}_i} \cap {\rm Uppe}{{\rm r}_i}} {{{{v}}_{ij}}} } \\ \end{gathered} \right) \\ \end{gathered} \right) = \\ -{K^{\rm{V}}}{{{v}}^{\rm{T}}}\left( {\left( {{{{L}}_N} + \left( {w - 1} \right){{L}}_N^{'}} \right) \otimes {{{I}}_D}} \right){{v}} \\ \end{gathered} $ | (16) |
由式(7)可知
| $\dot H \leqslant 0,\forall t \in [{t_{q - 1}},{t_q})$ | (17) |
由式(3)可知,若
| $H\left( t \right) \leqslant H\left( {{t_{q - 1}}} \right),\forall t \in [{t_{q - 1}},{t_q})$ | (18) |
即若
由式(3)和假设2可知,在切换时刻
| $V_{ij}^{\rm{f}}\left( {\left\| {{{{x}}_{ij}}} \right\|} \right) \leqslant V_{\max }^{\rm{f}}$ | (19) |
式中
假设在切换时刻
| $H\left( {{t_q}} \right) < {H_{\max }}{\rm{ = }}H\left( {{t_0}} \right) + V_{\max }^{\rm{f}}{\left( {N - 1} \right)^2} < \infty $ | (20) |
式中
由式(18)和式(20)可知,
由假设3可知,
| $\varOmega {\rm{ = }}\left\{ {{{\bar x}} \in {R^{D{N^2}}},{{v}} \in {R^{DN}}\left| {H < {H_{\max }},{H_{\max }} > 0} \right.} \right\}$ | (21) |
式中
由于
| $S{\rm{ = }}\left\{ {{{\bar x}} \in {R^{D{N^2}}},{{v}} \in {R^{DN}}\left| {\dot H{\rm{ = }}0} \right.} \right\}$ | (22) |
此时有
| $\begin{gathered} \dot H{\rm{ = }} - {K^{\rm{V}}}{{{v}}^{\rm{T}}}\left( {\left( {{{{L}}_N} + \left( {w - 1} \right){{L}}_N^{'}} \right) \otimes {{{I}}_D}} \right){{v}} {\rm{ = }} - \\ {K^{\rm{V}}}\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j \in {{\cal N}_i}} {{{({{{v}}_i} - {{{v}}_j})}^2}} }- \\ {K^{\rm{V}}}\left( {w - 1} \right)\displaystyle\sum\limits_{i \in {\rm Upper}} {\displaystyle\sum\limits_{j \in {{\cal N}_i}} {{{({{{v}}_i} - {{{v}}_j})}^2}} } = 0 \\ \end{gathered} $ | (23) |
则式(23)成立当且仅当
| ${{{u}}_1}{\rm{ = }}{{{u}}_2}{\rm{ = }} \cdots {\rm{ = }}{{{u}}_N}$ | (24) |
由式(8)可知,
| ${{u}}{\rm{ = }}\left[ {\begin{gathered} {\left( \begin{gathered} - {K^{\rm{f}}}\displaystyle\sum\limits_{j \in {\cal N}_1^1} {{\nabla _{{{{x}}_1}}}V_{1j}^{\rm{f}}\left( {\left\| {{{{x}}_{1j}}} \right\|} \right)} \\ - {\rm{info}}{{\rm{r}}_1}{K^{\rm{T}}}{\nabla _{{{{x}}_1}}}V_1^{\rm{T}}\left( {\left\| {{{{x}}_1} - {{{x}}_{\rm{T}}}} \right\|} \right) \\ \end{gathered} \right)} \\ {\left( \begin{gathered} - {K^{\rm{f}}}\displaystyle\sum\limits_{j \in {\cal N}_2^1} {{\nabla _{{{{x}}_2}}}V_{2j}^{\rm{f}}\left( {\left\| {{{{x}}_{2j}}} \right\|} \right)} \\ - {\rm{info}}{{\rm{r}}_2}{K^{\rm{T}}}{\nabla _{{{{x}}_2}}}V_2^{\rm{T}}\left( {\left\| {{{{x}}_2} - {{{x}}_{\rm{T}}}} \right\|} \right) \\ \end{gathered} \right)} \\ \vdots \\ {\left( \begin{gathered} - {K^{\rm{f}}}\displaystyle\sum\limits_{j \in {\cal N}_N^1} {{\nabla _{{{{x}}_N}}}V_{Nj}^{\rm{f}}\left( {\left\| {{{{x}}_{Nj}}} \right\|} \right)} \\ - {\rm{info}}{{\rm{r}}_N}{K^{\rm{T}}}{\nabla _{{{{x}}_N}}}V_N^{\rm{T}}\left( {\left\| {{{{x}}_N} - {{{x}}_{\rm{T}}}} \right\|} \right) \\ \end{gathered} \right)} \end{gathered}} \right]{\rm{ = }}0$ | (25) |
即鸽群内所有原鸽个体将会收敛至固定的几何构型。且由假设4可知,鸽群中的高层领导者可抵达至距目标点
本节通过仿真实验进一步研究鸽群交互模式切换模型中不同参数(包括原鸽个体数目
依照所建模型进行仿真,设定层级交互模式下最大通信距离
| 表 1 鸽群交互模式切换模型参数设置 Tab.1 Parameters of the pigeon flock interaction pattern switching model |
|
Download:
|
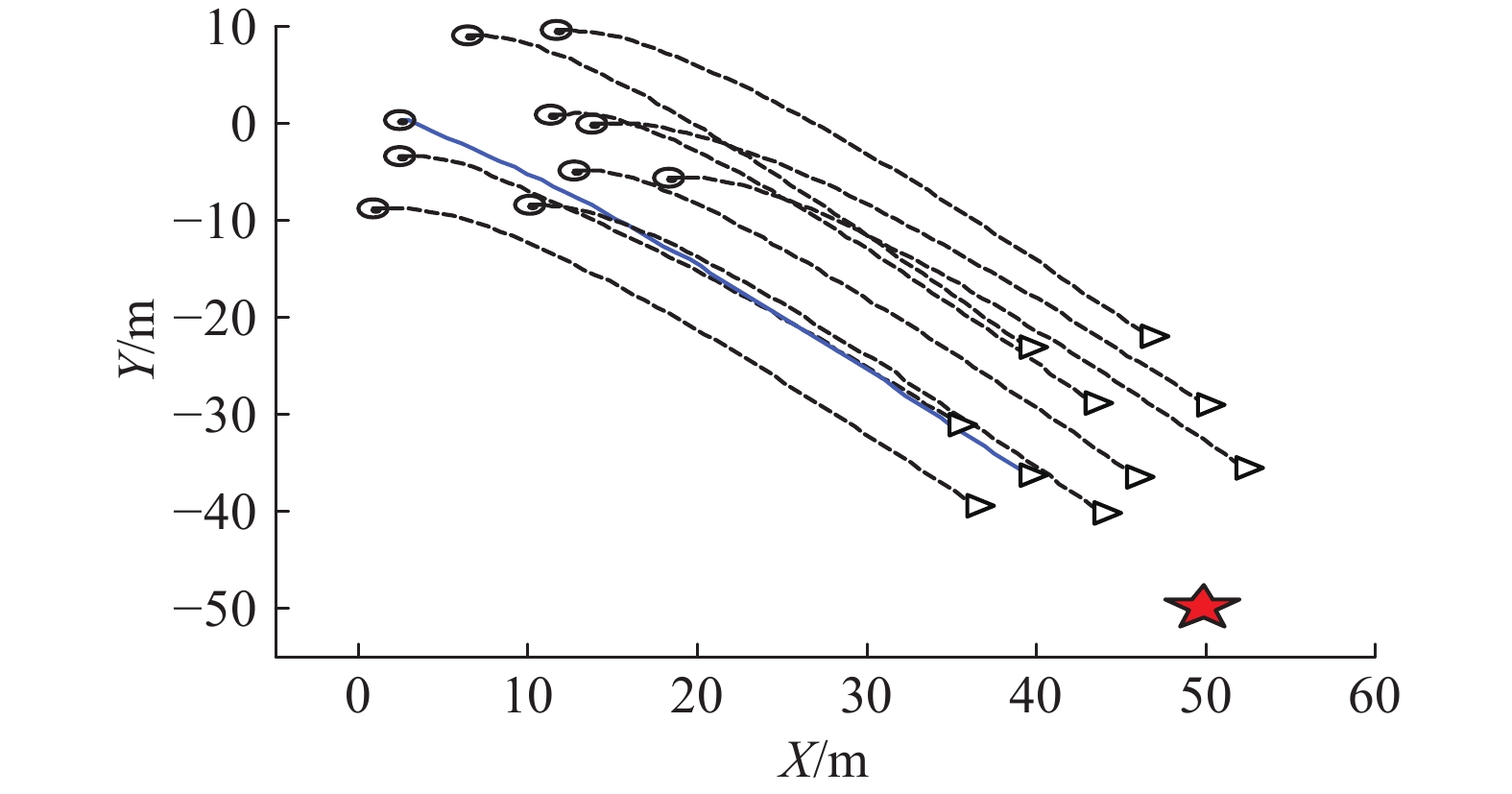
| 图 1 鸽群抵近目标点的仿真运动轨迹 Fig. 1 Motion trajectory of the pigeon flock approaching the target | |
|
Download:
|
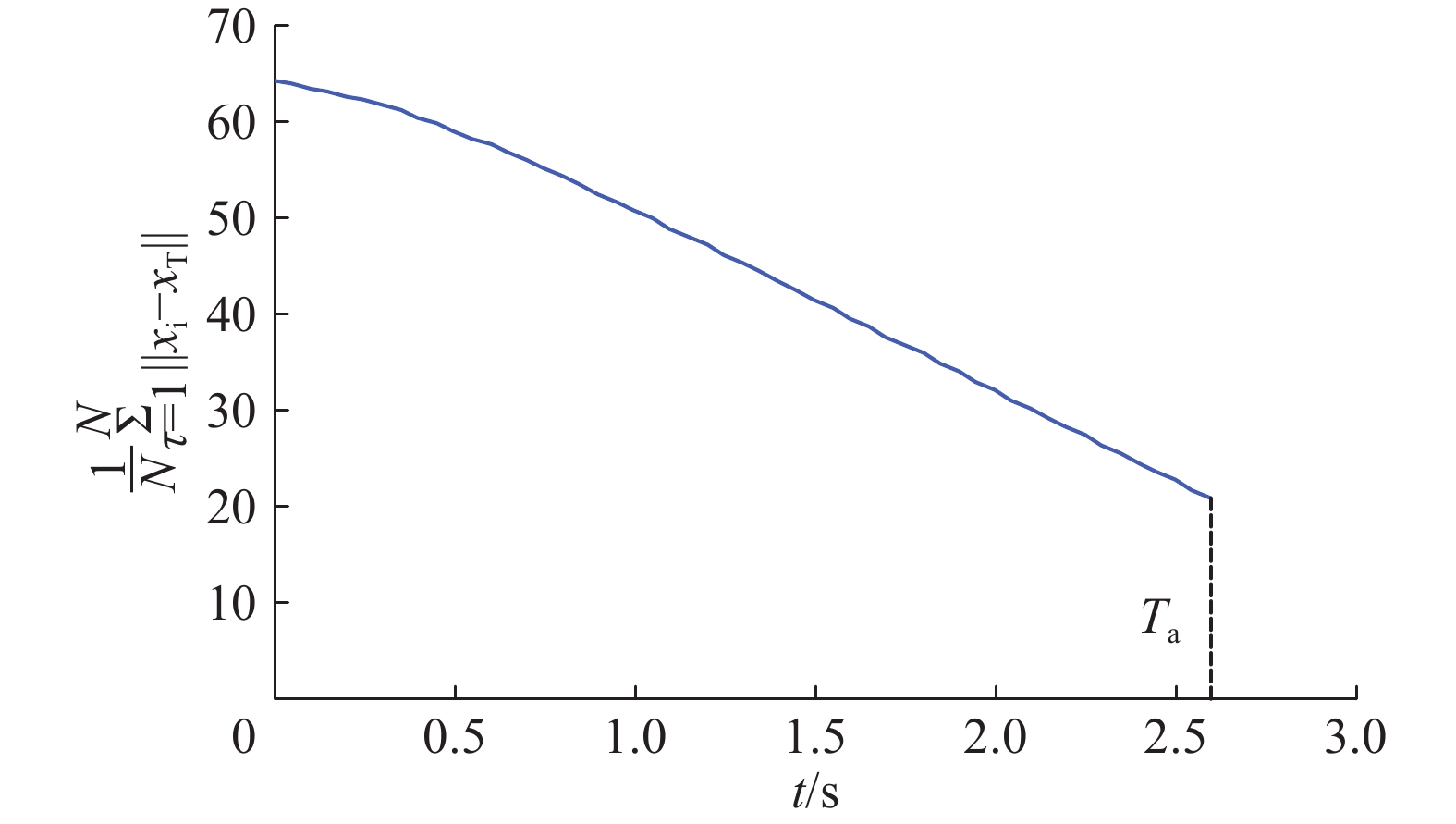
| 图 2 鸽群与目标点距离 Fig. 2 Distance between the pigeon flocks and the target | |
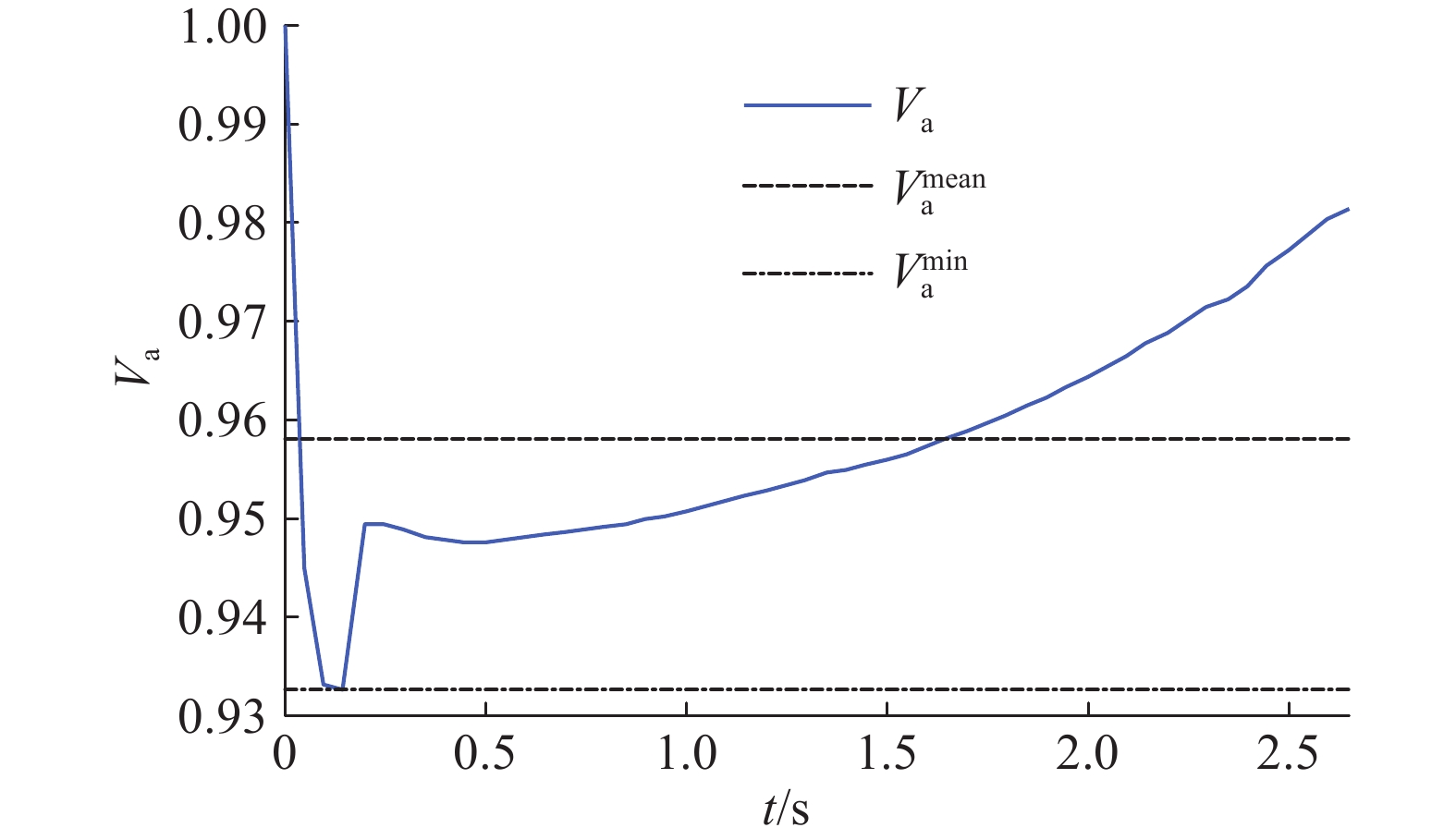
为衡量鸽群系统群集运动的同步程度,采用平均归一化速度的绝对值作为序参量(order parameter),具体如下[22-24]:
| ${V_{\rm{a}}}{\rm{ = }}\frac{1}{N}\left| {\sum\limits_{i = 1}^N {{{v}}_i^*} } \right|$ | (26) |
当鸽群内部原鸽个体归一化速度
|
Download:
|
| 图 3 鸽群序参量 Fig. 3 Order parameter of pigeon flocks | |
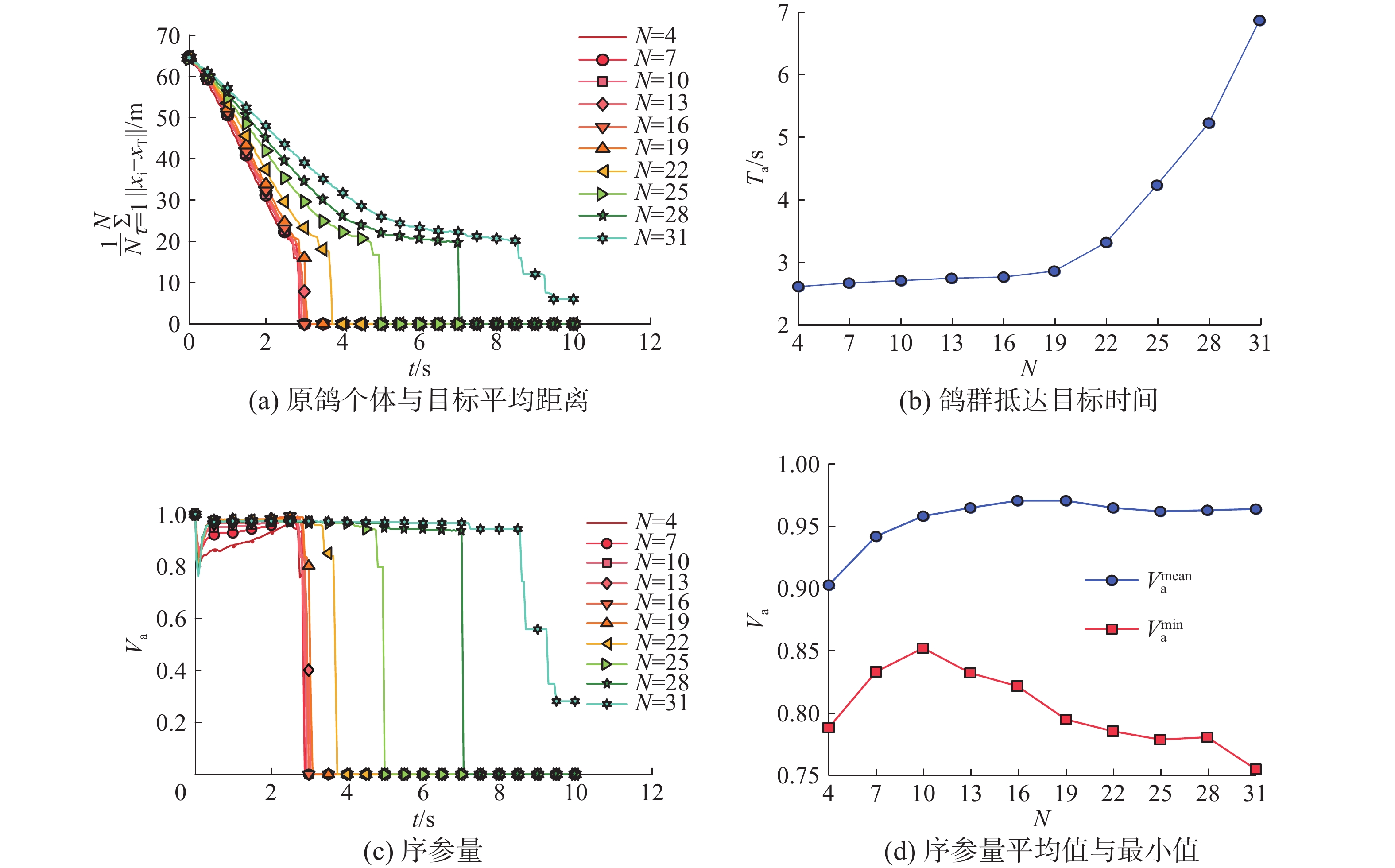
首先,研究原鸽个体数目
|
Download:
|
| 图 4 鸽群同步性参数随原鸽个体数目的变化曲线 Fig. 4 Curves of synchronization parameters of pigeon flocks with the number of individuals | |
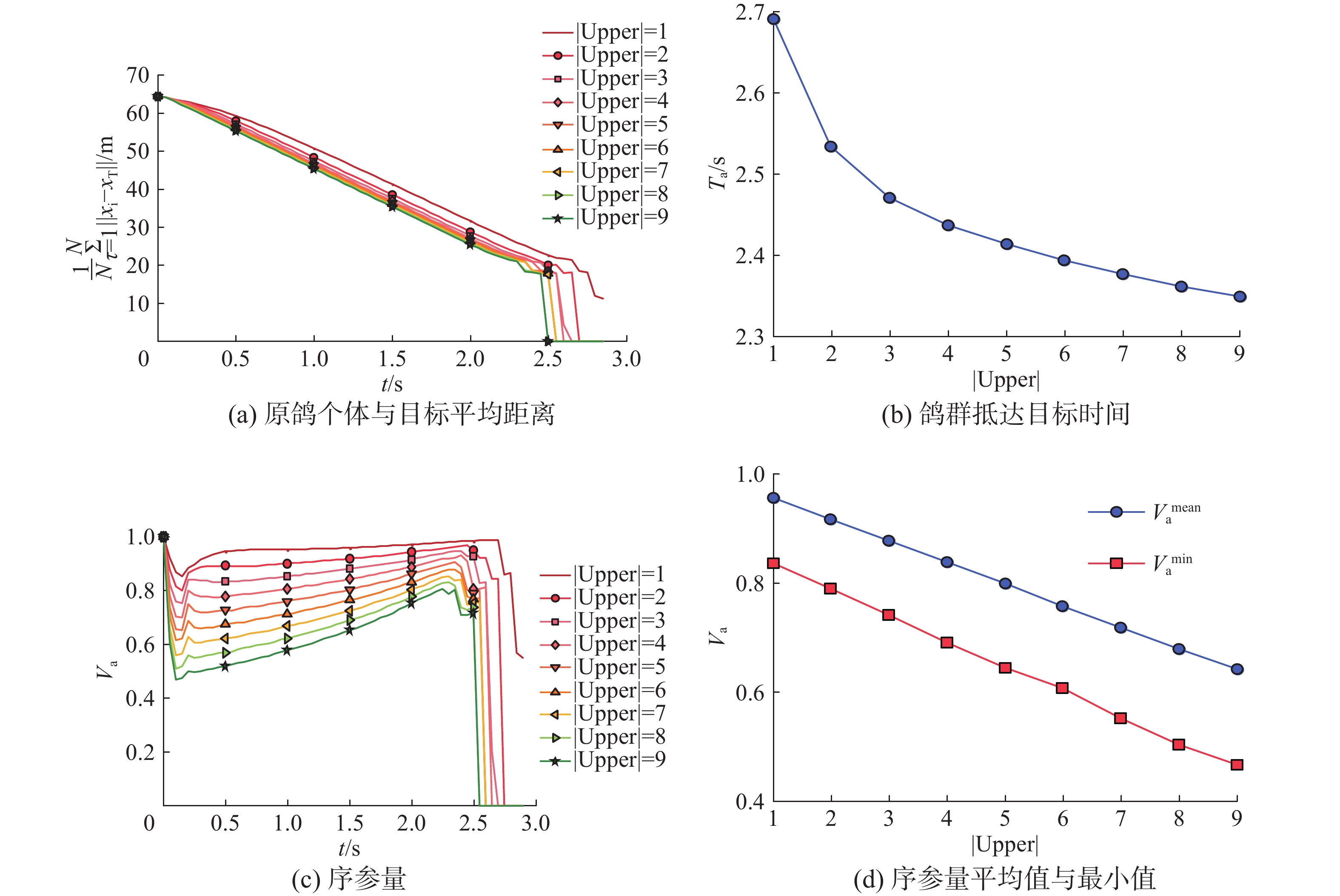
其次,研究高层级原鸽个体数目
|
Download:
|
| 图 5 鸽群同步性参数随高层级原鸽个体数目的变化曲线 Fig. 5 Curves of synchronization parameters of pigeon flocks with the number of higher-rank individuals | |
最后,研究个体最大速率
图6给出了100次独立重复仿真实验后,鸽群归巢群集运动同步性参数随原鸽个体最大速率

|
Download:
|
| 图 6 鸽群同步性参数随原鸽个体最大速率的变化曲线 Fig. 6 Curves of synchronization parameters of pigeon flocks with the maximum rate of individuals | |
图6(a)中横轴、纵轴设定与图4(a)及图5(a)相同,不同个体最大速率
具备群居性的鸟类,历经长期演化,在防御、繁殖、觅食、社群、节律、攻击等行为中均体现出共识自主性,涌现出具备无中心、简单和自组织特点的群体智能[25]。本文以原鸽为研究对象,归纳出原鸽归巢机制中的双模式决策原则、模式切换原则与优势个体原则,并基于上述原则建立鸽群交互模式切换模型。
基于LaSalle不变集理论,给出鸽群系统实现同步的条件,具体如下:首先亦定义包括势能函数和动能函数在内的鸽群Lyapunov函数,基于Lyapunov稳定性理论证明鸽群Lyapunov函数值在平等交互模式有向图相邻切换区间内递减;由鸽群编队势场函数以及原鸽个体平等交互模式下邻居集合的特殊设定,可得鸽群Lyapunov函数值在平等交互模式有向图切换时刻增加有限;继而可知鸽群Lyapunov函数存在上界,同时由鸽群编队势场函数特殊设定可知原鸽个体间不会发生碰撞;进而基于LaSalle不变集理论,可证鸽群内所有个体可实现速度同步,并可收敛至固定的几何构型,同时抵达目标。由蒙特卡罗仿真结果可见,若鸽群系统满足假设条件,不同原鸽个体数目、高层级原鸽个体数目以及个体最大速率下,鸽群系统同步性均可得到保障,且可抵达目标。
| [1] |
BAJEC I L, HEPPNER F H. Organized flight in birds[J]. Animal behaviour, 2009, 78(4): 777-789. DOI:10.1016/j.anbehav.2009.07.007 ( 0) 0)
|
| [2] |
REN Jiaping, SUN Wanxuan, MANOCHA D, et al. Stable information transfer network facilitates the emergence of collective behavior of bird flocks[J]. Physical review E, 2018, 98(5): 052309. ( 0) 0)
|
| [3] |
SAINZ-BORGO C, KOFLER S, JAFFE K. On the adaptive characteristics of bird flocks: small birds form mixed flocks[J]. Ornitología neotropical, 2018, 29: 289-296. ( 0) 0)
|
| [4] |
CHEN Duxin, LIU Xiaolu, XU Bowen, et al. Intermittence and connectivity of interactions in pigeon flock flights[J]. Scientific reports, 2017, 7(1): 10452. DOI:10.1038/s41598-017-09986-5 ( 0) 0)
|
| [5] |
CHEN Duxin, XU Bowen, ZHU Tao, et al. Anisotropic interaction rules in circular motions of pigeon flocks: an empirical study based on sparse Bayesian learning[J]. Physical review E, 2017, 96(2): 022411. DOI:10.1103/PhysRevE.96.022411 ( 0) 0)
|
| [6] |
BALLERINI M, CABIBBO N, CANDELIER R, et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study[J]. Proceedings of the national academy of sciences of the United States of America, 2008, 105(4): 1232-1237. DOI:10.1073/pnas.0711437105 ( 0) 0)
|
| [7] |
NAGY M, ÁKOS Z, BIRO D, et al. Hierarchical group dynamics in pigeon flocks[J]. Nature, 2010, 464(7290): 890-893. DOI:10.1038/nature08891 ( 0) 0)
|
| [8] |
ZAFEIRIS A, VICSEK T. Advantages of hierarchical organization: from pigeon flocks to optimal network structures[C]//Proceedings of Research in the Decision Sciences for Global Business: Best Papers from the 2013 Annual Conference. New Jersey, United States, 2015: 281−282.
( 0) 0)
|
| [9] |
FLACK A, BIRO D, GUILFORD T, et al. Modelling group navigation: transitive social structures improve navigational performance[J]. Journal of the royal society interface, 2015, 12(108): 20150213. DOI:10.1098/rsif.2015.0213 ( 0) 0)
|
| [10] |
CHEN Zhiyong, ZHANG Haitao, CHEN Xi, et al. Two-level leader-follower organization in pigeon flocks[J]. EPL (Europhysics letters), 2015, 112(2): 20008. DOI:10.1209/0295-5075/112/20008 ( 0) 0)
|
| [11] |
NAGY M, VÁSÁRHELYI G, PETTIT B, et al. Context-dependent hierarchies in pigeons[J]. Proceedings of the national academy of sciences of the United States of America, 2013, 110(32): 13049-13054. DOI:10.1073/pnas.1305552110 ( 0) 0)
|
| [12] |
BIRO D, SASAKI T, PORTUGAL S J. Bringing a time-depth perspective to collective Animal Behaviour[J]. Trends in ecology & evolution, 2016, 31(7): 550-562. ( 0) 0)
|
| [13] |
PETTIT B, PERNA A, BIRO D, et al. Interaction rules underlying group decisions in homing pigeons[J]. Journal of the royal society interface, 2013, 10(89): 20130529. DOI:10.1098/rsif.2013.0529 ( 0) 0)
|
| [14] |
PETTIT B, ÁKOS Z, VICSEK T, et al. Speed determines leadership and leadership determines learning during pigeon flocking[J]. Current biology, 2015, 25(23): 3132-3137. DOI:10.1016/j.cub.2015.10.044 ( 0) 0)
|
| [15] |
FREEMAN R, MANN R, GUILFORD T, et al. Group decisions and individual differences: route fidelity predicts flight leadership in homing pigeons (Columba livia)
[J]. Biology letters, 2010, 7(1): 63-66. ( 0) 0)
|
| [16] |
FLACK A, PETTIT B, FREEMAN R, et al. What are leaders made of? The role of individual experience in determining leader-follower relations in homing pigeons[J]. Animal behaviour, 2012, 83(3): 703-709. DOI:10.1016/j.anbehav.2011.12.018 ( 0) 0)
|
| [17] |
WATTS I, PETTIT B, NAGY M, et al. Lack of experience-based stratification in homing pigeon leadership hierarchies[J]. Royal Society open science, 2016, 3(1): 150518. DOI:10.1098/rsos.150518 ( 0) 0)
|
| [18] |
ZHANG Haitao, CHEN Zhiyong, VICSEK T, et al. Route-dependent switch between hierarchical and egalitarian strategies in pigeon flocks[J]. Scientific reports, 2014, 4(1): 5805. ( 0) 0)
|
| [19] |
CHEN Duxin, VICSEK T, LIU Xiaolu, et al. Switching hierarchical leadership mechanism in homing flight of pigeon flocks[J]. EPL (Europhysics letters), 2016, 114(6): 60008. DOI:10.1209/0295-5075/114/60008 ( 0) 0)
|
| [20] |
陈杰, 方浩, 辛斌. 多智能体系统的协同群集运动控制[M]. 北京: 科学出版社, 2017.
( 0) 0)
|
| [21] |
KHALIL H K. Noninear systems[M]. New Jersey: Prentice-Hall, 1996.
( 0) 0)
|
| [22] |
VICSEK T, CZIRÓK A, BEN-JACOB E, et al. Novel type of phase transition in a system of self-driven particles[J]. Physical review letters, 1995, 75(6): 1226-1229. DOI:10.1103/PhysRevLett.75.1226 ( 0) 0)
|
| [23] |
罗琪楠. 基于鸽群行为机制的多无人机协调围捕及验证[D]. 北京: 北京航空航天大学, 2017.
( 0) 0)
|
| [24] |
LUO Qi’nan. Research on cooperative control and pursuit-evasion strategy of multi-UAV based on pigeon behavioral mechanisms[D]. Beijing: Beihang University, 2017.
( 0) 0)
|
| [25] |
段海滨, 邱华鑫. 基于群体智能的无人机集群自主控制[M]. 北京: 科学出版社, 2018.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


