2. 浙江业大学 计算机科学与技术学院,浙江 杭州 310014
2. College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310014, China
聚类是数据分析的重要手段,将数据集分为若干类,使得簇内紧密且相似性大,簇与簇之间有明显区别,使得相似性最小,在数据挖掘、图像处理等领域被广泛应用[1-4]。k-means聚类算法是一种常用的动态聚类算法,具有聚类速度快,操做简单,效率高等特点,但其同时存在对初始聚类中心点较敏感、全局搜索能力弱的缺点,使得聚类效率低,准确性差。因此,很多学者为得到稳定、高效的聚类效果,对k-means聚类算法的局限性进行了改进与研究。
何熊熊等[5]提出一种基于密度和网格的簇心可确定聚类算法,通过网格对象的密度值进行划分以完成聚类;李亚等[6]引入轮廓系数作为聚类效果评价指标,并将改进的算法应用到台折损率的计算中;邢长征等[7]针对聚类结果对孤立点敏感的问题,提出了一种基于平均密度优化初始聚类中心的k-means算法;张天骐等[8]提出一种基于k-means聚类改进的软扩频信号伪码序列盲估计算法,利用相似度从分段数据中寻找初始聚类中心,并通过平均轮廓系数估计规模数;李晓瑜等[9]提出了一种基于Hadoop的分布式改进k-means算法,通过引入Canopy算法初始化k-means算法的聚类中心;Tzortzis G等[10]提出了MinMax k-means算法,在初始化不好的情况下通过赋予方差权重以优化目标提高聚类效果;Laith Mohammad Abualigah等[11]将k-means算法采用和声搜索方法进行优化并应用于文本聚类中,提高了聚类精度;Li Yanyan等[12]提出一种基于粒子群优化的k-means算法,并将其应用在岩体不连续数据分类中;Khanmohammadi等[13]为克服对初始聚类中心的敏感问题,提出了一种混合k-谐波均值和重叠k均值算法的混合方法来克服缺点。以上改进算法都起到了较好的聚类效果,但在初始聚类中心选取问题上仍存在首个初始聚类中心点落于稀疏边界的缺陷。
基于此,本文提出一种基于可拓距的改进k-means聚类算法,将可拓学思想与k-means算法有效的结合,通过引入可拓侧距和缩放因子,对首个初始聚类中心点进行优化,选出一组最优初始聚类中心点,并通过仿真对比检验本文改进算法的可行性。通过实验验证,该方法具有更好的聚类效果。
1 基本知识 1.1 可拓距相关知识可拓学是以蔡文教授为首的我国学者们创立的新学科,近年来,可拓学在计算机,人工智能、检测、控制等领域进行的应用取得了良好的成绩[14]。其中,可拓距在实例检索领域应用较为广泛,通过可拓距构造关联函数,依据样本间关联度识别案例类别[15-19],显著提高了案例检索效率与正确率。
在经典数学中,当点在区间内时,默认点与区间的距离为零,即“类内即为同”,无法将事物内部的“质变”、“量变”表达出来。因此,为了描述类内事物(区间内的点)的区别,在可拓学中规定:实轴上任意一点x与区间X0=<a, b>之距为[14]
| $\rho \left( {x,{X_0}} \right) = |x - \dfrac{{a + b}}{2}| - \dfrac{{b - a}}{2} = \left\{ \begin{array}{l} a - x,\;\;\;\;x \leqslant \dfrac{{a + b}}{2}\\ x - b,\;\;\;\;x \geqslant \dfrac{{a + b}}{2} \end{array} \right.$ | (1) |
当实例点在区间中点时,该实例最符合要求;
但在实际工作中,却不全如此,例如,误差要求越小越好;成本要求越低越好;性价比越高越好;洗衣机的洗净率越大越好等,一般而言,实例点并不是越在区间中点越好,因此在可拓距的基础上,引入可拓侧距的概念[14]:
给定区间X0=
| $\rho {_l}(x,{x_0},{X_0}) = \left\{ {\begin{array}{*{20}{l}} {a - x,}\\ {\dfrac{{b - {x_0}}}{{a - {x_0}}}(x - a),}\\ {x - b,} \end{array}\begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{x \leqslant a}\\ {x \in \left\langle a,{x_0} \right\rangle }\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{x \geqslant {x_0}} \end{array}} \right.$ | (2) |
为x与区间X0关于x0的左侧距。
给定区间X0=
| ${\rho _r}(x,{x_0},{X_0}) = \left\{ {\begin{array}{*{20}{l}} {a - x,}\\ {\dfrac{{a - {x_0}}}{{b - {x_0}}}(b - x),}\\ {x - b,} \end{array}\begin{array}{*{20}{c}} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{x \leqslant {x_0}}\\ {x \in \left\langle {x_0},b \right\rangle }\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{x \geqslant b} \end{array}} \right.$ | (3) |
为x与区间X0关于x0的右侧距。
1.2 k-means聚类算法基本原理k-means聚类算法基本思想是将样本划分成多个类,使得各簇内对象具有尽可能大的相似度,同时使簇间的相似度尽可能的小[20]。k-means聚类算法的处理过程如下:
1) 从数据集X中随机选择k个对象,分别作为k个类别的初始聚类中心;
2) 计算剩余每个对象与各个聚类中心的距离,并将其划分到距离最近的子类中;
3) 重新计算每个子类中所有对象的平均值,将其作为新的聚类中心。
重复上述过程,直到聚类中心不再改变[21]。
1.3 k-means聚类算法的不足分析k-means算法中,对于k个初始中心点的选取是随机完成的,而初始中心点选取的不同会导致不同的聚类效果,从而引起聚类结果的不稳定性。针对该不足,一些学者提出用密集度、差异度等[22-23]概念对初始聚类中心进行优化,都无法避免初始聚类中心点落在边界非密集区域,因此本文将从初始中心点选取方面对k-means算法提出相应的改进措施。
2 可拓距改进的k-means聚类算法 2.1 基本思想为便于表述,首先定义距离区间、距离可拓侧距、距离平均可拓侧距3个概念。对于n个样本的集合
定义1 样本集合X的距离区间Z为
| $Z = \left[ {A,B} \right] = \left[ {\min (D),\max (D)} \right]$ | (4) |
其中,
定义2 根据式(2)和式(3)定义两样本xi和xj (i
| $ \begin{array}{l} {\text{左侧距}}:\rho _l^{(i,j)} = {\rho _l}(d,A,Z) = \left\{ {\begin{array}{*{20}{l}} {A - d{\rm{,}}}\\ {{A_z}{\rm{,}}}\\ {d - B,} \end{array}\begin{array}{*{20}{c}} {d < A}\\ {d = A}\\ {d > A} \end{array}} \right.\\ {\text{其中}}:{A_z}{\rm{ = }}{\rho _l}(A,A,Z){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {0,}\\ {A - B,}\\ {0 \otimes \left( {A - B} \right),} \end{array}\begin{array}{*{20}{c}} {A \notin Z}\\ {A \in Z}\\ {A \notin Z{\text{且}}A \in Z.} \end{array}} \right. \end{array} $ | (5) |
| $ \begin{array}{l} {\text{右侧距}}:\rho _r^{(i,j)} = {\rho _r}(d,B,Z) = \left\{ {\begin{array}{*{20}{l}} {A - d{\rm{,}}}\\ {{B_z}{\rm{,}}}\\ {d - B,} \end{array}\begin{array}{*{20}{c}} {d < B}\\ {d = B}\\ {d > B.} \end{array}} \right.\\ {\text{其中}}:{B_z}{\rm{ = }}{\rho _r}(B,B,Z){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {0,}\\ {A - B,}\\ {0 \otimes \left( {A - B} \right),} \end{array}\begin{array}{*{20}{c}} {B \notin Z}\\ {B \in Z}\\ {B \notin Z{\text{且}}B \in Z.} \end{array}} \right. \end{array} $ | (6) |
定义3 根据定义2可计算所有两两样本的可拓侧距,则平均左、右侧距为
| $\overline \rho = \dfrac{{\displaystyle\sum\limits_{j = i + 1}^n {\displaystyle\sum\limits_{i = 1}^{n - 1} {{\rho ^{(i,j)}}} } }}{{C_n^2}}$ | (7) |
其中,
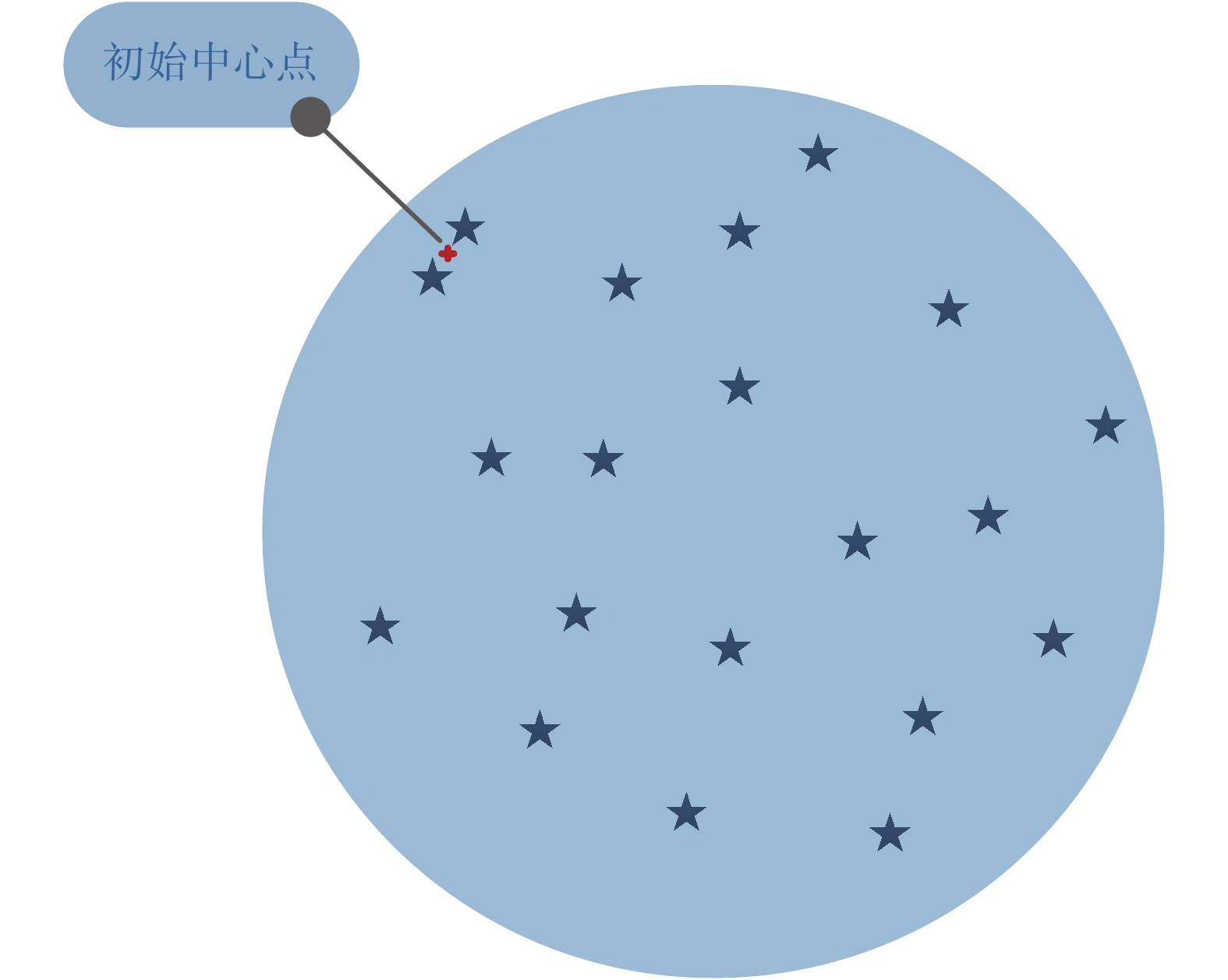
针对传统k-means算法初始中心点随机选取所引起聚类算法稳定性差问题,现有的改进算法虽取得了一定的效果,但仍无法避免初始聚类中心点落在边界非密集区域如图1所示,取样本间距离最小值所对应中心坐标作为首个初始聚类点,因下一初始聚类中心点的选取决定于首个初始中心的位置,当该点位于边界非密集区域,既降低了剩余初始聚类中心点质量,又会出现最终聚类集合中样本数为0或1的情况,使得聚类效果不均衡。
|
Download:
|
| 图 1 初始中心点展示图 Fig. 1 The display map of first initial center point | |
初始聚类中心的选取,不仅要求分布在较密集的范围内,还需要保证各初始聚类中心尽可能分散。针对上述问题,利用可拓距中数据分布情况对左右侧距平均值的影响,将经典平均距离映射为两个平均侧距值,如图2所示,其中平均左侧距值相对中心点靠左分布,平均右侧距值相对中心点靠右分布。特别指出,当数据在区间对称分布时,左右平均可拓侧距值重合于一点。将可拓平均左侧距

|
Download:
|
| 图 2 经典距向可拓距映射 Fig. 2 Mapping of classical distances to extension distances | |
当选出初始聚类中心点数未达到所要求个数时,引入缩放因子
| $ \eta = \left\{ {\begin{array}{*{20}{l}} {1 + \dfrac{{C_n^2 - k'}}{{C_n^2}}}&{k' \ne K}\\ 1\;,\;{k' = K} \end{array}} \right.$ | (8) |
其中,
最后按传统聚类算法进行聚类。选取的一组最优初始聚类中心点克服了中心点出现于边界非密集区域缺陷,最大限度分布在密集区且各聚类中心点均匀分布。
2.2 改进k-means算法初始聚类中心选取流程根据上述思想,得到改进k-means算法初始聚类中心选取的具体实施步骤如下:
1)按式(4)计算出两两样本间距离及等效密集距离区间[A,B];
2)按式(5)和式(6)将距离映射为可拓左侧距
3)遍历排序好的可拓距,将其中首个大于样本间可拓平均左侧距
4)计算排好序可拓距中下一个值对应中心点坐标并依次计算出其与已确定的初始聚类中心的可拓距,将其与样本平均可拓右侧距
5)如果遍历一次后,初始聚类中心未达到K,则按式(8)计算出缩小因子
6)若聚类中心数达到K时,则完成初始聚类中心的选取。
3 实验与分析为了验证本文所提出算法的有效性,将本文算法与传统k-means算法及文献[22-23]所提出的改进聚类算法进行对比分析。
实验所用的测试数据集为UCI数据库中用于测试聚类的Iris数据集和Wine数据集,各数据的特征如表1所示。
| 表 1 各数据集的基本特征 Tab.1 Characteristics of datasets |
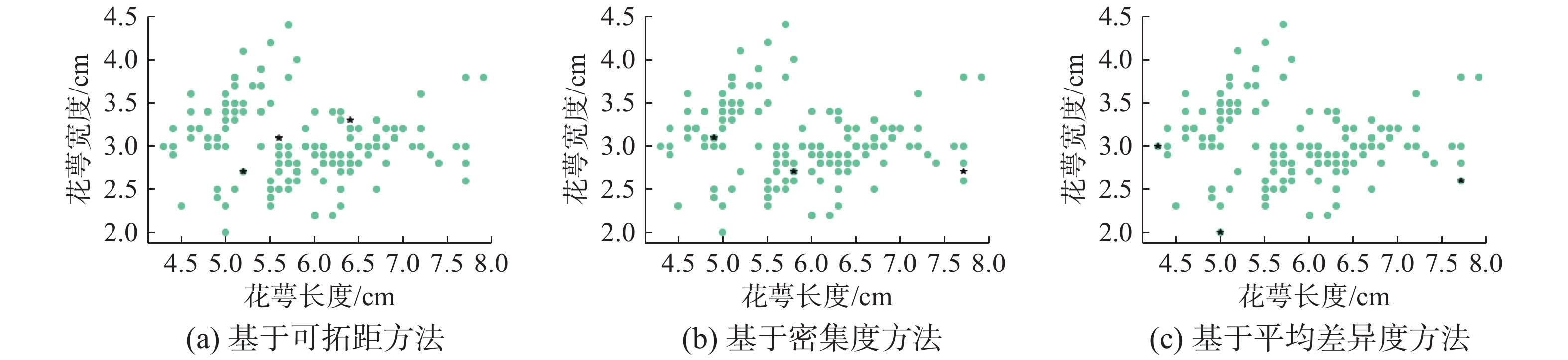
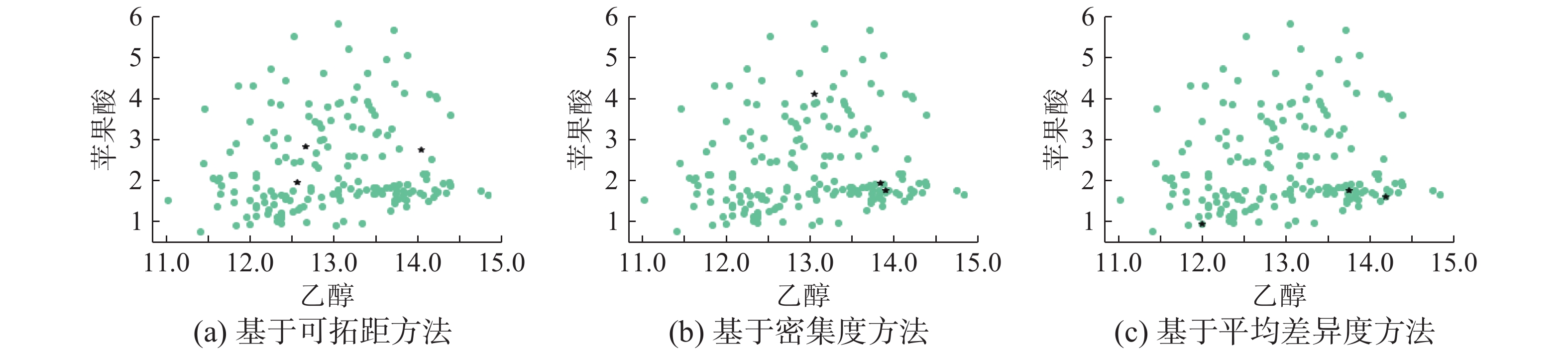
基于本文提出算法对Iris、Wine数据进行初始中心点选取,特别指出,为了观察初始聚类中心点选取位置的大体远近及分散程度,本文为节省篇幅,只展示数据集两属性的二维图3和图4。
|
Download:
|
| 图 3 基于Iris数据的初始聚类中心点分布对比 Fig. 3 Comparison of distribution of initial cluster centers based on Iris dataset | |
|
Download:
|
| 图 4 基于Wine数据的初始聚类中心点分布对比 Fig. 4 Comparison of distribution of initial cluster centers based on Wine dataset | |
从图3和图4中可看出本文提出改进算法选取的初始聚类中心点,对低维与高维数据选取的初始聚类中心点,相较于其他改进算法分布更均匀,位于边界区域初始聚类中心点,其周围数据点也相对密集。
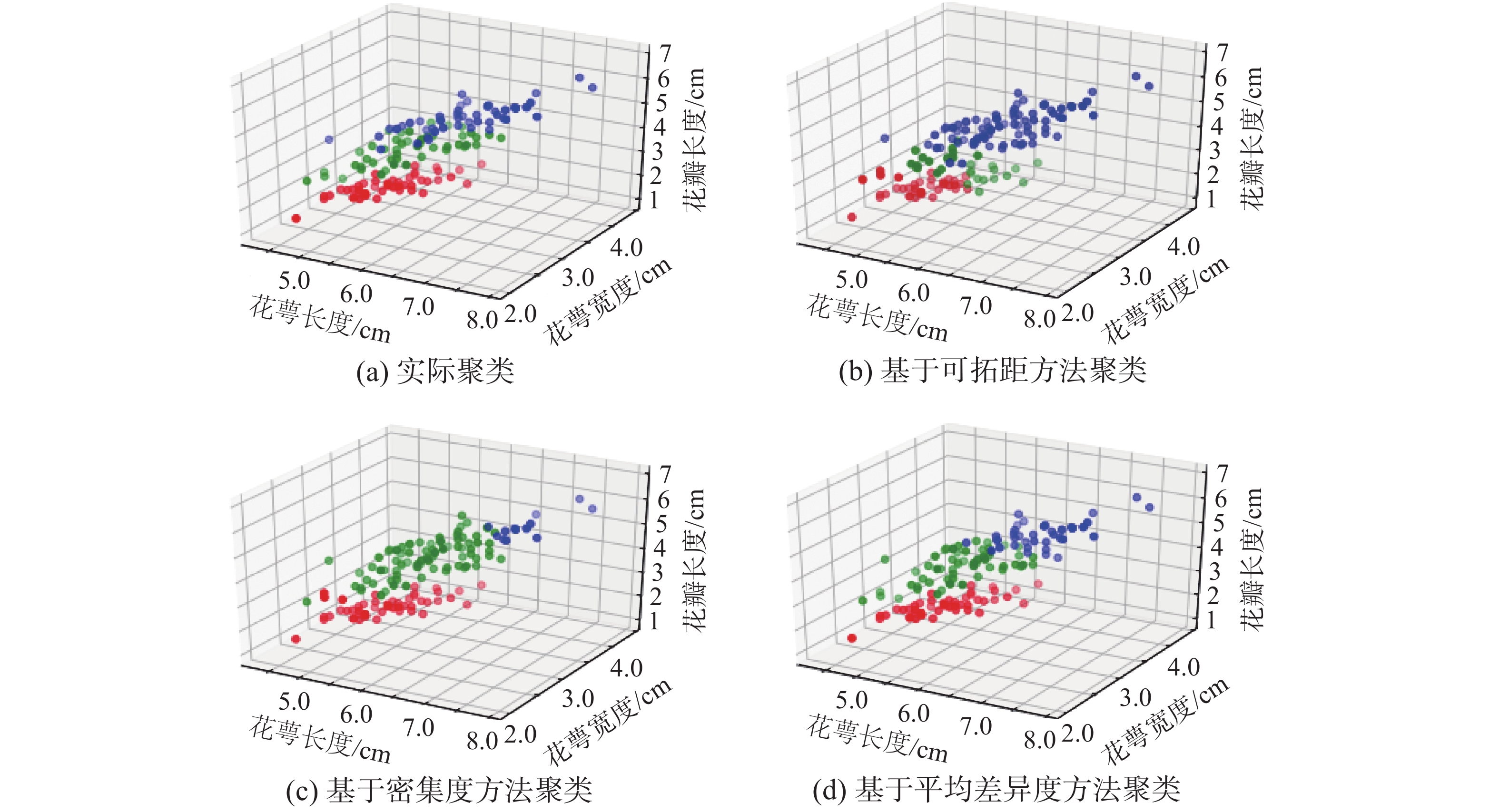
为了定量描述初始聚类中心点选取的质量,本文先将所选中心点聚类,将其与样本实际聚类情况和现有改进算法聚类情况进行对比,其聚类效果图5和图6。
|
Download:
|
| 图 5 基于Iris数据聚类对比图 Fig. 5 Comparison of clustering based on Iris dataset | |
|
Download:
|
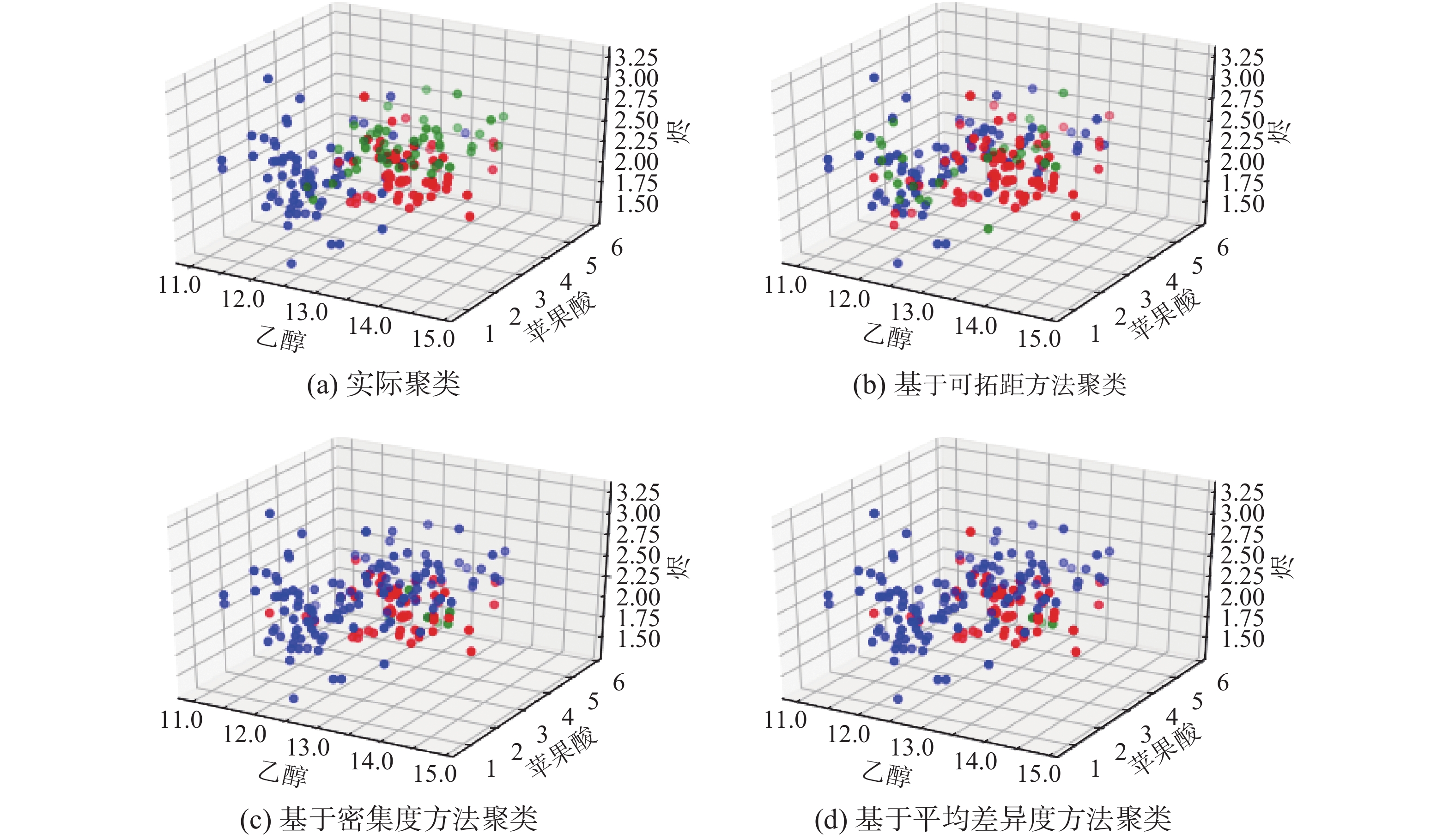
| 图 6 基于Wine数据聚类对比 Fig. 6 Comparison of clustering based on Wine dataset | |
其中,图5与图6中3种颜色代表3个聚类簇,可看出其他两种改进算法,由于初始中心点分布不均匀且有位于稀疏边界的中心点,从而导致对两组样本集聚类的结果存在一定误差,但本文提出的改进算法,虽然仍存在误差,但误差的大小有所缩小,尤其在对更高维的Wine数据集聚类时,优势更明显。
为了定量衡量算法的有效性,本文采用分类正确率指标,即被正确分到对应类别的样本个数与总样本个数比值以及聚类均衡性指标,即各类中样本个数与实际相应类中样本个数的方差,进行衡量。
对初始聚类中心点聚类后分类正确率统计如表2所示。对初始聚类中心点聚类后各簇类样本的个数统计如表3所示。由表3得出改进前后算法的均衡性指标如表4所示。从表2与表4中可看出当数据集样本维数不高时,本文算法与改进算法在聚类的均衡性上差异较小,但当维数增高时,现有改进算法聚类均衡性和分类准确性会降低,导致个别类中样本较多,相反也会出现有些类中样本过少的情况,使得之后聚类中心点更新时,较少样本数据的中心点在迭代更新时坐标变化不明显,从而导致最终聚类效果差。
| 表 2 改进前后算法聚类正确率指标 Tab.2 Accuracy of clustering algorithm before and after |
| 表 3 改进前后算法聚类后各簇类样本个数 Tab.3 The number of samples in each cluster |
| 表 4 改进前后算法聚类均衡性指标 Tab.4 Balance of clustering algorithm before and after |
本文提出一种基于可拓距的改进k-means聚类算法,将样本间平均距离映射为可拓距上对应两个平均侧距,作为初始聚类中心选取的约束范围,克服了首个选取的初始中心点可能位于较疏散边界的缺陷。实验表明在高维数据集的情况下,基于可拓距的改进k-means算法选取的初始聚类中心点聚类具有较高的正确率和均衡率,表明选取的初始聚类中心点较优,更适合大数据背景下的海量、高维数据聚类。
本文对k-means聚类算法初始聚类中心的选取展开了研究,由于时间和个人能力有限,还存在不足之处有待后续研究中深化、提高:1)本文算法对非数值型的数据集样本如何衡量相似度,并没有给出解决方法。2)文中提到的缩放因子并不能自适应的变化,对算法的性能有所影响。3)如何引入关联函数代替距离计算相似度,是值得深入研究的问题。4)在理论上和实用上的意义及价值。5)进一步深入研究本课题的建议。
| [1] |
于佐军, 秦欢. 基于改进蜂群算法的k-means算法[J]. 控制与决策, 2018, 33(1): 181-185. YU Zuojun, QIN Huan. k-means algorithm based on improved artificial bee colony algorithm[J]. Control and decision, 2018, 33(1): 181-185. (  0) 0)
|
| [2] |
HE Hong, TAN Yonghong. Automatic pattern recognition of ECG signals using entropy-based adaptive dimensionality reduction and clustering[J]. Applied soft computing, 2017, 55: 238-252. DOI:10.1016/j.asoc.2017.02.001 ( 0) 0)
|
| [3] |
PENG Chong, KANG Zhao, XU Fei, et al. Image projection ridge regression for subspace clustering[J]. IEEE signal processing letters, 2017, 24(7): 991-995. DOI:10.1109/LSP.2017.2700852 ( 0) 0)
|
| [4] |
RÖTHLISBERGER V, ZISCHG A P, KEILER M, et al. Identifying spatial clusters of flood exposure to support decision making in risk management[J]. Science of the total environment, 2017, 598: 593-603. DOI:10.1016/j.scitotenv.2017.03.216 ( 0) 0)
|
| [5] |
何熊熊, 管俊轶, 叶宣佐, 等. 一种基于密度和网格的簇心可确定聚类算法[J]. 控制与决策, 2017, 32(5): 913-919. HE Xiongxiong, GUAN Junyi, YE Xuanzuo, et al. A density-based and grid-based cluster centers determination clustering algorithm[J]. Control and decision, 2017, 32(5): 913-919. (  0) 0)
|
| [6] |
李亚, 刘丽平, 李柏青, 等. 基于改进K-Means聚类和BP神经网络的台区线损率计算方法[J]. 中国电机工程学报, 2016, 36(17): 4543-4551. LI Ya, LIU Liping, LI Baiqing, et al. Calculation of line loss rate in transformer district based on improved K-Means clustering algorithm and BP neural network[J]. Proceedings of the CSEE, 2016, 36(17): 4543-4551. (  0) 0)
|
| [7] |
邢长征, 谷浩. 基于平均密度优化初始聚类中心的k-means算法[J]. 计算机工程与应用, 2014, 50(20): 135-138. XING Changzheng, GU Hao. K-means algorithm based on average density optimizing initial cluster centre[J]. Computer engineering and applications, 2014, 50(20): 135-138. DOI:10.3778/j.issn.1002-8331.1311-0122 (  0) 0)
|
| [8] |
张天骐, 杨强, 宋玉龙, 等. 一种K-means改进算法的软扩频信号伪码序列盲估计[J]. 电子与信息学报, 2018, 40(1): 226-234. ZHANG Tianqi, YANG Qiang, SONG Yulong, et al. Blind estimation PN sequence in soft spread spectrum signal of improved K-means algorithm[J]. Journal of electronics & information technology, 2018, 40(1): 226-234. DOI:10.11999/JEIT170306 (  0) 0)
|
| [9] |
李晓瑜, 俞丽颖, 雷航, 等. 一种K-means改进算法的并行化实现与应用[J]. 电子科技大学学报, 2017, 46(1): 61-68. LI Xiaoyu, YU Liying, LEI Hang, et al. The parallel implementation and application of an improved K-means algorithm[J]. Journal of University of Electronic Science and Technology of China, 2017, 46(1): 61-68. DOI:10.3969/j.issn.1001-0548.2017.01.010 (  0) 0)
|
| [10] |
TZORTZIS G, LIKAS A. The MinMax k-means clustering algorithm[J]. Pattern recognition, 2014, 47(7): 2505-2516. DOI:10.1016/j.patcog.2014.01.015 ( 0) 0)
|
| [11] |
ABUALIGAH L M, KHADER A T, AI-BETAR M A. Unsupervised feature selection technique based on harmony search algorithm for improving the text clustering[C]//Proceedings of the 7th International Conference on Computer Science and Information Technology. Amman, Jordan, 2016: 1–6.
( 0) 0)
|
| [12] |
LI Yanyan, WANG Qing, CHEN Jianping, et al. K-means algorithm based on particle swarm optimization for the identification of rock discontinuity sets[J]. Rock mechanics and rock engineering, 2015, 48(1): 375-385. DOI:10.1007/s00603-014-0569-x ( 0) 0)
|
| [13] |
KHANMOHAMMADI S, ADIBEIG N, SHANEHBANDY S. An improved overlapping k-means clustering method for medical applications[J]. Expert systems with applications, 2017, 67: 12-18. DOI:10.1016/j.eswa.2016.09.025 ( 0) 0)
|
| [14] |
杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014.
( 0) 0)
|
| [15] |
管凤旭. 基于流形学习及可拓分类器的手指静脉识别研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. GUAN Fengxu. Research on finger vein recognition based on manifold learning and extension classifier[D]. Harbin: Harbin Engineering University, 2010. (  0) 0)
|
| [16] |
赵燕伟, 苏楠, 张峰, 等. 基于可拓实例推理的产品族配置设计方法[J]. 机械工程学报, 2010, 46(15): 146-154. ZHAO Yanwei, SU Nan, ZHANG Feng, et al. Configuration design method for product family based on extension case reasoning[J]. Journal of mechanical engineering, 2010, 46(15): 146-154. (  0) 0)
|
| [17] |
叶永伟, 张帆, 王运. 基于可拓距的起重机产品配置方法设计[J]. 中国制造业信息化, 2012, 41(23): 24-27. YE Yongwei, ZHANG Fan, WANG Yun. The crane products configuration design based on extension distance[J]. Manufacturing information engineering of China, 2012, 41(23): 24-27. (  0) 0)
|
| [18] |
NOUAOURIA N, BOUKADOUM M. Case retrieval with combined adaptability and similarity criteria: application to case retrieval nets[C]//Proceedings of the 18th International Conference on Case-Based Reasoning. Research and Development. Alessandria, Italy, 2010: 242–256.
( 0) 0)
|
| [19] |
赵燕伟, 任设东, 陈尉刚, 等. 基于改进BP神经网络的可拓分类器构建[J]. 计算机集成制造系统, 2015, 21(10): 2807-2815. ZHAO Yanwei, REN Shedong, CHEN Weigang, et al. Extension classifier construction based on improved BP neural network[J]. Computer integrated manufacturing systems, 2015, 21(10): 2807-2815. (  0) 0)
|
| [20] |
李敏. K-means算法的改进及其在文本聚类中的应用研究[D]. 无锡: 江南大学, 2018. LI Min. The research and application of text clustering based on improved K-means algorithm[D]. Wuxi: Jiangnan University, 2018. (  0) 0)
|
| [21] |
杨明极, 马池, 王娅, 等. 一种改进K-means聚类的FCMM算法[J]. 计算机应用研究, 2019, 36(7): 2007-2010. YANG Mingji, MA Chi, WANG Ya, et al. Algorithm named FCMM to improve K-means clustering algorithm[J]. Application research of computers, 2019, 36(7): 2007-2010. (  0) 0)
|
| [22] |
韩俊, 谈健, 黄河, 等. 基于改进K-means聚类算法的供电块划分方法[J]. 电力自动化设备, 2015, 35(6): 123-129. HAN Jun, TAN Jian, HUANG He, et al. Power-supplying block partition based on improved K-means clustering algorithm[J]. Electric power automation equipment, 2015, 35(6): 123-129. (  0) 0)
|
| [23] |
李武, 赵娇燕, 严太山. 基于平均差异度优选初始聚类中心的改进K-均值聚类算法[J]. 控制与决策, 2017, 32(4): 759-762. LI Wu, ZHAO Jiaoyan, YAN Taishan. Improved K-means clustering algorithm optimizing initial clustering centers based on average difference degree[J]. Control and decision, 2017, 32(4): 759-762. (  0) 0)
|
 2020, Vol. 15
2020, Vol. 15


