关联规则挖掘是数据挖掘研究领域重要任务之一，目标就是从事务数据集中发现隐藏的、有意义的联系，目前已广泛应用于购物篮分析、网络入侵检测、关联规则分类、交通事故模式分析、药物成分关联分析、病人症型判断等领域^[1-3]。常用关联规则算法有Apriori、FP-Growth、MagnumOpus、Closet等^{[1, 4]}，其中最常用也是最经典的挖掘算法是Apriori算法。

为了挖取规模合适的规则，大部分关联规则算法执行前需用户设置两个阈值：最小支持度和最小置信度，以期找到所有超过用户设定阈值的规则。因此，用户必须具备一定的先验知识才能寻找到合适的最小支持度和最小置信度以便获得有应用价值的规则。但在实际应用过程中，1)不同领域数据差异较大，导致算法在不同的数据集中设置的最小支持数和最小置信度存在较大差异，没有一个统一的标准；2)存在许多非专业用户，对算法参数的取值具有较大的随意性。因此如何利用数据集本身的特性自动确定阈值而无须先验知识是一个很有意义且亟待解决的问题。本文针对这一问题提出基于可决系数的自适应关联规则挖掘算法，依据待挖掘数据集中所有项的支持数和所有规则的置信度的数据分布特性，采用曲线拟合技术，根据可决系数自动确定拟合多项式，并在此基础上自动确定具有数据统计依赖意义的最小支持度和置信度，使其关联规则挖掘的应用门槛降低。

1 相关研究

针对上述所提的参数阈值设置方面问题，在过去的十多年中，研究者们从不同角度提出了一些解决方法。一种角度是优化参数或减少参数的方法。例如，Scheffer提出的预测Apriori算法^[5]，它自动解决了最小支持度和最小置信度这两个参数之间的平衡问题，最大限度地提高了对数据集进行精确预测的可能性。该算法利用贝叶斯方法计算了一个称为精确期望预测精度的参数，以实现精确的预测，从而提供规则的精确性信息。最后的结果表明，预测Apriori算法的性能优于使用增量因子的Apriori型算法。AI-Maqaleh等^[6]提出了一种有效的置信度综合算法，在挖掘频繁项集的过程中生成了真正有用的规则。吴瑞华等^[7]提出了一种多重支持度关联规则挖掘算法，根据不同数据项的特点定义多重支持度，通过挖掘数据库中的最大频繁项目集，计算最大频繁候选项目集在数据库中的支持度来发现关联规则，可解决关联规则中经常出现的稀少数据项问题。陈柳等^[8]提出了一个结合项集相关性的两级置信度阈值设置方法(PNMC-TWO)，该方法不仅可以更好地确保提取出的关联规则有效和有趣,还可以显著地降低可信度低的关联规则数。于海燕^[9]提出了一种最小相关度优化PNARC算法的审计数据关联规则挖掘模型，提高负关联规则的程度，减少不相关的关联规则，然后对最小相关度进行概率分析，降低无关规则的产生几率。董博等^[10]针对传统关联规则挖掘方法存在计算冗余度过高的问题，提出一种后处理闭包算子最小单约束的关联规则算法有效降低算法冗余计算，提高算法计算效率。Li等^[11]提出了一种新的联想分类器SigDirect，利用Fisher的精确检验作为一种剪枝策略，直接挖掘分类关联规则。在没有最小支持度和最小置信度等阈值设置的情况下，SigDirect能够找到非冗余的分类关联规则，这些规则在一组先前项和随后的类标签之间表现出统计上的显著依赖性。还有一些学者提出利用智能技术进行关联规则挖掘，而无需设置最小支持度和最小置信度，如Qodmanan等^[12]利用多目标遗传算法进行FP-Tree模式关联规则挖掘，Sarath等^[13]提出使用二进制粒子群优化策略，吴琼等^[14]针对量化关联规则的特点，提出基于多目标烟花算法全面搜索关联规则，Anping等^[15]提出了基于Pareto的多目标二进制BAT算法(MBBA)。Can等^[16]提出利用引力搜索算法(GSA)进行数值型关联规则挖掘。这些基于智能技术，通过搜索全域空间，无须设置最小支持度和最小置信度参数即可获取支持度最好、置信度最高的强关联规则，存在着需要很大计算量的问题。另一角度是利用数据内在的某些特性确定参数的方法。如王志愿等^[17]提出根据项集内部的语义相关度动态确定该项集的最小支持度，并采用了项集语义相关度的增量计算方法。实验结果表明，DS-Apriori算法在很大程度上提高了关联规则挖掘算法的效率和效果。Saurav等^[18]提出了一种基于动态阈值的FP-生长规则挖掘算法，该算法将基于加权最短距离的基因表达、甲基化和蛋白−蛋白质相互作用剖面结合起来，在多视点数据集中寻找不同基因对之间的新关联，该方法主要优点之一是它考虑了属于每个规则的所有成对基因之间的定量和交互意义。与以往的方法相比，该算法生成的规则更少，运行时间也更短，并且为得到的顶级规则提供了更大的生物学意义，但该方法是基于生物学基础的统计，缺乏通用性。Jitendra等^[19]提出了一种基于项集范围和相关系数的关联规则集粒子群算法SARIC，该算法能快速、客观地自动确定支持度和置信度。林甲祥等^[20]提出一种新的自动确定支持度和置信度阈值的方法，该方法采用数据分布特性进行曲线拟合确定阈值，为算法的更广泛合理应用提供了可能。但该方法对数据拟合时采用固定阶次的多项式拟合方式，实际应用中不同的数据往往需要采用不同阶次的多项式拟合。

因此，在文献[20]基础上提出一种多项式曲线拟合的阶次自动确定算法AARM_BR(Adaptation Association Rule Mining Based on Determination Coefficient R²)，为进一步自动确定支持度和置信度阈值提供更具有数据统计依赖意义的基础。

2 概念术语

定义1　 D是一个事务数据集，其中每个事务T是由一系列具有唯一标识TID的项目组成的项集。令I={i₁，i₂，···，i_m}是事务数据集D中所有项的集合，每个事务T对应I上的一个子集，即T $ \subseteq $ I，T可表示为T={t₁，t₂，···，t_n}，t_i∈I，n为自然数(n≤m)，表示事务T项集所含的项数。包含k个项的项集，称为k-项集。

定义2　项集X的支持度计数(n_sup(X))是指事务数据集D中包含项集X的事务个数。若项集X $ \subseteq$ I，Y $ \subseteq$ I，且X∩Y=Φ，则形如X $ \Rightarrow $ Y的蕴涵式称为关联规则。令事务数据集D中事务总个数为n_total。规则X $\Rightarrow $ Y的支持度Support(X $\Rightarrow $ Y)是指事务数据集D中同时出现X，Y的事务占事务数据库的百分比；规则X $\Rightarrow $ Y的置信度Confidence(X $\Rightarrow $ Y)是指事务数据集中同时出现X，Y的事务数与包含X的事务数之比。其计算表达式分别为

$ {\rm{Support}}(X \Rightarrow Y) = \frac{{{n_{\rm{sup}}}(X\;U\;Y)}}{{{n_{\rm{tatal}}}}} $

$ {\rm Confidence}(X \Rightarrow Y) = \frac{{{n_{\rm{sup}}}(X\;U\;Y)}}{{{n_{\rm{tatal}}}}} $

定义3　最小支持度minSup和最小置信度minConf是用户或专家定义的分别衡量支持度和置信度的两个阈值。最小支持数(minCount)是指某个项集X为达到最小支持度在事务数据集中至少应出现的次数，等于最小支持度minSup乘于所有事务数；频繁项集是指支持度不小于最小支持度minSup的项集；所谓强关联规则就是指满足最小支持度minSup和最小置信度minConf的关联规则。

通常地，给定一个数据库D，挖掘关联规则的过程可以转换成寻找满足最小支持度minSup和最小置信度minConf阈值的强关联规则过程，即分解成求解所有频繁项集和由频繁项集产生规则两阶段实现。

3 AARM_BR的设计与实现

以最经典的关联规则挖掘算法Apriori为基础，在文献[20]所提基于自适应支持度和置信度的基础上进一步改进，提出一种基于可决系数的自适应关联规则挖掘算法AARM_BR，该算法为进一步确定更具统计意义的支持度和置信度阈值提供可能。文献[20]提出一种支持度和置信度自适应的无参化关联规则挖掘算法AdapARM，该算法是通过数学方法，拟合频繁项集支持数和规则置信度数据的曲线及其二阶导函数，确定数理意义上最适合的数值作为关联规则挖掘的minCount和minConf阈值。该文提出的自适应方法很有应用价值，但文中求取自适应支持度和自适应置信度时采用的拟合多项式是固定次数多项式。本文提出基于可决系数的自适应k次多项式拟合方法，多项式次数k根据自动拟合精度确定，最后以此自适应确定最小支持度和置信度阈值。

3.1 自适应k次多项式

首先，根据事务数据集D中各项的支持数或某个关联规则集的置信度，按从大到小顺序排序并建立“序−值”队列，如式(1)所示。其中，V_t代表某个项在事务数据集D中的支持数或某个规则的置信度。对于支持数，序对的个数t等于事务数据集D中项的个数；而对于置信度，t等于所产生的所有规则数目。

$ \{ ({\text{序列值}},{\text{序号}})\} = \{ (y,x)\} = \left\{ {\left( {{V_1},1} \right),\left( {{V_2},2} \right), \cdots ,\left( {{V_t},t} \right)} \right\} $

(1)

然后，以“序−值”队列中的序号为x，序列值为y建立有序的平面坐标点序列(x_i，y_i)(i=1，2，···，t)。并采用k次多项式进行曲线拟合。拟合的多项式曲线模型为

$ y = f(x) = \sum_{i = 0}^k {{a_i}} {x^j} $

式中：k的取值根据自适应实现，从2次开始，每次递增1，求取对应多项式并判断曲线拟合程度，本算法中选取可决系数 ${R} _k^2 $ 判断曲线的拟合程度。可决系数 ${R} _k^2 $ 衡量因变量与自变量关系密切程度的指标，取值范围在[0，1]之间， ${R} _k^2 $ 越大代表曲线拟合越好。

本算法拟合结束以相邻两阶可决系数 ${R} _k^2 $ 的差小于某个值(设为Rend)为终止条件，Rend由用户指定。多项式次数取拟合结束时的k值。自适应k次拟合多项式算法的具体流程如图1所示，流程中Rend取0.05。

然后，根据确定的k次多项式求取拟合曲线的二阶导数 $f''\left( x \right)$ ：

$ y'' = f''(x) = \sum\limits_{i = 2}^t i \cdot (i - 1) \cdot {a_i} \cdot {x^{i - 2}} $

最后，求解拟合曲线中二阶导数 $f''\left( x \right)=0$ 的点(记x₀)及对应的函数值f(x₀)，x₀下取整作为最小支持数阈值minCount，f(x₀)作为最小置信度阈值minConf。

3.2 AARM_BR算法实现

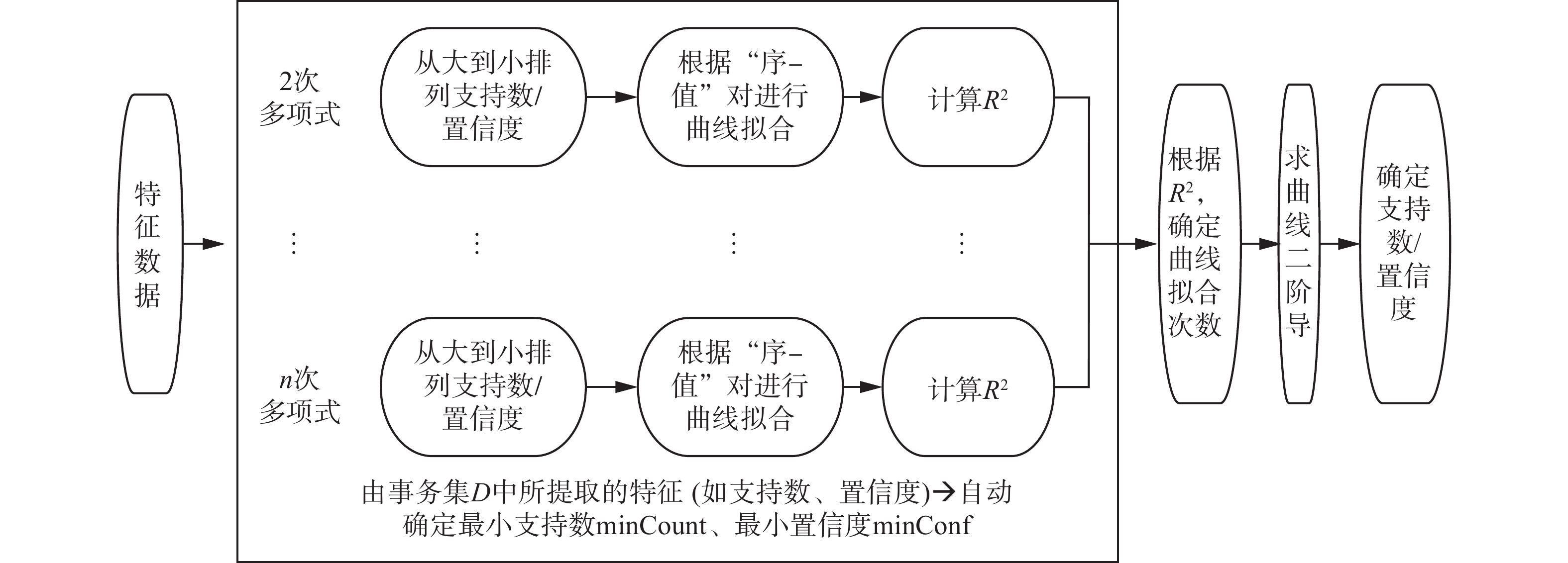
基于可决系数自适应阶次的多项式曲线拟合模型下确定最小支持数和置信度阈值的关联规则挖掘算法AARM_BR的核心流程如图2所示。

AARM_BR算法描述如下：

输入　事务数据集D，拟合结束条件Rend

输出　所有强规则SR，SR={SR₁, SR₂, ···, SR_r}

1) C₁ = find_candidate_1-itemsets(D);

2) C '₁= sort_InDescOrder(C₁); //降序排序

//自适应确定多项式拟合曲线的次数k;

3) k=find_k_polynomial_curve_fitting(C' ₁);

//产生支持数k次多项式;

4) f(x) = polynomial_curve_fitting(C ' ₁,k);

5) find x₀, where f"((x₀)=0;

6) minCount =int(x₀); //x₀下取整并赋给minCount;

7) {L₁, L₂, ···, L_k}= find_all_frequent_k-itemsets(D, minCount);

8) {R₁, R₂, ···, R_t}= generateRule_from_frequent_k-itemsets(L₁, L₂, ···, L_k); //对所有规则按置信度降序排序;

9) R'= sort_InDescOrder(R₁, R₂, ···, R_t); //自适应确定多项式拟合曲线的次数k

10) k=find_k_polynomial_curve_fitting(R');

//产生k次多项式

11) h(x) = polynomial_curve_fitting(R',k);

12) find x₀, where h"(x₀)=0;

13) minConf=h(x₀); //得到最小置信度;

14) {SR₁, SR₂, ···, SR_r} = find_strong_rules({R₁, R₂, ···, R_t}, minConf);

15) Return {SR₁, SR₂, ···, SR_r} //得到所有强规则。

4 实验与分析

为了比较分析，选取文献[12]使用的数据集进行实验。具体数据集为关联规则挖掘购物车Trolley数据集和开源软件R GUI里的Groceries数据集。Trolley数据集总共有9条消费记录(即9行)，包含7种不同商品；Groceries数据集有9 835条消费记录(即9 835行)，包含169种不同商品。下面对自适应k次多项式的挖掘流程进行介绍，并对挖掘结果进行分析和讨论。

4.1 不同阶次拟合对比

首先，分析不同阶次多项式对自动确定支持度阈值的影响。下面给出Trolley数据集和Groceries数据集两个数据集在不同阶次下曲线拟合得到的minCount，分别如表1、2所示。

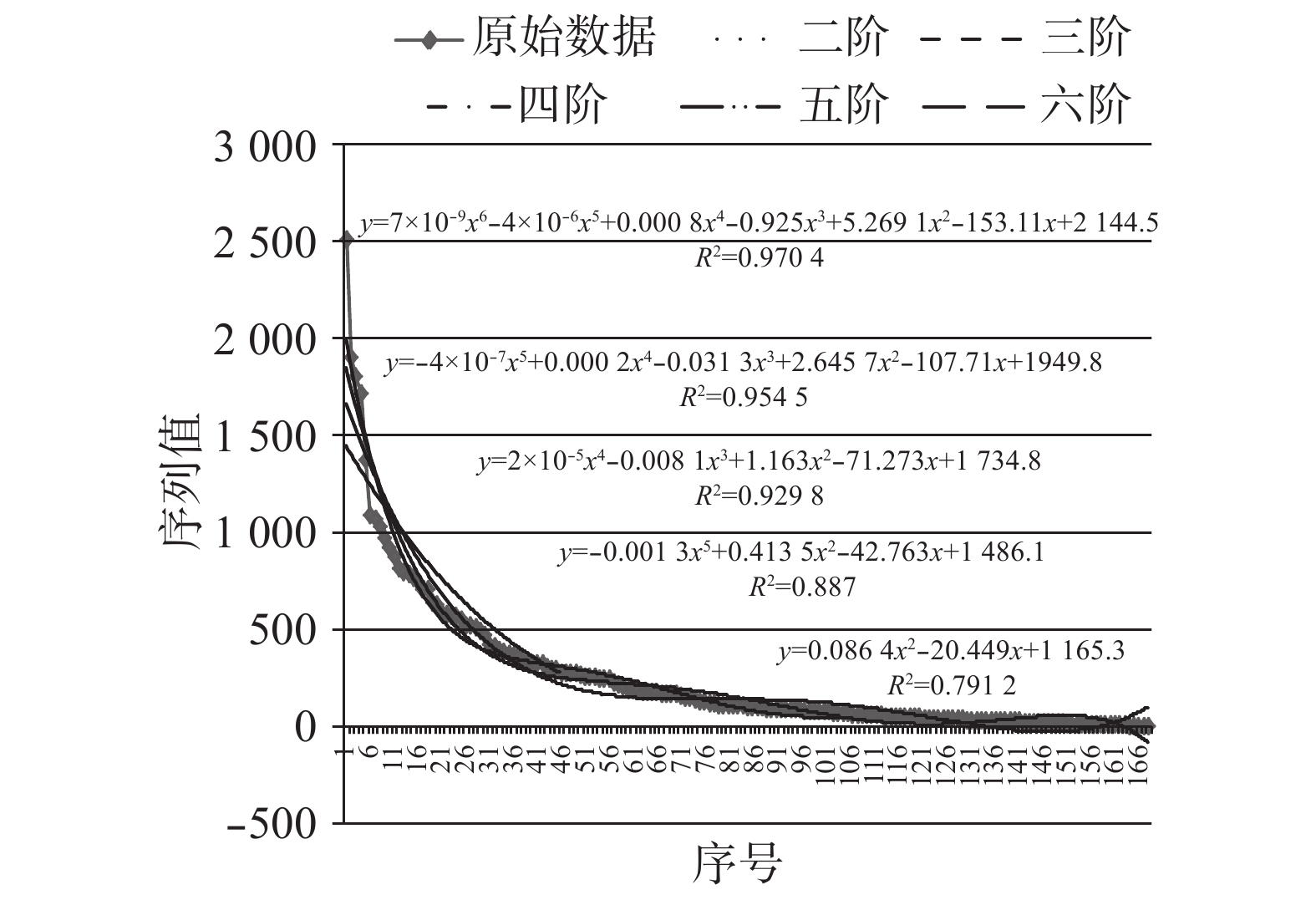
Groceries数据集下确定minCount的不同阶次的多项式拟合曲线如图3所示。

从表1和表2及图3可以看出：1)在相同的结束条件下，不同数据集拟合采用的多项式次数不一定相同，如本实验中数据集Groceries下确定最小支持度时k取4次，而Trolley数据集下k取3次；2)同一数据集下，拟合选取不同次数的多项式，会影响minCount的值，从而也会影响关联规则挖掘的效果。这说明不同的数据集下，不能采取统一阶次的多项次拟合，多项式拟合的阶次应该根据数据拟合的实际情况自适应确定。

其次，分析不同阶次多项式拟合对自动确定置信度阈值的影响。对于Trolley数据集和Groceries数据集在上步minCount约束下所得规则的基础上，自适应拟合确定最小置信度minConf，得到如表3和表4所示结果。

同理，不同数据集中根据自动确定多项式次数是不完全相同的，如本实验拟合精度差Rend取0.05时，数据集Trolley和数据集Groceries的多项式次数都是3次；而若拟合精度差Rend取0.02时，数据集Trolley下多项式次数为4次，而数据集Groceries的多项式次数为3次。同一数据集下不同阶次的多项式下得到的minConf也不尽相同，如Trolley数据集下k取3次时得到minConf为0.612，而k取4次时得到minConf为0.762；Groceries数据集下k取3次时得到minConf为0.094，而k取4次时得到minConf为0.116。综合上述两部分分析说明多项式的阶次会影响阈值，从而也会影响挖掘结果。如何自适应确定多项式阶次是很有必要的。

4.2 结果对比与分析

根据挖掘的流程，首先选取待挖掘数据集中各事务项支持数作为特征数据并按支持数大小进行降序排序建立“序−值”对序列。

其次，采用文中所提的自动阶次拟合方法建立“序−值”对序列的k次多项式曲线拟合模型，自动确定k的次数及对应的多项式。k从2开始，以相邻两阶精度差R²小于Rend为结束条件，本实验以Rend取0.05为例。本步实验结果与文献[12]所提的AdapARM算法比较如表5所示。

然后，根据k阶多项式二阶导函数求取最小支持数，得到对应的二阶导函数及最小支持数minCount如表6所示。

按照Apriori算法思想，在上步求得的最小支持数基础上，从一阶频繁项开始逐层向上，获取所有k阶频繁项集，并根据频繁项集产生关联规则，得到如表7结果。

根据数据集Trolley和数据集Groceries产生的关联规则的置信度从大到小排序并进行k次多项式曲线拟合，k从2开始，以相邻两阶精度差R²小于Rend为结束条件，本实验以Rend取0.05为例。在本步中，两个方法得到的阶次k均为3，确定的拟合多项式如表8所示。

根据k次多项式二阶导函数求取最小置信度，h_T(x)和h_G(x)的二阶导函数h"_T (x)和h"_G (x)公式及对应的最小置信度分别如表9所示。

最后，根据最小置信度确定强关联规则，得到结果如表10所示。

上述算法挖掘结果比较可以看出，自适应多项式挖掘的结果与人为确定多项式次数的挖掘结果不一定相同，如Groceries数据集下人为确定次数有可能遗漏一些重要的规则。根据数据本身的特性确定多项式的拟合次数算法，不需要用户具备先验知识，在不指定多项式阶数、不指定最小支持度和最小置信度阈值的情况下，自动获取数据统计意义下的强关联规则。自适应多项式曲线拟合方法为支持度和置信度的自动确定提供了更具数据依赖意义的解决方案。

从时间复杂度角度分析，本算法只在经典算法Aprori算法的基础上增加了两个步骤：排序和多项式阶次自动确定，其中排序的时间复杂度为O(nlogn)，多项式阶次的自动确定时间复杂度为O(kn)；与AdapARM算法比较，只多了一步自动确定多项式阶次的单层循环。这里增加的时间在整个算法中占用很小，可忽略不计，同时对自动确定最小支持度和最小置信度具有指导意义。

5 结束语

文中提出一种基于可决系数的数据自适应多项式拟合曲线确定支持度和置信度阈值的关联规则挖掘算法AARM_BR。以曲线拟合的精确程度R²为判断依据，自适应确定多项式拟合曲线的次数及多项式，在此基础上求取k次拟合多项式的二阶导函数为零的点x₀及其函数值f(x₀)，作为支持数和置信度阈值，进而获取数据依赖意义下最小支持数和最小置信度及其强关联规则。该方法根据数据自身特点，在用户不具备经验知识、不指定支持度和置信度阈值的情况下，自动确定拟合曲线、最小支持度和最小置信度阈值。在两个标准数据集Trolley和Groceries上的实验结果和分析表明，该方法对关联规则的进一步推广应用具有一定价值。