2. 中国科学院大学,北京 100089;
3. 中国科学院 脑科学与智能技术卓越创新中心,上海 200031;
4. 半导体神经网络智能感知与计算技术北京市重点实验室,北京 100083
2. University of Chinese Academy of Sciences, Beijing 100089, China;
3. Center for Excellence in Brain Science and Intelligence Technology, Chinese Academy of Sciences, Shanghai 200031, China;
4. Semiconductor Neural Network Intelligent Perception and Computing Technology Beijing Key Lab, Beijing 100083, China
近年来,由于大数据时代海量数据的获取以及计算机性能的显著提升,以卷积神经网络为代表的深度学习算法在许多领域体现出了巨大的优越性。在计算机视觉方向,深度学习的方法已经获得了超过人类的认知和分类水平[1]。然而像典型的分类网络VGG-16,需要15.5 G次乘加操作和138 M的参数量[2],巨大的计算量和参数量使得卷积神经网络的实际应用困难重重。
如何加速卷积神经网络计算,近年来一直是个活跃的研究领域。文献[3]研究了卷积神经网络的加速基本方法,并分析了加速设计的性能瓶颈。文献[4]比较了各种典型的并行展开方法,提出了适合实时卷积神经网络计算的数据流结构。文献[5]设计了多个卷积层处理器,分别加速不同的卷积层。文献[6]比较了不同的卷积计算展开方式,并提出了有效的数据复用和资源展开方法。
然而仅从计算性能和带宽瓶颈上入手对加速卷积神经网络计算来说还远远不够,有效利用神经网络本身的稀疏性,能够从算法层面大大加快网络计算速度[7]。卷积神经网络的稀疏性体现在激活结果和网络参数两个方面。
文献[8]利用激活稀疏性压缩了激活结果中的零值,节省了传输带宽开销并降低了计算功耗。文献[9]利用激活稀疏性对卷积计算激活结果压缩编码,在次层计算中跳过激活输入中的零值降低了卷积神经网络计算量。文献[10]利用参数稀疏性,将激活输入中权重无效的输入剔除,降低了卷积神经网络计算量。文献[11]同时利用激活稀疏性和参数稀疏性,实时选择激活输入中的有效值广播给所有PE,PE独立索引,将有效的激活输入和权重的乘积累加到对应位置完成卷积计算,有效降低了网络计算量和参数量。文献[12]同时利用激活稀疏性和参数稀疏性,PE内使用笛卡尔乘积的方法,完成稀疏激活输入与稀疏权重的乘积,再将乘积结果还原到对应位置进行累加完成卷积计算,有效降低了网络计算量和参数量。
尽管这些方法都能在一定程度上利用卷积神经网络的稀疏性优化计算,但是我们注意到它们很难兼顾计算灵活性、并行效率和资源开销。文献[8]虽然利用激活稀疏性压缩了激活结果,但受制于计算方式的规整,实际上并没有将它用于降低计算量。文献[9-10]、[12]没有对并行计算负载失衡导致的性能损失问题进行优化,进行卷积计算时平均有20%~40%的性能损失在负载失衡上[12]。文献[11]只对输出特征图方向进行了并行展开,在计算输出特征图较少的卷积层时不能完全利用计算性能,并行效率受到明显影响。文献[10-12]为了利用参数稀疏性,每个PE都需要庞大的逻辑和存储空间配套,这不利于大规模并行,尤其是在FPGA设备上不能将乘法器资源充分利用,并且这些设计对于计算量密集的卷积计算,最终体现出的加速效果也一般,性价比并不高。
针对这些问题,提出了一种利用稀疏性加速计算同时并行效率极高、额外资源开销较小的并行展开方法,设计并实现了能够高效利用稀疏性加速计算的卷积神经网络加速器。对于卷积层,我们通过使用内核脉动阵列展开与特征图平铺展开结合的并行展开方式,在有效利用激活稀疏性减少计算量加速计算的同时,降低了并行计算负载失衡对加速效果的影响;对于全连接层,我们选择使用压缩稀疏列的计算方式,同时利用激活稀疏性和参数稀疏性,明显的降低了参数量和计算量。
1 卷积神经网络的稀疏性自然界中的神经系统本身是稀疏的[13],卷积神经网络本身也是稀疏的。卷积神经网络的稀疏性体现在激活结果和网络参数的两个方面。
卷积神经网络的激活结果是稀疏的。卷积神经网络使用非线性激活函数模仿了生物中神经元的放电方式[14],近年来被广泛使用的ReLU激活函数将所有负值激活为零,给卷积神经网络的激活结果带来了显著的稀疏性[15]。例如AlexNet中卷积层有19%~63%的激活结果是0[16],而对0进行乘累加对计算结果没有任何影响,跳过这部分的无效计算,就能给卷积神经网络加速器带来明显的性能提升。
卷积神经网络的网络参数是冗余的。卷积神经网络使用了大量的参数来保证网络足够的复杂度和表现力,然而大量实验证明,增加参数量并不一定能提升网络效果,甚至会带来网络的过拟合[17]。特别地,虽然卷积神经网络的全连接层占用了绝大部分的参数量,却仅贡献了非常小的计算量。例如VGG-16中全连接层使用了89.4%的参数,却仅仅占用了0.8%的计算量。实验证明全连接层的连接是非常稀疏的,能够在不损失网络精度的情况下,通过剪枝移除超过90%的全连接层连接[18]。
如图1所示,实验随机选取了ImageNet数据集中的500张图,直接使用VGG-16网络不做任何优化的原始基础参数,统计了每一层的激活输入稀疏性。实验结果表明,对比VGG-16基准网络模型,在理想情况下利用激活稀疏性能够降低50.92%的计算量。

|
Download:
|
| 图 1 利用激活稀疏性前后VGG-16网络每层计算量的变化 Fig. 1 Changes of the computation amount of VGG-16 network layer before and after utilizing the sparsity of activation | |
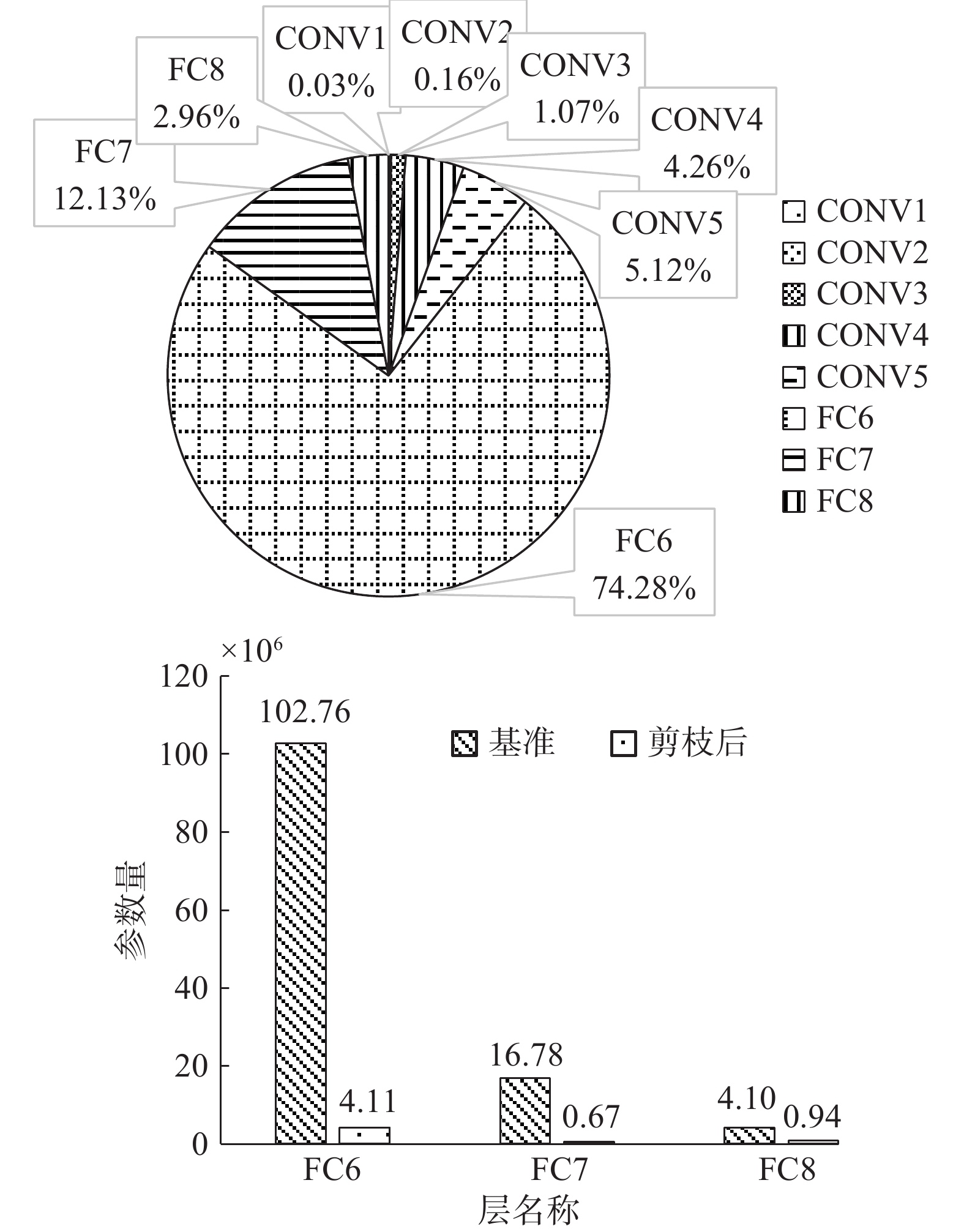
使用动态精度量化的方法[19],将参数与激活结果均量化为8 bit,并对全连接层进行了剪枝,比较了网络剪枝前后的参数量。实验结果如图2所示。实验结果表明,全连接层占据了大部分的参数量,对全连接层进行稀疏剪枝能够降低85.23%的参数量。以上两个实验证明了,即使不对网络结构进行任何额外的优化,利用稀疏性对卷积神经网络计算的提升也非常明显。如何有效利用稀疏性优化计算是当前的卷积神经网络加速器设计必须要认真考虑的问题。
|
Download:
|
| 图 2 VGG-16全连接层参数量比重与剪枝前后的变化 Fig. 2 Proportion and Changes of the parameters amount of VGG-16 full connected layer before and after pruning | |
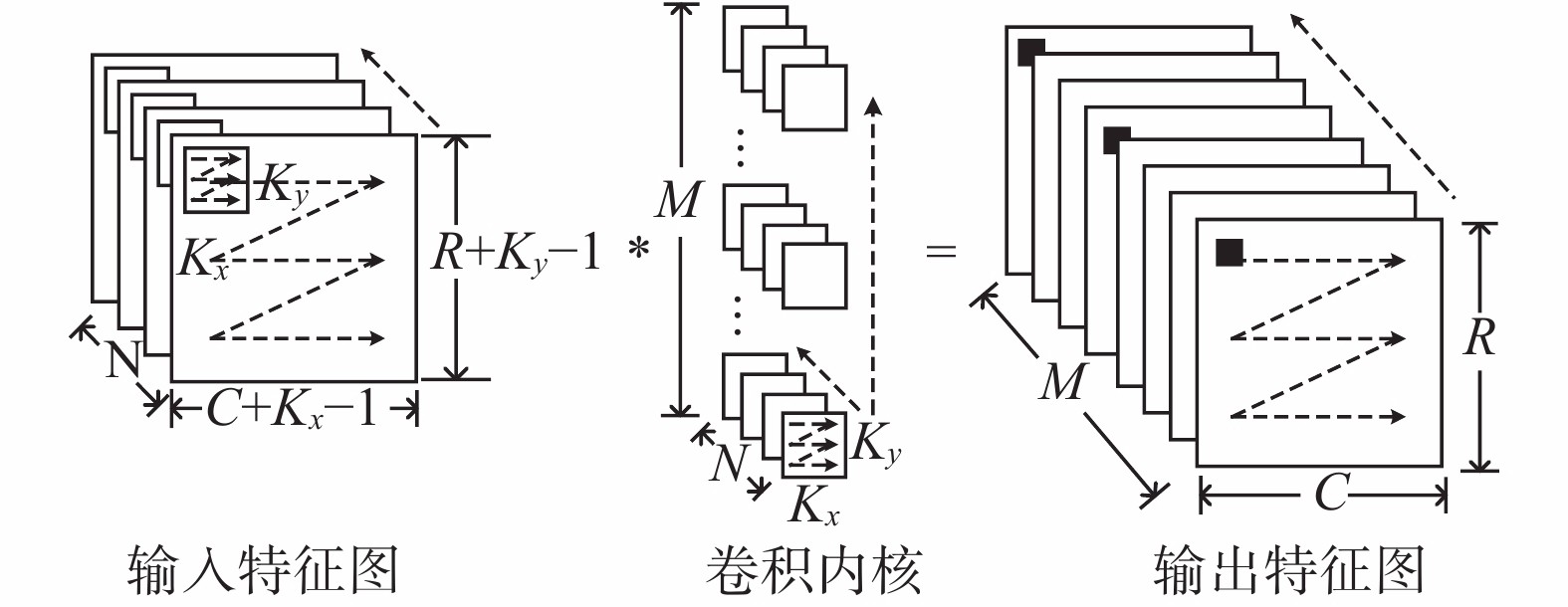
典型的卷积神经网络卷积计算如图3所示。输出特征图的行数为R、列数为C,输入特征图的尺寸考虑了边界补零,输入特征图通道深度为N,输出特征图的数量为M,内核行方向为Kx,内核列方向为Ky。进行卷积操作时,N个大小为Kx×Ky的窗口同时在输入特征图上滑动,每次获取一个大小为Kx×Ky×N的张量,分别与M个输出特征图的权重卷积。卷积的M个计算结果为输出特征图上的一个像素点,通过依次滑动窗口,最终获得完整的输出特征图。卷积计算的伪代码如算法1中表示。
|
Download:
|
| 图 3 卷积层计算示意 Fig. 3 Schematic diagram of convolution computing | |
| 算法1 典型的卷积计算伪代码 | |
|
|
//输出特征图 |
|
|
//输入特征图 |
|
|
//特征图的行 |
|
|
//特征图的列 |
|
|
//内核行方向 |
|
|
//内核列方向 |
|
|
//乘累加 |
| }}}}}} | |
利用稀疏性加速卷积神经网络计算会给硬件上带来两个问题:首先,稀疏的卷积计算是不平衡的,而并行计算时负载失衡会导致计算单元利用率下降,损失性能,在并行队列数量较多、队列长度不够长时,负载失衡的影响会非常明显;其次,对激活输入和权重的判断或选择会增加逻辑复杂度,可能会带来不能接受的面积开销,影响并行展开规模。
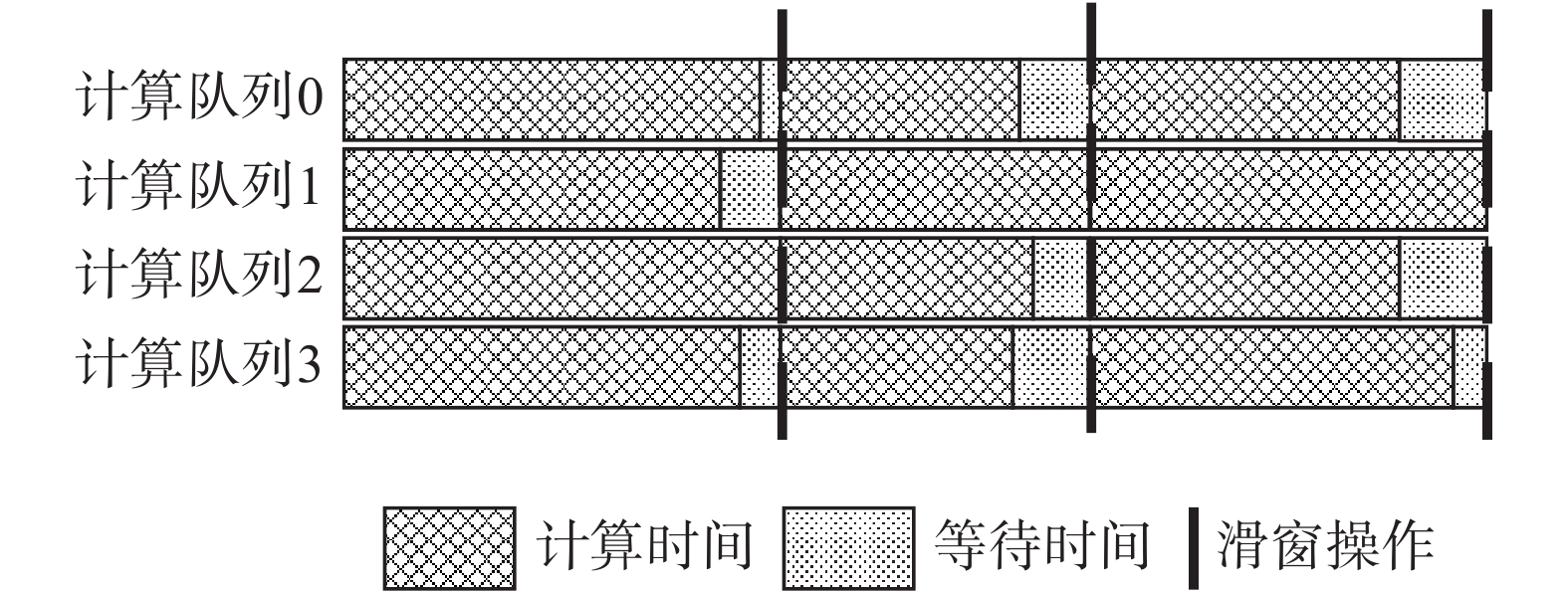
用系统并行自由度来表征并行计算的负载失衡。如图4所示,大部分卷积计算是以窗口滑动为时间基本单位控制时序的,窗口滑动之间需要等待所有并行化方向上的计算队列计算完成,所以系统并行自由度越高,负载失衡造成的性能损失就越严重。对于完全规则设计的卷积计算模型,所有并行计算队列的计算时间是相同的,这样的系统的并行自由度为1,而增加对权重
|
Download:
|
| 图 4 并行计算性能损失示意 Fig. 4 Schematic diagram of parallel computing performance losses | |
卷积计算硬件化设计的关键在于如何兼顾数据共享、复用和计算的灵活性,对于稀疏的卷积计算,需要最大化数据共享来降低并行计算时负载失衡导致的性能损失。本文分别从并行展开方式和利用稀疏性方式进行分析比较,确定并行效率极高、额外资源开销较小的稀疏卷积神经网络加速器设计。
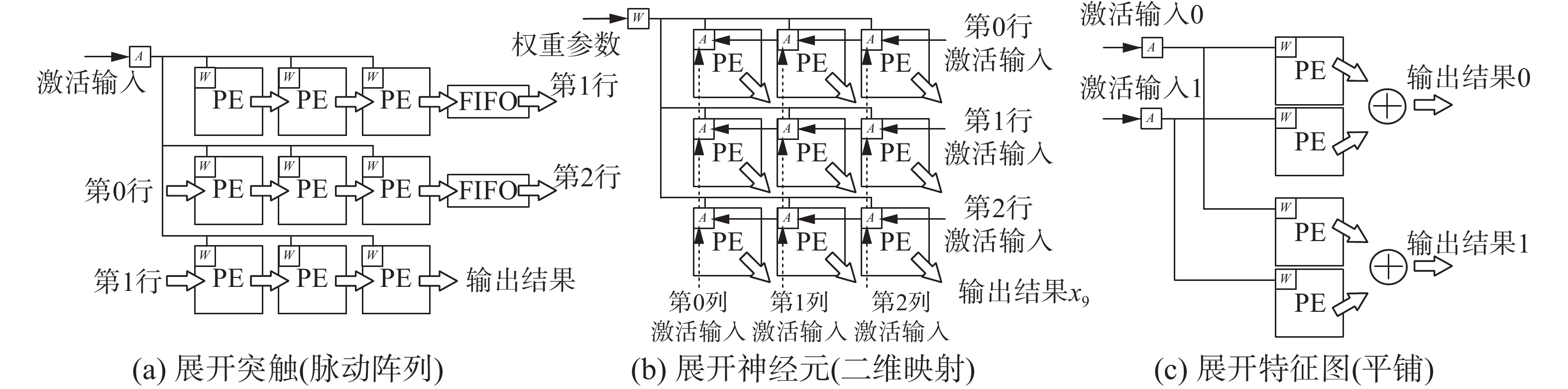
2.1 并行展开方式如图5所示,总体来说,卷积神经网络加速器设计的卷积计算的并行展开方式可以分为3种:展开突触(Kx、Ky)、展开神经元(R、C)、展开特征图(M、N)。大部分卷积神经网络加速器的设计都是按照这3种并行展开方式的其中的一种或者多种展开的[4]。
对突触进行并行展开通常使用脉动阵列[20]的方式。如图5(a)所示,图中Kx=Ky=3,PE缓存权重,按照内核行方向Kx从左到右级联,每次计算时PE将乘法运算结果与左边相邻PE输入的值做加法运算送往右边相邻PE,每行最右边PE通过一个深度为R的FIFO连接到次行,脉动阵列的输入为0,通过全部9个PE之后计算完成全部内核方向的计算。这种并行展开方式共享了激活输入,复用了权重。它利用激活稀疏性的系统并行自由度为1,利用参数稀疏性的系统并行自由度为Kx×Ky,同时利用两种稀疏性的系统并行自由度为Kx×Ky。
|
Download:
|
| 图 5 并行展开方式示意 Fig. 5 Schematic diagram of parallel expansion mode | |
对神经元进行并行展开通常使用二维映射的方式,如图5(b)所示,特征图的行方向R和列方向C被分块为Tr与Tc,图中Tr=Tc=3,计算开始时,Tr×Tc的激活输入被初始化到Tr×Tc个PE上,权重
对特征图进行并行展开通常使用平铺的方式。如图5(c)所示,输入特征图N和输出特征图M被分块为Tn与Tm,图5中Tn=1,Tm=2,对应相同输入特征图的乘法器共享激活输入,对应相同输出特征图的乘法器将计算结果经由一个加法树累加输出。这种并行展开方式共享了激活输入。它利用激活稀疏性的系统并行自由度为Tn,利用参数稀疏性的系统并行自由度为Tm,同时利用两种稀疏性的系统并行自由度为Tn×Tm。
假设同时利用权重
基于以上这些考虑,在卷积层计算时仅利用了激活输入
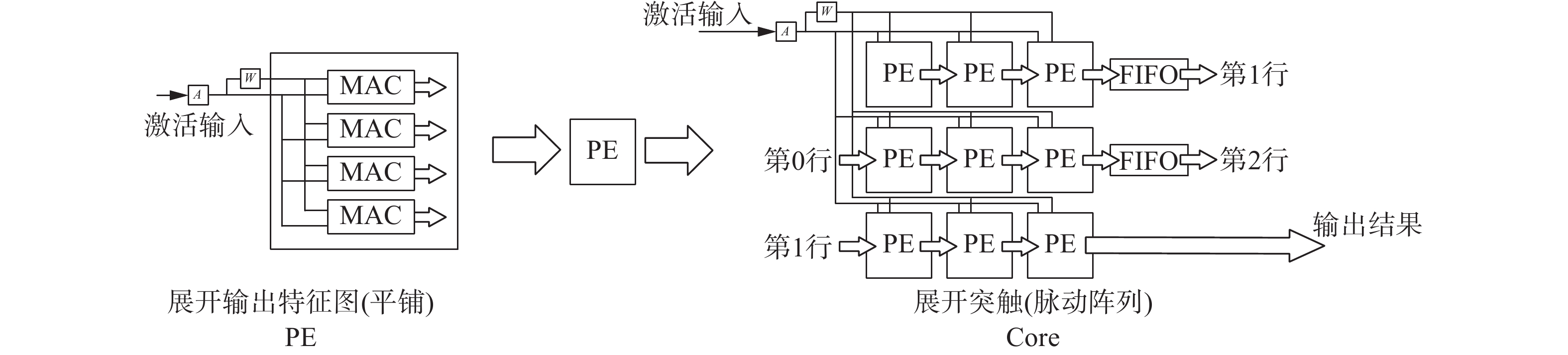
|
Download:
|
| 图 6 本设计使用的并行展开方式示意 Fig. 6 Schematic diagram of parallel expansion mode in our design | |
| 算法2 卷积层计算伪代码 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
注意到现代卷积神经网络的卷积核几乎只有3×3和1×1,并且对于大于3×3的卷积核(例如5×5)可以使用多次3×3卷积替代[2]。类似的,每个PE组分别独立计算输出特征图即可以将3×3卷积工作模式转换成1×1卷积工作模式。所以本文提出的这种并行展开方式展开3×3的卷积核是可以适应于大部分卷积神经网络的。
全连接层参数量巨大,片上片下传输带宽是全连接层计算瓶颈,不做任何算法优化在硬件上完成全连接层计算是效率极低的,并且本身全连接层稀疏性非常高(对于VGG-16,FC-6的有效参数密度为4%),计算队列的长度特别长(VGG-16,不分块情况下FC-6的激活队列长度为25 088),足以忽略负载失衡造成的性能损失,非常适合利用参数稀疏性进行计算,所以对全连接层计算使用压缩稀疏列(CSC)方式同时使用了激活稀疏性和参数稀疏性。全连接层计算是简单的矩阵乘法,使用平铺的方式并行展开输出特征图效率最高,此时系统并行自由度为Tm。对应的全连接层计算伪代码如算法3所示。
| 算法3 全连接层计算伪代码 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
卷积神经网络稀疏性分为激活稀疏性和参数稀疏性两种,利用稀疏性的方式直接决定了设计的复杂性和额外的资源开销量,我们分别分析不同的利用稀疏性方式。
利用激活稀疏性主要可以分为压缩编码和多路选择两种方式,如图7所示。压缩编码方式将激活结果分块,按顺序判断激活结果是否有效,记录有效激活结果的值和有效激活结果之间的距离。多路选择方式一次读入多个激活输入,按优先级从中选择有效的激活结果,输出激活结果的值和位置。压缩编码方式能够降低传输功耗,但不适合通道较浅的卷积层;多路选择方式不能降低传输功耗,但逻辑更简单,并且适应所有卷积层。

|
Download:
|
| 图 7 利用激活稀疏性的方式 Fig. 7 Method of using activate sparsity | |
文献[8-9]、[12]使用了压缩编码的方式,文献[11]使用了多路选择的方式。本文在上节中实际分析了VGG-16网络在ImageNet下的激活稀疏性在50%左右,使用压缩编码的方式能够降低50%的激活结果数据量,但与此同时对压缩编码的索引也是需要占用数据量的。几乎所有分类网络经过优化都能使用动态精度量化的方法量化成8 bit激活结果与8 bit权重[21]。如图8所示,随着激活结果量化程度的不断提高,对激活结果进行压缩编码的收益是在不断下降的。并且我们的设计充分靠虑了最大化共享激活输入,使用多路选择的方式消耗的激活压缩单元会非常少。基于资源开销和普适性的考虑,我们使用了多路选择的方式利用激活稀疏性。
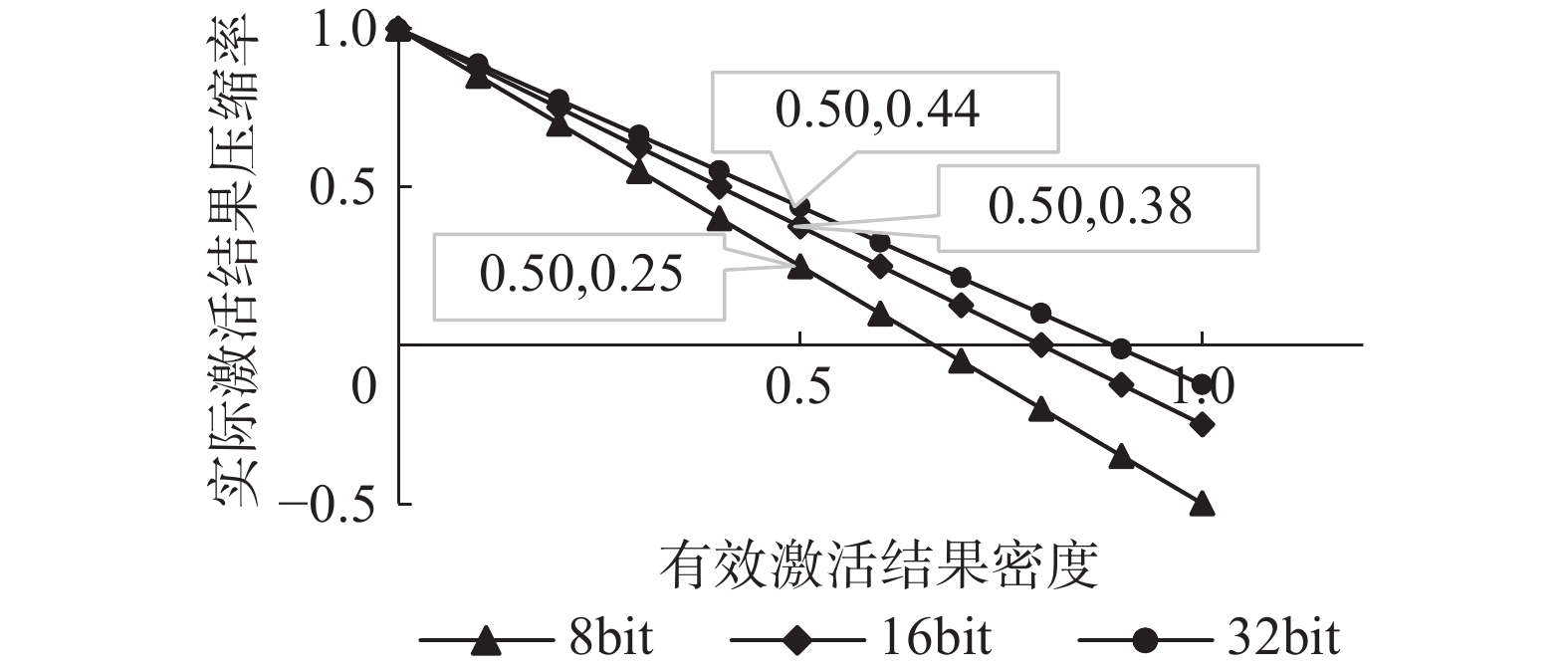
|
Download:
|
| 图 8 不同量化精度下VGG-16压缩编码实际压缩效率 Fig. 8 Actual compression efficiency of VGG-16 compression code with different quantization precision | |
利用参数稀疏性主要可以分为压缩稀疏行CSR和压缩稀疏列CSC两种方式[22],如图9所示。压缩稀疏行CSR,稀疏矩阵按照输出特征图分离成若干个独立计算,每个输出特征图共享输入特征图,并分别按照权重的有效性选择激活输入进行乘累加计算。压缩稀疏列CSC,稀疏矩阵按权重方向分离成若干个计算队列,每个计算队列对应一个激活输入,计算时依次选择有效权重与激活结果相乘,并将乘积累加到对应输出特征图位置。
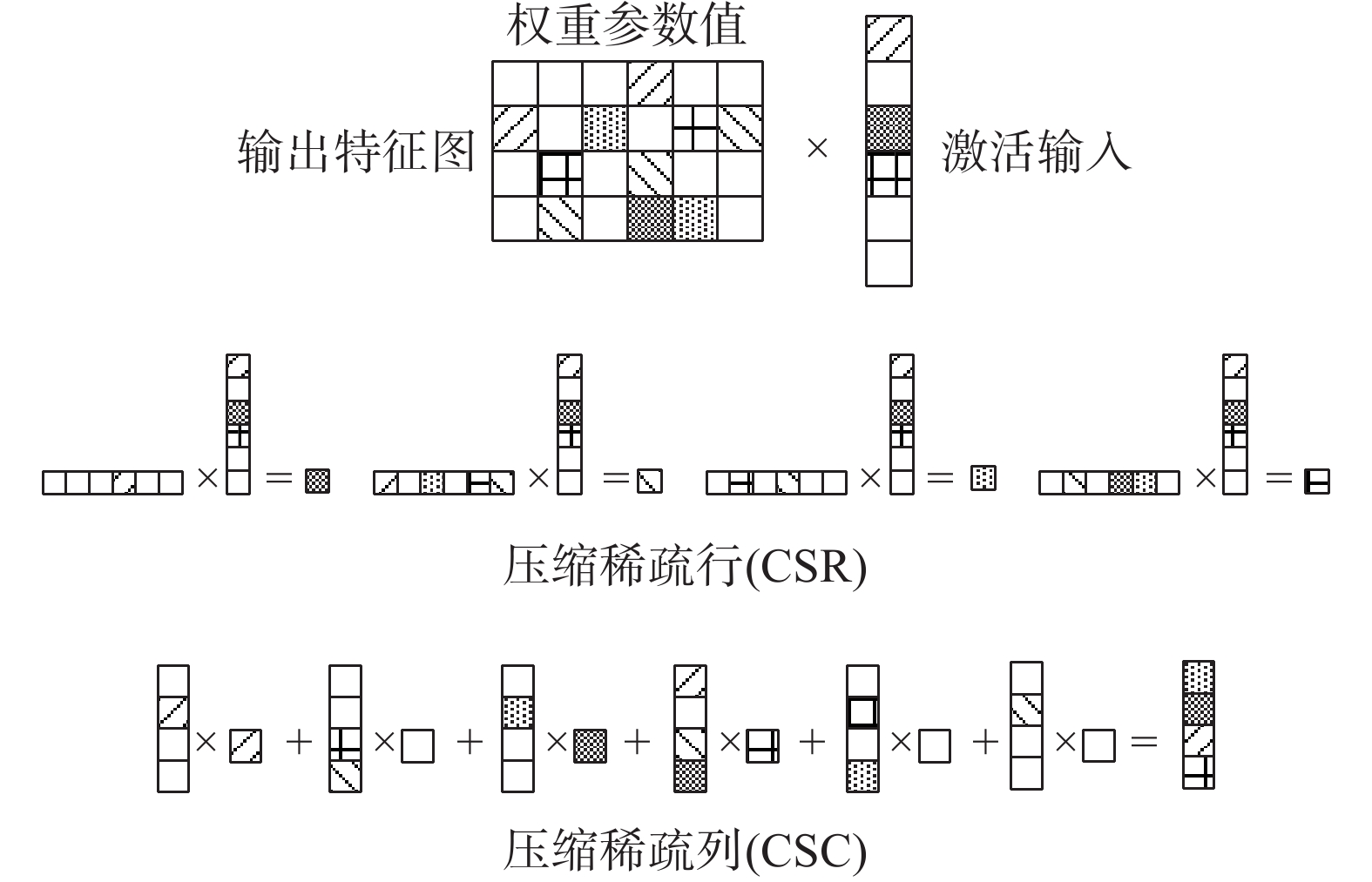
|
Download:
|
| 图 9 利用参数稀疏性方式 Fig. 9 Method of using parameter sparsity | |
CSR模式需要完成两个稀疏矩阵的乘法,复杂性较高,文献[12]利用笛卡尔乘法在CSR模式完成了稀疏矩阵计算,文献[10]使用CSR模式仅利用了参数稀疏性。CSC模式将计算分离成了若干个计算队列,选择有效队列就能利用激活稀疏性,更容易实现,文献[11]使用了CSC模式同时利用了激活稀疏性和参数稀疏性。使用CSC模式完成全连接层计算。
全连接层稀疏计算PE如图10所示。多路选择获得的有效激活输入和索引被送入PE,通过一个存储权重指针的逻辑获得这个有效激活输入对应的有效权重的头地址和长度,然后从权重缓存中依次读出权重。权重由位置索引和值两部分组成,在乘累加缓存区域获得位置索引对应位置的乘累加值,与新产生的乘积累加,再送回乘累加缓存区域,使用一个旁路逻辑缓存乘累加结果,避免相邻周期对同一个位置读写导致的一个周期的时间惩罚。
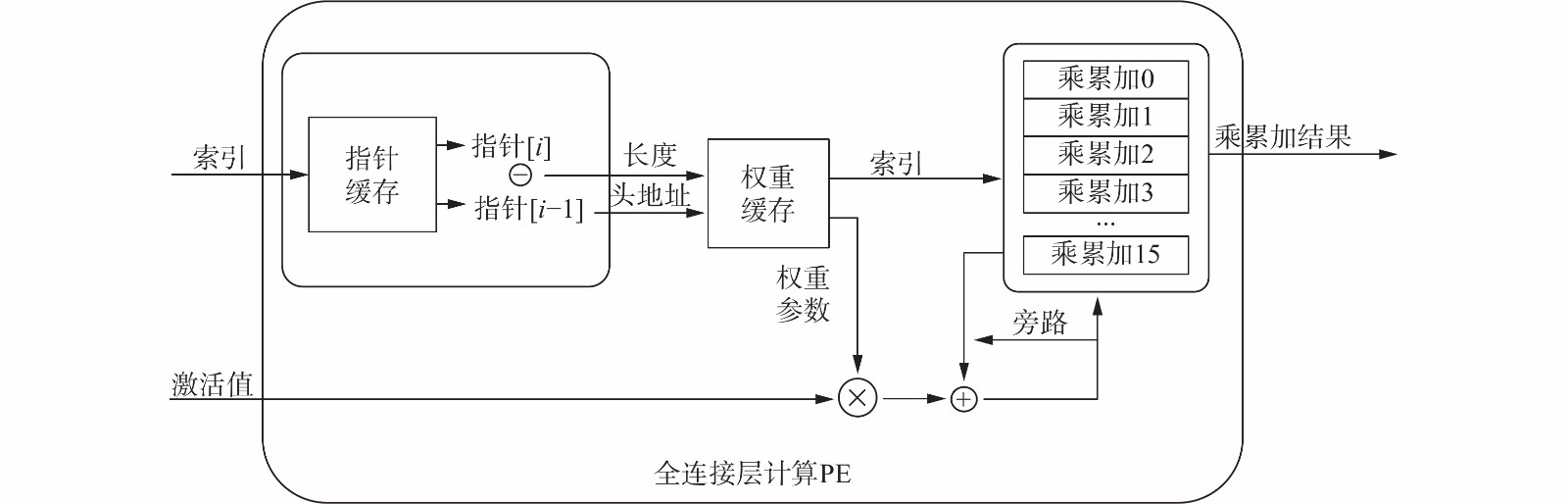
|
Download:
|
| 图 10 全连接层稀疏计算PE示意 Fig. 10 Schematic diagram of sparse computing PE for FC layer | |
我们分别比较了上述几种卷积神经网络加速器利用稀疏性的方式和并行展开方式,见表1。表1中稀疏性A代表激活稀疏性,稀疏性W代表参数稀疏性,CSR代表压缩稀疏行,CSC代表压缩稀疏列,展开方式S、N、F分别代表突触(synapse)、神经元(neuron)、特征图(feature map)。
| 表 1 并行展开方式和利用稀疏性的方式比较 Tab.1 Compare of parallel expansion and method of using sparsity |
从表1中可知,几乎所有利用稀疏性加速卷积神经网络计算的加速器都受到了负载失衡的影响。文献[11]系统并行自由度仅受到参数稀疏度不平衡性影响,这是因为它只对输出特征图方向进行了展开,然而这种并行展开是有上限的,当展开规模大于输出特征图数量时,继续并行展开并不能提升计算性能。不考虑利用参数稀疏性的情况下,和文献[11]相比,在同样负载失衡损失条件下实现了Kx×Ky倍的并行展开规模和更小的单位乘法器资源开销。和同样仅利用激活稀疏性加速卷积计算的文献[9]相比,本文实现了比它更低的负载失衡损失和更少的单位乘法器资源开销。综上所述,本文提出的利用激活稀疏性加速卷积神经网络计算,相比于同领域其他设计,并行效率更高、额外资源开销更小。
3 硬件设计与实现本文使用了具有ARM+FPGA的Zynq系列异构计算体来设计卷积神经网络加速器。ARM处理器部分被称为PS端,FPGA被称为PL端,两者之间通过多种接口互联。PS端即ARM处理器部分,我们运行了linux操作系统用于从文件中读取权重和输入、测量时间并控制DMA(direct memory access,直接内存存取)等各个模块进程。PL端即FPGA部分,我们使用HLS工具设计了共用端口的卷积计算模块与全连接计算IP核、可配置工作模式的输入网络和输出网络、非线性激活ReLU模块、极大池化模块和数据整合模块,使用SDSoC工具完成了DMA与PL-PS交互控制设计。PS与PL之间连接有4个高速的HP端口和4个中速的GP端口用于传输数据。整体架构如图11所示。
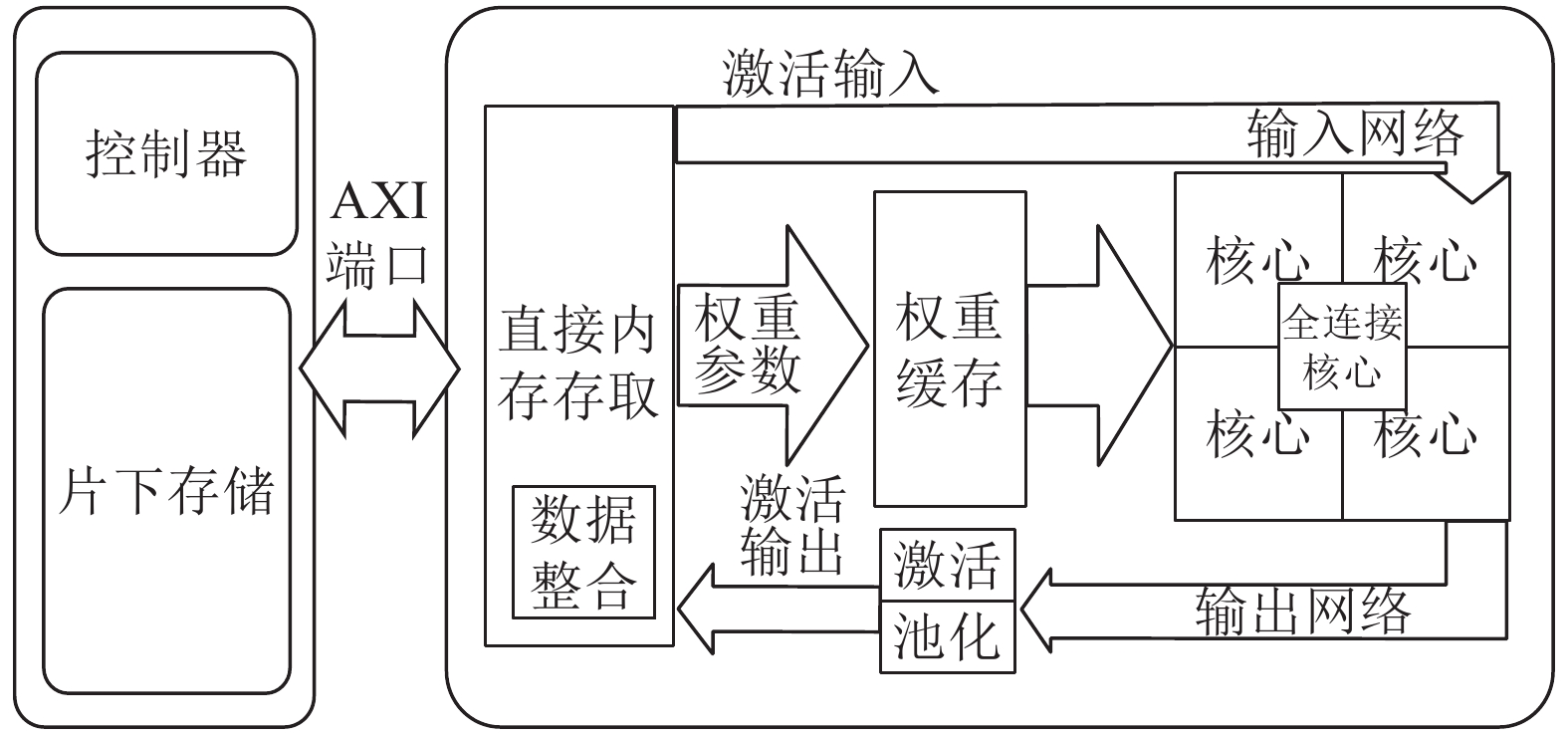
|
Download:
|
| 图 11 系统整体架构 Fig. 11 Schematic diagram of the overall architecture | |
网络参数和输入图片都被存储在文件系统中,在初始化时会读取到片下存储DRAM,再通过DMA传输到卷积神经网络加速器中。在卷积计算过程,ARM会控制卷积神经网络加速器按照规定顺序,以分块乒乓操作的形式读取权重并完成每一层网络的计算。计算完成之后ARM将卷积神经网络加速器计算结果与计算时间通过串口打印输出。
平铺展开设计的卷积神经网络加速器往往被认为对不同卷积层计算效率适应性不高,通过配置输入网络和输出网络的方式实现了多工作模式,这能让卷积神经网络加速器在计算不同卷积层时利用率更高。如图12所示,(a)代表所有核心共享激活输入,同时计算1组输入特征图和4组输出特征图,这种计算模式带宽压力最低,并行效率最高;(b)代表核心同时计算两个输入特征图两个输出特征图,这种计算模式适合卷积层输出特征图较少的情况;(c)代表所有核心计算不同的激活输入,这种计算模式适合输入特征图通道极深的情况;(d)代表核心左右分成两组分块计算,这种计算模式适合网络输入层尺寸极大的情况。通过多核心组合多种工作模式的方法,设计的卷积神经网络加速器能够支持最高2 048通道的输入特征图以及最大1 024尺寸的网络输入层计算。在计算VGG-16网络时,我们设计的卷积神经网络加速器每一层卷积计算的PE利用率均为100%,没有因为适应性导致性能损失。

|
Download:
|
| 图 12 多种工作模式示意 Fig. 12 Schematic diagram of multiple working modes | |
使用了高级语言硬件设计工具链vivado HLS和SDSoC进行FPGA上的实现。首先在vivado HLS上完成计算IP核的设计与功能时序验证,再修改接口,移植到SDSoC上完成IP核读写接口与软硬件环境的设计,系统级验证测试带宽影响。所有功能和时序验证通过后使用vivado综合实现,得到实际资源报表和比特流Bitstream。我们设计的卷积神经网络加速器资源使用情况如表2所示。工作频率保守的设置为100 MHz,AXI总线设置为200 MHz。每个卷积核心使用了32×9=288个乘加器,75%使用DSP实现,剩余的部分使用LUT实现,有4个这样的卷积核心;全连接层计算核心使用了16个乘加器,全部用DSP实现。
| 表 2 FPGA资源使用情况 Tab.2 Utilization report of FPGA |
生成的linux内核、可执行程序、Bitstream文件最终打包,通过SD卡移植到开发板上实际测试。程序中调用了SDSoC提供的高精度时钟计数接口,计算完成后会将计算结果和每层所用时间打印到串口。
4 性能分析评估与比较 4.1 加速效果与并行展开方式比较影响加速效果的最主要因素是激活输入的不平衡。局部上,多路选择需要一个周期,如果激活输入极为稀疏也要受到一个周期的时间惩罚;整体上,计算的整体时间取决于最长的计算时间队列,如果并行展开存在多个计算队列,负载失衡影响加速效果。基于这两个因素,我们使用TensorFlow环境,在ImageNet数据集下运行VGG-16网络,统计了不同的并行展开方式最终的加速效果,如图13所示。由于我们的设计单个核心内部无负载失衡损失(1 IFM),加速效果均比其他的并行展开方式优秀。相比于稠密卷积计算,设计的卷积神经网络加速器理论上能加速1.92倍。

|
Download:
|
| 图 13 VGG-16网络不同的并行展开方式加速效果比较 Fig. 13 Comparison of acceleration effects of VGG-16 networks with different parallel expansion modes | |
卷积神经网络加速器设计的一个重要考虑因素就是系统带宽。考虑到我们利用稀疏性加速了卷积计算,计算速度更快,系统带宽压力会比普通设计的加速器的带宽压力要高。分析了极限情况下(计算加速4倍)系统带宽情况,如图14所示,图中IFM代表输入特征图读操作,OFM代表输出特征图写操作,OFMDM代表输出特征图整合操作,W代表权重读操作。
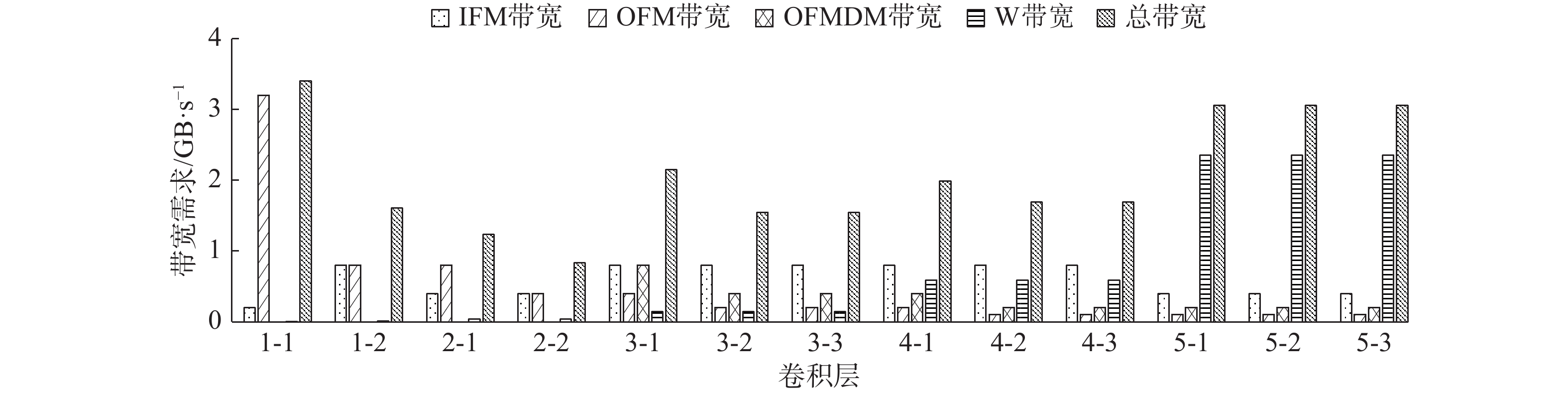
|
Download:
|
| 图 14 VGG-16网络极限情况下系统带宽需求 Fig. 14 Limit case system bandwidth requirements of VGG-16 network | |
系统带宽瓶颈来自于两个方面,我们使用的DDR3内存带宽上限为读写总共4.2 GB/s,对于PS与PL连接的HP端口,每个端口读带宽1.6 GB/s、写带宽1.2 GB/s。本文分配了3个HP端口用于权重读取,大部分情况下加速器都没有因为带宽瓶颈影响性能,卷积计算各层带宽占用如图14所示。本文使用将激活结果量化为了INT8,并且对需要分块计算的卷积层使用多核心共享激活输入的方式降低了带宽压力。
4.3 计算时间与有效激活输入密度关系本文测量了不同卷积层的实际有效激活输入密度和对应的计算时间,如图15所示,其中计算时间根据各层不加速情况进行了归一化。从图15中可以看出,加速器加速效果与有效激活输入密度在大部分区间成正比,当理论激活输入密度靠近0.25时,受到多路选择单元瓶颈影响(从4路输入中选择一路),即使激活输入密度更低加速效果也基本上不会增加。
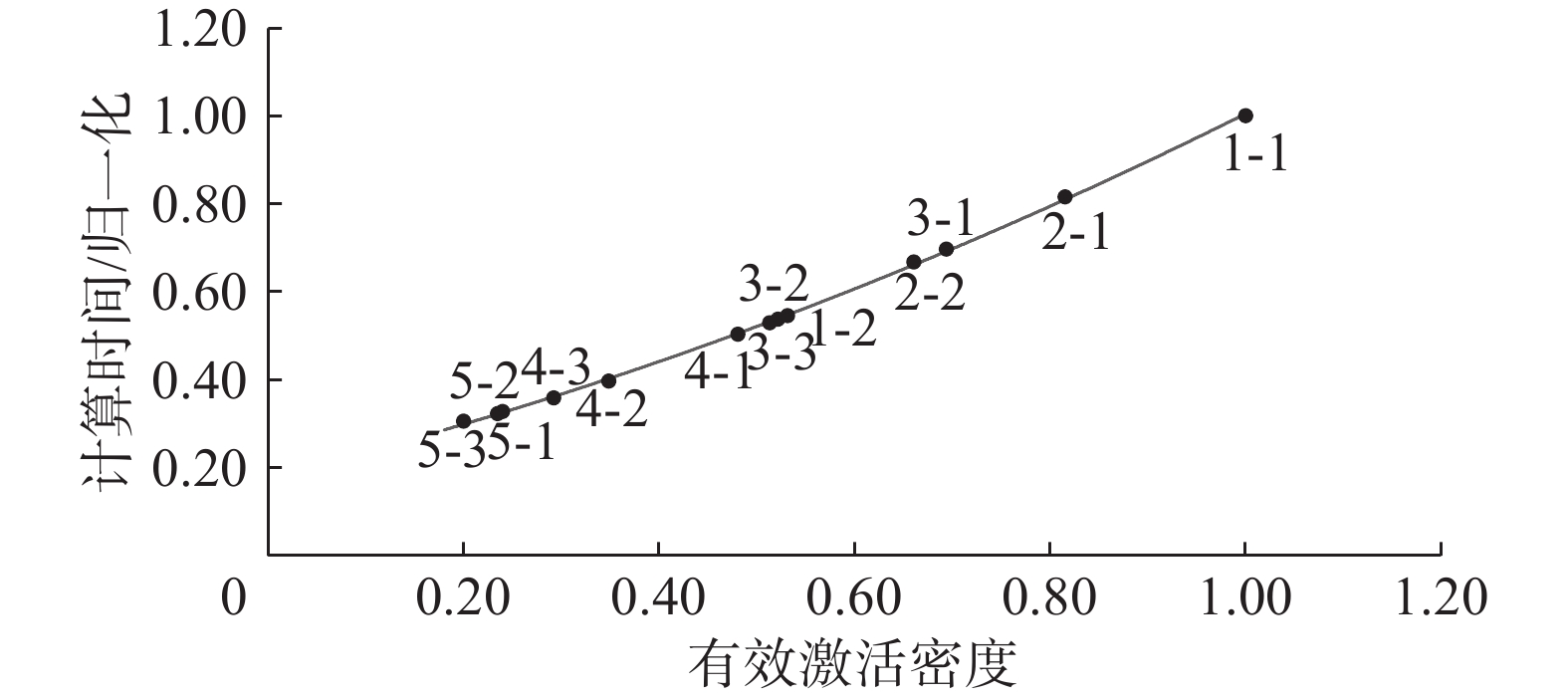
|
Download:
|
| 图 15 VGG-16网络计算时间和有效激活输入密度关系 Fig. 15 Relationship between computing time and effective activation input density of VGG-16 network | |
本文完整地测量了卷积神经网络计算时间,并与同领域FPGA实现的卷积神经网络加速器设计的性能作了比较。本文使用多核心组合多种工作模式实现了更高的乘加器利用率,并利用稀疏性减少了卷积计算计算量。从表3中可以看出,在VGG-16网络、ImageNet数据集环境下,本文设计的稀疏卷积神经网络加速器平均获得了392.10 GOP/s的卷积计算性能和362.48 GOP/s的整体网络性能。表4中显而易见的,和同领域FPGA实现的卷积神经网络加速器相比,本文的设计单位乘加器的卷积效率更高。与同器件实现的典型卷积神经网络加速器相比,本文设计的稀疏卷积神经网络加速器卷积性能提升了108.8%,整体性能提升了164.6%,优势显著。
| 表 3 稀疏卷积神经网络加速器VGG-16各层计算性能 Tab.3 Sparse convolutional neural network accelerator VGG-16 calculation performance of each layer |
| 表 4 与其他卷积神经网络加速器的VGG-16运行性能的比较 Tab.4 Comparison of VGG-16 performance with other convolution neural network accelerators |
卷积层庞大的计算量以及全连接层冗余的参数量为卷积神经网络硬件化实现带来了不小的挑战。本文分析了不同的并行展开方式和利用稀疏性的方式对并行效率和资源开销的影响,提出了相比于同领域其他设计,并行效率更高、额外资源开销更小的能够高效利用稀疏性加速卷积神经网络计算的并行展开方式,兼顾了并行效率和计算灵活度。本文设计的稀疏卷积神经网络加速器通过利用激活稀疏性和参数稀疏性的方式,降低了VGG-16网络47.9%的计算量和85.23%的参数量,极大地加快了卷积神经网络计算速度。
本文使用Zynq XC7Z045器件实现了ImageNet数据集下运行VGG-16网络11.7 帧·s−1的计算性能,平均卷积性能392.10 GOP·s−1、整体网络性能362.48 GOP·s−1。和使用同样器件的同领域设计相比,本文的卷积性能提升了108.8%,整体性能提升了164.6%,具有明显的性能优势。
| [1] |
RUSSAKOVSKY O, DENG Jia, SU Hao, et al. ImageNet large scale visual recognition challenge[J]. International journal of computer vision, 2014, 115(3): 211-252. ( 0) 0)
|
| [2] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]// The 3rd International Conference on Learning Representations (ICLR2015).San Diego, CA, 2015.
( 0) 0)
|
| [3] |
ZHANG Chen, LI Peng, SUN Guangyu, et al. Optimizing FPGA-based accelerator design for deep convolutional neural networks[C]//Proceedings of 2015 ACM/SIGDA International Symposium on Field-programmable Gate Arrays. New York, NY, USA, 2015.
( 0) 0)
|
| [4] |
NATALE G, BACIS M, SANTAMBROGIO M D. On how to design dataflow FPGA-based accelerators for convolutional neural networks[C]//2017 IEEE Computer Society Annual Symposium on VLSI (ISVLSI). Bochum, Germany, 2017.
( 0) 0)
|
| [5] |
SHEN Yongming, FERDMAN M, MILDER P. Maximizing CNN accelerator efficiency through resource partitioning[C]//2017 ACM/IEEE 44th Annual International Symposium on Computer Architecture (ISCA). Toronto, ON, Canada, 2016.
( 0) 0)
|
| [6] |
MA Yufei, CAO Yu, VRUDHULA S, et al. Optimizing loop operation and dataflow in FPGA acceleration of deep convolutional neural networks[C]//ACM/SIGDA International Symposium on Field-programmable Gate Arrays. Monterey, California, USA, 2017.
( 0) 0)
|
| [7] |
SHI Shaohuai, CHU Xiaowen. Speeding up convolutional neural networks by exploiting the sparsity of rectifier units[J]. Computer vision and pattern recognition, 2017, 4: 1-7. ( 0) 0)
|
| [8] |
CHEN Y H, KRISHNA T, EMER J S, et al. Eyeriss: an energy-efficient reconfigurable accelerator for deep convolutional neural networks[J]. IEEE journal of solid-state circuits, 2017, 52(1): 127-138. DOI:10.1109/JSSC.2016.2616357 ( 0) 0)
|
| [9] |
ALBERICIO J, JUDD P, HETHERINGTON T, et al. Cnvlutin: ineffectual-neuron-free deep neural network computing[C]//2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA). Seoul, South Korea, 2016.
( 0) 0)
|
| [10] |
ZHANG Shijin, DU Zidong, ZHANG Lei, et al. Cambricon-X: an accelerator for sparse neural networks[C]//201649th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO). Taipei, China, 2016: 1−12.
( 0) 0)
|
| [11] |
HAN Song, LIU Xingyu, MAO Huizi, et al. EIE: efficient inference engine on compressed deep neural network[J]. International symposium on computer architecture, 2016, 44(3): 243-254. DOI:10.1145/3007787.3001163 ( 0) 0)
|
| [12] |
Parashar A , RHU M , Mukkara A , et al. SCNN: An accelerator for compressed-sparse convolutional neural networks[C]//The 44th Annual International Symposium. TorontoCanada, 2017.
( 0) 0)
|
| [13] |
OLSHAUSEN B A, FIELD D J. Sparse coding with an overcomplete basis set: a strategy employed by V1?[J]. Vision research, 1997, 37(23): 3311-3325. DOI:10.1016/S0042-6989(97)00169-7 ( 0) 0)
|
| [14] |
DAYAN P, ABBOTT L F. Theoretical neuroscience: computational and mathematical modeling of neural systems[M]. Cambridge, USA: The MIT Press, 2001.
( 0) 0)
|
| [15] |
NAIR V, HINTON G E. Rectified linear units improve restricted Boltzmann machines[C]//Proceedings of the 27th International Conference on International Conference on Machine Learning. Haifa, Israel, 2010.
( 0) 0)
|
| [16] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada, 2012.
( 0) 0)
|
| [17] |
HAN Song, POOL J, TRAN J, et al. Learning both weights and connections for efficient neural networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal, Canada, 2015: 1135−1143.
( 0) 0)
|
| [18] |
HAN Song, MAO Huizi, DALLY W J, et al. Deep compression: compressing deep neural networks with pruning, trained quantization and Huffman coding[C]//International Conference on Learning Representations, San Juan, Puerto Rico,2016.
( 0) 0)
|
| [19] |
MA Yufei, SUDA N, CAO Yu, et al. Scalable and modularized RTL compilation of convolutional neural networks onto FPGA[C]//201626th International Conference on Field Programmable Logic and Applications (FPL). Lausanne, Switzerland, 2016: 1−8.
( 0) 0)
|
| [20] |
KU NG. Why systolic architectures[J]. IEEE Computer, 1982, 15(1): 300-309. ( 0) 0)
|
| [21] |
GYSEL P, MOTAMEDI M, GHIASI S. Hardware-oriented approximation of convolutional neural networks[J]. Computer Vision and Pattern Recognition, 2016, 10: 1-8. ( 0) 0)
|
| [22] |
DORRANCE R, REN Fengbo, MARKOVIĆ D, et al. A scalable sparse matrix-vector multiplication kernel for energy-efficient sparse-blas on FPGAs[C]//ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, California, USA, 2014: 161−170.
( 0) 0)
|
| [23] |
QIU Jiantao, WANG Jie, YAO Song, et al. Going deeper with embedded FPGA platform for convolutional neural network[C]//Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, California, USA, 2016: 26−35.
( 0) 0)
|
| [24] |
SUDA N, CHANDRA V, DASIKA G, et al. Throughput-optimized openCL-based FPGA accelerator for large-scale convolutional neural networks[C]//Proceedings of the 2016 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays. Monterey, California, USA, 2016.
( 0) 0)
|
| [25] |
ZHANG Chen, FANG Zhenman, ZHOU Peipei, et al. Caffeine: towards uniformed representation and acceleration for deep convolutional neural networks[C]//Proceedings of the 35th International Conference on Computer-Aided Design. Austin, Texas, USA, 2016.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


