2. 中国科学院自动化研究所 智能系统与工程研究中心,北京 110016
2. Center for Research on Intelligent System and Engineering, Institute of Automation, Chinese Academy of Sciences, Beijing 110016, China
近年来,由于硬件的发展,计算资源的增加, 深度学习在人工智能领域崛起。利用深度学习可以从高维原始数据中提取高层特征,研究者们不再受手工选取特征的影响,进而使得图像检测、语音识别和自然语言处理等领域的研究水平达到新高度[1]。
在强化学习和深度学习结合起来之后也获得了质的飞跃,促进了游戏、机器人、金融管理、健康医疗和智慧交通等领域的发展。引人注意的是深度强化学习深度Q网络在Atari游戏上的应用取得了重大的突破,达到人类水平[2]。深度强化学习在人工智能领域的作用日益显著,“围棋专家”AlphaGo到AlphaZero的水平也远远超过甚至碾压人类水平[3]。AlphaGo和AlphaZero 的主要贡献者David Silver在他的教程中明确指出人工智能就是深度学习与强化学习,并决定将其带领的Deepmind团队的重点研究转移到难度更大的实时策略性游戏星际争霸上,因此掀起了人工智能领域的另一波研究热潮。
星际争霸是一个微观操作和宏观计划相结合的战争对抗性实时策略游戏,游戏玩家在大面积而且部分信息可见的环境中必须学会控制大量的游戏单元以发展经济,建造建筑,建设军队,从而能够为获取战争的胜利打下坚实的基础。星际争霸状态空间和动作空间是十分巨大的,截至目前,学者们直接在整个游戏上研究是十分困难的,现在的研究主要集中在一些经典场景的微型操作中,期望成为研究整个游戏人工智能的基石。Deepmind团队与游戏星际争霸的拥有者暴雪公司合作将星际Ⅱ发展成为研究人工智能的环境,并在文献[4]中详细介绍了星际争霸Ⅱ的学习环境SC2LE(StarCraft Ⅱ Learning Environment)并且还针对星际争霸Ⅱ中的迷你游戏运用经典的深度强化学习算法A3C(Asynchronous Advantage Actor-Critic)训练出一些基线智能体。事实上,在Deepmind 团队决定研究星际争霸之前,其他研究者们在星际争霸上的研究工作就进行了很多年[5],只不过绝大部分的研究工作主要集中在星际争霸Ⅰ而不是星际争霸Ⅱ上,基于不同的机器学习算法在不同的方面进行研究并取得了一些成果,例如,对星际争霸中的战争结果进行估计[6-7],在宏观上进行管理[8],对智能体行为的可解释性进行研究[9-10],以及将强化学习应用到微操场景中去[11-13]。
注意力机制是自深度学习发展之后广泛应用在自然语言处理、图像检测、语音识别等领域的核心技术。神经网络中的注意机制[14]是基于人类的视觉注意机制提出的,虽然存在不同的模型,但它们都基本上归结为能够以高分辨率聚焦在图像的某个区域,同时以低分辨率感知周围的图像区域,然后不断调整关注点。近年来注意力机制也开始被应用于循环神经网络(recurrent neural networks)[15-16],主要涉及自然语言处理和图像检测等领域,主要思想是解码器在每一时间步中都能够关注到源输入序列的不同位置,重点是注意力模型可以关注到目前已经学习到的内容以及学习下一步应该主要关注的内容。本文创新灵感的来源主要是:在强化学习决策序列过程中,智能体需要关注到输入状态序列中有价值的状态。以星际争霸II中的3个经典迷你游戏作为测试平台,它们分别是战胜跳虫和毒爆虫(DefeatZerglingsAndBanelings),奔向烽火处(MoveToBeacon)以及收集矿物碎片(CollectMineralShards),在这些小游戏中,智能体只包含4种动作行为,即上下左右,这样就可以大大缩小动作空间。利用星际争霸II学习环境中提供的接口,可以获取很多状态特征,比如非空间特征和空间特征图层,进而来训练智能体,但是经过分析这3个迷你游戏发现智能体获取如此多的空间特征是没有必要的,因此我们挑选了部分特征,去掉冗余特征,以加快智能体的学习速度。
根据以上所谈论到的问题以及注意力机制的优势,本文的主要贡献包括到以下两个方面:
1)采用的网络结构比Deepmind提供的基线智能体的网络结构更加简洁。
2)将强化学习中的奖励与注意力机制结合起来,每一个时间步,智能体更加关注有价值的游戏状态。
通过以上两个方面相结合,不仅加速了智能体在星际争霸II中的学习速度,也使得智能体学习到更优的策略,取得更好的成绩。
1 强化学习在本节中,首先回顾一下经典的强化学习场景以及算法A3C[17]。
经典的强化学习场景中的一些基本概念描述如下:在某一时刻
| $ {R_t} = \sum\limits_{k = 0}^\infty {{\gamma ^k}r\left( {{s_{t + k}},{a_{t + k}}} \right)} $ |
其中
| $ {\max _\pi }{E_{s\sim {P_0}}}\left[ {{R_t}|{s_t} = s} \right] $ |
| $ {Q^\pi }\left( {s,a} \right) = {E_\pi }\left[ {{R_t}|{s_t} = s,{a_t} = a} \right] $ |
表示在状态
| $ {V^\pi }\left( s \right) = {E_\pi }\left[ {{R_t}|{s_t} = s} \right] $ |
表示在策略
A3C算法是将策略函数和价值函数相结合的强化学习方法,对目标函数式(1):
| $ {J_\theta }\left( s \right) = {E_{{\pi _\theta }}}\left[ {{R_t}|{s_t} = s} \right] $ | (1) |
运用梯度上升的方法以不断更新现有的策略
| ${\nabla _\theta }{J_\theta }\left( s \right) = {E_{{\pi _\theta }}}\left[ {\nabla _\theta }\ln {\pi _\theta }\left( {{a_t}|{s_t}} \right) {R_t}|{s_t} = s \right]$ |
但是只采用这种方式存在高方差的缺点,因此Williams等[18]提出了改进版本:
| ${\nabla _\theta }{J_\theta }\left( s \right) = {E_{{\pi _\theta }}}\left[ {\nabla _\theta }\ln {\pi _\theta }\left( {{a_t}|{s_t}} \right) \left[ {{R_t} - b\left( {{s_t}} \right)} \right]|{s_t} = s \right]$ |
通常情况下,
| $ {\nabla _\theta }{J_\theta }\left( s \right) = {E_{{\pi _\theta }}}\left[ \begin{array}{l} {\nabla _\theta }\ln {\pi _\theta }\left( {{a_t}|{s_t}} \right) \left[ {Q^\pi }\left( {{s_t},{a_t}} \right) - {V^\pi }\left( {{s_t}} \right) \right]|{s_t} = s \\ \end{array} \right] $ |
其中
基于价值函数的方法则主要是与环境进行交互后,对动作值函数和价值函数进行估计,然后获取较优的策略或者是促进策略优化,在A3C算法中主要采用后者,一般只对价值函数进行估计,通常最小化此损失函数:
| $ {\left[ {{G^\pi }\left( {{s_t}} \right) - V_{\theta '}^\pi \left( {{s_t}} \right)} \right]^2} $ | (2) |
其中,
| $ {G^\pi }\left( {{s_t}} \right) = {E_{{\pi _\theta }}}\left[ {\sum\limits_{k = 0}^n {\gamma ^k}r\left( {{s_{t + k}},{a_{t + k}}} \right) + {\gamma ^{n + 1}}V_{\theta '}^\pi \left( {{s_{t + n + 1}}} \right) } \right] $ |
为了提升策略的探索度,通常在A3C算法中加入熵正则化项
| $ {J_\theta }\left( {{s_t}} \right) = {E_{{\pi _\theta }}}\left[ {{A^\pi }\left( {{s_t},{a_t}} \right)} \right] + \delta H\left[ {{\pi _\theta }\left( {{s_t}} \right)} \right] $ |
其中
| $ {\nabla _\theta }{J_\theta }\left( {{s_t}} \right) = {E_{{\pi _\theta }}}\left[ {\nabla _\theta }\ln {\pi _\theta }\left( {{a_t}|{s_t}} \right) \left[ {Q^\pi }\left( {{s_t},{a_t}} \right) - {V^\pi }\left( {{s_t}} \right) \right]{\rm{ + }} \delta {\nabla _\theta }H\left[ {{\pi _\theta }\left( {{s_t}} \right)} \right] \right] $ |
A3C算法同时为了提高学习的稳定性并且加快学习速度,利用异步的方法,将多个智能体在不同的线程中运行,共同更新一个策略网络。
2 基于状态注意力的A3C算法在深度强化学习中,是否采用游戏环境默认的奖励是一个值得探讨的问题,即便是一些经典算法被提出以后,在实际的源码实现中也对环境原始的奖励进行了缩放[19]。因此,本文认为,原始环境中定义的奖励只是起到了一定的基础作用,并未真正体现出各个游戏状态的相对重要性,为了让智能体学会关注更有价值的游戏状态,引入了权重网络
| $ {R_t} = \sum\limits_{k = 0}^\infty {{\gamma ^k}{w_\vartheta }\left( {{s_{t + k}}} \right)r\left( {{s_{t + k}},{a_{t + k}}} \right)} $ |
当引入权重网络
| $ {Q^\pi }\left( {{s_t},{a_t}} \right) = {w_\vartheta }\left( {{s_t}} \right)r\left( {{s_t},{a_t}} \right) + \gamma {Q^\pi }\left( {{s_{t + 1}},{a_{t + 1}}} \right) $ | (4) |
| $ {V^\pi }\left( {{s_t}} \right) = {E_{{\pi _\theta }}}\left[ {w_\vartheta }\left( {{s_t}} \right)r\left( {{s_t}} \right) + \gamma {V^\pi }\left( {{s_{t + 1}}} \right) \right] $ | (5) |
由此可以看出,此算法和A3C算法是很相似的。所以基于注意力机制的A3C算法最大化的目标函数分别为式(3)、式(6),最小化目标函数为式(2):
| $ {J'_{{w_\vartheta }}}\left( {{s_t}} \right) = - {\left[ {G_{{w_\vartheta }}^\pi \left( {{s_t}} \right) - {V^\pi }\left( {{s_t}} \right)} \right]^2} $ | (6) |
其中,
| $ G_{{w_\vartheta }}^\pi \left( {{s_t}} \right) = {E_{{\pi _\theta }}}\left[ \displaystyle\sum\limits_{k = 0}^n {\gamma ^k}{w_\vartheta }\left( {{s_{t + k}}} \right) r\left( {{s_{t + k}},{a_{t + k}}} \right) + {\gamma ^{n + 1}}{V^\pi }\left( {{s_{t + n + 1}}} \right) \right] $ |
其式(2)则主要体现在不断调整价值网络的参数,使价值网络更靠近于真实的价值网络,式(5)则主要体现在通过不断调整权重网络
| $ {\nabla _\vartheta }{{J'}_{{w_\vartheta }}}\left( {{s_t}} \right) = - 2\left[ {G_{{w_\vartheta }}^\pi \left( {{s_t}} \right) - {V^\pi }\left( {{s_t}} \right)} \right] {\nabla _{{w_\vartheta }}}G_{{w_\vartheta }}^\pi \left( {{s_t}} \right){\nabla _\vartheta }{w_\vartheta }\left( {{s_t}} \right) $ |
在本节中,将本文提出的基于注意力机制的A3C算法在实时策略性游戏星际争霸II中的迷你游戏上进行实验验证网络结构与算法的有效性,有关于战胜跳虫和毒爆虫、奔向烽火处和收集矿物碎片这3个小游戏的具体描述如下:
战胜跳虫和毒爆虫:最初状态下,在地图的两侧分别有9个陆战队员和10个虫子(6个跳虫和4个毒爆虫),当任何一个跳虫和毒爆虫被陆战队员消灭,智能体都会获得奖励,当所有的跳虫和毒爆虫被消灭,又会恢复到刚开始的10个,此时也会额外增加4个满血状态的陆战队员,其他陆战队员的血量还是保持原来的样子。与此同时虫子和陆战队员的位置会被重置到地图的两侧。
奔向烽火处: 地图上有一个烽火标记和一个陆战队员,当陆战队员到达烽火标记的位置智能体就会获得奖励,同时,烽火的位置会重新设置。
收集矿物碎片:地图上有两个陆战队员和20个分散在屏幕各处的矿物碎片,当任何一个陆战队员移动到矿物碎片处智能体都会获得奖励,当然最优的策略应该是两个陆战队员独立行动,分开收集矿物,当所有的矿物被收集完之后,地图会继续随机生成20个矿物碎片。
更多关于星际争霸II迷你游戏的细节,请参考文献[20]。
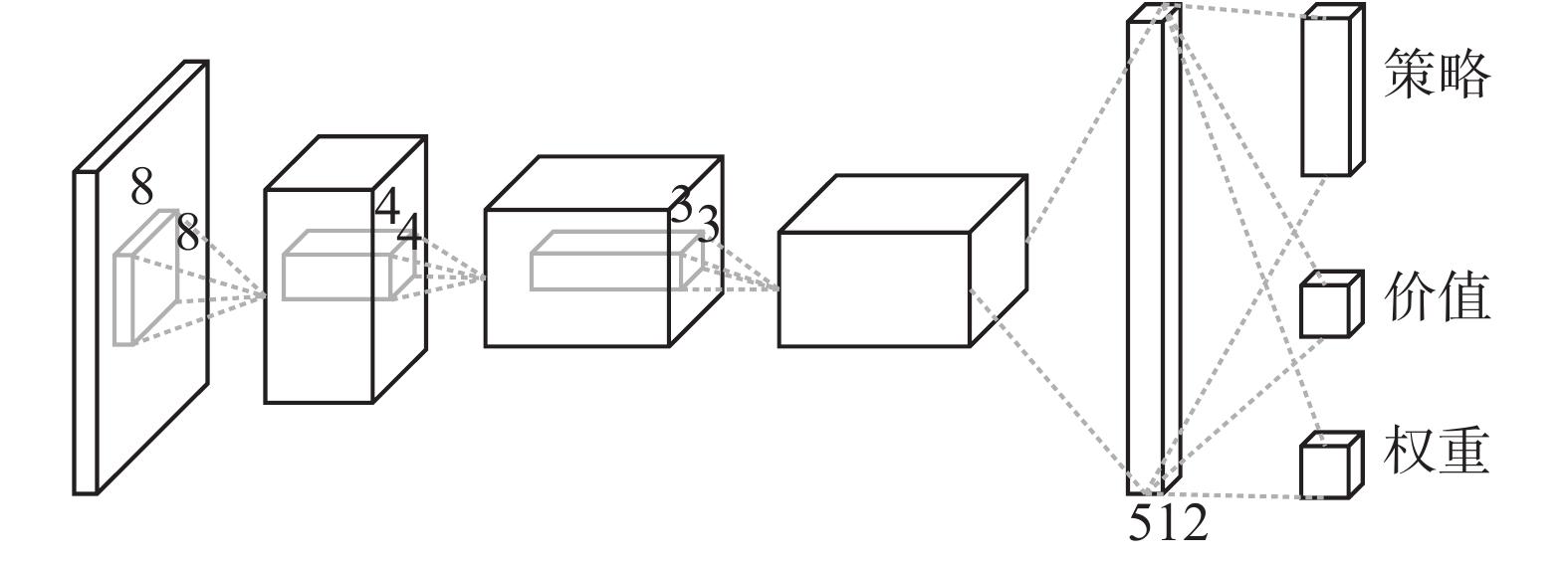
3.1 网络结构本文的学习环境与测试环境是基于Deepmind和暴雪合作的SC2LE,网络结构与传统的网络结构非常相似。如图1所示,我们利用很简单的三层卷积神经网络和一层全连接网络,将SC2LE中提供的部分屏幕特征图层(单元类型、已选择、生命值)输入到网络里,3个卷积层的过滤器的个数分别是32、64、64,大小分别是8、4、3,步长分别是4、2、1,每一层有RELU激活函数,在全连接层中有512个隐层单元和RELU激活函数,网络有3个输出,分别输出策略、价值和基于注意力机制的A3C算法中的注意力权重,我们使用RMSProp优化器,每次网络输入量的大小为32批。实验具体硬件环境的条件是拥有8 GB显存的GPU、16GB内存以及8核4.2 GHz的CPU。
|
Download:
|
| 图 1 网络结构 Fig. 1 Network architecture | |
从本节开始对游戏场景的介绍中可以知道,智能体玩好游戏的第一步应该关注的是如何选择陆战队员。在游戏战胜跳虫和毒爆虫中,有10个陆战队员,首先选择哪一个陆战队员对他发出命令,是否应该完全区别对待这10个陆战队员,是一个值的考虑的问题,本文认为随机选择陆战队员是一个不错的决策,随机的选择意味着不再区分陆战队员,所有的陆战队员将采取同一个策略,增加了策略的鲁棒性。比如,在图2中,随机选择2个相同状态的陆战队员交换他们的位置之后的状态其实和交换之前的状态是完全一样的,所以,随机选择的策略意味着缩小了状态空间,从实验过程中可以进一步发现,随机的选择有利于陆战队员分散开来,这种行为也有利于陆战队员击败虫子。从上面两种情况中可以看出,在游戏战胜跳虫和毒爆虫中随机选择是一个不错的策略,事实上,虽然在游戏收集矿物碎片中也每次随机选择一个陆战队员执行命令,但是这并不是一个明智的决策。比如,在某一段时间内,很有可能会出现一个陆战队员在忙碌地收集矿物碎片,而另一个陆战队员却一直在等待的情况。

|
Download:
|
| 图 2 战胜跳虫和毒爆虫游戏界面截图 Fig. 2 The screenshot of DefeatZerglingsAndBanelings | |
为了保证游戏智能体与人类的成绩相比较时操作速度是相当的,即对于人类是一场公平的竞争。Deepmind在整个游戏实验中每8帧执行一个动作,而在战胜跳虫和毒爆虫整个游戏中,因为每次随机选择一个陆战队员,然后对陆战队员发送命令。然而从SC2LE提供的程序接口pysc2中发现,如果每次都要随机选取一个陆战队员,那么每次选择陆战队员之前,就必须选择全部陆战队员然后从这些陆战队员中选择其中的一个。因此每次这种操作就会让陆战队员速度变慢,所以在战胜跳虫和毒爆虫实验中选择每4帧执行一个动作, 这种方式是很合理的,毕竟人类并不会在选择某一个陆战队员之前选择全部的陆战队员。
实验结果如表1所示,基于注意力机制的A3C算法的性能表现不错,与目前Deepmind提供的基准智能体ATARI网络的分数相比较在战胜跳虫和毒爆虫的迷你游戏中得分显著提高。
| 表 1 人类和智能体获取的平均分数表 Tab.1 Averaged results for human baselines and agents |
从表1可以看出,随机策略在战胜跳虫和毒爆虫、收集矿物碎片迷你游戏中的平均成绩要比Deepmind 随机策略的平均成绩要高一些,由此可见,虽然本文的网络结构比Deepmind的Atari网络结构简单一些,但是对于星际中的这3个游戏场景来说,简单的网络结构更适合。在游戏奔向烽火处中基于注意力机制的A3C算法的成绩并没有比Deepmind 的Atari网络的成绩高,经过分析原因后发现,由于基于注意力机制的A3C算法的智能体的可选择方向只包含上下左右,所以陆战队员不能直线到达目标位置,但是陆战队员所走的路线就是在规定方向的基础上的最短路径,而通过Deepmind发表的视频中可以发现,在这个小游戏上,游戏智能体直接定位到目标位置,陆战队员可以沿直线走过去,在这个小游戏上也许是一个好的办法,但是如果游戏中添加了障碍物,也许这就不是一个好的方法了。虽然在战胜跳虫和毒爆虫的游戏分数上基于注意力机制的A3C算法取得了较大的提高,但是与人类水平相比还存在较大的差距,这也意味着还存在较大的空间值得我们研究与探索。
4 结束语本文认为不同的游戏状态或者游戏帧有不同的重要性,智能体理应关注更有价值的状态,因此本文提出了基于注意力机制的A3C算法,由此将注意力机制和强化学习中的奖励结合起来,得到了一定的进步,但是智能体比起人类水平还是存在较大差距,深度强化学习的应用,虽然在很多游戏上取得了成功,但是在实时策略游戏上还面临很大的挑战。在战胜跳虫和毒爆虫迷你游戏中,本文做法也存在不足之处:1)人类不会采用随机选择陆战队员这样的策略,比如,大部分玩家会优先选择让受伤的陆战队员后退然后远距离攻击敌人,而不是站在那里被敌人杀死。2)系统预先给定好的奖励是否是有利于深度强化学习算法进行学习的最优奖励,这是不确定的,应该采用一定的策略来优化这个默认的奖励。以上两点也是我们未来工作考虑的两个方面。
| [1] |
LI Yuxi. Deep reinforcement learning: an overview[EB/OL]. [2018-01-17]https://arxiv.org/abs/1701.07274.
( 0) 0)
|
| [2] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529-533. DOI:10.1038/nature14236 ( 0) 0)
|
| [3] |
SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 ( 0) 0)
|
| [4] |
VINYALS O, EWALDS T, BARTUNOV S, et al. StarCraft II: a new challenge for reinforcement learning[EB/OL]. [2018-01-17]https://arXiv: 1708.04782, 2017.
( 0) 0)
|
| [5] |
ONTANON S, SYNNAEVE G, URIARTE A, et al. A survey of real-time strategy game AI research and competition in StarCraft[J]. IEEE transactions on computational intelligence and AI in games, 2013, 5(4): 293-311. DOI:10.1109/TCIAIG.2013.2286295 ( 0) 0)
|
| [6] |
SYNNAEVE G, BESSIERE P. A dataset for StarCraft AI & an example of armies clustering[C]//Artificial Intelligence in Adversarial Real-Time Games. Palo Alto, USA, 2012: 25–30.
( 0) 0)
|
| [7] |
SYNNAEVE G, BESSIÈRE P. A Bayesian model for opening prediction in RTS games with application to StarCraft[C]//Proceedings of 2011 IEEE Conference on Computational Intelligence and Games. Seoul, South Korea, 2011: 281–288.
( 0) 0)
|
| [8] |
JUSTESEN N, RISI S. Learning macromanagement in starcraft from replays using deep learning[C]//Proceedings of 2017 IEEE Conference on Computational Intelligence and Games. New York, USA, 2017: 162–169.
( 0) 0)
|
| [9] |
DODGE J, PENNEY S, HILDERBRAND C, et al. How the experts do it: assessing and explaining agent behaviors in real-time strategy games[C]//Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems. Montreal QC, Canada, 2018.
( 0) 0)
|
| [10] |
PENNEY S, DODGE J, HILDERBRAND C, et al. Toward foraging for understanding of starcraft agents: an empirical study[C]//Proceedings of the 23rd International Conference on Intelligent User Interfaces. Tokyo, Japan, 2018: 225–237.
( 0) 0)
|
| [11] |
PENG Peng, WEN Ying, YANG Yaodong, et al. Multiagent bidirectionally-coordinated nets for learning to play starcraft combat games[EB/OL]. [2018-01-17]https://arXiv: 1703.10069, 2017.
( 0) 0)
|
| [12] |
SHAO Kun, ZHU Yuanheng, ZHAO Dongbin, et al. StarCraft micromanagement with reinforcement learning and curriculum transfer learning[J]. IEEE transactions on emerging topics in computational intelligence, 2019, 3(1): 73-84. DOI:10.1109/TETCI.2018.2823329 ( 0) 0)
|
| [13] |
WENDER S, WATSON I. Applying reinforcement learning to small scale combat in the real-time strategy game StarCraft: Broodwar[C]//Proceedings of 2012 IEEE Conference on Computational Intelligence and Games. Granada, Spain, 2012: 402–408.
( 0) 0)
|
| [14] |
DENIL M, BAZZANI L, LAROCHELLE H, et al. Learning where to attend with deep architectures for image tracking[J]. Neural computation, 2012, 24(8): 2151-2184. DOI:10.1162/NECO_a_00312 ( 0) 0)
|
| [15] |
BAHDANAU D, CHO K, BENGIO Y, et al. Neural machine translation by jointly learning to align and translate[C]//Proceedings of International Conference on Learning Representations. 2015.
( 0) 0)
|
| [16] |
MNIH V, HEESS N, GRAVES A, et al. Recurrent models of visual attention[C]//Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal, Canada, 2014: 2204–2212.
( 0) 0)
|
| [17] |
MNIH V, BADIA A P, MIRZA M, et al. Asynchronous methods for deep reinforcement learning[C]//Proceedings of the 33rd International Conference on Machine Learning. New York USA, 2016: 1928-1937.
( 0) 0)
|
| [18] |
WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning[J]. Machine learning, 1992, 8(3/4): 229-256. DOI:10.1023/A:1022672621406 ( 0) 0)
|
| [19] |
ILYAS A, ENGSTROM L, SANTURKAR S, et al. Are deep policy gradient algorithms truly policy gradient algorithms? [EB/OL]. [2018-01-17]https://arXiv: 1811.02553, 2018.
( 0) 0)
|
| [20] |
DeepMind. DeepMind mini games[EB/OL]. (2017-08-10)[2018-09-10]. https://github.com/deepmind/pysc2/blob/master/docs/mini_games.md.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


