基于表示的分类(representation based classification，RBC)方法通过训练样本来近似表示查询样本，进而对查询样本进行分类^[1]。在RBC框架中，如何准确地计算查询样本和每个类之间的相似性，对查询样本的表示和分类起着重要的作用^[2]。一般地，RBC方法可以分为基于 ${L_1}$ 范数的表示方法^[3]和基于 ${L_2}$ 范数的表示方法^{[1-2, 4]}。基于 ${L_1}$ 范数表示方法是用 ${L_1}$ 范数对表示系数进行正则化，其中最典型的方法是基于稀疏表示的分类(sparse representation based classification，SRC)^[3]。SRC使用训练样本的稀疏组合来表示查询样本，并根据类的重构残差对查询样本进行分类。当使用 ${L_2}$ 范数对表示系数正则化时，可获得一个闭合解，提高了算法的稳定性，在分类时具有很好的区分性^[1]。最典型的方法是基于协同表示的分类(collaborative representation based classification，CRC)^[1]，它利用训练样本之间的协作来表示查询样本。受CRC的启发，文献[4]中提出了两阶段测试样本稀疏表示(two-phase test sample sparse representation，TPTSR)方法，该方法通过近邻来重构查询样本并进行分类。

在RBC方法中，表示系数可以用来描述样本之间的相似性^[5-10]，在设计分类器时可直接采用这些表示系数^[5-7]。例如，基于线性重构度量的最近邻(linear reconstruction measure nearest neighbor，LRMNN)分类^[5]使用 ${L_1}$ 范数或 ${L_2}$ 范数正则化的表示系数作为线性重构度量(linear reconstruction measure，LRM)来确定查询样本的最近邻，这里的表示系数也称为线性重构系数。Cheng等^[6]提出的稀疏性诱导相似性度量使用了 ${L_1}$ 范数正则化的表示系数作为标签传播和动作识别的相似性度量。Li等^[7]将 ${L_1}$ 范数的表示系数之和(sum of coefficient，SoC)用于分类决策。文献[8]指出类似的样本应该用相似的稀疏表示系数进行编码。文献[9]将样本权重的表示系数用于数据集的自动图构建。Ma等^[10]提出了基于 ${L_1}$ 范数正则化的稀疏系数 $k$ 近邻分类。文献[11]则在TPTSR基础上提出基于两阶段线性重构度量的分类(two-phase linear reconstruction measure based classification，TPLRMC)方法，它利用重构系数代替残差来选择近邻，再进行分类。由于表示系数可以保留原始高维数据和潜在分类信息的一些固有几何特性，因此表示系数可应用于降维。这些基于表示系数的降维方法可以统一到图嵌入框架中^[12]。最近，用于线性回归的非负稀疏图学习方法^[13]实现了标签预测和投影学习，并为基于图的学习提供了新的视角。因此，表示系数可以很好地应用于模式分类。

虽然基于表示系数的分类方法在许多实际的人脸识别任务中表现良好，但其分类性能会受到人脸图像变化的显著影响^[2]，且有些没有考虑过程中数据非平衡的问题^[14]。为了进一步提高对人脸图像的分类性能，本文提出了一种基于 ${L_1}$ 范数或 ${L_2}$ 范数的自适应多阶段线性重构表示的分类(self-adaptive multi-phase linear reconstruction representation based classification，MPRBC)方法。首先，用表示系数代替残差来表示查询样本与训练样本之间的相似性，系数越大表示它们越相似。用近邻类代替近邻样本，保留近邻类中的全部样本，保持样本数据的平衡。用多次选择近邻代替单次选择，同时利用自适应的方法控制算法的时间复杂度。在6个人脸数据集上的实验表明，MPRBC算法优于目前最先进的基于表示的分类方法。

1 相关RBC算法

本节主要回顾已有的一些RBC方法。给定训练样本 ${{X}} = \left[ {{{{X}}^{\rm{1}}}\;\;{{{X}}^2}\;\; \cdots \;\;{{{X}}^{{{{M}}_0}}}} \right] = \left[ {{{{x}}_{\rm{1}}}\;\;{{{x}}_{\rm{2}}}\;\; \cdots \;\;{{{x}}_{{n}}}} \right] \in {{{{\bf{R}}}}^{d \times n}}$ 为 $n$ 个属于 ${M_0}$ 类的 $d$ 维样本， ${{{X}}^i}$ 表示属于第 $i$ 类的训练样本子集，其对应的类标签为 ${{{c}}_i} \in \{ 1,\;2,\; \cdots ,\; {M_0}\} $ 。

1.1 基于线性重构度量的最近邻(LRMNN)分类

一般的线性重构度量(LRM)问题可表示为

$\mathop {{{\min}} }\limits_{{s}} \left\| {{{y}} - {{Xs}}} \right\|_2^2$

(1)

式中： ${{s}} = {\left[ {{{{s}}_1}\;\;{{{s}}_2}\;\; \cdots \;\;{{{s}}_n}} \right]^{\rm T}} \in {{\bf{R}}^n}$ 表示线性重构系数， ${{{s}}_i}$ 代表 ${{y}}$ 与 ${{{x}}_i}$ 的相似性。设 ${\hat{{s}}} = {\left[ {{{{\hat{{s}}}}_1}\;\;{{{\hat{{s}}}}_2}\;\; \cdots \;\;{{{\hat{{s}}}}_n}} \right]^{\rm T}} \in {{\bf{R}}^n}$ 是问题(1)的最优解，则 ${{\hat{{s}}}_i}$ 越大，说明 ${{y}}$ 与 ${{{x}}_i}$ 越相似。为了克服奇异值问题并控制过拟合，在LRM目标函数中增加正则化项对表示系数进行约束，得到以下正则化LRM模型：

$\mathop {{{\min}} }\limits_{{s}} \left\| {{{y}} - {{Xs}}} \right\|_2^2 + \lambda {\left\| {{s}} \right\|_p}$

(2)

式中 ： ${\rm{\lambda }}$ 是平衡参数，用来平衡重建误差项和正则化项之间的贡献； $p$ 通常设置为1或2，当 $p=$ 1时， ${{s}}$ 为稀疏表示系数，文献[3]中给出了详细的求解过程；当 $p=$ 2时， ${{s}}$ 为协同表示系数，其最优解为

${\hat{{s}}} = {({{{X}}^{\rm{T}}}{{X}} + {\rm{\lambda }}{{I}})^{ - 1}}{{{X}}^{\rm{T}}}{{y}}$

(3)

基于表示系数的相似性度量在分类中表现良好^{[5-6, 8]}。如果一个训练样本 ${{{x}}_i}$ 与查询样本 ${{y}}$ 非常相似，那么在重构 ${{y}}$ 时 ${{{x}}_i}$ 会有较大的表示系数。因此，LRMNN认为具有最大表示系数 ${{\hat{{s}}}_i}$ 的样本 ${{{x}}_i}$ 与 ${{y}}$ 最相似，从而可利用最相似样本对 ${{y}}$ 进行分类，分类规则如下：

$c = {\rm{arg ma}}{{\rm{x}}_{{{{c}}_i}}}\left\| {{{{\hat{{s}}}}_i}} \right\|$

(4)

式中 ： $i = 1,2, \cdots ,n$ ； ${{{c}}_i}$ 是训练样本 ${{{x}}_i}$ 的类标签。

1.2 表示系数之和(SoC)分类

SRC使用 ${L_1}$ 范数正则化约束，通过式(2)得到最优稀疏表示向量 ${\hat{{s}}}$ ，然后根据查询样本与训练样本的残差进行分类。SoC算法^[9]是在SRC的基础上用同类样本的表示系数之和对查询样本进行分类，其分类规则为

$c = {\rm{arg ma}}{{\rm{x}}_{{{{c}}_i}}}\sum {{\delta ^{{{{c}}_i}}}} ({\hat{{s}}})$

(5)

式中 $\sum {{\delta ^{{{{c}}_i}}}} ({\hat{{s}}})$ 为向量 ${\hat{{s}}}$ 中 ${{{c}}_i}$ 类训练类样本的表示系数之和。

1.3 两阶段线性重构度量分类(TPLRMC)

TPLRMC方法^[7]分为两个阶段。首先，利用正则化LRM模型获得查询样本的一个粗略的线性表示，并根据系数的大小依次从所有的训练样本中选择 $K$ 个近邻。假设对查询样本 ${{y}}$ 和训练样本集 ${{X}}$ ，由式(2)得到最优解为 ${\hat{{s}}}$ ，其分量是训练样本的表示系数。根据“训练样本的表示系数越大，则该训练样本对重构查询样本的贡献就越大”的原则^[9,11]，将所有训练样本的表示系数按由大到小的顺序排序，并选出前 $K$ 个较大的系数所对应的样本，记为 ${\bar{{ X}}} = [{{\bar {{x}}}_1}\;\;{{\bar {{x}}}_2}\;\; \cdots \;\;{{\bar {{x}}}_K}]$ ，这些样本所在的类共H个，类集合记为 ${\bar {{C}}} = \{ {\bar c_1},\;{\bar c_2},\; \cdots ,\;{\bar c_H}\} $ ，它是所有样本类别的一个子集，即 ${\bar {{C}}} \subseteq \{ {c_1},\;{c_2},\; \cdots ,\;{c_M}\} $ 。

其次，利用先前选出的 $K$ 个训练样本 ${\bar{\bf{ X}}}$ 对查询样本进行精细表示，其最优表示系数优化模型为

$\mathop {{{{\rm{min}}}} }\limits_{{s}} \left\| {{{y}} - {{{{\bar X}}s}}} \right\|_2^2 + \lambda {\left\| {{s}} \right\|_p}$

(6)

设式(6)的最优解为 ${{\bar s }}$ ，计算 ${{\bar s}}$ 中对应于同一类训练样本的表示系数之和，那么和最大的一个所对应的类即为查询样本的类别，分类规则类似于式(5)。

2 自适应多阶段线性重构表示分类

根据TPLRMC的思想，利用同类样本表示系数之和(以下称其为类系数)按由大到小的选择策略，经过对查询样本近邻类的多次选择，逐渐缩小训练样本范围，提出一种自适应多阶段线性重构表示的分类(MPRBC)方法。

2.1 MPRBC的基本思想

在SRC^[3]和TPTSR^[4]中，根据训练样本与查询样本之间的残差来对给定查询样本进行分类或选择近邻，是不够准确的^[5-7]。这是因为残差只能反映训练样本与查询样本的相似度，而不能反映训练样本对查询样本重构的贡献大小和贡献的正负属性。

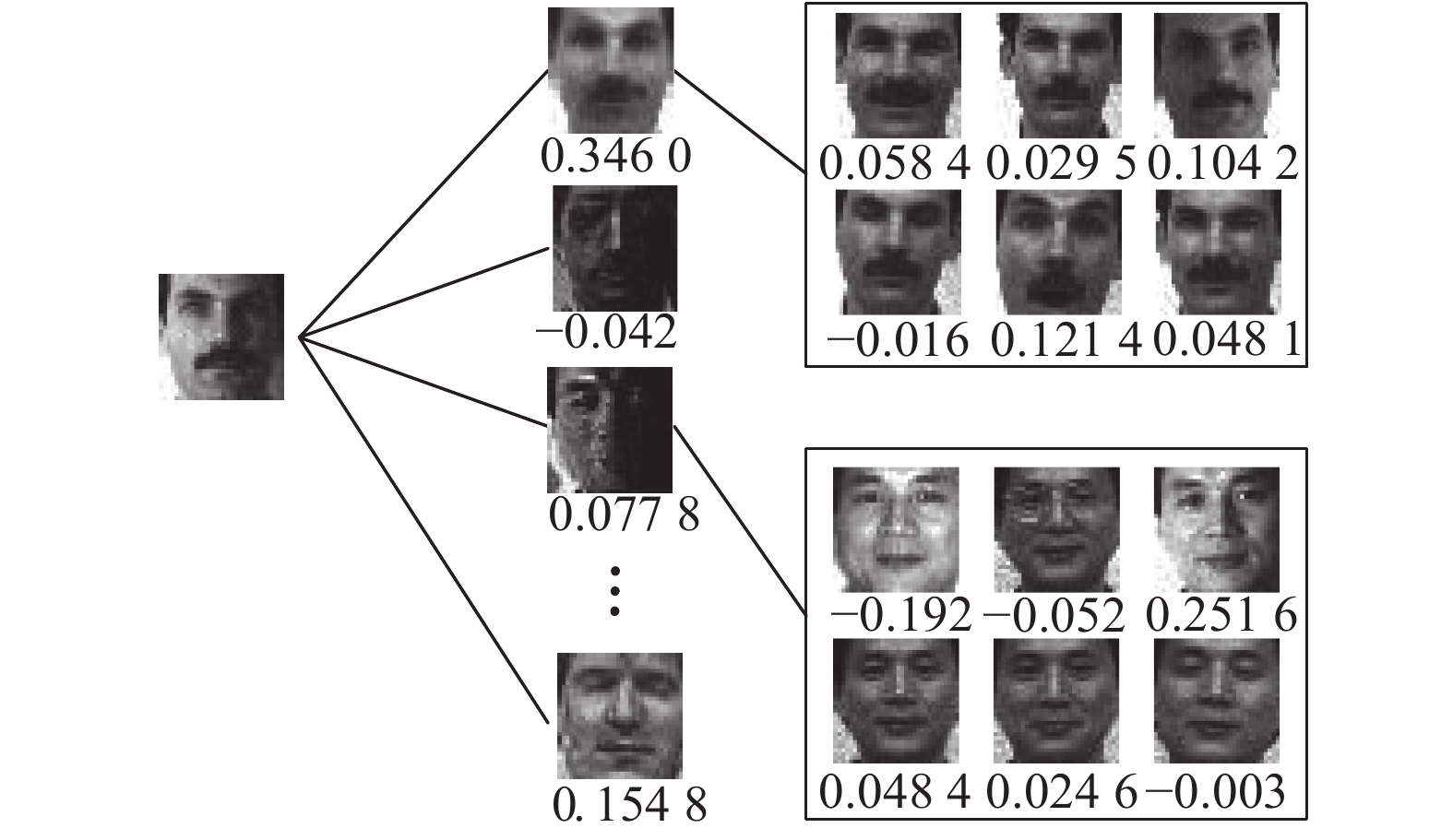
相比利用残差进行分类，直接通过表示系数进行分类，能很好地还原样本之间的关系，且易于实现。LRMNN正是基于此进行分类的，但其也有一定的局限性。例如，当各训练样本的表示系数比较平均时，LRMNN分类的准确性将显著下降。图1给出了重构查询样本时各训练样本的表示系数，由图可见，与查询样本同类的训练样本系数相对比较平均，而最大的表示系数(0.251 6)所对应的训练样本与查询样本是非同类的，此时通过LRMNN算法将得到错误的分类结果。

若利用类系数则可得到同类训练样本对重构查询样本的总贡献。在图1中，与查询样本同类的训练样本系数之和(0.3460)最大。此时，利用同类中训练样本做整体协同表示，可以捕捉到更多的变化，其表示能力比单个样本要强，这有利于对查询样本进行正确分类。该思想类似于集成学习中投票的方法，它充分利用了训练样本的类别信息^[7]，并且可以抵消表示系数较平均时产生的影响，筛选掉系数有较大方差的类，保留的样本数据具有平衡性的特点^[14]。但是在类别数较多的数据集上，由于类基数较大，且不同类别训练样本的类系数之间的差异不太明显，这些都会影响分类的精度。

运用TPLRMC算法选择近邻样本之后再进行重构表示的思想，本文使用了多阶段的方法，在每一阶段，利用查询样本重构后类系数的大小，筛选出与查询样本相似类别的所有训练样本，这也是熵减小理论的体现^[15]。随着过程的进行，选出的训练样本将集中在少数几类中，这样使得类别之间贡献的区分度更加明显，从而提高了分类精度。以Yale人脸数据集为例，从每一类中选出6张图片作为训练样本，而查询样本来自第15类，通过 ${L_2}$ 范数正则化问题(2)求得各训练样本的表示系数，各训练样本与查询样本的残差和表示系数及类系数分别如图2(a)~(c)所示，而图2(d)则是由MPRBC算法筛选出的5个类的类系数。在图2(a)中，两个最小残差之比为1∶1.4616，它们对应两个来自不同类的训练样本；图2(b)中两个最大表示系数之比为1∶1.9259，它们也对应于两个不同类的训练样本；在图2(c)中，两个最大的类系数之比为1∶3.2087；而图2(d)是在使用MPRBC算法经过3个阶段之后，训练样本的类别数由原来的15个减小到5个，此时两个最大的类系数之比为1∶6.3917，这表明，相比以往RBC算法，MPRBC算法的分类区分度最明显。

2.2 MPRBC的实现过程

记在第k阶段训练样本集为 ${{{X}}_k}$ ，通过以下 ${L_1}$ 范数或 ${L_2}$ 范数正则化的LRM，获得查询样本在 ${{{X}}_k}$ 上的表示系数向量

$\mathop {{\rm{min}}}\limits_{{s}} \left\| {{{y}} - {{{X}}_k}{{s}}} \right\|_2^2 + {\rm{\lambda }}{\left\| {{s}} \right\|_p}$

(7)

设式(7)的最优解为 ${{{s}}_k}$ ，将 ${{{s}}_k}$ 的各分量依据类别的不同求出类系数，并筛选出前 ${M_k}$ 个拥有较大类系数的类( ${M_k}$ 将在2.3节式(9)中给出确定方法)。然后，把属于这些类的训练样本重新组成新的训练样本集 ${{{X}}_{k + 1}}$ ，继续此过程，直到 ${{{s}}_k}$ 的各分量所对应的类别数不大于预先设定的阈值 $\beta $ 为止，并输出具有最大类系数的类标签。

$c = {\rm{arg ma}}{{\rm{x}}_{{{{c}}_i}}}\sum {{\delta ^{{{{c}}_i}}}} ({{{s}}_k})$

(8)

式中： $\displaystyle\sum {{\delta ^{{{{c}}_i}}}} ({{{s}}_k})$ 为向量 ${{{s}}_k}$ 中属于 ${{{c}}_i}$ 类的训练样本类系数。

2.3 自适应MPRBC算法

不同于以往的两阶段算法^{[4, 11]}和多阶段算法^[15]需要人为确定选取样本的数目，MPRBC算法可根据类系数的大小自适应地选取样本类别的数目。在前文中已经分析，类系数的大小可以较准确地反映该类对重构查询样本的贡献。当类系数为正时，表示该类对查询样本有正面影响，当类系数为负时，表示该类对查询样本有负面影响。在每一阶段中只选取类系数为正的类进入到下一阶段。

在算法中有两个参数 $\alpha $ 与 $\beta $ ， $\alpha $ 代表所选取类的类系数之和占所有正类系数总和的比例，取值范围为 $0 < \alpha \leqslant 1$ ； $\beta $ 代表算法终止时所选训练样本的类别数阈值，取值范围为 $1 \leqslant \beta \leqslant {M_0}$ ，其中 ${M_0}$ 是训练样本的总类别数。参数 $\alpha $ 控制每次选取的类别数，确定算法进行的阶段数，进而影响算法的时间复杂度，而参数 $\beta $ 则控制算法最后进行识别时所需要的类别数，其影响算法的识别率。在第k阶段，确定选取类别数的规则为

${M_k} = \mathop {\arg \max }\limits_{1 \leqslant M \leqslant {M_{k - 1}}} \left( {\sum_{i = 1}^M {{\rm{SU}}{{\rm{M}}^{{{{c}}_i}}} < } \alpha \times {\rm{SU}}{{\rm{M}}^{{{{c}}^ + }}}} \right)$

(9)

式中： ${\rm{SU}}{{\rm{M}}^{{{{c}}^ + }}}$ 表示所有为正的类系数求和； ${\rm{SU}}{{\rm{M}}^{{{{c}}_i}}}$ 表示第 ${{{c}}_i}$ 类的类系数。注意，这里的类系数已经按降序排列。找到前 ${M_k}$ 个拥有较大类系数的类，其类系数之和小于阈值 $\alpha \times {\rm{SU}}{{\rm{M}}^{{{{c}}^ + }}}$ ,并且前 ${M_k}$ +1个较大类系数之和不大于阈值 $\alpha \times {\rm{SU}}{{\rm{M}}^{{{{c}}^ + }}}$ 。 ${M_k}$ 的取值范围是 $1 \leqslant {M_k} \leqslant {M_{K - 1}}$ ， $\alpha $ 控制每次选取近邻类的步长，当 $\alpha = 1$ 时，则每次选取类系数为正的类。该策略能逐渐缩小查询样本近邻类的范围。MPRBC算法的具体过程如算法1^[16]所示。

算法1　MPRBC算法

输入　训练样本集 ${{X}}$ ，查询样本 ${{y}}$ ，类别数 ${M_0}$ ，k=0。

输出　查询样本 ${{y}}$ 的类别 ${{c}}$ 。

1) While ${M_k}$ 大于设定阈值 $\beta $ ，通过式(7)得出训练样本 ${{{X}}_k}$ 的表示系数 ${{{s}}_k}$ ；

2) 根据式(9)确定 $ {M_{k + 1}}$ ；

3) 选取与前 ${M_{k + 1}}$ 个较大的 ${\rm{SU}}{{\rm{M}}^{{{{c}}_i}}}$ 所对应的类中所有样本，构成训练集 ${{{X}}_{k + 1}}$ ；

4) $ k = k + 1$ ；

5) End while；

6) 根据式(8)确定查询样本 ${{y}}$ 的类别 ${{c}}$ 。

3 实验结果及分析

为了验证所提出的自适应多阶段线性重构表示的分类(MPRBC)方法的有效性，选择6个人脸数据集进行实验，各数据集的规模和特征如表1所示。将MPRBC算法的分类精度与RBC方法(如LRMNN(p=1，p=2)^[5]、SoC(p=1) ^[7]、SoC(p=2)、TPLRMC(p=1，p=2)^[11])进行比较。对每个数据集，从每类中随机选取 $L$ 个图像作为训练样本，而余下的样本作为查询样本。通过10次运行再求平均得到每种方法的分类精度。

3.1 识别精度的实验与分析

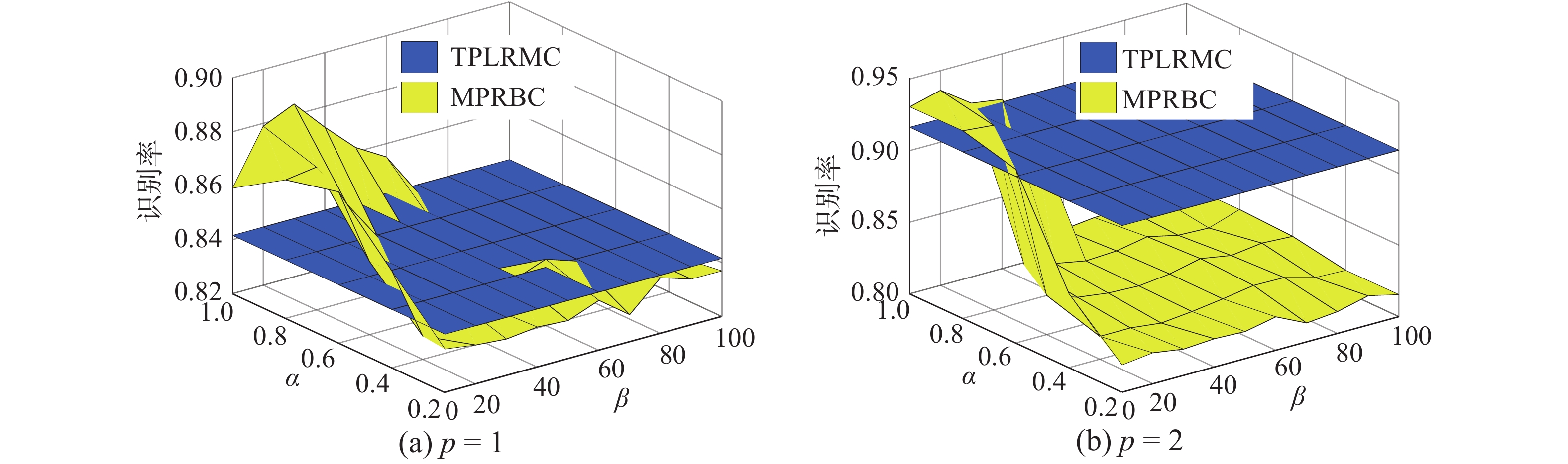
图3给出了在AR数据集上参数 $\alpha $ 和 $\;\beta $ 值的变化对识别率的影响，其中 $L = 7$ 。图3中，随着 $\alpha $ 值由大到小而 $\;\beta $ 值由小到大的变化，MPRBC的识别率由较高趋于稳定，且趋于退化为SoC，图中TPLRMC所表示的平面为TPLRMC算法识别率的参照平面。图4显示了在AR数据集上固定 $\;\beta $ =10，识别率随 $\alpha $ 值的变化。当 $\alpha $ 偏小时，说明算法选择类的步长较大，算法收敛较快，但识别率过低，随着 $\alpha $ 值的增大，其筛选类的过程逐渐精细化，算法的识别率得到提升。由图3和图4可知， $\alpha $ 值对较高识别精度的表达影响较小，但当 $\alpha $ 值较小时，随着 $\;\beta $ 值的由小到大，MPRBC算法的退化速度加快。当 $\alpha $ =1时，图5反映了MPRBC算法在各数据集上识别精度随 $\;\beta $ 值的变化情况。由此可知，要获得较好的识别性能， $\;\beta $ 的值不能太小也不能过大。当 $\;\beta $ 值较小时，最后一步用来进行识别判断的类的个数就较少；当 $\;\beta $ 值较大时，算法的阶段数较少，甚至完全退化为SoC算法，这些都会降低算法的识别精度。

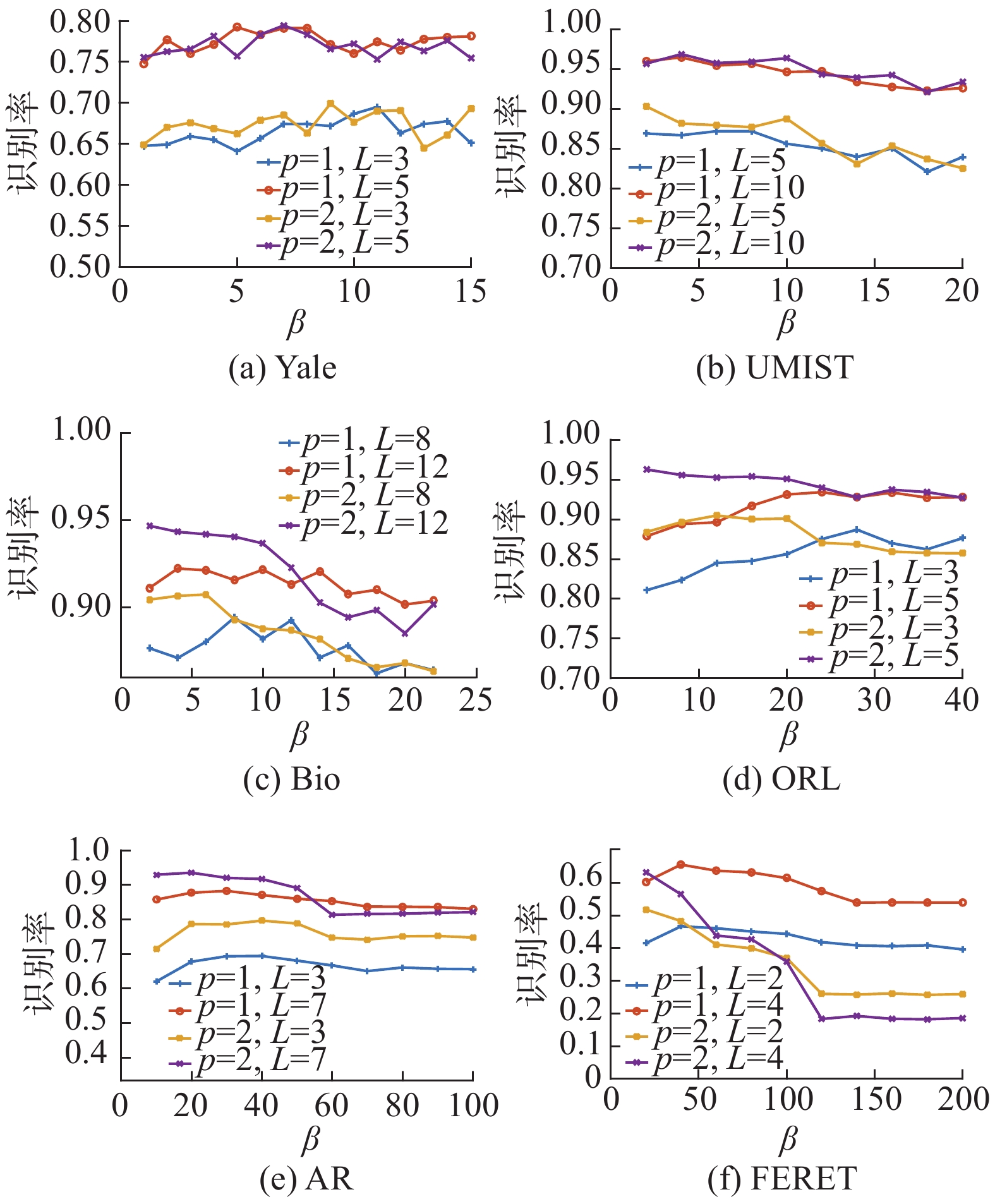
表2给出了MPRBC与其他算法识别精度的比较(MPRBC算法的识别精度由图5中的最高精度确定)。在所有数据集上，MPRBC算法均具有最好的识别性能。SoC算法要比LRMNN算法性能要好，这是因为SoC算法利用了样本的标签，通过同类样本进行协同表示，是一种有监督的算法，而LRMNN算法只考虑单个样本表示的作用。因此根据类系数来进行分类能提高分类精度，这也从侧面说明MPRBC筛选相似类的策略比TPLRMC筛选相似样本的策略更能提高分类性能。另外，SoC算法通过一阶段和TPLRMC算法通过两阶段筛选近邻样本并进行分类，其本质上是一种粗糙的筛选方法，且对于不同的查询样本，选择近邻的个数没有差异性。而MPRBC算法通过多阶段进行近邻类的筛选，是一种精细的筛选方法，且根据查询样本的不同，近邻类的筛选具有差异性。比较MPRBC算法、SoC算法和TPLRMC算法在各数据集上的实验结果，可以观察到多阶段比一阶段和二阶段更能提高分类精度，并且随着数据集样本类别数的增多其分类精度均有明显地提高。

3.2 时间复杂度的实验与分析

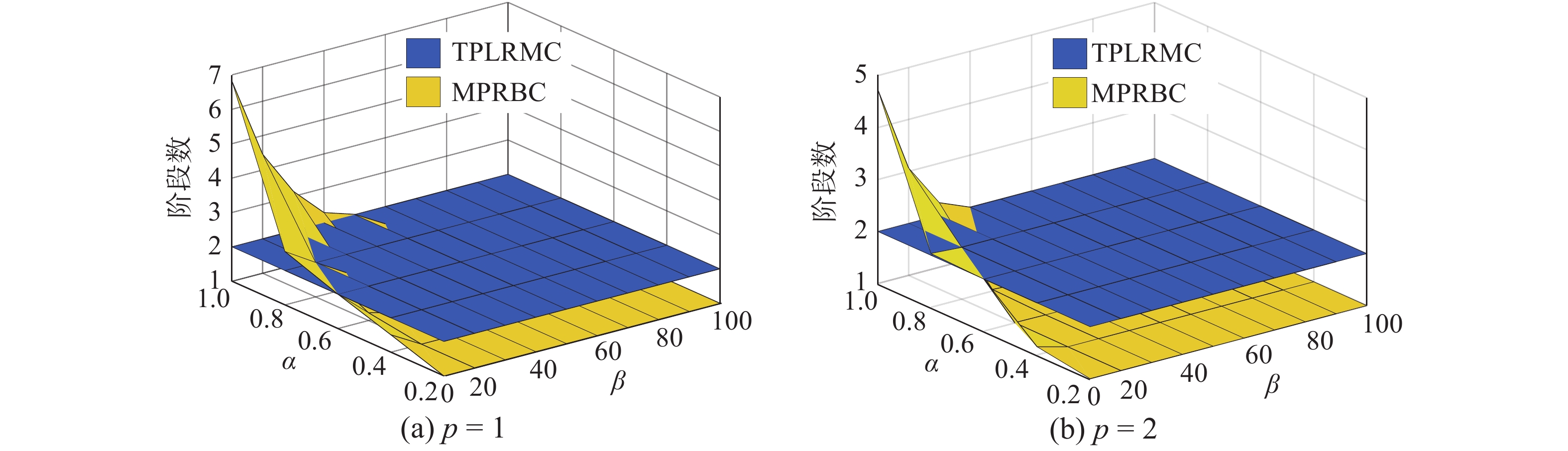
对于每一个查询样本，MPRBC与TPLRMC算法均通过 ${L_1}$ 范数或 ${L_2}$ 范数得到表示系数，其时间复杂度受训练样本数T的影响^{[1, 3]}。在MPRBC算法中，每阶段训练样本数随查询样本的不同自适应确定，而且MPRBC的阶段数P受T影响，不同查询样本也有差异。图6和图7分别给出了在AR数据集上 $L = 7$ 时参数 $\alpha $ 和 $\;\beta $ 对算法阶段数P和各阶段参与计算的训练样本的数量总和 $\displaystyle\sum\limits_1^P T$ 的影响。注意，图7中TPLRMC算法选取样本总数为两阶段相加，而MPRBC算法为多阶段相加。图8反映的是不同 $\alpha $ 和 $\;\beta $ ，MPRBC的CPU时间。图6~8中TPLRMC所表示的平面为TPLRMC算法达到最高识别精度时，阶段数、参与计算样本总数与CPU时间的参照平面。数据是所有查询样本分别计算10次后的平均值。由图6和图7看出，阶段数与选取样本总数之间呈现正相关。

当 $\alpha $ =1时，MPRBC算法在3个数据集上的最高识别精度所对应的CPU时间如表3所示，表中数据括号内为MPRBC算法所用平均阶段数。通过实验观察，在 ${L_1}$ 范数约束下，随着样本类别数的增加，MPRBC(p=1) 算法的阶段数也增加，算法的CPU时间也呈现递增趋势。在 ${L_2}$ 范数约束下，MPRBC(p=2)算法的CPU时间较高，这可能是因为不同类的训练样本在重构查询样本时其差异性不足，需要通过增加阶段数来提高识别精度。而由图3和图8可知，减小 $\alpha $ 值，在识别性能优于TPLRMC的情况下，MPRBC仍能减小算法的CPU时间。总之，自适应算法在保证较高识别精度的同时，由于对各查询样本进行差异化地表示，算法的CPU时间保持相对较低水平。

4 结束语

本文提出了一种自适应多段线性重构表示的分类(MPRBC)方法。基于熵减少原则，通过多阶段的方法，利用同类训练样本表示系数之和筛选样本，将分类集中在类别数较少的训练样本上，使得所选样本在具有较大重构贡献的同时保证了样本的稀疏类概率分布，达到了提高训练样本表示能力的目的。其次，算法拥有基于自适应的选择过程，能对不同查询样本进行差异化表示，并在部分数据集上减小了CPU时间。实验表明，该算法性能优于其他RBC算法，且在类别数较多的数据集上识别精度有明显的提升。