作为海洋资源开发的重要工具和军事领域的新型装备，水下无人航行器(autonomous underwater vehicle, AUV) 得到各国海洋工程领域的重点关注，并取得了长足的发展，但精确的水下导航定位方法一直是制约AUV长时间远距离深潜与自主作业的重要因素^[1-2]。常用于AUV的导航方法有水声学导航、航位推算导航、惯性导航以及近年兴起的地球物理导航等^[3-4]。水声学导航需要布置外部声学基阵，AUV无法独立作业，且定位范围受声学基阵布设范围限制。航位推算导航和惯性导航无需外部设备支持，但其长时间水下航行会产生较大的累积误差，需要定期上浮进行卫星定位校准。基于地磁场、重力场、海底地形等的地球物理信息导航由于具有全天候、无源性且不容易被干扰等优点，成为水下导航领域的研究热点之一。受限于测量传感器的测量精度等因素，地磁场、重力场辅助导航很难在现阶段应用于AUV导航系统。多波束地形测量技术的成熟，使得制作高精度的海底数字地图变为现实，所以海底地形辅助导航成为解决AUV水下精确导航的可行手段。AUV采用海底地形辅助导航无需布置外部传感器，不需要上浮修正误差，可满足AUV水下导航定位需求^[5-6]。

常用于海底地形辅助导航定位的方法是基于相关性的方法^[7-8]，它通过对比多波束实时测深数据和先验数字地形图(digital terrain map, DTM)中存储的水深数据，找出其相关度最大的位置作为最优匹配位置，并将其用于导航数据的修正。地形相关性算法的主要缺点是受到“误差均化”作用影响，在地形特征不明显区域存在伪定位点。对此，文献[9]提出一种基于Fisher判据的伪定位点的二次判别方法，但其大大增加了地形辅助定位程序的复杂性；文献[10]提出一种基于信息包的地形辅助导航定位方法，该方法考虑了相邻地形的联系，匹配精度较高，但其计算量较高，实时性较差。

由此可见，现有的改进相关性算法虽然具有理论上的优势，但由于其计算量较大，不能满足AUV水下实时导航需求。在现有各种状态估计算法中，粒子滤波(particle filter, PF)算法作为Bayesian滤波估计的一种近似最优估计方法，在处理非线性问题中具有较强优势^[11]，更适用于AUV海底地形辅助导航。本文在建立基于Bayesian估计的地形相关匹配定位模型基础上，采用改进后的粒子滤波方法解决Bayesian估计问题，该方法实现简单，具有较高的匹配精度，仿真实验结果表明了本文提出方法的有效性。

1 地形辅助定位算法模型 1.1 地形辅助定位的Bayesian估计

根据AUV水下运动规律，建立AUV海底地形辅助导航模型为

${{{X}}_{t + 1}} = {{{X}}_t} + {{{U}}_t} + {\nu _t}$

${{{Y}}_t} = {{{H}}_t}\left( {{{{x}}_t}} \right) + {{{E}}_t}$

(1)

式中： ${{{X}}_t}$ 为 $t$ 时刻参考导航(一般为惯性导航) 系统输出的AUV水平位置坐标； ${{{U}}_t}$ 为参考导航系统给出的相邻2个定位间隔内的位置偏移量； ${\nu _t}$ 为惯性导航误差； ${{{Y}}_t}$ 表示 $t$ 时刻的多波束实时测深数据； ${{{H}}_t}$ 为 ${{{x}}_t}$ 处的DTM数据； ${{{E}}_t}$ 为多波束测深误差，此处假定为Gaussian白噪声。为了简化分析，可将式(1)写成一维向量的形式：

${{{y}}_t} = {{{h}}_t}({{{x}}_t}) + {{{e}}_t}$

假设多波束实时测深数据由真实水深加上多波束测深误差组成，且该误差为独立Gaussian白噪声，则先验概率密度函数(probability density function, PDF)为

$p\left( {{y}_{t}}|{{x}_{t}} \right)=\frac{1}{{{\left( 2{\text{π}} {{\sigma }^{2}} \right)}^{\frac{N}{2}\;}}}\exp \left[ -\frac{1}{2{{\sigma }^{2}}}\sum\limits_{k=1}^{N}{{{\left( {{y}_{k}}\left( {{x}_{0}} \right)-{{h}_{k}}\left( {{x}_{t}} \right) \right)}^{2}}} \right]$

(2)

式中：N为匹配面中水深数据的数目； $\sigma $ 为独立Gaussian白噪声的方差。根据实时测量序列 ${y_t}$ 估计地形辅助定位误差，系统后验PDF可由Bayesian公式确定：

$p\left( {{x_t}|{y_t}} \right) = \frac{{p\left( {{y_t}|{x_t}} \right)p\left( {{x_t}} \right)}}{{\displaystyle \int_{{x_t} \in {S_t}} {} p\left( {{y_t}|{x_t}} \right)p\left( {{x_t}} \right){\rm{d}}{x_t}}}$

式中：分母是一个与 ${x_t}$ 无关的归一化常量， $p\left( {{x_t}} \right)$ 为参考导航系统的定位误差分布。假设条件独立，即 $p\left( {{y_t}|{Y_{t - 1}},{x_t}} \right) = p\left( {{y_t}|{x_t}} \right)$ ，根据Bayesian联合证据理论可得Bayesian更新公式：

$ \begin{array}{c} p\left( {{x_t}|{Y_t}} \right) = {\alpha _t} p\left( {{x_t}|{Y_{t - 1}}} \right)p\left( {{y_t}|{x_t}} \right)= \\ \;\;\;\;\;\;\;\;\;\dfrac{{p\left( {{x_t}|{Y_{t - 1}}} \right)p\left( {{y_t}|{x_t}} \right)}}{{\displaystyle\int_{{x_t} {_t \in {S_t}}} {} {p\left( {{x_t}|{Y_{t - 1}}} \right){p_{{\nu _t}}}\left( {{x_{t + 1}} - {x_t} - {u_t}} \right)} {\text{d}} {x_t}}} \end{array}$

(3)

式中 $p({X_t}|{Y_{t - 1}})$ 可由 $p({X_{t - 1}}|{Y_{t - 1}})$ 通过位置更新获得。假设位置变量相互独立，可得Bayesian预测公式为

$ \begin{array}{c} p({X_t}|{Y_{t - 1}}) = p({x_t}|{X_{t - 1}},{Y_{t - 1}})=\\ \;\; \;\displaystyle\int_{{x_t} \in {S_{t - 1}}} {p({X_{t - 1}}|{Y_{t - 1}})p({x_t}|{x_{t - 1}}){\rm{d}}{x_{t - 1}}} = \\ \;\; \displaystyle\int_{{x_t} \in {S_{t - 1}}} {p({X_{t - 1}}|{Y_{t - 1}})({x_t} - {x_{t - 1}} - {u_{t - 1}}){\rm{d}}{x_{t - 1}}} \end{array} $

(4)

式(2)、(3)、(4)为地形匹配的Bayesian滤波估计公式，其中式(3)、(4)分别为系统状态更新公式和系统状态预测公式。

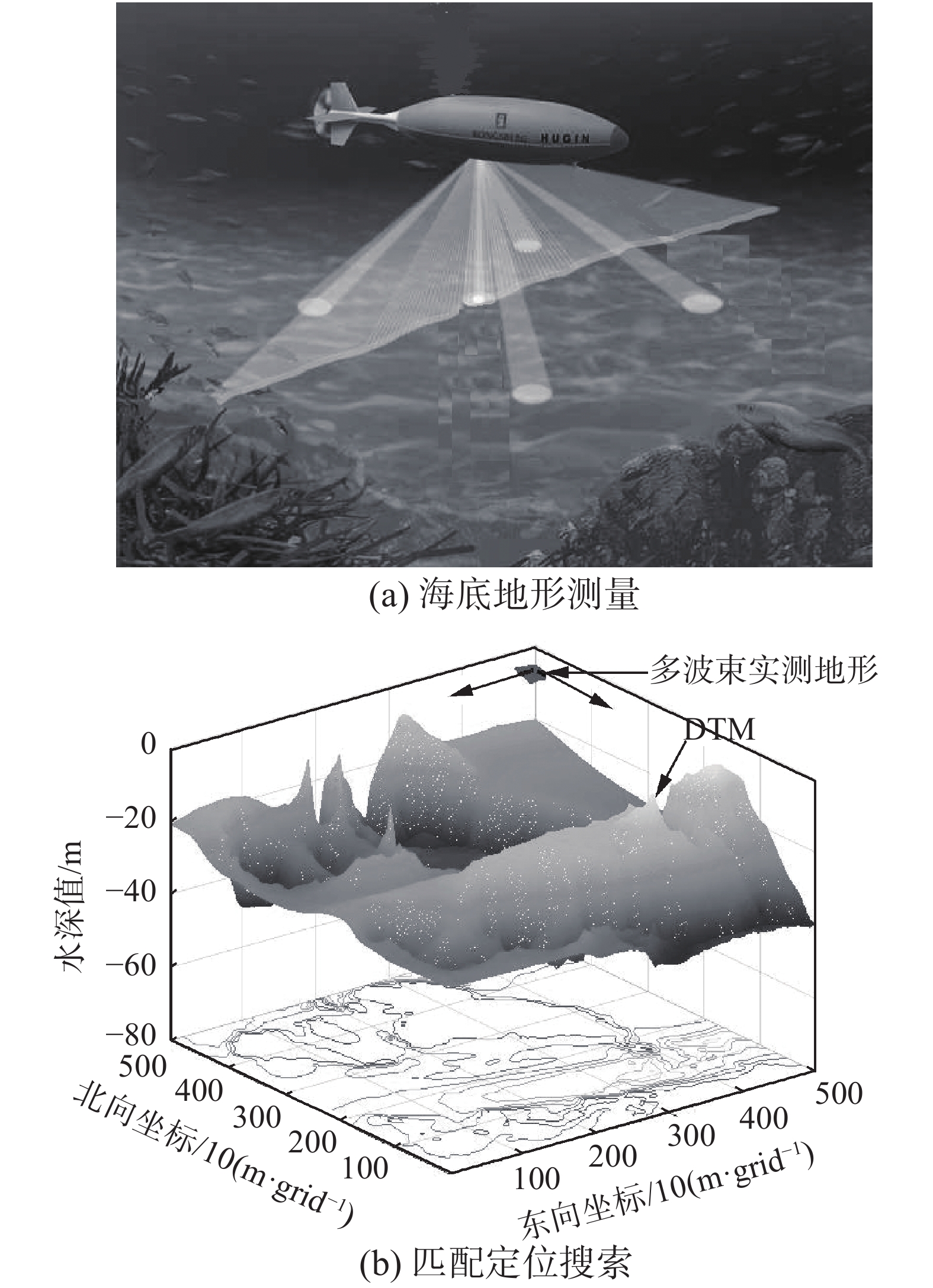
Bayesian滤波的最大困难是PDF的数值解法，即使对于线性高斯系统，其求解仍然面临着高维积分问题，计算难度较大。在Bayesian滤波的数值解法中，PF算法作为一种Bayesian滤波的近似最优方法得到了越来越多的关注，在解决这类问题上有着良好的实用性^[12]。基于多波束测探的AUV海底地形辅助导航示意如图1所示。

1.2 PF地形辅助定位算法

PF算法的本质是将连续积分运算变为随机样本集的求和运算，即系统状态的后验PDF可用一组在状态空间内随机抽取的加权粒子表示为

$p({X_t}|{Y_t}) \approx \frac{1}{{{N_s}}}\sum\limits_{i = 1}^{{N_s}} {\delta ({X_t} - X_t^i)} $

式中 ${N_s}$ 为抽取加权粒子的个数。PF的关键步骤是通过引入有权值的粒子集 $\left\{ {X_t^i} \right\},i = 1, 2, \cdots ,{N_s}$ ，并根据观测值更新粒子的权重，估计系统的状态。研究表明：随着迭代次数增加，粒子权值的方差随之增大，将产生粒子退化现象。为了消除粒子退化影响，PF通常引入重采样技术，复制高权值粒子，并淘汰低权值粒子，更新权值后的PDF可表示为

$p({X_t}|{Y_t}) \approx \sum\limits_{i = 1}^{{N_s}} {w_t^i\delta ({X_t} - X_t^i)} $

式中 $w_t^i$ 为第i个粒子在t时刻的权值，其计算公式为

$w_t^i = w_{t - 1}^i\frac{{p\left( {{z_t}|x_{t - 1}^i} \right)p\left( {x_t^i|x_{t - 1}^i} \right)}}{{q\left( {x_t^i|x_{t - 1}^i,{y_t}} \right)}}$

(5)

粒子滤波的状态估计和方差估计为

状态估计：

${\tilde {{x}}_t} = \frac{1}{{{N_j}}}\sum\limits_{i = 1}^{N_c^j} {w_t^i} x_t^i$

方差估计：

${p_t} = \sum\limits_{j = 1}^{{N_j}} {\sum\limits_{i = 1}^{N_c^j} {w_t^i(} {{x}}_t^i - {{\tilde {{x}}}_t}){{({{x}}_t^i - {{\tilde {{x}}}_t})}^{\text{T}}}} $

虽然基于重采样技术的PF算法可避免粒子退化现象，但重采样会造成高权值粒子被多次复制，从而损失粒子集的多样性，即出现“粒子贫化”现象。为了弥补重采样过程中的多样性损失问题，对重采样后粒子进行重新分布，在地形辅助定位中引入辅助采样技术。

1.3 辅助重采样技术

辅助采样是指是在重采样后的父代粒子的基础上，通过父代粒子的先验PDF进行再次采样。辅助采样后粒子是融合了父代先验知识的重新分布的粒子，可有效提高粒子多样性，使得粒子分布结果更接近于真实PDF。辅助重采样技术的实现方法如下：

1) 计算粒子滤波中的有效粒子个数 ${N_{{\text{eff}}}}$ ， ${N_{{\text{eff}}}}$ 的计算公式为

${N_{{\text{eff}}}} = {1 / {\sum\limits_{i = 1}^{{N_s}} {{{\left( {w_t^i} \right)}^2}} }}$

(6)

2) 若 ${N_{{\text{eff}}}}$ 小于设定的重采样阈值 ${N_{{\text{th}}}}$ ，从粒子集中根据重要性权值重新采样得到新的粒子集 $\left\{ {{{{x}}^*}_t^i} \right\},i = 1,2, \cdots ,N$ ，记录其父代粒子及其权值的集合 $\left\{ {{{x}}_t^j,{{w}}_t^j} \right\}_{j = 1}^M,j = 1,2, \cdots ,M$ ，以及每个父代粒子复制的次数 $\left\{ {{{N}}_c^j} \right\}_{j = 1}^M,j = 1,2, \cdots ,M$ 。其中M为父代粒子的个数。

3) 根据每个父代粒子的分布 $p(x_i^j)$ ，重新采样 $N_c^j$ 次，计算采样后粒子的权值：

$w_t^j = \dfrac{{p({y_t}|x_{t - 1}^i)}}{{p({y_t}|x_t^*)}}$

式中 $x_t^* = E({x_t}|x_{t - 1}^i)$ ， $i = 1,2, \cdots ,N_c^j$ 即为采样后的均值，归一化所有权值 $w_t^i = 1/N$ 。

2 地形辅助定位算法流程

引入辅助的改进粒子滤波(improved particle filter, IPF)算法步骤如下：

1) 初始化： $t = 0$ ，根据 $p\left( {{x_0}} \right)$ 的分布采样得到粒子数为N的粒子集 $\left\{ {{{x}}_0^i} \right\}_{i = 1}^N,i = 1,2, \cdots ,N$ ，粒子的初始重要性权值为 $w_0^i = {1 / N}$ ；

2) 重要性权值计算： $t = t + 1$ ，根据先验PDF采样得到 $x_t^i \sim q\left( {{x_t}|x_{t - 1}^i,{y_{t - 1}}} \right)$ ， $i = 1,2, \cdots ,N$ ，根据式(5)计算重要性权值 $w_t^i$ ；

3) 重要性权值归一化： ${w^*}_t^i = {{w_t^i} / {\displaystyle\sum\limits_{j = 1}^N {w_t^j} }}$ ；

4) 根据式(6)计算有效粒子个数 ${N_{{\text{eff}}}}$ ；

5) 若 ${N_{{\text{eff}}}}$ 小于重采样阈值 ${N_{{\text{th}}}}$ ，执行辅助重采样计算；

6) 输出地形匹配的状态估计和方差估计；

7) 判断滤波是否收敛，若滤波收敛，输出定位结果；若滤波未收敛转到步骤2)。

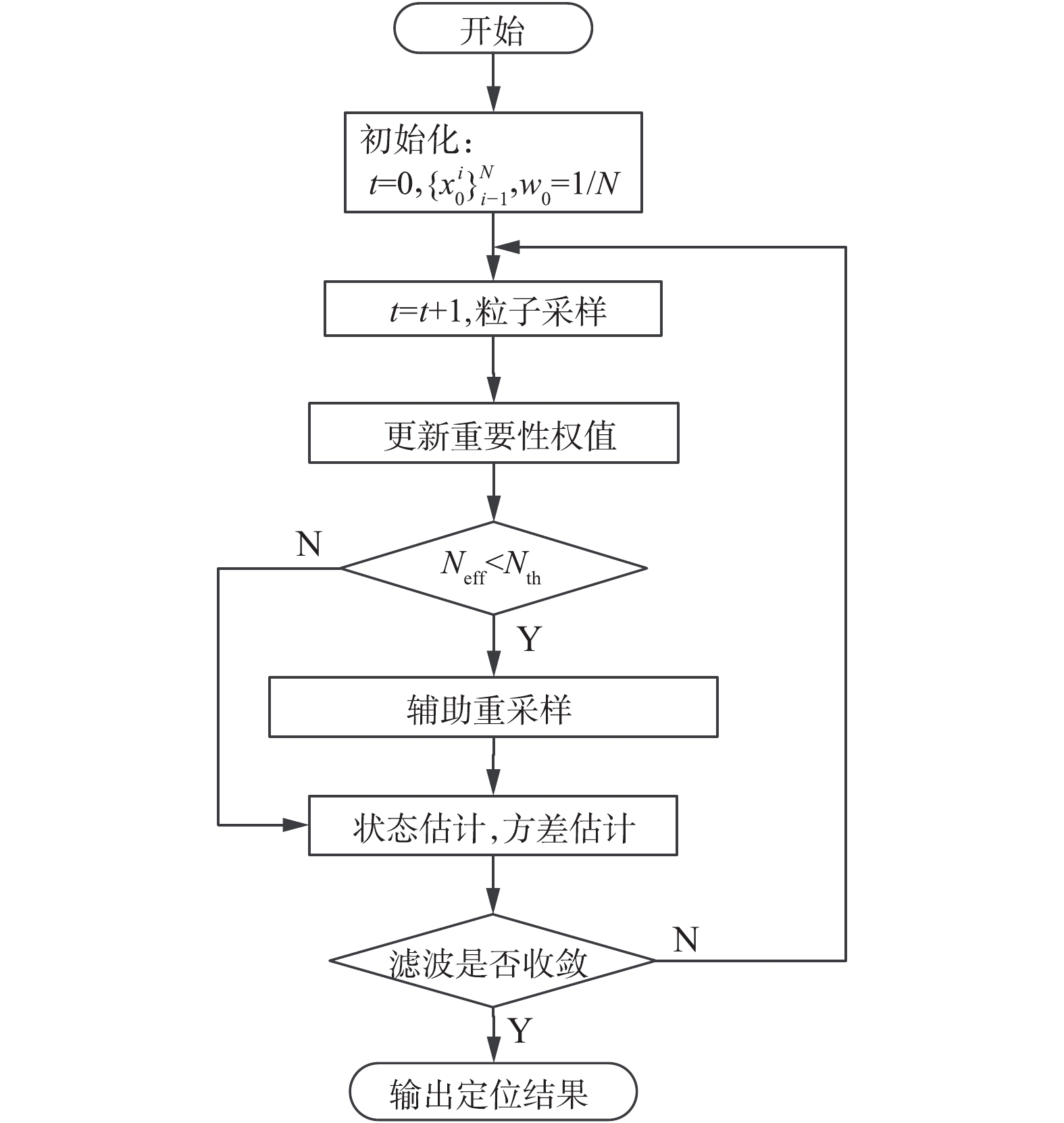
基于辅助采样粒子滤波的海底地形辅助定位算法流程图如图2所示。

3 仿真实验与结果分析 3.1 半物理测试平台

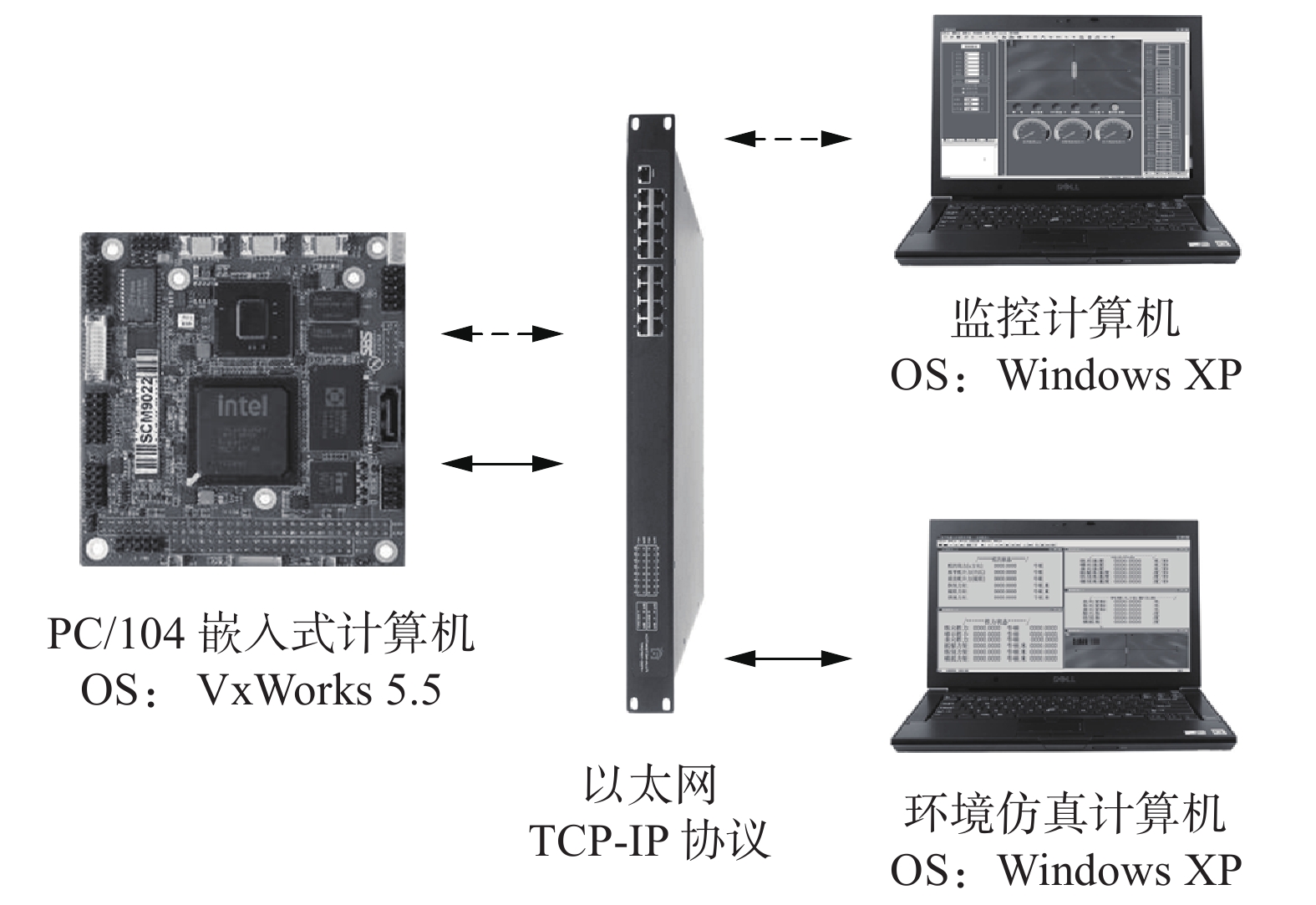
仿真实验在一个以PC/104嵌入式计算机为核心的AUV海底地形辅助导航半物理测试平台中进行，其结构如图3所示。

如图3所示，仿真平台由3部分组成：监控计算机、环境仿真计算机和PC/104嵌入式计算机。基于半物理测试平台，仿真试验分为2部分：

1) 基于电子海图数据的算法验证；

2) 使用真实多波束测深数据的回放式仿真。

3.2 算法验证

使用在环境仿真计算机中运行的Vega视景仿真软件模拟AUV运动，同时多波束测深系统由Vega的相交线检测功能模拟^[13]。Vega视景仿真界面如图4所示。

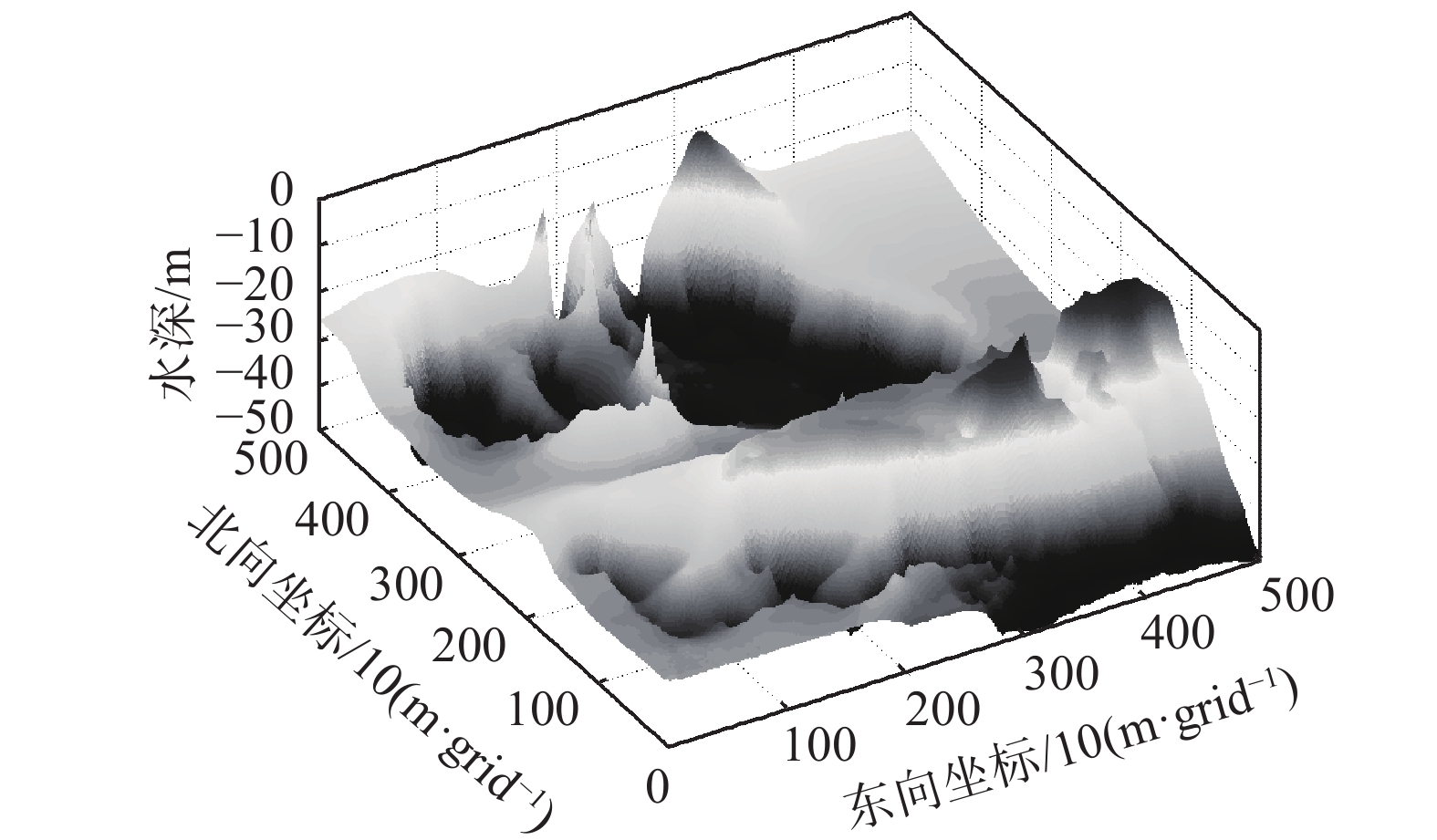
算法验证所使用的DTM通过对某海域电子海图中的水深数据进行网格化插值得到，如图5所示。DTM的尺度大小 $5\;{{\text{km}}} \times 5\;{{\text{km}}}$ ，网格数目1 000×1 000。根据文献[13]建立视景仿真所需的DTM并输入仿真平台，以实现地形数据的相交检测。

由于在真实地形辅助导航外场实验中使用的光纤罗经等姿态测量传感器具有较高的测量精度，在运算中往往忽略其误差影响^[14]。因此为了提高仿真效率，AUV自身姿态测量误差在仿真中也可忽略。设定AUV的航行路径，并在航行路径上选取5个地形匹配区域，规划路径和选取的匹配区域如图6所示。

选用 $60 \times 5$ 的实时地形数据进行匹配实验，其中乘号前表示每个地形剖面的测深点数量，乘号后表示测深剖面的个数，相邻两个地形剖面的间距为10 m。由于Vega相交线检测的精度很高，因此需要对检测结果加一定的噪声。

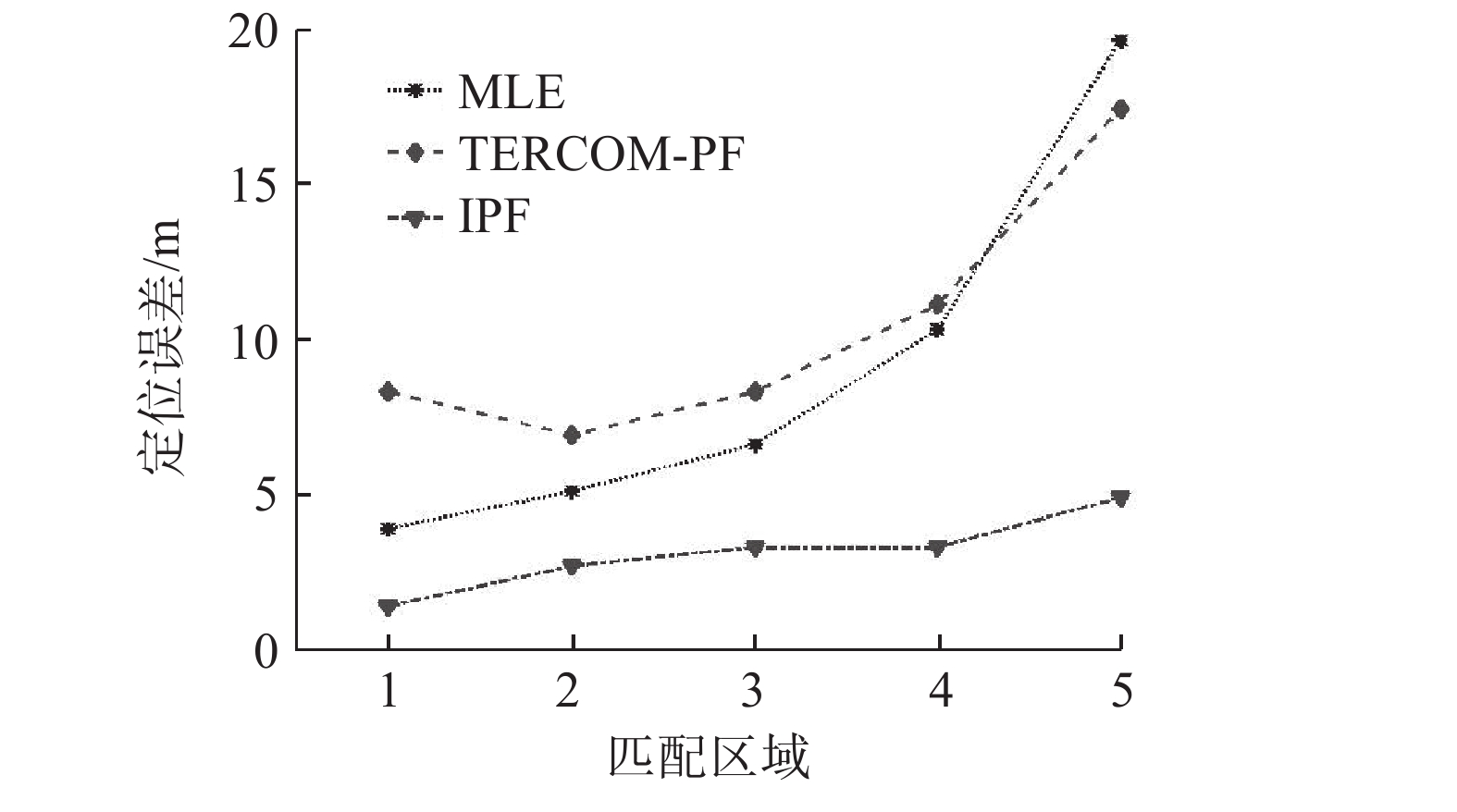
为了量化地形特征的丰富程度，计算匹配区域内的地形熵^[15]。分别基于极大似然估计(maximum likelihood estimation, MLE)算法^[9]、TERCOM和粒子滤波组合算法( terrain-aided navigation algorithm combined with the TERCOM algorithm and particle filter，TERCOM-PF )^[16]和基于辅助采样的IPF算法，各进行200次导航仿真实验并计算误差平均值，仿真结果如图7所示。

根据地形熵的定义可知，地形特征丰富程度随地形熵的增大而减少。由表1可知，定位区域1~5处的地形特征逐渐贫乏。由图7可以看出，随着地形熵的增大，MLE算法、TERCOM-PF算法、IPF算法的地形匹配误差均随之增大。当地形熵较小时，MLE算法的定位精度介于TERCOM-PF算法和IPF算法之间。随着地形熵的增大，MLE算法的定位误差增长较快，在定位区域5内，MLE算法的定位误差大于TERCOM-PF算法。这是由于MLE算法假设所有测深数据的误差对地形匹配定位的影响是相同的，总体误差是个体误差的平均，没有考虑个体误差的差别，即MLE算法的定位性能受“误差均化”作用的影响。在地形特征贫乏区域，总体间的误差差别很小，“误差均化”的干扰也随之增大，从而导致地形匹配精度的大幅降低。相比于TERCOM-PF算法，IPF算法引入辅助采样技术，滤波运算中的有效粒子个数大大增加，因此其精度有较大提高，且其受地形特征影响程度较低，5个区域的平均定位精度均小于5 m，对于地形特征有着较强的适应性。

3.3 回放式仿真

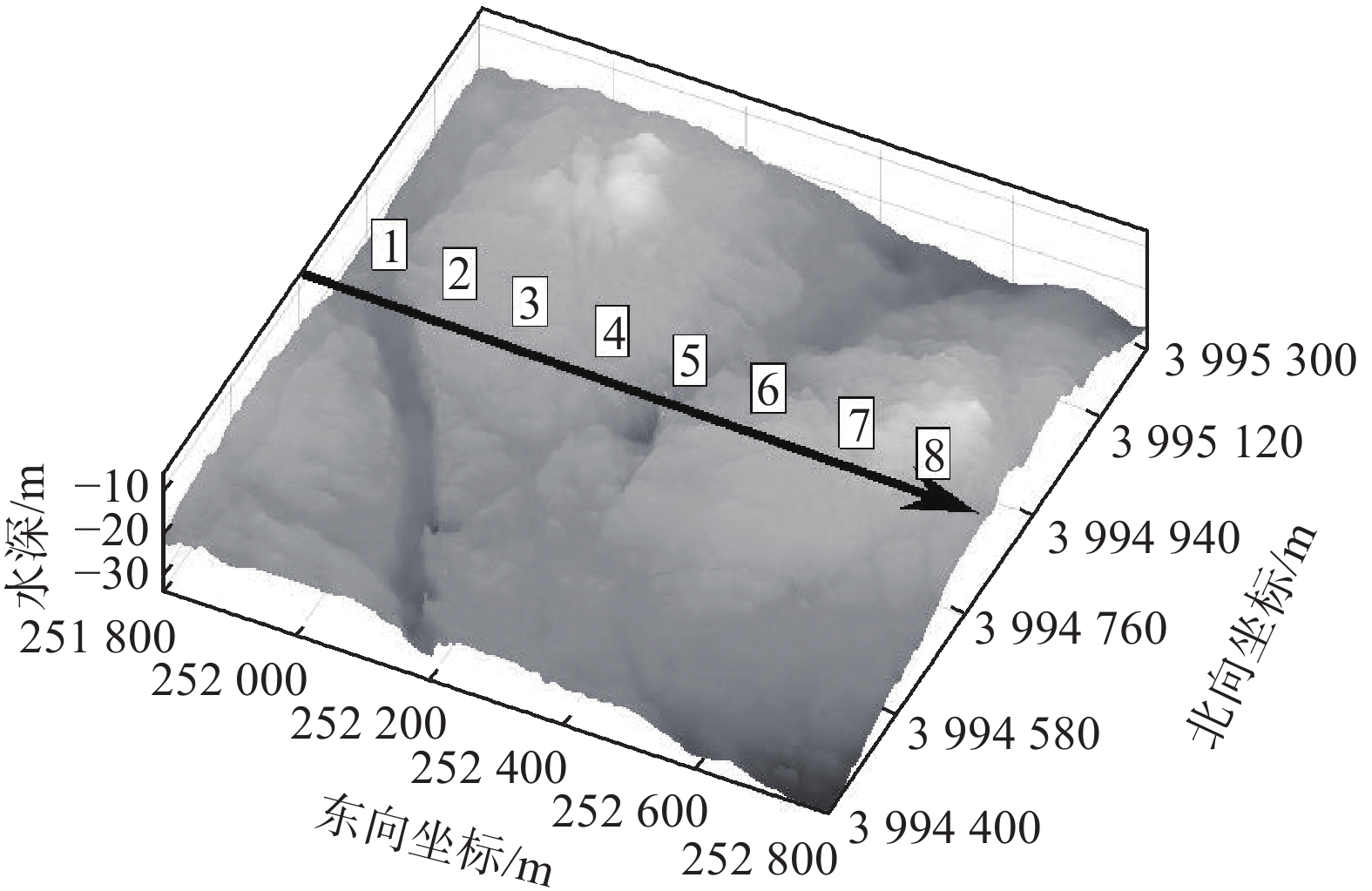
回放式仿真实验的数据源为AUV搭载多波束测深系统在胶州湾海区获得的海底测量数据。多波束测量区域大小约为1 000 m×900 m。滤波和网格化处理后，得到分辨率为1 m×1 m的DTM，如图8所示。

图8中箭头所示的路径是一条独立的多波束测线，用于模拟实时多波束测深数据。该测线由一次独立多波束测深实验获得，且测量时AUV航向不同于测量DTM时的航向，保证了数据独立性。

由于回放式仿真中的实验数据来源于真实海中实验，因此回放式仿真可验证算法在真实海洋环境中的适应性^[17]。沿独立测线方向选取8个区域作为地形辅助定位区域，计算地形熵。表2中所示为定位区域内的地形熵，表示地形特征丰富程度，正好与地形匹配区域内的定位精度相对应。

基于不同的波束组合模式和粒子数，进行回放式仿真实验，实验结果如下：

1) 设定仿真中的粒子数为2 000，选择不同波束组合进行仿真实验，仿真结果如图9所示。

由图9可以看出，当实时测深数据较少(40×3)时，增加波束的数目可以有效提高地形辅助定位的精度；当实时测深数据达到一定数目(60×5)时，随着测深数据的增加，地形辅助定位精度并不随之提高。这是由于60×5的实时测深数据对局部地形特征的描述已经能较为准确，此时增加测深数据将带来数据冗余，并不能有效提高定位精度。

2) 设定仿真中的波束组合为 $60 \times 5$ ，选择不同粒子数目进行仿真实验，仿真结果如图10所示。

由图10可以看出，当粒子数较少时，增加粒子个数可以有效提高地形辅助定位的精度；但随着粒子数的增加，地形辅助定位精度将稳定在一定范围，此时再增加粒子数目不能提高匹配定位精度。IPF地形辅助定位的计算量与粒子数呈正比，因此在匹配中应在保证定位精度的前提下取较少的粒子数目。

由于采用的DTM具有较高分辨率，在回放式仿真实验中沿独立测线选取的8个区域内的地形辅助定位精度均小于5 m，因此本文提出的地形辅助定位方法对真实海洋环境有较好的适应性。

4 结束语

针对AUV海底地形辅助导航问题，在PF中引入辅助采样技术，提出一种适用于AUV的IPF海底地形辅助定位算法，并进行了基于半物理测试平台的算法验证实验和回放式仿真。本文提出的方法具有容易实现、定位精度较高、对地形特征的适应能力较强等优势。由于地形辅助定位精度与匹配区域内的地形特征丰富程度相关，后续的研究工作将重点研究如何根据海底地形特征实时选取恰当的测深数据组合模式和粒子数，实现定位精度和计算量的平衡。