当前移动机器人自主运动是衡量机器人性能的重要指标,而路径规划是完成这一指标的关键技术。路径规划[1]是指存在障碍物的环境中,按照一定的评价标准,找到一条适当的从起点到终点的路径,机器人在运动的过程中避开所有障碍。移动机器人路径规划大致分两种,分别是全局路径规划方法[2-3]和局部路径规划方法[4-5]。目前国内外路径规划算法主要采取的方法有:传统方法,如A*算法、人工势场法、Bidirectional RRT算法等[6-8];智能算法,如神经网络算法[9]、粒子群算法和模糊控制算法等。这些算法各有优缺点,例如:人工势场法实现简单,但容易陷入局部最小值;Bidirectional RRT算法能够有效地解决高维空间和复杂约束问题,但路径由随机采样点搜索一次生成,缺乏可重复性,导致路径不是最优;粒子群算法[10]具有收敛速度快、设置参数少的特点,但寻优效率能力差;模糊控制算法[11]不需要精确的数学模型,鲁棒性强,但是控制系统精度降低,动态品质变差,缺乏系统性。国内外学者针对每种算法存在的不足提出了很多方法:文献[8]提出了基于双向势函数的抽样路径规划算法,通过启发式函数证明收敛得到路径最优解,文献[10]提出一种与Morphin算法混合路径规划,同时改进QPSO自适应局部搜索的策略,引入交叉操作,提高性能避免局部最优。其中Morphin搜索树[12]算法计算量小、实用性好,适合处理具有动态障碍物的路径规划问题。文献[13]中使用双层栅格地图方法对A*算法进行优化,高层A*算法决定下一块大栅格局部地图,低层A*算法对合并的局部地图进行路径规划。A*算法是一种搜索速度快,使用广泛的路径规划算法。针对传统A*算法节点多,转折角大且无法动态避障等问题,本文提出一种融合改进A*算法与Morphin算法的结合算法。该算法主要利用改进A*算法进行全局路径规划,在全局路径的基础上,利用Morphin搜索树算法进行局部路径修正,使移动机器人在遇到行走的人、打开的门等动态障碍物时,进行局部路径规划,绕过障碍物后回到全局路径上,实现动态避障。
1 基于改进A*算法的全局路径规划传统A*算法[13]获取的路径存在搜索节点多、折线多、转折角大等不足之处,本文针对上述问题主要对A*算法[14-15]进行了两方面改进。首先改进关键节点的选取方式,删除冗余节点,假设P为保存路径的j行2列数组,每列元素分别代表栅格地图中x轴与y轴上的坐标点,每次更新P时,对已知节点与当前节点进行判断是否在同一直线上,如果为真,则去除中间节点,如果不在同一直线上,则将当前节点保存到P中。然后对规划的路径平滑处理[16],文献[16]中面对传统A*算法生成的路径转折角大且移动机器人转向困难等问题采用了创建函数判断连接点是否存在障碍物,若无障碍物删除连线中间节点。而本文利用移动平均滤波的方法进行路径平滑处理,实现简单,效果同样明显。根据数据统计方法,将连续的采样数据作为一个固定长度为N的队列,在新的一次测量后,去掉上述队列中首数据,剩余的
1)初始化地图信息包括起点、目标点、障碍物信息等;
2)创建Open列表与Closed列表,将起点的节点信息放入Open列表中;
3)如果Open列表中为空,表示没有找到路径,退出;
4)寻找起点周围可以到达的方格(周围8个方格),并把起点设置为这些方格的“父节点”,然后把周围节点加入到“Open列表中”,根据列表中节点
5)从Open列表中找到最佳节点,作为新的“父节点”,并将上一个父节点移到Closed列表中;
6)在Closed列表中选取扩展节点,将扩展节点的周围节点加入Open列表中。判断当前父节点是否为目标点,如果是,则通过当前父节点向上遍历到起点,找到组成路径的所有节点,否则,转到4);
7)设置变量
8)将Closed列表中最后得到的路径节点进行移动平均滤波处理,得到平滑路径。
2 Morphin搜索树算法局部路径规划 2.1 Morphin搜索树算法Morphin算法是CMU根据Ranger[17]算法提出的基于地面分析的局部路径规划算法,也是一种基于先验栅格地图进行可行性统计分析的局部避障算法[18-20]。其核心思想是:根据机器人自身的传感器对环境信息进行实时检测,根据不同的转向角度生成一组可行驶路径集,然后根据机器人当前的状态,包括俯仰角、转向角以及前方路径的可通行率、安全性,选出一条最适宜通行的路径。该算法不仅计算量较少、效率较快,能够较好地处理环境建模的不确定性,也能较好地与全局路径规划算法结合,共同决策机器人的运动行为[21]。Morphin算法预测线如图1所示,其中圆环为机器人,Target菱形为目标,黑色块为障碍物。

|
Download:
|
| 图 1 Morphin算法路径选择 Fig. 1 Path selection by Morphin algorithm | |
Morphin算法由运动模型和评价函数两部分组成。运动模型的核心思想是根据前进方向按照同样的时间、不同的转移角生成一组路径,利用评价函数对每条路径进行估计,得到最优路径。Morphin算法运动模型的建立就是建立搜索路径组和搜索弧线组[22]。搜索路径组是指由当前环境信息得到的可能运行的位置。搜索弧线组由多条预测线组成。已知机器人当前位置、速度及运动方向角,即
| $\begin{array}{l} \left[ \begin{array}{l} x(t + \mu ) \\ y(t + \mu ) \\ \end{array} \right] = \left[ \begin{array}{l} x(t) \\ y(t) \\ \end{array} \right] - \left[ \begin{array}{l} {\textit{v}}(t)\mu \cos {{\bf{\theta }}_s}(t) \\ {\textit{v}}(t)\mu \sin {{\bf{\theta }}_s}(t) \\ \end{array} \right] \end{array} $ | (1) |
式中:
| $\begin{array}{l} \left[ \begin{array}{l} x(t + \ell i) \\ y(t + \ell i) \\ \end{array} \right] = \left[ \begin{array}{l} x(t + \ell (i - 1)) \\ y(t + \ell (i - 1)) \\ \end{array} \right]{\rm{ - }}\left[ \begin{array}{l} {\textit{v}}(t)\ell \cos {{{\theta }}_s}(t) \\ {\textit{v}}(t)\ell \sin {{{\theta }}_s}(t) \\ \end{array} \right] \end{array} \!\!\!\!\!$ | (2) |
式中:
从图1中可以看出,机器人为了避开障碍物会选择碰撞机率最小的路径,7条弧线中AB与AC为无碰撞的备选路径,AC路径到达目标点会导致路径复杂,因此AB路径更加合理。对于Morphin搜索树算法产生的多条备选路径规划用评价函数决定最优度,评价函数为
| $f = \left\{ \begin{array}{l} \infty ,\quad {\text{弧线上有障碍物}}\\ {\gamma _1}L + {\gamma _2}M + {\gamma _3}\Delta d + {\gamma _4}N,\quad {\text{无障碍物}} \end{array} \right.$ | (3) |
式中:
本文算法的流程如图2所示。机器人首先基于改进A*算法进行全局规划,然后根据自身传感器实时检测周围环境信息,并感知是否存在未知障碍物,预测障碍物的运动轨迹与速度,判断机器人是否会与障碍物发生碰撞,如果与未知障碍物碰撞,调用Morphin算法进行局部规划。

|
Download:
|
| 图 2 融合算法流程图 Fig. 2 Flow chart of the fusion of algorithms | |
融合算法中的Morphin算法基于动态窗口原理,采用时间滚动窗口思想搜索可行轨迹空间。根据动态窗口中评价函数来进行动态预测:
| $G = \alpha \cdot X_{\rm{angle}} + \beta \cdot Y_{\rm{dist}} + \lambda \cdot Z_{\rm{velocity}}$ | (4) |
设定以机器人为中心的工作区域,依靠实时的传感器每隔一段时间以3个栅格的距离对周围环境信息进行采集,式(4)作为判断局部路径的评价函数。航向对目标的偏离角由
1)机器人根据探测障碍物信息每隔一段时间更新栅格地图信息,同时保存当前节点;
2)确定将要驶向的子目标点;
3)以机器人当前节点为起点,画出指向子目标点的直线,在直线两侧45°均匀地画出弧线,弧线利用附近的栅格点或已保存的节点表示;
4)根据评价函数
5)将机器人旋转一定角度或等待一段时间进行尝试,如果不行,停止局部路径规划;调用A*算法重新进行全局规划,然后返回1);
6)机器人成功绕开障碍物后回到全局路径上继续行驶到目标点。
3 仿真结果与分析为了验证本文提出的A*算法与Morphin搜索树算法相融合的方法的有效性,进行了多组仿真实验,首先对比分析传统A*算法与改进A*算法在全局路径规划中的效果,然后引入动态障碍物,采用Morphin搜索树算法进行局部路径规划,修正全局路径。仿真实验在MATLAB R2014a实验平台上进行。计算机配置CPU 2.5 GHz,内存4 GB。在栅格地图模型20×20(网格间距1 m)下进行多组传统A*与改进A*的对比实验。障碍物覆盖率为30%,实验中起点坐标为(2,2)目标点坐标为(18,18)。改变环境信息以验证改进算法优化效果明显。
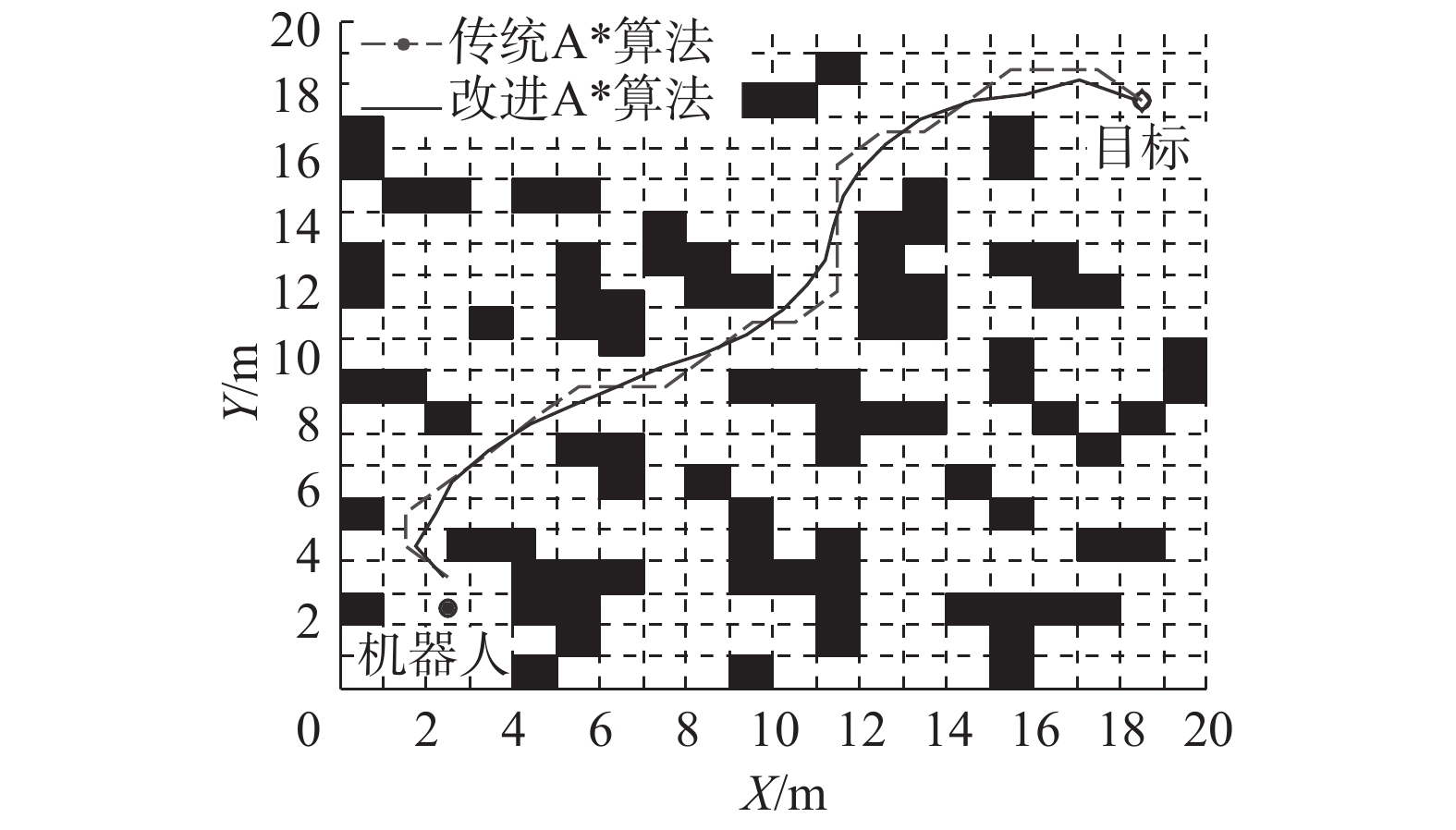
3.1 A*算法与改进A*算法仿真实验对比分析在地图相同的情况下,使用传统A*算法与改进A*算法进行路径规划,对比2种算法的仿真结果。在普通室内环境,经过A*算法和改进A*算法全局路径规划后的结果如图3所示。在随机生成的环境下经过A*算法和改进A*算法全局路径规划后的结果如图4所示。

|
Download:
|
| 图 3 普通地图传统A*算法与改进A*算法实验 Fig. 3 Experiment of traditional A* algorithms and improved A* algorithms on general map | |
|
Download:
|
| 图 4 随机地图传统A*与改进A*算法实验 Fig. 4 Randomly generated map traditional A* algorithms and improved A* algorithms experiment | |
对比2种算法路径规划结果,即起点与终点间的连线,可以看出改进A*的路径比传统A*的路径更平滑,路径中拐点的转折角得到了优化。
通过图3室内地图与图4随机地图的比较可知,该算法在复杂环境中依然可以选择出最优的路径。室内固定障碍环境只有1条或2条可到达目标的路径,而随机障碍物具有多条可通行路径,可选择的路径增加,而改进A*算法仍然可以在多条路径中选择最优路径。表1是对两组A*算法与改进A*分别进行10次的平均值。
| 表 1 传统A*算法与改进A*算法比较结果 Tab.1 Comparison of traditional and improved A* algorithms |
从表1中可以看出,改进A*算法路径长度缩短了15%,所耗费的时间缩短了8%,节点数减少了36%。在时间、距离、节点数等方面优化了传统A*算法。
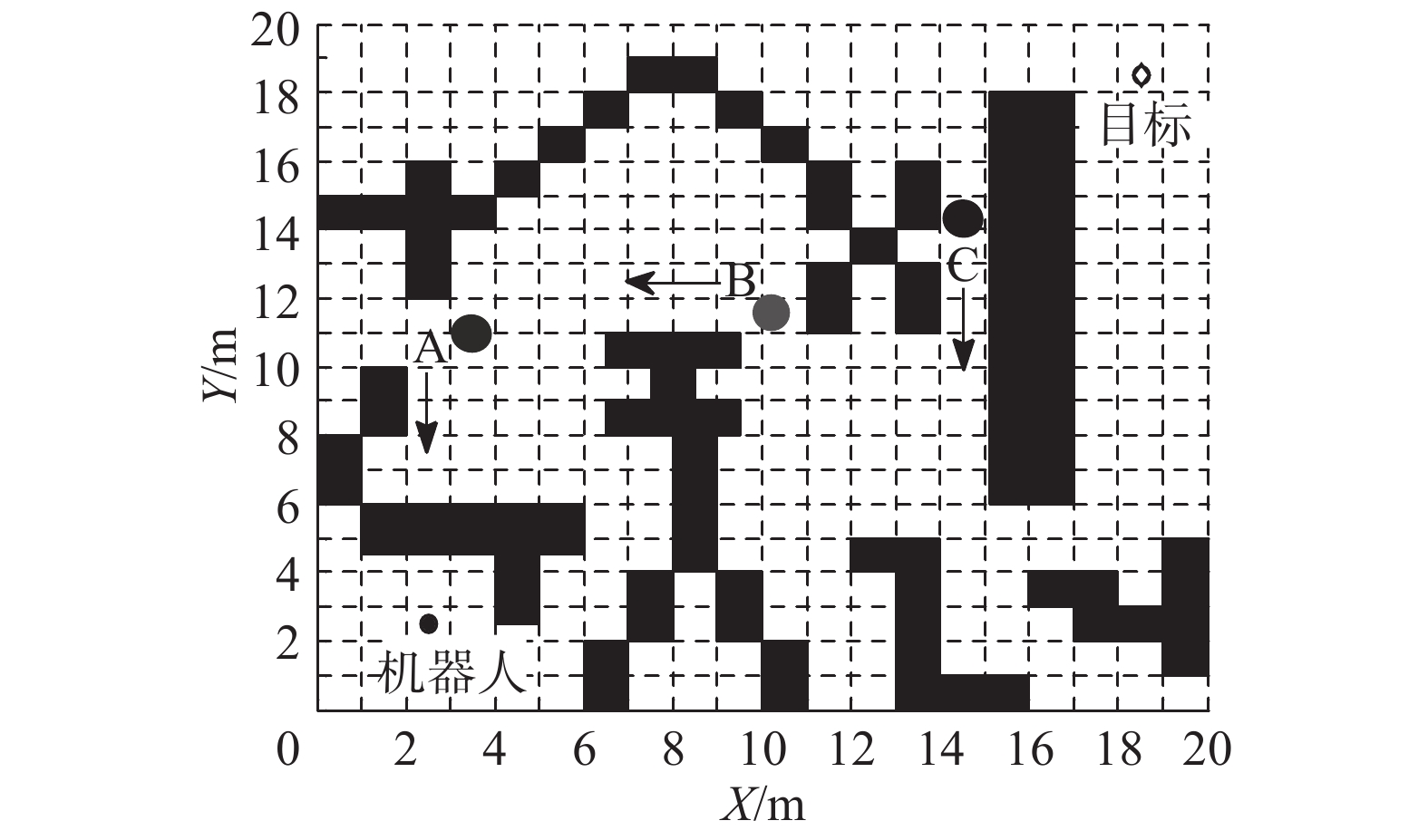
3.2 引入Morphin算法后动态避障效果分析图5是动态障碍物在初始位置时的地图。机器人首先按照改进A*算法规划的全局路径行驶。假设在机器人行驶过程中栅格地图中存在A、B、C 3个动态障碍物小球,实验参数如下:小球平均速度为0.23 m/s,小车平均速度为2.2 m/s。小球位置分别为(6,10)、(11,8)、(15,13);Bidirectional RRT算法每步搜索节点为10,搜索次数最大值1 000,RRT双向搜索树算法在相同地图下进行对比实验,如图6所示;模糊控制算法中初始航向为45°,机器人的安全距离为1 m,距离阈值偏差为30 cm,最大转向角60°,如图7所示,对于动态算法的时间、路径、精度进行对比。
|
Download:
|
| 图 5 动态障碍物运动前位置 Fig. 5 Initial position before dynamic obstacle movement | |

|
Download:
|
| 图 6 Bidirectional RRT算法规划路径 Fig. 6 Path planned by Bidirectional RRT algorithm | |
|
Download:
|
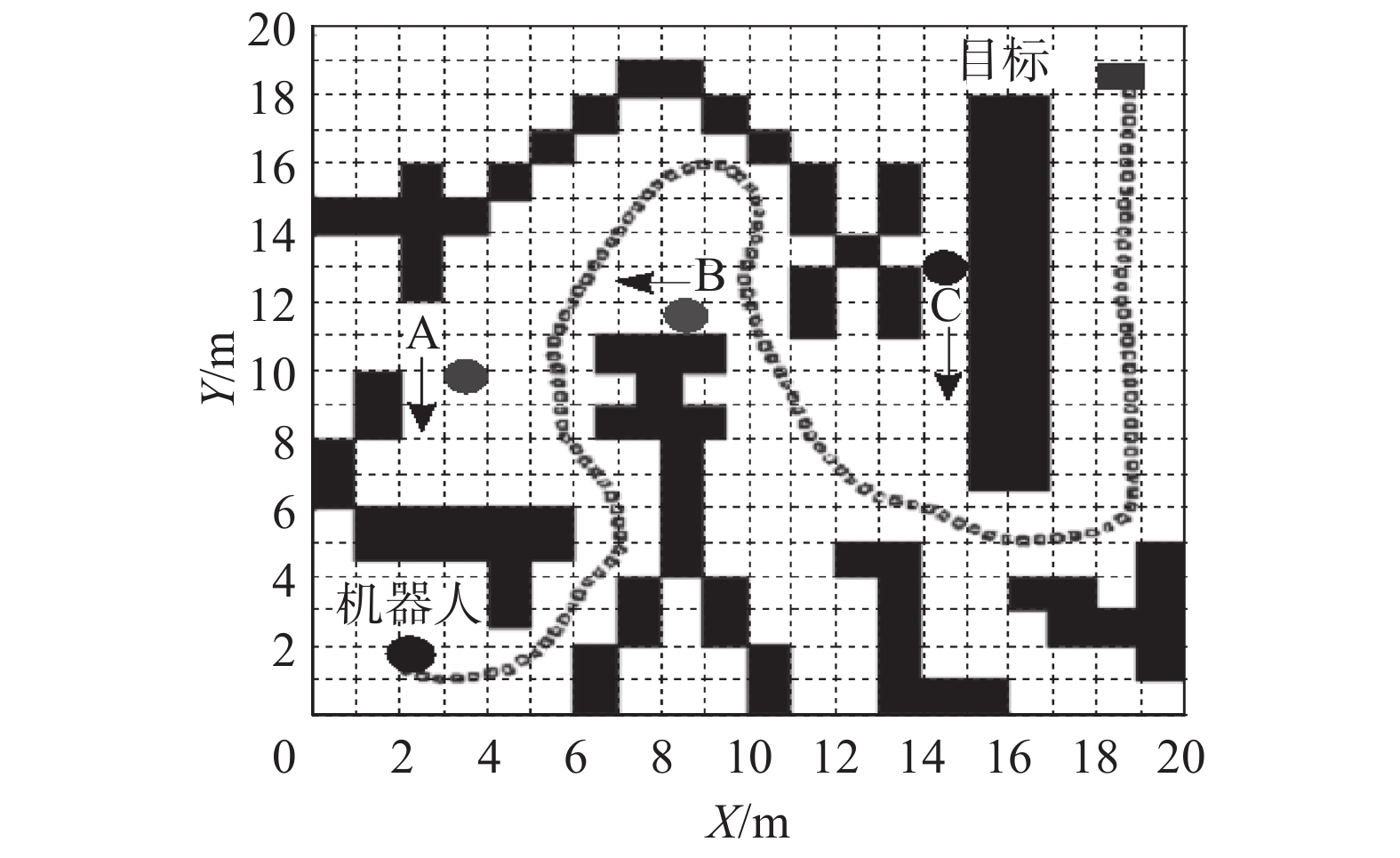
| 图 7 模糊控制算法规划路径 Fig. 7 Path planned by fuzzy control algorithm | |
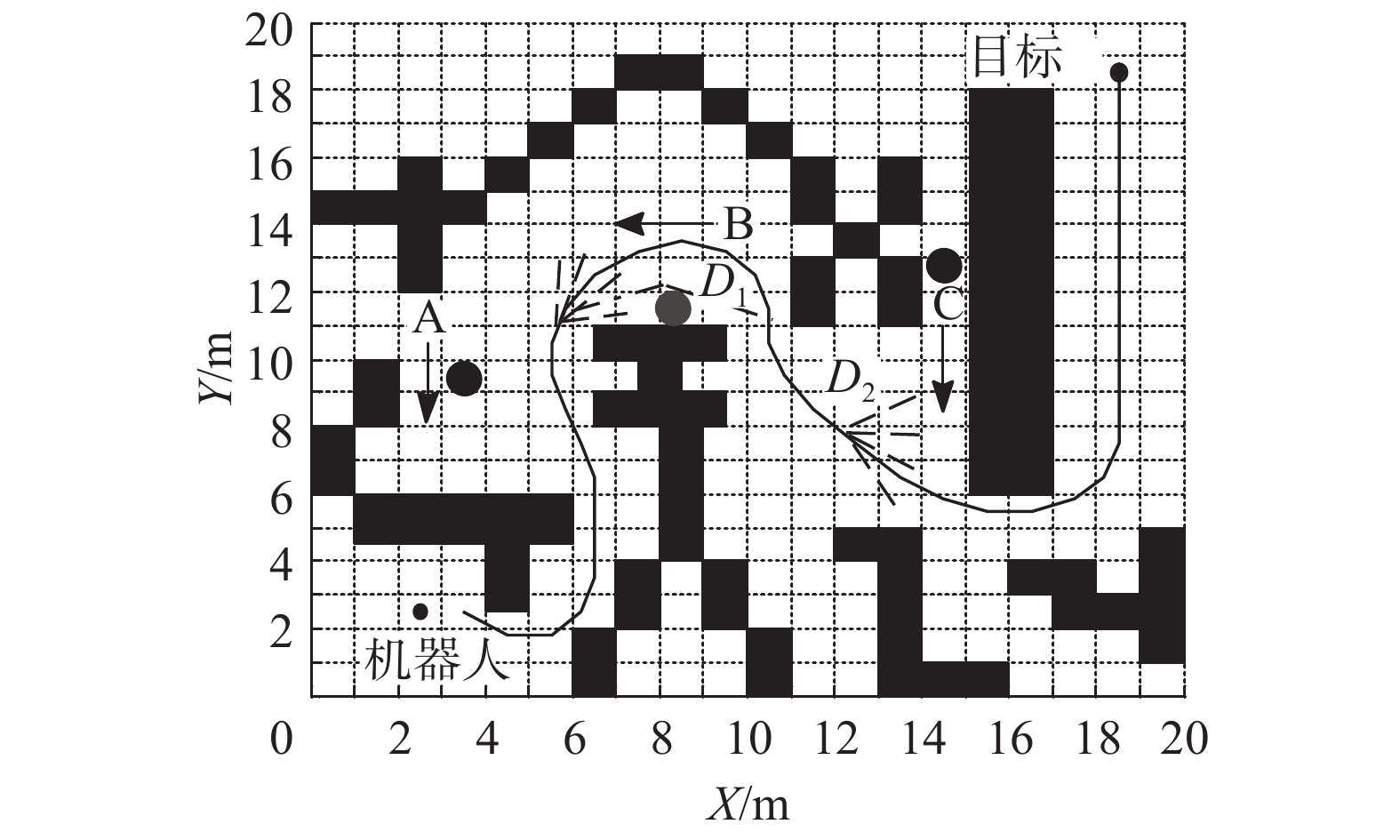
Morphin算法对机器人与障碍物是否碰撞进行预测,从而进行局部路径规划,如图8所示。由于小球A与小车运动路线无干扰,小车正常行驶;通过预测可知在虚线的D1点,将会与小球B碰撞,小车进行局部避障选择预测弧线G值最小的路径,避开后回到全局路径继续行驶。运动小球C在障碍物之间的通道中,此处机器人无法通过。对于运动小球C有2种情况。第1种情况,小球C速度为0.4 m/s,短时间内从机器人要行驶的通道内出来并且不阻挡机器人的运动。如图8所示,机器人在D2点等待球C运动出来,再按照规划好的全局路径行驶到目标点。

|
Download:
|
| 图 8 全局路径动态避障 Fig. 8 Global-path dynamic obstacle avoidance | |
第2种情况小球C速度为0.1 m/s,运动之后停在通道内,机器人无法按照规划好的全局路径行驶,障碍物之间的通道被堵住,如图9所示。此时,机器人重新调用改进A*算法进行全局路径规划,修改原来的规划路线,行驶到目标点。
|
Download:
|
| 图 9 动态避障重新规划路径 Fig. 9 Re-planned path using dynamic obstacle avoidance | |
图6与图7的对比实验静态与动态障碍物相同。Bidirectional RRT算法通过生成随机数的方式来搜索可通行路径,缺乏可重复性,找到的路径并不是最优的。同时在初始阶段双向搜索树会对地图进行大面积探索,包括不可通行的死区,导致节点增多,占用内存增加。模糊算法根据设定的转向角、阈值、安全距离等因素会出现死锁现象,使机器人停在原地无法移动到目标。同时在复杂的室内环境转向困难当转向角过大将会陷入死锁。所以同等环境下本文动态算法在灵活性与适应性方面更优。表2是A*算法、改进A*算法、Bidirectional RRT、模糊控制算法、动态算法的数据对比。
| 表 2 路径规划算法比较结果 Tab.2 Comparison of path planning results |
通过动态算法在相同环境下与Bidirectional RRT算法和模糊控制的对比可以看出,在路径长度、耗费时间、与路径节点等方面得到明显的改善。耗费更少的资源得到更优的结果同时保证机器人安全有效地到达目标点。
4 结束语本文针对传统A*算法面对动态障碍发生碰撞或者路径规划失败问题,提出了一种改进A*算法与Morphin算法相结合的动态路径规划方法。首先对A*算法进行改进,优化传统A*算法的搜索节点多,路径不平滑,不易运动控制等问题。并根据改进的A*算法进行路径规划;然后机器人按照规划出的全局路径行驶,如果碰到未知的静态或动态障碍物时,根据传感器检测到的信息调用Morphin算法进行局部规划。通过仿真验证了改进A*算法规划出的路径更加平滑,搜索节点更少;Morphin算法可以有效地避开动态障碍物。动态算法通过A*算法与Morphin算法相融合,使机器人获得最佳的路径、时间,有效地提升了机器人的工作效率和安全性。
| [1] |
QURESHI A H, AYAZ Y. Potential functions based sampling heuristic for optimal path planning[J]. Autonomous robots, 2016, 40(6): 1079-1093. DOI:10.1007/s10514-015-9518-0 ( 0) 0)
|
| [2] |
SONG Baoye, WANG Zidong, ZOU Lei. On global smooth path planning for mobile robots using a novel multimodal delayed PSO algorithm[J]. Cognitive computation, 2017, 9(1): 5-17. DOI:10.1007/s12559-016-9442-4 ( 0) 0)
|
| [3] |
LEE J. Heterogeneous-ants-based path planner for global path planning of mobile robot applications[J]. International journal of control, automation and systems, 2017, 15(4): 1754-1769. DOI:10.1007/s12555-016-0443-6 ( 0) 0)
|
| [4] |
李元, 王石荣, 于宁波. 基于RGB-D信息的移动机器人SLAM和路径规划方法研究与实现[J]. 智能系统学报, 2018, 13(3): 445-451. LI Yuan, WANG Shirong, YU Ningbo. RGB-D-based SLAM and path planning for mobile robots[J]. CAAI transactions on intelligent systems, 2018, 13(3): 445-451. DOI:10.11992/tis.201702005 (  0) 0)
|
| [5] |
FAZLOLLAHTABAR H, HASSANLI S. Hybrid cost and time path planning for multiple autonomous guided vehicles[J]. Applied intelligence, 2017, 48(2): 482-498. ( 0) 0)
|
| [6] |
HAN J, SEO Y. Mobile robot path planning with surrounding point set and path improvement[J]. Applied soft computing, 2017, 57: 35-47. DOI:10.1016/j.asoc.2017.03.035 ( 0) 0)
|
| [7] |
SUDHAKARA P, GANAPATHY V. PRIYADHARSHINI B, et al. Obstacle avoidance and navigation planning of a wheeled mobile robot using amended artificial potential field method[J]. Procedia computer science, 2018, 133: 998-1004. DOI:10.1016/j.procs.2018.07.076 ( 0) 0)
|
| [8] |
TAHIR Z, QURESHI A H, AYAZ Y, et al. Potentially guided bidirectionalized RRT* for fast optimal path planning in cluttered environments[J]. Robotics and autonomous systems, 2018, 108: 13-27. DOI:10.1016/j.robot.2018.06.013 ( 0) 0)
|
| [9] |
朱大奇, 孙兵, 李利. 基于生物启发模型的AUV三维自主路径规划与安全避障算法[J]. 控制与决策, 2015, 30(5): 798-806. ZHU Daqi, SUN Bing, LI Li. Algorithm for AUV’s 3-D path planning and safe obstacle avoidance based on biological inspired model[J]. Control and decision, 2015, 30(5): 798-806. (  0) 0)
|
| [10] |
伍永健, 陈跃东, 陈孟元. 改进QPSO和Morphin算法下移动机器人混合路径规划[J]. 电子测量与仪器学报, 2017, 31(2): 295-301. WU Yongjian, CHEN Yuedong, CHEN Mengyuan. Hybrid path planning of mobile robot based on improved QPSO and Morphin algorithm[J]. Journal of electronic measurement and instrumentation, 2017, 31(2): 295-301. (  0) 0)
|
| [11] |
MAOUDJ A, HENTOUT A, BOUZOUIA B, et al. On-line fault-tolerant fuzzy-based path planning and obstacles avoidance approach for manipulator robots[J]. International journal of uncertainty, fuzziness and knowledge-based systems, 2018, 26(5): 809-838. DOI:10.1142/S0218488518500368 ( 0) 0)
|
| [12] |
万晓凤, 胡伟, 郑博嘉, 等. 基于改进蚁群算法与Morphin算法的机器人路径规划方法[J]. 科技导报, 2015, 33(3): 84-89. WAN Xiaofeng, HU Wei, ZHENG Bojia, et al. Robot path planning method based on improved ant colony algorithm and Morphin algorithm[J]. Science & technology review, 2015, 33(3): 84-89. DOI:10.3981/j.issn.1000-7857.2015.03.014 (  0) 0)
|
| [13] |
秦玉鑫, 王红旗, 杜翠杰. 基于双层A*算法的移动机器人路径规划[J]. 制造业自动化, 2014, 36(24): 21-25, 40. QIN Yuxin, WANG Hongqi, DU Cuijie. A path planning approach to moving robot based on double layer A* Algorithm[J]. Manufacturing automation, 2014, 36(24): 21-25, 40. DOI:10.3969/j.issn.1009-0134.2014.24.006 (  0) 0)
|
| [14] |
XU Yaru, LIU Rong. Path planning for mobile articulated robots based on the improved A* algorithm[J]. International journal of advanced robotic systems, 2017, 14(4): 1-10. ( 0) 0)
|
| [15] |
ZHANG Hongmei, LI Minglong. Rapid path planning algorithm for mobile robot in dynamic environment[J]. Advances in mechanical engineering, 2017, 9(12): 1-12. ( 0) 0)
|
| [16] |
王红卫, 马勇, 谢勇, 等. 基于平滑A*算法的移动机器人路径规划[J]. 同济大学学报(自然科学版), 2010, 38(11): 1647-1650. WANG Hongwei, MA Yong, XIE Yong, et al. Mobile robot optimal path planning based on smoothing A* algorithm[J]. Journal of Tongji University (Natural Science), 2010, 38(11): 1647-1650. DOI:10.3969/j.issn.0253-374x.2010.11.016 (  0) 0)
|
| [17] |
SIMMONS R, KROTKOV E, CHRISMAN L, et al. Experience with rover navigation for lunar-like terrains [C]//Proceedings of 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots. Pittsburgh, USA, 1995: 441–446.
( 0) 0)
|
| [18] |
张飞, 白伟, 乔耀华, 等. 基于改进D*算法的无人机室内路径规划[J]. 智能系统学报, 2019, 14(4): 662-669. ZHANG Fei, BAI Wei, QIAO Yaohua, et al. UAV indoor path planning based on improved D* algorithm[J]. CAAI transactions on intelligent systems, 2019, 14(4): 662-669. DOI:10.11992/tis.201803031 (  0) 0)
|
| [19] |
BELGHITH K, KABANZA F, HARTMAN L. Randomized path planning with preferences in highly complex dynamic environments[J]. Robotica, 2013, 31(8): 1195-1208. DOI:10.1017/S0263574713000428 ( 0) 0)
|
| [20] |
诸葛程晨, 唐振民, 石朝侠. 基于多层Morphin搜索树的UGV局部路径规划算法[J]. 机器人, 2014, 36(4): 491-497. ZHUGE Chengchen, TANG Zhenmin, SHI Zhaoxia. A local path planning algorithm for UGV based on multilayer Morphin search tree[J]. Robot, 2014, 36(4): 491-497. (  0) 0)
|
| [21] |
曹清云, 倪建军, 王康, 等. 一种改进的未知动态环境下机器人混合路径规划方法[J]. 计算机与现代化, 2016(4): 54-58. CAO Qingyun, NI Jianjun, WANG Kang, et al. A robot hybrid path planning algorithm under improved unknown and dynamic environment[J]. Computer and modernization, 2016(4): 54-58. DOI:10.3969/j.issn.1006-2475.2016.04.012 (  0) 0)
|
| [22] |
张兆宁, 魏中慧. 危险天气下基于多重Morphin算法的终端区三维实时改航方法[J]. 南京航空航天大学学报, 2015, 47(4): 467-473. ZHANG Zhaoning, WEI Zhonghui. 3-D real-time deviation method for avoiding hazardous weather in terminal airspace based on Morphin planning algorithm[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2015, 47(4): 467-473. (  0) 0)
|
 2020, Vol. 15
2020, Vol. 15


