仿人机器人由于拥有与人体结构相似的双足式结构,可以较好地适应轮式机器人难以适应的高低落差较大的地形场景,且在崎岖多变的地形环境中机动性好,因此仿人机器人可以代替人类在复杂和危险的环境下工作,同时也被广泛应用到服务、医疗康复和教育娱乐等领域。因此仿人机器人的研究也就成为了机器人领域的重要研究方向之一。
控制机器人的稳定步行,传统上是通过规划ZMP轨迹,并通过逆运动学等方法求取机器人的驱动角度完成的。而人为规划的ZMP轨迹和质心轨迹过分依靠仿人机器人运动学模型,这种方法在对机器人建模时需进行大量的计算,且运动模式僵硬单一[1-6]。由于人体结构与仿人机器人的结构有很强的相似性,通过人体示教的方式,机器人模仿其动作的方式,能使机器人动作自然,运动方式多样[7-10],但是二者之间的质量分布存在差异,直接使用人体示教的关节角度,容易导致仿人机器人在运动过程中摔倒。使用ZMP补偿或线性反馈等方式补偿关节角度可使仿人机器人在步行过程中的稳定性提高,但补偿角的计算过程过于复杂。Seleem等[11]使用Kinect-V2传感器捕捉人体步态数据同时使用多项式拟合并利用反馈线性化技术稳定双足机器人步行过程,获得了较为自然且多样的步态轨迹,但未能充分利用人体的示教数据,使计算过程过于复杂。面对计算量大这一问题,机器学习通过构建“模型”思想,大大减少了传统算法的运算量和计算过程。Hwang等[12]应用机器学习的思想对仿人机器人的ZMP轨迹进行规划,并将机器人的关节角度构成离散的动作空间,以构建机器人步行模型,进行步态控制,但只有16个动作的离散动作空间机器人动作僵硬单一。支持向量回归(support vactor regression, SVR)由Cortes等[13]提出,是建立在结构风险最小化原则基础之上的一种机器学习算法。相较于传统的机器学习算法的经验风险最小化原则,它在最小化训练误差的同时最小化了泛化误差的上限,并且其算法复杂度与样本的训练维数无关,避免了维数灾难,是一种有着很强理论基础的小样本学习方法。
1 基于SVR的机器人步态平衡泛化模型的构建采用人体示教的方法,可以使仿人机器人在不同的步长、步态周期下动作自然地行走且大大简化了动力学建模的计算过程。但在机器人模仿人体步行动作时,由于两者质量分布不同,质心在运动过程中极易发生偏移,需要通过人体示教信息经过大量计算得到使机器人稳定步行的关节补偿角度[14]。考虑基于SVR算法建立步态平衡泛化模型,根据得到的人体示教信息直接得到经稳定性补偿的关节角度。在保留人体示教优点且保证稳定性的同时降低计算复杂度,增强机器人动作模仿的实时性。
1.1 支持向量回归算法支持向量回归模型分为线性回归模型和非线性回归模型。考虑到人体示教数据和机器人驱动关节角度是非线性关系,需要建立非线性回归模型。给定样本:
| ${{D = }}\left\{ {\left( {{{{x}}_1},\;\;{{{y}}_1}} \right),\left( {{{{x}}_2},\;\;{{{y}}_2}} \right), \cdots ,\left( {{{{x}}_i},\;\;{{{y}}_{{i}}}} \right),\;\;{{i = }}1,2, \cdots ,\;l} \right\}$ |
式中:
| ${{f}}\left( {{x}} \right) = \omega {{\cdot}}\varPhi \left( {{x}} \right){{ + b}}$ |
式中:x为模型输入的n维变量;
在SVM间隔最大化思想下,引入不敏感损失函数
| $\left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_{\left( {\omega ,b,{\xi _i},{\xi _i}^*} \right)} \dfrac{1}{2}{\left\| \omega \right\|^2} + C\displaystyle\sum\limits_{i = 1}^l {\left( {{\xi _i} + {\xi _i}^*} \right)} \\ {\rm{s}}{\rm{.t}}{\rm{.\; }}{y_i} - \omega \varPhi \left( x \right) - b \leqslant \varepsilon + {\xi _i}\\ {\rm{ }}\omega \varPhi \left( x \right){\rm{ + }}b \leqslant \varepsilon + {\xi _i}^*\\ {\rm{ }}{\xi _i},{\xi _i}^* \geqslant 0 \end{array} \right.$ | (1) |
为了计算更加便捷,通过引入拉格朗日乘子
| $ \left\{ \begin{array}{l} \mathop {{\rm{max}}}\limits_{\left( {{\alpha _i},{\alpha _i}^*} \right)} \displaystyle\sum\limits_{i = 1}^l {{\alpha _i}\left( {y - \varepsilon } \right)} - \displaystyle\sum\limits_{i = 1}^l {{\alpha _i}^*\left( {y + \varepsilon } \right)} +\\ {\rm{ }}\;\;\;\;\;\;\;\; \displaystyle\sum\limits_{i,j = 1}^l {\left( {{\alpha _j} - {\alpha _j}^*} \right)} \left( {{\alpha _i} - {\alpha _i}^*} \right)K\left( {{x_i},{x_j}} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.\; 0}} \leqslant {\alpha _i} \leqslant C,{\rm{0}} \leqslant {\alpha _i}^* \leqslant C,i = 1,2, \cdots ,l\\ \displaystyle\sum\limits_{i = 1}^l {\left( {{\alpha _i} - {\alpha _i}^*} \right) = 0} \end{array} \right. $ | (2) |
式中:
由于不等式约束问题需满足的KKT条件可解得SVR的解形式为
| $ f(x)=\sum _{i=1}^{l}\left({\alpha }_{i}-{\alpha }_{i}^{*}\right)K\left({x}_{i},{x}_{j}\right)+b $ | (3) |
式中
综上所述,决定SVR算法非线性模型性能的参数为
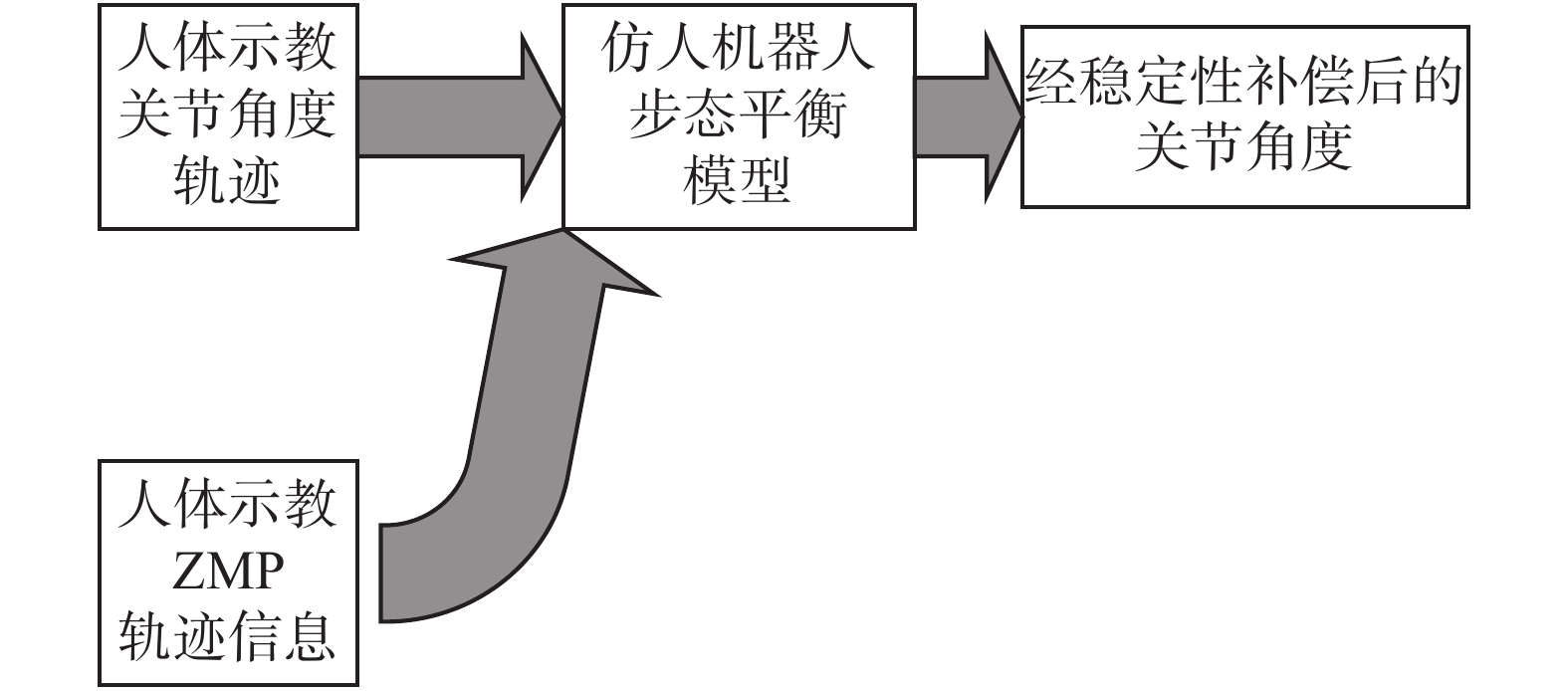
构建步态平衡泛化模型需要在SVR算法非线性回归模型结构的基础上,确定合适的输入和输出。二者之间需有一定的相关关系,才能保证模型有良好的泛化效果。具体选择如下:以人体示教的关节角度和人体步行的ZMP信息作为步态平衡模型的输入。首先,人体示教的关节角度是机器人模仿人体动作的基础。其次,在计算关节稳定性补偿角度时人体示教的ZMP信息(以示教者支撑脚底部的骨骼点轨迹作为人体示教的ZMP轨迹)是在计算关节稳定性补偿角度时的重要依据,并且由其定义式如式(6)所示,ZMP信息包含了人体示教的质心信息和质心加速速度信息:
| ${{p}} = c - \frac{h}{g}{{\ddot c}}$ | (4) |
式中:
以平衡补偿后的关节角度(即机器人驱动角度)作为输出。在稳定的基础上省去稳定性补偿角的复杂计算,完成仿人机器人的步行控制。
对模型输入人体的关节角度和人体在步行运动时的ZMP信息,由SVR非线性回归模型代替人体示教信息和稳定性后的关节角度之间的函数关系直接泛化出经补偿的关节角度,构建模型结构如图1所示。在充分利用人体示教信息的基础上,保证了仿人机器人的稳定性并简化了稳定性补偿角的计算。
|
Download:
|
| 图 1 机器人步态平衡泛化模型结构 Fig. 1 Robot gait balance generalization model structure | |
模型结构确立后,由1.1节可知,确定步态平衡泛化模型的SVR算法中的
采用人为确定C、p、
鲸鱼优化算法(whale optimization algorithm, WOA)是一种全局随机优化算法,是一种新颖且效果很好的优化算法[15]。其过程分为2个阶段:开发阶段和探索阶段。从一组随机解开始,通过开发阶段找到最优解的大体范围,再通过螺旋收缩包围的机制找到最优解的具体位置。其数学模型建立如下:
| $\left\{ \begin{array}{l} {{D}} = \left| {{{C}} \cdot {{{x}}^{{*}}}\left( t \right) - {{x}}\left( t \right)} \right| \\ {{x}}\left( {t + 1} \right) = {{{x}}^{{*}}}\left( t \right) - {{A}} \cdot {{D}} \\ {{A}} = 2{{a}} \cdot {{r}} - {{a}} \\ {{C}} = 2 \cdot {{r}} \\ \end{array} \right. $ | (5) |
式中:
| ${{x}}\left( {{\rm{t}} + 1} \right) = \left\{ {\begin{array}{*{20}{l}} {{{{x}}^{{*}}}\left( t \right) - {{A}} \cdot {{D}},\quad{{p}} < 0.5}\\ {{{D}} \cdot {{\rm{e}}^{{{bl}}}} \cdot {\rm{cos}}\left( {2{{{\text{π}} l}}} \right){{ + }}{{{x}}^{{*}}}\left( t \right),\quad{{p}} \geqslant 0.5} \end{array}} \right.$ | (6) |
式中:l为(−1,1)的随机数;
当迭代次数达到最大时,最终采用式(9)进行最优解的确定:
| $\left\{ {\begin{array}{*{20}{l}} {{{D}} = \left| {{{C}} \cdot {{{x}}_{{\rm{rand}}}} - {{x}}\left( t \right)} \right|} \\ {{{x}}\left( {t + 1} \right) = {{{x}}_{{\rm{rand}}}} - {{A}} \cdot {{D}}} \end{array}} \right.$ | (7) |
式中
在SVR非线性回归模型中,p过大会使模型过于简单,学习精度不够;p过小,会出现过拟合,模型泛化能力变差。C和
为了比较WOA和常用寻优算法对SVR非线性回归模型寻优性能的差异。分别使用3种算法(GA、PSO算法和WOA)对SVR非线性回归模型进行参数寻优并对3种算法的寻优效果进行对比,具体方法如下:使用风速时间序列预测的数据集(非线性回归问题与步态问题同样具有周期性和非线性的特点)在同一寻优空间内,分别使用GA、PSO算法和WOA对SVR非线性回归模型进行参数寻优,使用均方误差(MSE)作为性能指标来评估3种算法的参数寻优效果,其结果如表1所示。
| 表 1 3种算法对SVR非线性回归模型寻优效果比较 Tab.1 Comparison of effects of three algorithms for SVR nonlinear regression model |
从表1的结果可以看出,WOA在与GA对比中虽然训练误差差距不明显,但其泛化误差有着显著优势(GA过拟合)。而与PSO算法对比,训练误差和泛化误差都有着明显的提升。因此可以看出,WOA在寻优精度上高于其他2种算法,训练误差和泛化能力都优于2种常用的SVR参数优化算法。
2.3 基于WOA优化算法的机器人步态平衡泛化模型的参数优化在以SVR为基础的步态平衡模型中,为了获取最佳的仿人机器人步态平衡泛化模型,需对3个参数使用WOA进行寻优,在此之前,需确定3个参数的寻优空间,过小会导致最佳参数在寻优空间之外,过大会影响寻优的效率。结合SVR模型在关节角度控制应用中的3个关键参数的寻优范围的经验[16],对该寻优范围的上下限进行适当地扩大,具体步骤如下:
1)确定3个参数的寻优范围分别为
2)构建WOA的适应性函数。针对
3)使用WOA迭代寻优,在寻优空间内确定一组C、p、
经WOA寻优得到的
为了验证上述方法的有效性,设计构建仿真环境及过程如下:
1)使用Kinect2.0对人体步行动作进行数据采集。Kinect2.0是一款能对人体的骨骼点信息进行跟踪,记录体感的采集器,它能对人体的25个骨骼点进行跟踪,并记录其三维坐标(x,y,z)。
2)在MATLAB中,对人体示教数据进行处理并构建平衡泛化模型,具体步骤为:运用空间向量法进行人体关节角度的计算;通过人体在步行运动双脚的高度选取支撑脚,以此脚底部的骨骼点作为ZMP信息提取,并进行数据预处理(归一化);SVR非线性模型构建;利用模仿学习计算平衡性补偿角的方式到经补偿后的机器人关节角度构成训练集和测试集;WOA参数寻优;步态平衡泛化模型训练和泛化。
3)在WEBOTS的仿真平台上,使用模型泛化补偿后的关节角驱动NAO机器人,观察其运动效果。其中,NAO机器人是由Aldebaran Robotics公司研发的有着13个关节25个自由度的仿人机器人,适合作为仿人机器人算法的研究平台。
仿真整体结构如图2所示。

|
Download:
|
| 图 2 仿真流程图 Fig. 2 Simulation flowchart | |
Kinect2.0采集一组人体行走数据,共177个数据点(一个步态周期),前130个作为训练集,后47个作为测试集。由于仿人机器人的关节较多,在其步行运动过程中,通过调整髋关节和踝关节8个关节角度便可以实现稳态步行。因此以左腿为例,对左腿髋关节和踝关节的4个关节角度进行步态平衡模型的构建和训练。机器人踝关节的平衡泛化模型结构如图3所示。

|
Download:
|
| 图 3 踝关节步态平衡泛化模型结构图 Fig. 3 Ankle joint gait balance generalization model structure diagram | |
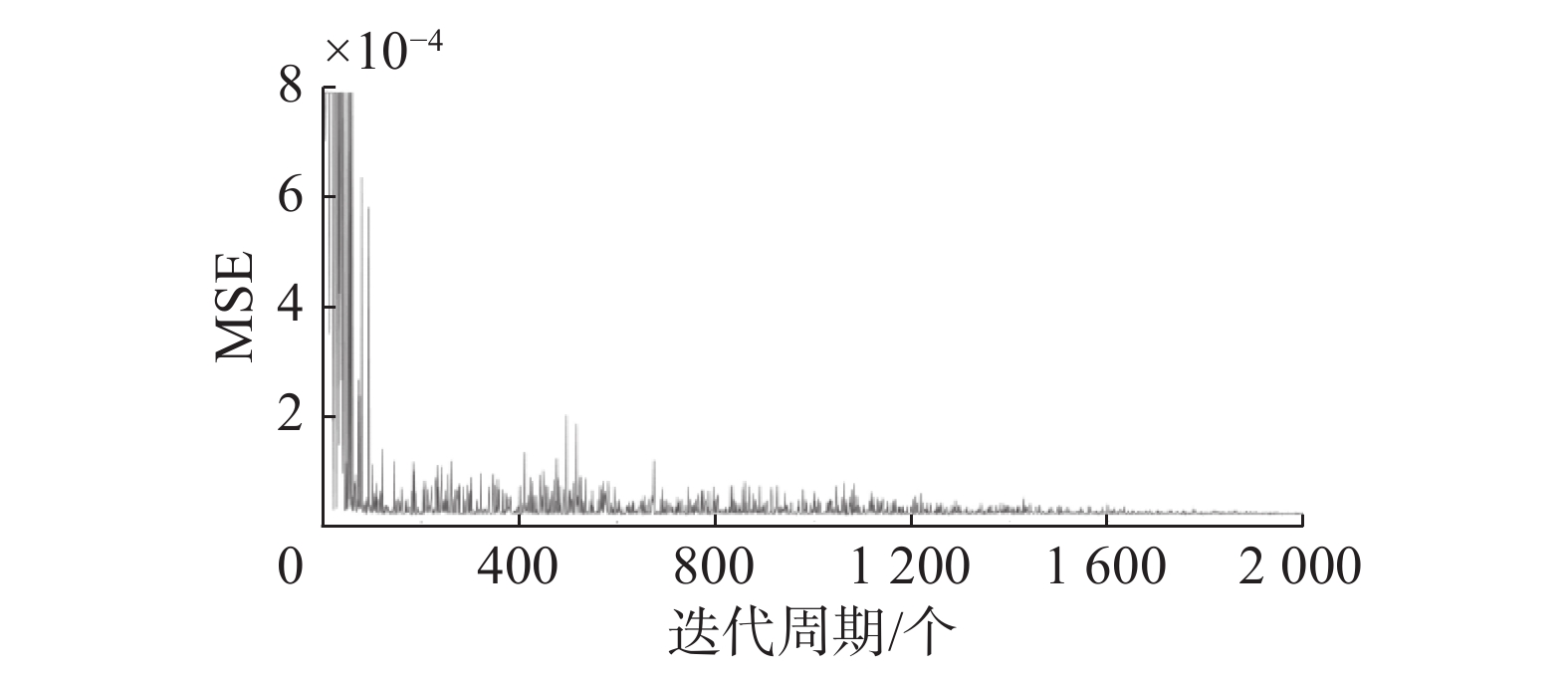
运用WOA对左腿的不同关节角的平衡模型进行参数寻优,以踝关节滚动角为例,其寻优过程的MSE值(均方误差)变化曲线如图4所示。
|
Download:
|
| 图 4 WOA寻优MSE变化曲线图 Fig. 4 WOA optimization MSE curve | |
在寻优确定参数的条件下,使用训练集对模型进行训练,训练结果如表2所示。
| 表 2 仿人机器人步态平衡泛化模型的训练参数及训练性能指标 Tab.2 Training parameters and training performance indicators of humanoid robot gait balance generalization model |
分析表2中的数据可以看出,由WOA寻优确定的仿人机器人步态平衡泛化模型,对训练集样本关节角度的拟合效果较为理想,精确度和相关性较高。
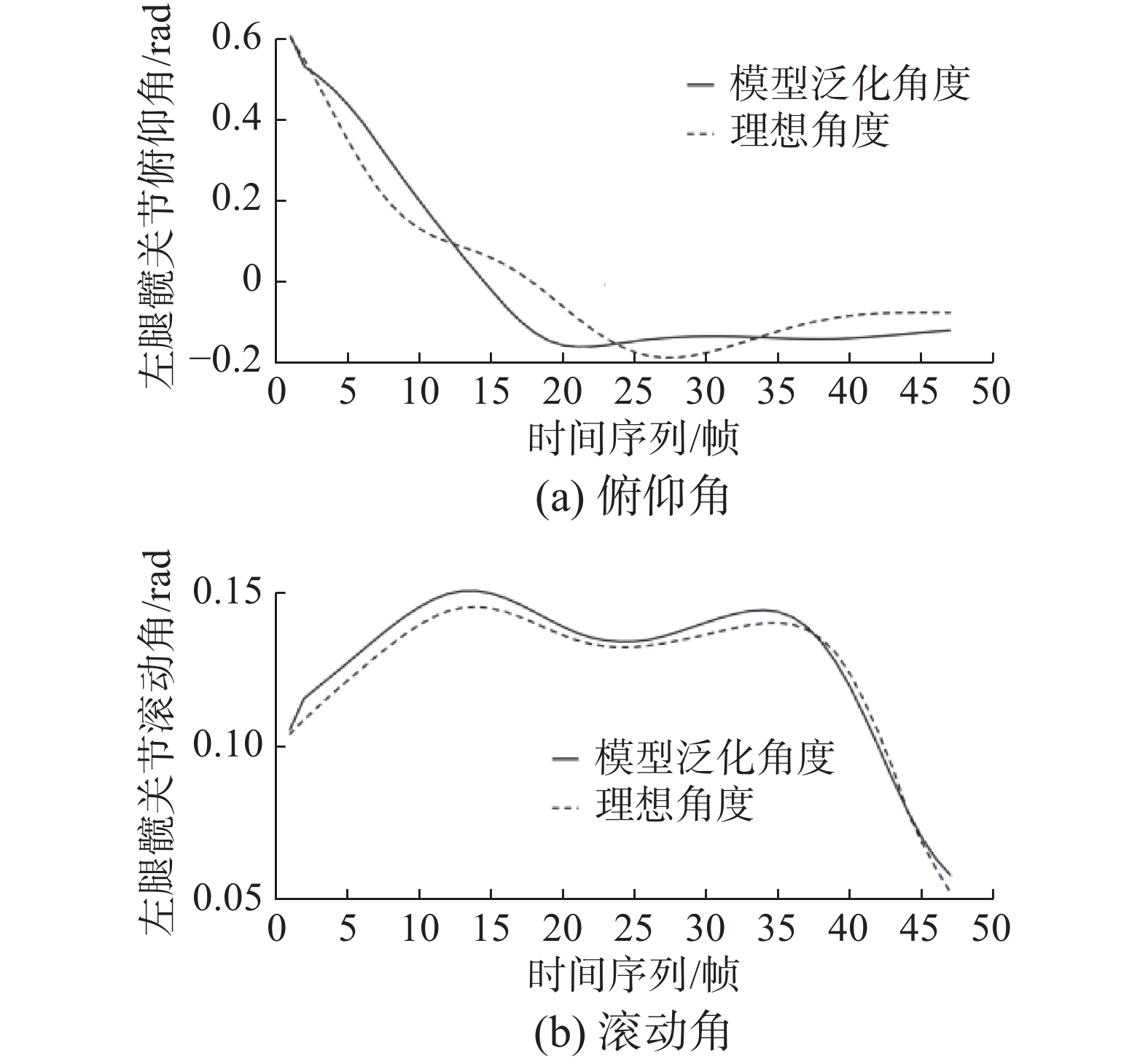
3.2 仿人机器人步态平衡模型的泛化使用测试集对训练好的步态平衡模型进行测试,由模型直接泛化得到的经补偿的关节角度与由传统算法得到的关节角度(理想角度)对比,如图5、图6所示。
|
Download:
|
| 图 5 髋关节泛化结果 Fig. 5 Hip generalization results | |

|
Download:
|
| 图 6 踝关节泛化结果 Fig. 6 Ankle generalization results | |
从图5、图6中可以看出,对比模型泛化得到的关节角度与理想的关节角度,其均方误差和相关系数如表3所示。
| 表 3 仿人机器人步态平衡泛化模型在同一步长、步态周期下的泛化性能指标 Tab.3 Generalized performance indicators of humanoid robot gait balance generalization model under the same step and gait cycle |
从表3中可以看出,模型得到的关节角度序列与理想的关节角度序列的相关系数在0.866以上而均方误差则控制在了0.011 7以内,证明仿人机器人步态平衡模型有着很好的泛化能力。
为了验证机器人在泛化得到的关节角度的驱动下具有稳定性。利用模型的泛化结果与理想的关节角度的差值及式(8)得到机器人的质心偏移量:
| $ {\delta _{{c}}} = {{J}}{\delta _\alpha } $ | (9) |
式中:
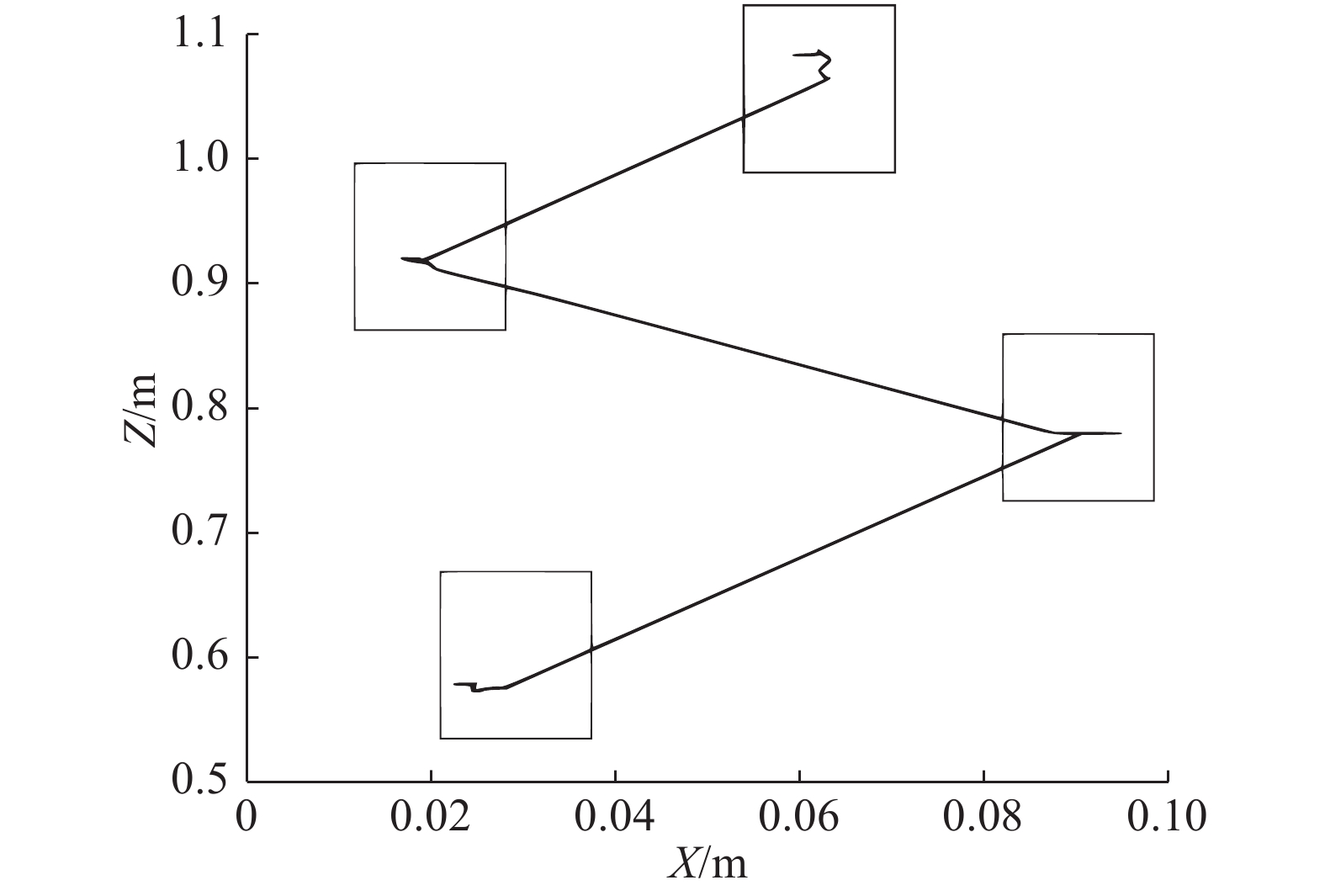
机器人的在模型泛化角度下驱动机器人运动的ZMP轨迹如图7所示。
|
Download:
|
| 图 7 同一步长、步态周期下在泛化驱动角度下机器人ZMP轨迹 Fig. 7 Robot ZMP trajectory at generalized driving angle under the same step and gait cycle | |
从图7中可以看出,通过模型泛化出的关节角度驱动机器人运动,其ZMP轨迹波动很小,且在机器人足部的支撑方框之内,证明机器人在模仿人体步行运动时不会摔倒。
由如图8可以看出,NAO机器人在WEBOTS环境下可以平稳地步行。

|
Download:
|
| 图 8 模型泛化角度值在WEBOTS仿真平台上的稳定步行 Fig. 8 Model generalized angle values for stable walking on the WEBOTS simulation platform | |
从上述结果可以看出,通过引入步态平衡泛化模型可以在减少复杂计算过程的基础上使机器人能够完成稳态步行,且具有很好的稳定性。
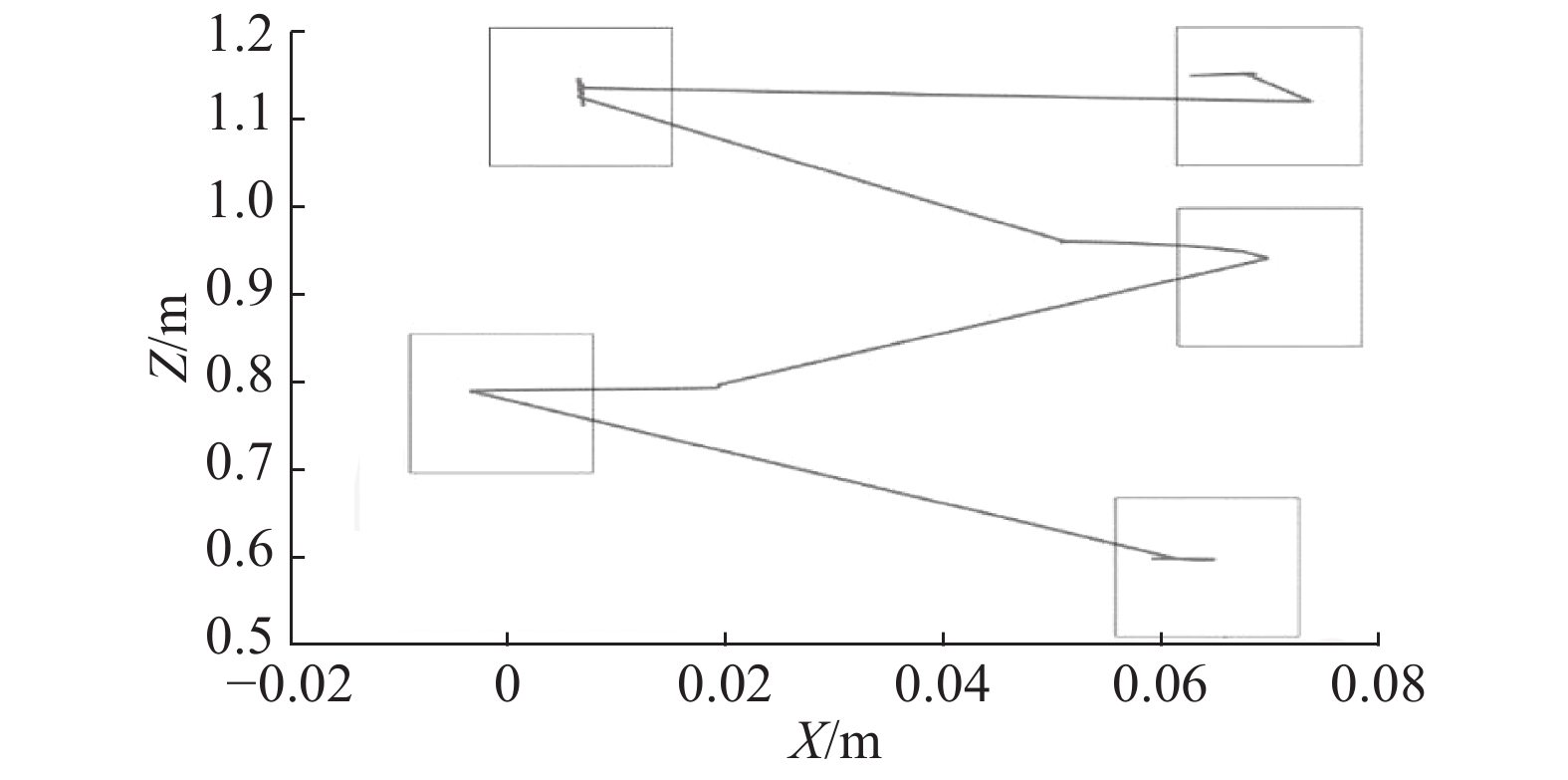
以上泛化结果为同一次示教的数据拆分成的训练集和测试集,因此示教步行动作的步长和步态周期相同。但不同示教人在示教时(甚至同一示教人在非同一次示教时)可能会产生步长和步态周期上的差异。为了验证步态平衡泛化模型不同示教人的示教信息的泛化能力,使用Kinect采集76个与训练集步长,步态周期均不同的人体行走数据点(两个步态周期),用上一节中训练好的步态平衡模型对其进行泛化。模型得到的经补偿后的关节角度与理想角度的对比如图9、图10所示,所计算的机器人实际ZMP轨迹如图11所示。

|
Download:
|
| 图 9 不同步长、步态周期下左腿髋关节泛化结果 Fig. 9 Generalization of left hip pitch under different gait long and gait cycles | |
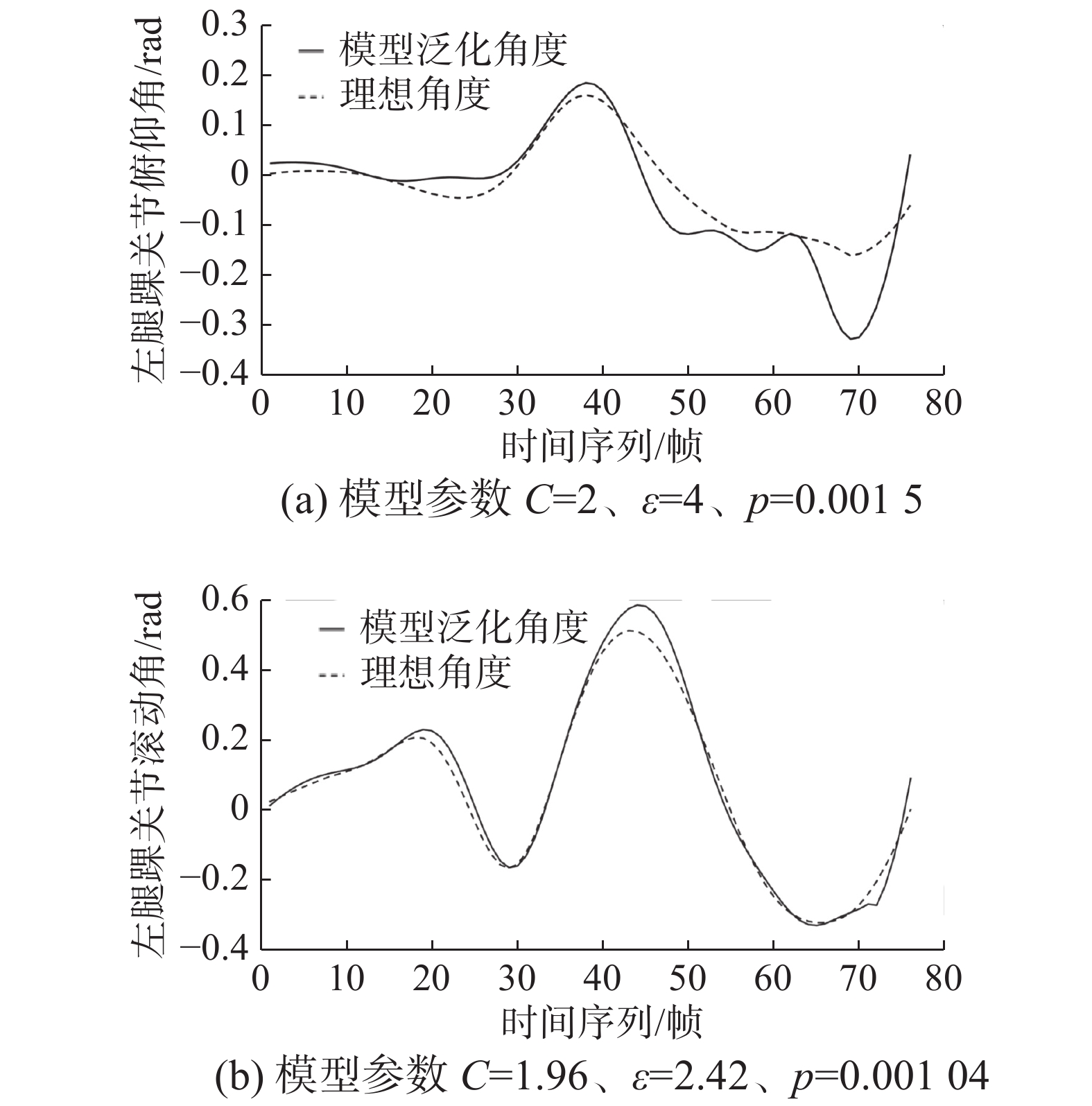
|
Download:
|
| 图 10 不同步长、步态周期下左脚踝关节泛化果 Fig. 10 Generalization of left ankle roll under non-synchronized and gait cycles | |
|
Download:
|
| 图 11 不同步长、步态周期下的机器人ZMP轨迹 Fig. 11 Robot ZMP trajectory under different gait long and gait cycle | |
从表4的模型泛化结果中可以看到,与同一步长、步态周期下的泛化效果相比,模型对不同步长、步态周期下的示教数据泛化得到的4个关节角度值与理想的关节角度值相比虽然最大均方误差增加到了0.011 8,相关系数也降低到了0.794,机器人的实际ZMP也有轻微波动,机器人的稳定性方面也与同一步长、步态周期下的数据训练的模型存在一定差距。但在WEBOTS仿真平台上进行仿真,NAO机器人仍能进行较为平稳的步行运动。
| 表 4 不同步长、步态周期下的泛化性能指标 Tab.4 Generalized performance indicators of unsynchronized and long gait cycles |
在不同步长和步态周期的示教数据下模型泛化的关节角度误差较小,ZMP轨迹还在机器人足部支撑方框内,因此步态平衡泛化模型能在不同示教者示教的情况下减少补偿角计算并保证步行稳定。不足之处有以下两点:
1)由于Kinect是一款非专业的体感采集器,其测量范围有一定的限制,太远或太近都会使测量误差过大,无法进行一组两个以上步行动作的采集。同时结合同一步长、步态周期下,泛化的起始点与理想的起始点有一些偏差,导致在循环动作时机器人会有一定不自然动作,甚至会导致机器人不稳定、摔倒。因此,在保证机器人稳定的基础上,步态周期间的平滑切换(连续步态周期的关节角度时间序列预测)是下一阶段工作的重点之一[17-19]。
2)在不同步长、步态周期下的模型泛化效果与同一步长、步态周期下的相比不够理想。因此,进一步优化模型的算法和选择训练模型数据是构建针对仿人机器人不同组步行数据下的平衡泛化模型和构建步态循环模型的需要解决的问题。
4 结束语仿真结果表明,仿人机器人步态平衡泛化模型可以在相同和不同步长和步态周期下有效地泛化机器人经稳定性补偿的关节角度,其泛化角度与理想角度的误差较小。使用泛化得到的角度在WEBOTS仿真平台上驱动NAO机器人,可使其稳定步行。证明了步态平衡泛化模型在保留模仿学习动作自然,运动方式多样的优点的同时,简化了稳定性补偿角的计算过程,增强了机器人模仿人体运动的实时性,并保证了机器人运动过程的稳定性。
| [1] |
WANG Fei, WANG Yaning, WEN Shiguang, et al. Nao humanoid robot gait planning based on the linear inverted pendulum[C]//Proceedings of 2012 24th Chinese Control and Decision Conference. Taiyuan, China, 2012: 986−990.
( 0) 0)
|
| [2] |
DONG Enzeng, WANG Dandan, CHEN Chao, et al. Realization of biped robot gait planning based on NAO robot development platform[C]//Proceedings of 2016 IEEE International Conference on Mechatronics and Automation. Harbin, China, 2016: 1073−1077.
( 0) 0)
|
| [3] |
ZHANG Ying, LI Shuanghong, HAN Boyu, et al. Research on gait planning and inverse kinematics solving of biped walking robots[C]//Proceedings of 2015 8th International Symposium on Computational Intelligence and Design. Hangzhou, China, 2015: 629−632.
( 0) 0)
|
| [4] |
KHAZENIFARD A, BAHRAMI F, ANDANI M E, et al. An energy efficient gait trajectory planning algorithm for a seven linked biped robot using movement elements[C]//Proceedings of 2015 23rd Iranian Conference on Electrical Engineering. Tehran, Iran, 2015: 1006−1011.
( 0) 0)
|
| [5] |
付根平, 杨宜民, 黄春林. 基于粒子群优化算法的双足机器人步态优化[J]. 华中科技大学学报(自然科学版), 2011, 39(S2): 355-358. FU Genping, YANG Yimin, HUANG Chunlin. Walking pattern optimization based on particle swarm optimization for biped robot[J]. Journal of Huazhong University of Science and Technology (nature science edition), 2011, 39(S2): 355-358. (  0) 0)
|
| [6] |
YAMAGUCHI A, HYON S H, OGASAWARA T. Reinforcement learning for balancer embedded humanoid locomotion[C]//Proceedings of 2010 10th IEEE-RAS International Conference on Humanoid Robots. Nashville, USA, 2010: 308−313.
( 0) 0)
|
| [7] |
KANG Zhongrun, DENG Muqing, WANG Cong. Frontal-view human gait recognition based on kinect Features and deterministic learning[C]//Proceedings of 2017 36th Chinese Control Conference. Dalian, China, 2017: 10834−10839.
( 0) 0)
|
| [8] |
SELEEM I A, ASSAL S F M. Sliding mode control of underactuated five-link biped robot for climbing stairs based on real human data[C]//Proceedings of 2017 IEEE International Conference on Industrial Technology. Toronto, Canada, 2017: 878−883.
( 0) 0)
|
| [9] |
赵姝颖, 徐文杰, 郑雪林, 等. 基于体感的机器人展示系统研究与开发[J]. 机器人技术与应用, 2012(6): 54-57. ZHAO Shuying, XU Wenjie, ZHENG Xuelin, et al. Research and development of display system of Nao humanoid robot based on posture perception[J]. Robot technique and application, 2012(6): 54-57. DOI:10.3969/j.issn.1004-6437.2012.06.016 (  0) 0)
|
| [10] |
于建均, 门玉森, 阮晓钢, 等. 基于Kinect的Nao机器人动作模仿系统的研究与实现[J]. 智能系统学报, 2016, 11(2): 180-187. YU Jianjun, MEN Yusen, RUAN Xiaogang, et al. The research and implementation of behavior imitation system about Nao robot based on Kinect[J]. CAAI transactions on intelligent systems, 2016, 11(2): 180-187. DOI:10.11992/tis.201511020 (  0) 0)
|
| [11] |
SELEEM I A, ASSAL S F M, MOHAMED A M. Cyclic gait planning and control of underactuated five-link biped robot during single support and impact phases for normal walking[C]//Proceedings of 2018 IEEE International Conference on Industrial Technology. Lyon, France, 2018: 123−128.
( 0) 0)
|
| [12] |
LIN Jinling, HWANG K S, JIANG Weicheng, et al. Gait balance and acceleration of a biped robot based on Q-learning[J]. IEEE access, 2016, 4: 2439-2449. DOI:10.1109/ACCESS.2016.2570255 ( 0) 0)
|
| [13] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297. ( 0) 0)
|
| [14] |
于建均, 张远, 左国玉, 等. 基于ZMP判据的仿人机器人步态模仿[J]. 北京工业大学学报, 2018, 44(9): 1187-1192. YU Jianjun, ZHANG Yuan, ZUO Guoyu, et al. Humanoid robot gait imitation based on ZMP criterion[J]. Journal of Beijing University of Technology, 2018, 44(9): 1187-1192. (  0) 0)
|
| [15] |
ALZAQEBAH A, MASADEH R, HUDAIB A. Whale optimization algorithm for requirements prioritization[C]//Proceedings of 2018 9th International Conference on Information and Communication Systems. Irbid, Jordan, 2018: 84−89.
( 0) 0)
|
| [16] |
FERREIRA J P, CRISÓSTOMO M, COIMBRA A P. SVR control of the sagittal balance of a biped robot combining torso and ankle joints[C]//Proceedings of 2010 World Automation Congress. Kobe, Japan, 2010: 1−9.
( 0) 0)
|
| [17] |
DING Zhen, YANG Chifu, XING Kai, et al. The real time gait phase detection based on long short-term memory[C]//Proceedings of 2018 IEEE Third International Conference on Data Science in Cyberspace. Guangzhou, China, 2018: 33−38.
( 0) 0)
|
| [18] |
雷森, 史振威, 石天阳, 等. 基于递归神经网络的风暴潮增水预测[J]. 智能系统学报, 2017, 12(5): 640-644. LEI Sen, SHI Zhenwei, SHI Tianyang, et al. Prediction of storm surge based on recurrent neural network[J]. CAAI transactions on intelligent systems, 2017, 12(5): 640-644. DOI:10.11992/tis.201706015 (  0) 0)
|
| [19] |
FENG Yang, LI Yuncheng, LUO Jiebo, et al. Learning effective Gait features using LSTM[C]//Proceedings of 2016 23rd International Conference on Pattern Recognition. Cancun, Mexico, 2016: 325−330.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


