机制主义人工智能理论框架包括：机制主义人工智能理论^[1]、泛逻辑学理论^[2]和因素空间理论^[3]。因素空间理论是机制主义人工智能的数学基础。背景基理论是因素空间理论框架下的一个重要分支。因素空间理论是现有人工智能数学理论的进一步提升，该理论从形成事物的本质出发，以构成事物的“基因”为维度，形成一个描述事物的“基因空间”。基因最早的英文名称是Factor，因素就是广义的基因，所以用“因素空间”描述事物更具有普适价值。背景分布是因素空间理论下的一个重要概念。2013年，汪培庄^[4]在讨论因素空间与因素库的关系时提出背景分布概念。2014—2015年，汪培庄^[5-6]在因素空间与数据科学一文中讨论了数据科学与因素背景关系的深刻联系。“背景分布−背景关系−背景基”模型是人对客观事物从观察到认识事物，再到知识形成的过程^[7-9]。背景基的提出就是为了描述因素的背景关系。曲国华等^[10-11]研究了背景分布与模糊背景之间的关系。与此同时，汪培庄提出了一种构造背景基的判别方法：内点判别法。该算法简单、高效，可以近似描述背景关系。吕金辉等^[12]为了弥补该算法的近似性，给出了完整的夹角判别定理，使得内点判别法成为一种精确的算法，但该方法计算较复杂，且在高维空间中提取的基点较冗余。此外，目前大数据计算复杂性理论仍然需要时间突破^[13]。跳出时间复杂度成指数增长的约束仍是专家学者们继续研究的热点。针对以上问题，提出了一种基于背景基的数据分类算法：基点分类算法。该算法可以模仿人类认识事物的过程，把人类学习到的知识用背景基刻画，不同的背景基容纳不同知识体，最终实现知识的分类与预测。从机制主义人工智能理论的角度来看，该算法不但有监督学习和预测的能力，而且在遇到全新知识时，有自我判断和自我分类的能力，所以说，该算法从原理上可以认为是具有一定的智能生长能力^[14]。本文提出可继承可扩展的改进的背景基提取算法(improved background-base extraction, IBBE)，设计基点分类算法，通过定义 $\lambda $ -背景基优化预测模型，数值实验验证算法有效性。

1 背景基理论基本概念

因素空间理论中，认为因素是事物的质根，强调事物构成的根本。背景基则强调用集合理论表达知识

定义1　一类事物的集合称为论域，用U表示。

定义2　映射。 $f:U \to X(f) $ 称为一个因素，其中 $X(f)$ 是f从事物所映射出来的性状的集合，称为f的性状空间。

对于给定论域U上的一组因素 ${f_j}:U \to X({f_j})$ $(j = 1,2, \cdots ,n)$ ，称集合 ${F^*} = \left\{ {{f_1}, {f_2},\cdots ,{f_n}} \right\}$ 为当前论域U的一个因素集。 $P({F^*})$ 为F^*的幂集，元素个数为 ${2^{|{F^*}|}}$ ，此处 $\left| {{F^*}} \right| = n$ ， $P({F^*})$ 的任意元素 ${F_i} = \left\{ {{f_{(j)}}, \cdots ,{f_{(k)}}} \right\}$ ，其中 $i = 1,2, \cdots ,{2^{|{F^*}|}}$ ， $\left\{ {{f_{(j)}}, \cdots ,{f_{(k)}}} \right\}$ 是 $P({F^*})$ 的一个子集合，定义一个U上的合成因素 ${F_i}: U \to X({F_i})$ ，其性状空间是

$X\left( {{F_i}} \right) = X\left( {{f_{(j)}}} \right) \times \cdots \times X\left( {{f_{(k)}}} \right)\\ $

(1)

记为 ${F_i} = {f_{\left( j \right)}} \cup \cdots \cup {f_{\left( k \right)}}$ 。式(1)的含义是：合成因素F_i的性状空间 $X({F_i})$ 被定义成一个笛卡尔乘积 $X({f_{(j)}}) \times \cdots \times X({f_{(k)}})$ 。

定义3　因素空间。记 ${X_{{F^*}}} = {\left\{ {X\left( F \right)} \right\}_{(F}}_{ \in P({F^*}))}$ ，称 $\varPhi = (U,{X_{{F^*}}})$ 为U上的一个因素空间。

记 ${X_{{\rm{max}}}} = X({f_1}) \times X({f_2}) \times \cdots \times X({f_n})$ 称为最大性状空间。对于离散型性状空间而言，任意 ${{a}} = ({a_1}, {a_2},\cdots ,{a_n}) \in X$ 称为一个性状颗粒。

因素空间定义的更多解释，可参考文献[3]中第1章的相关内容。

定义4　背景关系。给定U上的定性因素空间 $\varPhi = (U,{X_{{F^*}}})$ ，对任意相 ${{a}} = ({a_1},{a_2}, \cdots ,{a_n}) \in X$ ，记其在U上的原相为

$[{{a}}] = {{{F}}^{ - 1}}({{a}}) = \{ u \in U|{{F}}(u) = {{a}}\} \\$

(2)

$[{{a}}]$ 可能是空集，若 $[{{a}}] \ne {\text{Ø}} $ ，则称a是一个实性状颗粒，否则称a是一个虚组态。全体实性状集合记为

$ \begin{array}{l} R = {{{F}}^*}(U) = \{ {{a}} = ({a_1},{a_2}, \cdots ,{a_n}) \in X|\exists u \in U \\ {\rm{ }}{f_1}(u) = {a_1},{f_2}(u) ={a_2},\cdots ,{f_n}(u) = {a_n}\},\\ \end{array} $

(3)

R称为因素 ${f_1}, {f_2},\cdots ,{f_n}$ 之间的背景关系，也称为因素F^*的背景集。

机器学习中a可以视为一条样本，[a]表示a的对应标签。如果一个a有对应标签，则a是有意义的，即a是一个实性状颗粒，否则a是没有意义的，称a是一个虚组态。背景关系可以理解为：所有有意义的样本构成的集合S与样本的标签之间的因果关系。若要深入讨论集合S的分布问题，则引出定义5。

定义5　背景分布。设论域 $U = \left( {U,{{A}},p} \right)$ 是一个概率场， $\varPhi = (U,{X_{{F^*}}})$ 是定义在U上的一个因素空间， $X = (X,{{B}})$ 是最大性状空间上的一个可测结构。若所有 ${F^*}$ 中的 ${f_j}$ 都是可测映射，记 $p = {p_{{F^*}}}$ 为p经过 ${F^*}$ 在X上所诱导出来的概率，亦即对任意 $B \in {{B}}$ ，都有 $p(B) = p\left( {{{({F^*})}^{ - 1}}(B)} \right)$ 。B称为因素 ${F^*}$ 的背景分布。

定义6　背景基。若每个性状空间 $X({f_j})$ 都是有序集，背景关系R是X中的凸集，记R的所有顶点所构成的集合为B=B(R)={P|P是R的顶点}，称作背景基。S表示样本集合，当S=R时，记B的所有顶点构成的集合为 B(S)={P|P是S的顶点}，称为样本背景基。

背景基可以生成背景关系，是背景关系的无信息损失的压缩，对因素库^[4]的实际应用具有重要的意义。

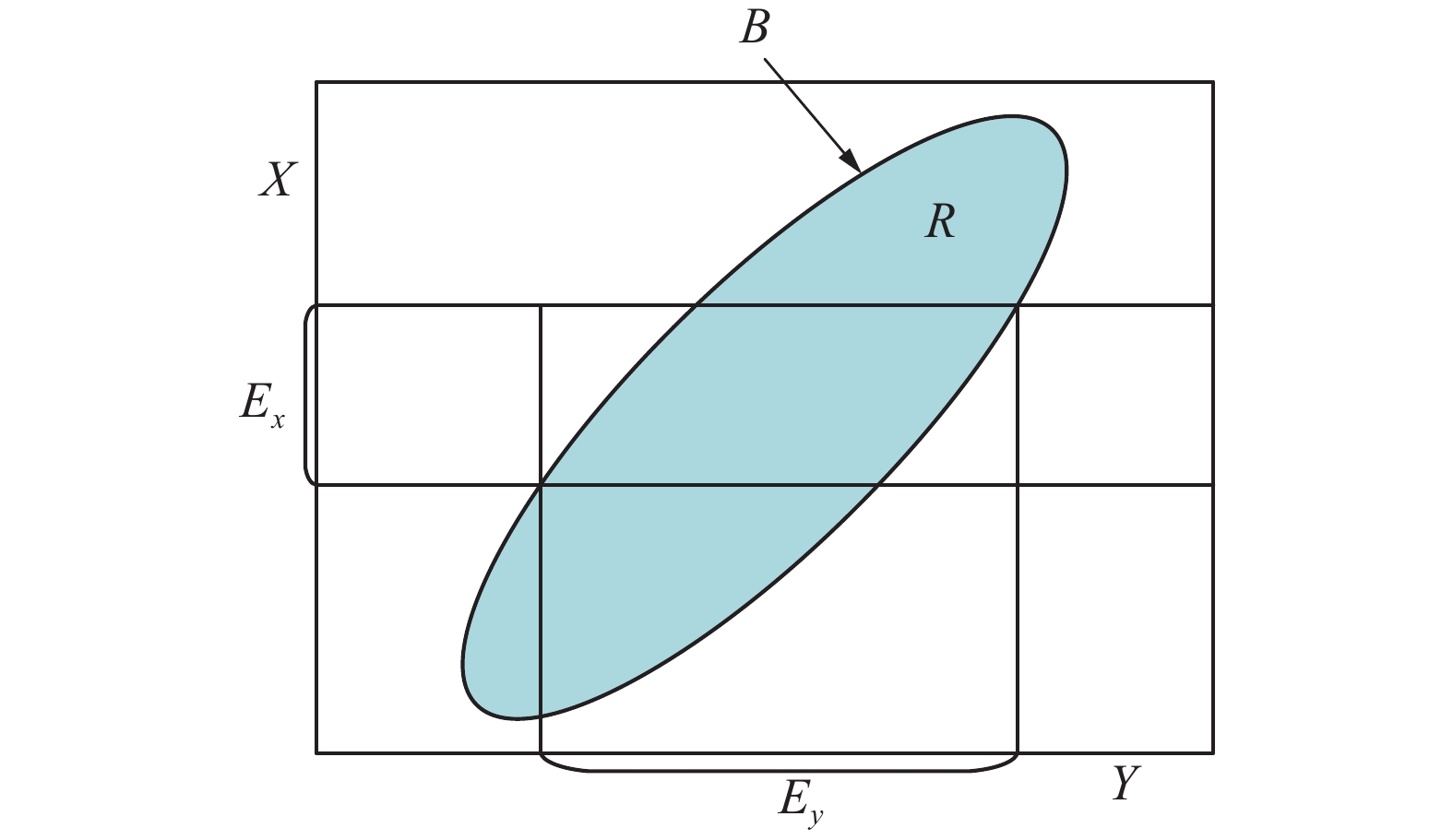
为了更好地说明背景关系、背景分布、背景基三者概念之间的联系，以图1为例进行图示说明。

设集合X、Y、R，其中 $E_x \subseteq X,E_y \subseteq Y$ ，集合R称为背景关系，集合R的“边缘”构成背景基B，p是背景分布，视为集合R的概率密度，可以由样本的相a的频率逼近来实现。背景关系R表示集合X和集合Y之间的关联性。这里有

$E_x\;R\;E_y $

可得逻辑推理：

$E_x \to R_y{\rm{ }}(R \text{表示} \to ) $

因此可以认为，背景关系R保证了X与Y的因果关系，背景基则限定了背景关系区域，背景分布表示了因果关系的概率。

2 改进的背景基提取算法

集合论的诞生，使得数学与认知实现了潜在的融合。人类对事物的认知表现可以用数学中的集合刻画，集合可以表现概念，认知的逻辑特性被集合论充分地表现出来。因素空间的背景基理论就是力求用数学刻画人的学习过程。从技术层面来讲，目前由夹角判别定理实现的知识归纳算法有背景基提取算法^[12]，但是该算法判别条件复杂、时间复杂度较大，搜寻到的基点数量太多。这些导致表达的知识不利于继承和保存。为此，本章对现有算法改进，使其在减少复杂度同时，更符合人的思维逻辑。

2.1 背景基提取原理

用技术手段实现背景基的提取，是“背景关系−背景分布−背景基”从理论到实践的关键。目前背景基提取主要用到夹角判别定理。

夹角判别定理^[12] 　设S是一个样本集。 ${S^*}$ 是S的一个基点集合，其中心为O。 $P \in X$ \ ${S^*}$ 是一个新的样本点。它可被删除当且仅当存在一点 $Q \in {S^*}$ ，使射线PQ与射线PO形成钝角，亦即 $ (Q - P,\;O - P) < 0$ 。而且，对于任意 $Q' \in {S^*}$ \ $\left\{ Q \right\} $ ，都有

$(P - O,{O^*} - O) \leqslant ({O^*} - O,{O^*} - O) $

这里， ${O^*} $ 是O在直线QQ’上的垂足。

内点判别法　设S为数据样本集，P是S的一个内点当且仅当在S中存在一点Q，使射线PQ与射线PO形成钝角，亦即(Q−P, O−P)<0。

夹角判别定理是一种精确求取背景基的方法，但该方法在计算时较复杂，在高维空间提取的基点较冗余。为此，在简化计算的同时，减少背景基点个数，同时保证信息不损失是本章算法改进的目的。

内点判别法计算简单，基点提取率高效，有利于处理大样本高维度数据。为此，本章采用内点判别法作为改进背景基提取算法的理论基础。

2.2 改进的背景基提取算法

给定一组样本集合 $S = \left\{ {{{{x}}_i} = ({x_i}_1,{x_i}_2, \cdots ,{x_{in}})} \right\}$ ，n表示样本个数， $|S|$ 表示样本数量，|S|=m， $i = 1, 2,\cdots ,m$ ，且m>n。设B为背景基，初始值B=Ø，含义表示人对事物的认知初始处于混沌状态，随着对样本的学习，B≠Ø，表示人对事物开始有了一定的判断力，随着样本量的增加，B的泛化能力越来越强，当样本足够充分时，就会形成对特定事物的认知包，一个认知包就是一个知识，或者一个概念。

改进的背景基提取算法就是在模仿人学习过程同时提取知识轮廓，保存学到的知识。下面给出改进的背景基提取算法步骤。

算法　改进的背景基提取算法(IBBE算法)。

输入　样本 $S = \left\{ {{x_i} = ({x_i}_1, {x_i}_2,\cdots ,{x_{in}})} \right\}$ 。

初始化　背景基 $B = {\text{Ø}} $ ；样本个数|S|；计数器count=0； $\theta $ 为初始基点个数。

1)取S中样本x_i，若|B|< $\theta $ ，则 ${x_i} \in B$ ，否则，转至2)。

2)计算B的几何中心o：

${{o}} = \frac{1}{k}\sum\limits_{j = 1}^k {{{{b}}_j},\quad{{{b}}_j} \in {{B}}}\\ $

计算内积：

$({{\alpha}} ,{{{\beta}} _{{j}}}) = {{\alpha}} {{{\beta }}^{\rm{T}}_{{j}}} \\ $

其中： ${{\alpha}} = {{o}} - {{{x}}_{{i}}}$ , ${{{\beta}} _{{j}}} = {{{b}}_{{j}}} - {{{x}}_{{i}}}$ , $j = 1,2, \cdots ,{{|}}B{{|}}$ 。

若存在 ${{{\beta}} _j}$ 使得 $({{\alpha}} ,{{{\beta}} _{\rm{j}}}) < 0$ ，那么x_i是背景基B的内点，舍去，并转至1)；否则x_i是B的一个基点，即 ${{{x}}_i} \in B$ ，然后转至3)。

3)在 2)中加入x_i可能会导致一个或多个基点再次变成内点，而内点需要被剔除，因此3)功能是剔除B中内点。具体如下：

①取基点 ${{{b}}_j} \in {{B}}$ 视为待测点，B中剩余的基点 ${B^{\rm{*}}} = B $ \ ${{{b}}_j} $ 视为临时背景基；然后计算B^*的几何中心 ${{o}}'$ 以及内积：

$({{\alpha}} ',{{{\beta}} _i}') = {{\alpha}} '{({{{\beta}} _i}')^{\rm{T}}}, $

其中： ${{\alpha}} ' = {{o}}' - {{{b}}_j},\;{{{\beta}} _i}' = {{b}}_i^* - {{{b}}_j},\;{{{b}}^*} \in {{{B}}^*}$ 。

②若 $({{\alpha}} ',{{{\beta}} _i}') < 0$ ，则继续判断 ${b_j}$ 是否为极点，即 ${{{b}}_j} = {{P_j}^ + }$ ？或 ${{{b}}_j} = {{P_j}^ - }$ ？其中

${{P_j}^ + } = {\rm{argma}}{{\rm{x}}_i}\{ {b_{ij}}|{b_{ij}} \in {{B}}\} $

${{P_j}^ - } = {\rm{argmi}}{{\rm{n}}_i}\{ {b_{ij}}|{b_{ij}} \in B\} {\rm{ }}\left( {j = 1,2, \cdots ,|{{B}}|} \right)$

如果不是各因素的极点，则标记b_i为待删除点d_i；依此类推，检测B中所有基点。

4)若B中存在内点，则删除标记点d_i标记的基点，得到 ${{B'}}$ ，更新B： ${{B}} \leftarrow {{B'}}$ ；再返回1)读取全部样本后转至5)。

5)输出背景基B。

通常背景基B是由矩阵存储，若样本S有n个因素，B的基点个数| B |=m，则B是一个m×n的矩阵：

$ {{{B}}_{m \times n}} = \left[ \begin{array}{l} {b_{11}}\;\;{b_{12}}\;\; \cdots \;\;{b_{1n}} \\ {b_{21}}\;\;{b_{22}}\;\; \cdots \;\;{b_{2n}} \\ \;\ \vdots \ \ \ \ \;\; \ \vdots\ \ \ \ \ \ \ \ \;\;\; \vdots \\ {b_{m1}}\;\;{b_{m2}}\;\; \cdots \;\;{b_{mn}} \\ \end{array} \right] $

B的每一行表示一个基点。

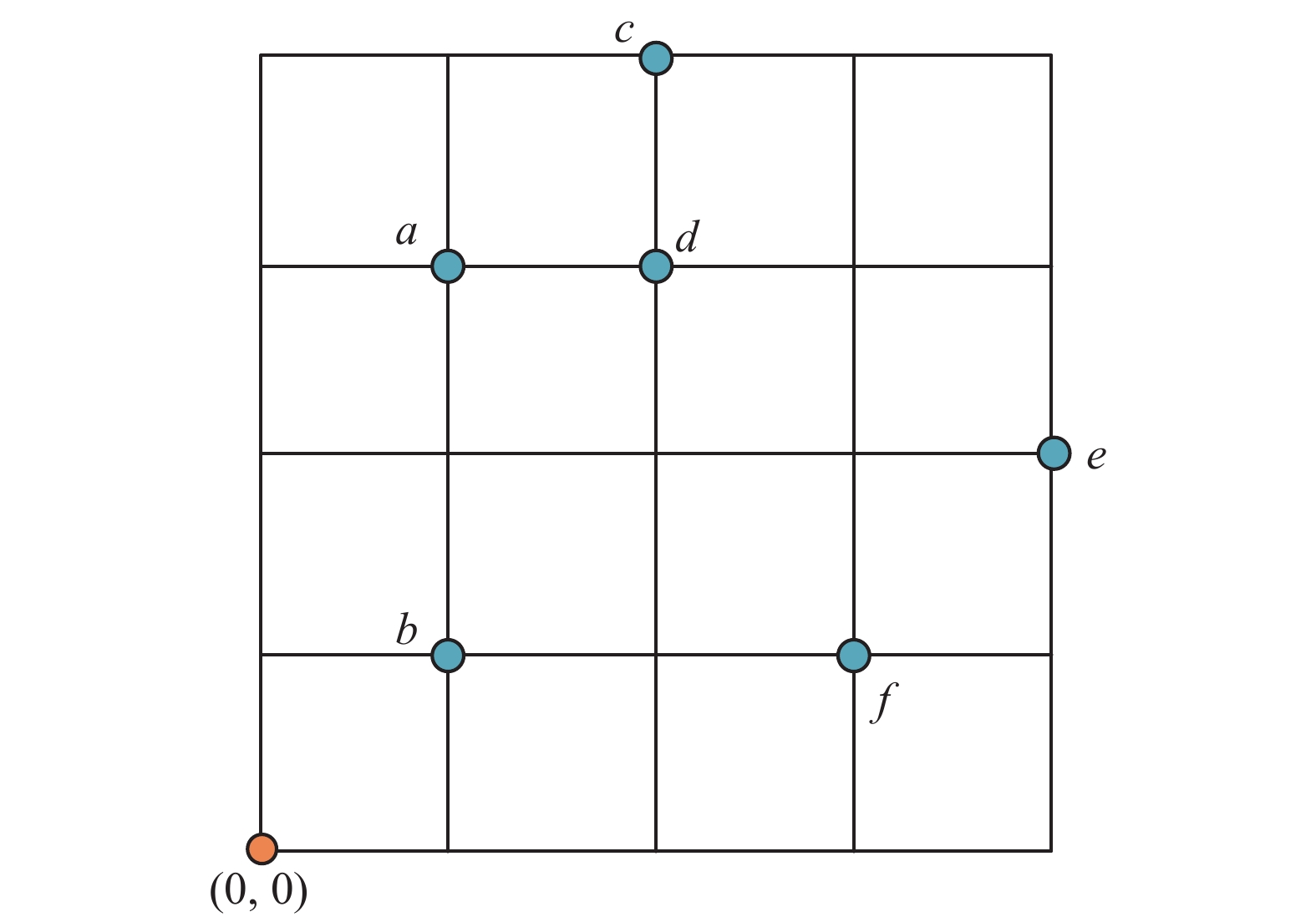
2.3 算例

图2中，样本集合S包含点a=(1,3)、b=(1,1)、c=(2,4)、d=(2,3)、e=(4,2)和f=(3,1)，利用上述改进算法生成样本集合S的背景基B。

计算步骤如下：

输入　样本集合S={a, b, c, d, e, f}。

初始化　背景基 ${{B}} ={\text{Ø}}$ ；样本个数|S|=6; 计数器count=0。

选代t=1：

1)从S中读取一个样本a，count=1，此时|B|=1，|B|<3，不做任何判断，此时B={a};

从S中取样本b，count=2，此时|B|=2，|B|<3,不做任何判断，此时B={a, b}；

从S中取样本c, count=3，此时|B|=2，|B|<3，条件不成立，转至2)。

2)先计算B的中心：

${{o}} = \frac{1}{k}\sum\limits_{j = 1}^k {{b_j} = \frac{1}{2}} (a + b) = (1,2)\\ $

再计算内积：

(o−c,a−c)=(o−c)(a−c)^T=(−1,−2)(−1, −1)^T=3>0

(o−c,b−c)=(o−c)(b−c)^T=(−1,−2)(−1, −3)^T=7>0

因为上述内积结果都为正，即交成锐角，所以认为c是一个基点，即B={a, b, c}。

3)在2)中B的更新可能产生新的内点，需要进一步筛选和剔除：

①将B中的a视为内点，B^*=B\a={b,c}，按照2)方法判断，得到a不是B^*中的内点；

②将B中的b视为内点，B^*=B\b={a,c}，按照2)方法判断，得到b不是B^*中内点；转至4)。

4)B中没有内点，故B={a,b,c}；此时count=3<|S|，则转至1)。

选代t=2：

1)从S中取样本d，count=4，此时|B|=3，|B|<2，条件不成立，转至2)。

2)~4)与上述对应步骤相同，此处省略，得到B={a, b, c, d}。

选代t=3：

1)从S中取样本e，count=5，此时|B|=4，|B|<2，条件不成立，转至2)。

2)与上述对应步骤相同，此处省略，得到B={a, b, c, d, e}。

3) ①取B中a为待测点，B^*=B\a={b, c, d, e}，判断得到a不是B^*中内点；

②取B中b为待测点，B^*=B\b={a, c, d, e}，判断得到b不是B^*中内点；

③取B中c为待测点，B^*=B\b={a, b, d, e}，判断得到c不是B^*中内点；

④取B中d为待测点，B^*=B\b={a, b, c, e}，判断得到d是B^*中的内点，再根据极点公式P_j⁺、P_j⁻判断得到d不是极点，因此标记d点为待删除点d₁。

4) B中有内点存在，删除标号d₁的点，所以B={a, b, c, e}；此时count=5<|S|，则转至1)。

选代t=4：

1)从S中取样本f，count=6，此时|B|=4，|B|<2，条件不成立，转至2)。

2)、3)与上述对应步骤相同，此处省略，得到B={a, b, c, e, f}。

4) B中没有内点，故B={a, b, c, e, f}；此时count=6=|S|，循环结束。

输出　背景基B。

输出的背景基B是5×2矩阵，为表达上的美观，采用B的转置表达，即

${{B}} = {\left[ \begin{array}{l} {\rm{1 }}\;1\;{\rm{ 2\; 4\; 3}} \\ {\rm{3 }}\;1\;{\rm{ 4 \; 2 \; 1}} \\ \end{array} \right]^{\rm{T}}}$

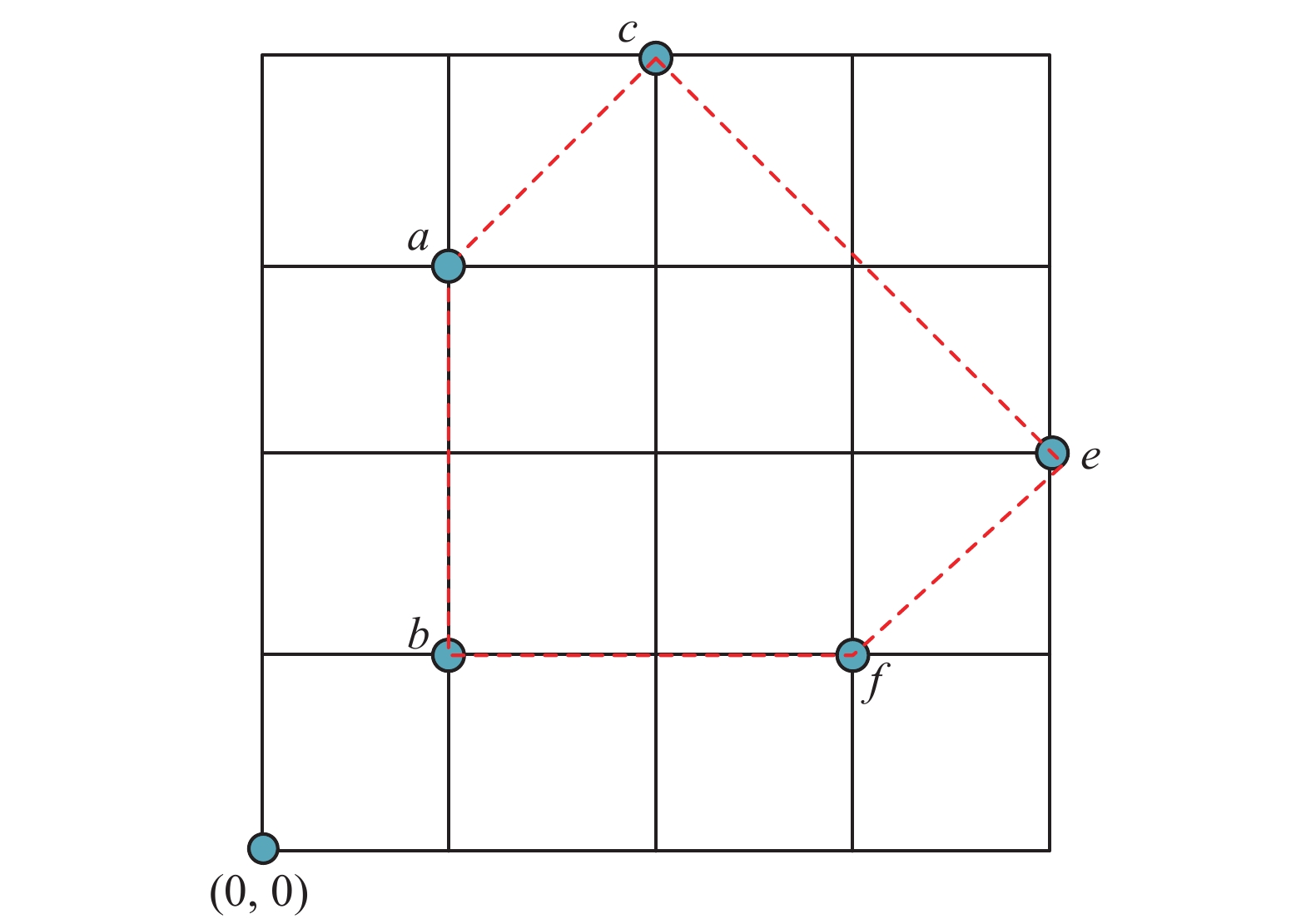
B的每列代表一个因素，如图3所示，虚线包含的区域可以近似视为由样本数据生成的背景分布，此时背景基为背景分布轮廓的特征点集合。由上述算例可得背景基在信息压缩、知识表达与存储等方面有着独具创新的优势。

结合算法和算例，总结IBBE算法的优点：

①IBBE算法极大简化了计算难度和编程难度；

②算法初始化阶段不需要依赖各因素极值；

③极大降低了基点数量，有利于高维度数据提取基点。

3 基点分类算法

人工智能对数据的分类其实质是对同一类别的数据形成概念。本文提出的基点分类算法(base point classification algorithm)，简称BPC算法，以背景基提取算法为核心。通过对不同类别样本进行分类打包和学习，最终将给定样本归纳成以各类别为单位的认知包，一个认知包就是一个概念。

3.1 基本定义

BPC算法训练得到的模型相对固定。在实际中，决策者的主观因素常常扮演重要角色，基于此，BPC算法在做决策时需要加入决策者主观参数，由主观参数 $\lambda $ 变换得到的背景基称为 $\lambda $ -背景基。

定义7　设集合 ${B_i} \ne \text{Ø}$ ，由c个类别生成的背景基 ${{B}}{\rm{ = }}\mathop\cup\limits_{i = 1}^{{c}} {{{{B}}_i}}$ ，各类别用i表示， $i = 1,2, \cdots ,c$ ， ${b_j} \in {{B}}$ ，则有

${[{{B}}]_{{i}}} = \{ {{b}}_{{j}}^{{i}}|i \in c,j = 1,2, \cdots ,n\},\\ $

(4)

其中 $n = |[{{B}}{]_i}|$ ，称 ${[{{B}}]_{{i}}}$ 为类别i的背景基。

命题1　如果 ${[{{B}}]_{{i}}}$ 为类别i的背景基，则 ${{{B}}_i} = {[{{B}}]_i}$ 。

证明　设 ${[{{B}}]_{{i}}}$ 为类别i的背景基， $i = 1, 2, \cdots , c$ ，B为由c个类别生成的背景基，则有

${{B}} = \mathop\cup\limits_{i = 1}^{{c}} {{{[{{B}}]}_i}} \\ $

而由定义7得

${{B}} = \mathop\cup\limits_{i = 1}^{{c}} {{{{B}}_i}} \\ $

因此有

${{{B}}_i} = {[{{B}}]_i}$

证毕。

定义8　设B为c个类别的背景基，[B]_i为类别i的背景基，b_j∈[B]_i，向量 ${{\varLambda}} {\rm{ = (}}{\lambda _1},{\lambda _2}, \cdots ,{\lambda _c}{\rm{)}}$ ， ${\lambda _i}{\rm{ > 0}}$ ， $i = 1,2, \cdots ,c$ ，使得

${[{{{B}}_{{\lambda}} }]_i} = {{\varLambda}} \otimes {[{{B}}]_i} = \{ {\lambda _{{i}}}{{{b}}_{{j}}}|j = 1,2, \cdots ,|{[{{B}}]_i}|\} \\ $

(5)

则称 ${{{B}}_\lambda } = \mathop\cup\limits_{i = 1}^n {{{[{{{B}}_\lambda }]}_i}}$ 为 $\lambda $ -背景基。

从几何学角度看， $\lambda $ -背景基 ${{{B}}_\lambda }$ 是普通背景基B的放大或缩小。当 $\lambda \in [0,1)$ 时，背景基B锁定的区域R(B)包含 ${{{B}}_\lambda }$ 锁定的区域 R( ${{{B}}_\lambda }$ )，即R( ${{{B}}_\lambda }$ ) $ \subset $ R(B)；当 $\lambda = 1$ 时，满足关系R( ${{{B}}_\lambda }$ ) = R(B)；当 $\lambda \in (1,\infty )$ 时，R( ${{{B}}_\lambda }$ ) $ \supset $ R(B)。综上所言，对于区域R关系满足：

$R = \left\{ \begin{array}{l} R({{{B}}_\lambda }) \subset R\left( {{B}} \right),\quad \lambda \in [0,1) \\ R({{{B}}_\lambda }) = R\left( {{B}} \right),\quad \lambda = 1 \\ R({{{B}}_\lambda }) \supset R\left( {{B}} \right),\quad \lambda \in [1,\infty ] \\ \end{array} \right.$

实现 $\lambda $ -背景基具体方法见定义9。

定义9　设O为第i类背景基 ${[{{B}}]_i}$ 的重心，其中 $m = |{[{{B}}]_i}|$ ， $j \in m$ ，b_ij∈ ${[{{B}}]_i}$ ，则

${{b}}_{ij}^\lambda = O{\rm{ + }}\lambda {\rm{(}}O{\rm{ - }}{{{b}}_{ij}})\\ $

(6)

这里 ${[{{{B}}_\lambda }]_i} = \mathop\cup\limits_{j = 1}^m {{{b}}_{ij}^\lambda }$ 。

3.2 构造基点分类算法

据第2章的IBBE算法和第3.1节中相关定义，本节设计一种新型的分类算法：基点分类算法(BPC算法)。下面采用图示方法对BPC算法的构造原理进行详细阐述和说明。

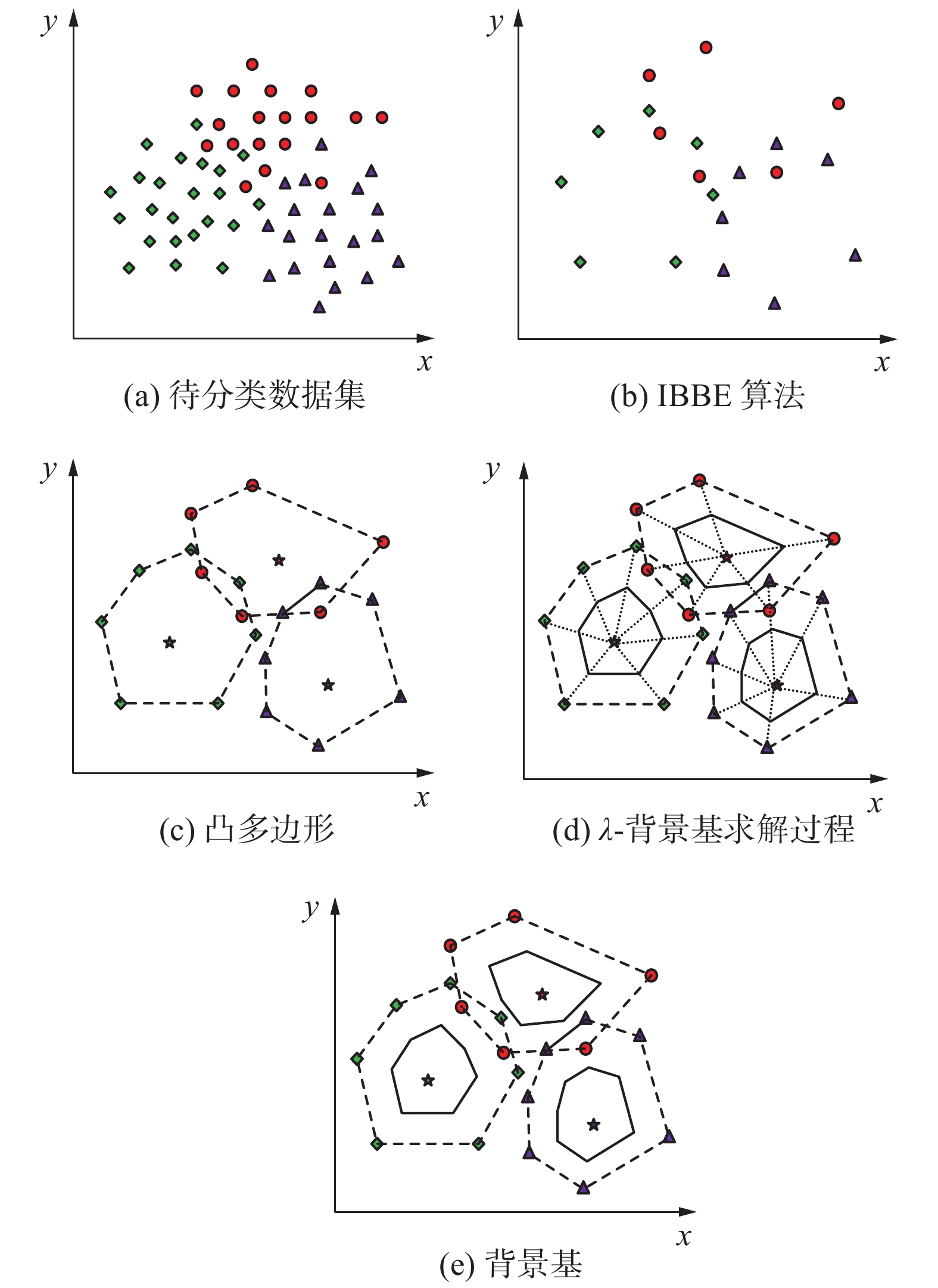
如图4所示：图(a)为待分类的数据集，不同符号代表不同的类别，共3个类别；图(b)呈现了由IBBE算法提取的每个类别的基点；为了形象表示基点围成的区域，图(c)表示在图(b)基础上围成凸多边形，其中该凸多边形可用来近似代替各类别的背景分布，其中“☆”表示每个类别的重心(由样本生成，而非由基点生成)，这在一定程度上还原了样本背景分布的情形；图(d)表示的是 $\lambda $ -背景基的求解过程，其中实线段围成的凸多边形是 $\lambda $ -背景基；图(e)就是分类器最后呈现出的背景基，由 $0 < \lambda < 1$ 和 $\lambda = 1$ 两层背景基构成，可以形象区别为边缘区域和核心区域。

基于以上思想，下面给出BPC算法的具体步骤。

算法　基点分类算法(BPC算法)。

输入　 c个类别的样本集合S，各类别用i表示；参数向量 ${{\varLambda}} {\rm{ = (}}{\lambda _1},{\lambda _2}, \cdots ,{\lambda _c}{\rm{)}}$ ， ${\lambda _i}{\rm{ > 0}}$ ， $i = 1,2, \cdots ,c$ 。

初始化　背景基B= $ \text{Ø} $ 。

1)从S中取样本x_k，判定x_k类别i；从B中提取类别为i的背景基[B]_i。

2)利用函数IBBE(x_k, [B]_i)，更新B中原来的背景基[B]_i，具体做法为

$[{{B}}]_i' = \operatorname{IBBE} ({x_k},{[{{B}}]_i}) \\ $

${{B}} = \operatorname{update} ([{{B}}]_i',{[{{B}}]_i})\\ $

函数update()功能是更新B中[B]_i。

3)计算每个类别的重心O。

4)对B中每个类别做 $\lambda $ 变换得到 ${[{{{B}}_\lambda }]_i}$ 。

5)输出 ${{{B}}_\lambda }$ 。

设M表示样本个数，N表示因素个数，p表示基点个数。当样本数量较少时，p²与M的数量级接近；当样本数量远远大于N和p²时，此时N和p²可以忽略不计，时间复杂度为O(MNp²)≈O(M)。因此，BPC算法在处理大样本数据时优势明显。

4 数值实验

采用两个实验对BPC算法进行测试。实验1采用二维数据作测试样本，用来说明BPC算法在对二维数据分类时效果良好，且有发现新类别的优点。实验2用三维数据作测试样本，用来说明BPC算法在对三维数据分类效果同样良好，并突出了 $\lambda -$ 背景基的在预测时的优势。

4.1 二维数据

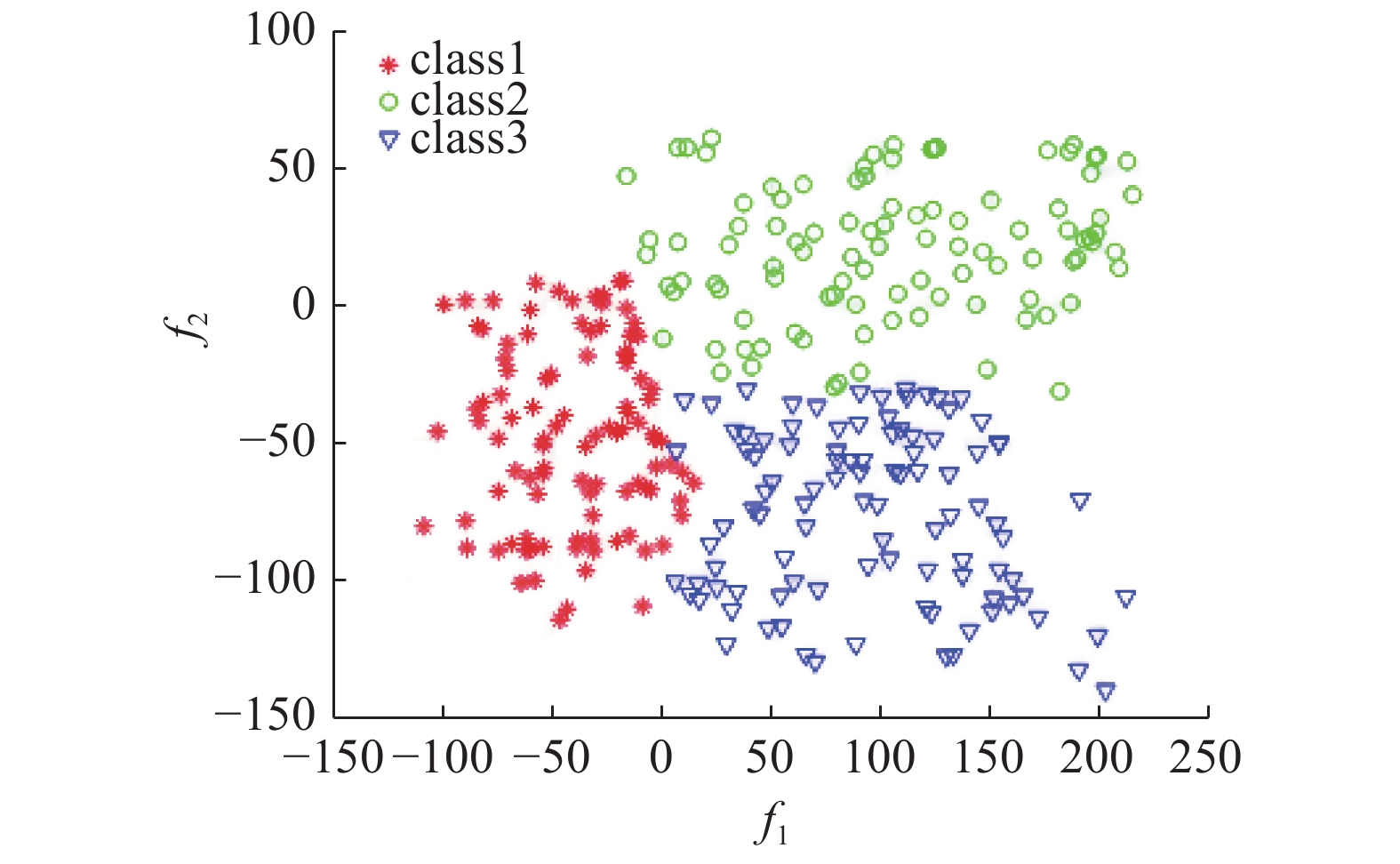
为了验证BPC算法的可行性以及实际分类效果，实验1采用二维数据作为样本数据。数据由Matlab软件仿真得到，仿真数据为均匀分布，每类样本集均为凸集，有2个因素，3个类别，每个类别100个样本，共计300个样本。不同类别用不同符号标记，如图5的图例所示。

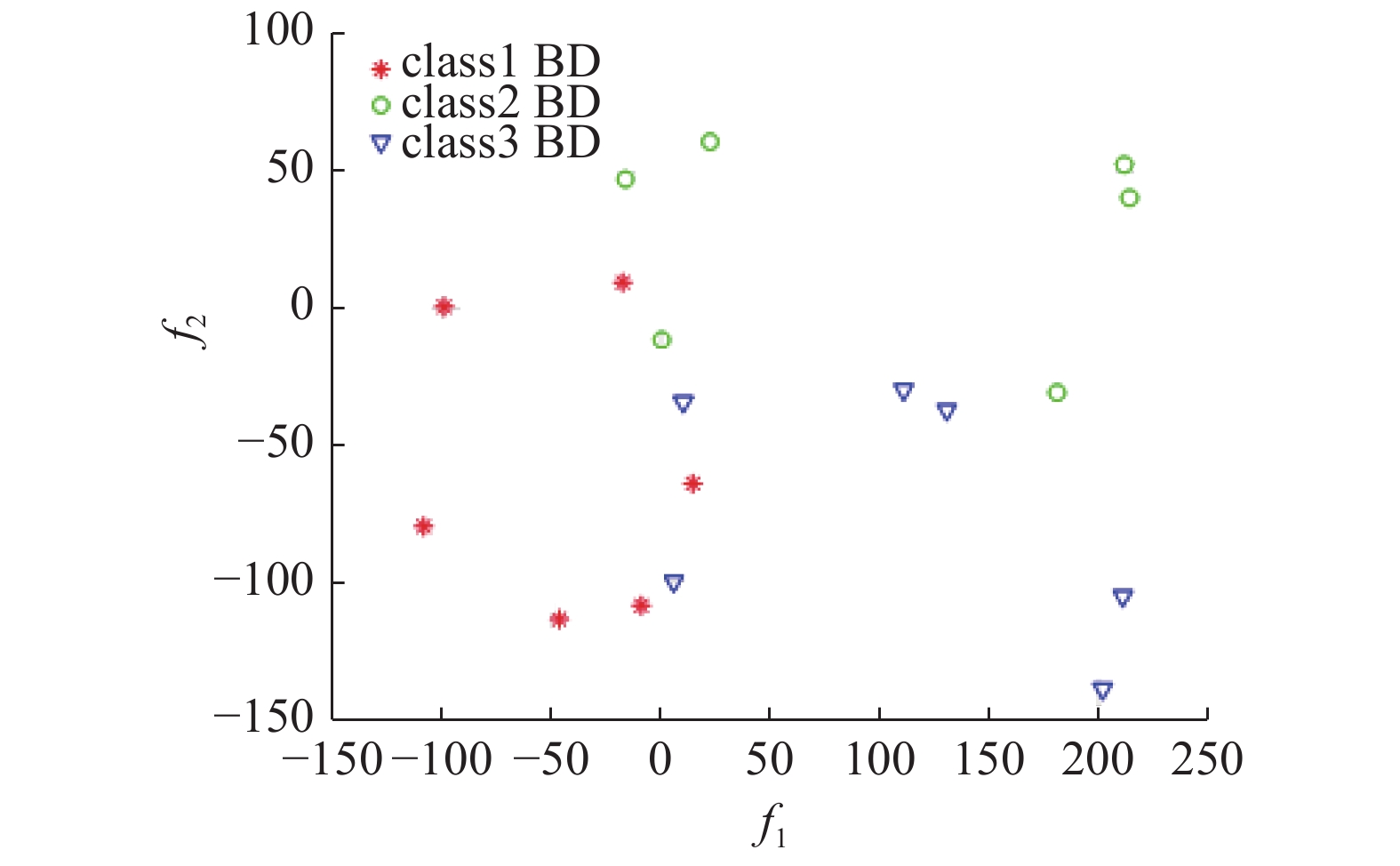
图5为3个类别样本集的分布情况；图6展现由基点分类法找到的各类别样本的基点，3个类的基点用不同的符号表示；图7是删除各类别内点保留基点的示意图。

BPC算法采用基点限定区域原理学习和预测，由于其原理与SVM算法原理具有相似性，所以实验结果与SVM(libsvm)算法进行比较是合理的。训练数据与测试数据为同一组数据。通过Matlab编程得到BPC算法的训练函数和预测函数。实验结果表明，BPC算法准确率为98.33%，SVM算法准确率为100.00%，两者结果相当。从实验结果来看，BPC算法在开始阶段表现良好。

除此之外，通过分析实验，还能得到以下结论：

1)在线性可分的样本分布下，BPC算法与SVM算法预测结果相近，但BPC算法原理更简单易懂、实验结果可解释性强，在一定程度上更符合人的思维逻辑。

2)BPC算法分类是通过构建每个类别的背景基来限定各类别区域范围，这种划分原理比SVM算法用超平面划分原理更加精准。当出现新类别样本时，BPC算法可以及时发现远离它的类别，并为其定义新标签，而SVM算法只会将该样本归类到已学习到的类别中，不会产生新类别。所以，BPC算法的一个非常明显的优势是在预测中可以发现新类别。

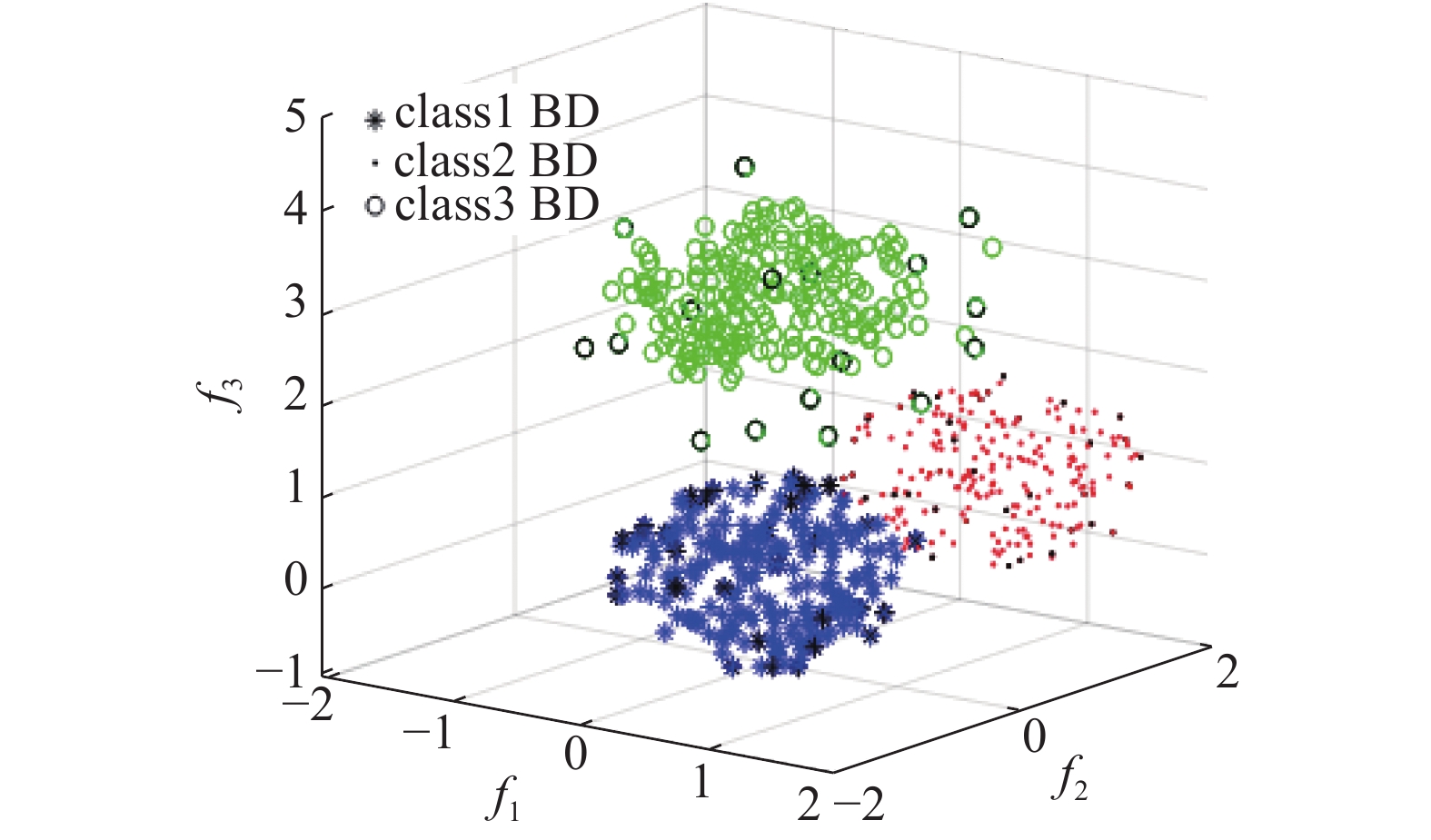
4.2 三维数据

实验2数据由Matlab仿真结果得到。仿真数据特点：每类数据集均为凸集，3个因素，3个类别class1、class2和class3，每一类220个样本，其中class1与class2数据为均匀分布，class3为非均匀分布，3个类别线性可分，见表1。

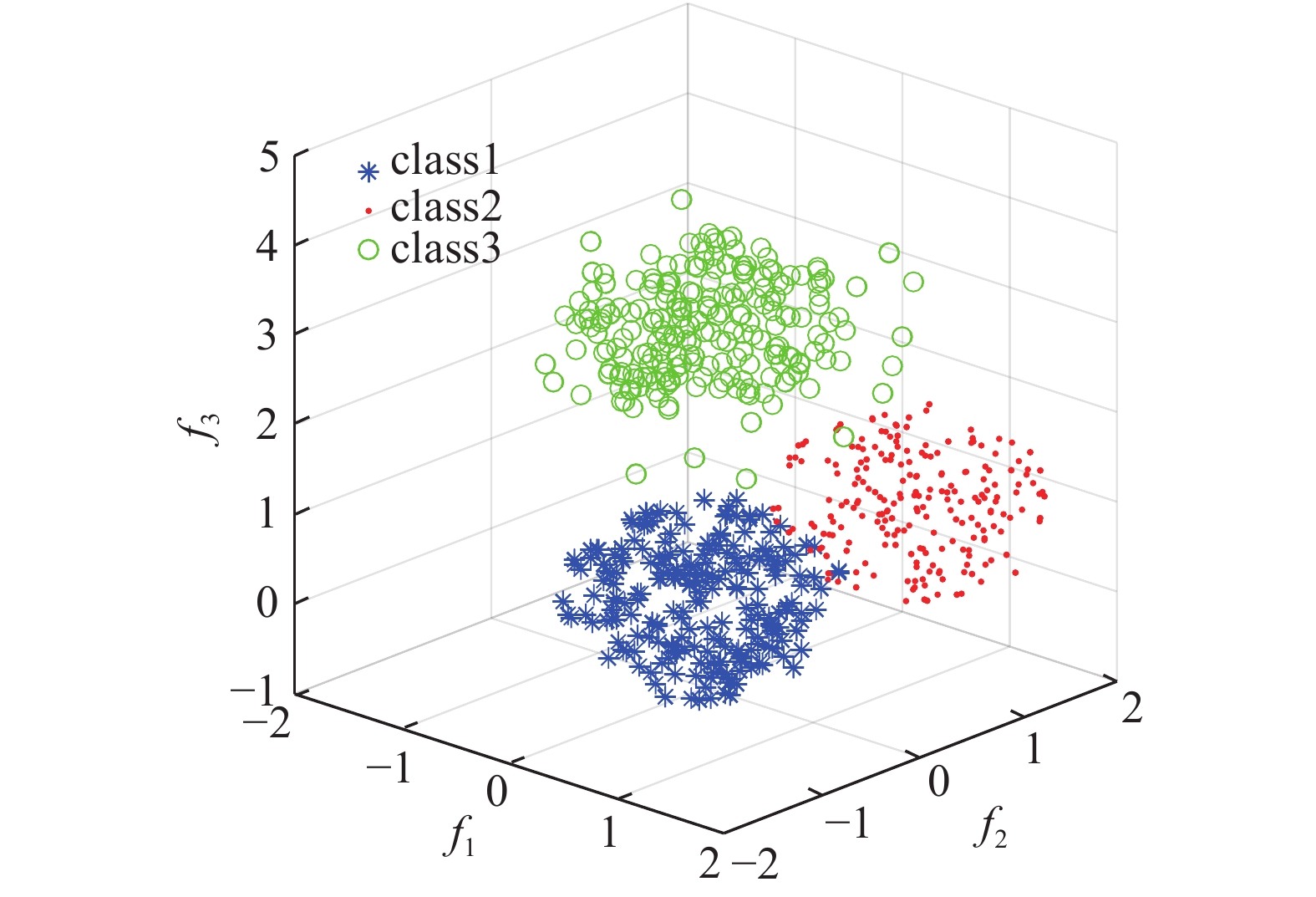
图8展示了数据集的分布情况，不同符号代表不同类别。

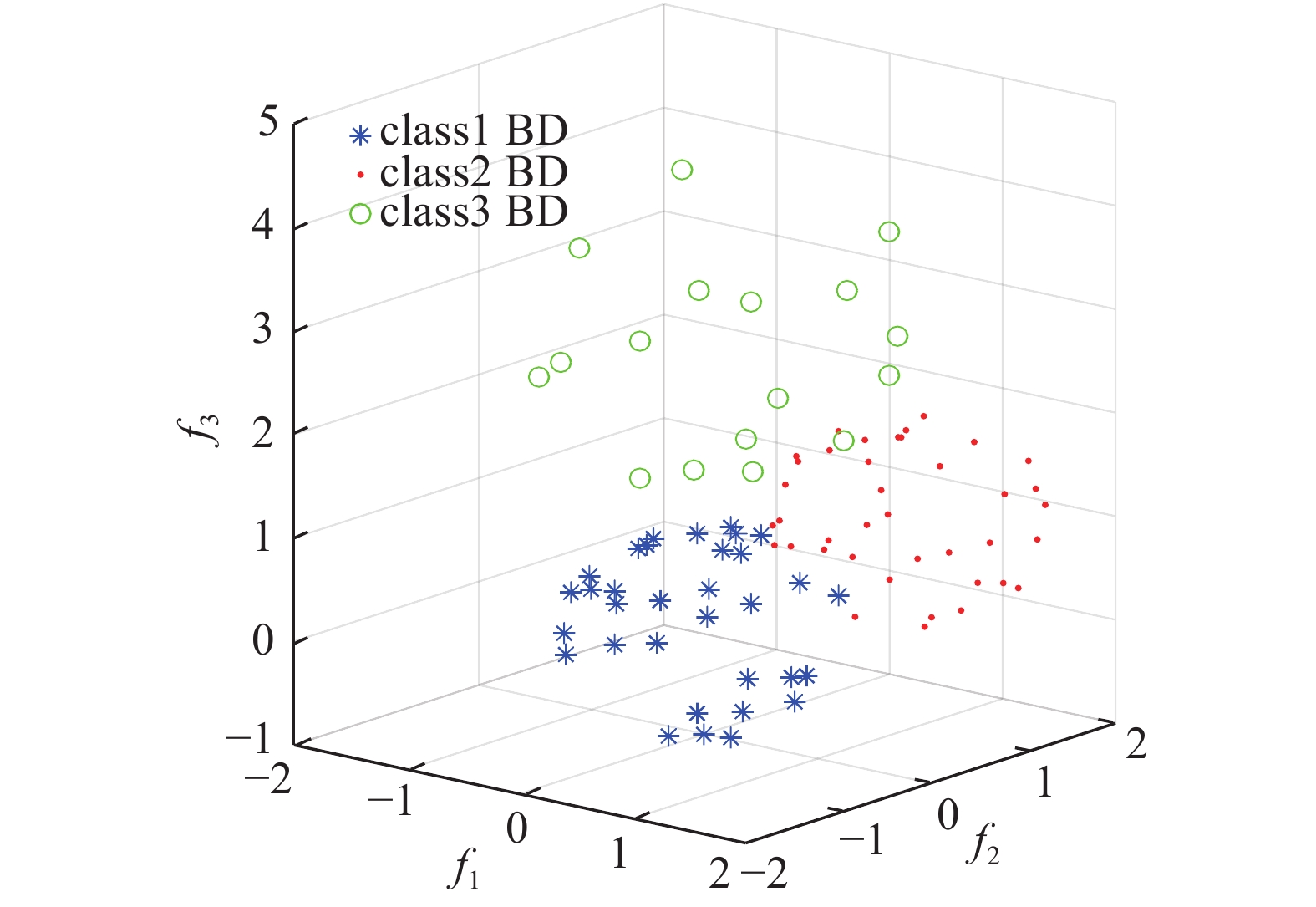
BPC算法可以提取三维数据的背景基。图9展示的是用BPC算法提取到实验2数据的背景基。由于BPC算法继承了IBBE算法的优点，所以提取到的基点数量少，却又能高效覆盖所要表达的信息。从图10可以看出，各类别的背景基数量远小于样本边界的数量。

通过学习和预测实验2的数据，实验得出：BPC算法准确率为97.73%，SVM算法准确率为99.09%。从结果来看，BPC算法结果与SVM算法结果相当。但是从预测模型来看，BPC算法比SVM算法更具有灵活性，这主要体现在 $\lambda $ -背景基的优势。

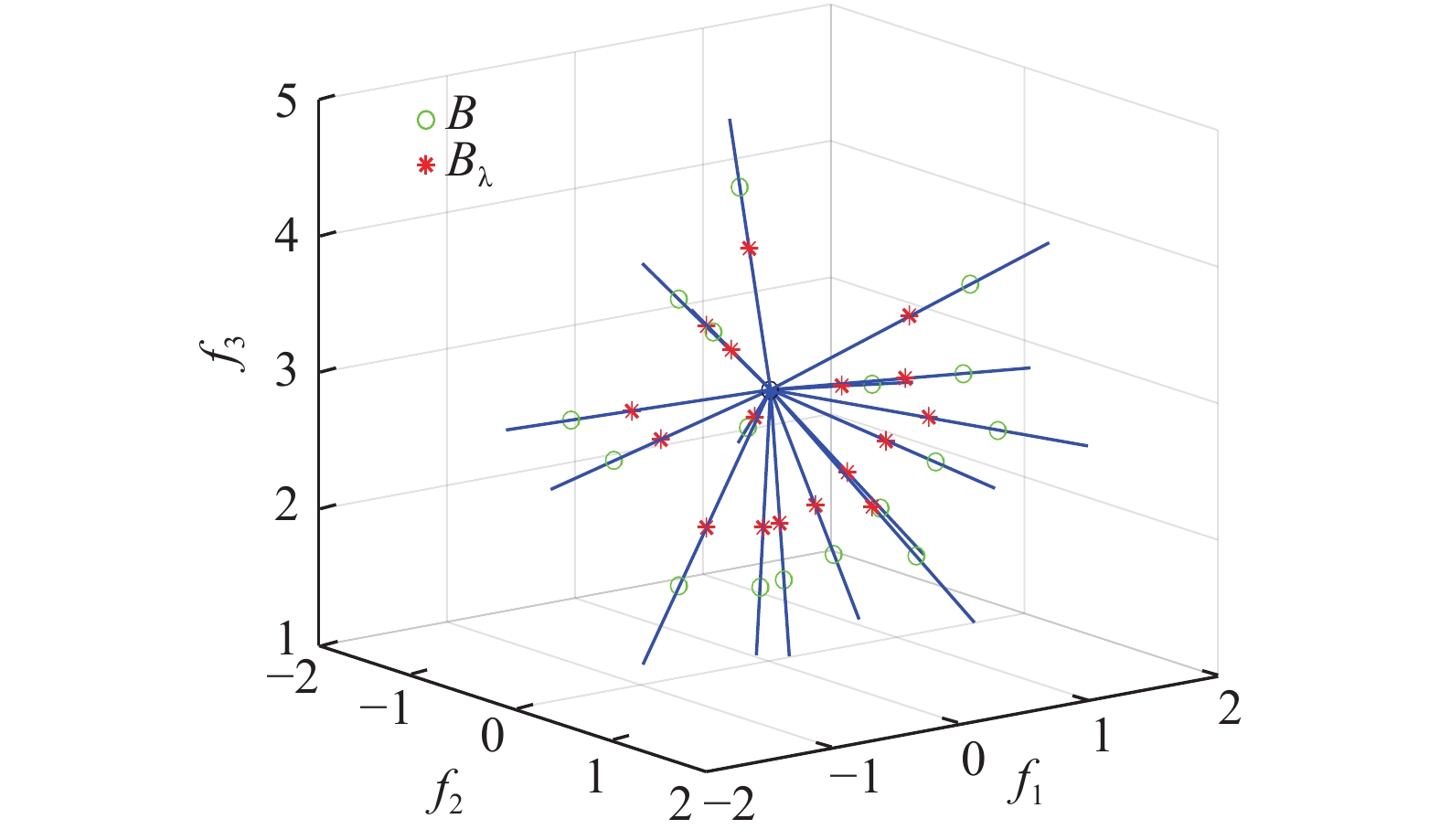
从图8可以看出，class3样本集的外围数据明显处于游离状态，其结合紧密程度远不如核心区域，采用 $\lambda $ -背景基，可以缩小区域范围，使其决策的可信度更高。

通过试错实验方法，最后得到当 $\lambda $ =0.7时背景基能刚好包含核心数据。图11为class 3数据集的背景基B和 $\lambda $ -背景基 ${{{B}}_\lambda }$ 的示意图，此时 $0 < \lambda < 1$ ， ${{{B}}_\lambda } \subset {{B}}$ 。通过调节 $\lambda $ 参数，改变由基点限定的区域，这有利于抓取数据集核心特征。该方法除了分类应用以外，也可为决策者提供决策依据。

4.3 总结

BPC算法的特点如下：

1)上述实验只是针对二维、三维数据进行的，实际上，BPC算法可以扩展到n维数据集上，且时间复杂度随着维度增加呈线性增长，避免了高维数据基点冗余的现象。

2) BPC算法具有智能的生长机制。由于BPC算法可以发现新类别，新类别可以衍生新概念。从机制主义人工智能理论出发，机器能产生新概念则具有自我学习和扩展学习的能力。据此可得，BPC算法是具有一定智能生长机制的。

3) BPC算法使用 $\lambda $ -背景基使得预测或决策更灵活。分类器重复训练模型的代价很大，为了减小代价、充分利用已训练模型， $\lambda $ -背景基可以在原训练模型基础上，根据需要扩大或缩小预测区域，这种处理可以减少重复训练的代价，同时可以继承原有知识。

4) BPC算法原理完全由智能数学描述，其算法和原理较传统数学更加简单高效。

5) BPC算法得到的模型不是“黑箱”，而是具有可解释的、符合人类逻辑思维的“白箱”。理论上，该模型是决策者思维的同构映射。

5 结束语

本文从因素空间的背景基理论出发，首先改进了背景基提取算法，简化了计算步骤，降低了时间复杂度，从整体上提高了算法效率。其次，构造了基点分类算法，并通过2个实验展示了该算法在线性可分数据集的独特优势。下一步工作将研究非线性数据集处理、非凸数据集类别处理和精准识别新类别等。主要工作思路有：1)对于线性不可分数据集，采用分块链式策略。将数据按照一定规则划分成块状，然后用子背景基进行包络，最终链式连接多个子背景基；2)对于非凸数据集类别，可以采用因素映射方法，即通过分析因素值变化的单调性进行相应的映射变换。