在数据分类的研究中，普遍存在类别分布不平衡^[1]的问题，即某一类别的样本数量远远多于另一类(分别称为多数类和少数类)，具有这样特征的数据集视为不平衡。传统的分类算法，如支持向量机(SVM)在处理不平衡数据时，分类超平面往往会向少数类偏移，导致对少数类的识别率降低，而随机森林(random forest，RF^[2])分类时易出现分类不佳、泛化误差变大等问题。针对支持向量机在训练样本点过程中存在的噪声和野点问题，不少研究学者提出了相应的改进算法。如台湾学者Lin等^[3]提出模糊支持向量机(fuzzy support vector machines，FSVM)，根据不同数据样本对分类的贡献不同，赋予不同的隶属度，将噪声和野点与有效样本区分开，然而实际数据集中除了存在噪声和野点，不同类别的样本个数差异也会影响算法的分类精度。目前对不平衡数据分类的研究主要集中在算法层面和数据层面的改进，如通过对不平衡数据集进行欠采样(under-sampling^[4])、过采样(SMOTE^[5])、不同惩罚因子的方法(different error costs，DEC^[6])和集成学习方法^[7]等，这些方法在处理不平衡数据时一定程度上提高了少数类的分类精度，然而欠采样在删除样本点时易造成重要信息的丢失，过采样又会带来信息的冗余，并增大算法时间复杂度，代价敏感学习算法虽然定义了正负类不同的惩罚因子，但却没有考虑到样本点的实际分布情况，这些问题又会直接影响算法的分类效果。传统的分类方法在构建分类模型时仅考虑了数据样本点的物理特征(如距离、相似度等)，并没有更深层次地挖掘数据点之间的关联特征，但实际应用中的数据集样本之间并不是孤立存在的，它们之间除了位置上的差异，关联信息也是不可忽略的。

Silva等^[8-9]将仅考虑样本点物理特征的传统分类方法视为低层次分类，把数据样本点看作网络节点，提出了基于网络信息特征的高层次数据分类方法，在训练样本点分类模型时既考虑了样本点的位置关系，又考虑到了数据点之间的拓扑特征，将两个层次的分类器有效地结合，并在数字图像识别中取得较高的准确度。Carnerio等^[10]提出了基于复杂网络的新型分类器，通过KNN法或KAOG^[11]法建立子网络模型，利用谷歌PageRank度量方法赋予网络节点不同影响力概念，依据Spatio structural effi-ciency和节点间的距离特征实现分类。文献[12]针对复杂网络中的链路预测问题介绍了多种基于局部和全局结构的节点相似度模型，分析出实际复杂系统中网络节点的相互影响关系，两个节点之间产生连边的概率大小是由网络拓扑结构和几何结构共同决定的。文献[13]中把链路预测问题视为一个二分类问题，提出了一个数据分类问题的概率模型，将待测样本点的类别归属于相似度分数高的类。

鉴于高层次数据分类方法在无偏数据集上的优越性，本文从数据样本点的物理特征和拓扑特征方向出发，综合考虑数据点之间的位置关系和关联信息，提出基于网络拓扑特征的不平衡数据分类方法(imbalanced data classification of network tolopogy characteristics，NT-IDC)。首先利用KNN法建立与每类数据点对应的网络结构，将数据样本实例对应网络中的节点，使具有相同类别的网络节点之间产生连边，并依据其连接特性计算出每个节点的局部效率作为拓扑信息，应用基于距离倒数的相似度作为两个节点产生连边概率的物理特征，将拓扑特征与样本点的物理特征一起作为判别测试点类别归属的依据，为了克服由不同类别的数据样本点个数差异带来的影响，构建了一种引入不平衡因子 $c$ 的新型概率模型。本文所建立的基于数据点物理特征和拓扑特征的分类模型更加符合实际数据集样本点的分布情况，实验验证了本文所提方法具有可行性和有效性，与传统的分类器模型有着一定的区别。

1 相关概念

基于网络拓扑特征的不平衡数据分类算法包括两个阶段：网络的构建和测试点的类别预测。利用较为常见的KNN法对训练数据集 $X = \{ {x_1}, {x_2}, \cdot \cdot \cdot , {x_N}\} $ 中的每一个样本点，从其前 $k$ 个最近的邻居节点中找到标签信息相同的节点并在两点之间建立一条有向边，每个数据样本点 $ {x_{ i}} (i = 1 , 2 , \cdot \cdot \cdot ,N)$ 与网络中的节点 $ {v_{ i}} (i = 1 , 2, \cdot \cdot \cdot , N )$ 对应，且节点 $ {v_{ i}} $ 与样本点 $ {x_{ i}} $ 具有相同的标签类型，建立网络邻接矩阵A，这样就将整个数据集映射成带有节点标签信息的网络 $G(V,E,L)$ ， $V$ 是节点集合，E是边的集合，L = $ \{ {l_1}, {l_2}, \cdot \cdot \cdot , {l_m}\} $ 是标签集合。在预测阶段，利用文中构建的分类模型去判断测试数据样本点Y = $ \{ {x_{N + 1}},{x_{N + 2}}, \cdot \cdot \cdot , x{}_{N + m}\} $ 的标签类型，对于已经判断过标签类型的测试节点，选择直接丢弃的策略，不再归合到由训练点所建立的子网络结构中，图1为本文实现数据分类的几个步骤的图解，假设建立网络中 $k = 3$ ，最终将测试点归为整体性测度大的类别。

1.1 节点局部效率

复杂网络由图论逐渐发展而来，基于图论的网络结构模型在表达数据之间的关系时具有明显的优势^[14-16]，本文所提出的方法在计算网络节点局部效率时正是建立在图论的基础上。网络中的节点可以既是起点又是尾点，因此由数据样本点的连接关系所建立的图是有向的，为了更多地挖掘网络中的数据点之间的拓扑关系，在数据样本点训练阶段，充分考虑每个节点的连接特性，赋予节点不同的效率，使节点之间具有差异性，本文计算网络节点的局部效率公式^[17]为

${p_i} = \left\{ {\begin{array}{l} {\delta ,}\quad{{D_{ i}} = 0} \\ {\frac{1}{{{D_{ i}}}}\sum\limits_{{e_{ ij}}} {{d_{ ij}},} }\quad{{D_{ i}} > 0} \end{array}} \right.$

(1)

式中： ${p_i}$ 为节点 $ {v_{ i}} $ 的局部效率； ${D_i}$ 为以节点 $ {v_{ i}} $ 为起点的有向边的个数； $ {e_{ i j}} $ 表示以节点 $ i$ 为起点， $ j $ 为尾点的边； $ {d_{ i j}} $ 是节点 $ i$ 与 $ j $ 间的距离； $\delta $ 是一个很小的正数，利用数据样本点建立的网络分类器可有效地减弱噪声和野点的影响，当节点是噪声点或野点时，其局部效率为 $\delta $ ，可忽略不计。

1.2 基于相似度的类别归属

将数据样本点映射成网络节点，则待测样本点的类别归属与网络中的每个节点都有关系，一般来说，距离越近的两个节点属于同类的可能性就越大。

基于这种思想，本文用距离倒数表示网络节点之间的物理特征，则节点 $ {v_{ i}} $ 和 $ {v_{ j}} $ 之间的相似度可表示为

${S_{i,j}} = \frac{1}{{D(i ,j)}}$

式中 $D(i ,j)$ 代表节点 $ {v_{ i}} $ 和 $ {v_{ j}} $ 之间的欧式距离。

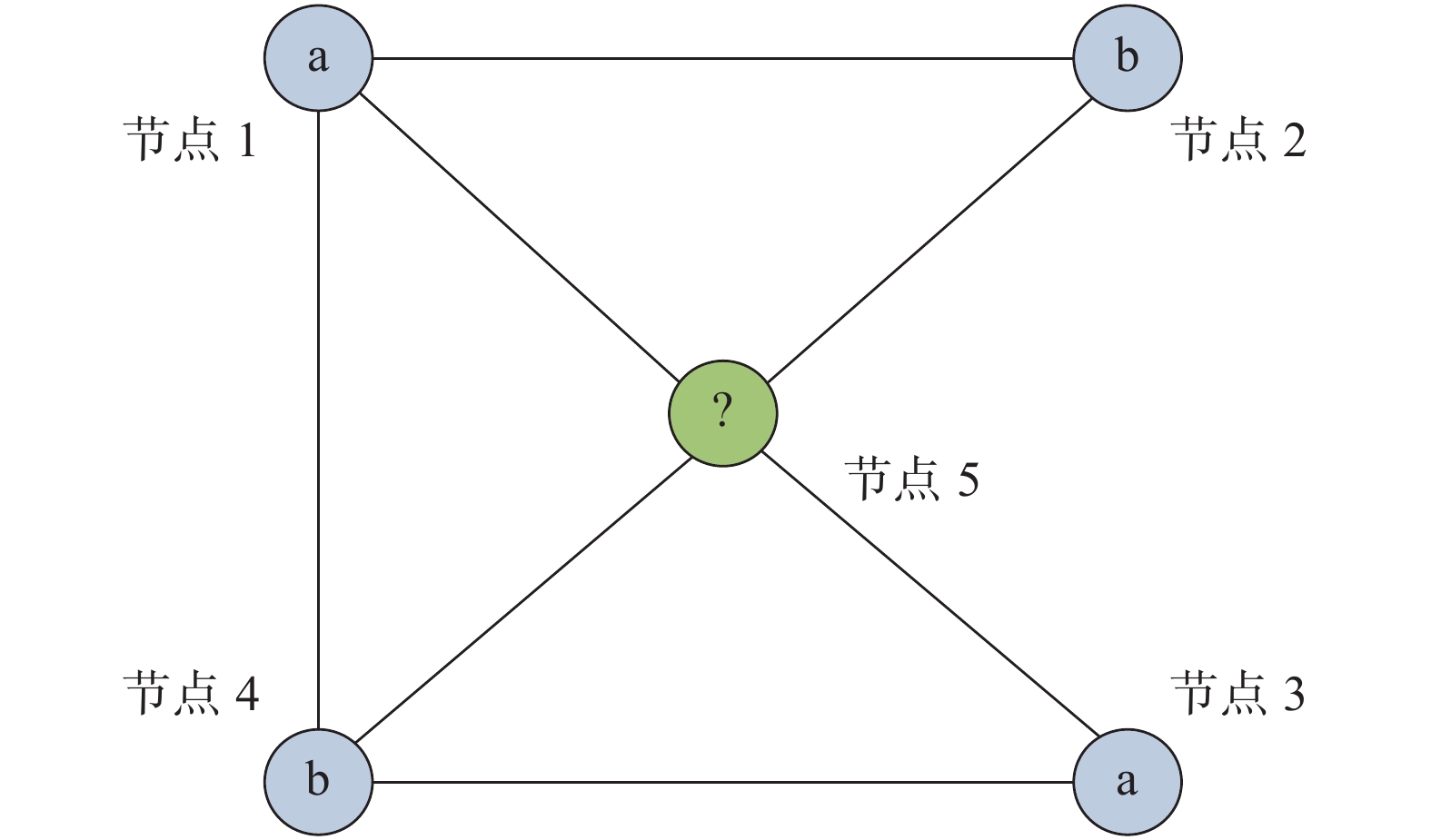
任给一个网络，未知标签信息的节点类别用0表示，对网络中任意一对节点 $ u $ 和 $ v $ ，存在相应的距离相似度 $ {S_{u,v}}$ ，则无标签节点 $ u $ 属于 $ {l_i}$ 的概率为

$p({l_i}\left| u \right.) = \frac{{\sum\limits_{\{ v\left| {v \ne u} \right.,{\rm{Index}}(v) = {l_i}\} } \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{S_{u,v}}} }}{{\sum\limits_{\{ v\left| {v \ne u} \right.,{\rm{Index}}(v) \ne 0\} } \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{{S_{u,v}}} }}$

式中： $ {l_i} \in L$ ；节点 $ u $ 的预测标签类别是由最大的 $ p ( {l_i} \left| { u} \right. ) $ 决定，如果最大值不止一个，随机选择其中一个。其解释性过程如图2所示，节点5处于由节点1、2、3、4所围成的正方形的中心，且节点1、3属于a类，节点2、4属于b类，计算未知标签节点与其余节点之间的距离，满足关系 ${S_{1,5}} + {S_{3,5}} =$ $ {S_{2,5}} + {S_{4,5}}$ ，故节点5属于a类和b类的概率相等，此时随机选择所属类别。

2 不平衡数据分类

本文算法是从网络节点的连接特性中提取出拓扑特征与数据样本点的距离相似度，并一起用于实现数据分类。具体地，在引入不平衡因子的条件下，将子网络中每个节点的局部效率与节点间的欧式距离结合起来，根据测试样本点与每个子网络的整体性测度来确定类别归属。

2.1 相似性测度

文献[10]中是将子网络效率与待测节点之间的物理特征结合在一起，考虑到网络中摇摆节点的存在，仅仅利用平均功率无法有效地分辨出对分类结果影响较小的节点，为了更好地区别单个节点对测试点分类结果的影响，本文将每个节点的局部效率分别与物理特征结合到一起，可以对影响较小的样本点有较好的识别，其表达式为

${\varepsilon _{t n}} = \sum\limits_i {\frac{{{p_{ i}}}}{{{S_{ t,i}}}}} $

(2)

式中： ${p_i}$ 为网络中每个节点的局部效率； $i $ 是子网络 $n$ 中的节点； ${\varepsilon _{t n}}$ 为每个测试点 $t$ 与子网络 $n$ 的相似性测度； ${p_i} > {S_{t ,i}}$ 时说明该测试点更符合节点 $i$ 所在的子网络结构模式。

2.2 整体性测度

传统的有监督和无监督的分类器构建多是以数据样本点的物理特征作为判别依据，但实际数据集中的数据点并不是孤立存在的，正如链路预测问题中一个节点的两个邻居节点之间是否建立连边除了受共同邻居个数的影响外，还与共同邻居的性质，如度、聚类系数和介数中心性等有关。把每个节点看成独立或同等分布是有缺陷的，不符合实际数据集的样本点之间的关系，利用整体性测度大小去判断待测样本点的类别归属，正是将数据点的物理特征和关联特征结合在一起的体现，对于测试样本点 $t$ ，整体性测度定义为

${\varphi _{t n}} = \frac{{{\varepsilon _{t n}} + c}}{{\sum\limits_{n = 1}^m {{\varepsilon _{t n}} + {\rho _{ n}} \cdot c} }}$

(3)

式中： $n$ 为任一子网络； $m$ 为整个网络中的子网络个数； ${\varphi _{tn}}$ 为测试点 $t$ 与子网络 $n$ 的整体性测度； ${\rho _n}$ 为训练样本集中每类的训练样本数； $c$ 为不平衡调节因子，用来降低由不同类别的样本个数差异对分类结果造成的影响，对于不同的数据集 $c$ 的取值一般不同， $c$ 值的大小可根据不同类别的样本个数确定，也可以通过网格搜索结合交叉验证的方法确定。最后根据待测节点 $t$ 与每个子网络的整体性测度大小来确定标签信息，测度越高，节点属于该类的可能性就越大，即判定节点属于此类别。

2.3 算法步骤和时间复杂度

算法　网络拓扑特征的不平衡数据分类

输入　训练集 $X = \{ ({x_1},{C_1}) ,({x_2},{C_2}) , \cdot \cdot \cdot , (x{}_N,{C_N})\} $ ，其中 $N$ 是训练样本个数，每个数据样本点 ${x_i} = \{ {a_1} , {a_2}, \cdot \cdot \cdot ,{a_d}\} $ 都是一个 $d$ 维特征向量， ${C_i} \in L$ 表示第 $i$ 个样本的标签；测试集 ${{Y}} = \{ {{{x}}_{N + 1}}, {{{x}}_{N + 2}}, \cdot \cdot \cdot , $ ${ x}{}_{N + m}\} $ ；KNN中的参数 $k$ ；不平衡因子 $c$ 。

输出　测试集标签 $\{ {C_{N + 1}}, {C_{N + 2}}, \cdot \cdot \cdot , {C_{N + m}}\} $ 。

1) 构建网络；

2) 根据式(1)计算网络节点局部效率；

3) 根据式(2)计算待测节点与每个子网络的相似性测度；

4) 根据式(3)计算待测节点与每个子网络的整体性测度；

5) 依据整体性测度的大小预测待测样本点的标签。

对于本文所提算法的时间复杂度分析：假设用于建立网络的样本点个数为 $N$ ，邻居节点数为 $k$ ，且满足 $k \ll N$ ，以每个节点为起点的最大有向边数为 $k$ ，故整个网络中的有向边最多为 $kN$ 条；1)构建网络时需要计算任意一对节点之间的距离，耗时较长，计算量为 $ O({N^2} + kN)$ ；2)在计算节点局部效率时需要计算节点的度，其时间复杂度为 $ O(N)$ ；3)中计算待测点与每个子网络的相似性测度，已知网络节点个数为 $N$ ，故这一阶段时间复杂度为 $ O(N)$ ；4)中最坏的情况是整个网络节点的类别数较多，其计算量不大于 $ O(N)$ ；5)中依据测试样本点与哪类子网络的整体性测度大，就确定该节点的类别，这步完成需要时间量为 $O(1)$ 。通过上面的分析，把算法步骤各个阶段的时间复杂度整合到一起，得出本文方法时间复杂度为 $ { O}({N^2} + kN + N + N + N + 1)$ ，取最高阶，时间复杂度为 $ { O}({N^2})$ ，这与SVM的时间复杂度^[18] ${ O}(N) \sim { O}({N^{2.3}})$ 仍具有可比性。

3 实验结果及分析 3.1 评价指标

传统的分类方法多采用正确率(测试样本点中正确分类的个数占总的个数的比例)作为评价指标，其对应的混淆矩阵可用来表示实际分类情况，见表1所示。表1中，TP+FN=N ⁺，FP+TN=N ⁻，N ⁺为测试样本正类数，N ⁻为测试样本负类数。

然而，对于非平衡数据集则采用不平衡分类中的敏感性Se和特异性Sp作为性能评价的两个辅助指标，几何平均值Gm和F-value作为综合性指标，它们在一定程度上可用来衡量算法的优劣，其定义为

$\rm{Se} = {\rm{TP}}/({\rm{TP}} + {\rm{FN}})$

(4)

$\rm{Sp} = {\rm{TN}}/({\rm{FP}} + {\rm{TN}})$

(5)

$\rm{Gm} = \sqrt {{\rm{Se}} \times {\rm{Sp}}} $

(6)

式中：Se代表分类器在少数类样本上的预测能力；Sp代表分类器在多数类样本上的预测能力。Se和Sp的值越大表示分类效果越好，但现实不平衡数据中往往少数类样本携带更有价值的信息，所以在实际应用中更应该想着如何提高Se值。

F-value是查全率Rc和敏感性Se的平均值， $\beta $ 是一个相对重要性参数，在不平衡数据分类问题中一般设置为1，查全率定义为 $\rm{Rc} = {\rm{TP}}/({\rm{TP}} + {\rm{FP}})$ ，则指标F-value为

$\rm{F} - {\rm{value}} = \frac{{(1 + {\beta ^2}) \times {\rm{Rc}} \times {\rm{Se}}}}{{{\beta ^2} \times {\rm{Rc}} + {\rm{Se}}}}$

(7)

3.2 实验结果及分析

为了验证本文所提分类方法的有效性，首先用一个人造数据集给出证明，实验中得出的结果均是在MATLAB 2012a软件上运行得出的，台式计算机具体配置为：系统为64位的Windows10企业版，处理器为Intel(R) Core(TM) i7-6700CPU，内存大小8 GB。本文实验中非线性的核函数使用较为广泛的Gauss径向基(RBF)核函数。考虑到SVM在数据分类上是具有代表性的算法，本文用来对比的算法均使用SVM作为基分类器，Under-sampling中使用基于欧氏距离的欠采样方法^[19]，DEC中正负类样本的惩罚因子设置为样本个数不平衡比，SMOTE中最近邻个数设置 $k = 5$ ，通过网格搜索算法得到 $\lambda $ 和惩罚参数 $C$ ，所有对比算法中惩罚参数 $C$ 的候选集设定为 $\{ {2^0}, {2^1}, \cdot \cdot \cdot ,{2^{13}}\} $ ， $\lambda $ 的候选集设定为 $\{ 1 , 2, \cdot \cdot \cdot , $ $20\} $ ，均取最优时的数值参加计算。本文使用五折交叉验证的方法对数据集进行验证，每次迭代选择其中4组作为训练集，1组作为测试集，每组训练集和测试集中的正负类样本点数量差异均定义为不平衡比，把本文算法分类结果与SVM、FSVM、DEC、SMOTE和Under-sampling算法结果进行比较，每种算法在数据集上运行20次五折交叉验证取平均值，并将最大的Gm值和F-value值用黑体标出。

3.2.1 人造数据集

在二维空间中随机生成样本点不平衡比为1000:50的线性不可分数据集(见图3)，其样本点符合正态分布，多数类含有1 000个样本点，少数类含有50个样本点，采用基于网络拓扑特征的不平衡数据分类方法与其他经典算法相比较，表2给出了各算法在该数据集上的分类结果，从表中可以看出，本文所提方法对不平衡数据集具有良好的分类性能。

3.2.2 真实数据集

从UCI机器学习数据库选择了10组不平衡的数据集来进行实验。所用数据集样本点个数范围为214~5 000，样本点的属性维数范围为3~34，有的数据集可能有多种类别，本文仅考虑二分类问题，对于类别不是两类的就先把数据集都变为两类，把其中某类或某几类看作正类，剩下的所有类合并为负类，10个数据集的详细信息如表3所示。

为了验证算法在真实数据集上的有效性，表4和表5分别给出了不同算法在少数类和综合指标性能上的对比结果。在表4中，本文算法在少数类预测能力上效果较好，除Yeast和Ecoli外，其余数据集都优于对比算法。表5中，相比较SVM，其他算法在不平衡数据分类中的精度都有了一定的提高，当不平衡比率较大时，SVM的分类效果会变得较差，DEC算法虽然考虑了数据的不平衡性，但没能很好地考虑到样本点的分布情况，本文算法则较好地处理了这一问题，对样本点间有关联特征的数据集如Haberman、Ecoli、Glass、Imagesegment、wireless和contraceptive本文算法均取得了最优的分类结果。

对于数据集Haberman、Ecoli和waveform，本文算法的Gm值平均提高了2%左右，但是在数据集Yeast和Vowel上，由于节点之间的关联信息不明显，算法所能挖掘的网络信息受限，对部分测试点无法做出正确地判断，没有取得最好的效果，但与SVM、FSVM、DEC、SMOTE和Under-sampling分类方法所取得分类结果相差不大，表明NT-IDC算法仍有待改进。对于正负类样本不平衡比率大的数据集，因为本文算法提高了少数类分类性能，在Gm值一定的前提下，当FP值变大时，Rc值变小，使得Glass、Vowel和Yeast数据集上的F-value值有所波动，在处理样本点个数较多的数据集如waveform上正是因为考虑了数据点间的关联信息，所以才表现出一定的优越性。综上分析，本文所提算法在考虑到影响不平衡数据分类因素的条件下，表现出良好的分类性能，充分说明了将数据点之间关联特征作为数据分类性能影响因素的合理性。

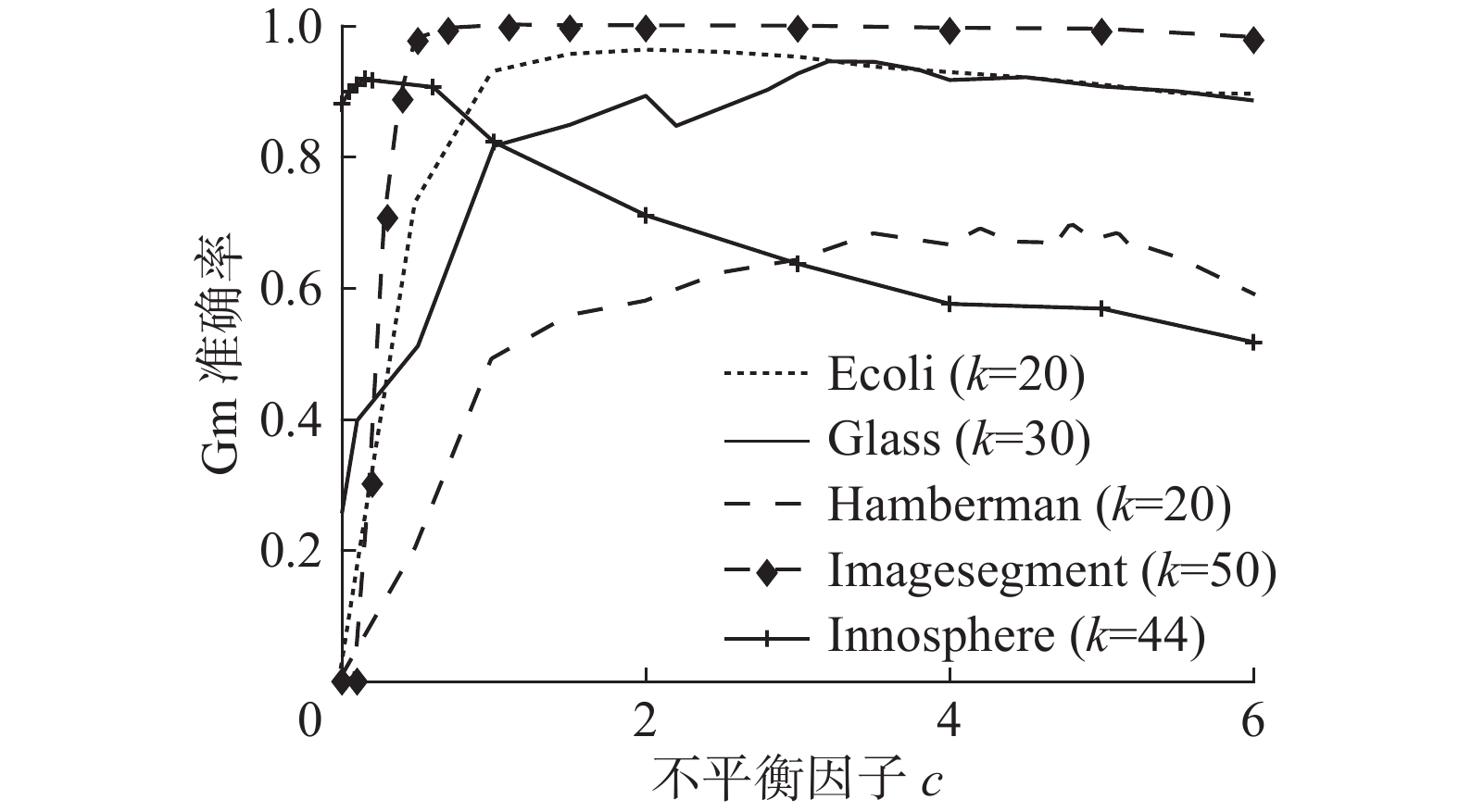
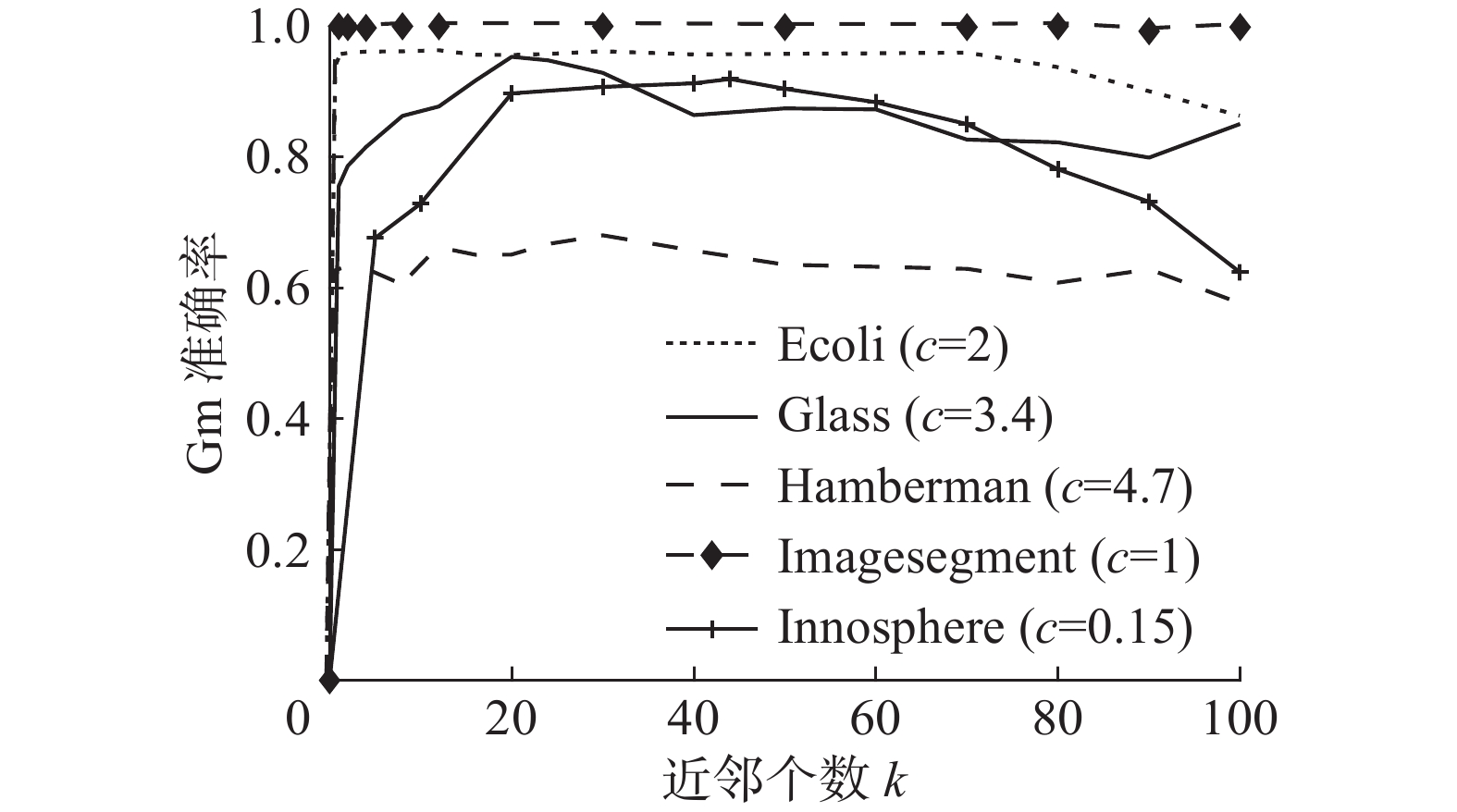
3.3 参数敏感性分析

为了更好地了解本文算法中参数对数据分类效果的影响，在实际数据集Haberman、Glass、Inno-sphere、Ecoli、和Imagesegment上分析不平衡因子 $c$ (见图4)和KNN中的参数 $k$ (见图5)对分类性能的影响。

从图4中观察到，不平衡因子 $c$ 对Gm影响较明显，对于数据集Imagesegment、Glass和Ecoli，当 $c$ 值大于2的时候，本文算法所取得的Gm值波动范围较小，但Innosphere数据集对 $c$ 值比较敏感，实验过程中较难根据经验确定 $c$ 的取值；相比 $c$ ，参数 $k$ 的取值对分类精度影响较小，当 $k$ 值从10增加到100时，除Innosphere外，其他数据集的Gm值并没有太大的波动，说明不平衡数据分类的问题中，正负类数据点样本个数的差异对分类性能有较大影响，需要采用合适的策略和方法来降低不平衡比。

4 结束语

本文针对不平衡数据分类问题，考虑到传统分类方法在实际数据集中存在的缺陷，提出一种更符合数据集样本点真实关系的数据分类方法，算法中除利用数据点的物理特征外，还充分挖掘了由这些数据点所建立的网络拓扑特征，实验结果表明基于网络结构去解决不平衡数据分类问题是一个可行的途径，除此之外，本文提出的算法仍能够应用于多分类问题。在未来的研究中，将探索如何更有效地挖掘隐藏在网络中的节点行为，找到更加符合数据样本点之间的拓扑特征，例如考虑除节点局部效率外的其他性质，不同的数据集 $c$ 值选取一般不固定，后续可以在参数的优化上做进一步的研究。