聚类技术作为机器学习领域中的一种无监督技术，在检测数据的内在结构和潜在知识方面发挥着重要的作用。在过去的几十年中，许多聚类方法得到了发展，如基于分区的方法(k-means)、基于模型的方法、基于密度的方法、层次聚类方法、模糊聚类方法(fuzzy c-means)和基于图的方法(spectral clustering)^[1]。由于谱聚类在处理非凸形结构的数据集方面的高效性，谱聚类在图像分割^[2-4]、社区检测^[5]、人脸识别^[6]等方面得到了广泛的研究和应用。

然而，传统的谱聚类算法在使用高斯核函数构造亲和矩阵时，需要先验信息来设置合适的参数以控制邻域的尺度；并且以距离来度量数据点之间的相似性，没有考虑到整体数据点的变化情况，对于高维数据来说，较难得到更高的聚类精度。近年来有很多学者对谱聚类算法进行了研究。赵晓晓等^[7]结合稀疏表示和约束传递，提出一种结合稀疏表示和约束传递的半监督谱聚类算法，进一步提高了聚类准确率。林大华等^[8]针对现有子空间聚类算法没有利用样本自表达和稀疏相似度矩阵，提出了一种新的稀疏样本自表达子空间聚类方法，所获得的相似度矩阵具有良好的子空间结构和鲁棒性。Chang等^[9]提出了一种通过嵌入标签传播来改进谱聚类的方法，通过密集的未标记数据区域传播标签。以上方法虽然一定程度上提高了谱聚类算法的聚类性能，但是，在大部分谱聚类算法中，高斯核函数中尺度参数 $\sigma $ 的选取往往都是通过人工选取，对聚类结果有一定的影响。NJW算法^[10]对预先给定几个尺度参数 $\sigma $ 进行谱聚类，最后从这几个聚类结果中选择具有最佳聚类结果的 $\sigma $ 作为尺度参数，该方法消除了尺度参数 $\sigma $ 选择的人为因素，但是也增加了计算时间。Ye等^[11]在有向KNN图中考虑了一种基于共享最近邻的鲁棒相似性度量，大大提高了谱聚类的聚类精度。Jia等^[12]提出了一种基于共享近邻的自校正p谱聚类算法，该算法利用共享最近邻来度量数据间的相似性，然后应用果蝇优化算法找到p-laplacian矩阵的最优参数p，从而更好地进行数据分类。王雅琳等^[13]提出一种基于密度调整的改进自适应谱聚类算法，通过样本点的近邻距离自适应得到尺度参数，使算法对尺度参数相对不敏感。

传统的谱聚类以及上述大部分改进的谱聚类算法都是单一的针对距离度量或者尺度参数进行调整，本文从一个新的角度出发，在公理化模糊集(AFS)理论的基础上，结合局部密度估计和共享近邻的定义，提出一种基于AFS理论的共享近邻自适应谱聚类算法——公理化模糊共享近邻自适应谱聚类算法。利用AFS理论提出了一种模糊相似性度量方法，并将其作为谱聚类算法输入的亲和矩阵。同时采用共享近邻的方法发现密集区域样本点分布的结构和密度信息，并且根据每个点所处领域的稠密程度自适应调节参数 $\sigma $ ，与高斯核距离测度相比，本文的解决方案对参数具有较强的鲁棒性，增强了对各种数据集的适应性，减少了噪声数据带来的不良影响。

1 相关算法理论 1.1 谱聚类算法

在谱聚类中，设 ${{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_n} \in {{\bf{R}}^d}$ 为 $n$ 个具有 $d$ 个特征的样本，数据集可用一个加权无向图来描述，该图由 $\left| V \right|$ 个顶点和 $\left| E \right|$ 个边组成。对于 ${{ v}_i} \in V$ ， ${{{v}}_i}$ 表示一个样本 ${{{x}}_i}$ ， ${{{e}}_{ij}}$ 表示 ${{{v}}_i}$ 和 ${{{v}}_j}$ 之间的权重。 ${{{e}}_{ij}}$ 通常是由 ${{{x}}_i}$ 和 ${{{x}}_j}$ 之间的相似性来度量的。通常引入高斯核函数来构造相似矩阵 ${{S}}$ ，其定义为

${{{S}}_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{{\rm{e}}^{ - \frac{{\left( {{{\left\| {{{ x}_i} - {{ x}_j}} \right\|}^2}} \right)}}{{2{\sigma ^2}}}}}, \quad i \ne j} \\ {0, \quad i = j} \end{array}} \right.$

(1)

作为一种简单而有效的聚类准则，归一化割(Ncut)在文献[14]中提出，其定义为

$ {\rm{Ncut}}\left(A,B \right) = \frac{{{{{y}}^{\rm{T}}}\left( {{{D}} - {{W}}} \right){{y}}}}{{{{{y}}^{\rm{T}}}{{Dy}}}} $

(2)

式中： ${{D}}$ 是对角矩阵； ${{y}}$ 是最优分割向量。谱聚类的一般过程为：

1)构造图 ${{G}}$ 的相似度矩阵 ${{S}}$ ,对于给定的 $\sigma $ ， ${{S}}$ 是由式(1)构造的；

2)计算对角矩阵 ${{D}}$ ，构造对角矩阵 ${{D}}$ ， ${{{D}}_{ii}} = \sum\limits_{1 \leqslant j \leqslant n} {{{{S}}_{ij}}} $ ；

3)计算归一化拉普拉斯矩阵，拉普拉斯矩阵 L 为 ${{L}} = {{D}} -{{S}} $ ，L被归一化为

${{L}} = {{{D}}^{{{ - 1} / 2}}}{{L}}{{{D}}^{{{ - 1} / 2}}} = {{I}} - {{{D}}^{{{ - 1} / 2}}}{{S}}{{{D}}^{{{ - 1} / 2}}};$

4)对 ${{L}}$ 进行特征分解，得到前 $k$ 个特征向量，并构建特征向量空间；

5)利用经典的聚类算法如k-means对特征向量空间中的特征向量进行聚类。

1.2 AFS理论

AFS理论是刘晓东^[15-18]在1998年提出的一种基于AFS代数和AFS结构的模糊理论，AFS理论放弃使用距离度量来计算数据之间的相似性关系，而是将观测数据转化为模糊隶属函数，并实现其逻辑运算。然后，可以从AFS空间而不是原始特征空间中提取信息。在AFS空间中利用模糊关系来构建数据之间的相似性度量。采用模糊隶属度来表示数据之间的距离关系，增强了在处理现实数据中对各种数据集的适应性，为处理离群点提供了有效方法。

在文献[15]中，根据EI代数的定义，对于任意概念集合 $A \subseteq M$ ， $\mathop \Pi\limits_{m \in A} m $ 表示A中模糊概念的集合，为了更好地提取数据结构，清楚地说明可将AFS理论结合以下场景：

设 $X = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_6}} \right\}$ 是6个人的样本集合及其特征(属性)，由真实数字(年龄、身高、体重)、布尔值(性别)、额定值(黑色素)和顺序关系(发黑、发白)描述； $M = \left\{ {{m_1},{m_2}, \cdot \cdot \cdot ,{m_6}} \right\}$ 是样本 $X$ 上的模糊概念集。 $M$ 中的每一个元素都被看作描述事物的简单概念，它们相应的语言标签被定义为： ${m_1}$ (老年人)、 ${m_2}$ (高的人)、 ${m_3}$ (重的人)、 ${m_4}$ (头发黑色素更多的)、 ${m_5}$ (男性)、 ${m_6}$ (女性)。则 ${A_1} = \left\{ {{m_1},{m_6}} \right\} \subseteq $ M， $\mathop \Pi\limits_{m \in {A_1}} {m = {m_1}{m_6}} $ 是一个新的复杂概念“老年女人”； ${A_2} = \left\{ {{m_1},{m_3}} \right\} \subseteq M$ ， $\mathop \Pi\limits_{m \in {A_2}} {m = {m_1}{m_3}} $ 表示“重的老年人”； ${A_3} = \left\{ {{m_3}} \right\} \subseteq M$ ， $\mathop \Pi\limits_{m \in {A_3}} {m = {m_3}} $ 表示“高的人”。对于 $\gamma = {m_1}{m_6} + {m_1}{m_3} + {m_2}$ ，它的概念为“老年女人”或者“重的老年人”或者“高的人”，是一个复杂概念的集合。一个新的模糊集可以被写成:

$\sum\limits_{i = 1}^3 {\left( {\mathop \Pi \limits_{m \in {A_i}} m} \right)} = \mathop \Pi \limits_{m \in {A_1}} m + \mathop \Pi \limits_{m \in {A_2}} m + \mathop \Pi \limits_{m \in {A_3}} m$

(3)

这些基于简单概念的EI代数运算生成的概念被认为复杂的概念。

因此，概念的逻辑表达可以用 $\sum\limits_{i \in I} {\left( {\mathop \Pi\limits_{m \in {A_i}} m } \right)} $ 表示 $\left( {{A_i} \subseteq M,i \in I} \right)$ 。若 $m$ 是非空集，集合 $E$ 定义为

$ E = \left\{ {\sum\limits_{i \in I} {\left( {\mathop \Pi\limits_{m \in {A_i}} m } \right)\Big| {{A_i} \subseteq M,i \in I} } } \right\} $

(4)

式中 $I$ 为非空索引集。

其中，每个模糊集可以被唯一地分解：

$\xi = \sum\limits_{i \in I} {\left( {\mathop \Pi\limits_{m \in {A_i}} m } \right)} $

(5)

式中 ${A_i}$ 是M 的子集。

2 所提算法 2.1 在模糊空间建立距离度量

本文提出的亲和矩阵构造方法是建立在AFS理论基础上的，该过程允许我们在发现的判别模糊子空间中表示不同模糊项的样本。这些子空间由模糊隶属函数选择，消除了不明显或噪声特征。因此，它们被认为能够改善内部相似和减少相互相似。此外，利用AFS中定义的模糊隶属度和逻辑运算，放宽了欧氏假设对数据距离推断的影响。更具体地说，本文使用一个样本的隶属度属于另一个样本的描述，用模糊集表示为距离度量。在最初的AFS聚类^[19-21]基础上，在AFS空间上构建相似性度量。

首先建立隶属度函数，需要定义以下有序关系：设X是一个样本集合，M是X上的一组模糊集合。对于任意 ${A_i} \subseteq M$ ， $x \in X$ ，可以写成：

${A_i} \geqslant \left( x \right) = \left\{ {y \in X\left| {x{{\geqslant }_m}y,\,{\rm{for}}\,\,\forall m \in {A_i}} \right.} \right\} \subseteq X$

(6)

式中： $m \in M$ ；“ $x \geqslant_my$ ”表示 $m$ 代表 $x$ 的模糊关系大于或等于 $m$ 代表 $y$ 的模糊关系； ${A_i} \geqslant \left( x \right)$ 是 $x$ 中所有模糊关系小于或等于 $\mathop \Pi\limits_{m \in {A_i}} m $ 的 $x$ 样本中的元素的集合。 ${A_i} \geqslant \left( x \right)$ 是由 ${A_i}$ 模糊集的语义和观测数据集的概率分布决定的。

对于模糊集合 $\xi \in E$ ， ${\mu _\xi }:X \to \left[ {0,1} \right]$ 。根据文献[17]， $\left\{ {{\mu _\xi }\left( x \right)\left| {\xi \in E} \right.} \right\}$ 是AFS模糊逻辑系统 $\left( {E, \vee , \wedge } \right)$ 的一组相关隶属度函数，则满足条件：

1)对于 $\alpha ,\beta \in E$ ，如果 $\alpha \leqslant \beta $ 在系统 $\left( {E, \vee , \wedge } \right)$ 内，并且对于任意 $x \in X$ ， ${\mu _\alpha }\left( x \right) \leqslant {\mu _\beta }\left( x \right)$ 都成立；

2)对于 $x \in X$ ， $\eta = \sum\limits_{i \in I} {\left( {\mathop \Pi\limits_{m \in {A_i}} m } \right)} \in E$ ，如果对于任意 $i \in I$ ， ${A_i} \geqslant \left( x \right) = \varnothing$ ，则 ${\mu _\eta }\left( x \right) = 0$ ；

3)对于 $x,y \in X$ ， ${A_i} \subseteq M$ ， $\eta = \mathop \Pi\limits_{m \in {A_i}} m \in E$ ，如果 ${A_i} \geqslant \left( x \right) \subseteq {A_i} \geqslant \left( x \right)$ ，则 ${\mu _\eta }\left( x \right) \leqslant {\mu _\eta }\left( y \right)$ ；如果 ${A_i} \geqslant \left( x \right) = X$ ，则 ${\mu _\eta }\left( x \right) = 1$ 。

确定相关性隶属函数首先要确定 $X$ 上的测度。下面给出了实现该测度的具体内容。设 $\gamma $ 是关于 $X$ 的一个模糊项。文献[17]中 ${A_i}$ 的权重函数被定义为：

设 ${\rho _\gamma }:X \to {R^ + } = \left[ {0,\infty } \right),$ 如果 ${\rho _\gamma }$ 满足条件：

1) ${\rho _\gamma }\left( x \right) = 0 \Leftrightarrow x{ <_m}x,x \in X;$

2) ${\rho _\gamma }\left( x \right) \geqslant {\rho _\gamma }\left( y \right) \Leftrightarrow x{ \geqslant _m}y,x,y \in X$ 。

则称 ${\rho _\gamma }$ 为模糊项 $\gamma $ 的权重函数。

设 $\left( {\varOmega ,f,P} \right)$ 是一个概率测度空间， $M$ 是 $X$ 上的一组模糊集合， ${\rho _\gamma }$ 是模糊项 $\gamma \in M$ 的权重函数， $X \subseteq \varOmega $ 是概率空间 $\left( {\varOmega ,f,P} \right)$ 上的一个有限观测样本集。如果对于任意的 $m \in M$ ， $x \in \varOmega $ ； $m \geqslant \left( x \right) \in f$ ，则 $\left\{ {{\mu _\xi }\left( x \right)\left| {\xi \in E} \right.} \right\}$ 是 $\left( {E, \vee , \wedge } \right)$ 的一组相关隶属度函数，条件是每个模糊集 $\xi = \sum\limits_{i \in I} {\left( {\mathop \Pi\limits_{\gamma \in {A_i}} m } \right)} \in E$ 的隶属函数被定义为

$ {\mu _\xi }\left( x \right) = \mathop {\sup }\limits_{i \in I} \mathop {\inf }\limits_{\gamma \in {A_i}} \frac{{\sum\limits_{u \in \left( {{A_i}{ \geqslant} \left( x \right)} \right)} {{\rho _\gamma }\left( u \right)} }}{{\sum\limits_{u \in X} {{\rho _\gamma }\left( u \right)} }},\quad \forall x \in X $

(7)

$ {\mu _\xi }\left( x \right) = \mathop {\sup }\limits_{i \in I} \mathop {\inf }\limits_{\gamma \in {A_i}} \frac{{\int_{{A_i}\underline { > \left( x \right)} } {{\rho _\gamma }\left( t \right){\rm{d}}{P_t}} }}{{\sum\limits_\varOmega {{\rho _\gamma }\left( t \right){\rm{d}}{P_t}} }},\quad \forall x \in \varOmega $

(8)

如果对于每个 $\gamma \in M$ ， ${\rho _\gamma }\left( x \right)$ 在 $\varOmega $ 上是连续的且 $\left| X \right|$ 是从概率空间 $\left( {\varOmega ,f,P} \right)$ 中随机抽取的一组样本集，则式(7)所定义的隶属函数等于式(8)所定义的隶属函数。

根据以上可知，在 E 中模糊概念的隶属函数可以由 ${\rho _\gamma }\left( x \right)$ 和 ${A_i} \geqslant \left( x \right)$ 来确定，这既考虑了模糊性又考虑了随机性。根据文献[17]，对于任意模糊概念 $\xi = \sum\limits_{i \in I} {\left( {\mathop \Pi\limits_{\gamma \in {A_i}} m } \right)} \in E$ ，对于任意 $x \in X$ ， $\xi $ 的隶属函数被定义为

$ {\mu _\xi }\left( x \right) = \mathop {\sup }\limits_{i \in I} \left\{ {\frac{{\left| {{A_i} \geqslant \left( x \right)} \right|}}{{\left| X \right|}}} \right\} $

(9)

$ {\mu _\xi }\left( x \right)\mathop { = \sup }\limits_{i \in I} \left\{ {\frac{{\left| {y \in X\left| {x{{ \geqslant }_{{\rho _m}}}y,\forall m \in {A_i}} \right.} \right|}}{{\left| X \right|}}} \right\} $

(10)

式中 $\;{\rho _m}$ 是一个权重函数。

接着设样本集为 $X = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_n}} \right\} \subseteq {\rm{R}}$ ， $X$ 上的一个特征集合 $F = \left\{ {{f_1},{f_2}, \cdot \cdot \cdot ,{f_l}} \right\}$ ， $M = \{ {{m_{i,j}}\left| {1 \leqslant i \leqslant l,}\right. 1 \leqslant}$ $ j \leqslant {k_i} \} $ 表示一组相对于特征 ${f_i}$ 的选择的 ${k_i}$ 个模糊概念的集合， ${m_{i,1}},{m_{i,2}}, \cdot \cdot \cdot ,{m_{i,{k_i}}}$ 是其中与特征 ${f_i}$ 相对应的一组简单模糊概念。在新的测度空间中，对于每一个样本 $x$ ，发现一个显著的模糊子集 ${\zeta _x} =\mathop \Pi\limits_{m \in M} m $ ，以便 ${\zeta _x}$ 有效地表示 $x$ ，而不是整个模糊集。这里，如果 ${x_k}$ 属于 ${m_{i,j}}$ 的隶属度大于某一阈值，则模糊隶属函数用作特征的度量， ${m_{i,j}}$ 足够好地将 ${x_k}$ 与其他值区分开。在这里定义：

$ B_x^\varepsilon = \left\{ {m \in M\left| {{\mu _m}\left( x \right) \geqslant \max \left\{ {{\mu _m}\left( x \right)} \right\} - \varepsilon } \right.} \right\} $

(11)

式中： $\varepsilon $ 表示误差阈值^[20]，在这里设 $\varepsilon = 0.3$ ，通过设定误差阈值避免了使用模糊隶属函数的不明显特征，使样本的表示方法能够更好地表达数据中的底层语义结构，排除了噪声对数据样本特征的干扰，若对误差阈值运用自适应策略，将明显增加算法的计算复杂度。考虑本文算法的总体性能表现，实验中参考文献[20]中的经验数值进行设定。 $B_x^\varepsilon $ 表示关于数据样本 $x$ 的全部的模糊项的集合。然后将 ${\zeta _x}$ 描述为

$ {\zeta _x} = \mathop \wedge \limits_{m \in B_x^\varepsilon } m $

(12)

式中 $ \wedge $ 是AFS代数中的模糊隶属关系运算。通过这样表示，所有理想的模糊项都结合在一起作为样本表示。然后，通过AFS代数和AFS理论中的模糊运算，结合模糊隶属度的关系，通过逻辑运算的数据距离推理，将模糊集表示的另一个描述样本的隶属度用作距离度量。根据AFS聚类^[19-21]，对于两个数据样本 ${X_i}$ 和 ${X_j}$ ，它们之间的距离定义为：

$ {D_{ij}} = 1 - \min \left\{ {{{\bar \mu }_{{\zeta _{{X_i}}}}}\left( {{X_i}} \right),{{\bar \mu }_{{\zeta _{{X_j}}}}}\left( {{X_j}} \right)} \right\} $

(13)

$ {\bar \mu _{{\zeta _{{X_i}}}}}\left( {{X_j}} \right) = \left\{ {{m_k} \in {\zeta _{{X_i}}}\left| {\frac{{\sum\limits_{k = 1}^N {{\mu _{{m_k}}}\left( {{X_j}} \right)} }}{N}} \right.} \right\} $

(14)

式中： ${\mu _{{m_k}}}\left( {{X_j}} \right)$ 表示数据样本模糊项 ${m_k}$ 的 ${X_j}$ 的模糊隶属度； ${m_k}$ 表示模糊项集合 ${\zeta _{{X_i}}}$ 中的每个模糊项； ${\bar \mu _{{\zeta _{{X_i}}}}}\left( {{X_j}} \right)$ 表示模糊项集合 ${\zeta _{{X_i}}}$ 的数据样本 ${X_j}$ 的平均隶属度。

在AFS理论的基础上，为了更好地提取数据结构，在AFS空间中建立了距离测量，公式为

$A\left( {{x_i},{x_j}} \right) = \exp \left( { - \frac{{{D_{ij}}^2}}{{2{\sigma ^2}}}} \right)$

(15)

式中 ${D_{ij}}$ 为式(13)所示基于公理化模糊集理论的距离定义。

2.2 所提算法

在2.1小节中虽然利用AFS理论在谱聚类算法中构建了新的距离度量，即 $A\left( {{x_i},{x_j}} \right) = \exp \left( { - {{{D_{ij}}^2} /{2{\sigma ^2}}}} \right)$ ,但是高斯核函数中 $\sigma $ 是一个人工指定的参数，为每个数据集指定一个合适的参数 $\sigma $ 是一件很复杂的事，需要花费大量的时间和精力。本文将数据点的领域信息加入相似度的计算中，并结合共享近邻的思想，在AFS理论距离测量的基础上定义了一个能够自适应得到尺度参数 $\sigma $ 的高斯核函数——基于AFS理论的共享近邻自适应高斯核函数，其定义为

$ A\left( {{x_i},{x_j}} \right) = \left\{\!\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {\exp \left( { - \dfrac{{{D_{ij}}^2}}{{{\sigma _i}{\sigma _j}\left( {\operatorname{SNN} \left( {{x_i},{x_j}} \right) + 1} \right)}}} \right),}&{i \ne j} \\ {0,}\quad{i = j} \end{array}} \end{array}} \right. $

(16)

式中 ${\sigma _i}$ 的取值由数据点 ${x_i}$ 的 K 个最近邻确定，通常为 $K = 7$ ^[22]。根据文献[22]可知， $K$ 的选择与尺度参数无关，并且是嵌入空间数据维数的函数，通过 $K$ 共享近邻的方法能够根据数据样本本身之间的关系自适应的获得更加适合的尺度参数，避免了选取尺度参数给算法带来的不确定性。其计算方法为

${\sigma _i} = \frac{1}{K}\sum\limits_{m = 1}^K {d\left( {{x_i},{x_m}} \right)} $

(17)

式中： ${\sigma _i}$ 表示样本点 ${x_i}$ 和其 $K$ 个最近邻距离的平均值；同理 ${\sigma _j}$ 表示样本点 ${x_j}$ 和其K个最近邻距离的平均值。 $\operatorname{SNN} \left( {{x_i},{x_j}} \right)$ 表示样本点 ${x_i}$ 和 ${x_j}$ 在 $K$ 邻域内所共有的邻居个数。 $\operatorname{SNN} \left( {{x_i},{x_j}} \right)$ 反映了 ${x_i}$ 和 ${x_j}$ 点的局部密度，可以用来提高数据点间的相似性，有助于样本点正确的划分。

2.3 所提算法流程

算法　公理化模糊共享近邻自适应谱聚类算法(AFSSNNSC)

输入　数据集 $X = \left\{ {{x_1},{x_2}, \cdot \cdot \cdot ,{x_n}} \right\}$ ，目标聚类数 $k$ ；

输出　聚类实际产生 $y$ 类。

1)首先为数据点的每个特征 ${f_i}$ 构造模糊关系模糊项 ${m_{i,j}}$ ；

2)使用式(10)计算每个数据点的隶属度函数 ${\mu _{m \in M}}\left( x \right)$ ；

3)通过式(11)找出模糊项的集合 $B_x^\varepsilon $ ；

4)通过 ${\zeta _x} = \mathop \wedge \limits_{m \in B_x^\varepsilon } m$ 构建每个样本的描述 ${\zeta _x}$ ；

5)根据 ${\zeta _x}$ 利用式(13)计算成对距离 ${D_{ij}}$ ；

6)通过式(17)计算 ${\sigma _i}$ 和 ${\sigma _j}$ ；

7)利用式(16)构建亲和矩阵 ${{A}}$ ；

8)根据 ${{{D}}_{ii}} = \sum\limits_{1 \leqslant j \leqslant n} {{{{S}}_{ij}}} $ 计算对角矩阵 ${{D}}$ ；

9)计算归一化拉普拉斯矩阵，拉普拉斯矩阵 ${{L}}$ 由 ${{L}} = {{D}} - {{S}}$ 被归一化为

${{L}} = {{{D}}^{{{ - 1} / 2}}}{{L}}{{{D}}^{{{ - 1} / 2}}} = {{I}} - {{{D}}^{{{ - 1} / 2}}}{{S}}{{{D}}^{{{ - 1} / 2}}}$

10)对 ${{L}}$ 进行特征分解，得到前 $k$ 个特征向量，并构建特征向量空间；

11)利用经典的聚类算法如k-means对特征向量空间中的特征向量进行聚类。

3 实验与结果分析 3.1 实验环境及性能指标

在UCI、USPS手写数字的相同数据集上，采用本文提出的方法和文献[10]的NJW谱聚类(SC)、文献[21]的AFS聚类算法(AFS)、文献[22]的self-tuning spectral clustering(STSC)算法、基于K均值的近似谱聚类(KASP)^[23]、基于Nystrom近似谱聚类(Nystrom)^[24]和基于地标点谱聚类算法(LSC-R，LSC-K)^[25]进行对比实验。本文算法实验是在MATLAB 2014b，计算机的硬件配置为Intel i7-4770 CPU 3.40 GHz、16 GB RAM的平台下进行。为了评估所提算法的聚类性能，本文使用聚类误差(CE)^[26]和归一化互信息(NMI)^[27]2种性能指标对本文算法与其他聚类方法的聚类结果进行了比较。其中CE被广泛用于评价聚类性能，CE越低聚类性能越好。NMI也是一种广泛使用的评估算法聚类性能的测量标准，NMI越大性能越好。

3.2 UCI数据集实验结果与分析

为了验证所提出算法的有效性，本文将所提的算法和其他方法应用于UCI数据库中的11个基准数据集作为测试样本，表1为这11类数据集的特征，分别是数据总量、维数以及类的个数。

基于聚类误差(CE)的实验结果如表2所示，由表2可知所提的方法在大部分实验数据集上均获得了优于对比算法的CE值；所提出的方法在Heart、Hepatitis、Wdbc、Protein和Libras数据集上的CE分别为15.27%、27.14%、6.03%、51.12%、52.31%，相比较AFS算法而言均改进了10%以上，在其他5个数据集上的CE相比较AFS也均有所提高。证明了利用谱理论对相似矩阵进行划分比之前提出的传递闭包理论好得多，考虑到传递闭包方法的验证循环，所提出的方法也相对更快、更容易实现。在Iris、Wine数据集中，所提算法的CE分别为7.42%和2.89%，相对聚类错误率略高于STSC算法。因为这两个数据集中只有150个样本和178个样本，但是差异实际上只有一两个样本，但相对于总体而言，所提算法CE普遍低于其他算法在各数据集上的结果，仍具有较好的优越性；与基于距离度量的方法相比所提算法在给出的所有数据集中都显示出了优越性，在Sonar数据集上更加改进5%以上，本文算法与基于Nystrom近似谱聚类方法相比在所有数据集上均有1%以上的优势。本文算法与基于地标点的谱聚类方法LSC-R和LSC-K相比也展现出较好的聚类性能。这是因为通过模糊隶属函数代替距离度量数据之间的相似性，利用模糊语义结构解释数据之间的复杂的相互关系，增强了算法的鲁棒性。对于Protein、Libras等多聚类数据集，AFS的聚类错误率偏高，因为AFS聚类需要根据每个集群的边界选择最好的数据聚类分区。随着集群规模数量的不断增加，将很难去清晰地找到边界，这样聚类误差也会随之增高。总体而言，与对比文献方法相比，所提算法的CE值在所有实验数据集上均得到了改善，降低了算法的聚类错误率。

在归一化互信息(NMI)中测量的聚类性能如表3所示。所提出的算法的聚类结果NMI与其他方法的NMI相比都得到了改善，尤其在Heart和Protein数据集上，所提算法相对于KASP、SC、STSC、AFS和Nystrom对比算法而言NMI均提高了5%以上。只是在Wine数据集上，所提算法的NMI为87.86%，与其他算法相当，但在整个对比表格中为最好的聚类性能。由于所选Covertype数据集是一个从地图变量预测森林覆盖类型的数据集，它们都主要是在荒野地区发现的，所以覆盖类型在实际地理上是非常接近的，相对于其他数据集而言，这个数据集数据特性更加复杂。所以在Covertype数据集下所有算法的NMI都普遍较低，但是所提算法获得了比其他算法更好的聚类效果。

从实验结果可以看出，STSC不是很稳定，它在Hepatitis和Sonar数据集上的NMI情况都非常差，由于在STSC和本文算法中都考虑到了数据之间的相互关系，利用到了数据邻居的近邻作用，所以可以从中得出结论，与考虑到数据样本关系之间的传统距离度量作为相似性度量相比，采用具有数据样本模糊关系的模糊隶属度作为距离度量，在相似性度量上更具有鲁棒性。总体而言，所提算法相较于对比算法都具有明显的改善。

3.3 USPS数据集实验结果与分析

选择两个典型谱聚类算法SC和STSC与所提方法在广泛使用的USPS数据库中的手写数字数据集进行对比实验。该数据集包含美国邮政总局通过扫描信封中的手写数字获得的数字数据。原始扫描的数字是二进制的，大小和方向不同。本文使用的图像经过了大小归一化，得到了1 616张256维的灰度图像。它包含7 291个训练实例和2 007个测试实例(总共9 298个)。为了展示该方法的可伸缩性，考虑了不同数量的集群。具体来说，数字子集{0,8}、{4,9}、{0,5,8}、{3,5,8}、{1,2,3,4}、{0,2,4,6,7}和整个集合{0,1,···,9}用于测试本文提出的算法。这些子集的详细信息如表4所示。分别在每个子集上进行实验，并使用CE和NMI来测量性能。

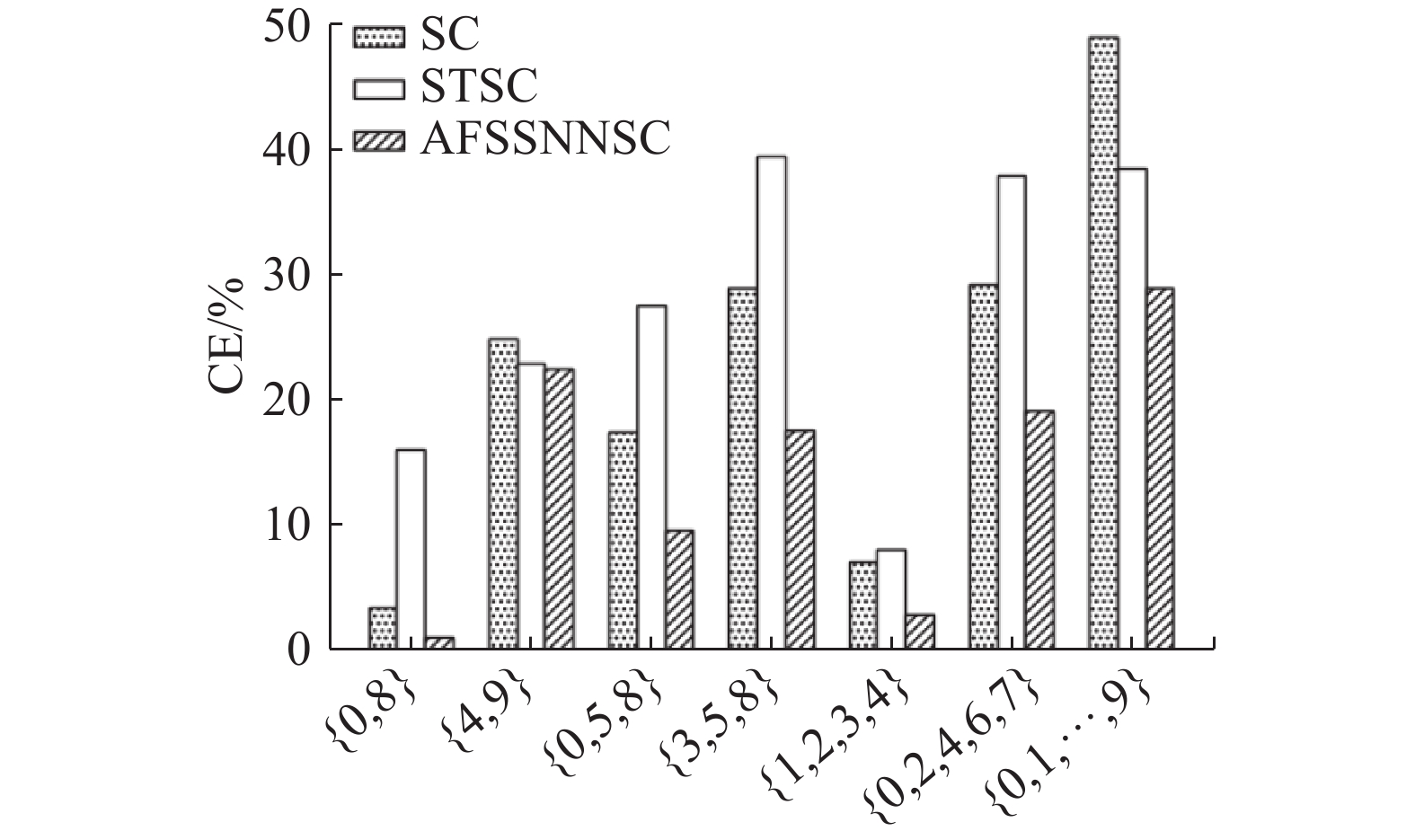
从图1可以看出，在CE方面，所提算法在所有的情况下都优于STSC和SC，尤其在{0,8}、{0,5,8}、{3,5,8}、{0,2,4，6,7}、{0,1,···,9}数据集上CE均改善了5%以上，甚至在{3,5,8}上CE相较于其他对比算法，所提算法改进了10%以上。总体而言与SC和STSC相比，可以从图1中看出所提出的方法均得到明显的改善。

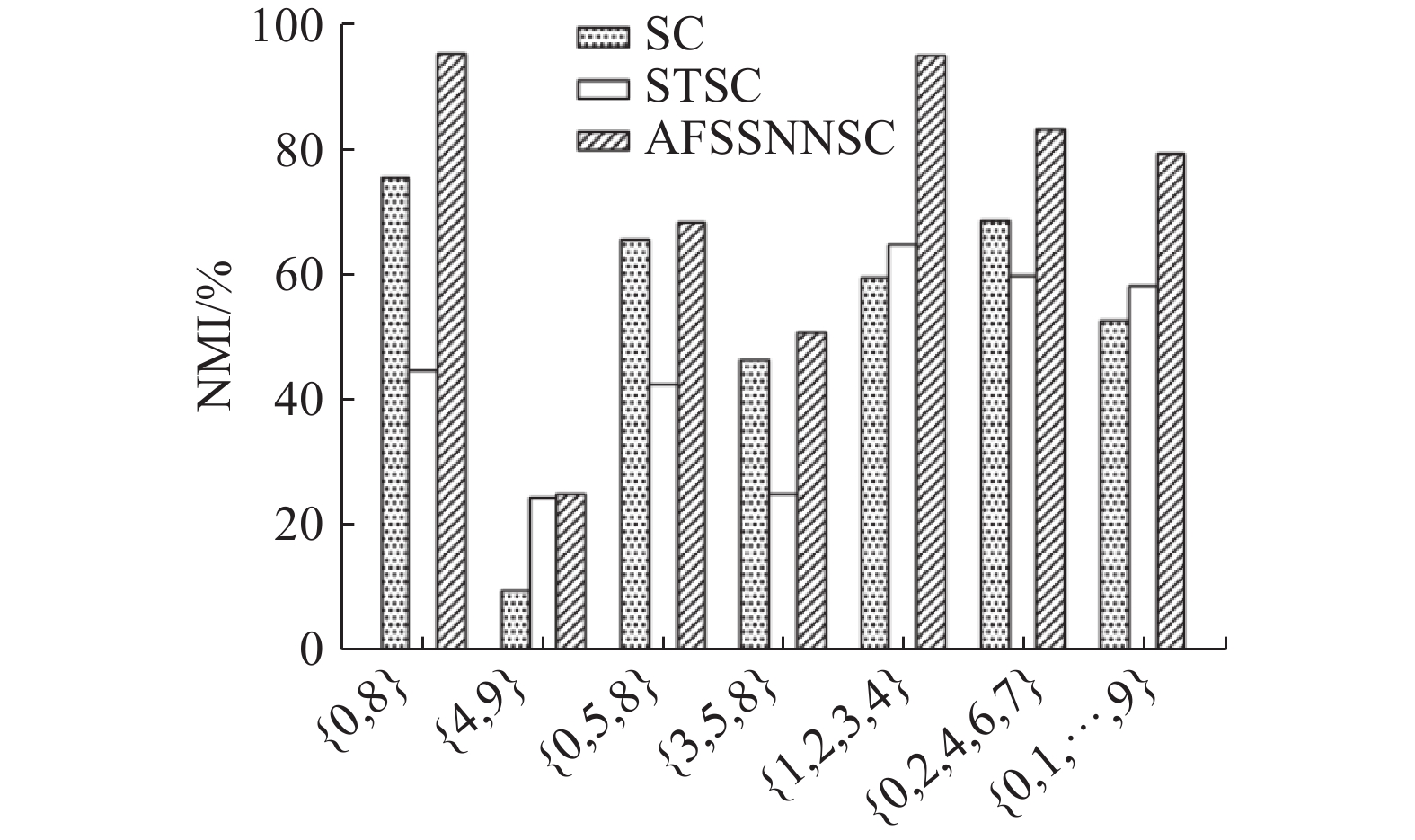
图2显示了基于NMI的USPS数据集的结果。从图2中可以看出，所提出的方法在所有情况下都比SC和STSC有优势。在{0,8}、{1,2,3,4}、{0,1,···,9}上相较于其他对比算法，所提算法的NMI都提高了10%以上，特别是对于具有挑战性的情况{3,5,8}和多类情况{1,2,3,4}、{0,2,4,6,7}、{0,1,···,9}，所提出的算法都具有一定的优越性。

4 结束语

本文提出了一种新的无监督广义数据亲和图的构造方法，该方法具有更强的鲁棒性和更有意义的数据亲和图，以提高谱聚类精度。采用模糊理论定义数据相似度，利用模糊隶属度函数导出亲和图。此外，亲和图不是盲目地相信所有可用变量，而是通过捕捉和通过对每个样本的模糊描述，确定了特征子空间中组合分布的微妙两两相似关系。同时采用共享近邻的方法发现密集区域样本点分布的结构和密度信息，并且根据每个点所处领域的稠密程度自动调节参数 $\sigma $ ，从而生成更强大的亲和矩阵，进一步提高聚类准确率，证明了该方法对不同类型数据集的有效性。实验结果表明，该方法与其他先进的方法相比具有一定的优越性。数据大小的多样性在一定程度上体现了该方法对于大数据集的可扩展性。在未来将通过系统地将所提出的算法与一些采样或量化策略相结合来处理一般的可伸缩性问题。