近年来，深度学习在图像识别和语音识别领域取得了突破性的进展。深度学习逐渐成为机器学习最热的研究方向之一。由于RBM(restricted boltzmann machine)^[1-3]具有表达能力强、易于推理等优点被成功用作深度神经网络的结构单元。当前，以RBM^[4-5]为基本构成模块的DBN(深度信念网络)、DBM(深度玻尔兹曼机)等模型被认为是最有效的深度学习算法。其中深度信念网络(DBN)是深度学习的典型代表，通常DBN在进行图像及语音等模式识别上有较高的精度，但是训练一个DBN的复杂度非常高，因为DBN在微调阶段使用了BP算法，这种算法很难做到多机并行，所以在大规模的数据上进行学习会非常困难。综上，DBN主要存在两个问题：1)训练一个DBN的时间复杂度仍然较高；2)达到好的效果通常需要较多的隐含节点数，然而当隐含节点数较多时又易产生过拟合。虽然邓力等^[6-8]通过改进DBN的网络结构来提升其性能，但仍然没有突破以上问题。

分类是深度学习的核心问题，提高分类器的分类性能是分类器研究的主要目标之一。通常将模糊理论与分类器相结合，用于处理不确定问题。在构建分类模型时，为了对所构建的目标模型的局部细节有更好的逼近程度，通常的做法是将输入空间划分成多个模糊区域或模糊子空间，即模糊划分^[9-10]，在各个子空间中分别构建分类子模型，最后将各子模型的结果集成输出^[11-12]。有3种模糊划分方法，即格状划分、树状划分和散状划分。格状划分是将每一维度的输入空间作划分，求得其模糊集合，再根据模糊系统理论，将模糊集映射成模糊区域。树状划分是，一次产生一个与模糊区域相对应的一个划分，每做一次划分就会产生出划分面。散状划分是，将输入输出的数据作分析，将预产生相似结果的输入空间以模糊区域作划分，每一模糊区域可作描述输入输出数据的行为。该划分是一种较为灵活的划分方法，吸收了前两种方法的优点，同时摒弃了它们存在的不足。在本文的研究中，采用散状划分这种方式。

为了更好地挖掘深度模型的表达能力，在实际应用中进一步提高DBN的精度并加快DBN的训练。受到上述思想的启发，本文提出了一种基于模糊划分和模糊加权的集成深度信念网络，将对应的集成分类算法命名为FE-DBN。首先通过模糊聚类算法FCM将训练数据划分为多个子集；然后在各个子集上并行训练不同结构的DBN；最后借鉴模糊集合理论的思想，将各个分类器的结果进行模糊加权。该算法能够有效且快速解决大样本数据的分类问题，克服了单个DBN用于数据分类时时间复杂度较高等缺点；而且，FE-DBN可以避免过拟合问题，具有分类精度高等优点；并在人工数据集、UCI数据集上得到了有效验证。

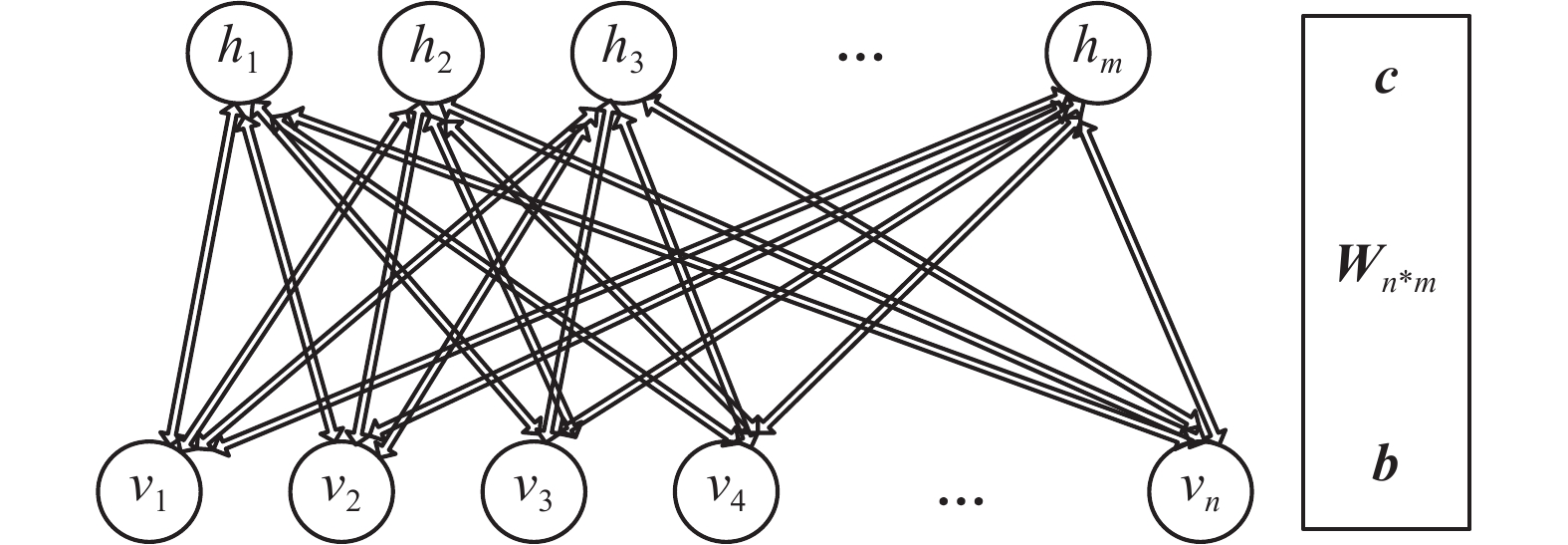
1 RBM和DBN

受限玻尔兹曼机是由Hinton和Sejnowski于1986年提出的一种生成式随机网络^[1]，该网络是一种基于能量的概率图模型，它由一个可见层和一个隐含层组成，如图1所示，v和h分别表示可见层与隐含层，W表示两层之间的连接权值。对于可见层与隐含层，其连接关系为层间全连接，层内无连接。注意，图1中h有m个节点，v有n个节点，单个节点用 ${v_i}$ 和 ${h_j}$ 描述。可见层用于观测数据，隐含层用于提取特征。RBM的隐单元和可见单元可以为任意的指数族单元。本文只讨论所有的可见层和隐含层单元均为伯努利分布，假设所有的可见单元与隐单元均为二值变量，即对 $\forall i,j,{v_i} \in \left\{ {0,1} \right\},{h_j} \in \left\{ {0,1} \right\}$ 。

RBM是一种能量模型，能量函数定义为

$ {E} ({{v}},{{h}}|{{\theta }}) = - \sum\limits_{i = 1}^n {{b_i}} {v_i} - \sum\limits_{j = 1}^m {{c_j}{h_j} - \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{v_i}{W_{ij}}} } } {h_j} $

式中：b和c分别为可见层和隐含层的偏置向量； $ {{\theta }} \in \{ {{b,c,W}}\} $ ，W表示权值矩阵。基于能量函数，可以得到v和h的联合概率分布：

$ \left\{ \begin{split} & P ({{v}},{{h}},{{\theta }}) = \frac{{{{\rm e}^{ - E({{v}},{{h}},{{\theta }})}}}}{Z} \\ & Z = \sum\limits_{\tilde v} {\sum\limits_{\tilde h} {{{\rm e}^{ - E(\tilde v,\tilde h,\theta )}}} } \end{split} \right. $

(1)

式中Z函数为归一项。

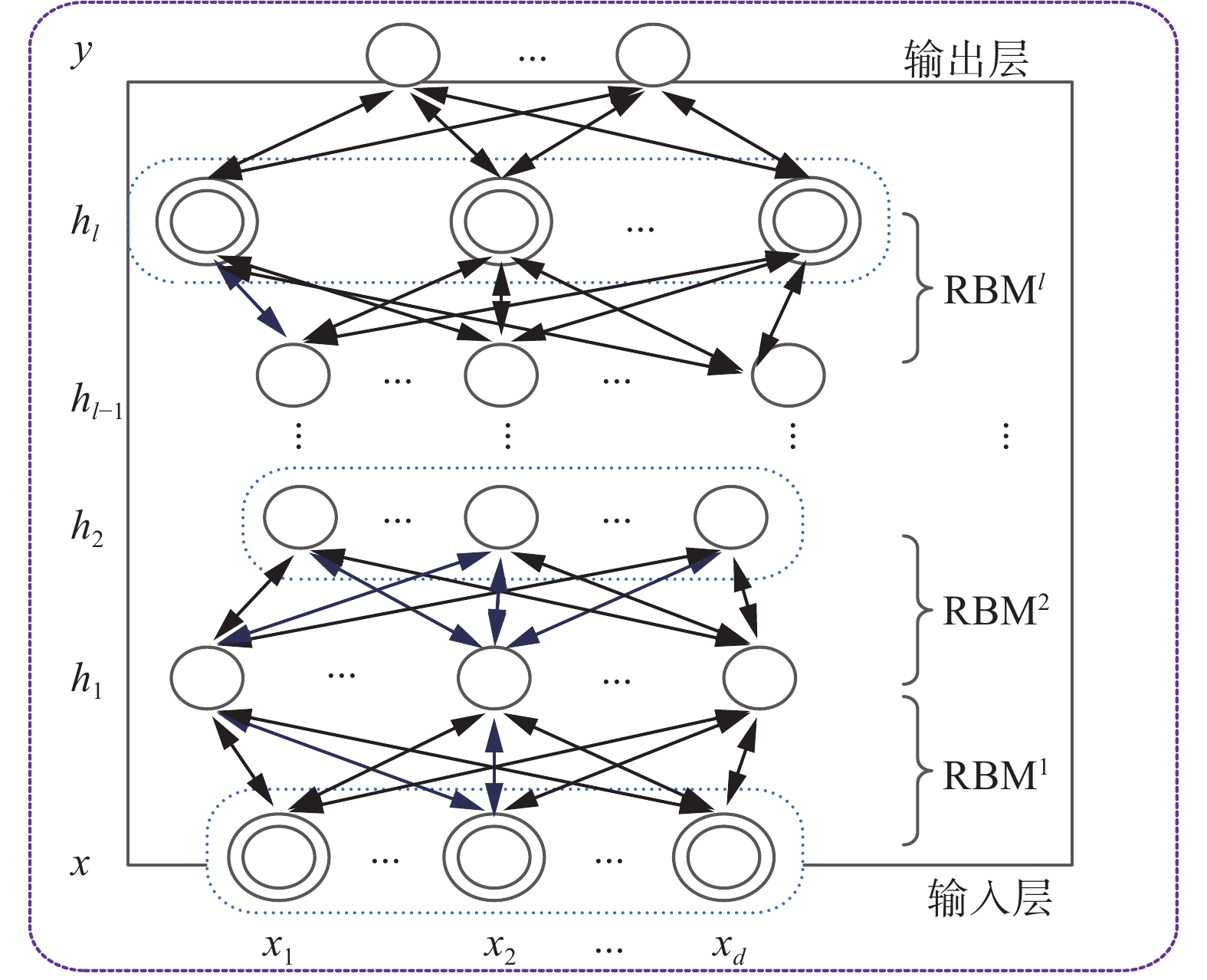
多个RBM的堆栈组合构成了DBN^[5]，前一个RBM的输出作为后一个RBM的输入。如图2所示，最底层是输入层，最顶层是输出层，中间层是隐含层。DBN的学习包括两个阶段：预训练和微调。预训练是以贪婪的无监督的方式逐层进行训练的，将输入层映射到输出层从而学习到复杂的非线性函数；微调是在监督的方式下实现的，它使用反向传播(BP)算法从最顶层到最底层对整个DBN网络参数进行微调。

尽管DBN具有强大的知识表达能力，但是当处理大规模数据甚至大数据时，DBN在微调阶段需要花费大量的时间去训练模型，这样导致训练时间特别长。

2 基于模糊划分和模糊加权的DBN分类器集成

针对不同的子空间，从不同的角度来刻画一个物体各个方面的性质，利用各种不同结构分类器的组合来形成一个综合的决策。大量的实验和应用证明：将多个分类器的决策结果按照一定的规则集成在一起，往往可以得到比其中最优分类器还要好的性能^[12-15]。针对经典的DBN算法时间复杂度高，容易过拟合，本文将具有多个不同隐含层结构的DBN分类器进行集成，提出了一种基于模糊划分和模糊加权的集成DBN，即FE-DBN。提出的FE-DBN性能优于经典的DBN分类算法，主要有两个原因：1)在分类之前首先进行预处理、聚类，能够更好地增强分类精度；2)将训练集分为多个子集，每个子集用不同结构的DBN训练，最后将结果进行模糊加权。根据集成学习原理，多个弱分类器的组合能够组成一个强分类器。

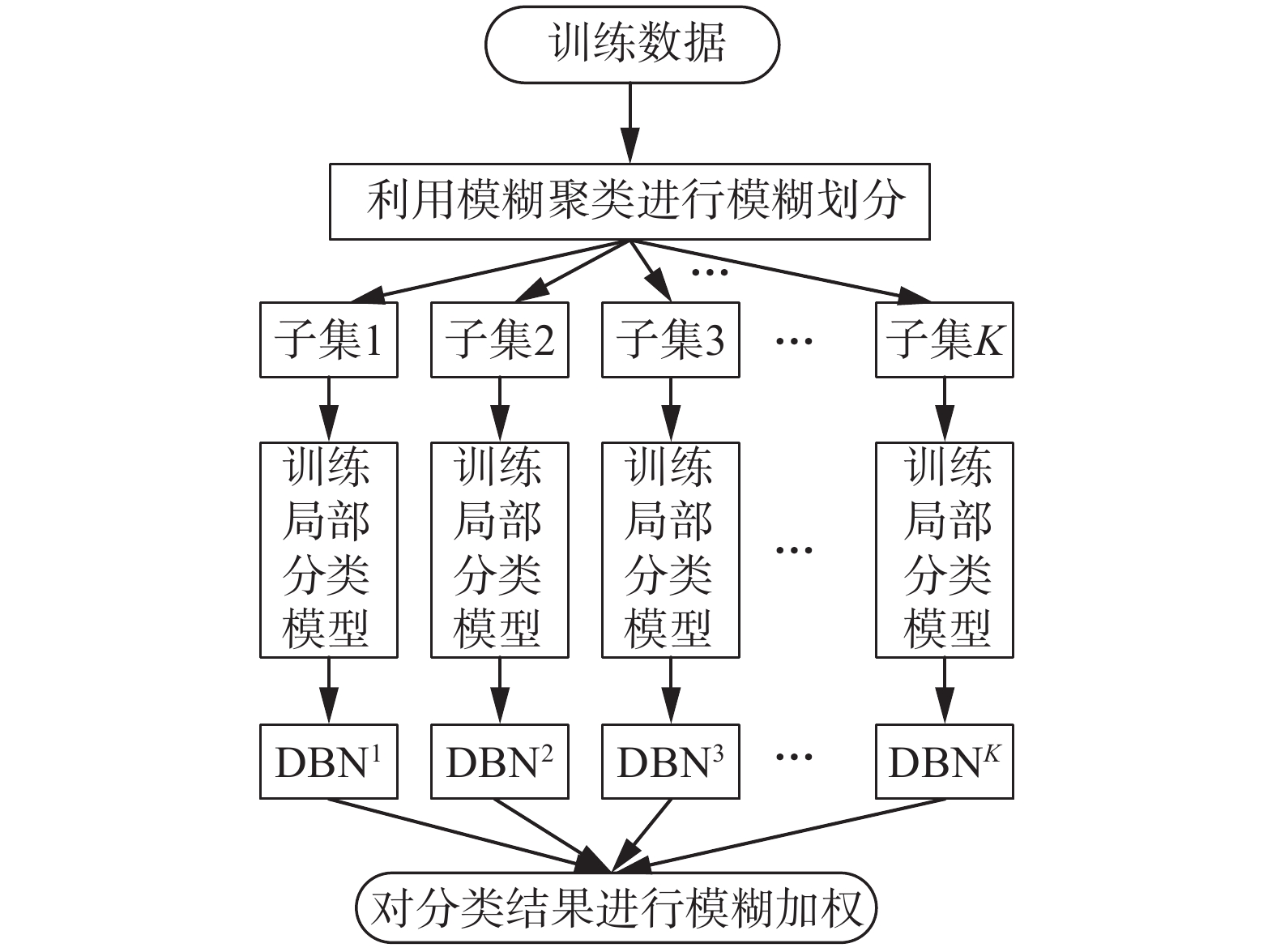
2.1 FE-DBN结构图

FE-DBN结构图如图3所示，首先利用模糊聚类算法FCM，将训练数据集划分为K个子集，每个子集分别采用不同结构的DBN模型进行建模(每个DBN子模型中每层隐节点数不一样，由此构成了K个DBN模型)，各模型独立并行训练，最后将各模型所得结果进行模糊加权形成最终输出。在进行模糊加权时，采用高斯型隶属度函数进行权值计算。在FE-DBN中，各DBN子模型并行训练，由于各个训练子集的数据规模远远小于原数据规模，需要较少的隐节点数，因此训练时间较短。

2.2 实现过程

首先，使用模糊聚类算法FCM对训练数据集进行模糊分组。利用FCM算法进行模糊聚类，FCM的目标函数为^[16-19]：

$ \begin{split} & \mathop {\min }\limits_{\mu ,{\rm v}} {\rm{ }}J = \sum\limits_{i = 1}^K {\sum\limits_{j = 1}^N {\mu _{ij}^m({{\left\| {{x_j} - {\upsilon _i}} \right\|}^2})} } \\ & {\rm{ s.t.}}{\rm{ }}\sum\limits_{i = 1}^K {\mu _{ij}^m = 1,\forall j = 1,2, \cdots ,n} \end{split} $

式中：K是划分数；N是样本数； ${\upsilon _i} = \left( {{\upsilon _{i_1}},{\upsilon _{i_2}}, \cdots ,{\upsilon _{i_d}}} \right)$ 为第 $i$ 类的中心点； ${\mu _{ij}}$ 表示第 $j$ 个样本属于第 $i$ 类的隶属度；m是模糊指数，必须满足 $m \geqslant 2$ ，本文取为2； ${x_j}$ 表示第 $j$ 个样本点。引入拉格朗日因子构造新的目标函数，推导得到隶属度和聚类中心的迭代计算公式分别为^[20]：

$ {\mu _{ij}} = \dfrac{1}{{\displaystyle\sum\limits_{k = 1}^K {{{\left(\dfrac{{||{x_j} - {\upsilon _i}|{|^2}}}{{||{x_j} - {\upsilon _k}|{|^2}}}\right)}^{1/(m - 1)}}} }} $

(2)

$ {\upsilon _i} = \sum\limits_{j = 1}^N {\mu _{ij}^m} {x_j}/\sum\limits_{j = 1}^N {\mu _{ij}^m} ,{\rm{ 1}} \leqslant i \leqslant K $

(3)

根据式(2)、式(3)，当迭代终止后，所获得的隶属矩阵 U 在去模糊化后便得到空间划分矩阵。

根据式(2)、式(3)，计算宽度为

$ \gamma _j^s = \sqrt {\frac{{\sum\limits_{i = 1}^N {\mu _{ij}^m \cdot {{\left\| {x_i^s - \upsilon _j^s} \right\|}^2}} }}{{\sum\limits_{i = 1}^N {\mu _{ij}^m} }}} $

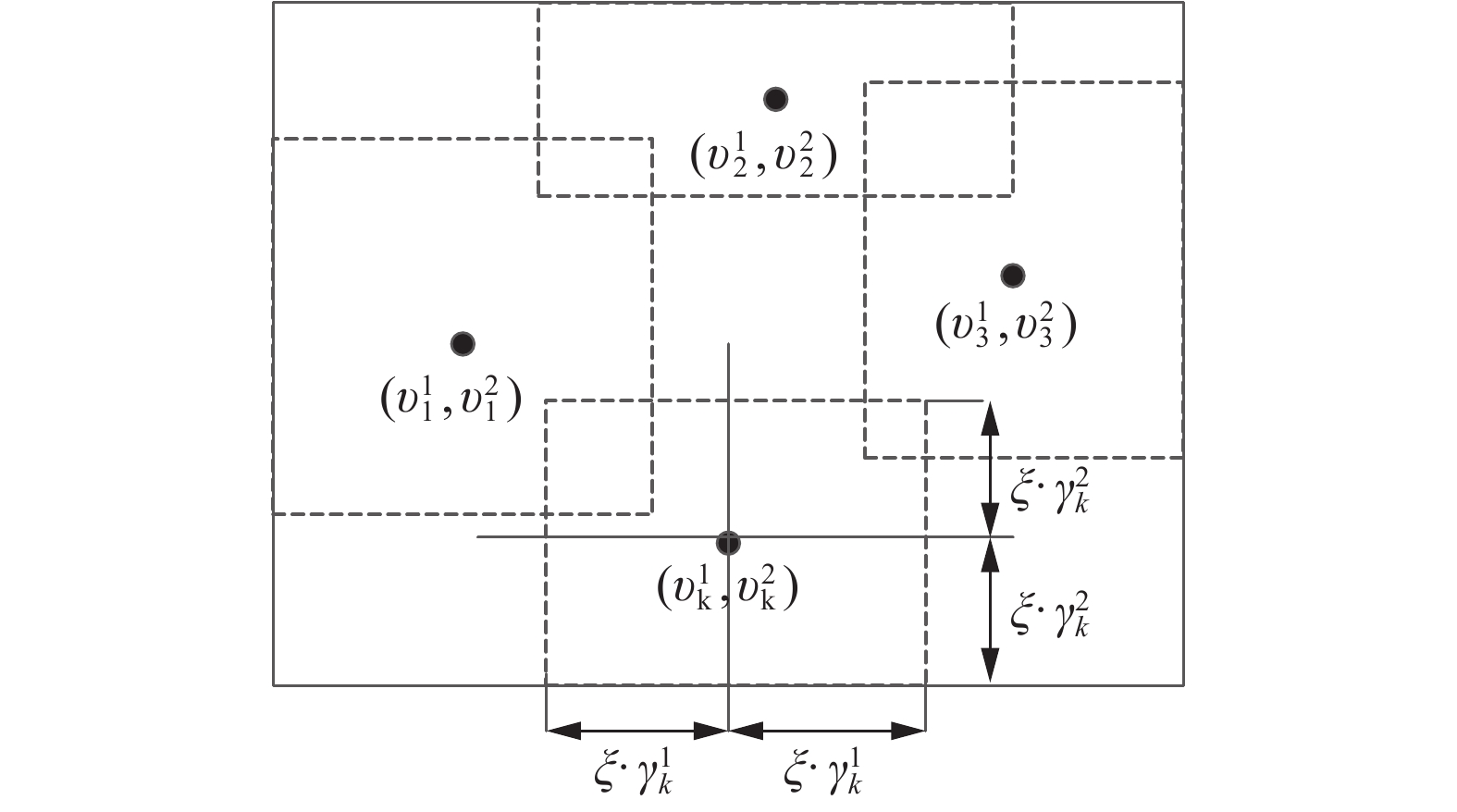
根据聚类中心和宽度的值，并利用式(4)对训练数据集进行模糊划分：

$ \begin{split} & {\vartheta _j} = \left\{ {\left( {{{{x}}_i},{y_i}} \right)\left| {\upsilon _j^s - \xi \cdot \gamma _j^s \leqslant x_i^s \leqslant \upsilon _j^s + \xi \cdot \gamma _j^s} \right.} \right\} \\ & \qquad\; s = 1,2, \cdots ,q;{\rm{ }}j{\rm{ = 1,2,}} \cdots {\rm{,}}K \end{split} $

(4)

式中： ${\vartheta _j}$ 为定义的划分子集；q为维数； $\xi $ 为重叠因子， $\xi $ 越大子集划分也就越模糊。模糊划分示意图如4所示。在对原数据集模糊划分完成后，再在各个子集上并行训练不同结构的DBN。

在式(1)中最关心的是联合概率分布所确定的边缘概率分布 $P({{v}}|{{\theta }})$ ，由于RBM模型层内无连接，因此当给定可见单元的状态时，各隐单元的激活状态是条件独立的。此时，第j个隐单元的激活概率为

$ P({h_j} = 1|{{v}},{{\theta }}) = \sigma ({c_j} + \sum\limits_{i = 1}^n {{v_i}} {W_{ij}}) $

(5)

式中 $\sigma ({{x}}) = \dfrac{1}{{1 + \exp ( - {{x}})}}$ 为sigmoid激活函数。第i个可见单元的激活概率为

$ P({v_i} = 1|{{h}},{{\theta }}) = \sigma ({b_i} + \sum\limits_{i = 1}^m {{W_{ij}}} {h_j}) $

(6)

RBM采用Hinton提出的CD-k(对比散度)算法进行参数学习，并证明，当使用训练样本初始化 ${{{v}}^{\left( 0 \right)}}$ 时，仅需较少的抽样步数(一般k=1)就可以得到很好的近似。采用CD-k算法，各参数的更新准则如下^[3]：

$ \begin{array}{l} \varDelta {w_{ij}} = \varepsilon ( < {v_i}{h_j}{ > _{\rm data}} - < {v_i}{h_j}{ > _{{\rm recon} }}) \\ \quad \varDelta {b_i} = \varepsilon ( < {v_i}{ > _{{\rm data} }} - < {v_i}{ > _{\rm recon}}) \\ \quad\varDelta {c_j} = \varepsilon ( < {h_j}{ > _{\rm data}} - < {h_j}{ > _{\rm recon}}) \\ \end{array} $

(7)

式中： $\varepsilon $ 为预训练的学习率； $ < \cdot { > _{{\rm{data}}}}$ 为训练数据集所定义的分布之上的数学期望； $ < \cdot { > _{{\rm{recon}}}}$ 为重构后的模型所定义的分布上的期望。利用式(7)，通过迭代更新得到DBN各子模型的参数。各子模型训练好之后，给定测试数据 ${{{x}}_i}$ ，计算得到该数据在每个模型的输出结果，利用三角形隶属度函数计算权值：

$ {{{\omega }}_k}({{{x}}_i}) = \omega _k^1({{x}}_i^1) \;\; \omega _k^2({{x}}_i^2) \;\; \cdots \;\; \omega _k^q({{x}}_i^q) $

(8)

$ \begin{array}{l} \omega _k^s({{x}}_i^s) = \max\left\{ {\min \left(\dfrac{{x_i^s - (\upsilon _k^s - \xi \cdot \gamma _k^s)}}{{\upsilon _k^s - (\upsilon _k^s - \xi \cdot \gamma _k^s)}},\dfrac{{(\upsilon _k^s + \xi \cdot \gamma _k^s) - x_i^s}}{{(\upsilon _k^s + \xi \cdot \gamma _k^s) - \upsilon _k^s}}\right),0} \right\} \\ \\ \end{array} $

(9)

式中： $ k = 1,2, \cdots ,K;i = 1,2, \cdots ,N;{\rm{ }}s = 1,2, \cdots ,q$ 。

划分好样本空间，每一个分类器在样本子空间进行运算，样本在分类器中具有局部分类性能最好的，其所对应的权值就越大。

最后，将各DBN分类器所得结果进行模糊加权，即

$ {\hat y}({{{x}}_{{i}}}) = \frac{{\sum\limits_{k = 1}^K {{{{\omega }}_k}({{{x}}_{{i}}}){\rm{LCM}}_{{\rm{DBN}}}^k({{{x}}_{{i}}})} }}{{\sum\limits_{k = 1}^K {{{{\omega }}_k}({{{x}}_{{i}}})} }} $

(10)

式中： ${\rm{LCM}}_{{\rm{DBN}}}^k({{{x}}_{{i}}})$ 为样本 ${{{x}}_{{i}}}$ 在第k个模型的分类结果；LCM为局部分类模型； ${\hat y}$ 为K个模型分类结果模糊加权后所得的最终输出。

FE-DBN算法实现过程如下：

1)初始化。设定划分子集个数K及重叠因子 $\xi $ ，各子模型DBN的隐节点数及DBN的迭代周期，初始化W，b，c的值，学习率 $\varepsilon $ 。

2)划分子集。利用模糊聚类算法FCM求得每簇的中心点和宽度，根据式(4)将源数据集划分为K个子集。

3)并行训练各子模型DBN¹~DBN^K，对于所有的可见单元，利用式(5)计算 $P({h_j} = 1|{{v}},{{\theta }})$ ，并抽取 ${h_j}$ 且 ${h_j} \in \left\{ {0,1} \right\}$ 对于所有的隐单元，利用式(6)计算 $P({v_i} = 1|{{h}},{{\theta }})$ ，并抽取 ${v_i}$ 且 ${v_i} \in \left\{ {0,1} \right\}$ ，利用式(7)更新RBM参数W，b，c的值，即

$ {{W}} = {{W}} + \varDelta {{W}}, \;{{b}} = {{b}} + \varDelta {{b}}, \;{{c}} = {{c}} + \varDelta {{c}} $

重复3)，直到满足迭代周期为止。

4)利用式(8)、式(9)计算每个测试数据对各个子集的隶属度，将测试数据代入3)所得的K个子模型中并输出K个分类结果。利用式(10)进行集成得到最终输出。

3 实验与分析

本文在实验部分将分别利用人工数据和UCI数据对所提的基于模糊划分和模糊加权的集成DBN分类算法(FE-DBN)进行验证和评估。并将该算法的性能同深度信念网络(DBN)^[1-3]算法进行比较。为了验证本文所提出的算法FE-DBN的有效性，采用的对比算法有局部分类模型DBN^K和全局分类模型DBN，其中DBN^K表示将原数据集分为K个子集，在每个子集上构建一个局部深度信念网络分类模型。所有的实验结果都采用五折交叉，运行10次取均值。

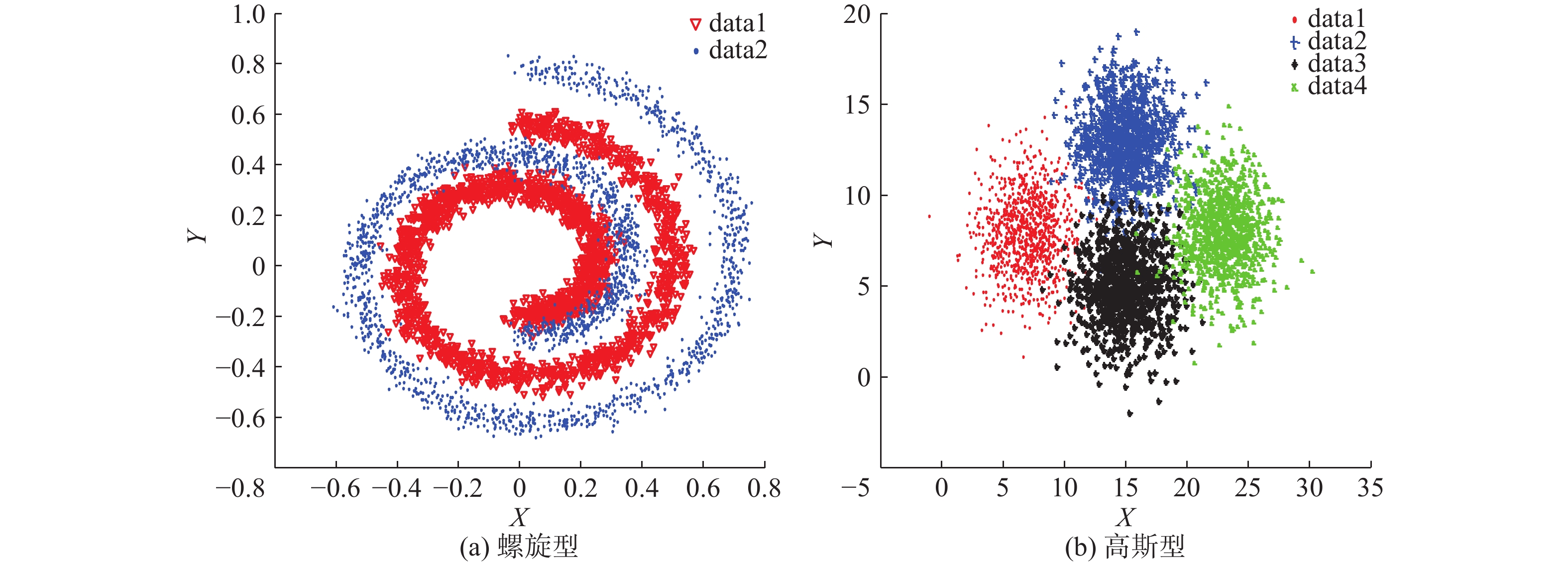
3.1 实验设置 3.1.1 数据集

人工数据集生成两种：左螺旋型、右高斯型，如图5。两种数据均生成4 000个样本，螺旋型2类，2维；高斯型4类，2维。构造的螺旋型数据集正负类样本数各2 000，高斯型数据集每类样本数1 000，高斯型各类的中心分别是：[7 8]、[15 13]、[15 5]、[23 8]，协方差均为 $\left[\begin{array}{l} 4 \quad 0\\ 0 \quad 4 \end{array}\right] $ 。真实数据集全部来自于UCI^[21]。数据集详细信息如表1、表2所示。

3.1.2 参数设置及实验运行环境

实验中采用三层的DBN，ξ用于控制子集的伸缩宽度，在实验中发现，当ξ=3时，能够取得较好的结果，也可根据具体的数据集分布进行微调。DBN代码参照http://www.cs.toronto.edu/~hinton/，RBM迭代周期maxepoch=20，用于控制RBM的预训练迭代次数和模型参数的微调次数。权重的学习率epsilonw=0.05；显层偏置的学习率epsilonvb=0.05；隐层偏置的学习率epsilonhb=0.05；权损失系数weightcost=0.000 2；动量学习率initialmomentum=0.5，finalmomentum=0.9。

本文使用平均测试精度、均方差、运行时间(训练时间+测试时间)进行算法性能度量。实验环境为intel(R) Core(TM) i3 3.40 GHz CPU，8 GB内存，Windows10操作系统，MATAB2016a。

3.2 实验结果及分析

为进一步探索数据集模糊划分个数对提升分类精度及算法运行时间的重要性，本文将数据集划分为不同的子集个数，及采用不同的隐节点数组合分别进行实验比较。如表3所示，局部分类模型DBN^K分别有3个子集和4个子集，“28+22+19”表示DBN¹中第一层、第二层、第三层的隐节点数分别为28、22、19。

3.2.1 人工数据集

该实验部分主要是通过构造模拟数据集来验证本文提出的FE-DBN算法的有效性。从表3、表4的实验结果可以看出：螺旋线数据集不太好区分，精度不高，但是FE-DBN仍有所提升；高斯型数据集精度，FE-DBN比各局部模型DBN^K略高，和全局模型DBN基本持平，因为其精度已经很高，故很难再有较大的提升。

3.2.2 UCI数据集

本部分实验选的UCI数据集，既有中等规模数据，又有大规模数据，既有二分类，也有多分类，3种算法在各UCI数据集上的对比实验结果如表5~9所示。

从表5~9的实验结果，可以得出如下结论：

1)在测试精度上，和全局分类模型DBN相比，FE-DBN在数据集Adult、shuttle和Magic_gamma_telescope上增长较多，在数据集pendigits和waveform3上有略微上浮。在样本划分子集确定的情况下，FE-DBN高于任何一个局部分类模型DBN^K。总的来看，FE-DBN算法的分类效果在三者中为最优。从表5~9中还可以看出，在划分的子集数确定时，具有不同隐节点数组合的各局部分类模型DBN^K分类器的精度并无明显差异。随着划分子集数的增加，FE-DBN的精度在不同数据集上基本均有增长的趋势。其主要原因在于，根据集成原理^[14,22−23]，对于集成FE-DBN分类模型，增加各子模型的多样性，能够提高集成分类器的性能。

2)和全局模型DBN相比较，FE-DBN中每个局部分类模型需要较少的隐节点数，就可以达到较高的精度，这主要是因为组成FE-DBN的每个局部分类器都是弱分类器。

3)对于所有数据集，在运行时间上，当划分子集数逐渐增多时，由于每个子集的样本数在减少，隐节点数也在减少，运行时间相应也会减少。由于要进行模糊划分和模糊集成，FE-DBN的运行时间比各局部分类模型DBN^K要多，但是FE-DBN的运行时间要小于全局模型DBN的运行时间，因为在FE-DBN中各局部分类模型是并行运行的，且每个子模型的隐节点数均小于全局模型DBN的隐节点数。

无论是模拟数据集还是UCI数据集，基于模糊划分和模糊加权的DBN集成分类器(FE-DBN)比单分类器(DBN)的性能好，比最优的局部分类模型DBN^K也要高。由表3~9中结果，根据统计分析得出，样本划分粒度越细，分类精度会越高，表明细划分能得到更多的样本特征信息。但也不是子集划分得越多，精度就越高，数据集shuttle在划分子集数为4时取得最大值。

4 结束语

采用集成的方法解决DBN训练时间复杂度高的问题。根据数据之间的相似性信息对数据进行模糊分组，构造样本空间子集，然后在各样本空间子集中训练具有不同结构的DBN子分类器，最后使用模糊加权的方法，得到最终的集成分类器和分类结果。人工数据集和UCI数据集上的实验结果显示，FE-DBN算法可以得到比其他分类算法更好的分类结果。未来的研究工作将主要集中在如何确定样本空间子集上。