自闭症又叫孤独症，是一种广泛性神经失调的发展障碍疾病，其临床表现主要为社会交往障碍、言语交流障碍和动作刻板重复等^[1-3]。自1943 年利奥·坎纳医生首次对自闭症做出经典性描述以来，该疾病因其病因不明确，又集多种障碍于一身，已经得到了广泛的关注。目前，在美国平均每68名儿童中就有1名自闭症儿童；在世界范围内，自闭症患者超过1%。据统计，约2/3孤独症患儿成年后无法独立生活，需要终生照顾和看护。为此，人们迫切希望寻找科学而高效的手段对自闭症进行准确诊断以达到早发现早治疗的目的。

已有研究表明，自闭症患者行为和认知缺陷与潜在的脑功能异常有关。静息态fMRI技术^[4-9]通过使用血氧水平依赖(blood oxygenation level dependent, BOLD)信号可以有效地反映患者在静息状态下脑部血流和代谢活动等功能性变化，因此在自闭症的辅助诊断中起着重要的作用。基于静息态的医学影像诊断大致可分为特征提取和分类器设计这两个阶段。在特征提取阶段，通过使用相关性特征选择等方法从高维医学影像特征中得到有鉴别意义的特征；在分类器设计阶段，通过使用线性或非线性分类器进行分类。但是目前多采用线性特征学习方法，虽然具有简单高效等优点，但是尚不能有效挖掘出医学影像数据中的复杂信息。

本文基于静息态fMRI提出了一种新型的无监督模糊特征学习方法，并在此基础上构造多视角分类器从而实现自闭症的辅助诊断。其技术路线可概括为：首先，将静息态fMRI经过预处理后，基于Pearson相关系数构造低阶功能连接矩阵，并使用文献[7]的方法构造高阶功能连接矩阵；然后，提出新型的无监督模糊特征学习方法，将2种功能连接矩阵分别映射到不同的低维嵌入空间中；最后，以低阶和高阶功能连接在脑疾病诊断中的互补性为出发点，设计多视角SVM^[10]分类器进行分类。

1 实验数据集及处理

本文使用的数据集来自ABIDE(autism brain imaging datae xchange)数据库(http://preprocessed-connectomes-project.org/abide/download.html)的NYU子集和USM子集，采集对象的FIQ(full-scale intelligence quotient)范围为65～150。实验所处理对象的相关信息如表1和表2所示。

每个对象的fMRI数据使用DPARSF(data processing assistant for resting-state fMRI)^[11]工具进行处理。处理步骤主要包括：1）去除功能磁共振图像序列前10个时间点的数据；2）时间层校正和头部运动校正；3）数据通过统一使用T1加权图像分割并将其归一化到MNI152(montreal neurological institute 152)标准空间中；4）使用AAL (anatomical automatic labeling)模板将大脑划分成116个脑区，每个区域重新采样3×3×3 mm³的体素；5）使用半高全宽高斯核进行空间平滑处理；6）应用带通滤波(0.01～0.1 Hz)去除噪声；7）去线性漂移并进行全局信号校正去干扰变量；8）计算每个脑区的平均时间序列。

2 基于fMRI数据的无监督模糊特征学习方法 2.1 方法流程

基于静息态fMRI进行自闭症辅助诊断包括训练和测试两个阶段。本文所采用的训练过程如图1所示，各步骤包括：

1）根据预处理后的静息态功能磁共振成像数据，提取出各脑区的平均时间序列信号，计算脑区之间的Pearson系数，得到低阶功能连接矩阵 ${{M}}_{{\rm{tr}}}^{\rm{l}}$ 。

2）将低阶功能连接矩阵的每一行作为各脑区的特征描述，再次计算脑区之间的Pearson系数，得到高阶功能连接矩阵 ${{M}}_{{\rm{tr}}}^{\rm{h}}$ 。

3）分别取低阶和高阶功能连接矩阵 ${{M}}_{{\rm{tr}}}^{\rm{l}}$ 和 ${{M}}_{{\rm{tr}}}^{\rm{h}}$ 的上三角阵，按行串联形成新的特征向量，然后将所有对象的特征向量进行排列，生成基于低阶和高阶功能连接的所有对象的特征矩阵；对两种不同的特征矩阵计算各特征与类标的相关性，选择与类标相关性最高的D个特征，构成矩阵 ${{X}}_{{\rm{tr}}}^{\rm{l}} = \left( {{{\left( {{{x}}_1^{\rm{tr,l}}} \right)}^{\rm{T}}};{{\left( {{{x}}_2^{\rm{tr,l}}} \right)}^{\rm{T}}}; \cdots ;{{\left( {{{x}}_N^{\rm{tr,l}}} \right)}^{\rm{T}}}} \right) \in {{\bf{R}}^{N \times D}}$ 和 ${{X}}_{{\rm{tr}}}^{\rm{h}} = \left( {{\left( {{{x}}_1^{\rm{tr,h}}} \right)}^{\rm{T}}}; \right.$ $\left.{{\left( {{{x}}_2^{\rm{tr,h}}} \right)}^{\rm{T}}};\cdots;{{\left( {{{x}}_N^{\rm{tr,h}}} \right)}^{\rm{T}}} \right) \in {{\bf{R}}^{N \times D}} $ ，其中 ${{x}}_i^{\rm{tr,l}} \in {{\bf{R}}^D}$ ， ${{x}}_i^{\rm{tr,h}} \in {{\bf{R}}^D}$ ，i = $ 1,2, \cdots ,N$ 。

4）使用无监督模糊特征映射方法对低阶和高阶功能连接的特征矩阵进行特征学习，得到相应的变换矩阵 ${{{\beta}} _g}$ ，并将 ${{X}}_{{\rm{tr}}}^{\rm{l}}$ 和 ${{X}}_{{\rm{tr}}}^{\rm{h}}$ 变换到低维空间中得到相应的嵌入矩阵 ${{E}}_{{\rm{tr}}}^{\rm{l}}$ 和 ${{E}}_{{\rm{tr}}}^{\rm{h}}$ 。

5）基于4）得到的嵌入矩阵 ${{E}}_{{\rm{tr}}}^{\rm{l}}$ 和 ${{E}}_{{\rm{tr}}}^{\rm{h}}$ ，分别计算相应的核矩阵。

6）将2种不同的核矩阵进行线性组合得到复合核矩阵。

7）构造相应的SVM分类器。

2.2 低阶和高阶功能连接矩阵的生成

虽然大脑各脑区在空间上相互隔离，但它们之间的神经活动相互影响，通常使用功能连接矩阵来表示脑区之间的时间相关性^[12]。本文使用文献[8]中的方法，基于每个脑区fMRI时间序列来计算每个对象各脑区之间的Pearson相关系数，得到低阶功能连接矩阵 ${{M}}_{{\rm{tr}}}^{\rm{l}}$ 。将低阶功能连接矩阵的每一行作为一个脑区的特征描述，使用同样的方法再次计算脑区之间的Pearson相关系数，从而得到高阶功能连接矩阵 ${{M}}_{{\rm{tr}}}^{\rm{h}}$ 。

2.3 基于流形正则化约束的模糊特征学习

为了在无监督环境中将高维空间中的样本点映射到S维的低维空间，本文引入多输出TSK模糊建模方法。TSK模糊系统是由形式为“IF-THEN”的模糊规则组成的，对于多输出TSK模糊系统，给定任意一个D维输入向量 $ {{x}} =$ $ {[{x_1}\;\;{x_2}\;\; \cdots \;\;{x_D}]^{\rm{T}}}$ ，第k条模糊规则可以表示为：

$ \begin{split} & {\rm{if}}\;\;\;\;{x_1}\;{\rm{is}}\;A_1^k \wedge {x_2}\;{\rm{is}}\;A_2^k \wedge \cdots\;\wedge {x_D} \wedge\;A_D^k, {\rm{then}} \\ & \left\{ \begin{array}{l} f_1^k\left( {{x}} \right) = \beta _0^{k,1} + \beta _1^{k,1}{x_1} + \cdots + \beta _D^{k,1}{x_D}\\ f_2^k\left( {{x}} \right) = \beta _0^{k,2} + \beta _1^{k,2}{x_1} + \cdots + \beta _D^{k,2}{x_D}\\ \qquad\qquad\qquad \vdots \\ f_S^k\left( {{x}} \right) = \beta _0^{k,S} + \beta _1^{k,S}{x_1} + \cdots + \beta _D^{k,S}{x_D} \end{array} \right. \end{split} $

式中： $A_d^k$ 表示输入特征向量 ${{x}}$ 第 $d$ 维特征所对应的第 $k$ 条模糊规则的模糊子集； $ \wedge $ 表示模糊合取操作； $k = 1,2, \cdots ,K$ ； $d = 1,2, \cdots ,D$ ，d 表示统称； $s = 1,2, \cdots ,S$ ； $K$ 表示模糊规则数； $S$ 表示模型输出的个数。

本文采用高斯函数表示模糊规则的模糊集，即

${\mu _{A_d^k}}\left( {{x_d}} \right) = {\rm{exp}}\left( {\frac{{ - {{\left( {{x_d} - c_d^k} \right)}^2}}}{{2\delta _d^k}}} \right)$

(1)

并使用式(2)、式(3)来计算每个样本相对于每条模糊规则的点火强度：

${\mu ^k}\left( x \right) = \prod\limits_{d = 1}^D {{\mu _{A_d^k}}\left( {{x_d}} \right)} $

(2)

${\tilde \mu ^k}\left( x \right) = \frac{{{\mu ^k}\left( x \right)}}{{\displaystyle\sum\limits_{k = 1}^K {{\mu ^k}\left( x \right)} }}$

(3)

参数 $c_d^k$ 和 $\delta _d^k$ 的值可以使用聚类技术或其他划分方法^[13-14]计算得出。本文使用FCM聚类算法进行数据集的模糊划分，其中 $c_d^k$ 和 $\delta _d^k$ 可通过式(4)、式(5)计算得到：

$c_d^k = \sum\limits_{i = 1}^N {{u_{ik}}{x_{id}}} /\sum\limits_{i = 1}^N {{u_{ik}}} $

(4)

$\delta _d^k = h \cdot \sum\limits_{i = 1}^N {{u_{ik}}{{\left( {{x_{id}} - c_d^k} \right)}^2}} /\sum\limits_{i = 1}^N {{u_{ik}}} $

(5)

式中： ${u_{ik}}$ 表示每个样本 ${x_i}$ 属于第 $k$ 类的模糊隶属度； $h$ 是隶属度函数的可调尺度参数。多输出TSK模糊系统的输出可以表示为

${y_s} = \sum\limits_{k = 1}^K {{{\tilde \mu }^k}\left( {{x}} \right) \cdot f_s^k\left( {{x}} \right)} $

(6)

式中 $s = 1,2, \cdots ,S$ 。

令 ${{X}} = \left( {{{x}}_1^{\rm{T}};{{x}}_2^{\rm{T}};\cdots;{{x}}_N^{\rm{T}}} \right)$ ，1为全1列向量，多输出TSK模糊系统的建模过程可用式(7)~ (13)的计算方法表述^[15]：

${{{X}}_e} = \left( {{\bf{1}},{{X}}} \right)$

(7)

${\tilde {{X}}^k} = {\rm{diag}}\left( {{{\tilde \mu }^k}\left( {{{{x}}_1}} \right),{{\tilde \mu }^k}\left( {{{{x}}_2}} \right), \cdots ,{{\tilde \mu }^k}\left( {{{{x}}_N}} \right)} \right){{{X}}_e}$

(8)

${{{X}}_g} = {\left( {{{\left( {{{\tilde {{X}}}^1}} \right)}^{\rm{T}}}{{\left( {{{\tilde {{X}}}^2}} \right)}^{\rm{T}}} \cdots {{\left( {{{\tilde {{X}}}^K}} \right)}^{\rm{T}}}} \right)^{\rm{T}}}$

(9)

${{{\beta}} ^{s,k}} = {\left( {\beta _0^{s,k},\beta _1^{s,k}, \cdots ,\beta _D^{s,k}} \right)^{\rm{T}}}$

(10)

${{{\beta}} ^s} = {\left( {{{\left( {{{{\beta}} ^{s,1}}} \right)}^{\rm{T}}},{{\left( {{{{\beta}} ^{s,2}}} \right)}^{\rm{T}}}, \cdots ,{{\left( {{{{\beta}} ^{s,K}}} \right)}^{\rm{T}}}} \right)^{\rm{T}}}$

(11)

${{{\beta}} _g} = \left[ {{{{\beta}} ^1}\quad{{{\beta}} ^2}\quad \cdots\quad {{{\beta}} ^S}} \right]$

(12)

$f\left( {{X}} \right) = {{{X}}_g}{{{\beta}} _g}$

(13)

式(7)~(13)表述的多输出TSK模糊系统建模过程可以看作将 $K\left( {D + 1} \right)$ 维空间中的数据通过变换矩阵 ${{{\beta}} _g}$ 降维到S维数据空间的过程，通常 $S < K\left( {D + 1} \right)$ 。为了学习得到适合的 ${{{\beta}} _g}$ ，本文构造的目标学习准则为

$ \begin{array}{c} \mathop {\min }\limits_{{{{\beta}} _g} \in {R^{\left( {D + 1} \right)K \times S}}} \parallel {{{\beta}} _g}{\parallel _F} + {\textit{λ}} {\rm{tr}}\left( {{{\beta}} _g^{\rm{T}}{{X}}_g^{\rm{T}}{{L}}{{{X}}_g}{{{\beta}} _g}} \right) \\ {\rm{s.t.}} {\left( {{{{X}}_g}{{{\beta}} _g}} \right)^{\rm{T}}}{{{X}}_g}{{{\beta}} _g} = {{{I}}_S} \end{array} $

(14)

式中： ${\textit{λ}} $ 为惩罚项系数；单位矩阵 ${{{I}}_S} \in {{\bf{R}}^{S \times S}}$ ； ${{L}}$ 为定义在功能连接矩阵 X 上的拉普拉斯矩阵。式(14)在 ${{{\beta}} _g}$ 全为零时取得最小值。为了避免平凡解，引入约束条件 ${\left( {{{{X}}_g}{{{\beta}} _g}} \right)^{\rm{T}}}{{{X}}_g}{{{\beta}} _g} = {{{I}}_S}$ 。本文引入流形正则化项 tr $\left( {{{\beta}} _g^{\rm{T}}{{X}}_g^{\rm{T}}{{L}}{{{X}}_g}{{{\beta}} _g}} \right)$ ，将处于流形上的特征数据映射到低维空间中，并尽可能保留特征数据间相似度。

本文中所涉及的场景是典型的高维小样本问题，故满足 $\left( {D + 1} \right)K > N$ 。式(14)可以转化为式(15)所描述的广义特征值问题：

$\left( {{{{I}}_N} + {\textit{λ}} {{L}}{{{X}}_g}{{X}}_g^{\rm{T}}} \right){{u}} = \gamma {{{X}}_g}{{X}}_g^{\rm{T}}{{u}}$

(15)

在得到最小 S 个特征值 ${\gamma _1},{\gamma _2}, \cdots ,{\gamma _S}( {\gamma _1} \leqslant {\gamma _2} \leqslant \cdots \leqslant $ $ {\gamma _S} )$ 及其对应的广义特征向量 ${{{u}}_1},{{{u}}_2}, \cdots ,{{{u}}_S}$ (因 ${{{u}}_1} = 0$ ，故不用)后，可以求得最优解为：

${{{\beta}} _g} = {{X}}_g^{\rm{T}}\left( {{{\tilde {{u}}}_2},{{\tilde {{u}}}_3},\cdots,{{\tilde {{u}}}_{S + 1}}} \right)$

(16)

式中： ${\tilde {{u}}_d} = {{{u}}_d}/||{{{X}}_g}{{X}}_g^{\rm{T}}{{{u}}_d}||$ 表示归一化特征向量，d = 2, $3, \cdots ,S + 1$ 。

无监督模型模糊特征学习的过程如图2所示。

在模型训练过程中，本文分别对低阶功能连接数据 ${{X}}_{{\rm{tr}}}^{\rm{l}} = \left( {{{x}}_1^{\rm{tr,l}};{{x}}_2^{\rm{tr,l}}; \cdots ;{{x}}_N^{\rm{tr,l}}} \right) \in {{\bf{R}}^{N \times D}}$ 和高阶功能连接数据 ${{X}}_{{\rm{tr}}}^{\rm{h}} = \left( {{{x}}_1^{\rm{tr,h}};{{x}}_2^{\rm{tr,h}}; \cdots ;{{x}}_N^{\rm{tr,h}}} \right) \in {{\bf{R}}^{N \times D}}$ 采用上述过程进行处理，分别将它们映射到S维的低维空间中去，记相应的变换矩阵分别为 ${{\beta}} _g^{\rm{l}}$ 和 ${{\beta}} _g^{\rm{h}}$ ，则低维空间中的嵌入矩阵由式(17)和式(18)计算而得：

${{E}}_{{\rm{tr}}}^{\rm{l}}{\rm{ = }}{\left( {{{X}}_{\rm{tr}}^{\rm{l}}} \right)_g}{{\beta}} _g^{\rm{l}}$

(17)

${{E}}_{{\rm{tr}}}^{\rm{h}}{\rm{ = }}{\left( {{{X}}_{\rm{tr}}^{\rm{h}}} \right)_g}{{\beta}} _g^{\rm{h}}$

(18)

2.4 基于功能连接矩阵的多视角SVM

基于上述模糊特征学习过程得到低阶和高阶嵌入矩阵 ${{E}}_{{\rm{tr}}}^{\rm{l}}$ 和 ${{E}}_{{\rm{tr}}}^{\rm{h}}$ ，本文采用文献[16]中的方法构造SVM分类器。对于拟构造的SVM分类器，采用线性核计算其核矩阵 ${{K}}_{{\rm{tr}}}^{\rm{l}}$ 和 ${{K}}_{{\rm{tr}}}^{\rm{h}}$ ：

${{K}}_{{\rm{tr}}}^{\rm{l}} = {{E}}_{{\rm{tr}}}^{\rm{l}}{\left( {{{E}}_{{\rm{tr}}}^{\rm{l}}} \right)^{\rm{T}}}$

(19)

${{K}}_{{\rm{tr}}}^{\rm{h}} = {{E}}_{{\rm{tr}}}^{\rm{h}}{\left( {{{E}}_{{\rm{tr}}}^{\rm{h}}} \right)^{\rm{T}}}$

(20)

使用式(21)对核矩阵进行线性组合，得到最终的复合核矩阵 ${{{K}}_{{\rm{tr}}}}$ ：

${{{K}}_{{\rm{tr}}}} = {\theta _1}{{K}}_{{\rm{tr}}}^{\rm{l}} + {\theta _2}{{K}}_{{\rm{tr}}}^{\rm{h}}$

(21)

式中： ${\theta _1}$ 和 ${\theta _2}$ 是复合核矩阵的组合系数，满足 ${\theta _1}{\rm{ + }}{\theta _2}=1$ 。

3 实验结果与分析 3.1 性能指标及参数设置

本节通过实验验证本文方法的有效性并与已有方法进行比较。本文选取精确度(ACC)、AUC值、敏感度(SEN)、特异性(SPE)作为实验的评价指标，实验的参数设置使用嵌套五折交叉验证来进行寻优。相关方法的表述及各参数的详细设置等信息如表3所示。

本文采用式(22)~(24)计算性能指标，以此进行算法性能评估：

${\rm{ACC}} = \frac{{{\rm{TP}} + {\rm{TN}}}}{{{\rm{TP}} + {\rm{FN}} + {\rm{TN}} + {\rm{FP}}}}$

(22)

${\rm{SEN}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}$

(23)

${\rm{SPE}} = \frac{{{\rm{TN}}}}{{{\rm{TN}} + {\rm{FP}}}}$

(24)

式中：TP和TN分别代表正确分类为自闭症患者的人数和正确分类为正常对照组的人数；FP和FN分别代表正常个体被分类为自闭症患者的人数以及自闭症患者被分类为正常对照组的人数^[17]；灵敏度SEN作为衡量该方法准确预测出自闭症患者的能力的指标；特异性SPE是衡量该方法准确预测出健康个体的能力指标。本文实验使用LIBSVM^[18]工具包中的高斯核SVM。

3.2 分类结果及分析

从表4和表5中可以看到，UFFM-M2SVC使用无监督模糊特征映射算法UFFM进行特征学习，在此基础上构造分类器M2SVC，可以取得比LOFCC、HOFCC及M2SVC等传统分类器更好的性能。

M2SVC算法联合使用两个视角的数据进行分类，其分类结果要明显优于基于单视角的分类器LOFCC和HOFCC；而本文方法采用新型的模糊特征学习技术进行特征学习，在此基础上使用M2SVC进行分类，从而取得了比仅使用M2SVC更好的效果，这表明本文所使用的模糊特征学习技术能够得到更有鉴别能力的特征，这对自闭症的诊断具有更优的判别能力。

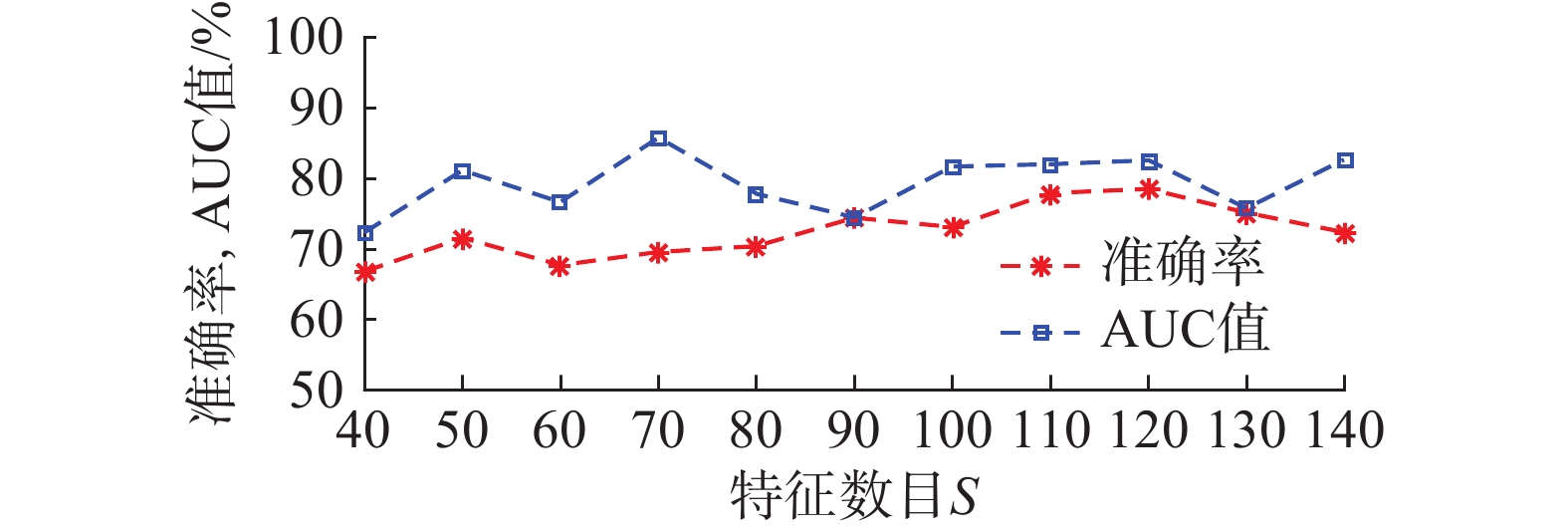
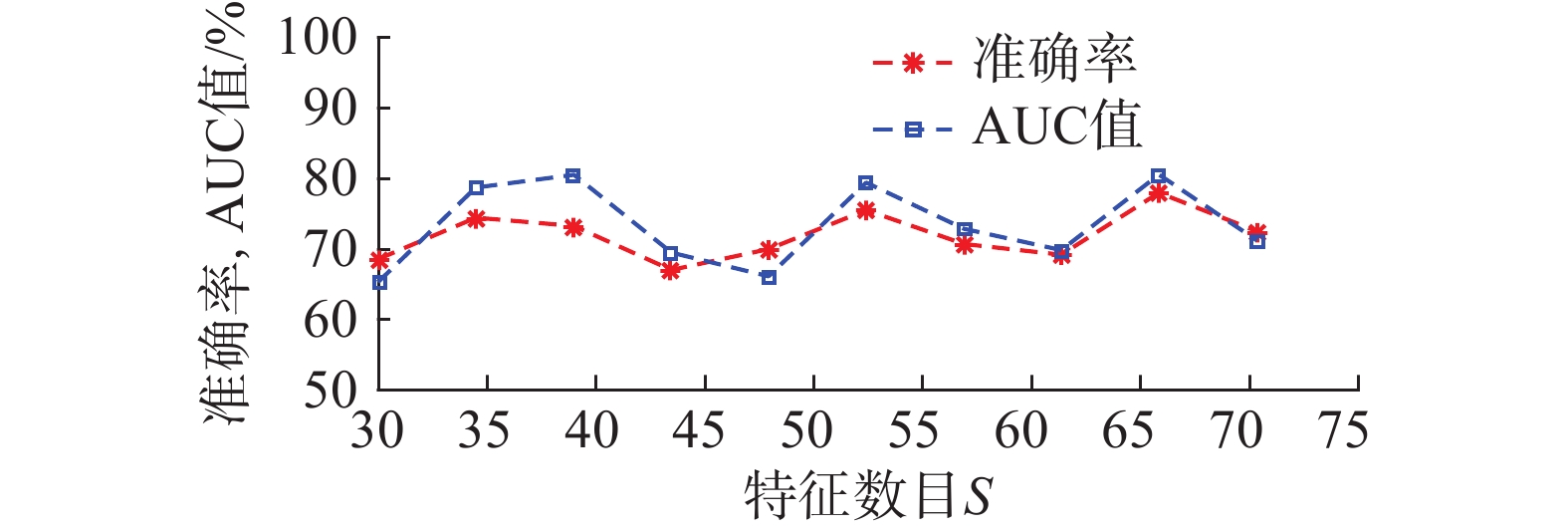
3.3 特征数目对实验结果的影响

本节研究UFFM所提取的特征数目S对M2SVC性能的影响，图3和图4中给出了算法在数据集NYU和USM上S取不同值时M2SVC的分类结果。从图3和图4可以看出，UFFM-M2SVC算法的分类准确率随着S取值的不同而发生变化，图3中最高达到78.38%，图4中最高达到78.95%，均比M2SVC算法提高了约5%。可知，在特征提取数S合理取值的情况下，本文使用UFFM进行无监督模糊特征学习，不仅可以有效保留原始有效的特征信息，而且去除了其中包含的冗余信息，使得自闭症患者和正常对照组之间的特征差异更有区分性。

4 结束语

自闭症患者的脑区神经活动异于常人。以此为出发点，本文基于静息态fMRI提出了一种面向自闭症辅助诊断的无监督模糊特征学习方法UFFM，并与M2SVC相结合，从而实现了自闭症的辅助诊断。相对于目前传统的分类算法，UFFM-M2SVC算法训练出的分类模型具有优越且稳定的分类性能。实验结果表明，本文所使用的无监督模糊特征学习方法能够有效地提取出fMRI数据中的重要特征，从而有助于自闭症的临床辅助诊断。但是，本文仅基于静息态fMRI数据进行实验，针对任务态fMRI数据的分类效果还未可知，有待进一步的研究。