现代社会中的信息呈爆炸式增长，使得社会系统极具复杂性。研究表明，各种系统之间的交互信息可以通过对应的复杂网络表示，其中，网络中的节点代表系统中的个体，连边代表个体之间的关系^[1]。网络科学是专门用于研究各种复杂网络系统的定性和定量规律的一门交叉学科^[2]。然而，由于隐私政策和个体设置等原因，实际获取的网络连边信息往往是不完整的，加大了网络科学研究的难度。链路预测能够对缺失信息进行还原和预测，是网络科学研究的有力辅助工具，具有重要的理论研究和实际应用价值。一方面，链路预测可以帮助人们理解各种复杂网络的演化机制^[3-4]，为不同演化模型的优劣比较提供统一平台；另一方面，链路预测的结果可以指导生物网络中的实验，降低实验成本并提高准确率，还可以建立网络中的推荐系统^[5]。

网络中的链路预测，是指如何根据网络中已知的节点和结构信息，预测网络中尚未产生连边的两个节点之间产生连接的可能性^[6]，包括未来链接和未知链接的预测，常用的方法可分为两大类：基于相似性的方法和智能方法。

基于相似性方法的一个基本假设是：两个节点越相似，在未来连接的可能性越大，而节点的相似程度可通过相似性指标量化，即根据相似性指标计算相似性得分，得分越高，两个节点越相似。已有相似性指标可分为三大类：基于节点局部信息的方法，如共同邻居(CN)^[7]、Adamic-Adar(AA)^[8]和资源分配(RA)^[9]指标等；基于全局路径的方法，如Katz^[7]和局部路径(LP)^[9]等；基于随机游走的方法^[10]。

上述方法中，基于节点局部信息的方法运算复杂度最低，且预测准确度较高，因此常被用作基准指标。吕琳媛等^[11]对几种基准指标的研究发现，无论是否加权，RA均表现最好，且无权指标的性能均优于加权指标。由此得出：复杂网络中的弱连接不容忽视，强调弱连接的贡献可以极大提高预测准确度。此外，作者意识到这些指标存在共同缺点，即认为所有共同邻居对于节点对的贡献相同。为此，Liu等^[12]假设每个共同邻居的贡献不同，有些促进链接的产生，有些则抑制，因此共同邻居数量相同的节点对产生链接的概率可能不同。然后将朴素贝叶斯理论应用到链路预测中，提出了局部朴素贝叶斯(LNB)模型。最近，Valverde-Rebaza等^[13]认为每个用户可能同时属于多个社团，且扮演角色不同，预测时应充分考虑用户所属的所有社团信息。基于此思想，Valverde-Rebaza在文献[14]中提出了基于重叠组的朴素贝叶斯(GNB)链路预测模型。此外，考虑到共同邻居之间并非完全相互独立，文献[15]使用互信息量化共同邻居的相关性，对LNB进行推广，提出了广义的树增广朴素贝叶斯(TAN)概率模型，并扩展到了CN、AA和RA指标，在运行效率和有效性等方面均优于基准方法。然而，上述方法仅考虑了共同邻居的作用，忽略了节点自身的影响。闫玲玲等^[16]提出了一种基于度和聚类系数的新指标，对中国航空网络中的节点重要性进行分析。Pujari等^[17]认为节点对的每个属性代表不同信息，可以将所有属性对应特征进行加权整合以提高预测性能。Li等^[18]以新浪微博为研究对象，根据其自身特点提出了包含用户临近特征、属性特征和拓扑特征的特征集用于预测。但这些方法仅考虑了节点自身作用，忽略了共同邻居的影响。

为解决上述问题，本文基于局部朴素贝叶斯(LNB)模型提出了融合朴素贝叶斯(syncretic naive Bayes，SNB)模型。本文的主要贡献如下。1)认为链接的产生受到内部和外部两方面因素的影响。其中，节点对自身特点属于内部影响，可以通过节点度量化；共同邻居的作用属于外部影响，可以通过LNB模型量化，将两者结合提出一个新模型。2)模型的优劣不仅体现在其自身的预测精确度上，还体现在它与其他思想的融合效果上，后者可以通过其在基准指标推广后的预测精确度定性描述。因此，文中将SNB推广到CN、AA和RA形式，说明其具有普适性。

近些年，智能方法受到广泛关注。已有研究包括支持向量机^[19]、BP神经网络^[20-21]、3层隐含的贝叶斯(3-HBP)链路预测模型^[22]、最大熵模型^[23]以及可变贝叶斯概率矩阵分解模型^[24]等。与直接给节点对分配相似性得分不同，这些方法都是通过学习已知知识建立模型进行预测，是将来的研究重点。

1 预备知识

本部分首先给出了链路预测的概念，然后介绍了本文的理论基础——朴素贝叶斯理论，接着阐述了一些常用的基准指标，最后简要介绍了局部朴素贝叶斯(LNB)链路预测模型。

1.1 问题描述

一个无权无向的网络图可表示为 $G(V,E)$ ，其中 $V$ 代表节点集， $E \subseteq V \times V$ 代表节点之间的连边集合，本文不考虑自环和重复边。假设有两个节点 $x \subseteq V,y \subseteq V$ ，则 ${e_{xy}} = \left\langle {x,y} \right\rangle \in E$ 表示节点 $x$ 和 $y$ 之间存在链接，而 $\overline {{e_{xy}}} = \left\langle {x,y} \right\rangle \notin E$ 表示节点 $x$ 和 $y$ 之间不存在链接。网络中所有可能连边的集合为 $A$ ，则 $|A| = \displaystyle\frac{{|V| \times (|V| - 1)}}{2}$ 。因此，不存在的连边集合为 $N = A - E$ 。文中 $N(x)$ 代表节点 $x$ 的邻居集合，则节点 $x$ 和节点 $y$ 的共同邻居集合可以记为 $N(x,y) =$ $ N(x) \cap N(y)$ 。

通常，按照某种比例 $r$ 将网络中所有连边划分为训练集 ${E^T}$ 和测试集 ${E^P}$ 。其中， ${E^T}$ 代表已知连边集合， ${E^P}$ 代表缺失连边集合，链路预测的任务是根据 ${E^T}$ 建立模型预测出 ${E^P}$ 中的连边。

1.2 朴素贝叶斯理论

朴素贝叶斯分类器简单易懂，受到了众多学者的青睐。假设 $C$ 为类变量， ${{X}} = ({X_1},{X_2}, \cdots ,{X_n})$ 代表 $n$ 维特征向量。根据贝叶斯理论，已知特征向量 ${{X}}$ 求类变量 $C$ 取某值的概率为后验概率 $P(C|{{X}})$ ：

$\begin{array}{c} P(C|{{X}}) = P(C|{X_1},{X_2}, \cdots ,{X_n}) = \\ \displaystyle\frac{{P(C) \cdot P({X_1},{X_2}, \cdots ,{X_n}|C)}}{{P({X_1},{X_2}, \cdots ,{X_n})}} \end{array}$

(1)

朴素贝叶斯的基本假设是：当类变量 $C$ 取值固定时，各特征变量 ${X_i}(i = 1,2, \cdots ,n)$ 之间相互独立，即

$P({X_1},{X_2}, \cdots ,{X_n}|C) = \prod\limits_{i = 1}^n {P({X_i}|C)} {\rm{ }}$

(2)

将式(2)代入式(1)可得

$P(C|{{X}}) = \frac{{P(C) \cdot \prod\limits_{i = 1}^n {P({X_i}|C)} }}{{P({X_1},{X_2}, \cdots ,{X_n})}}$

1.3 基准指标

1) 共同邻居指标(CN)

通常认为，共同邻居越多，节点对越相似。CN指标通过直接计算共同邻居数目来量化节点对的相似性^[7]，定义如下：

$s_{xy}^{\rm{CN}} = |N(x) \cap N(y)| = |N(x,y)|$

2) Adamic-Adar指标(AA)

AA指标^[8]以CN指标为基础，认为度越大的共同邻居对于节点对的贡献越小。因此，可以通过惩罚度大的邻居节点提高预测准确度，其定义为

$s_{xy}^{\rm{AA}} = \sum\limits_{{\textit{z}} \in N(x,y)} {\frac{1}{{\log {k_{\textit{z}}}}}} $

式中 ${k_{\textit{z}}}$ 表示节点 z 的度。

3) 资源分配指标(RA)

受到资源分配动力学的启发，RA指标^[9]根据资源在节点间的传递情况，结合惩罚大度节点的思想，定义了节点对的相似性：

$s_{xy}^{\rm{RA}} = \sum\limits_{{\textit{z}} \in N(x,y)} {\frac{1}{{{k_{\textit{z}}}}}} {\rm{ }}$

1.4 LNB链路预测模型

LNB模型^[11]假设节点 $x$ 和 $y$ 是否连接取决于它们的共同邻居集合，即节点 $x$ 和 $y$ 在未来连接和未连接的概率为后验概率 $P({e_{xy}}|N(x,y))$ 和 $P(\overline {{e_{xy}}} |N(x,y))$ ，根据贝叶斯理论有

$P({e_{xy}}|N(x,y)) = \frac{{P({e_{xy}}) \cdot P(N(x,y)|{e_{xy}})}}{{P(N(x,y))}}$

(3)

$P(\overline {{e_{xy}}} |N(x,y)) = \frac{{P(\overline {{e_{xy}}} ) \cdot P(N(x,y)|\overline {{e_{xy}}} )}}{{P(N(x,y))}}$

(4)

其中， ${e_{xy}},\overline {{e_{xy}}} $ 是类变量 $C$ 的两个取值，分别表示节点 $x$ 和 $y$ 连接与未连接，由于各个共同邻居之间相互独立，则：

$P(N(x,y)|{e_{xy}}) = \prod\limits_{{\textit{z}} \in N(x,y)} {P({\textit{z}}|{e_{xy}})} {\rm{ }}$

(5)

$P(N(x,y)|\overline {{e_{xy}}} ) = \prod\limits_{{\textit{z}} \in N(x,y)} {P({\textit{z}}|\overline {{e_{xy}}} )} $

(6)

将式(5)和式(6)分别代入式(3)和式(4)，然后两式相除，得：

$r_{xy}^{\rm{LNBCN}} = \underbrace {\frac{{P({e_{xy}})}}{{P(\overline {{e_{xy}}} )}} \cdot \prod\limits_{{\textit{z}} \in N(x,y)} {\frac{{P(\overline {{e_{xy}}} )}}{{P({e_{xy}})}}} }_{{\rm{constant \; value }}}{\rm{ }} \cdot \underbrace {\prod\limits_{{\textit{z}} \in N(x,y)} {\frac{{P({e_{xy}}|{\textit{z}})}}{{P(\overline {{e_{xy}}} |{\textit{z}})}}} {\rm{ }}}_{{\rm{role \; of \; }} {\rm{node \; {\textit{z}}}}}$

(7)

式中 $P({e_{xy}})\text{、}P(\overline {{e_{xy}}} )$ 分别表示节点 $x$ 和 $y$ 连接与未连接的先验概率：

$P({e_{xy}}) = \frac{{|{E^T}|}}{{|A|}}$

$P(\overline {{e_{xy}}} ) = \frac{{|A| - |{E^T}|}}{{|A|}}$

显然， $P({e_{xy}})\text{、} P(\overline {{e_{xy}}} )$ 均为常数，则 ${s^{ - 1}} = \displaystyle\frac{{P({e_{xy}})}}{{P(\overline {{e_{xy}}} )}} =$ $ \displaystyle\frac{{|{E^T}|}}{{|A| - |{E^T}|}}$ 也为常数，表示网络中存在边与不存在边的比值，可以忽略。而 $P({e_{xy}}|{\textit{z}})$ 表示节点 z 的聚类系数：

$P({e_{xy}}|{\textit{z}}) = {c_{\textit{z}}} = \frac{{2T({\textit{z}})}}{{{k_{\textit{z}}} \cdot ({k_{\textit{z}}} - 1)}}$

(8)

$P(\overline {{e_{xy}}} |{\textit{z}}) = 1 - {c_{\textit{z}}}$

(9)

式中 $T({\textit{z}})$ 代表节点 ${\textit{z}}$ 的 ${k_{\textit{z}}}$ 个邻居之间真实存在的边数。令 ${R_{\textit{z}}} = \displaystyle\frac{{P({e_{xy}}|{\textit{z}})}}{{P(\overline {{e_{xy}}} |{\textit{z}})}}$ 表示 z 的邻居之间连接与未连接的比值， ${R_{\textit{z}}}$ 值越大，说明节点 z 的邻居之间更倾向于相互连接，即节点 z 的促进作用越强。不同节点的 ${R_{\textit{z}}}$ 值一般不同，因此称 ${R_{\textit{z}}}$ 为节点 z 的角色函数。将式(8)、式(9)代入式(7)，等式两边取对数得：

$s_{xy}^{{\rm{LNBCN}}} = \sum\limits_{{\textit{z}} \in N(x,y)} {(\log s + \log {R_{\textit{z}}})} $

将其推广可得：

$s_{xy}^{{\rm{LNBAA}}} = \sum\limits_{{\textit{z}} \in N(x,y)} {\frac{1}{{\log {k_{\textit{z}}}}}} (\log s + \log {R_{\textit{z}}})$

$s_{xy}^{{\rm{LNBRA}}} = \sum\limits_{{\textit{z}} \in N(x,y)} {\frac{1}{{{k_{\textit{z}}}}}} (\log s + \log {R_{\textit{z}}})$

2 融合朴素贝叶斯链路预测模型

在介绍SNB模型之前，首先考虑一个问题，节点之间链接的产生到底与什么因素有关？图1给出了3种不同的思路。

最简单的一种思路是：两节点的共同邻居数目越多，它们的兴趣属性等越接近，未来越有可能产生链接，这便是图1(a)中CNs指标的主要思想。因此，图中节点 $c$ 和 $d$ 的共同邻居数目多，它们产生链接的可能性大于节点 $a$ 和 $b$ 。

在CNs的基础上，有学者指出，每个共同邻居扮演角色不同，对于节点对产生链接的贡献不同，因此不能通过简单计算共同邻居的数目得到相似性，而应该累加共同邻居的贡献以得到最终的相似性分数。按照此思想，图1(b)中节点 $a$ 和 $b$ 的共同邻居只有2个，但每个共同邻居的邻居之间大多存在链接，说明这两个共同邻居对其邻居间链接的产生有促进作用；节点 $c$ 和节点 $d$ 的共同邻居有3个，但每个共同邻居的邻居之间基本没有链接，说明这些共同邻居对其邻居间链接的产生有抑制作用。综上，节点 $a$ 和 $b$ 在未来产生链接的可能性更大。

实际生活中，节点间链接的产生不仅受到共同邻居的影响，与其自身的活跃程度也是密不可分的。在共同邻居数目相等的条件下，节点倾向于和更活跃的个体产生链接；当共同邻居数目不等时，如图1(c)中，节点 $a$ 和 $b$ 的共同邻居少且均为促进作用，但其自身的度比较小；节点 $c$ 与 $d$ 的共同邻居多且均为抑制作用，但其自身的度比较大。共同邻居与节点自身究竟谁的作用更大，需要具体计算，这便是SNB模型的核心思想。

本文认为，节点 $x$ 和 $y$ 之间链接的产生受到内部和外部因素的影响。其中，共同邻居的作用属于外部影响，根据LNB的相关知识，每个共同邻居的作用不尽相同，或促进或抑制。另一方面，链接的产生与节点 $x$ 和 $y$ 自身的活跃程度密切相关，影响大小可以通过节点的度进行量化。这意味着，度相同的两对节点产生链接的概率会因共同邻居贡献不同而不同，受共同邻居作用相同的两对节点也会因其自身的度不同而产生差异。基于此思想，本文综合考虑了共同邻居与节点对自身的作用，提出了融合朴素贝叶斯(SNB)链路预测模型。

在SNB模型下，节点 $x$ 和 $y$ 产生链接的后验概率为:

$\begin{array}{c} P({e_{xy}}|N(x,y),{k_x},{k_y}) = \\ \displaystyle\frac{{P({e_{xy}}) \cdot P(N(x,y),{k_x},{k_y}|{e_{xy}})}}{{P(N(x,y),{k_x},{k_y})}} \end{array}$

(10)

$\begin{array}{c} P(\overline {{e_{xy}}} |N(x,y),{k_x},{k_y}) = \\ \displaystyle\frac{{P(\overline {{e_{xy}}} ) \cdot P(N(x,y),{k_x},{k_y}|\overline {{e_{xy}}} )}}{{P(N(x,y),{k_x},{k_y})}} \end{array}$

(11)

由概率论相关知识，可得：

$\begin{array}{c} P(N(x,y),{k_x},{k_y}|{e_{xy}}) = \\ P(N(x,y)|{e_{xy}}) \cdot P({k_x}|{e_{xy}},N(x,y)) \cdot \\ P({k_y}|{e_{xy}},N(x,y),{k_x}) \end{array}$

(12)

$\begin{array}{c} P(N(x,y),{k_x},{k_y}|\overline {{e_{xy}}} ) = \\ P(N(x,y)|\overline {{e_{xy}}} ) \cdot P({k_x}|\overline {{e_{xy}}} ,N(x,y)) \cdot \\ P({k_y}|\overline {{e_{xy}}} ,N(x,y),{k_x}) \end{array}$

(13)

将式(12)和式(13)分别代入式(10)和式(11)，可得:

$\begin{array}{c} r_{x,y}^{{\rm{SNBCN}}} = \displaystyle\frac{{P({e_{xy}}|N(x,y),{k_x},{k_y})}}{{P(\overline {{e_{xy}}} |N(x,y),{k_x},{k_y})}}{\rm{ = }}\\ \underbrace {\frac{{P({e_{xy}})}}{{P(\overline {{e_{xy}}} )}} \cdot \frac{{P(N(x,y)|{e_{xy}})}}{{P(N(x,y)|\overline {{e_{xy}}} )}}}_{{\rm{LNBCN}}} \cdot \underbrace {\frac{{P({k_x}|{e_{xy}},N(x,y))}}{{P({k_x}|\overline {{e_{xy}}} ,N(x,y))}}}_{{\rm{influence}}\;{\rm{of}}\;{\rm{node}}\;x} \cdot \\ \underbrace {\frac{{P({k_y}|{e_{xy}},N(x,y),{k_x})}}{{P({k_y}|\overline {{e_{xy}}} ,N(x,y),{k_x})}}}_{{\rm{influence}}\;{\rm{of}}\;{\rm{node}}\;y}{\rm{ }} \end{array}$

(14)

由式(14)可知， $r_{x,y}^{{\rm{SNBCN}}}$ 的值由3部分决定：共同邻居的影响，可以通过LNB模型的式(7)得到；节点 $x$ 的度的影响 ${R_x}$ 以及节点 $y$ 的度的影响 ${R_y}$ ，可以通过下面的分析得到。其中，节点 $x$ 和 $y$ 的度的影响统称为节点度的影响，图2给出了式(14)的图解。可以看出，一个复杂的链路预测问题可以分解为2个子问题，箭头左边相当于本文的SNB模型，箭头右边的第1部分相当于只考虑共同邻居的影响，属于外部因素；第2部分相当于只考虑节点对自身的影响，属于内部因素。

首先考虑式(14)中的第2项，即节点 $x$ 的度的影响。假设网络中总的节点数为 $m = |V|$ ，已知 $x$ 和 $y$ 连接，且它们的共同邻居数为 $n = |N(x,y)|$ ，若节点 $x$ 产生新的链接，则新链接中另一个节点有 $m - n - 1 - 1$ 种可能，其中第1个1表示节点 $x$ 不可能形成自环，第2个1表示节点 $x$ 和 $y$ 不可能存在一条以上的连边，即不考虑重复边。进一步的，若想要节点 $x$ 的度为 ${k_x}$ ，则除了与它和节点 $y$ 的共同邻居相连接外，还需要连接 ${k_x} - n - 1$ 个节点，其中1表示它与节点 $y$ 已连接。对于后验概率 $P({k_x}|{e_{xy}},N(x,y))$ ，即在节点 $x$ 与 $y$ 相连接且两者的共同邻居已知的条件下，求节点 $x$ 的度为 ${k_x}$ 的概率，是一个如何在可与节点 $x$ 产生新链接的所有节点中选取 ${k_x} - n - 1$ 个节点的组合问题。因此，

$P({k_x}|{e_{xy}},N(x,y)) = C_{m - n - 2}^{{k_x} - n - 1} $

(15)

同理可得：

$P({k_x}|\overline {{e_{xy}}} ,N(x,y)) = C_{m - n - 2}^{{k_x} - n}$

(16)

然后考虑式(14)的第3项，即节点 $y$ 的度的影响。在式(14)中第2项已知条件的基础上，已知节点 $x$ 的度为 ${k_x}$ 。若节点 $y$ 产生新链接，则可与 $y$ 形成新链接的另一个节点有 $m - {k_x} - 1$ 种可能，其中 ${k_x}$ 代表节点 $y$ 不可能与节点 $x$ 的邻居相连，增加共同邻居数，由于节点 $x$ 的邻居已经包括 $y$ ，所以节点 $y$ 不可能形成自环；1表示节点 $y$ 与 $x$ 不可能形成重复边。进一步的，若想要节点 $y$ 的度为 ${k_y}$ ，则除了与之相连的它和节点 $x$ 的共同邻居外，还需要连接 ${k_y} - n - 1$ 个节点，其中1表示节点 $y$ 与 $x$ 已连接。则后验概率 $P({k_y}|{e_{xy}},N(x,y),{k_x})$ ，即节点 $x$ 与 $y$ 已连接且两者的共同邻居数和节点 $x$ 的度已知时，求节点 $y$ 的度为 ${k_y}$ 的概率，是一个在可与 $y$ 产生新链接的所有节点中选取 ${k_y} - n - 1$ 个节点的组合问题：

$P({k_y}|{e_{xy}},N(x,y),{k_x}) = C_{m - {k_x} - 1}^{{k_y} - n - 1}$

(17)

同理，当节点 $x$ 和 $y$ 未连接时，节点 $x$ 的邻居不包括 $y$ 。若节点 $y$ 产生新链接，则可与 $y$ 形成新链接的另一个节点有 $m - {k_x} - 1 - 1$ 种可能，其中第1个1表示节点 $y$ 不可能形成自环，第2个1表示节点 $x$ 和 $y$ 不可能连接。进一步的，若想要节点 $y$ 的度为 ${k_y}$ ，它还需要连接 ${k_y} - n$ 个节点，则后验概率 $P({k_y}|\overline {{e_{xy}}} ,N(x,y),{k_x})$ ，即在可与节点 $y$ 产生新链接的所有节点中选取 ${k_y} - n$ 个节点的组合问题：

$P({k_y}|\overline {{e_{xy}}} ,N(x,y),{k_x}) = C_{m - {k_x} - 2}^{{k_y} - n}$

(18)

将式(7)，式(15)~(18)代入式(14)，可得：

$\begin{array}{c} r_{xy}^{{\rm{SNBCN}}} = \underbrace {\frac{{P({e_{xy}})}}{{P(\overline {{e_{xy}}} )}} \cdot \prod\limits_{{\textit{z}} \in N(x,y)} {\frac{{P(\overline {{e_{xy}}} )}}{{P({e_{xy}})}}} }_{{\rm{constant}}\;{\rm{value}}} \cdot \\ \underbrace {\prod\limits_{{\textit{z}} \in N(x,y)} {\frac{{P({e_{xy}}|{\textit{z}})}}{{P(\overline {{e_{xy}}} |{\textit{z}})}}} }_{R{\textit{z}}} \cdot \underbrace {\frac{{C_{m - n - 2}^{{k_x} - n - 1}}}{{C_{m - n - 2}^{{k_x} - n}}}}_{Rx} \cdot \underbrace {\frac{{C_{m - {k_x} - 1}^{{k_y} - n - 1}}}{{C_{m - {k_x} - 2}^{{k_y} - n}}}}_{Ry} \end{array}$

(19)

忽略常数 $\displaystyle\frac{{P({e_{xy}})}}{{P(\overline {{e_{xy}}} )}}$ ，式(19)等号两端取对数，可得其简化形式：

$s_{xy}^{{\rm{SNBCN}}} = \sum\limits_{{\textit{z}} \in N(x,y)} {(\log s + \log {R_{\textit{z}}})} + \log {R_x} + \log {R_y}$

受LNB模型的启发，本文将SNBCN推广到了AA和RA形式，以证明所提SNB模型的有效性。可以得到：

$\begin{array}{c} s_{xy}^{{\rm{SNBAA}}} = \displaystyle\sum\limits_{{\textit{z}} \in N(x,y)} {\displaystyle\frac{1}{{\log {k_{\textit{z}}}}}(\log s + \log {R_{\textit{z}}})} + \\ \displaystyle\frac{{\log {R_x}}}{{\log {k_x}}} + \frac{{\log {R_y}}}{{\log {k_y}}} \end{array}$

$\begin{array}{c} s_{xy}^{{\rm{SNBRA}}} = \displaystyle\sum\limits_{{\textit{z}} \in N(x,y)} {\displaystyle\frac{1}{{{k_{\textit{z}}}}}(\log s + \log {R_{\textit{z}}})} + \\ \displaystyle\frac{{\log {R_x}}}{{{k_x}}} + \frac{{\log {R_y}}}{{{k_y}}} \end{array}$

显然，当节点 $x$ 和 $y$ 相连的节点全部相同时，SNB模型会退化为LNB模型，则SNBCN、SNBAA和SNBRA指标会退化为相应的LNB指标。

3 链路预测实验

所提SNB模型的有效性需要实验的验证，为此，本文将从以下几个方面做详细介绍。

3.1 数据集

本文采用的数据集为美国航空网络(USAir)，包含332个机场和2 126条航线。网络的聚类系数 $C = 0.749$ ，同配系数 $r = - 0.208$ ，平均度 $\left\langle k \right\rangle = 12.81 $ ，平均最短距离 $\left\langle d \right\rangle = 2.74$ ，度异质性 $H = \displaystyle\frac{{\left\langle {{k^2}} \right\rangle }}{{{{\left\langle k \right\rangle }^2}}} = $ 3.46。原网络为含权网络，文中忽略了权重信息，将其当作无权网络处理。

3.2 基准方法与评价指标

1) 基准方法

为方便评判SNB模型的性能优劣，本文采用CN、AA和RA(记为CNs)与LNBCN、LNBAA和LNBRA(记为LNBs)等作为基准指标。由于CNs和LNBs指标在前文已作介绍，此处不再赘述。

2) 评价指标

链路预测算法多种多样，需要统一的评价指标对其进行性能优劣比较，本文选用AUC和精确度量化算法的准确度。

AUC (area under the receiver operating characteristic curve)表示随机从测试集 ${E^P}$ 中选择一条边的分数值比随机选择一条不存在的边分数高的概率^[6]。假设一共进行了 $n$ 次独立比较，其中有 ${n'}$ 次测试集里的边得分高于不存在的边得分，有 ${n{''}}$ 次两者得分相等，则AUC值为

$AUC = \frac{{{n'} + 0.5{n{''}}}}{n}$

精确度(precision)表示前 $L$ 条预测边中预测准确的比例^[6]。计算精确度时，将所有未知连边(包括测试集中的边和不存在的边)按照其相似性分数降序排列，然后选择排名靠前的前 L 条边，若有 $m$ 条边在测试集中，即有 $m$ 条边预测准确，则

${\rm{Precision}} = \frac{m}{L}$

本实验中设置 $L = 100$ 。

3.3 实验设置

本实验中训练集与测试集的划分比例为9∶1。由于网络中存在数据类别不平衡问题，即已知连边与不存在连边的数目相差很大，直接采取随机采样方式会严重影响预测效果。为此，本实验采用了分层采样，在保证训练集与测试集中存在边和不存在边的比例与原网络相同的条件下，随机划分数据集。另外，为消除随机误差的影响，实验中采用了10折交叉验证方法，且重复10次后取平均值作为最终结果。

3.4 实验结果与分析

本部分通过两方面内容评估SNB模型的性能：与基准指标的预测结果比较；当训练集大小发生变化时，预测结果的变化情况。

3.4.1 不同方法性能比较

当按照9∶1的比例划分训练集与测试集时，在USAir网络得到的预测结果如表1所示。可以看出：

1) SNBs的AUC值最高，LNBs和CNs次之。说明SNBs模型整体的预测准确度最高。

2) SNBs比LNBs的AUC值高，说明与单独考虑共同邻居相比，将共同邻居与节点自身综合考虑效果更好。

3) SNBs系列指标中，SNBRA的AUC值最高，SNBAA次之，之后是SNBCN，LNBs系列指标也有类似规律，这与之前的认识相符，即RA指标预测效果优于AA指标，AA指标预测效果优于CN指标，说明惩罚大度节点确实可以提高预测准确度，证实了文献[11]中的结论。

4) SNBCN相对于LNBCN和CN的AUC的提高幅度最大，SNBAA次之，接着是SNBRA。究其原因，一方面是因为预测效果越差的指标越容易提高，另一方面是因为直接计算共同邻居的贡献时，节点自身的影响是最大的，不容忽视。且节点的度越大，越倾向于形成链接，符合优先连接原则，因此考虑节点度的影响可以极大地提高准确度。而SNBAA和SNBRA认为，度越大的节点贡献越小，这与优先连接思想相悖，相当于将节点度对其自身的影响中和掉了一部分，导致AUC提高的幅度变小。

5) 对于精确度值，SNBs整体上与LNBs和CNs相差不大，甚至有所下降，可能是因为在预测的前100条边中，节点受其自身度的影响不大。

综上，可以得到如下结论：

1) SNBs的AUC值较LNBs和CNs明显提高，说明SNB模型倾向于赋予预测集中的链接更高的分数，即整体上SNBs能够更好地将测试集中的边与不存在的边区分开。

2) 3种方法的精确度变化不明显，说明三者对测试集中边的排序位置相差不大。

3) SNBs能够在基本保证前100条边中预测准确率一定的条件下，将更多地测试链接识别出来，证明了其有效性。

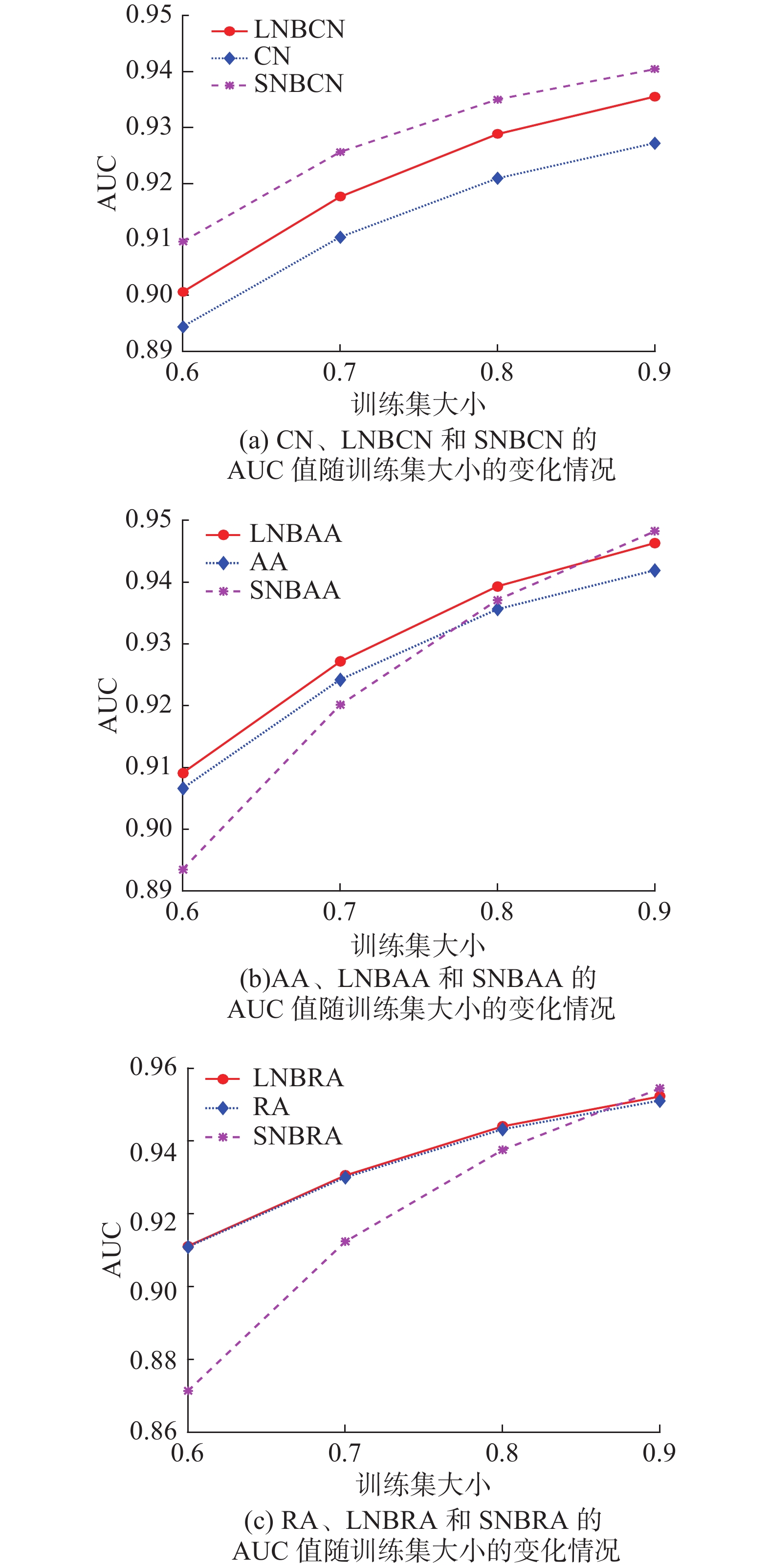
3.4.2 预测效果随训练集大小的变化情况

本实验中，训练集比例从0.6开始，步长为0.1，直到比例达到0.9，得到的CNs, LNBs, SNBs的AUC和精确度随训练集大小变化情况如图3和4所示。

图3(a)中，SNBCN的AUC值始终高于LNBCN和CN，证明了SNB模型的高效性；图3(b)和(c)的变化趋势相似，当训练集比例较小时，SNBRA和SNBAA的AUC值均最低，随着训练集的增大，SNBs与其他指标的差距逐渐减小，并在训练集比例为0.9时超过其他指标，说明SNB模型在训练集比例为0.9时的总体预测准确度最高。

图4(a)和图4(b)具有一致的变化趋势，即SNBs的精确度略低于LNBs和CNs指标，而图4(c)中SNBRA的精确度值一直处于或接近最高值，可能是因为：节点自身影响不能简单地用度进行量化，将节点度与资源分配思想结合可以取得更好的预测性能。

结合图3与图4，可以得出以下结论：

1) 随着训练集比例增大，几种指标的AUC值均呈增长趋势，而精确度值均呈递减趋势，这可能是由于AUC和精确度本身的侧重点不同造成的。其中，AUC侧重于总体的预测准确率，当训练集比较大(已知信息丰富)时，预测缺失边越容易，AUC值越高；精确度侧重于前 $L$ 条边的预测准确率，当测试集比例较大时，前 $L$ 条预测边在测试集的可能性越大，精确度越高。

2) 当SNB模型的AUC值较低时，精确度值一般最高或接近最高；同理，当其精确度值较低时，AUC值一般最高或接近最高，说明SNB模型的AUC和精确度一定有一个最高值，进一步从侧面印证了SNB模型的有效性。

4 总结与展望

近来，有文献指出：社交网络中链接的产生受内部和外部因素的影响。受此思想的启发，本文在局部朴素贝叶斯(LNB)的基础上，结合节点度的自身影响，提出了融合朴素贝叶斯(SNB)模型。该模型易于推广到其他的基于共同邻居的指标形式，如AA和RA具有良好的可扩展性。在美国航空网(USAir)上的实验结果表明：与基准方法相比，提高了链路预测性能，证实了该方法的有效性。由此得出结论：链接的产生不仅受到共同邻居的影响，也受到其自身度的影响，将二者综合考虑更加合理。

未来，将尝试将该思想推广到智能方法做链路预测，如支持向量机、相关向量机等。另外，考虑到本文研究的是无权无向网络，以后可以先在更多不同领域的网络上实现，然后再着眼于加权网络的研究。