中国象棋是一种广为流传的完全知识二人零和博弈游戏，形式上与国际象棋极为相似^[1-2]，在博弈技术上二者也有许多共通之处。2016年以来，谷歌相继推出AlphaGo^[3]、AlphaGo Zero^[4]、AlphaZero^[5]等博弈模型，不仅在围棋领域完胜人类棋手，在国际象棋、日本将棋上也超越了之前最先进的博弈引擎，计算机博弈受到人们广泛关注。

中国象棋博弈常提及的一个问题就是中国象棋空间复杂度，即中国象棋状态总数。现有文献仅给出中国象棋空间复杂度数值却没有提供计算方式，同时不同文献给出的数值存在较大差异。长期以来，中国象棋状态总数这一计数问题无人问津，却又莫衷一是。本文利用中国象棋棋子着法特点把求解中国象棋状态总数问题分解为若干个子问题，通过动态规划方法分别求解各个子问题，最终准确求出中国象棋状态总数，为以后描述中国象棋状态总数提供可靠依据。同时，这种计算中国象棋状态总数的方法除了可用于计算其他棋类的空间复杂度，也可以用于构造中国象棋棋盘局面哈希函数^[6]、构造中国象棋残局库^[7-8]等方面。

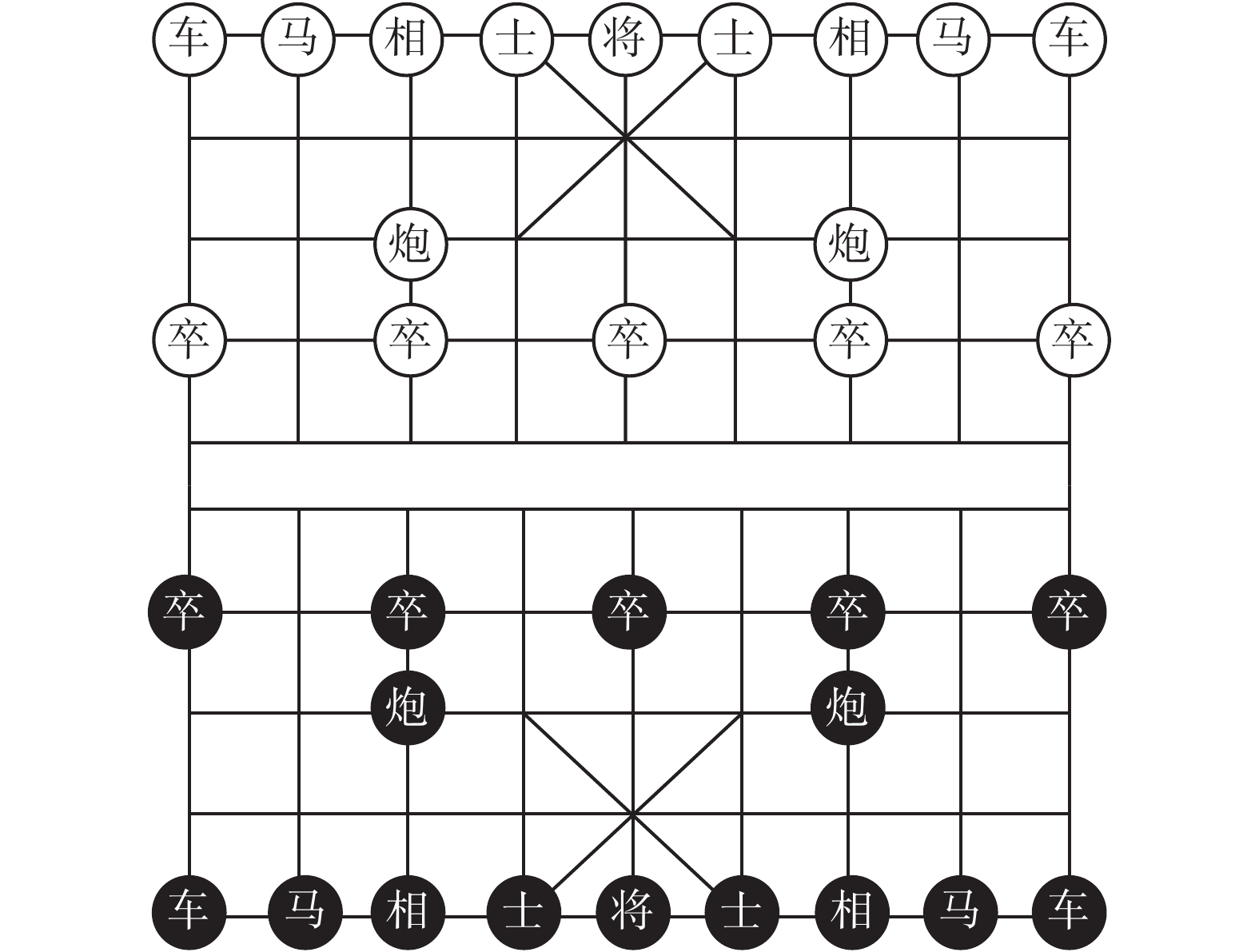
1 问题描述 1.1 中国象棋棋盘棋子

中国象棋棋盘9条竖线，10条横线，总计90个位置^[9-10]。棋子分为红黑两色，每方16枚棋子，棋子分为7类：车、马、炮、相、士、将、卒。开始局面如图1所示。

中国象棋中，“将”和“帅”、“相”和“象”、“卒”和“兵”描述的是同一类棋子。为叙述方便，本文对这3类棋子分别采用“将”、“相”、“卒”的叫法。

为便于用公式表示，本文使用英文缩写表示相关棋子，表1描述了棋子的缩写及其含义，本文使用缩写表示棋子，例如使用K_R表示红将，K_B表示黑将。

1.2 走子规则

车、马、炮3类棋子可以出现在棋盘的任意位置；相不能过河，只能出现在己方空间中的7个位置，为便于下文叙述，从左到右、从上到下对“相”的可去位置依次编号为0~6，如图2所示。

士和将只能在九宫格中，士有5个可去位置，将有9个可去位置。如图3，将九宫格中的9个位置按照从左到右、从上到下的顺序依次编号为0～8。

卒的着法分为过河和未过河两种情况，过河卒可以出现在敌方半棋盘空间中的任意一个位置，未过河的卒只可能出现在己方最上方2行5列共10个位置格点上，并且每列至多有一个卒。

1.3 问题定义

定义中国象棋状态总数问题首先需要定义子问题：给定若干棋子，在满足中国象棋规则的情况下，把这些棋子摆放在棋盘上，有多少种可能的放置方式。这里给定的每类棋子个数必然都不大于开局时每类棋子的个数。中国象棋状态总数可以用式(1)表示，式中S即为中国象棋状态总数，put表示从棋型到放置方法个数的映射，棋型指14种棋子组成的14维向量，每维数字表示每类棋子的个数。

$ S = \mathop \sum \limits_{{\rm{ChessType}} \in {\text{全部棋型}}} {\rm{put}}\left( {{\rm{ChessType}}} \right) $

(1)

关于计算的中国象棋状态总数，需要说明3点：

1) 本文讨论的是中国象棋可能出现的全部状态，在每步着法都完美的情况下，从初始状态出发可能无法到达全部状态。

2) 本文统计的状态集合中每个状态双方“将”都是存在的，即本文计算的全部局面都是游戏尚未结束的局面。

3) 本文讨论的状态包括“将帅见面”的情况。在中国象棋规则中，促成“将帅见面”局面的一方为输。

本节对中国象棋棋子、着法进行了简要介绍，对棋子、棋盘进行了一些符号约定，对问题给出了形式化描述并明确了中国象棋状态总数所包括的局面。

2 问题求解 2.1 摆放次序

计数问题的两个基本方法是分类加法和分步乘法^[11-12]。当使用分步乘法时，合理的步骤可以减少分类个数^[13-14]，从而简便地解决计数问题。

给定若干棋子之后计算摆放方式的个数时，摆放次序至关重要。下面举例描述摆放次序的重要性。给定2个红车、2个红相共4枚棋子，计算摆放方式个数。车的位置比较随意，可以摆放在棋盘上90个格点的任意位置，相的位置限制较多，只能摆放在如图2所示的7个位置上。如果先考虑相再考虑车，可知有 $C_7^2 \times C_{88}^2$ 种摆放方式；而如果先考虑车再考虑相就需要分3类情况进行讨论：

1) 当车占用0个相位时，车有83个位置可选，相有7个位置可选，这种情况有 $C_{83}^2 \times C_7^2$ 种局面。

2) 当车占用1个相位时，第1个车有7种相位可选，第2个车有83个位置可选，2个相有6个位置可选，这种情况有 $C_7^1 \times C_{83}^1 \times C_6^2$ 种局面。

3) 当车占用2个相位时，摆放方式有 $C_7^2 \times$ $ C_5^2$ 种。

以上3类情况摆法个数之和与“先摆放相，再摆放车”所得结果相同，但显然第一种方法需要较少的分类讨论。由此例可以看出，计算状态个数时合理规划摆放棋子的顺序能够极大简化问题。

计算中国象棋状态总数时，需按照一定次序放置棋子，核心思想是“先难后易”，即先放置限制较多、活动范围窄的棋子，然后再放置行动灵活、位置自由的棋子。

2.2 问题分解

车、马、炮可以到达棋盘上的任何一个位置，放置最为自由，只需要知道棋盘上有多少个空白格点，即可通过排列组合计算出摆法总数，因此最后考虑这3种棋子的摆放。卒过河后可以到达敌方阵地的每一个位置，自由度占半个棋盘，放在倒数第2位考虑。将的位置会影响士相的摆放，相的位置会影响未过河卒子的摆放。考虑将、士、相、卒这4类棋子之间的互相影响关系及着法特点，拟定摆放顺序为：将、士、相、卒。

综上，根据先考虑受限制多的棋子再考虑受限制少的棋子的思路，最终摆放顺序为：将、士、相、卒、车马炮。

利用分步乘法原理依次处理棋子的摆放，这个过程可以对问题进行层层分解，把问题划分为若干个有依赖关系的子问题。先摆放“将”，“将”摆放完成之后，后面要摆放的“士”和“相”会受到“将”的影响，所以把“将”的位置作为输入参数向后续求解模块传递。摆放“士”的时候可以根据已摆放“将”的位置，来决定“士”可以摆放的位置有哪些。

整体求解思路为：把已摆放的棋子对未摆放的棋子的影响作为参数传递给后续子问题，摆放棋子时参考已摆放棋子的位置来决定当前可行的摆放方法。

本节详细描述把中国象棋摆法总数这个问题划分成将、士、相、卒、“车马炮”5个子问题，每个子问题都有明确的输入，每个子问题的输出都是摆法个数。子问题之间逐层调用，最终能够求得中国象棋状态总数。子问题的定义及其输入的形式化是整个求解过程中较为关键的部分。

2.2.1 将

先摆放好双方的“将”，再考虑子问题：在“将”位置确定的情况下，“士相卒车马炮”总共有多少种摆法。记此子问题为getShi(K_R, K_B)，该子问题输入K_R, K_B为红黑双方“将”的位置。

对“将”的每一种摆放方式，将其余棋子的摆法个数累加起来即为中国象棋状态总数。伪代码如下：

函数名称　getJiang

输入　无；

输出　摆法种数s。

1) s = 0；

2) 对于红将的每个位置K_R∈[0, 9)；

3) 对于黑将的每个位置K_B∈[0, 9)；

4) s+=getShi(K_R, K_B)

在以上代码中，K_R表示红方将的位置，K_B表示黑方将的位置，累加双将位置确定之后“士相卒车马炮”的摆法个数即得到中国象棋状态总数，如式(2)：

$ S = \mathop \sum \limits_{{K_R} = 0}^8 \mathop \sum \limits_{{K_B} = 0}^8 {\rm{getShi}}\left( {{K_R},{K_B}} \right) $

(2)

2.2.2 士

在2.2.1中，在给定“将”位置的情况下，需要计算“士相卒车马炮”有多少种摆法。当“将”的位置确定后，“士”的可选位置随之确定。如果“将”在图3中的0、2、4、6、8号位置，则“将”占用一个士位，“士”有4个位置可选；如果“将”在1、3、5、7、9号位置，“将”没有占领士位，士有5个位置可选。

对于“士”的每一种摆法，累加“相卒车马炮”的摆法个数，即可得到在“将”位置确定情况下“士相卒车马炮”的摆法个数。记子问题“相卒车马炮”的摆法个数为getXiang(K_R, K_B, Space_R, Space_B)，其中K_R、K_B输入表示红黑双方将的位置，Space_R、Space_B表示双方空白格点数。getShi函数输入参数为红将位置和黑将位置，输出“士相卒车马炮”摆法总数。伪代码如下：

函数名称　getShi

输入　红将位置K_R；黑将位置K_B；

输出　“士相卒车马炮”的摆法总数s。

1) s=0；

2) 定义红士可去位置个数：若K_R不在士位上N_R=5，否则N_R=4；

3) 定义黑士可去位置个数：若K_B不在士位上N_B=5，否则N_B=4；

4) 对于红士个数的可取值A_R∈{0, 1, 2}；

5) 对于黑士个数的可取值A_B∈{0, 1, 2}；

6) 红方空白格点数Space_R=45−1−A_R；

7) 黑方空白格点数Space_B=45−1−A_B；

8) s+= $C_{{N_R}}^{{A_R}}C_{{N_B}}^{{A_B}}$ getXiang(K_R, K_B, Space_R, Space_B)

在上述伪代码中，摆放好“士”之后，需要乘以“相卒车马炮”的摆法个数，“相卒车马炮”摆法个数通过getXiang函数实现。考虑已摆放的“将”、“士”对“相卒车马炮”的影响，可以发现后续棋子的摆放只依赖于红将位置、黑将位置、红方空白格点数、黑方空白格点数4个变量。

2.2.3 相

经过以上两步，“将”和“士”的位置确定了，这两种棋子对后续棋子的“影响因素”包括：

1) “将”可能会占用相位，影响“相”的可摆放位置的个数；

2) 红方和黑方各自的空白格点数，影响“卒车马炮”的摆放。

问题转化为给定“将”的位置和红黑双方空白格点个数之后，“相卒车马炮”有多少种摆法。

“相卒车马炮”的摆法只跟4个变量有关：红将位置、黑将位置、红方空白格点数、黑方空白格点数。这4个变量一旦确定，“相卒车马炮”的摆法个数便随之确定。求解子问题“相卒车马炮”需要先考虑相的摆法。根据“将”是否已经放在如图3的1号位置，可以确定相的可选位置的个数。

对于“相”的每一种摆法，累加“卒车马炮”的摆法个数，即得“相卒车马炮”的摆法总数。记子问题“卒车马炮”的摆法个数为getZu(BP_R, BP_B, Space_R, Space_B)，BP_R、BP_B分别表示红相、黑相占用卒位的个数，Space_R、Space_B分别表示红黑双方空白格点数。伪代码如下：

函数名称　getXiang

输入　红将位置K_R；黑将位置K_B；红方空白格点数Space_R；黑方空白格点数Space_B；

输出　“相卒车马炮”的摆法总数s。

1) 定义红相可去位置个数：若K_R不在相位上N_R=7否则N_R=6；

2) 定义黑相可去位置个数：若K_B不在相位上N_B=7否则N_B=6；

3) s=0；

4) 对于红相个数的可取值B_R∈{0, 1, 2}；

5) 对于黑相个数的可取值B_B∈{0, 1, 2}；

6) 对于红相占用红卒位置的个数BP_R∈{0, 1, 2}；

7) 对于黑相占用黑卒位置的个数BP_B∈{0, 1, 2}；

8) 相的放法种数 ${\rm{placeXiang}} = C_2^{B{P_R}}C_2^{B{P_B}}C_{{N_R} - 2}^{{B_R} - B{P_R}}$ $C_{{N_B} - 2}^{{B_B} - B{P_B}}$ ；

9) s+=placeXiang×getZu(BP_R, BP_B, Space_R−B_R, Space_B−B_B)。

2.2.4 卒

经过以上步骤，“将士相”摆放完成，“卒车马炮”子问题的输入包括4个变量：红相占用卒位个数(可取值0、1、2)、黑相占用卒位个数(可取值0、1、2)、红方空白格点数、黑方空白格点数。

“卒”需要分为2类进行讨论：过河卒和未过河卒。各方过河卒个数加上未过河卒的个数不超过5，需考虑红方、黑方各自的过河卒、未过河卒共4类棋子的摆放。

为便于叙述，下面进行一些符号约定：

1) Space_B表示黑方棋盘空白格点数，Space_R表示红方棋盘空白格点数；

2) P_R表示红方未过河卒的个数，P_B表示黑方未过河卒的个数；

3) $P_R'$ 表示红方过河卒的个数， $P_B'$ 表示黑方过河卒的个数。

下面以红方为例，讨论过河卒和未过河卒的摆放。

对于过河卒，有 $C_{{\rm{Spac}}{{\rm{e}}_B} - {P_B}}^{P_R'}$ 种摆法，其中Space_B−P_B表示黑方空白格点数，从这些空白格点选择 $P_R'$ 个格点分配给 $P_R'$ 个红方过河卒。

对于红方未过河卒，需要根据相占用的卒位个数和未过河卒的个数两个变量求出有多少种放置方法，这个问题可以明确定义为：在2行5列共10个位置上，放置P个卒子，其中BP个相占用了卒位，每列至多放置1个卒子，在这些约束下求P个卒子的摆法总数。这个子问题解法如下：假设有i个卒子放在了被占用的列上，这i个卒子只有唯一位置。而剩下的P-i个卒子都有2个空白格点可选，共计2^P-i种情况。未过河卒放法种数如式(3)所示：

$ \mathop \sum \limits_{i = 0}^{\min \left( {BP,P} \right)} {2^{P - i}}C_{5 - BP}^{P - i} $

(3)

对于卒子的每一种摆放方式，累加“车马炮”的摆放方式即得“将士相”确定后，“卒车马炮”的摆放方式。

2.2.5 车马炮

“车马炮”的摆放仅与一个变量有关，即整个棋盘上空白格点数。枚举红黑双方车、马、炮的个数，使用分步乘法计算有多少种摆法，如式(4)：

$ \mathop \sum \limits_{{R_B} = 0}^2 \mathop \sum \limits_{{R_R} = 0}^2 \mathop \sum \limits_{{H_B} = 0}^2 \mathop \sum \limits_{{H_R} = 0}^2 \mathop \sum \limits_{{C_B} = 0}^2 \mathop \sum \limits_{{C_R} = 0}^2 {\rm{jvmapao}}\left( {{R_B},{R_R},{H_B},{H_R},{C_B},{C_R}} \right) $

(4)

jvmapao(R_B, R_R, H_B, H_R, C_B, C_R)函数可以使用分步乘法实现。例如，摆完“将相士卒”之后剩余80个空白格点，在这些空白位置上摆放2个红车、2个红马、2个黑炮。根据分步乘法很容易得出摆法总数为 $C_{80}^2 \times C_{78}^2 \times C_{76}^2$ 。jvmapao函数实现如以下伪代码所示：

函数名称　jvmapao

输入　空白格点数Space；红黑双方的车马炮的个数R_B、R_R、H_B、H_R、C_R、C_B；

输出　 s，表示“车马炮”的摆法总数。

1) $s = C_{{\rm{Space}}}^{{R_B}} \times C_{{\rm{Space}} - {R_B}}^{{R_R}}$ ；

2) Space=Space−R_B−R_R；

3) $s = s \times C_{{\rm{Space}}}^{{H_B}} \times C_{{\rm{Space}} - {H_B}}^{{H_R}}$ ；

4) Space=Space−H_B−H_R；

5) $s = s \times C_{{\rm{Space}}}^{{C_B}} \times C_{{\rm{Space}} - {C_B}}^{{C_R}}$ 。

2.3 动态规划方法加速求解

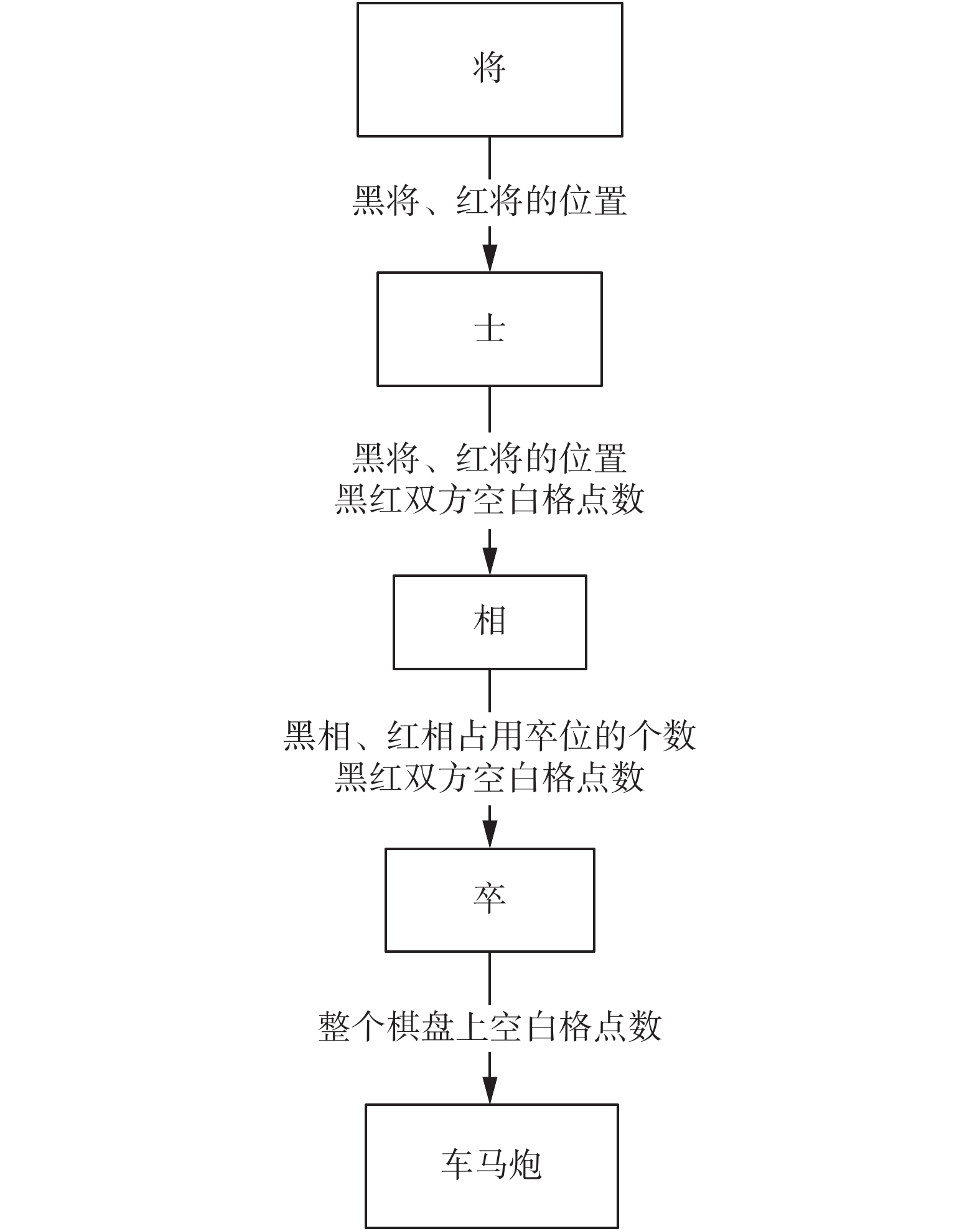
利用2.2节中各个子问题的性质，可以对上述计数方法进行优化。各个部分输入参数如图4。

图4描述了中国象棋状态总数求解的5个子问题：

1) 将的摆放；

2) 士的摆放，输入为红将、黑将的位置；

3) 相的摆放，输入为红将、黑将的位置、红黑双方空白格点数4个变量；

4) 卒的摆放，输入为红黑双方空白格点数、红黑双方相占用卒位的个数；

5) 车马炮的摆放，输入为整个棋盘上空白格点数。

每个子问题都有一条重要性质：输入到输出为单射。根据这条性质可以为每个子问题建立一个映射表，保存函数输入和输出的映射关系。当求解某个子问题时，先查询映射表，如果存在答案则不必再调用后续子问题进行求解，直接查表得出；如果不存在，则求解该问题并把最终结果存储到映射表中，以备下次查询。这种方法相当于为每个子问题加一层缓存，若未命中缓存则进行求解并使用求解结果更新缓存，若命中缓存则直接返回缓存的答案。这种动态规划技巧又叫备忘录方法^[15-18]，是动态规划的一种变形。

各个子问题之间具有单向依赖性，动态规划方法避免了子问题之间层层调用和重复调用。

3 实验结果与验证

实验得出中国象棋状态总数具体数值为7 547 040 878 332 418 571 694 532 043 654 081 760 159，用科学计数法表示为7.54×10^39.88。现有文献中提到的中国象棋状态总数如表2所示，这些结果都远远高估了中国象棋空间复杂度。

如果用定长编码来描述中国象棋的一个状态，只需对中国象棋状态总数取以2为底的对数，得到结果132.47 bit，这就是描述一个棋盘状态最少需要的bit数。若将中国象棋全部状态使用定长编码存储下来，需要将状态占用bit数乘以状态个数，结果为1.14×10²⁹ TB。

为佐证本文结论，使用另一种粗略方法估计中国象棋状态总数。下面给出一种简略的计算中国象棋状态总数的方法，这种方法给出的是中国象棋状态总数的上界。

首先，只考虑红方的棋子摆放，记为s。中国象棋包括红方和白方两方，所以全部状态总数为s²。下面介绍s的计算方法。

将和士摆放方法为 ${\rm{jiangShi}} = C_9^3 \times 3 + C_9^2 \times 2 + C_9^1$ 。将士在九宫中， $C_9^3$ 表示选定3个位置，乘以3表示为“将”分配3个位置中的1个位置。

相的摆放方法数为： ${\rm{xiang}} = C_7^2 + C_7^1 + C_7^0$ 。卒的摆放需要考虑过河卒和未过河卒，过河卒有45个格点空间，未过河卒有5列，每列有2种摆放方式。故卒的摆放方式有 ${\rm{zu}} \!=\!\! \mathop \sum \nolimits_{i = 0}^5 \mathop \sum \nolimits_{j = 0}^{5 - i} C_{45}^i \times C_5^j \times {2^j}$ 种。车的摆放方式： ${\rm{jv}} = C_{90}^2 + C_{90}^1 + C_{90}^0$ 。马和炮的摆法与车完全相同。

在这种简略计算方法中，忽略了棋子之间的互相影响，所以应该采用分步乘法的方式计算s，只考虑红方共有s=jiangShi×xiang×zu×jv³种摆法。

中国象棋状态总数即为s²，约为10^42.78。可见粗略估计结果与本文计算结果更为接近，即便是粗略估计，现有文献中的数据都是极不准确的。

4 结论和展望

基于动态规划的方法求解中国象棋状态总数充分挖掘了中国象棋棋子着法规律，快速而准确地求出了中国象棋状态总数，为描述中国象棋空间复杂度提供了充分依据，实验证明现有文献提供的数据远远不够准确。

该计数方法创新点包括两方面：1)先难后易，把问题分解为若干个子问题，先摆放约束较多的棋子，后摆放约束较少的棋子，把影响后续摆放的因素作为参数向后传递；2)在求解每个子问题时，动态规划可以减少重复计算。

本文提出的计数方法可能的应用方向包括：1)计算其他博弈游戏状态总数；2)用于构造中国象棋棋盘局面哈希函数，建立棋盘局面和数字之间的一一映射；3)寻找可暴力枚举全部状态的棋型，为构建中国象棋残局库提供依据。