2. 北京大学 工学院,北京 100871;
3. 北京大学 海洋研究院,北京 100871
2. College of Engineering, Peking University, Beijing 100871, China;
3. Institute of Ocean Research, Peking University, Beijing 100871, China
强化学习是受动物能有效适应环境的启发发展而来的一种算法。基本思想是以试错的机制与环境进行交互,在没有导师信号的情况下,使奖励累积最大化,来寻求最优的策略[1-3]。目前强化学习的行业应用颇广泛,比如无人驾驶、人形机器人、智能交通和多智能体协同等。其中多智能体编队的强化学习研究是一个重要的方向[4-5]。文献[4]设计多动作回放的马尔可夫模型,在此框架下,多智能体
事件驱动机制已经被证明可以有效地减小大规模网络的通信量[6-7]。综合已有研究成果,事件驱动条件设计主要分为两类:状态相关[8]和状态无关[9]。其主要做法都是通过检测智能体采样前后状态的偏差值大小,判断是否满足事件驱动条件,来决定间歇性的更新控制输入,减小控制器与多智能体系统的通信频率和计算量[10-12]。文献[10]较早在状态反馈控制器中引入事件驱动控制机制。文献[11]考虑多智能体间同步采样异步触发机制解决多智能体环形编队问题,其中智能体可独立地选择触发条件参数。但是当前强化学习与事件驱动的结合相对较少[13-14]。文献[13]设计事件驱动控制器并应用于非线性连续系统的强化学习中,解决了自适应动态规划问题。文献[14]提出根据智能体观测信息的变化率设计触发函数,减少学习过程中的计算资源消耗。
综合以上分析,本文区别于传统的多智能体强化学习算法,在资源有限的情况下,考虑将事件驱动和强化学习相结合,侧重于事件驱动在强化学习过程中动作决策频率方面的研究。
1 问题描述 1.1 基于强化学习的编队问题
综上所述,基于强化学习的多智能体编队问题可描述为:智能体与环境进行交互,学习动作决策策略,最小化群体的动作总量

|
Download:
|
| 图 1 编队问题 Fig. 1 Formation problem | |
博弈论中智能体的每一个决策都会导致状态的转移,此时的决策序列称为一个随机策略。具有马尔可夫(Markov)特性的随机策略称为Markov策略(MG)。MG是研究具有离散时间特性的多智能体系统的重要理论框架。
考虑一个分散式马尔可夫模型(decentralized Markov decision processes,DEC-MDPs),DEC-MDPs是一个五元组<I,S,Ai(s),P,{ri}>,其中:

|
Download:
|
| 图 2 Q学习流程图 Fig. 2 Flow chart of Q-learning | |
图2采用的是折扣累积奖赏,策略
| ${V^{\text{π}} }(s) = \sum\limits_{t = 0}^\infty {{\gamma ^t}{r_t}} ({s_t},{a_t})\left| {s = {s_0},\quad{a_t} = {\text{π}}({s_t})} \right.$ |
式中,
| $ {Q^{\text{π}} }({s_t},{a_t}) = r({s_t},{a_t}) + \gamma {V^{\text{π}} }({s_{t + 1}}) $ |
此时最优策略可以根据式(1)得到:
| $ {{\text{π}} ^*} = \arg \mathop {\max }\limits_{a \in A(s)} {Q^{^{\text{π}} }}(s,a) $ | (1) |
那么可借助时间差分误差来更新
| $ \nabla {Q_{t + 1}}({s_t},{a_t}) = {r_{t + 1}} + \gamma \max {Q_t}({s_{t + 1}},{a'}) - {Q_t}({s_t},{a_t}) $ |
| $ {Q_{t + 1}}({s_t},{a_t}) = {Q_t}({s_t},{a_t}) + {\alpha _t}\nabla {Q_{t + 1}}({s_t},{a_t}) $ |
式中,
为解决经典强化学习过程中存在通信和计算资源消耗大问题,本节在经典强化学习中引入事件驱动控制机制。
2.1 事件驱动条件设计在DEC-MDPs中,每个智能体可独立地观测局部状态信息,同时广播给附近的其他智能体。观测结束后,其根据上一时刻观测与当前观测的状态偏差值大小,决定是否要执行更新动作。这里采用状态值
| $ {e_i}(t) = {Q_{t,i}}({s_{t,i}},{a_{t,i}}) - {Q_{t - 1,i}}({s_{t - 1,i}},{a_{t - 1,i}}) $ |
式中,
在基于事件驱动的强化学习编队问题中,如果智能体
| ${\delta _{t,i}} = {\left( {\frac{{\sum\limits_{j \in {N_{t,i}}} {{r_{t,j}}} - \left| {{N_{t,i}}} \right|{r_{t,i}}}}{{\left| {{N_{t,i}}} \right|}}} \right)^2}$ |
式中,Nt,i为智能体
| $ {e_i}(t) = {\sigma _i}\left( {{Q_{t,i}}({s_{t,i}},{a_{t,i}}) - \sqrt {{\delta _{t,i}}} } \right) $ | (2) |
式中
如图3所示,智能体执行过程为:当智能体感知自己附近有障碍物时,即优先避碰,避碰结束后重新进行编队。在通信无障碍的情况下,考虑基于事件驱动的DEC-MDPs,由六元组<I,S,Ai(s),P,{ri},e>构成,其中
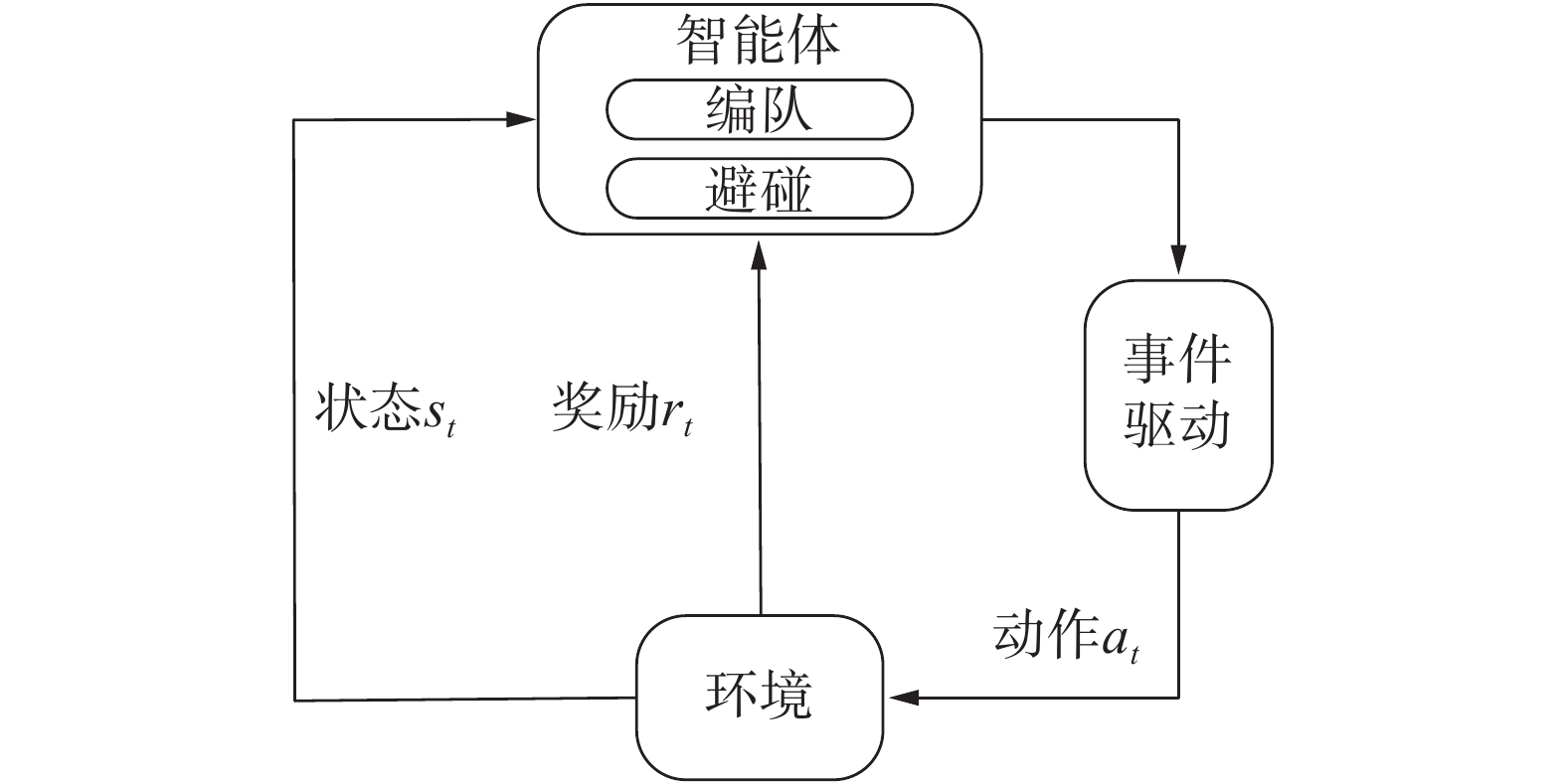
|
Download:
|
| 图 3 基于事件驱动的强化学习框架 Fig. 3 The frame of reinforcement learning with event-triggered | |
图2经典的
1)初始化Q矩阵;
2)初始化多智能体的当前状态
3)智能体
4)智能体
5)智能体
| $ \Delta {Q_{t,i}}({s_{t,i}},{a_{t,i}}) = {r_{t,i}} + \gamma \max {Q_{t,i}}(s_{t,i}',{a_{t,i}}) - {Q_{t,i}}({s_{t,i}},{a_{t,i}}) $ |
| $ {Q_{t,i}}({s_{t,i}},{a_{t,i}}) \leftarrow {Q_{t,i}}({s_{t,i}},{a_{t,i}}) + \alpha \Delta {Q_{t,i}}({s_{t,i}},{a_{t,i}}) $ |
式中,
6)如果每个智能体都抵达各自期望位置,则终止一轮Episode;
7)判断是否满足事件触发条件,如果满足返回步骤3),不满足返回步骤4)。
2.3 资源消耗对比
为了定量比较经典

|
Download:
|
| 图 4 多智能体编队 Fig. 4 Formation of multi-agents systems | |
| $ {r_i} = \omega + 0.1\beta + \chi + \xi $ | (3) |
式中,当智能体
表1比较了事件驱动
| 表 1 事件驱动与经典
|
| $ \eta = \frac{{{\kappa _{\rm{1}}}{{ - }}{\kappa _2}}}{{{\kappa _{\rm{1}}}}} $ | (4) |
在同一组
如图5所示,基于事件驱动
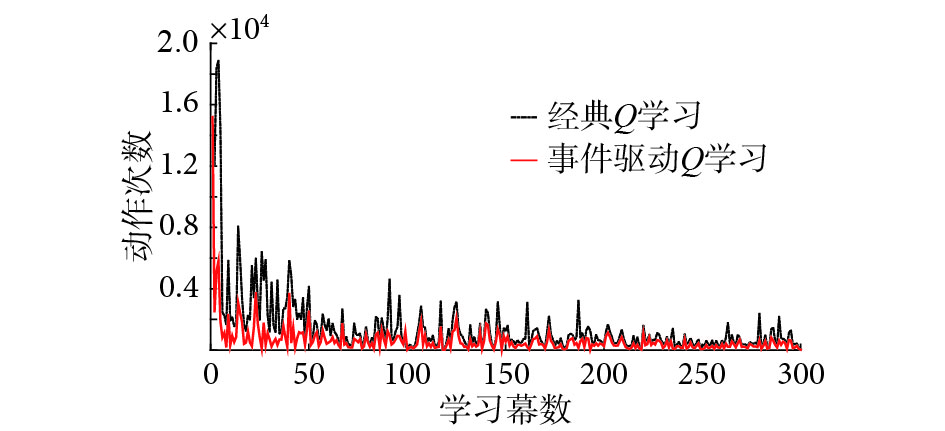
|
Download:
|
|
图 5 基于事件驱动
|
|
图6对比了在不同参数下的事件驱动条件编队动作次数的演变情况。结合表1,在一个Episode中,虽然
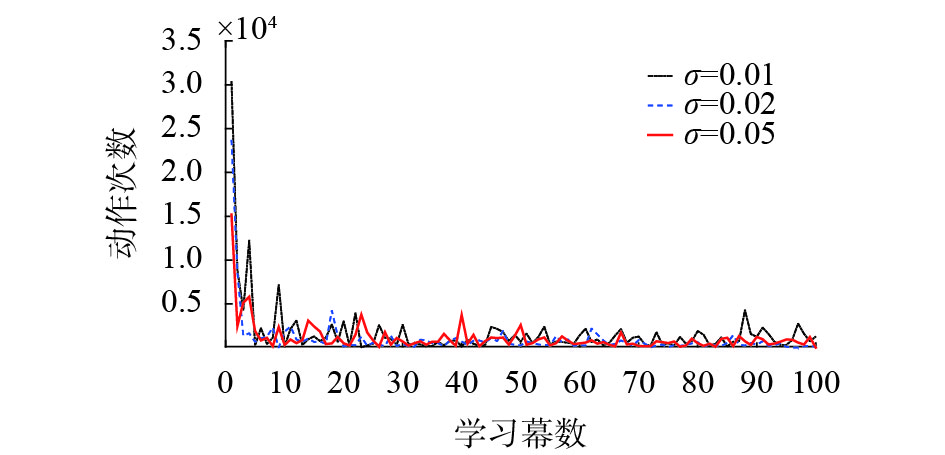
|
Download:
|
|
图 6 基于事件驱动
|
|
本文主要研究基于事件驱动的强化学习多智能体编队问题,侧重于学习过程中动作决策层面的研究。智能体在与环境交互中,根据观测状态值的变化与设计的事件驱动条件比较,决定是否执行动作更新。研究结果表明,在相同时间内,保证系统可允许编队性能的前提下,事件驱动机制可以降低智能体的动作决策频率和减少通信和计算资源消耗。因此,引入事件驱动机制有助于强化学习在实际有限资源环境中的工程应用。未来的工作会基于现有研究,将事件驱动机制优势与更多种类的强化学习算法相结合,开展相关的理论和应用研究。
| [1] |
POLYDOROS A S, NALPANTIDIS L. Survey of model-based reinforcement learning: applications on robotics[J]. Journal of intelligent & robotic systems, 2017, 86(2): 153-173. ( 0) 0)
|
| [2] |
TSAURO G, TOURCTZKY D S, LN T K, et al. Advances in neural information processing systems[J]. Biochemical and biophysical research communications, 1997, 159(6). ( 0) 0)
|
| [3] |
梁爽, 曹其新, 王雯珊, 等. 基于强化学习的多定位组件自动选择方法[J]. 智能系统学报, 2016, 11(2): 149-154. LIANG Shuang, CAO Qixin, WANG Wenshan, et al. An automatic switching method for multiple location components based on reinforcement learning[J]. CAAI transactions on intelligent systems, 2016, 11(2): 149-154. (  0) 0)
|
| [4] |
KIM H E, AHN H S. Convergence of multiagent Q-learning: multi action replay process approach[C]//Proceedings of 2010 IEEE International Symposium on Intelligent Control. Yokohama, Japan, 2010: 789–794.
( 0) 0)
|
| [5] |
IIMA H, KUROE Y. Swarm reinforcement learning methods improving certainty of learning for a multi-robot formation problem[C]//Proceedings of 2015 IEEE Congress on Evolutionary Computation. Sendai, Japan, 2015: 3026–3033.
( 0) 0)
|
| [6] |
MENG Xiangyu, CHEN Tongwen. Optimal sampling and performance comparison of periodic and event based impulse control[J]. IEEE transactions on automatic control, 2012, 57(12): 3252-3259. DOI:10.1109/TAC.2012.2200381 ( 0) 0)
|
| [7] |
DIMAROGONAS D V, FRAZZOLI E, JOHANSSON K H. Distributed event-triggered control for multi-agent systems[J]. IEEE transactions on automatic control, 2012, 57(5): 1291-1297. DOI:10.1109/TAC.2011.2174666 ( 0) 0)
|
| [8] |
XIE Duosi, XU Shengyuan, CHU Yuming, et al. Event-triggered average consensus for multi-agent systems with nonlinear dynamics and switching topology[J]. Journal of the franklin institute, 2015, 352(3): 1080-1098. DOI:10.1016/j.jfranklin.2014.11.004 ( 0) 0)
|
| [9] |
WU Yuanqing, MENG Xiangyu, XIE Lihua, et al. An input-based triggering approach to leader-following problems[J]. Automatica, 2017, 75: 221-228. DOI:10.1016/j.automatica.2016.09.040 ( 0) 0)
|
| [10] |
TABUADA P. Event-triggered real-time scheduling of stabilizing control tasks[J]. IEEE transactions on automatic control, 2007, 52(9): 1680-1685. DOI:10.1109/TAC.2007.904277 ( 0) 0)
|
| [11] |
WEN Jiayan, WANG Chen, XIE Guangming. Asynchronous distributed event-triggered circle formation of multi-agent systems[J]. Neurocomputing, 2018, 295: 118-126. DOI:10.1016/j.neucom.2018.03.018 ( 0) 0)
|
| [12] |
MENG Xiangyu, CHEN Tongwen. Event based agreement protocols for multi-agent networks[J]. Automatica, 2013, 49(7): 2125-2132. DOI:10.1016/j.automatica.2013.03.002 ( 0) 0)
|
| [13] |
ZHONG Xiangnan, NI Zhen, HE Haibo, et al. Event-triggered reinforcement learning approach for unknown nonlinear continuous-time system[C]//Proceedings of 2014 International Joint Conference on Neural Networks. Beijing, China, 2014: 3677–3684.
( 0) 0)
|
| [14] |
张文旭, 马磊, 王晓东. 基于事件驱动的多智能体强化学习研究[J]. 智能系统学报, 2017, 12(1): 82-87. ZHANG Wenxu, MA Lei, WANG Xiaodong. Reinforcement learning for event-triggered multi-agent systems[J]. CAAI transactions on intelligent systems, 2017, 12(1): 82-87. (  0) 0)
|
| [15] |
KRÖSE B J A. Learning from delayed rewards[J]. Robotics and autonomous systems, 1995, 15(4): 233-235. DOI:10.1016/0921-8890(95)00026-C ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


