2. 天津市智能机器人重点实验室,天津 300350
2. Key Laboratory of Intelligent Robotics of Tianjin, Tianjin 300350, China
自20世纪20年代PID控制律应用于船舶航向控制以来,出于航行安全、节能,进一步解放船员劳动力的考虑,航向控制一直受到人们的高度重视。航运业承担着约90%的国际贸易数额,人们对于其经济性和安全性关注度越来越高,因此对大型船舶航向控制的研究和分析有非常重要的意义[1]。船舶的系统参数会受到船舶装载状态、船速、外界干扰等的影响,使船舶运动表现出系统参数不确定性和外部扰动不确定性,因此,研究船舶航向的控制具有重要的意义[2]。
船舶航向的控制问题即令船舶航向跟踪上设定值实质上包含两部分内容:一是当船舶在目标航向上受到扰动时,舵角改变量应尽量小以减少燃料损耗;二是当航向设定值改变时,船舶航向可以快速准确地跟踪上新的设定值[3]。为了达到这两个目标,近年来国内外的研究者们提出了众多的控制方法应用到船舶自动舵的设计中,大致可以分为3类:早期的经典PID控制,上世纪70年代出现的自适应控制和现在应用较多的智能控制。文献[4]针对船舶运动模型中的参数不确定性和外扰不确定性的问题,将PID与补偿控制相结合,提出了一种船舶航向鲁棒PID型自动舵;文献[3,5]借鉴反步法的思想,设计了船舶航向控制器;文献[6]考虑到船舶所受外扰的不确定性和舵机舵角的实际物理约束,设计了自适应鲁棒控制器,引入动态面简化控制器计算;文献[7]首次将系统状态和控制输入由平面输出和它的导数表示,结合滑模控制和微分平坦的特点设计了有效的航向控制器;文献[8]对于船舶航向保持问题提出了基于特征值分解的自适应滑模控制器;文献[9]将模糊神经网络与内模控制相结合设计了航向控制器。到目前为止,已经有多种方法用于航向控制,并且取得了不错的控制效果;但由于上述大多数算法结构复杂,计算量大,对模型要求较高等原因,不易于工程实现。
韩京清教授提出自抗扰控制后[10],自抗扰控制技术凭借其鲁棒性强、易于理解、结构简单且不依赖于模型等特点受到了国内外学者的广泛关注[11],理论证明的结果也层出不穷[12]。ADRC凭借其结构简单、鲁棒性强也被应用于船舶控制中。文献[13]将自抗扰控制技术应用于航向控制,仿真表明该控制器具有良好的适应能力;文献[14]基于船舶非线性Bech模型设计了高阶ADRC控制器。通过对已有自抗扰控制航向的相关文献学习发现,目前在船舶自动舵设计中的参数大多都是在初始设计时给定,因此当船舶受到较大的扰动或者船舶航行状态发生较大改变时,难以达到较好的控制效果。
受到上述不同控制方法所具有的不同特点的启发,考虑到船舶航向系统具有不确定性和非线性的特点,本文针对船舶模型非线性、时变的特点设计了一个线性自抗扰(LADRC)控制器。为了解决被控对象受到环境等影响变化范围大从而恶化控制效果的问题,进一步提高控制器的鲁棒性,引入了自适应ESO和自适应PD的概念,利用ANFIS实现参数的在线调整,设计了一种自适应新型航向控制器,与固定参数的控制器进行对比,观察其在风、浪等环境扰动和载重变化等引起的参数摄动下的控制效果。
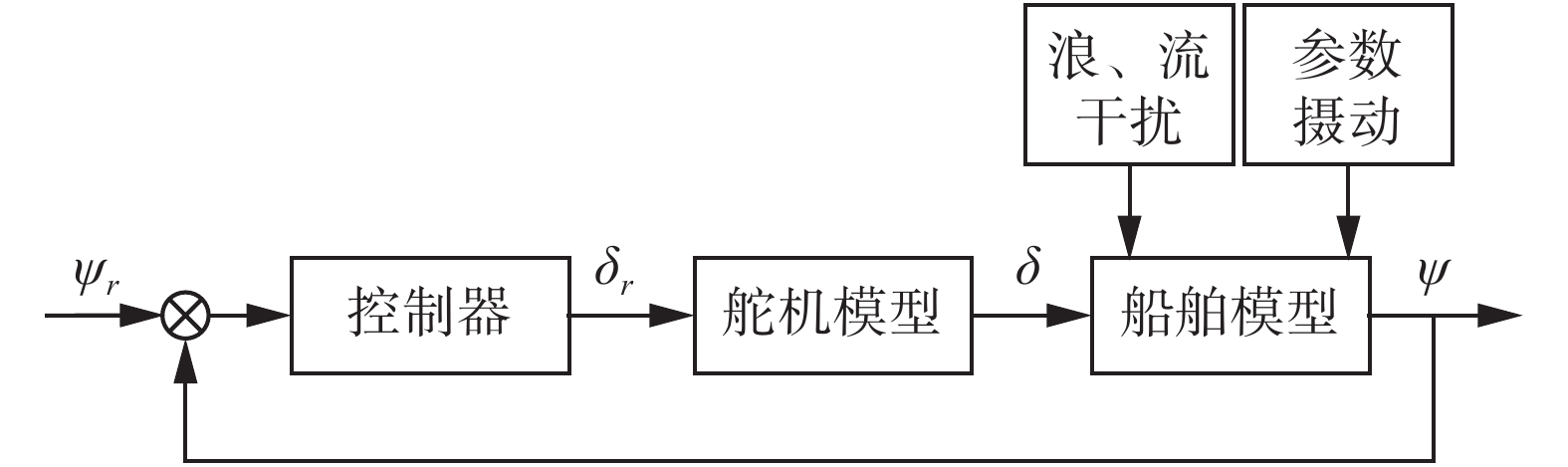
1 船舶航向控制模型常规水面船舶的主要操纵设备为螺旋桨和舵机,螺旋桨产生推进力用来控制船舶的前进速度,舵机产生舵角来保持和改变船首方向。
图1中,船舶的实时航向
|
Download:
|
| 图 1 船舶航向控制示意 Fig. 1 Schematic diagram of ship course control | |
船舶模型具有大惯性、大时滞的特点,且其操舵机构能量有限,可提供的舵角变化速度通常较低,为
| $T\dot r + r = K\delta $ | (1) |
式中:
实际航向中,船舶纵向速度的变化和流体动力的非线性特性都会使船舶的操舵响应呈现出非线性,非线性的影响通过引入非线性项
| $T\dot r + r + \alpha {r^3} = K\delta $ | (2) |
其中,
从而可得船舶航向的非线性响应模型为
| $\left\{ \begin{array}{l} \dot \psi = r \\ \dot r = - \dfrac{1}{T}r - \dfrac{\alpha }{T}{r^3} + \dfrac{K}{T}\delta \\ \end{array}\right.$ | (3) |
为了更具一般性,同时考虑外部扰动,通常将式(3)写为
| $\left\{ \begin{array}{l} \dot \psi = r \\ \dot r = f(r) + w(t) + b\delta \\ \end{array} \right.$ | (4) |
式中:
船艏方向的保持和改变主要是通过合理操作舵机实现的。舵机是一个动态系统,受实际物理条件的制约,有最大操舵角和最大操舵角速度的限制,目前应用较多的为一阶惯性模型,表达式为
| $\dot \delta = {K_E}({\delta _r} - \delta )/{T_E}$ | (5) |
式中:
结合式(4)和式(5),考虑舵机特性的船舶航向控制系统的非线性响应数学模型可以表示为
| $\left\{ \begin{array}{l} \dot \psi = r \\ \dot r = f(r) + w(r) + b\delta \\ \dot \delta = {K_E}({\delta _r} - \delta )/{T_E} \\ \end{array} \right.$ | (6) |
船舶在运动中会受到多种环境干扰,大致可分为3类:
1)船舶航行时的载重、航行速度、吃水深度等的变化,会造成船舶的水动力系数发生改变,这种扰动为系统内部不确定性,表现为系统的参数摄动,很难计算。
2)船舶在航行过程中总是存在风、浪、流等外界干扰,表现为干扰力和干扰力矩,是不可测的,但可以通过一些器件进行模拟,设计控制器时应予以考虑。
3)船舶航行时电源和油源的波动和测量噪声的存在,其属于低频干扰,影响相对小得多,设计控制器时不予考虑。
2 基于ADRC的船舶航向控制器设计高志强教授与韩京清研究员长期合作,在深刻理解抗扰思想、深入分析和思考控制问题本质的基础上,提出了频率尺度这一与工程应用紧密相关的概念,将ADRC参数与控制器和观测器的带宽相关联,解决了传统ADRC技术参数整定困难的问题,简化了参数的整定过程[16]。线性ADRC由3部分组成,分别为跟踪微分器(TD)、线性扩张状态观测器(LESO)和线性误差反馈控制律(LSEF)。其中,在某些情况下,TD的设计步骤可以省略,更加简化了LADRC的控制结构。
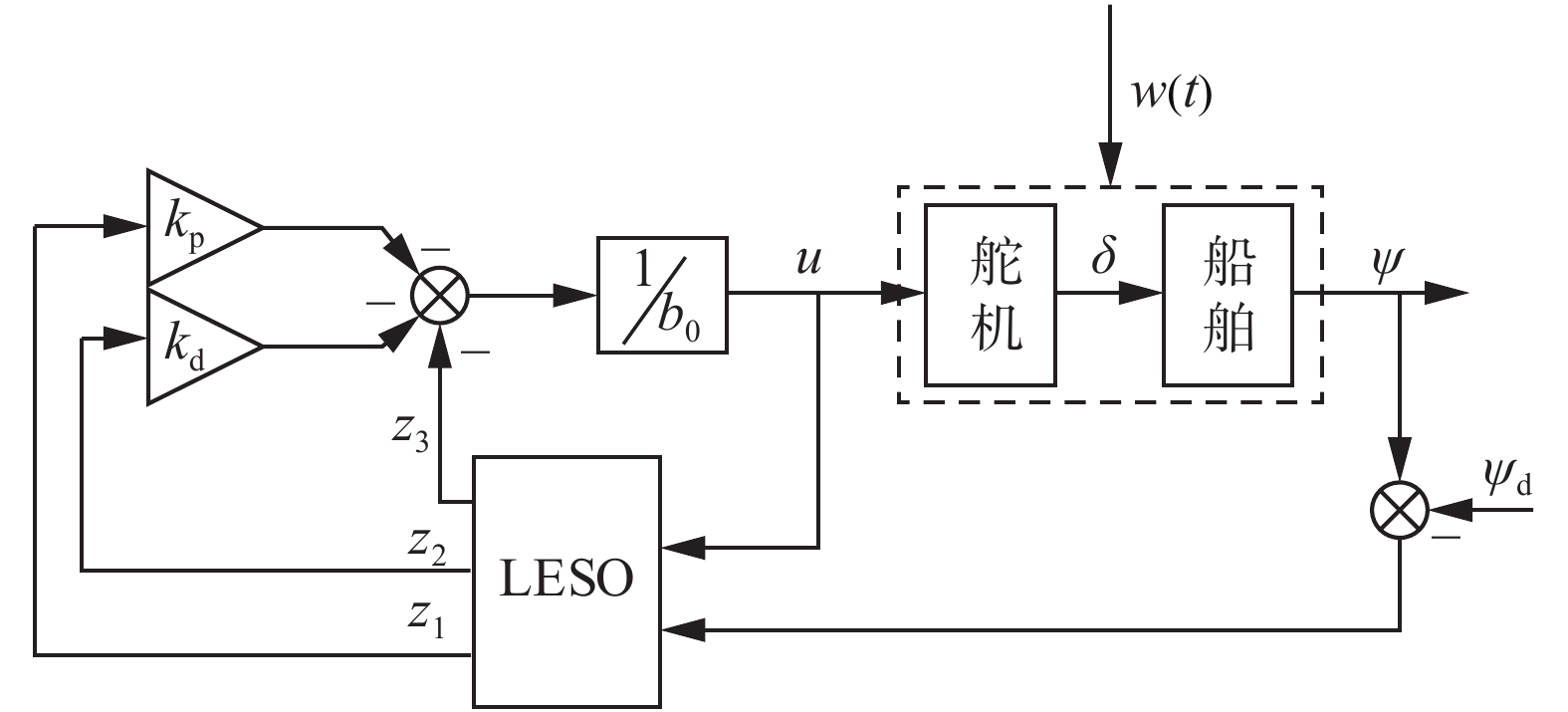
2.1 船舶航向控制器设计为了使设计简单,设计控制器时把船舶和舵机看作一个整体,将舵机特性作为航向控制系统的扰动,利用线性扩张状态观测器(LESO)进行观测,控制系统的结构框图如图2所示。
|
Download:
|
| 图 2 船舶航向自抗扰控制结构 Fig. 2 Structure of ADRC control for ship course | |
控制目标是求得控制舵角
| $\frac{{{\psi _d}}}{{{\psi _r}}} = \frac{{\omega _n^2}}{{{s^2} + 2\xi {\omega _n}s + \omega _n^2}}$ | (7) |
式中:
当期望的航向角信号
| $\left\{ \begin{array}{l} y = \psi - {\psi _d} \\ \dot y = {y_1} \\ {{\dot y}_1} = f + bu \\ f = - \dfrac{1}{T}r - \dfrac{\alpha }{T}{r^3} - {{\ddot \psi }_d};b = \dfrac{K}{T};u = \delta \\ \end{array} \right.$ | (8) |
控制器的控制目标为:
则式(8)的线性ESO可设计为
| $\left\{ \begin{array}{l} {e_0} = {z_1} - y \\ {{\dot z}_1} = {z_2} - {\beta _{01}}{e_0} \\ {{\dot z}_2} = {z_3} - {\beta _{02}}{e_0} + {b_0}u \\ {{\dot z}_3} = - {\beta _{03}}{e_0} \\ \end{array} \right.$ | (9) |
式中:
误差反馈律采用线性PD组合,得到误差反馈控制律为
| $\left\{ \begin{array}{l} {u_0} = - ({k_{\rm{p}}}e + {k_{\rm{d}}}\dot e) = - {k_{\rm{p}}}{z_1} - {k_{\rm{d}}}{z_2} \\ u = \dfrac{{{u_0} - {z_3}}}{{{b_0}}} \\ \end{array} \right.$ | (10) |
式中:
自适应神经模糊推理系统(ANFIS)是由J-S R Jang提出的一种基于T-S模型的自适应神经模糊推理系统。该系统将神经网络与模糊推理结合,根据输入−输出对的信息,采用混合算法可以自动产生if-then规则,实现隶属度函数的在线调整。
ANFIS通过对未知函数训练集样本的聚类分析可近似未知函数,还可用于模式识别,分类问题,过程控制等。ANFIS的典型结构如图3[17-18]。

|
Download:
|
| 图 3 ANFIS的典型结构 Fig. 3 Typical structure of ANFIS | |
图3中给出的是一个MISO系统,其中
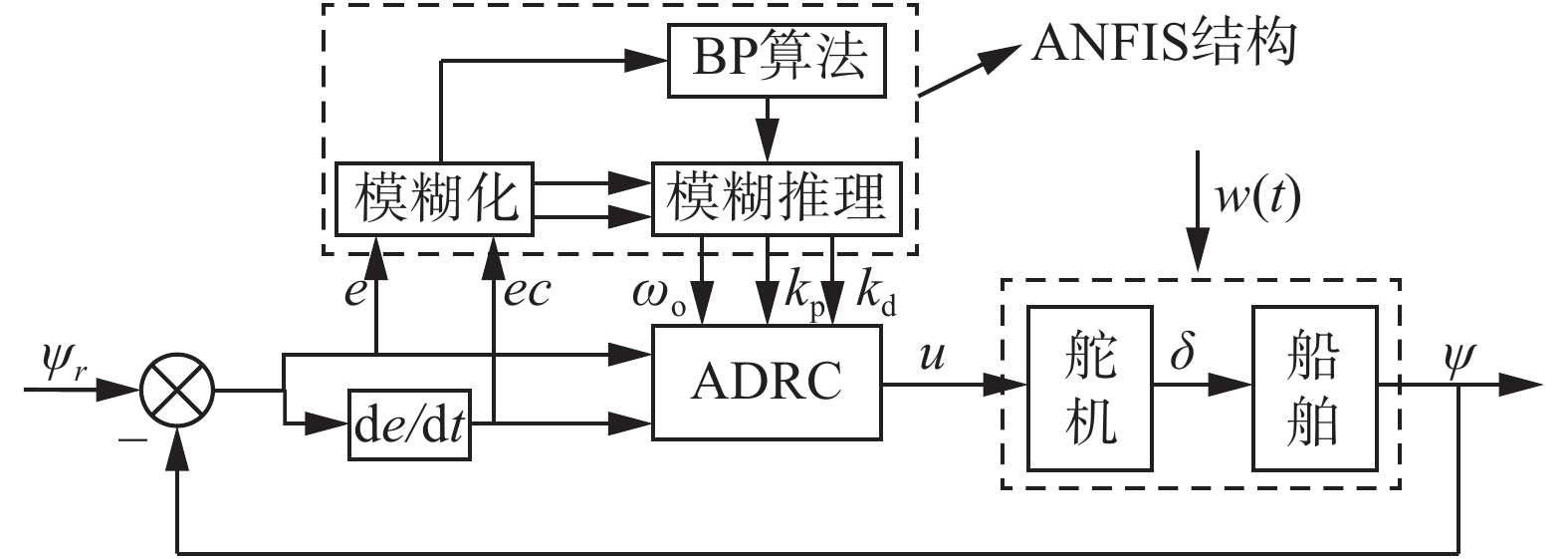
为了解决被控对象变化范围大而快使得控制效果变差的问题,进一步提高ADRC的鲁棒性,利用ANFIS网络分别实现ESO带宽
|
Download:
|
| 图 4 ANFIS-ADRC结构 Fig. 4 Diagram of ANFIS-ADRC | |
为了实现控制器所期望的功能,设计了两个ANFIS系统,每一个系统都是一个5层的前馈神经网络:输入层变量都选为2个,分别为航向误差
由式(9)可知,ESO有3个重要参数:

|
Download:
|
| 图 5 ANFIS网络结构 Fig. 5 Network structure diagram of ANFIS | |
ANFIS的参数优化算法分为正向计算和反向计算两个过程。
1) ANFIS的正向计算:
第1层隶属度选择高斯函数:
| $\mu _i^j = {e^{ - \frac{{{{({x_i} - {c_{ij}})}^2}}}{{\sigma _{ij}^2}}}};i = 1,2;j = 1, \cdots ,5$ | (11) |
第2层计算每一条规则的适应度:
| ${w_k} = \mu _1^{{j_1}}\mu _2^{{j_2}};{j_1},{j_2} \in \left\{ {1, 2,\cdots ,5} \right\};k = 1, 2,\cdots ,25$ | (12) |
第3层对每一个适应度进行归一化:
| ${\bar w_k} =\dfrac{{{w_k}}}{{ \displaystyle\sum\limits_{k = 1}^{25} {{w_k}} }}$ | (13) |
第4层为模糊规则的输出,每条规则的输出是输入变量的线性组合,即
| ${f_k} = {p_{1k}}{x_1} + {p_{2k}}{x_2} + {p_0}_k$ | (14) |
第5层是网络的输出层,有
| ${\omega _o} = y = \sum\limits_{k = 1}^{25} {{{\bar w}_k}{f_k}} $ | (15) |
2) ANFIS的反向计算:
ANFIS的反向计算选择BP算法进行参数调整,性能指标函数为
| $J(k) = \frac{1}{2}{(\psi (k) - {\psi _d}(k))^2} = \frac{1}{2}e{(k)^2}$ | (16) |
该网络中可以调整的参数包括式(11)中的前提参数
| $\Delta {{\varOmega }} = - \frac{{\partial J}}{{\partial {{\varOmega }}}} = - \frac{{\partial J}}{{\partial e}} \cdot \frac{{\partial e}}{{\partial \psi }} \cdot \frac{{\partial \psi }}{{\partial {\omega _o}}} \cdot \frac{{\partial {\omega _o}}}{{\partial {{\varOmega }}}}$ | (17) |
其中,
由于
| $\begin{gathered} {y_\beta } = \frac{{\partial \psi (k)}}{{\partial {\omega _o}(k)}} \approx {\rm{sign}}(\partial \psi (k)/\partial \Delta {\omega _o}(k)) = \\ \left\{ {\begin{array}{*{20}{l}} {{\rm{sign}}\dfrac{{\psi (k) - \psi (k - 1)}}{{\Delta {\omega _o}(k) - \Delta {\omega _o}(k - 1)}},\Delta {\omega _o}(k) \ne \Delta {\omega _o}(k - 1)}\\ {{\rm{sign}}(\psi (k) - \psi (k - 1)),\Delta {\omega _o}(k) = \Delta {\omega _o}(k - 1)} \end{array}} \right. \end{gathered}$ | (18) |
式(18)代入式(17),并化简得
| $\Delta {{\varOmega }} = - \frac{{\partial J}}{{\partial {{\varOmega }}}} = - e \cdot {y_\beta } \cdot \frac{{\partial {\omega _o}}}{{\partial {{\varOmega }}}}$ | (19) |
网络输出分别对各参数求偏导得
| $\begin{array}{c} \dfrac{{\partial {\omega _o}}}{{\partial {p_{ik}}}} = \left\{ {\begin{array}{*{20}{l}} {{{\bar w}_k}\;\;\;i = 0}\\ {{{\bar w}_k}{x_i}\;\;i \ne 0} \end{array}} \right.\\ \dfrac{{\partial {\omega _o}}}{{\partial {c_{ij}}}} = \dfrac{{\left( {\displaystyle\sum\limits_{k = 1}^{25} {{w_k}} - \displaystyle\sum\limits_{l = 1}^{{n_l}} {{w_l}} } \right) \cdot \displaystyle\sum\limits_{l = 1}^{{n_l}} {{w_l}{f_l}} }}{{{{\displaystyle\sum {{w_k}} }^2}}} \cdot \dfrac{{2\left( {{x_i} - {c_{ij}}} \right)}}{{\sigma _{ij}^2}}\\ \dfrac{{\partial {\omega _o}}}{{\partial {\sigma _{ij}}}} = \dfrac{{\left( {\displaystyle\sum\limits_{k = 1}^{25} {{w_k}} - \displaystyle\sum\limits_{l = 1}^{{n_l}} {{w_l}} } \right) \cdot \displaystyle\sum\limits_{l = 1}^{{n_l}} {{w_l}{f_l}} }}{{{{\displaystyle\sum {{w_k}} }^2}}} \cdot \dfrac{{2{{\left( {{x_i} - {c_{ij}}} \right)}^2}}}{{\sigma _{ij}^3}} \end{array} $ | (20) |
式中
采用改进BP算法,附加一个加快搜索速度的惯性项,则参数的学习算法为
| ${{\varOmega }}(k + 1) = {{\varOmega }}(k) + \eta \Delta {{\varOmega }}(k) + \alpha \Delta {{\varOmega }}(k - 1)$ | (21) |
与自适应ESO的设计方法类似,PD参数的在线调整也利用ANFIS网络实现。除网络第5层变为两个输出变量(考虑图中的点划线部分)之外,网络其他部分结构与上一节相同。
由于网络结构细微的不同,网络正向计算和反向的公式略有改变。
正向计算:
第4层:
| $ {f_{1k}} = p_{1k}^1{x_1} + p_{2k}^1{x_2} + p_{0k}^1 \\ {f_{2k}} = p_{1k}^2{x_1} + p_{2k}^2{x_2} + p_{0k}^2 \\ $ | (22) |
第5层:
| $\begin{array}{l} {k_{\rm{p}}} = {y_1} = \displaystyle\sum\limits_{k = 1}^{25} {{{\bar w}_k}f_k^1} \\ {k_{\rm{d}}} = {y_2} = \displaystyle\sum\limits_{k = 1}^{25} {{{\bar w}_k}f_k^2} \end{array} $ | (23) |
性能指标仍为式(16),类似地,采用符号函数代替难求解的偏导项,可得
| $\Delta {{\varOmega }} = - \frac{{\partial J}}{{\partial {{\varOmega }}}} = - e \cdot {y_u} \cdot \left( { - {z_1} \cdot \frac{{\partial {k_{\rm{p}}}}}{{\partial {{\varOmega }}}} + \left( { - {z_2}} \right) \cdot \frac{{\partial {k_{\rm{d}}}}}{{\partial {{\varOmega }}}}} \right)$ | (24) |
| $\begin{gathered} {y_u} = \dfrac{{\partial \psi (k)}}{{\partial {\omega _o}(k)}} \approx {\rm{sign}}({{\partial \psi (k)}/ {\partial \Delta {u_0}(k)}}) = \\ \left\{\begin{array}{l} {\rm{sign}}\dfrac{{\psi (k) - \psi (k - 1)}}{{\Delta {u_0}(k) - \Delta {u_0}(k - 1)}},\Delta {u_0}(k) \ne \Delta {u_0}(k - 1) \\ {\rm{sign}}(\psi (k) - \psi (k - 1)),\Delta {u_0}(k) = \Delta {u_0}(k - 1) \\ \end{array} \right. \\ \end{gathered} $ |
本文以“育龙”轮为仿真对象,选择航速为7.2 m/s的状态进行控制,操纵性指数
选取仿真参数为:h=0.01, b0=0.002 2;
AESO控制器:
APD-ADRC控制器:
利用MATLAB进行仿真实验,分别进行了理想状态下和有扰动情况下的仿真;扰动表现为参数摄动和外界扰动;参数摄动为随机参数摄动;外界扰动包括恒值干扰和低频正弦干扰两种情况。各控制器的仿真结果如下。
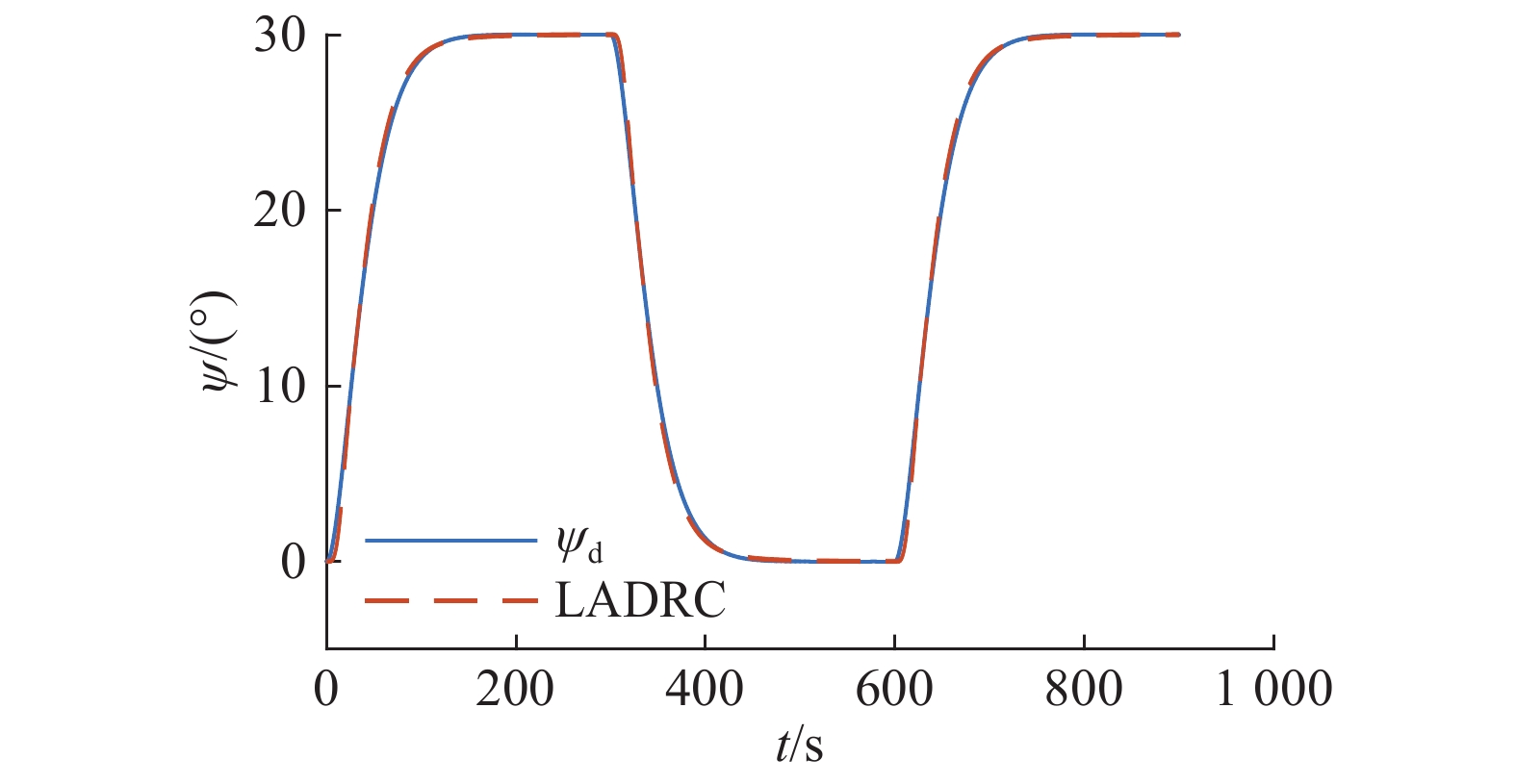
3.2.1 理想状态图6~8分别为在不考虑外界扰动和参数摄动时,设定航向为幅值
|
Download:
|
| 图 6 无干扰时LADRC的航向曲线 Fig. 6 Heading curve of LADRC without interference | |
|
Download:
|
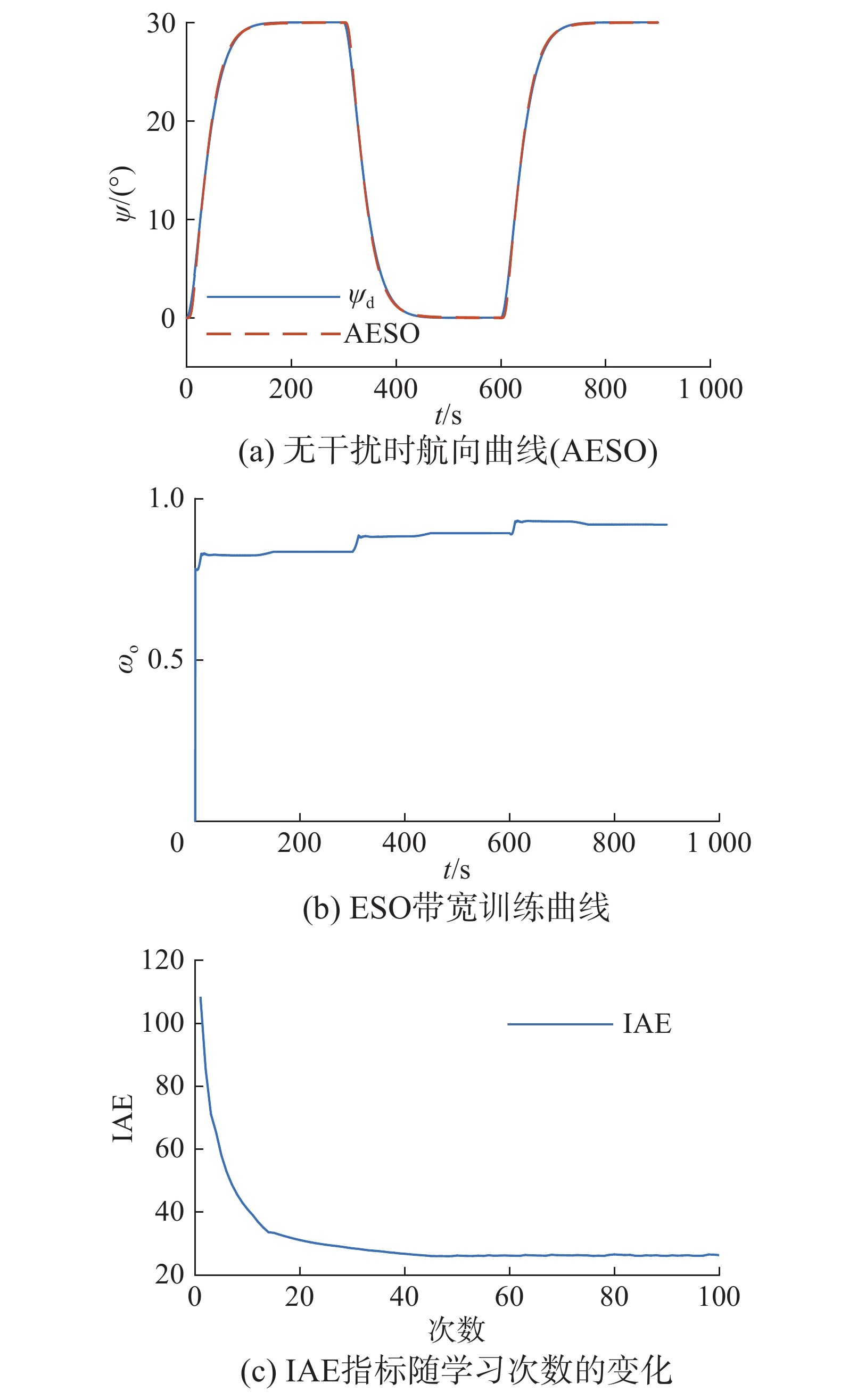
| 图 7 无干扰时AESO的航向和参数曲线 Fig. 7 Heading and parameter curves of AESO without interference | |
|
Download:
|
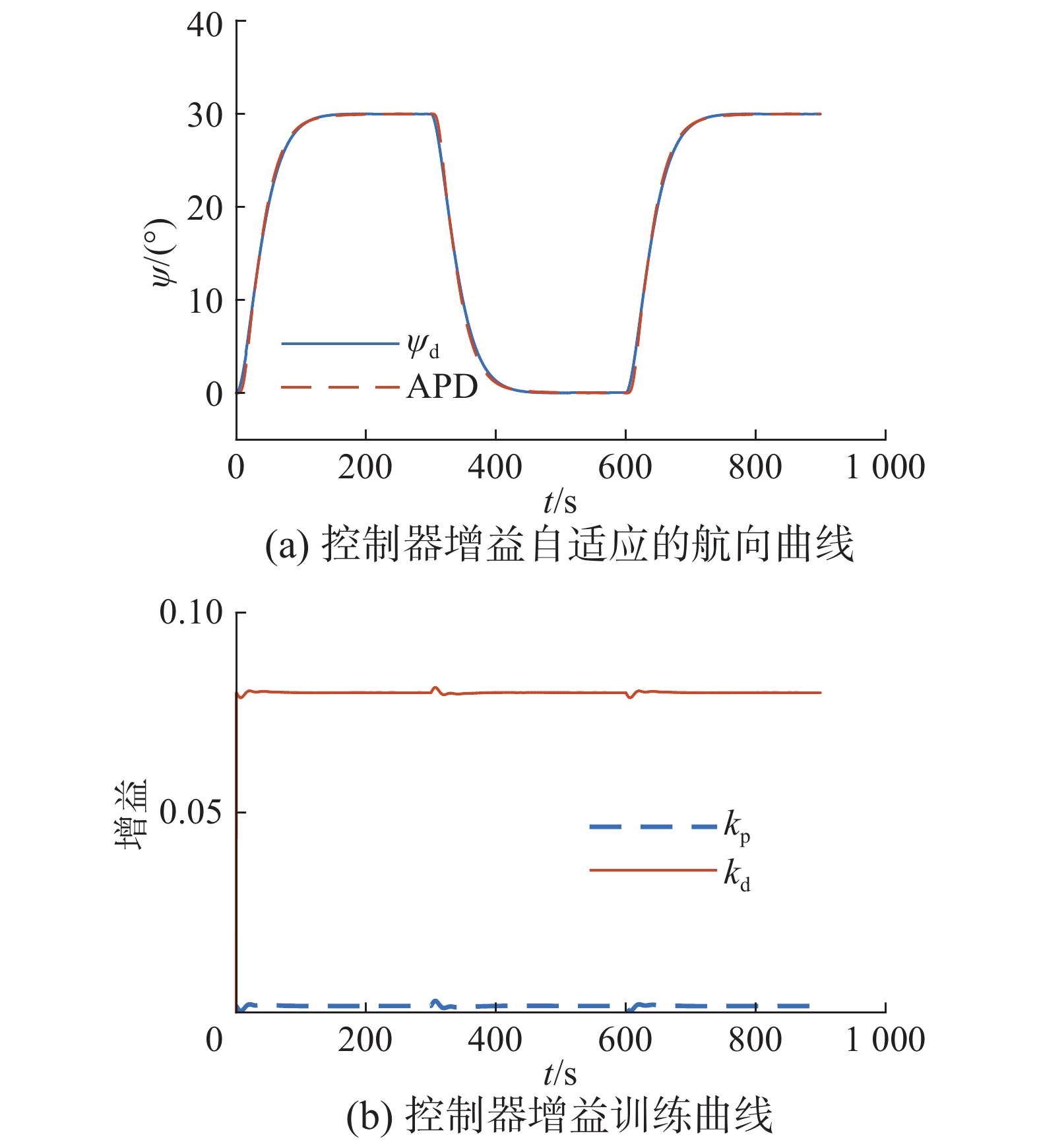
| 图 8 无干扰时自适应PD的航向和参数曲线 Fig. 8 Heading and parameter curves of APD without interference | |
观察无扰动标称模型情况下的仿真结果可知,3种控制器都可以实现不错的控制效果,表明自抗扰控制器可以用于船舶航向的控制,并且在不受扰动的情况下,可以达到良好的控制效果。由图7(c)可知,随着网络离线学习次数的增大,误差绝对值积分性能指标(IAE)减小,说明网络参数在朝着好的方向变化;图7(b)和图8(b)均为参数的在线调整曲线,由于APD-ANFIS的离线训练以LADRC的PD增益作为期望输出,所以在线参数调整时,其控制器增益的值在{0.08,0.001 6}上下波动。
3.2.2 存在外部扰动时的仿真结果1) 恒值干扰。
在200 s时施加幅值为7°的等效恒值扰动时,控制器的仿真结果如图9。

|
Download:
|
| 图 9 恒值干扰时的航向曲线 Fig. 9 Heading of constant interference | |
观察图9可以看出,基于ANFIS的在线参数调整控制器在受到扰动时仍旧可以很好的跟踪目标航向,并且不会产生大的超调;比较图9(b)和图9(c)可知,自适应ESO-ADRC控制器在受到恒值干扰时的控制性能优于自适应PD-ADRC控制器;而由图9(a)可知,当系统受到扰动时,船舶航向产生了明显超调,这是在实际控制中不希望看到的。
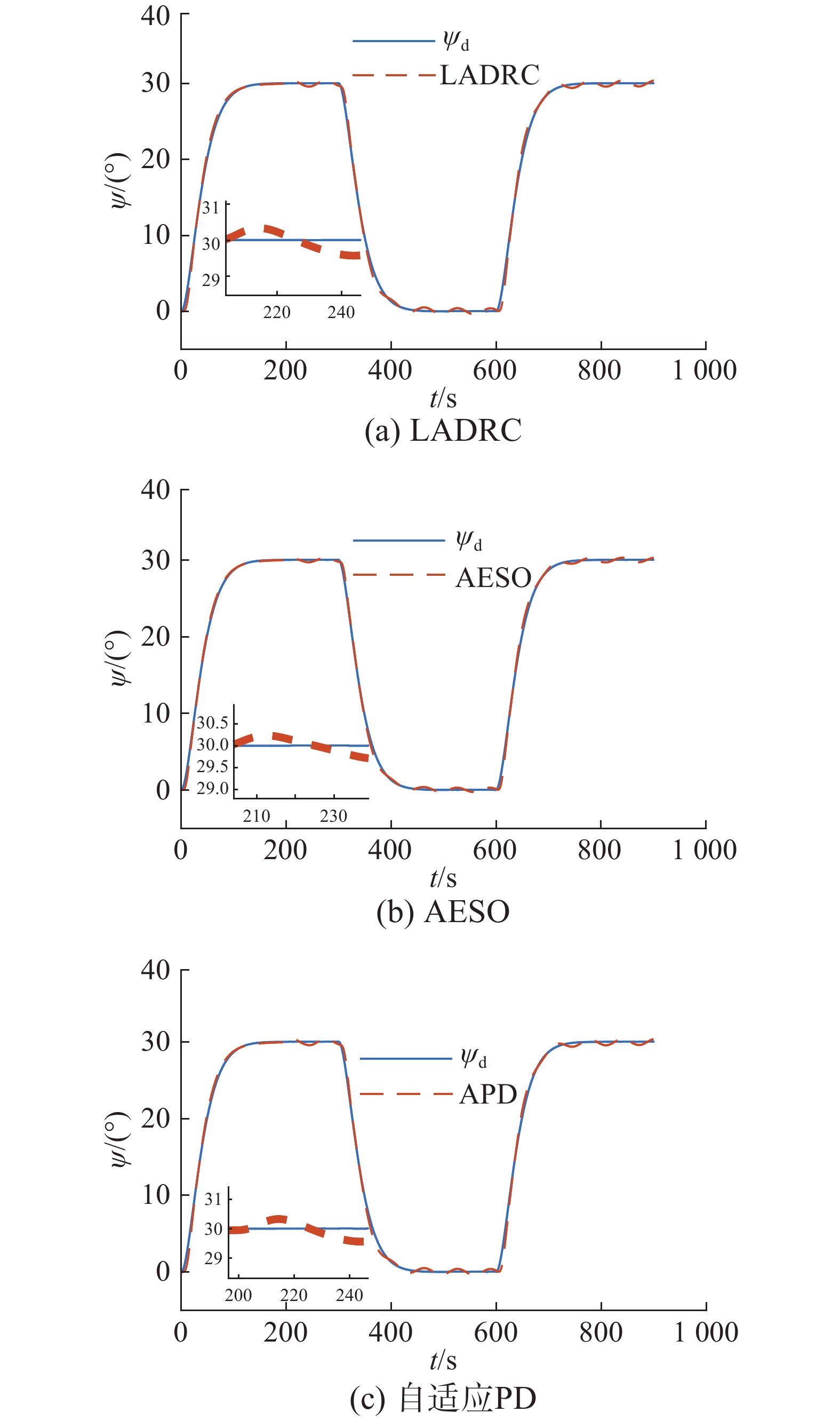
设定值不变,在200~800 s施加一个幅值为4°,频率为
|
Download:
|
| 图 10 低频干扰时的航向曲线 Fig. 10 Heading of low frequency interference | |
由图10可以看出,当系统受到低频正弦扰动时,自适应参数的控制器的鲁棒性和跟踪性能优于常规LADRC控制器;其中,AESO-ADRC控制器的控制效果最好,在受到扰动时航向曲线的上下波动幅值最小;由于APD-ADRC控制器中的ANFIS网络离线学习时间是以LADRC的PD增益作为期望输出进行训练得到的初始参数,因此其控制性能虽然优于LADRC控制器,但其优势性不够明显,还有很大的提升空间。这就意味着对于APD的初始ANFIS参数的选择可以考虑更好的策略,这也是之后可以进行深入研究的方向。
3.2.3 控制器的IAE指标对比为了对控制器的控制性能进行更清晰的比较,记录了在不同状况下的IAE的值,如表1。
| 表 1 各控制器在不同条件下的IAE值 Tab.1 IAE of controllers under different conditions |
由表1可知,对同一控制器来说,随着扰动的变化,IAE的值在逐渐变大。其中,无干扰的情况下IAE的值最小,正弦干扰下的IAE值最大;横向读表1可知,在同种情况的干扰下,AESO-ADRC控制器的IAE值最小,APD-ADRC次之,LADRC最大,也就是说在同等情况下,AESO-ADRC控制器的控制效果最好。
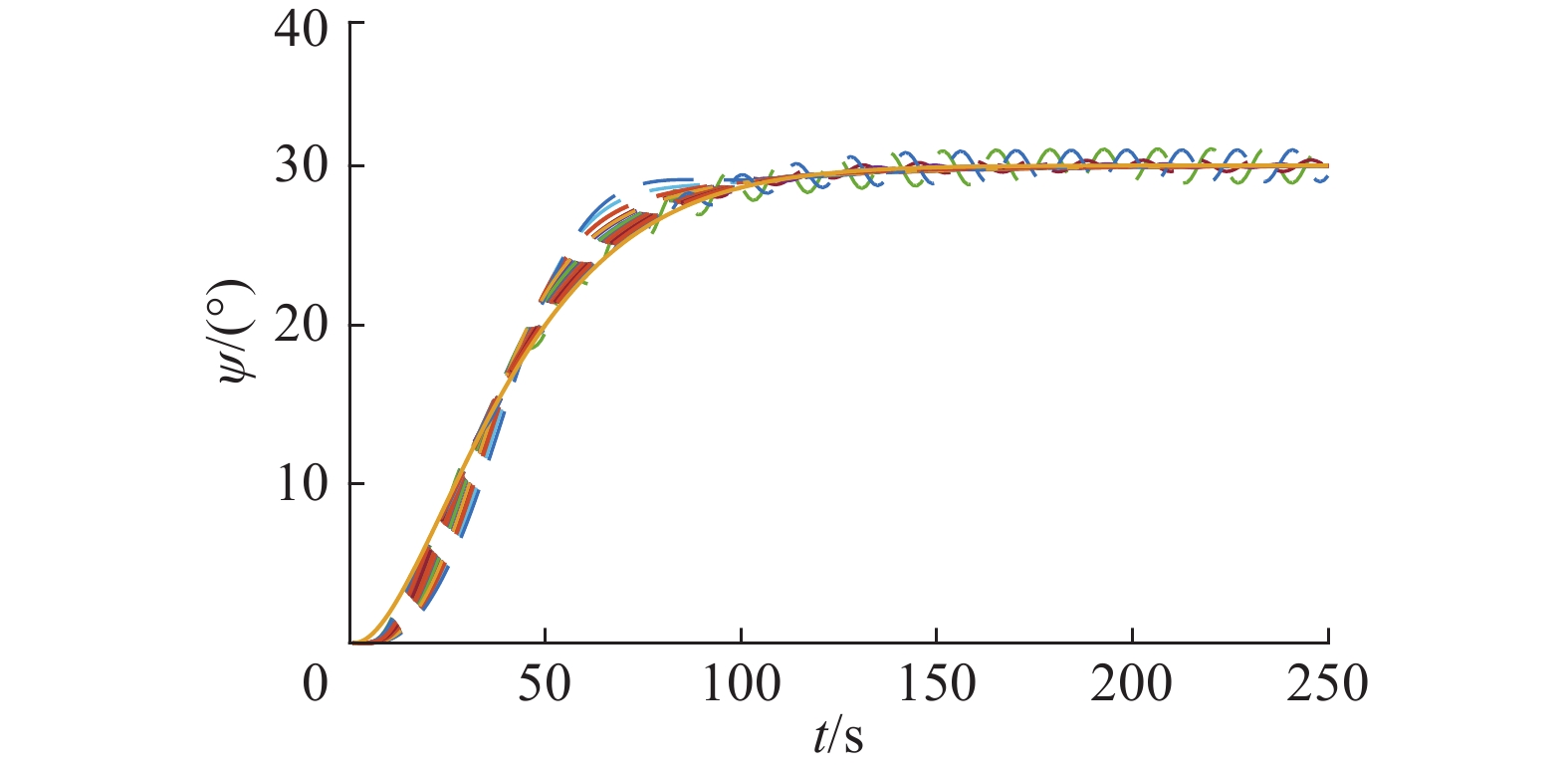
3.2.4 参数摄动下的蒙特卡罗仿真结果为了比较3种控制器的鲁棒性,在控制器参数不变的情况下,令船舶参数
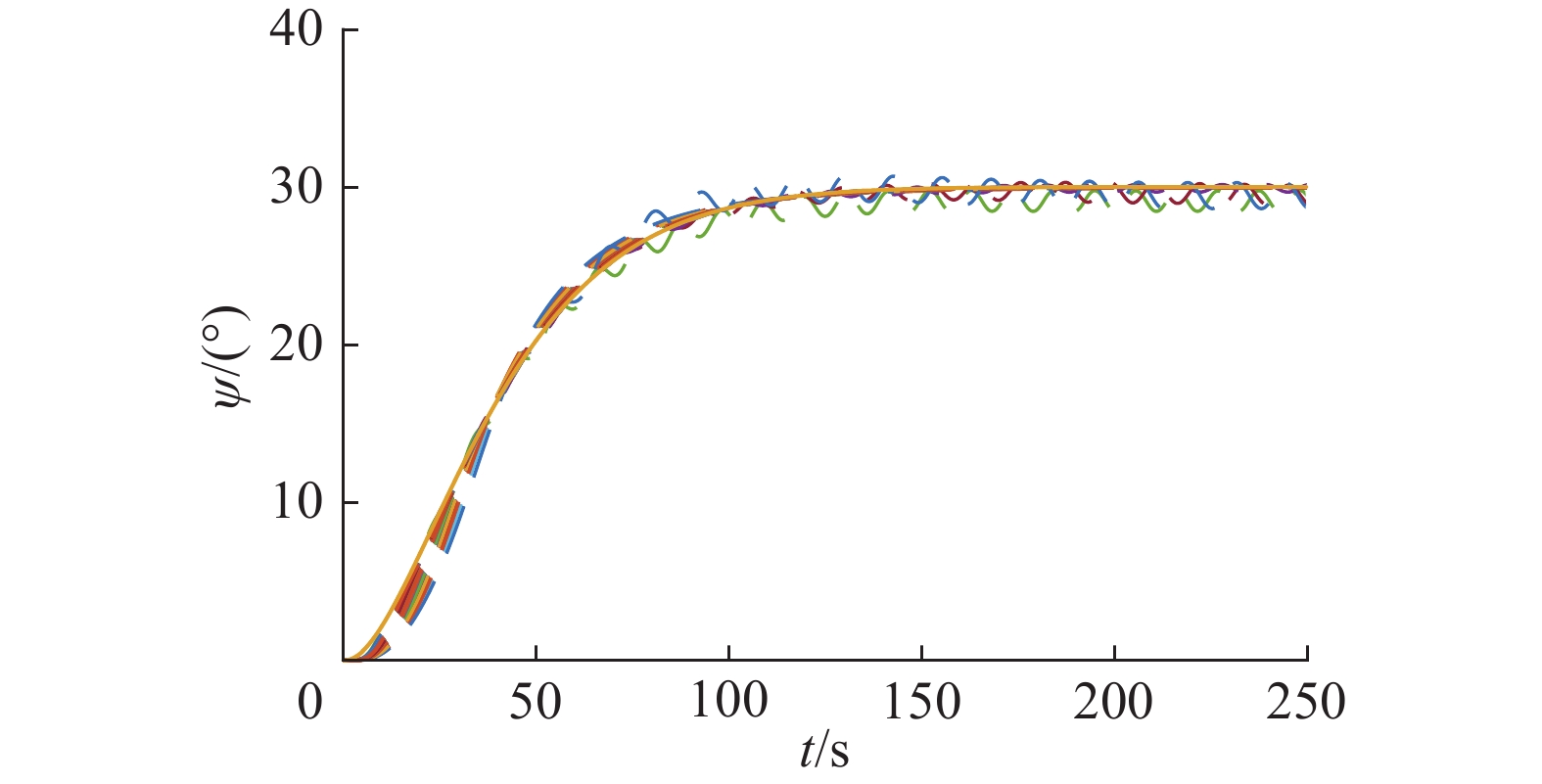
观察仿真结果图11~13可以发现,当系统存在参数摄动时,3种控制器都可以实现不错的控制效果,且自适应ESO与自适应PD控制器的控制效果优于LADRC控制器。
|
Download:
|
| 图 11 参数摄动时LADRC的航向角曲线 Fig. 11 Heading of LADRC with parameter perturbation | |
|
Download:
|
| 图 12 参数摄动时AESO的航向角曲线 Fig. 12 Heading of AESO with parameter perturbation | |

|
Download:
|
| 图 13 参数摄动时APD的航向角曲线 Fig. 13 Heading of APD with parameter perturbation | |
为了更清晰地比较不同控制器对于参数摄动的控制效果,选用表征系统暂态性能的性能指标进行评判:最大超调量
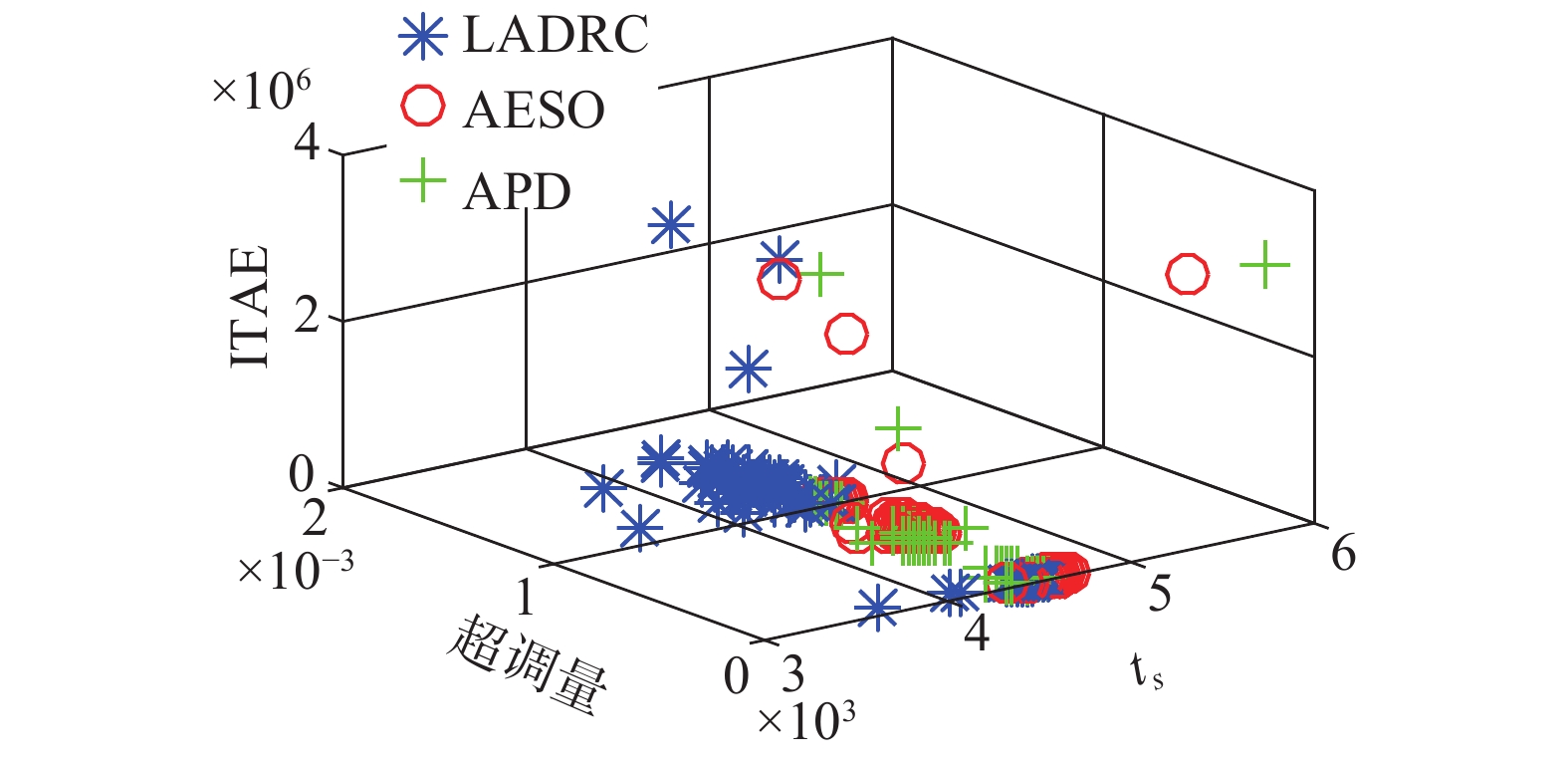
图14表明在发生参数摄动的情况下,两种自适应控制器均具有较小的最大超调量,并且点的分布更为密集;3种控制器的调节时间
|
Download:
|
| 图 14 蒙特卡罗实验结果 Fig. 14 Monte Carlo experimental result | |
本文给出了两种基于ANFIS网络的自适应ADRC设计方法,仿真结果表明自适应ADRC控制器在系统受到扰动时自适应策略具有更好的控制性能。当船舶受到扰动时,自适应ADRC可以较高精度地保持船舶航向;当航向设定值改变时,该类控制算法可以快速、平滑地跟上新的设定值,并且不会产生很大的操舵角,参数的适应性广,对于船舶航向的控制效果较为理想。在船舶参数发生摄动时,蒙特卡罗实验表明,基于ANFIS网络的自适应ADRC具有更强的鲁棒性。综上所述,基于ANFIS网络的自适应ADRC控制器具有更好的控制性能,鲁棒性更强。
本文所设计的自适应ADRC没有同时实现ADRC 3个参数同时在线调整,这将是未来研究的方向。另外,采用智能算法,例如粒子群算法、强化学习等进行控制参数的选择,也是未来需要进行探索的内容。
| [1] |
奚庆潮. 船舶航向自抗扰控制的研究[D]. 大连: 大连海事大学, 2014: 1-2. XI Qingchao. Research on ship course control based on the ADRC[D]. Dalian: Dalian Maritime University, 2014: 1–2. (  0) 0)
|
| [2] |
邱峰. 船舶航向与航迹积分滑模自抗扰保持控制[D]. 大连: 大连海事大学, 2018: 1–4. QIU Feng. Ship course and track sliding mode keeping control based on auto disturbance rejection control[D]. Dalian: Dalian Maritime University, 2018: 1–4. (  0) 0)
|
| [3] |
WITKOWSKA A, TOMERA M, ŚMIERZCHALSKI R. A backstepping approach to ship course control[J]. International journal of applied mathematics and computer science, 2007, 17(1): 73-85. DOI:10.2478/v10006-007-0007-2 ( 0) 0)
|
| [4] |
杨盐生, 于晓利, 贾欣乐. 船舶航向鲁棒PID自动舵设计[J]. 大连海事大学学报, 1999, 25(4): 11-15. YANG Yansheng, YU Xiaoli, JIA Xinle. Robust PID autopilot for ships[J]. Journal of Dalian Maritime University, 1999, 25(4): 11-15. DOI:10.3969/j.issn.1006-7736.1999.04.003 (  0) 0)
|
| [5] |
DU Jialu, GUO Chen. Nonlinear adaptive ship course tracking control based on backstepping and Nussbaum gain[C]//Proceedings of 2004 American Control Conference. Boston, MA, USA: IEEE, 2005: 3845–3850.
( 0) 0)
|
| [6] |
DU Jialu, HU Xin, SUN Yuqing. Adaptive robust nonlinear control design for course tracking of ships subject to external disturbances and input saturation[J]. IEEE transactions on systems, man, and cybernetics: systems, 2017. DOI:10.1109/TSMC.2017.2761805 ( 0) 0)
|
| [7] |
YU Renhai, LI Tieshan, LI Wei. Ship course control based on differential flatness and sliding mode[C]//Proceedings of the 4th International Conference on Information, Cybernetics and Computational Social Systems (ICCSS). Dalian, China: IEEE, 2017: 648–652.
( 0) 0)
|
| [8] |
LIU Zhiquan, GU Wei, GAO Diju. Ship course keeping using eigenvalue decomposition adaptive sliding mode control[C]//Proceedings of 2016 Techno-Ocean. Kobe, Japan: IEEE, 2016: 687–691.
( 0) 0)
|
| [9] |
ZHAO Jin, ZHANG Huajun. The application of fuzzy neural network in ship course control system[C]//Proceedings of 7th International Conference on Fuzzy Systems and Knowledge Discovery. Yantai, China: IEEE, 2010: 338–342.
( 0) 0)
|
| [10] |
韩京清. 自抗扰控制技术: 估计补偿不确定因素的控制技术[M]. 北京: 国防工业出版社, 2008: 255–263.
( 0) 0)
|
| [11] |
陈增强, 刘俊杰, 孙明玮. 一种新型控制方法——自抗扰控制技术及其工程应用综述[J]. 智能系统学报, 2018, 13(6): 865-877. CHEN Zengqiang, LIU Junjie, SUN Mingwei. Overview of a novel control method: active disturbance rejection control technology and its practical applications[J]. CAAI transactions on intelligent systems, 2018, 13(6): 865-877. (  0) 0)
|
| [12] |
王永帅, 陈增强, 孙明玮, 等. 一阶惯性大时滞系统Smith预估自抗扰控制[J]. 智能系统学报, 2018, 13(4): 500-508. WANG Yongshuai, CHEN Zengqiang, SUN Mingwei, et al. Smith prediction and active disturbance rejection control for first-order inertial systems with long time-delay[J]. CAAI transactions on intelligent systems, 2018, 13(4): 500-508. (  0) 0)
|
| [13] |
HAN Yaozhen, XIAO Hairong, WANG Changshun, et al. Design and simulation of ship course controller based on auto disturbance rejection control technique[C]//Proceedings of 2009 IEEE International Conference on Automation and Logistics. Shenyang, China: IEEE, 2009: 686–691.
( 0) 0)
|
| [14] |
刘文江, 隋青美, 周风余, 等. 基于Bech模型的船舶航向自抗扰控制器设计与仿真[J]. 船舶工程, 2011, 33(6): 61-64. LIU Wenjiang, SUI Qingmei, ZHOU Fengyu, et al. Active disturbance rejection controller design and simulation for ship course based on Bech’s equation[J]. Ship engineering, 2011, 33(6): 61-64. DOI:10.3969/j.issn.1000-6982.2011.06.016 (  0) 0)
|
| [15] |
贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999: 234–250. JIA Xinle, YANG Yansheng. Ship motion mathematical model: the mechanism modeling and identification modeling[M]. Dalian: Dalian Maritime University Press, 1999: 234–250. (  0) 0)
|
| [16] |
GAO Zhiqiang. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of 2003 American Control Conference. Denver, USA: IEEE, 2003: 4989–4996.
( 0) 0)
|
| [17] |
JANG J S R. ANFIS: adaptive-network-based fuzzy inference system[J]. IEEE transactions on systems, man, and cybernetics, 1993, 23(3): 665-685. DOI:10.1109/21.256541 ( 0) 0)
|
| [18] |
BURAGOHAIN M, MAHANTA C. A novel approach for ANFIS modelling based on full factorial design[J]. Applied soft computing, 2008, 8(1): 609-625. DOI:10.1016/j.asoc.2007.03.010 ( 0) 0)
|
| [19] |
PREMKUMAR K, MANIKANDAN B V. Adaptive neuro-fuzzy inference system based speed controller for brushless DC motor[J]. Neurocomputing, 2014, 138: 260-270. DOI:10.1016/j.neucom.2014.01.038 ( 0) 0)
|
| [20] |
李荣辉. 欠驱动水面船舶航迹自抗扰控制研究[D]. 大连: 大连海事大学, 2013: 32–34. LI Ronghui. Active disturbance rejction based tracking control of underactuated surface ships[D]. Dalian: Dalian Maritime University, 2013: 29–34. (  0) 0)
|
 2020, Vol. 15
2020, Vol. 15


