机器视觉有广泛的应用领域，如目标跟踪、视频监控、智能交通等。大多数计算机视觉算法都是假定输入为理想无噪声图像。然而，对于现实中的户外视觉系统来说，恶劣天气通常是不可避免的，它们将显著降低户外视觉系统的性能。由于雨、雪等动态大粒子随机分布在图像中，通常会影响图像局部强度，去除难度大。基于去雨研究通常分为视频去雨和单幅图像去雨。由于视频去雨的方法可利用时间相关的多帧图像信息^[1-2]，因而不适用于单幅图像去雨。而单幅图像去雨的方法可以应用于视频去雨中，解决视频去雨中不能较好处理背景变换过快的动态场景问题。因此，基于单幅图像去雨的研究显得更加有挑战性和重要性。

现如今，单幅图像去雨已引起了学术界的较大关注，可将这些单幅图像去雨方法分为3类。第1类是基于稀疏编码的去雨方法^[3-8]，第2类是基于模型的去雨方法^[9-14]，第3类是基于深度学习的去雨方法^[15-17]。其中，基于稀疏编码的去雨方法是根据雨线及背景边缘信息呈现出高频特性，而背景中的非边缘信息则呈现出低频特性。据此，这类去雨算法大多将待处理雨图预处理为高频子图和低频子图，对高频子图进行稀疏表示与字典学习，然后将高频子图学习出的背景边缘部分与低频子图相加，得到最终的去雨图。这类方法中，以Kang等^[4]为典型代表，通过稀疏表示和字典学习的方法来区分高频中的背景边缘与雨线，但存在误将背景字典原子认为是雨线字典原子，导致结果图出现模糊化的现象。后续去雨研究有依据背景与雨线对应稀疏编码系数的不同^[6]，或通过优化几何分量等^[7]方式进行去雨，这些方法在最后同样是加上低频分量，得到最终的去雨图。以上均是基于一种稀疏模型进行单幅图像去雨，还有基于融合解析和综合稀疏模型进行去雨^[8]，对融合模型迭代一定次数后，可逐步提取出背景细节，但该方法所得的背景图存在一定量的雨线残留。总之，基于稀疏编码的去雨方法效果较理想，但其中字典原子的学习过程耗时较长，实时性有待进一步提高。

基于模型的去雨方法主要依据背景与雨线结构特征的差异性，直接对图像进行去雨^[9-14]。如：基于引导滤波^[9]或基于McClellan变换^[18]设计相应的频域方向滤波器^[10]进行去雨，这些方法虽可有效地去除雨线，但计算复杂度较高。为了降低复杂度，通过分阶段^[11]或基于低阶特性模型^[12]进行去雨，均可实现有效去雨的同时，降低去雨复杂度的目标。另外，对待处理雨图添加稀疏先验项，构建稀疏约束模型进行去雨^[13-14]，去雨结果图的视觉效果也较佳。但上述去雨方法当雨线偏离垂直方向时，未将待处理雨图进行旋转或只进行大致旋转，此时去雨的视觉效果会出现一定程度下降。

最后一类是通过深度学习的方法进行去雨^[15-17]。典型的有：基于深度卷积神经网络^[15-16]或对抗网络^[17]，利用干净图像块和雨线图像块的映射关系训练神经网络进行去雨。总之，这些基于深度学习的去雨算法所得结果图视觉效果较好，但其网络结构复杂，训练过程中数据量大，较难满足实时性要求。

针对现有单幅图像去雨算法很少考虑风力对雨线主方向的影响，当雨线偏离垂直方向时，去雨后的结果图出现了雨线残留明显或背景模糊化的问题，本文提出了一种基于雨线主方向自适应的全局稀疏去雨模型。所提算法实现了有效去除雨线的同时，较大程度地保留背景信息的目标。

1 单向全变分模型去噪

一般，雨图模型^[13]可用如下的加性噪声模型表示：

${ r} = { t} + { s}$

(1)

式中： ${ r} \in {\rm{R}^{MN \times 1}}$ 为待处理雨图； ${ t} \in {\rm{R}^{MN \times 1}}$ 为待求的背景图； ${ s} \in {\rm{R}^{MN \times 1}}$ 为雨线图。

加性噪声模型也应用于遥感图去除条形噪声：

${ I}\left( {x,y} \right) = {{ I}_u}\left( {x,y} \right) + {{ I}_s}\left( {x,y} \right)$

(2)

式中： ${ I}\left( {x,y} \right)$ 表示含条形噪声的观测图； ${{ I}_u}\left( {x,y} \right)$ 和 ${{ I}_s}\left( {x,y} \right)$ 分别表示待求的背景图和条形噪声图。当条形噪声沿垂直方向时，雨线与遥感图的条形噪声具有方向相似性，故雨线的方向特性也可以基于文献[19]所提的单向全变分(unidirectional total variation，UTV)模型进行表征，其单向全变分模型的最小能量函数为

$\mathop {\min }\limits_{{{ I}_u}} { E}\left( {{{ I}_u}} \right) = {\rm T}{{\rm V}_y}\left( {{{ I}_u} - { I}} \right) + \tilde {\text{λ}} {\rm T}{{\rm V}_x}\left( {{{ I}_u}} \right)$

(3)

即：

$\mathop {\min }\limits_{{{ I}_u}} { E}\left( {{{ I}_u}} \right) = \int_\varOmega {\left( {\left| {\frac{{\partial \left( {{{ I}_u} - { I}} \right)}}{{\partial y}}} \right|} \right.} + \left. {\tilde {\text{λ}} \left| {\frac{{\partial {{ I}_u}}}{{\partial x}}} \right|} \right){\rm d}x{\rm d}y$

(4)

由式(4)对应的全变分模型可得以下结论：

1)为了有助于条形噪声的去除，可将梯度信息分离为沿着垂直方向的保真项 $\int_\varOmega {\left| {\dfrac{{\partial \left( {{{ I}_u} - { I}} \right)}}{{\partial y}}} \right|} {\rm d}y$ 和沿着水平方向的正则化项 $\int_\varOmega {\left| {\dfrac{{\partial {{ I}_u}}}{{\partial x}}} \right|{\rm d}x} $ ；

2)对保真项和正则化项应使用边缘保持范数，例如 ${\rm{TV}}$ 范数或 ${l_1}$ 范数等，避免背景图出现伪影现象。

2 基于雨线主方向自适应的全局稀疏去雨模型 2.1 自适应调节雨线主方向角度

由于在YCbCr颜色空间中，雨线只出现在Y通道分量图，剩余2通道分量图几乎看不见雨线。因此，将输入的RGB空间的雨图像转换到YCbCr空间，本文只需对Y通道分量图进行处理，最后进行通道重组可减少计算量。

首先，确定待处理雨图的雨线主方向。由于受风力的影响，导致雨线在垂直方向向左或右偏转，一般在90°±45°的范围内，即雨线降落角度 $\theta \in \left[ {{{45}^ \circ },{{135}^ \circ }} \right]$ 。将长度为90°的降落区间分成9格，每格区间长度设置为10°，以每格均值(如50°，60°，···，130°)为雨线主降落方向，对应图像库编号分别为 ${{\rm{I}}_1}, \;{{\rm{I}}_2},\;\cdots,\;{{\rm{I}}_9}$ 。本文之所以设置区间长度为10°，是确保每一幅雨图中即便雨线在不同区域存在偏差，±5°的角度偏差仍然满足要求。由于图像库中的雨线图的作用是为了确定待处理雨图的雨线主方向，为了清晰显示雨线在图中的分布情况，本文以二值图的形式进行展示所建立的纯雨线图像库，如图1所示。

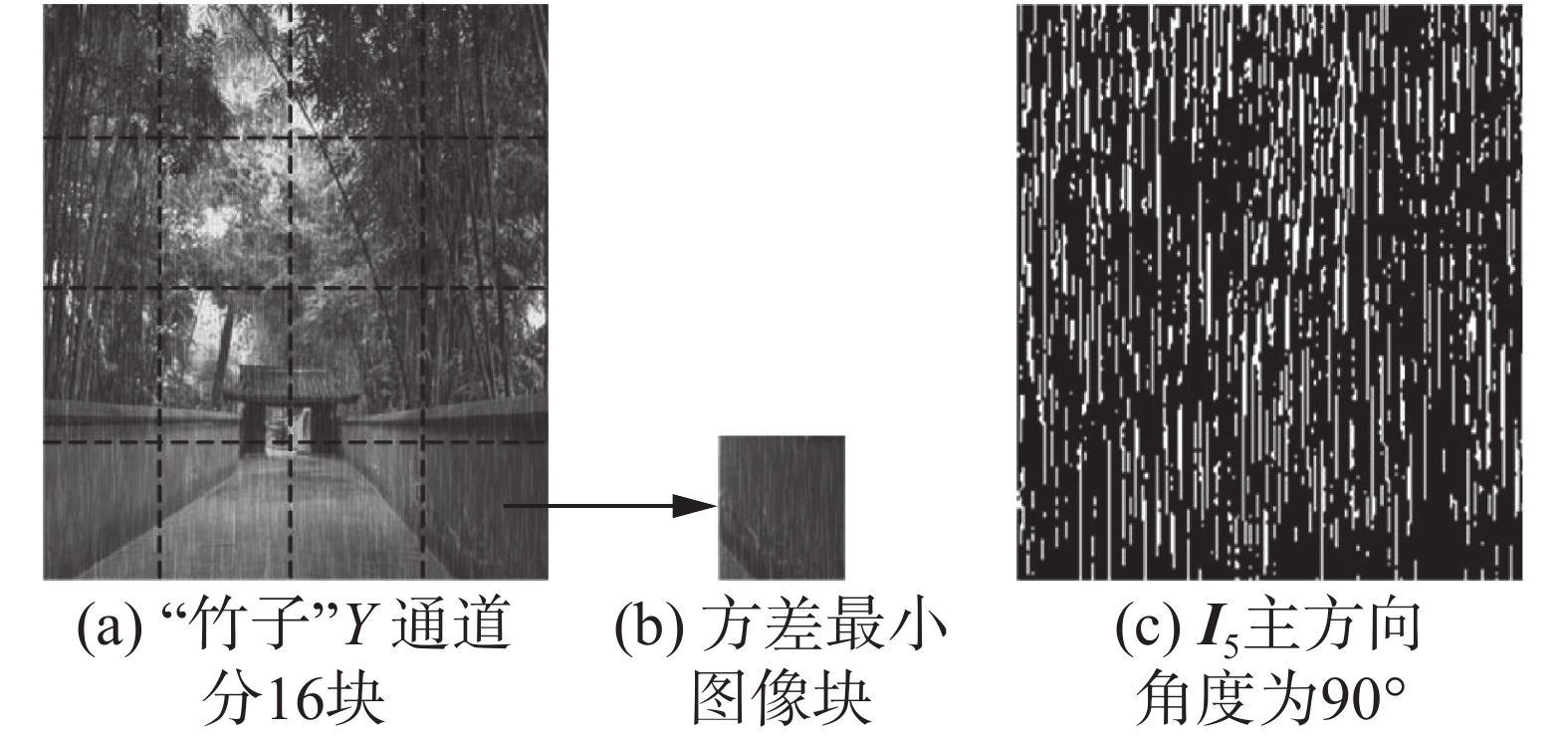
每一幅雨图都存在一个雨线降落主方向，由于在同一幅雨图中雨线降落方向近似相同，雨线的方差较小，而背景边缘方向各异，其方差较大。为了较为准确确定雨线降落主方向，将输入的雨图均分为16块，取方差最小的图像块用于确定雨线降落主方向。

图2以“竹子”图为例进行说明，“竹子”图的第16小块方差最小，该图像块中主要呈现为墙壁、地面等，其背景相对平滑，则该图像块受背景干扰小，故可选取方差最小的图像块用于确定雨线降落主方向。

接着，将以方差最小的图像块，依据HOG特征进行匹配，将匹配度最高的图像库中的雨线图的主方向降落角度 $\tilde \theta $ 视作待处理雨图的雨线主方向降落的角度，旋转待处理雨图直到其雨线主方向沿垂直方向，记旋转角为 $\theta $ 。

同样，以“竹子”图为例说明，“竹子”图的第16小块方差最小，以该图像块的HOG特征与雨线图像库中雨图的HOG特征进行匹配，此时匹配度最高的雨图为 ${{{I}}_5}$ ，将 ${{{I}}_5}$ 的雨线主方向视作待处理雨图的雨线主方向，记雨线主方向角 $\tilde \theta $ 为90°，则旋转角 $\theta = {0^ \circ }$ ，此时无需旋转待处理雨图。总之，待处理雨图的旋转角 $\theta $ 为：

$\theta = \left\{ \begin{array}{l} {90^ \circ } - \tilde \theta ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{{I}}_1},{{{I}}_2},{{{I}}_3},{{{I}}_4}\\ {0^ \circ },\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{{I}}_5}\\ - \left| {\tilde \theta - {{90}^ \circ }} \right| = {90^ \circ } - \tilde \theta ,\;\;{{{I}}_6},{{{I}}_7},{{{I}}_8},{{{I}}_9} \end{array} \right.$

(5)

式中旋转角 $\theta $ 的正负性可用来进行旋转方向的判断，具体为：

$\theta = \left\{ \begin{array}{l} \theta > {0^ \circ },\;\;\;\;\;\;{{{I}}_1},{{{I}}_2},{{{I}}_3},{{{I}}_4}\\ \theta = {0^ \circ },\;\;\;\;\;\;{{{I}}_5}\\ \theta < {0^ \circ },\;\;\;\;\;\;{{{I}}_6},{{{I}}_7},{{{I}}_8},{{{I}}_9}{\rm{ }} \end{array} \right.$

(6)

综上所述，当雨线以不同角度偏离坐标轴时，旋转角 $\theta $ 由以下3种情况确定：

1) $\theta > {0^ \circ }$ ，需要逆时针旋转 $\theta $ ，旋转角的大小为 ${90^ \circ } - \tilde \theta $ ，从而使雨线近似沿着垂直方向降落；

2) $\theta = {0^ \circ }$ ，此时待处理雨图的雨线主方向近似垂直方向，(图像库中编号为 ${{{I}}_5}$ 的雨线图与方差最小图像块的HOG特征匹配度最高，即：待处理雨图的雨线主方向在 ${90^ \circ } \pm {5^ \circ }$ 的区间)，无需旋转待处理雨图，即旋转角 $\theta $ 取 ${0^ \circ }$ ；

3) $\theta < {0^ \circ }$ ，需要顺时针旋转 $\theta $ ，旋转角的大小为 $\left| {\tilde \theta - {{90}^ \circ }} \right|$ ，从而使雨线近似沿着垂直方向降落。

然后，基于雨线主方向建立优化模型，为方便起见，本文将垂直雨线主方向统一使用 $\hat x$ 表示，雨线主方向统一使用 $\hat y$ 表示。

2.2 全局稀疏模型的确定

受文献[14]启发，本文先确定雨线主方向后，构建雨线主方向自适应的全局稀疏去雨模型，该模型由3个稀疏先验项对待处理雨图进行稀疏约束，包括一个雨线稀疏先验项，以及背景在 $\hat x$ 方向和雨线在 $\hat y$ 方向的梯度稀疏先验项。

1)雨线的稀疏正则项： ${l_0}$ 范数可对雨线的稀疏性起到较好的稀疏约束作用，但 ${l_0}$ 范数的非凸性会使模型收敛到局部最优解； ${l_1}$ 范数既可以表示稀疏性又具有凸性，会使稀疏模型收敛到全局最优。故本文基于 ${l_1}$ 范数对雨线添加稀疏正则项：

${\rm{Re}}{{\rm{g}}^{\left( {\rm{1}} \right)}}\left( { s} \right) = {\left\| { s} \right\|_1}$

(7)

2)雨线主方向( $\hat y$ 轴方向)上的梯度稀疏性：在该方向上，雨线梯度沿降落方向具有稀疏平滑性。即可对 $\hat y$ 方向的雨线梯度添加稀疏正则项进行约束：

${\rm{Re}}{{\rm{g}}^{\left( {\rm{2}} \right)}}\left( { s} \right) = {\left\| {{\nabla _{\hat y}}{ s}} \right\|_1}$

(8)

${\nabla _{\hat y}}$ 是 $\hat y$ 方向上的差分算子。该项可看作式(3)的第一个正则项的变换。

3)垂直于雨线主方向( $\hat x$ 轴)上的梯度稀疏性：受单向总变分(UTV)的启发，背景梯度在 $\hat x$ 方向受雨水影响最小，即：背景梯度具有稀疏性。在自然雨图像中，雨线图 ${ s}$ 具有非负性。线性叠加后，待处理含雨图 ${ r}$ 的强度值最大。因此，非负性约束条件为：

${ r} \geqslant { s} \geqslant 0$

(9)

由式(1)可得背景为 ${ t} = { r} - { s}$ 。因此，背景梯度在 $\hat x$ 方向的稀疏正则项为：

${\rm{Re}}{{\rm{g}}^{\left( {\rm{3}} \right)}}\left( { s} \right) = {\left\| {{\nabla _{\hat x}}\left( {{ r} - { s}} \right)} \right\|_1}$

(10)

式中 ${\nabla _{\hat x}}$ 是 $\hat x$ 方向上的差分算子。该项对应式(3)的第2个正则项的变换。

记 ${D_\theta }$ 为旋转角为 $\theta $ 的旋转运算符，则带有 ${D_\theta }$ 的3个稀疏正则项分别为 ${\left\| {{D_\theta }{ s}} \right\|_1}$ 、 ${\left\| {{\nabla _{\hat y}}\left( {{D_\theta }{ s}} \right)} \right\|_1}$ 、 ${\left\| {{\nabla _{\hat x}}\left( {{D_\theta }\left( {{ r} - { s}} \right)} \right)} \right\|_1}$ 。

因此，本文算法的优化模型为：

$\begin{gathered} \underset{{ s}}{\mathop{\min }}\,E\left( s \right)=\underset{s}{\mathop{\min }}\,\left\{ {{\textit{λ}}_{1}}{\rm T}{{{\rm V}}_{x}}\left( {{D}_{\theta }}\left( { r}-{ s} \right) \right)+{{\textit{λ}}_{2}}{{\left\| {{D}_{\theta }}{ s} \right\|}_{1}}+ \right. \\ \left. {\rm T}{{{\rm V}}_{y}}\left( {{D}_{\theta }}{ s} \right) \right\}=\underset{{ s}}{\mathop{\min }}\,\left\{ {{\textit{λ}}_{1}}{{\left\| {{\nabla }_{{\hat{x}}}}\left( {{D}_{\theta }}\left( { r}-{ s} \right) \right) \right\|}_{1}}+ \right. \\ \left. {{\textit{λ}}_{2}}{{\left\| {{D}_{\theta }}{ s} \right\|}_{1}}+{{\left\| {{\nabla }_{{\hat{y}}}}\left( {{D}_{\theta }}{ s} \right) \right\|}_{1}} \right\} \\ \end{gathered}$

(11)

式中： ${ r} \geqslant { s} \geqslant 0$ ； ${{\textit{λ}}_{\rm{1}}}$ 、 ${{\textit{λ}}_{\rm{2}}}$ 是两个正则化参数且 ${{\textit{λ}}_{\rm{1}}} > 0$ 、 ${{\textit{λ}}_2} > 0$ 。

本文算法流程图如图3所示。

采用约束条件解决式(11)对应的等价问题：

$\mathop {\min }\limits_{ s} \left\{ {{\lambda _1}{{\left\| { u} \right\|}_1} + {\lambda _2}{{\left\| { v} \right\|}_1} + {{\left\| { w} \right\|}_1}} \right\}$

(12)

式中： ${ u} = {\nabla _{\hat x}}\left( {{D_\theta }\left( {{ r} - { s}} \right)} \right)$ ； ${ v} = {D_\theta }{ s}$ ； ${ w} = {\nabla _{\hat y}}\left( {{D_\theta }{ s}} \right)$ 。

为了方便，本文将 ${D_\theta }\left( { r} - { s} \right)$ 、 ${D_\theta }{ r}$ 、 ${D_\theta }{ s}$ 分别表示为 ${{ r}_{{D_\theta }}} - {{ s}_{{D_\theta }}}$ 、 ${{ r}_{{D_\theta }}}$ 、 ${{ s}_{{D_\theta }}}$ 。因此，式(12)对应的增广拉格朗日函数为

$\!\!\mathop {\min }\limits_{{ u},{ v},{ w},{ s}} \left. {\left\{ \begin{gathered} L\left( {{ u},{ v},{ w},{ s},{p_1},{p_2},{p_3}} \right) = \\ {{\textit{λ}}_1}{\left\| { u} \right\|_1} + {{\textit{λ}}_2}{\left\| { v} \right\|_1} + {\left\| { w} \right\|_1} + \left\langle {{p_1},{\nabla _{\hat x}}\left( {{r_{{D_\theta }}} - {{ s}_{{D_\theta }}}} \right) - { u}} \right\rangle + \\ \dfrac{{{\beta _1}}}{2}\left\| {{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - {{ s}_{{D_\theta }}}} \right) - { u}} \right\|_2^2 + \\ \left\langle {{p_2},{{ s}_{{D_\theta }}} - { v}} \right\rangle + \dfrac{{{\beta _2}}}{2}\left\| {{{ s}_{{D_\theta }}} - { v}} \right\|_2^2 +\\ \left\langle {{p_3},{\nabla _{\hat y}}{{ s}_{{D_\theta }}} - { w}} \right\rangle + \dfrac{{{\beta _3}}}{2}\left\| {{\nabla _{\hat y}}{{ s}_{{D_\theta }}} - { w}} \right\|_2^2 \end{gathered} \right.} \right\}$

(13)

式中： $\;{\beta _1}$ 、 $\;{\beta _2}$ 、 $\;{\beta _3}$ 是正则化参数； ${p_1}$ 、 ${p_2}$ 、 ${p_3}$ 分别表示3个拉格朗日乘子。采用方向乘子法来解决 ${l_1}$ 范数问题，式(13)中的问题可以分解成4个简单且具有闭合解的子问题。

1) $ u$ 的子问题：固定 $ v$ 、 $ w$ ，最小化能量泛函：

$\begin{gathered} \hat { u}{\rm{ = arg }}\mathop {{\rm{min}}}\limits_{ u} {{\textit{λ}}_{\rm{1}}}{\left\| { u} \right\|_1} + \left\langle {{p_1}{\rm{,}}{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - {{ s}_{{D_\theta }}}} \right) - { u}} \right\rangle + \\ \dfrac{{{\beta _1}}}{2}\left\| {{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - {{ s}_{{D_\theta }}}} \right) - { u}} \right\|_2^2 = \\ {\rm{arg }}\mathop {{\rm{min}}}\limits_{ u} {{\textit{λ}}_{\rm{1}}}{\left\| { u} \right\|_1} + \dfrac{{{\beta _1}}}{2}\left\| {{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - {{ s}_{{D_\theta }}}} \right) - { u}{\rm{ + }}\dfrac{{{p_1}}}{{{\beta _1}}}} \right\|_2^2 \end{gathered}$

(14)

式(14)可通过式(15)的软阈值方法^[18]来解决：

${{ u}^{k{\rm{ + 1}}}} = {\rm{Shrink}}\left( {{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^k} \right) + \frac{{p_1^k}}{{{\beta _1}}},\frac{{{\lambda _{\rm{1}}}}}{{{\beta _1}}}} \right)$

(15)

${\rm{Shrink}}\left( {a{\rm{,}}b} \right) = {\rm{sign}}\left( a \right)\max \left( {\left| a \right| - b,0} \right)$

(16)

式中 ${\rm{sign}}\left( a \right)$ 为 $a$ 的符号函数，即：

$\text{sign}\left( a \right)=\left\{ \begin{matrix} \begin{matrix} 1, \\ 0, \\ -1, \\ \end{matrix} & \begin{matrix} a > 0 \\ a = 0 \\ a < 0 \\ \end{matrix} \\ \end{matrix} \right.$

(17)

2) $ v$ 的子问题：固定 $ u$ 、 $ w$ ，最小化能量泛函：

$\begin{gathered} \hat { v}{\rm{ = arg }}\mathop {{\rm{min}}}\limits_{ v} {{\textit{λ}}_{\rm{2}}}{\left\| { v} \right\|_1} + \left\langle {{p_2}{\rm{,}}{{ s}_{{D_\theta }}} - { v}} \right\rangle + \dfrac{{{\beta _2}}}{2}\left\| {{{ s}_{{D_\theta }}} - { v}} \right\|_2^2 = \\ _{}^{}{\rm{arg }}\mathop {{\rm{min}}}\limits_{ v} {{\textit{λ}}_{\rm{2}}}{\left\| { v} \right\|_1} + \dfrac{{{\beta _2}}}{2}\left\| {{{ s}_{{D_\theta }}} - { v} + \dfrac{{{p_2}}}{{{\beta _2}}}} \right\|_2^2 \\ \end{gathered} \!\!\!\!\!\!\!\!$

(18)

式(18)的闭合解也通过软阈值方法来获得：

${{ v}^{k + 1}} = {\rm{Shrink}}\left( {{ s}_{{D_\theta }}^k + \frac{{p_2^k}}{{{\beta _2}}},\frac{{{\lambda _{\rm{2}}}}}{{{\beta _2}}}} \right)$

(19)

3) $ w$ 的子问题：固定 $ u$ 、 $ v$ ，最小化能量泛函：

$\begin{gathered} \hat { w}{\rm{ = arg }}\mathop {{\rm{min}}}\limits_{ w} {\left\| { w} \right\|_1} + \left\langle {{p_3}{\rm{,}}{\nabla _{\hat y}}{{{ s}}_{{D_\theta }}} - { w}} \right\rangle + \dfrac{{{\beta _3}}}{2}\left\| {{\nabla _{\hat y}}{{{ s}}_{{D_\theta }}} - { w}} \right\|_2^2 = \\ _{}^{} {\rm{arg }}\mathop {{\rm{min}}}\limits_{ w} {\left\| { w} \right\|_1} + \dfrac{{{\beta _3}}}{2}\left\| {{\nabla _{\hat y}}{{{ s}}_{{D_\theta }}} - { w} + \dfrac{{{p_3}}}{{{\beta _3}}}} \right\|_2^2 \\ \end{gathered} \!\!\!\!\!\!\!\!\!$

(20)

子问题(20)的闭合解给出为：

${w^{k + 1}} = {\rm{Shrink}}\left( {{\nabla _{\hat y}}{\rm{s}}_{{D_\theta }}^k + \frac{{p_3^k}}{{{\beta _3}}},\frac{1}{{{\beta _3}}}} \right)$

(21)

4) ${{ s}_{{D_\theta }}}$ 的子问题：

$ \begin{gathered} {{{\hat{ s}}}_{{{D}_{\theta }}}}=\text{arg}\underset{{{ s}_{{{D}_{\theta }}}}}{\mathop{\text{min}}}\,\left\langle {{p}_{1}},{{\nabla }_{{\hat{x}}}}\left( {{ r}_{{{D}_{\theta }}}}-{{ s}_{{{D}_{\theta }}}} \right)-{ u} \right\rangle +\left\langle {{p}_{2}},{{ s}_{{{D}_{\theta }}}}-{ v} \right\rangle \text{+} \\ \left\langle {{p}_{3}},{{\nabla }_{{\hat{y}}}}{{ s}_{{{D}_{\theta }}}}-{ w} \right\rangle +\dfrac{{{\beta }_{1}}}{2}\left\| {{\nabla }_{{\hat{x}}}}\left( {{ r}_{{{D}_{\theta }}}}-{{ s}_{{{D}_{\theta }}}} \right)-{ u} \right\|_{2}^{2}+ \\ \dfrac{{{\beta }_{2}}}{2}\left\| {{ s}_{{{D}_{\theta }}}}-{ v} \right\|_{2}^{2}+\dfrac{{{\beta }_{3}}}{2}\left\| {{\nabla }_{{\hat{y}}}}{{ s}_{{{D}_{\theta }}}}-{ w} \right\|_{2}^{2}=\text{arg}\underset{{{ s}_{{{D}_{\theta }}}}}{\mathop{\text{min}}}\,\dfrac{{{\beta }_{1}}}{2} \\ \left\| {{\nabla }_{{\hat{x}}}}\left( {{ r}_{{{D}_{\theta }}}}-{{ s}_{{{D}_{\theta }}}} \right)-{ u}\text{+}\dfrac{{{p}_{1}}}{{{\beta }_{1}}} \right\|_{2}^{2}+\dfrac{{{\beta }_{2}}}{2}\left\| {{ s}_{{{D}_{\theta }}}}-{ v}\text{+}\dfrac{{{p}_{2}}}{{{\beta }_{2}}} \right\|_{2}^{2}+ \\ \dfrac{{{\beta }_{3}}}{2}\left\| {{\nabla }_{{\hat{y}}}}{{ s}_{{{D}_{\theta }}}}-{ w}\text{+}\dfrac{{{p}_{3}}}{{{\beta }_{3}}} \right\|_{2}^{2} \end{gathered}$

(22)

由于式(22)可微， ${{ s}_{{D_\theta }}}$ 的子问题的闭合解可通过式(23)求解：

$\begin{gathered} \left( {{\beta _1}\nabla _{\hat x}^T{\nabla _{\hat x}}{\rm{ + }}{\beta _2}{{I + }}{\beta _3}\nabla _{\hat y}^T{\nabla _{\hat y}}} \right)\tilde { s}_{{D_\theta }}^{k{\rm{ + 1}}} = \nabla _{\hat y}^T\left( {{\beta _{3{w^{k{\rm{ + 1}}}}}} - \dfrac{{p_{\rm{3}}^k}}{{{\beta _3}}}} \right){\rm{ + }}\\ {\beta _2}{{ v}^{k{\rm{ + 1}}}} - p_{\rm{2}}^k + \nabla _{\hat x}^T\left( {{\beta _1}{\nabla _{\hat x}}{{ r}_{{D_\theta }}} - {\beta _1}{{ u}^{k{\rm{ + 1}}}} + p_{\rm{1}}^k} \right)\pi \end{gathered}$

(23)

式中： $ I$ 表示单位矩阵。而式(23)可通过快速傅里叶变换(FFT)解决。

由非负性约束条件式(9)所得到的 $\tilde{ s}_{{D_\theta }}^{k + 1}$ ，可由式(24)进行投影：

${ s}_{{D_\theta }}^{k + 1} = {\rm{min}}\left( {{{ r}_{{D_\theta }}},{\rm{max}}\left( {\tilde { s}_{{D_\theta }}^{k{\rm{ + 1}}},0} \right)} \right)$

(24)

根据ADMM方法，可通过式(25)更新拉格朗日乘子 ${p_1}$ 、 ${p_2}$ 、 ${p_3}$ ：

$\begin{gathered} p_{\rm{1}}^{k + 1} = p_{\rm{1}}^k + {\beta _1}\left( {{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^{k + 1}} \right) - {{ u}^{k{\rm{ + 1}}}}} \right) \\ p_{\rm{2}}^{k + 1} = p_{\rm{2}}^k + {\beta _2}\left( {{ s}_{{D_\theta }}^{k + 1} - {{ v}^{k{\rm{ + 1}}}}} \right) \\ p_{\rm{3}}^{k + 1} = p_{\rm{3}}^k + {\beta _3}\left( {{\nabla _{\hat y}}{ s}_{{D_\theta }}^{k + 1} - {{ w}^{k{\rm{ + 1}}}}} \right) \\ \end{gathered} $

(25)

本文算法将式(13)对应的复杂问题分解为4个简单的子问题，这4个子问题均具有闭合解，可以确保算法的准确性和快速性。其中 $ u$ 、 $ v$ 、 $ w$ 子问题均通过软阈值法求解， ${{ s}_{{D_\theta }}}$ 子问题通过FFT来解决。

2.3 颜色掩膜保护背景

当背景和雨线的梯度相近时，无法正确区分背景和雨线，会出现雨线残留严重或过度平滑现象。基于此，本文受文献[20]的启发，考虑到雨线独特的颜色信息，利用颜色掩膜将Y通道中部分深灰色背景像素保持原值。

通过对Y通道归一化处理，雨线处像素值一般较大，在原始Y通道中大多呈现较亮的灰白色，而背景对应的像素大多表现出各种深浅不同的灰色。虽然无法确定像素值较大的灰白色像素一定为雨像素，但是像素值较小的黑色及深灰色像素一定不会是雨像素，这部分像素视作未受雨水影响的背景像素。设定原始Y通道像素值用 ${p_{y_i}}$ 表示， ${w_i}$ 表示每一个像素点 $i$ 的颜色与白色之间的差异值，以及 $T \in \left[ {0,1} \right]$ 表示整幅图像的阈值。当像素点的 ${w_i}$ 越大，即当 ${w_i} > T$ 时，可认为该像素为未受雨水影响的背景像素。再定义掩膜图像的像素值为 ${m_i}$ 。其表达式为：

${m_i} = \left\{ {\begin{array}{*{20}{c}} {1,\;\;{w_i} > T} \\ {0,\;\;{w_i} < T} \end{array}} \right.$

(26)

式中 ${w_i} = 1 - {p_{{\hat y}_i}}$ 。

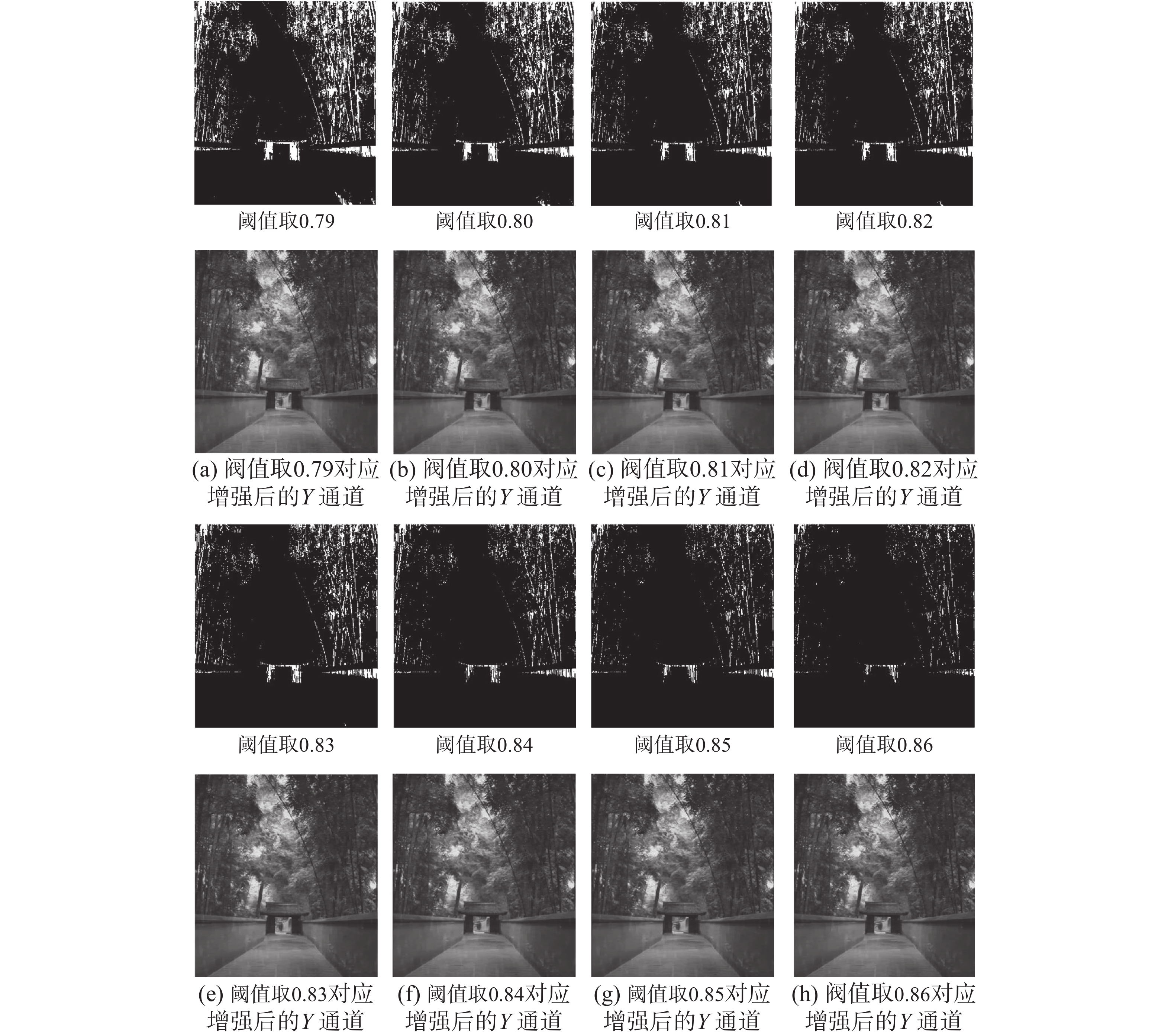
本文以“竹子”图为例来说明取不同数值的阈值 $T$ ，遍历整幅Y通道分量图后，得到对应的掩膜图以及对应增强后的Y通道分量图，如图4所示。

由图4可得，掩膜图的形成是基于原始Y通道分量图，在颜色掩膜图中用白色像素表示原始Y通道中像素满足 ${w_i} > T$ 的深灰色或黑色像素，这些深灰色或黑色像素可视作未被雨水覆盖的背景像素，这部分像素需在最终输出的去雨图中保留原值。而在颜色掩膜图中用黑色像素表示的像素处，最终的输出去雨图仍采用全局稀疏模型去雨后的像素值。

通过对UCID数据集的50幅图像进行实验，阈值 $T$ 取均值0.82时，峰值信噪比(PSNR)、结构相似性(SSIM)取得较高值。为了更加客观地评价，本文以“竹子”图为例，列出不同阈值 $T$ 对应的峰值信噪比(PSNR)、结构相似性(SSIM)数值，如表1所示。由表1可得：当阈值 $T$ 取值逐渐增大时，PSNR、SSIM值先增大后逐渐趋于平稳。

本文算法的步骤如下：

1)输入　雨图 $ r$ ，通过式(5)确定旋转角 $\theta $ ，

初始化 ${{\textit{λ}} _1} = 0.08$ ， ${{\textit{λ}} _2} = 0.95 $ ； $\;{\beta _1} = {\beta _2} = {\beta _3} = 200 $ ， $T=0.82;p_1^0 = p_2^0 = p_3^0 = 0,{s^0} = 0,k = 0$ 。

2)循环　 $k = k + 1$

$\begin{gathered} \left\| {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^k} \right\|/\left\| {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^{k - 1}} \right\| > {\rm tol} = {{\rm e}^{ - 3}} \\ {\rm and}\;k < {M_{{\rm ite}{ r}}} = {{2}}00 \\ \end{gathered} $

3)通过式(15)、(19)、(21)对应求解 ${{ u}^{k + 1}}{\text{、}} $ ${{ v}^{k + 1}}{\text{、}}{{ w}^{k + 1}}$ ；通过式(24)求解 ${ s}_{{D_\theta }}^{k + 1}$ ，通过式(25)求解 $p_1^{k + 1}{\text{、}}p_2^{k + 1}{\text{、}}p_3^{k + 1}$ ，即：

${{ u}^{k{\rm{ + 1}}}} = {\rm{Shrink}}\left( {{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^k} \right) + \frac{{p_1^k}}{{{\beta _1}}},\frac{{{{\textit{λ}} _{\rm{1}}}}}{{{\beta _1}}}} \right)$

${{ v}^{k{\rm{ + 1}}}} = {\rm{Shrink}}\left( {{ s}_{{D_\theta }}^k + \frac{{p_2^k}}{{{\beta _2}}},\frac{{{{\textit{λ}} _{\rm{2}}}}}{{{\beta _2}}}} \right)$

${{ w}^{k{\rm{ + 1}}}} = {\rm{Shrink}}\left( {{\nabla _{\hat y}}{{s}}_{{D_\theta }}^k + \frac{{p_3^k}}{{{\beta _3}}},\frac{1}{{{\beta _3}}}} \right)$

${ s}_{{D_\theta }}^{k{\rm{ + 1}}} = {\rm{min}}\left( {{{ r}_{{D_\theta }}},{\rm{max}}\left( {\tilde { s}_{{D_\theta }}^{k{\rm{ + 1}}},0} \right)} \right)$

$\begin{gathered} p_{\rm{1}}^{k + 1} = p_{\rm{1}}^k + {\beta _1}\left( {{\nabla _{\hat x}}\left( {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^{k + 1}} \right) - {{ u}^{k{\rm{ + 1}}}}} \right) \\ p_{\rm{2}}^{k + 1} = p_{\rm{2}}^k + {\beta _2}\left( {{ s}_{{D_\theta }}^{k + 1} - {{ v}^{k{\rm{ + 1}}}}} \right) \\ p_{\rm{3}}^{k + 1} = p_{\rm{3}}^k + {\beta _3}\left( {{\nabla _{\hat y}}{ s}_{{D_\theta }}^{k + 1} - {{ w}^{k{\rm{ + 1}}}}} \right) \\ \end{gathered} $

4)当有下式成立时

$\begin{gathered} \left\| {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^k} \right\|/\left\| {{{ r}_{{D_\theta }}} - { s}_{{D_\theta }}^{k - 1}} \right\| > {\rm tol} = {{\rm e}^{ - 3}} \\ {\rm{or }}\;k < {M_{\rm iter}} = {\rm{2}}00 \\ \end{gathered} $

通过全局稀疏模型所得的最小化能量泛函的解对应Y通道去雨图，即：

${{ t}_{{D_\theta }}} = {{ r}_{{D_\theta }}} - {{ s}_{{D_\theta }}}$

最后，通过式(26)，对未受雨水影响的部分背景进行保护，通道重组后，颜色空间转换到RGB空间中，得最终的去雨结果图。

3 实验结果与分析 3.1 合成数据定性分析

为验证本文算法的有效性，并与近期典型对比文献[6]、[13]、[14]所提算法进行对比实验及分析。如图5所示。

在硬件配置为Intel(R) Core (TM) i5-3210M CPU @2. 50 GHz 4 GB RAM的PC机，软件使用Matlab R2014a进行实验。

以“竹子”、“熊猫”、“女孩”、“树林”这4张合成图为例，展示4种算法视觉上的差异，可发现：Luo等^[6]算法背景保存最为完整，但是雨线残留较明显，如“竹子”图的地面等处。Li等^[13]算法虽然有效地去除了雨线，但背景细节模糊化较为明显，如“竹子”图的竹子纹理等处。

本文算法和Deng等^[14]相比，在较大程度保护背景信息的前提下，比文献[14]去雨稍彻底，同时背景信息也能较好地保留。整体上看，本文算法比文献[6]可更有效地去除雨线，同时比文献[13]更好地保留图像背景的细节信息。当雨线偏离垂直方向时，文献[14]只进行大致旋转，而本文算法由于采取了更精确的雨图旋转策略，故本文算法比文献[14]去雨更加彻底。同时，由于本文算法采用颜色掩膜对于未受雨水影响的背景进行保护，从而也较大程度地保留了背景细节信息。

3.2 合成数据定量分析

为了更加客观地评价本文与对比算法的效果，使用峰值信噪比(PSNR)、结构相似性(SSIM)以及运行时间作为客观评价指标，如表2所示。

从表2中的实验数据可看出，本文算法的PSNR值、SSIM值比文献[6]、[13]、[14]高，表示本文得到的去雨结果图与真实图更为近似。本文算法的计算时间比文献[6]、[13]短，稍长于文献[14]。

3.3 真实数据分析

本文以“花朵”、“奥巴马”、“树木”、“自行车”作为真实图的实验数据。

图6展现出了不同去雨算法在真实图上的去雨效果。从结果图中可看出，Luo等^[6]所提算法出现雨线残留较明显的情况，如“花朵”图上方的天空、草地等处。Li等^[13]所提算法雨线去除较彻底，但是出现一定程度的背景模糊化，如“花朵”图中草地等处。文献[14]存在少许雨线残留，如“花朵”图的天空等处。本文算法将整幅雨图的雨线去除更为彻底，同时背景信息也较大程度地被保护。

真实雨图的实验结果如图6所示。真实雨图为现实中真实存在的雨图，其不存在对应的无雨图，故无法计算PSNR值、SSIM值。本文以各算法取得最佳视觉效果的运行时间作为评价指标，4种算法的运行时间如表3所示。由表3可得，本文算法的运行时间明显比对比文献[6]、[13]的运行时间短，由于本文采用了自适应确定雨线主方向的策略以及对部分背景进行保护，运行时间稍长于文献[14]。整体上看，本文算法的实时性相对较高。

4 结束语

现有的单幅图像去雨算法很少考虑风力对雨线主方向的作用，当雨线偏离垂直方向时，现有方法未采取旋转或只是进行大致旋转，去雨后的雨图出现雨线残留明显或背景模糊的现象。针对该问题，本文提出一种基于雨线主方向自适应的全局稀疏去雨模型。实验结果表明，本文算法在有效去雨的同时能较大程度地保留背景信息，PSNR和SSIM值相对高，运行时间相对短。