因时序逻辑语言与自然语言高度相似，具有强大的表达力，近年来，越来越多的学者开始做基于时序逻辑理论的路径规划研究^[1-3]。文献[4]提出了基于计算树逻辑的智能体规划，文献[5-6]着重从单一的、全局的线性时序逻辑规范上来规划一组机器人的行为。文献[7]已经将一个线性时序逻辑片段作为车辆路径问题的一种规范语言。文献[8]在有时间限制的动态环境中进行线性时序逻辑约束下的路径规划研究。文献[9-10]认可了一种自上而下的线性时序逻辑规划方法，其中，机器人团队被给予一种全局性线性时序逻辑规范，并努力将任务公式分解为独立的局部线性时序逻辑规范，以至于可以根据局部规范单独处理每一个独立的机器人。文献[11]探讨了一种基于线性时序逻辑规范的自下而上的规划算法，提出了一种部分分散性的解决方案，即只是考虑具有相互依赖性的智能体的集群，不再去研究整个团队的智能体行为。

然而，尽管上述方法解决了时序逻辑综合问题，但不能处理依赖于时变参数(动态)的优化问题，此时，可通过在智能体规划上应用滚动时域方法来解决这个问题。其中，滚动时域控制是一种考虑整个固定时域范围的控制方法，对于每次由优化算法得到的最优控制序列，仅取序列中的第一个元素作为当前时刻的控制率。目前，滚动时域控制的应用几乎遍及各个领域^[12-16]。同时，在滚动时域控制方法与满足时序逻辑公式的控制策略相结合的应用方面，文献[17]中提出了一种用于控制自动车辆的滚动时域控制方法，该方法必须满足在分区环境区域内所发生的服务请求的丰富任务规范。滚动时域控制也曾被用于文献[18-19]中，使一个单独智能体的线性时序逻辑规划达到一个局部最优行为。此外，文献[20-21]也通过应用滚动时域方法来规划智能体的运动，然而，作者没有考虑要优化任何回报的收集问题。

本文针对有限确定性系统中的路径规划问题，根据给定的回报动态假设和局部回报感知特点，开发出具有高级线性时序逻辑任务规范和局部最优回报收集的智能体运动规划的通用框架，将控制综合问题划分为更小的子问题，并以类似于滚动时域的方式逐渐获得可行的正确控制策略。其中，将智能体的运动环境抽象建模为有限且确定性的加权切换系统。同时，为了保证满足时序逻辑规范，从线性时序逻辑模型检测^[22]中获得灵感，在切换系统和满足线性时序逻辑公式的 ${\rm{B\ddot uchi}}$ 自动机^[23]之间构造Product自动机，用于获取满足任务的所有可行路径。并遵循类似于离散李雅普诺夫函数的构造，提出了一种将成本函数分配给Product自动机状态的算法。即该方法利用自动机的方法进行模型检测，通过对有限时域范围内的成本函数进行重新规划和优化，迭代地从所有局部路径中寻找回报值最大化的一条局部路径，从而确保系统朝着任务满意度的方向前进。而且，为使得研究结果更符合实际，我们在势函数中引入地势影响因子，使得改进的势函数可以更加精细地描述智能体移动的环境。

1 预备理论

定义1　滚动时域控制

滚动时域控制的理论思路为：在每个时刻，当前状态的代价函数在有限时域内被优化，并在该时刻，仅取最优控制序列中的第一个控制信号实际作用到系统中，舍去后面各项。接着，在下一时刻，对于新的测量状态重复以上过程。这个过程随着时间的推进反复滚动进行。对于一个复杂环境下的路径规划问题，采用滚动时域策略，路径的每一小段都通过求解一个有限时域约束优化问题得到。因此，滚动时域控制方法能够极大地减少计算时间。

定义2　有限加权确定性切换系统

一个有限加权的确定性切换系统是一个元组 $\varGamma = (Q{\text{，}}{q_0}{\text{，}}\Delta {\text{，}}\omega {\text{，}}\varPi {\text{，}}h)$ ，其中

$Q$ 是状态的有限集合，每个状态代表道路网络中的一个节点；

${q_0} \in Q$ 是初始状态，代表初始位置；

$\Delta \subseteq Q \times Q$ 是切换函数，代表节点与节点之间切换关系的集合；

$\omega :\Delta \to {\rm{R}^ + }$ 是权重函数，为所有节点之间的有效切换分配一个正权值成本，如时间或距离等；

$\varPi $ 是观测状态的集合，即原子命题集合；

$h:Q \to {2^\varPi }$ 是观测图，即观测状态的命题函数。

定义3　线性时序逻辑任务公式

线性时序逻辑(linear temporal logic, LTL)语句 $\phi $ 是由切换系统的原子命题、布尔算子逻辑连接词[ $\neg $ (Negation)、 $ \wedge $ (Conjunction)、 $ \vee $ (Disjunction)]和时序逻辑算子[ $G$ (Always)、 ${\rm{F}}$ (Eventually)、 $X$ (Next)、 $U$ (Until)]组合构成的表达式。例如， $XQ$ 表示状态 $Q$ 对应的区域是智能体将要到达的下一个目标位置， ${Q_1}U{Q_2}$ 表示智能体必须经过状态 ${Q_2}$ 对应的区域才能到达 ${Q_1}$ 对应的区域。

定义4　 ${\rm{B\ddot uchi}}$ 自动机

一个 ${\rm{B\ddot uchi}}$ 自动机是用 $B = {\rm{(}}{S\!\!_{B}}{\text{，}}{S\!\!_{{B}0}}{\text{，}}\varSigma {\text{，}}\delta {\text{，}}{F\!\!_{B}}{\rm{)}}$ 描述的元组，其中

${S\!\!_B}$ 是状态的有限集合；

${S\!\!_{B0}} \subseteq {S\!\!_B}$ 是初始状态的集合；

$\varSigma $ 是输入字母表；

$\delta :{S\!\!_B} \times \varSigma \to {2^{{S\!\!_B}}}$ 是切换函数；

${F\!\!_B} \subseteq S$ 是接受状态的集合。

对于 $\varPi $ 上的任意LTL公式 $\phi $ ，可以构造一个输入字母表为 $\varSigma = {2^\varPi }$ ，接受满足 $\phi $ 的 ${2^\varPi }$ 上所有序列的 ${\rm{B\ddot uchi}}$ 自动机。

定义5　加权Product自动机

给定一个加权确定性切换系统和一个 ${\rm{B\ddot uchi}}$ 自动机，则Product自动机为 $P = \varGamma \otimes B$ ，被表示为 P = ${\rm{(}}{S\!\!_P}{\text{，}}{S\!\!_{P0}}{\text{，}}{\Delta _P}{\text{，}}{\omega _P}{\text{，}}{F\!\!_P}{\rm{)}}$ ，其中

${S\!\!_P} = Q \times {S\!\!_B}{\text{；}}$

${S\!\!_{P0}} = {\rm{\{ }}{q_0}{\rm{\} }} \times {S\!\!_{B0}}{\text{；}}$

${\Delta _P} \subseteq {S\!\!_P} \times {S\!\!_P}$ 是切换的集合，被定义为：如果 $q \to \varGamma q'$ ， $s\mathop \to \limits^{h(q)} Bs'$ ， $\left( {{\rm{(}}q,s{\rm{),(}}q',s'{\rm{)}}} \right) \in {\Delta _P}$ ；

${\omega _P}{\rm{: }}{\Delta _P} \to {\rm{R}^ + }$ 是权重函数，被定义为

${\omega _P}((q,s),(q',s')) = \omega ((q,q')){\text{；}}$

${F_P} = Q \times {F_B}$ 是 $P$ 上接受状态的集合。

其中， $P$ 上的一个轨迹 ${{p}} = ({q_0},{s_0})({q_1},{s_1})\cdots$ 是一个无穷序列，且 $({q_0},{s_0}) \in {S\!\!_{P0}}$ ，对于 $k \geqslant 0$ 时， $({q_k},{s_k}) \to $ $ P({q_{k + 1}},{s_{k + 1}})$ 。同时，我们通过移除 ${\rm{B\ddot uchi}}$ 自动机的状态定义 ${{p}}$ 在 $\varGamma $ 上的投影 ${\gamma _\varGamma }$ ，即可得，若 ${{p}} = ({q_0},{s_0})({q_1},$ ${s_1})\cdots $ ，则

${\gamma _\varGamma }({{p}}) = {{q}} = {q_0}{q_1}\cdots$

(1)

2 问题描述

给定一个有限加权确定性切换系统 $\varGamma $ ，一个线性时序逻辑任务公式 $\phi$ 以及一个假设的回报函数。本文的目的是设计一个控制器，使获得的回报以滚动时域控制的方式最大化，同时保证产生的最优轨迹满足 $\phi$ 。

2.1 切换系统

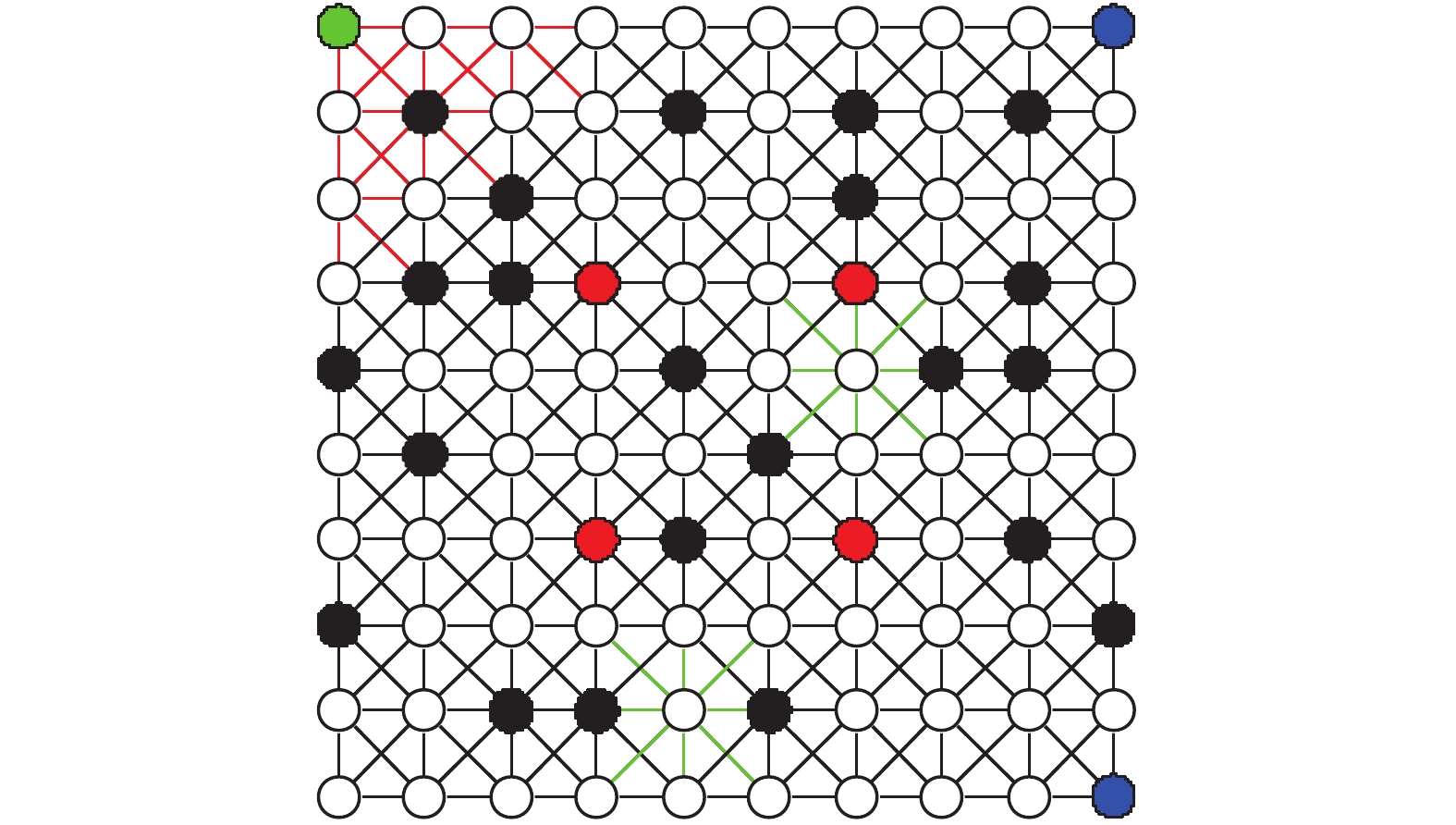
一个确定性加权切换系统的例子如图1所示。观测状态的集合为 $\varPi = {\rm{\{ a,b,c,d\} }}$ ，其中，观测状态a、b、c、d分别用黑色、绿色、蓝色和红色的实心圆圈表示。同时，白色圆圈表示非观测状态。

图1模拟了一个智能体在类似图形中运动的环境建模。在这个例子中， $\varGamma $ 共有100个状态，位于矩形网格的顶点，单元大小为10。权重函数 $\omega $ $ (q,q')$ 是顶点 $q$ 与 $q'$ 之间的欧几里得距离，如果两个顶点之间的欧几里得距离小于15，则两个顶点之间存在切换关系 $q \leftrightarrow q'$ 。

此外，由于智能体的运行环境中各区域地势不可能完全相同，而不同的地势就会影响智能体的运行距离或速度，本文把在不同地势中影响智能体运动的因素称为地势影响因子，并用符号 $\rho $ 来表示。图1的切换系统是按照空间距离均匀划分的模拟单元格，假设智能体分别在图1上的其中两种地势区域横向行驶了一个单元格，虽然在图1上的行驶距离是相同的，但是由于地势的影响，智能体在不同地形运行相同距离时耗用时间不同。因仿真中需要实时规划最优路径，故需要将地势影响因子的影响考虑在内，最直接的表达即是将地势影响因子对智能体行使速度或距离的影响相应的附加在原有的状态点距离上，以定量的准确表达智能体在状态点之间的“实际距离”(若切换系统中一个横向单元格的距离为10，假设智能体在第一种地势区域中，横向行驶一个单元格需要10 min，而在第2种地势区域中，横向行驶一个单元格需要运行12 min，此时可将第一种地势的影响因子设为1，第2种地势的影响因子设为1.2，并在仿真中分别将两种地势区域中连接横向单元格的状态点之间的实际距离表示为10和12)。即地势影响因子表示为一个可以定量表达地貌形态特征和地形属性对智能体实际运行距离影响的因子，人类完全可以通过经验获取地势影响因子的大小以准确描述状态点之间的实际距离。

在本例子中，设定图1切换系统网格中的红色线条区域、黑色线条区域、绿色线条区域分别为不同的地势区域，具有不同的地势影响因子。假设3个区域的地势影响因子 $\rho $ 的大小如下：

红色线条区域：

$\rho {\rm{ = }}\left\{ \begin{gathered} 1.5,\;\;\;\;{\rm{10 < }}\omega (q,q') < 15 \\ 1.2,\;\;\;\;{\rm{ 0 < }}\omega (q,q') \leqslant 10{\rm{ }} \\ \end{gathered} \right.{\rm{ }}$

(2)

黑色线条区域：

$\rho {\rm{ = }}\left\{ \begin{gathered} 1.2,\;\;\;\;{\rm{10 < }}\omega (q,q') < 15 \\ 1,\;\;\;\;{\rm{0 < }}\omega (q,q') \leqslant 10{\rm{ }} \\ \end{gathered} \right.{\rm{ }}$

(3)

绿色线条区域：

$\rho {\rm{ = }}\left\{ \begin{gathered} 1.3,\;\;\;\;{\rm{10 < }}\omega (q,q') < 15 \\ 1.1,\;\;\;\;{\rm{0 < }}\omega (q,q') \leqslant 10{\rm{ }} \\ \end{gathered} \right.{\rm{ }}$

(4)

若在本例中，不顾及区域之间的地势差别而粗糙地描述智能体的工作环境，则将导致仿真中智能体判断最优路径时出现差错，使最终得到的仿真结果不切合实际情况，这也与智能体可以应用在各种复杂环境的目的相斥。若引入地势影响因子，则可以更精细地描述智能体运动的环境模型，使研究结果更符合实际，更真实接近智能体在实际情况下的最优路径判断。

2.2 线性时序逻辑公式ϕ

将下面的LTL公式作为智能体的监视任务：

$\begin{gathered} {\rm{ }} \phi : ={\rm{G}}\neg a \\ \wedge {\rm{GFb}} \\ {\rm{ }} \wedge {\rm{G(b}} \to {\rm{X}}\neg {\rm{bUc)}} \\ {\rm{ }} \wedge {\rm{G(c}} \to {\rm{X}}\neg {\rm{cUd}}){\rm{ }} \\ \end{gathered} $

(5)

$\phi $ 的第一行， ${\rm{G}}\neg a$ 确保智能体在任何时间避免a观测状态。第二行， ${\rm{GFb}}$ 强制智能体重复访问观测状态b。第三行，确保智能体到达观测状态b后，并在返回状态b之前进入观测状态c。同样，第四行确保了智能体到达观测状态c之后并在重新回到c之前，智能体被驱动到观测状态d。即智能体要完成 ${{b}} \to {{c}} \to {{d}}$ 的监视任务。

2.3 假设的回报函数

假定本文描述的系统在具有回报的环境中操作，令在 $k$ 时刻，与状态 $q \in Q$ 相关的回报是 $R{\rm{(}}q,k{\rm{)}}$ 。其中，回报 $R{\rm{(}}q,k{\rm{)}}$ 与 $Q$ 中的状态以时间变化的方式联系在一起。并假设在 $k$ 时刻，系统只能观测当前状态 $q$ 的邻域 $\mathcal{N}(q,k) \subseteq Q$ 中各个状态的回报值。同时，假设在每个状态 $q \in Q$ ，如果 $q$ 与 $q'$ 的欧几里得距离不大于29，则在状态 $q$ 处可以观测到状态 $q'$ 处的回报量。在本案例研究中，定义 $R(q,k)$ 的算法步骤如下：

算法1　回报值定义算法

1) 定义回报最大值为25

2) 定义回报最小值为10

3) 在 $k = 0$ 时刻：当 $\omega (q,q') \leqslant 29$ ，并且随机函数randi(2,1)≠1成立时，设置实际回报值在可取范围内随机产生

4) 在 $k > 0$ 时刻：当 $\omega (q,q') \leqslant 29$ 时，设置实际回报值在可取范围内随机产生

根据上述定义算法，回报最大值设置为25，最小值设置为10。在 $k = 0$ 时刻，是否可以观测到邻域内每个状态点的回报 $R(q,0)$ 只有50%的可能性，并且回报的实际值是从范围[10,25]内的均匀分布中随机生成的。相似地，在以后的每个时刻 $k > 0$ ，回报值从[10,25]范围内的均匀分布中随机地重新分配。

本文的目的是合成一个控制器，在满足时序逻辑任务的同时，使回报值以滚动时域的方式最大化。其中，本文提出的滚动时域控制策略的主要组成部分如下：在时刻 $k$ ，状态为 ${q_k}$ ，通过在时域 $N$ 上求解最大化回报值的在线优化问题生成了一个有限轨迹 ${q_{k + 1}}{q_{k + 2}}\cdots{q_{k + N}}$ 。应用第一个控制动作 ${\rm{(}}{q_k},{q_{k + 1}}{\rm{)}}$ ，然后在时刻 $k + 1$ ，再次计算最优轨迹。

3 构建势函数

本文在Product自动机的状态上引入一个正值势函数 ${{V}}$ ，它使用权重 ${\omega _P}$ 来执行满足自动机的接受条件。从概念上讲，这个函数类似于李雅普诺夫能量函数，其创建满足给定公式的“进展”。它将先被离线计算一次，然后将与滚动时域控制器一起在线使用。

首先，令 $D\left( {{p_i},{p_j}} \right)\! =\! \left\{ {{p_1}{p_2} \cdots {p_n}|{p_1} \!= \!{p_i},{p_n}\! =\! {p_j}{\text{；}}{p_k} \to } \right.$ $\left. {P{p_{k + 1}},k = 1, \cdots ,n - 1} \right\}$ 表示从状态p_i∈S_P到状态p_j∈S_P的所有有限轨迹的集合。若 $D\left( {{p_i},{p_j}} \right) \ne{\text{Ø}}$ ，则表明状态p_i可以到达状态p_j，或者状态p_j可以到达状态p_i，即两个状态之间存在有效切换。

其次，为一个有限路径 ${{p}} = {p_1}{p_2}\cdots{p_n}$ 定义一个路径长度函数：

$L({{p}}) = \sum\limits_{k = 1}^{n - 1} {\rho {\omega _P}} ({p_k},{p_{k + 1}})$

(6)

其中，地势影响因子 $\rho $ 根据式(2)~(4)中的定义取值。

此外，定义从状态 $p \in {S\!\!_P}$ 到状态 $p' \in {S\!\!_P}$ 的距离函数为

$d(p,p') = \left\{ \begin{array}{l} \mathop {\min }\limits_{{{p}} \;\in D(p,\;p')} L({{p}}) \;{\text{若}}\;D({p_i},{p_j}) \ne {\text{Ø}} \\ \infty\;\;\;\;\;\;\;{\text{若}}\;D({p_i},{p_j}) = {\text{Ø}} \end{array} \right.$

(7)

因为 ${\omega _P}$ 是一个正值函数，对于所有 $p,p' \in {S_P}$ ， $d(p,p') > 0$ 。其中，可以通过Dijkstra算法等最短路径算法有效计算 $d(p,p')$ 。

定义6　 P中一个状态的势函数

状态点的势函数 ${{V(}}p),p \in {S\!\!_P}$ 被定义为

$V(p) = \left\{ \begin{array}{l} \mathop {\min }\limits_{p' \in F_P^*} {\rm{ }}d(p,p')\;\;{\text{若}}p \notin F_P^*\\ 0\;\;{\text{若}}p \in F_P^*{\rm{ }} \end{array} \right.$

(8)

式中： $F_P^ * $ 为 ${F_P}$ 的最大自我可达集合，同时，对于所有的 $p \in {S\!\!_P}$ ， ${{V}}(p) \geqslant 0$ 。当且仅当 $p \in F_P^ * $ 时， ${{V}}(p) = $ 0；当且仅当 $p$ 可到达集合 $F_P^ * $ 中的一个状态，则 $V(p) \ne $ $\infty $ 。因此，可得知 ${{V}}(p)$ 代表 $p$ 到集合 $F_P^ * $ 的最短距离。

本文通过提出算法2来获得对应于任务公式 $\phi $ 的 ${\rm{B\ddot uchi}}$ 自动机，Product自动机，最大自我可达集合 $F_P^ * $ 和势函数 ${{V}}(p)$ 。

算法2　势函数计算算法

1) 构建 ${\rm{B\ddot uchi}}$ 自动机： $B = {\rm LTL2BA}(\phi )$ ；

2) 构建Product自动机： $P = T \otimes B$ ；

3) 对于所有 $p \in {S_P}$ ， $p' \in {F_P}$ ，计算 $d(p,p')$ ；

4) 设置 $F_P^ * = {F_P}$ ；

5) 若存在 $q \in F_P^ * $ 使 $\mathop {\min }\limits_{p \;\in F_P^ * } d(q,p) = \infty $ ，则从 $F_P^ * $ 中移除 $q$ 以此获得最大自我可达集合 $F_P^ * $ ；

6) 若 $F_P^ * {\rm{ = }}\text{Ø} $ ，则返回无满足任务的路径；

7) 对于所有 $p \in {S_P}$ ，使用定义(8)获得 ${{V}}(p)$ 。

4 滚动时域控制器设计

控制设计的核心组成部分是一个运行在Product自动机上的状态反馈控制器，该控制器在一定的约束条件下，在预定的固定时域内优化有限轨迹。同时，这些约束确保了Product自动机状态上的势函数在有限时间内减少，从而保证在满足LTL公式方面取得进展。

为了说明控制器的工作原理，首先，将 $k$ 时刻的当前状态表示为 ${p_k}$ ，并在 $k$ 时刻，定义有限固定时域 $N$ 内Product自动机上的一个有限预测轨迹 ${{{p}}_k}$ 为： ${{{p}}_k}: = {p_{1|k}}{p_{2|k}}\cdots{p_{N|k}}$ ，其中， ${p_{i|k}}$ 表示在 $k$ 时刻时，预测轨迹的第 $i$ 个状态。其次，定义 ${{P}}({p_k},N)$ 为从状态 ${p_k} \in {S\!\!_P}$ 出发，时域 $N$ 内所有预测轨迹的集合。此外，由于Product自动机 $P$ 上的有限预测轨迹会被唯一地映射到切换系统 $\varGamma $ 上的一个有限轨迹 ${{{q}}_k} = {\gamma _\varGamma }({{{p}}_k})$ ，因此，若定义与 $k$ 时刻的预测轨迹 ${{{p}}_k} \in {{P}}({p_k},N)$ 相关的预测回报为 ${R_k}({{{p}}_k})$ ，则可将其表示为切换系统 $\varGamma $ 中有限轨迹 ${\gamma _\varGamma }({{{p}}_k})$ 上各状态点回报值的累积总和，如式(9)所示:

$ {R_k}({{{p}}_k}) = \sum\limits_{i{\rm{ = }}1}^N {{R_k}({\gamma _\varGamma }({p_{i\;|k}}))} $

(9)

4.1 滚动时域控制器

根据Product自动机和滚动时域控制的特点，可以将滚动时域控制器的设计分为两部分，即k = 0时刻和 $k > 0$ 时刻。

4.1.1 k = 0时刻的滚动时域控制器

在 $k = 0$ 时刻，由于 $P$ 的初始状态不是唯一的，因此，可以从集合 ${S_{P0}} = \{ {q_0}\} \times {S_{B0}}$ 中选取任意初始初始状态。并将在初始时刻执行的控制器表示为 ${\operatorname{RH} ^0}({S_{P0}})$ ，定义如下:

$\begin{array}{l} {{p}}_0^* = {{\mathop{\rm RH}\nolimits} ^0}({S_{P0}})\\ {\rm{ : = }}\mathop {{\rm{agrmax}}}\limits_{{p_0} \;\in {{P}}({p_0},N)} {R_0}({{{p}}_0}) \end{array}$

(10)

约束条件： $V({p_0}) < \infty $

控制器从势函数有限的初始状态 ${p_0} \in {S_{P0}}$ 开始运行,在时域 $N$ 内，使所有可能的投影轨迹上的预测累积回报值最大化，并返回最优投影轨迹 ${{p}}_0^*$ 。 $V({p_0}) < \infty $ 的约束十分重要，否则，从 ${p_0}$ 出发的轨迹不可能被接受。即若无满足 ${{V}}({p_0}) < \infty $ 的 ${p_0}$ ，则 $\varGamma $ 上不存在满足LTL公式的轨迹。

4.1.2 k > 0时刻的滚动时域控制器

$k > 0$ 时刻，控制器的形式表示为

${{p}}_k^* = \operatorname{RH} ({p_k},{{p}}_{k - 1}^{\rm{*}})$

(11)

即，它取决于当前状态 ${p_k}$ 和上一时刻获得的最优预测轨迹 ${{p}}_{k - 1}^* = p_{1|k - 1}^*\cdots p_{N|k - 1}^ * $ 。根据滚动时域控制方案的性质，先前预测轨迹的第一个控制信息被利用。因此，可获得等式(12)：

$ {p_k} = p_{1|k - 1}^{\rm{*}},{\rm{ }}k = 1,2,\cdots $

(12)

为满足线性时序逻辑任务， ${{p}}_{k - 1}^{\rm{*}}$ 将用于强制重复执行此控制器以使 $P$ 上状态的势函数最终减少到0。同时，使用以下3种情况来定义控制器(11)：

情况1　 $V({p_k}) > 0$ , 任意 $k \geqslant 1$ 都使得 ${{V}}(p_{i|k - 1}^*) \ne 0$

滚动时域控制器被定义如下：

$ \begin{array}{l} {{p}}_k^* = {\mathop{\rm RH}\nolimits} ({p_k},{{p}}_{k - 1}^{\rm{*}})\\ {\rm{ : = }}\mathop {{\bf{argmax}}}\limits_{{{{p}}_k} \in {{P}}({p_k},N)} {R_k}({{{p}}_k}) \end{array} $

(13)

约束条件： ${{V}}({p_{N|k}}) < V(p_{N|k - 1}^*)$ 。

在此情况下，保证 $P$ 上状态的势函数最终减少的关键是终端约束条件 ${{V}}({p_{N|k}}) < V(p_{N|k - 1}^*)$ ，即最优预测轨迹 ${{p}}_k^*$ 必须结束在比先前预测轨迹 ${{p}}_{k - 1}^{\rm{*}}$ 势函数低的一个状态。

情况2　 $V({p_k}) > 0$ ，存在 $i = 1,2, \cdots ,N$ 使 ${{V}}(p_{i|k - 1}^*){\rm{ = }}0$

若定义 ${i^0}({{p}}_{k - 1}^*)$ 为 ${{p}}_{k - 1}^*$ 中第一次出现势函数为0的标志，即 ${V}({{p}}_{{i^0}(p_{k - 1}^*)|k - 1}^*) = 0$ 。则控制器为

$\begin{array}{l} {{p}}_k^* = {\mathop{\rm RH}\nolimits} ({p_k},{{p}}_{k - 1}^{\rm{*}})\\ {\rm{ : = }}\mathop {{\bf{argmax}}}\limits_{{{{p}}_k} \in {{P}}({p_k},N)} {R_k}({{{p}}_k}) \end{array}$

(14)

约束条件： $V({{p}}_{{i^0}({{p}}_{k - 1}^*) - 1|k}^*) = 0$ 。

其中，若先前的预测轨迹包含这种状态，则强制最优预测轨迹中的一个状态具有0值的势函数。

情况3　 $V({p_k}) = 0$

控制器定义如下：

$\begin{array}{l} {{p}}_k^* = {\mathop{\rm RH}\nolimits} ({p_k},{{p}}_{k - 1}^{\rm{*}})\\ {\rm{ : = }}\mathop {{\bf{argmax}}}\limits_{{p_k} \in {{P}}({p_k},N)} {R_k}({{{p}}_k}){\rm{ }} \end{array}$

(15)

约束条件： $V({p_{N|k}}) < \infty $ 。

此种情况的终端约束为：终端状态的势函数数值大小是有限的。

4.2 控制算法

切换系统 $\varGamma $ 的总体控制策略在算法3中给出。在离线计算势函数之后，该算法在 $k = 0$ 时应用滚动时域控制器 ${\operatorname{RH} ^0}({S_{P0}})$ ，在 $k > 0$ 时刻，应用滚动时域控制器 $\operatorname{RH} ({p_k},p_{k - 1}^{\rm{*}})$ 。在算法的每次迭代中，滚动时域控制器返回最优预测轨迹 ${{p}}_k^*$ ，立即切换 $({p_k},p_{1|k}^{\rm{*}})$ 应用在 $P$ 上，对应的切换 $({q_k},{\gamma _\varGamma }(p_{1|k}^ * ))$ 应用在 $\varGamma $ 上。然后在 $k + 1$ 时刻重复该过程。

算法3　滚动时域控制算法

输入　 $\varGamma = (Q,{q_0},\Delta ,\omega ,\varPi ,h)$ ，线性时序逻辑公式 $\phi $

输出　控制策略

离线初始化：

　1) 构建对应于 $\phi $ 的 ${\rm{B\ddot uchi}}$ 自动机

$B = {\rm{(}}{S_B},{S_{B0}},{2^\varPi }{\rm{,}}{\delta _B}{\rm{,}}{F_B}{\rm{)}};$

　2) 构建Product自动机：

$P = \varGamma \otimes B = {\rm{(}}{S_P},{S_{P0}},{\Delta _P},{\omega _P},{F_P}{\rm{)}};$

　3) 计算所有状态 $p \in {S_p}$ 的势函数 ${{V}}(p)$ 。

在线滚动时域控制

　1) 若存在 ${p_0} \in {S_{P0}}$ 使 ${{V}}({p_0}) \ne \infty $ ，则设置 $k = 0$

　2) 观测 $q \in \mathcal{N}({q_0},k)$ 邻域内各状态的回报值，获得 ${R_0}(q)$ ；

　3) 获得 ${{p}}_0^* = {\operatorname{RH} ^0}({S_{P0}})$ ；

　4) 在Product自动机 $P$ 上执行切换 $({p_0},p_{1|0}^*)$ ，在切换系统 $\varGamma $ 上执行 $({q_0},{\gamma _\varGamma }(p_{1|0}^ * ))$ 切换；

　5) 设置 $k = 1$ ，进入循环；

　6) 观测 $q \in \mathcal{N}({q_k},k)$ 邻域内各状态的回报值，获得 ${R_k}(q)$ ；

　7) 获得 ${{p}}_k^* = \operatorname{RH} ({p_k},{{p}}_{k - 1}^{\rm{*}})$ ；

　8) 在Product自动机 $P$ 上执行切换 $({p_k},p_{1|k}^*)$ ，在切换系统 $\varGamma $ 上执行 $({q_k},{\gamma _\varGamma }(p_{1|k}^ * ))$ 切换；

　9) 设置 $k \leftarrow k + 1$ ；

　10) 结束循环；

　11) 否则，将无源于 ${q_0}$ 的满足 $\phi $ 的运行路径；

　12) 结束。

5 仿真结果分析

将有限切换系统 $\varGamma $ ，LTL公式 $\phi $ ，时域 $N$ 作为输入，函数 $R(q,k){\rm{ }}$ 生成了定义在 $\varGamma $ 状态上的时变回报值。通过执行算法3概述的控制算法，在 $\varGamma $ 中产生满足 $\phi $ 的轨迹，并根据提出的滚动时域控制律使获得的局部回报值最大化。在此案例研究中，具有回报值的状态可以被看作是“目标”，回报值的大小可以被视为与每个目标相关的“吸引力”。回报值最大化的控制目标，可以被解释为：使系统在具有高度吸引力的测量状态中所收集到的信息量获得最大化。

在本案例研究中，选择时域 $N = 4$ 。通过应用算法3，系统轨迹的前4个截图如图2所示。

在图2中，具有回报量的状态(回报感知状态)都用青色标出，青色圆圈的大小与相应状态点的回报值大小成正比。各子图的含义如下：

图2(a)：在 $k = 0$ 时刻，初始状态被标记为紫色。

图2(b)：滚动时域控制器 ${\operatorname{RH} ^0}({S_{P0}})$ 在初始状态下开始运行，将有限时域内的最优预测轨迹 ${{p}}_0^*$ 用一系列黄色状态标记。

图2(c)：第一次切换 ${q_0} \to \varGamma {q_1}$ 应用在有限加权切换系统 $\varGamma $ 上，同时，切换 ${p_0} \to P{p_1}$ 应用在Product自动机 $P$ 上。系统的当前状态 $({q_1})$ 被标记为紫色。

图2(d): 滚动时域控制器 ${{p}}_1^{\rm{*}} = {\rm{RH}}({p_1},{{p}}_0^*)$ 在 ${p_1}$ 处被计算。有限时域内的最优预测轨迹 ${{p}}_1^{\rm{*}}$ 用一系列黄色状态标记。

同时，将仿真时间设置为100个时间步长，并将势函数与时间步长的关系以及回报值总和与时间步长的关系绘制在图3中。

在每个时刻上绘制了势函数 $V(p)$ 。可得知，经过51个时间步长后，势函数大小变为0，这意味着到达了Product自动机的接受状态。鉴于每次到达接受状态时，系统至少访问一次b、c、d，即完成 ${{b}} \to {{c}} \to d$ 监视任务的一个周期。同时，可从图片看出，势函数的曲线几乎总是在下降，即始终朝着任务公式“进展”。

从图3可以看出回报值在每个离散时刻变化，收集到的回报量总和在稳步增长。其实，控制器通常选择满足终端约束，而不是选择增加势函数以便获得更多回报。因此，在这种情况下，对势函数的约束控制了局部回报量的最大化。

此外，本文对未引入地势影响因子的情况进行了仿真，其中，将式(6)表述的路径长度函数重新定义为

$ L({{p}}) = \sum\limits_{k = 1}^{n - 1} {{\omega _P}} ({p_k},{p_{k + 1}}) $

(16)

由于式(6)与式(8)所定义的势函数严格相关，而式(6)与式(16)存在差异，因此，未引入地势影响因子与引入地势影响因子的区别实质为势函数定义的差异。根据算法1和算法2，以及滚动时域控制算法3，通过MATLAB仿真，绘制了未引入地势影响因子情况下的势函数以及回报值总和与时间步长的关系，如图4所示。

对比图3和图4的势函数仿真结果，可知，在两图中的每一相同时刻，状态点的势函数大小不同(当前状态到Product自动机接受状态的最大自我可达集合 $F_P^ * $ 的最短距离不同)，并且相邻时刻的势函数变化率不同，因此，两种情况下控制器产生的轨迹完全不同。对比回报值总和的仿真结果，也可得出获取的累积回报值大小不同。两种情况的仿真结果对比突出了在地势不同的运行区域内，必须要引入地势影响因子的意义。

然而，本文只是比较客观的加入了几个假设的地势影响因子来阐述不同地势对智能体在状态点之间运行距离的影响，所假设的因子数值大小与智能体的实际工作环境无关，即本文只是在一个模拟的复杂多变地势环境下，通过假设的地势影响因子来实现满足控制目标的路径规划。在实际状况下，便可通过人为经验获得地势影响因子的大小来准确规划每一时刻的最优路径以获得最大累积回报值。

6 结束语

本文提出了一种线性时序逻辑约束下的在线实时求解滚动时域控制的新方法来解决有限确定性系统中的路径规划问题。该方法描述了保证无限轨迹满足给定线性时序逻辑公式的情况下，局部优化有限确定性系统轨迹的滚动时域控制框架，其优化标准被定义为最大化与系统状态相关联的时变回报值，同时，也开发了基于类能量函数定义的强化自动机接受条件的可证明正确的控制策略。

有关线性时序逻辑约束下的滚动时域控制问题，将来会有多个研究方向。例如，可以将所提出的框架扩展到有限概率系统，马尔可夫决策过程和部分可观测马尔可夫决策过程。还可以尝试将研究成果扩展到其他有限系统模型，如非确定性系统。