在某些复杂、环境恶劣的工业生产过程中，由于产品可靠性要求的不断提高，因此需要严格地监控一些直接或间接影响产品质量的关键变量。然而考虑到测量成本或者一些技术条件的制约，导致这些关键变量无法采用在线仪器测量获得。为了实时精确地预测这些难以测得的变量，基于数据驱动的软测量技术^[1-3]得到了快速的发展，并逐渐地应用到了化工、制药等工业过程中。

针对某些工况容易随时间发生变化的工业过程，传统的全局软测量模型难以满足工业过程的实时性要求且外推能力差^[4]，比较普遍的一种解决方案是采用即时学习^[5-6](just-in-time learning，JITL)策略，对于JITL相似度准则这一核心，学者们做出了大量的研究。Chen等^[7]考虑到常见的相似度准则仅将样本的输入信息联系起来，没有综合样本的输出信息，因此其把输入和输出信息共同考虑构造自适应加权距离作为相似度指标；Niu等^[8]结合模糊C-均值和传统的JITL这两种方法，首先采用模糊C-均值方法重构收集的历史样本，然后采用JITL方法在重构的历史样本集中选取当前的局部相似样本建立软测量模型。然而，该类方法没有考虑到JITL的耗时问题，在一些实时性要求较高的工业过程中无法有效运用。

针对上述提出的问题，Ge等^[9]首先计算相邻待测样本之间的一阶相似度，然后与相似度阈值比较判断是否更新当前时刻模型，仿真结果表明可以有效地解决模型耗时问题。但是，此方法忽略了过程变化较慢时产生的累计误差问题，文献[10]将计算相邻两待测数据之间的相似度改进为计算当前时刻待测样本与前一模型更新时刻待测样本之间的相似度，可以很好地解决累计误差问题。但是，上述方法在选择局部样本建模时均采用的是一阶相似度(first-order similarity, FOS)准则，若只在FOS的基础上降低模型更新频率，那么可以很好地解决模型的耗时问题，但是局部模型的精度会有所降低。牛大鹏等^[11]在文献[9]的框架上增加时序性，同时将投影算法用于估计模型未更新时刻的输出，取得了良好的成果。

综上，本文在FOS选取局部样本建模的基础上，提出一种二阶相似度(second-order similarity, SOS)准则，SOS准则既考虑到样本总体分布特性，同时可以更有效地判断当前模型是否需要更新。对于当前到来的待测样本，采用给定的相似度阈值判定模型是否更新，若更新，采用所提的SOS策略选择与待测样本邻居最多的二阶相似数据，同时采用累积相似度因子自适应的确定局部建模样本的个数，并将得到的二阶相似样本代入高斯过程回归 (Gaussian process regress, GPR)建立当前模型，否则，继续采用前一更新之初的模型估计当前待测样本，最后，采用青霉素发酵过程对所提方法进行验证，结果表明该方法既解决JITL耗时问题，且提高了模型精度。

1 基于二阶相似度的即时学习方法 1.1 传统的即时学习方法

JITL是根据相似输入产生相似输出的思想，假设有N个历史训练样本的数据集 ${ X}\{ {{ x}_i} \in {{\rm R}^m},$ $i = 1,2 \cdots N\} $ ，其中m表示输入数据的维度。若预测某一时刻待测样本 ${{{x}}_q}$ ，JITL的方式是在历史集中选择与 ${{{x}}_q} $ 拥有最高相似性的一组样本来构建当前的局部模型，同时采用该模型预测 ${{{x}}_q} $ 。相似度准则是JITL的核心，现对常用的FOS进行描述：

${\rm SI} = \gamma \sqrt {\exp ( - {d^2})} + (1 - \gamma ) \cos\; \theta $

(1)

式中:SI表示某一时刻待测数据 ${{{x}}_q} $ 与训练数据 ${{{x}}_1} $ 之间的相似度值；γ表示权重系数且 $\gamma \in [ {0,1} ] $ ；d为两样本的欧氏距离； $\theta $ 为两样本间的夹角，二者计算公式为

$d{\rm{ = }}{\left\| {{{ x}_q} - {{ x}_i}} \right\|_2}$

(2)

$\theta = {\rm{arc}}\cos \frac{{{ x}_q^{\rm{T}}{{ x}_i}}}{{{{\left\| {{{ x}_q}} \right\|}_2} \cdot {{\left\| {{{ x}_i}} \right\|}_2}}}$

(3)

1.2 二阶相似度策略 1.2.1 二阶相似度的定义

SOS^[12]定义为：如果两样本的一阶相似样本大多相同，那么认为两样本拥有较高的二阶相似性。FOS准则仅关注单独两样本之间的相似度，忽略了样本集总体的二阶相似性。如图1所示，数据1与2的FOS很高，数据1和8的近邻大多数相同，因此，二者的SOS很高，同理数据2与8的二阶相似性也较高。假设当前到来待测数据1，若采用FOS准则选取相似集，仅仅选择到数据2；但改用SOS策略时，不仅可以选择到数据2，还能选择到数据8。

SOS算法的伪代码如下：

输入　训练样本集 ${ X}\{ {{ x}_i} \in {{\rm R}^m},i = 1,2 \cdots N\} $ ，测试样本 ${{ x}_q}$

for $i = 1:N$

　 for $j = 1:N$

通过式(1)计算训练样本 ${{ x}_i}$ 和 ${{ x}_j}$ 之间的FOS

　 end for

end for

得到训练样本两两之间的相似度矩阵 ${{\bf{S}}_{N \times N}}$

对列方向上进行降序排序，得到对应的索引值矩阵 ${{I}} = \left[ {\begin{array}{*{20}{c}} {{{ i}_1}}&{{{ i}_2}}&{\begin{array}{*{20}{c}} {{{ i}_i}}& \cdots \end{array}}&{{{ i}_N}} \end{array}} \right]$

for $i = 1:N$

　通过式(1)计算测试样本 ${{ x}_q}$ 和训练样本 ${{ x}_i}$ 之间的FOS

end for

得到 ${{ x}_q}$ 和 ${{ x}_i}$ 相似度的列向量 ${{{S}}_{N \times 1}}$ ，对其进行降序排序，得到索引值向量 ${{ i}_q}$ ，取 ${{ i}_q}$ 和 ${{I}}$ 的前半行得到 ${{ \bar{ i}}_q}$ 和 ${{\bar I}} = \left[ {\begin{array}{*{20}{c}} {{{{ \bar{ i}}}_1}}&{{{{ \bar{ i}}}_2}}&{\begin{array}{*{20}{c}} {{{{ \bar{ i}}}_i}}& \cdots \end{array}}&{{{{ \bar{ i}}}_N}} \end{array}} \right]$

for $i = 1:N$

　计算 ${{ \bar{ i}}_q}$ 和 ${{ \bar{ i}}_i}$ 拥有相同索引值的个数

end for

输出　索引值的个数，即是 ${{ x}_q}$ 和 ${{ x}_i}$ 的SOS

1.2.2 SOS的特性分析

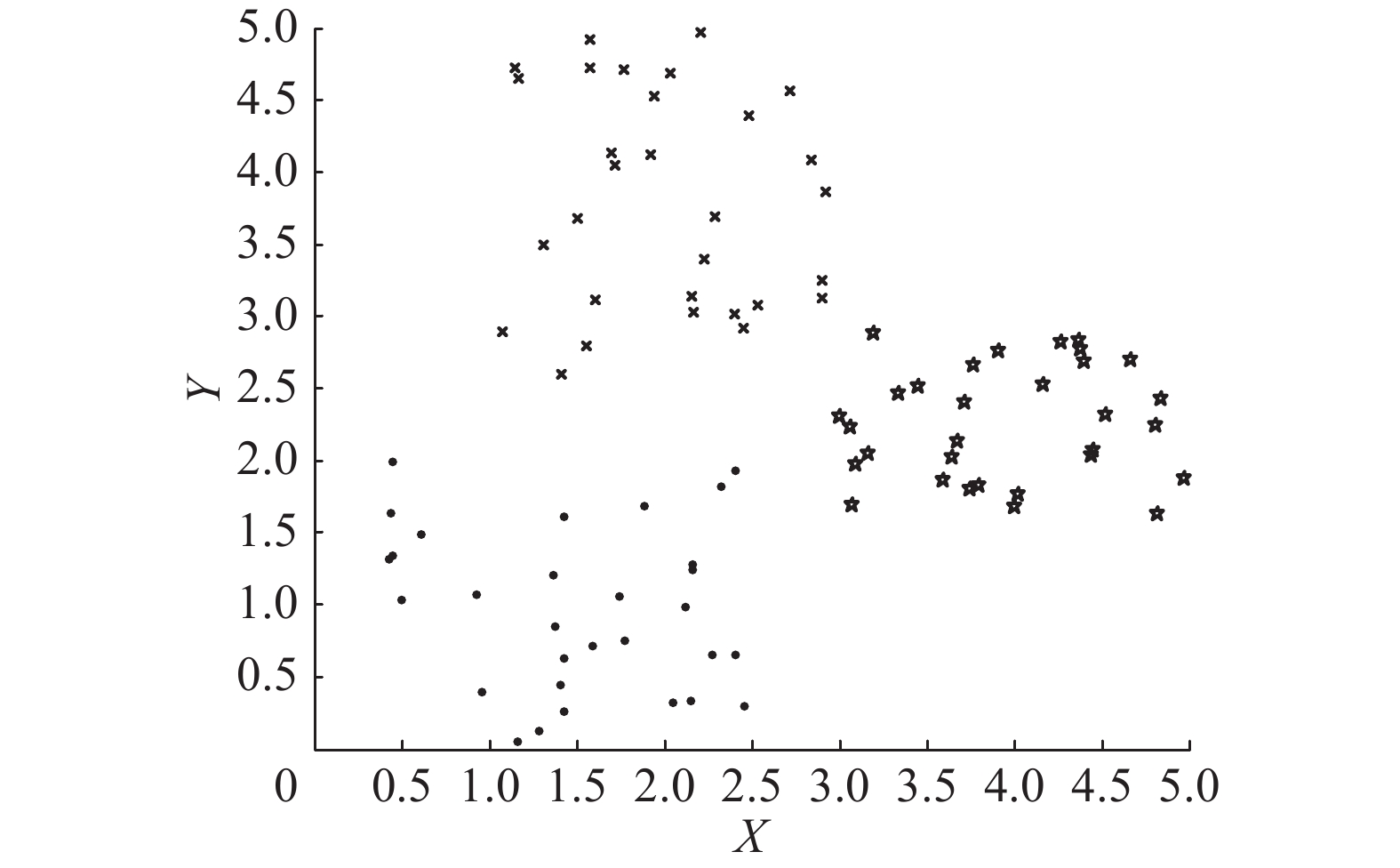
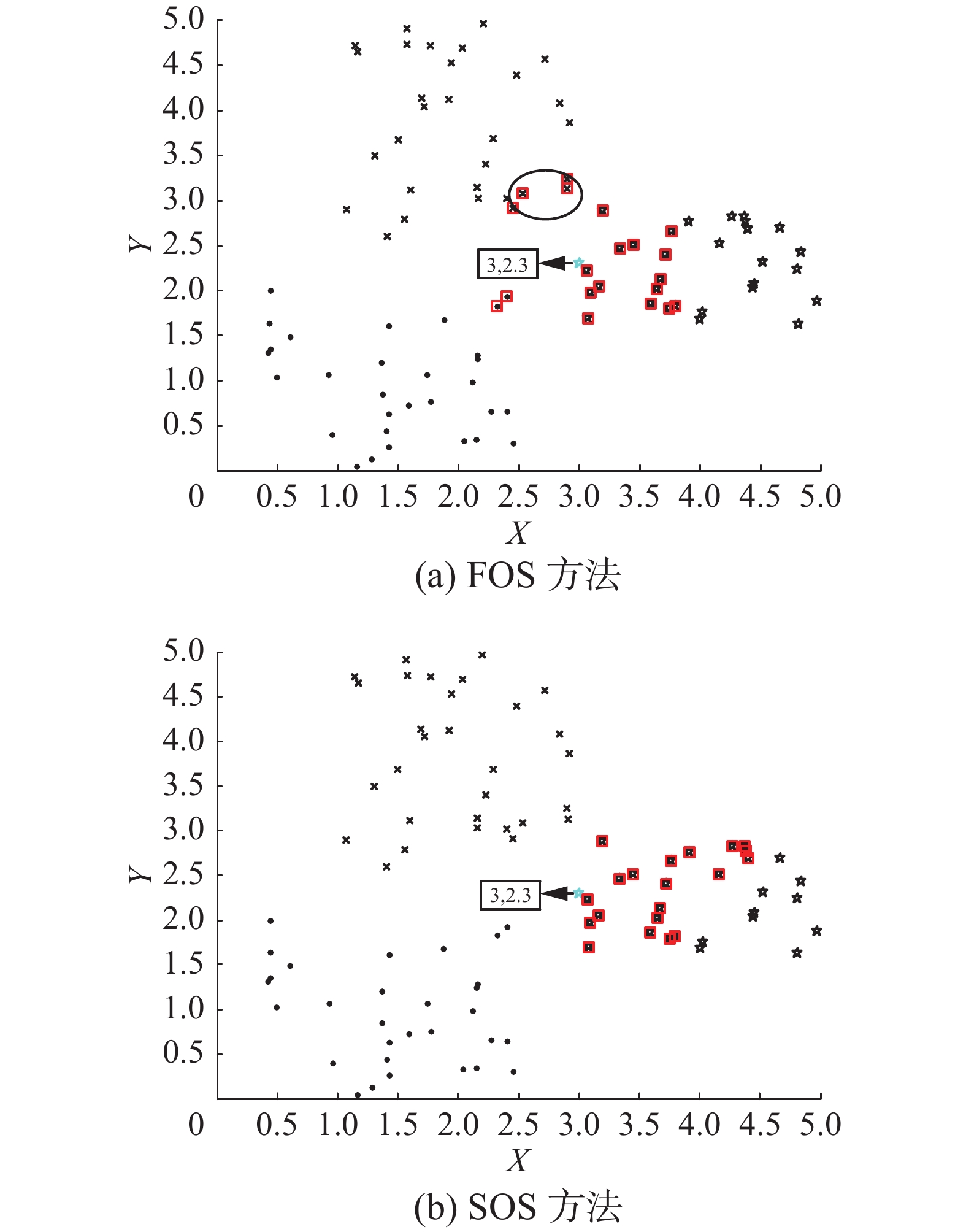
采用二维空间中的数值仿真，进一步探讨FOS、SOS准则的区别及特点。图2为二维空间中以3个类别中心随机产生的三类数据集。对于“星型”标记类上一点(3,2.3)，图3(a)、(b)中正方形标记框标记的样本分别是通过FOS与SOS准则选择到的，与FOS准则相比，SOS准则选择到的相似数据全是同类数据集，这是由于SOS准则在选择相似数据时不仅考虑数据单点间的相似性，而且充分考虑了数据集总体分布特征。选择同类别数据建立的局部模型更合理，精度更高。

如图3(a)所示，假设当前时刻到来椭圆中“叉号”标记类的数据点，使用FOS方法计算其与数据点(3,2.3)之间的相似度，那么计算出来的FOS很高，致使模型不会更新，仍采用更新之初模型估计会使模型精度下降；而将SOS准则用于计算其与点(3,2.3)的相似度，二者的SOS较低，使得模型会更新，进而选择到的局部相似数据更合理。因此，无论从数据集选取的角度还是从更新模型角度考虑，SOS在某种程度上都具有优势。

1.3 累计相似度因子

建立局部模型时，数据集个数的选取也是影响JITL模型精度的一个重要因素。若选择的数据过多会导致信息的冗余，失去了JITL相似输入产生相似输出的本意；过少会引起信息的丢失，这两种情况都不利于模型精度的提升。常用的解决方式是根据经验选取局部模型的数据个数，然而这样的选取方式具有盲目性。为了有效解决这一问题，本文引用累积相似度因子^[13-14]自适应的选取相似数据的数量，其计算公式为

${s_k} = \frac{{\displaystyle\sum\limits_{i = 1}^k {{s_{qi}}} }}{{\displaystyle\sum\limits_{i = 1}^N {{s_{qi}}} }},0 \leqslant k \leqslant N$

(4)

式中： ${s_{qi}}$ 为待测数据 ${{ x}_q}$ 与第 $i$ 个训练样本之间的相似度，且 ${s_{qi}}$ 是经过降序排序，即 ${s_{q1}} > {s_{q2}} > \cdots {s_{qi}} \cdots > $ ${s_{qN}} $ ，类似于PCA，取 ${s_k}$ 的值为0.85或0.9，表示前 $k$ 个最大的相似度占总相似度的贡献率，采用这样的方式可以在避免冗余的情况下获得大部分数据信息，比经验选取更有意义。

2 自适应更新机制的GPR模型 2.1 模型更新机制

针对每个新来的待测数据，JITL都是通过选择到的相似样本建立局部模型，并对待测数据进行估计。但是，一般的工业生产过程不会频繁发生工况变化。因此，可以继续采用之前建立好的的局部模型预测工况变化较小时刻的待测样本，从而减少模型耗时。

通常通过比较两相邻样本相似度与当前阈值(THR)的大小来降低模型更新频率，若小于THR，则更新模型估计当前待测数据；否则，沿用之前建立的局部模型进行估计输出。然而，当生产过程的工况变化较为缓慢时，如果仅计算相邻数据之间的相似度，可能会一直大于THR，从而使模型未及时更新引起累计误差问题。所以，可以改进为计算当前时刻与前一模型更新时刻数据间的相似度来克服累计误差问题。详细描述如下：

1) 若当前为q时刻，经过计算且模型需要更新，当来到新的测试数据 ${{ x}_q} $ ，采用1.2节的方法从历史样本集中选择与 ${{ x}_q} $ SOS最高的一批数据建立当前的GPR模型，同时估计 ${{ x}_q} $ ，并将SOS最高的值乘以某一数值(参数)用于判断之后时刻模型是否需要更新的THR。

2) 当 $q + 1 $ 时刻数据 ${{ x}_{q + 1}} $ 到来，计算其和 ${{ x}_{q }} $ 之间的SOS，同时与THR比较，若小于THR，则更新模型进行估计，同时更新相似度阈值，否则，认为当前工况变化较小，仍采用q时刻的局部模型对 ${{ x}_{q + 1}} $ 进行估计。

3) 如果 $q + 1 $ 未更新模型，在 $q + 2 $ 时刻，计算测试数据 ${{ x}_{q + 2}} $ 和前一模型更新时刻数据 ${{ x}_{q }} $ 之间的SOS，其他的判断方式与 ${{ x}_{q + 1}} $ 相同。

2.2 GPR建模方法

GPR是一种非参数概率模型，已经成为机器学习领域的一种重要的建模方法，并在近些年来得到广泛关注与应用^[15-17]，其基本原理描述如下。

现有历史训练数据集 ${ X}\{ {{ x}_i} \in {{\rm R}^m},i = 1,2 \cdots N\} $ 和Y $\{ {y_i} \in {\rm R},i = 1,2 \cdots N\} $ ，分别代表 $m$ 维输入样本和1维输出标签。可以采用如下的关系式表示输入与输出间的关系：

${y_i} = f({{ x}_i}) + \varepsilon $

(5)

式中： $f$ 为某种未知的函数； $\varepsilon $ 为均值为0，方差为 $\sigma _N^2$ 的高斯白噪声。

对于某一待测数据 ${{ x}_q}$ ，它的输出预测值 ${y_q}$ 满足高斯分布，其均值和方差可以分别表示为

${y_q}({{ x}_q}) = {{ c}^{\rm T}}({{ x}_q}){{ C}^{ - 1}}{ Y}$

(6)

$\sigma _{{y_q}}^2({{ x}_q}) = c({{ x}_q},{{ x}_q}) - {{ c}^{\rm T}}({{ x}_q}){{ C}^{ - 1}}{ c}({{ x}_q})$

(7)

其中， ${ c}({{ x}_q}) = {[c({{ x}_q},{{ x}_1}), c({{ x}_q},{{ x}_2}),\cdots ,c({{ x}_q},{{ x}_N})]^{\rm{T}}}$ 为待测输入数据与每个历史数据协方差构成的矩阵， ${ C} = {{\varSigma }} + \sigma _N^2{{I}}$ 是历史输入数据自身之间的协方差矩阵， $c({{ x}_q},{{ x}_q})$ 为待测输入自身的协方差值。

GPR有不同的协方差函数可以选择，本文选取径向基协方差函数，其详细描述如下：

$c({{ x}_i},{{ x}_j}) = v\exp \left[ { - \frac{1}{2}\sum\limits_{{{t}} = 1}^m {{\omega _t}{{({{ x}_{it}} - {{ x}_{jt}})}^2}} } \right] + \sigma _N^2{\delta _{ij}}$

(8)

其中， $v$ 是先验知识的总体度量； ${\omega _t}$ 为第t维样本的权重； ${\delta _{ij}}$ 是Kronecher算子，代表每个辅助变量的重要程度。

通常采用极大似然估计计算式(8)中的参数 ${ \theta } = \left[ {v,\sigma _N^2,{\omega _1}, \cdots ,{\omega _m}} \right]$ ，其对数似然函数为

$L({ \theta }) = - \frac{1}{2}\log (\det ({ C})) - \frac{1}{2}{{ Y}^{\rm T}}{{ C}^{ - 1}}{ Y} - \frac{N}{2}\log (2\pi )$

(9)

首先对超参 ${ \theta }$ 进行初始化，然后采用共轭梯度法得到优化的参数^[18]。参数确定后，当来到新的待测样本，根据式(6)得到模型输出。

3 基于二阶相似度的即时学习建模步骤

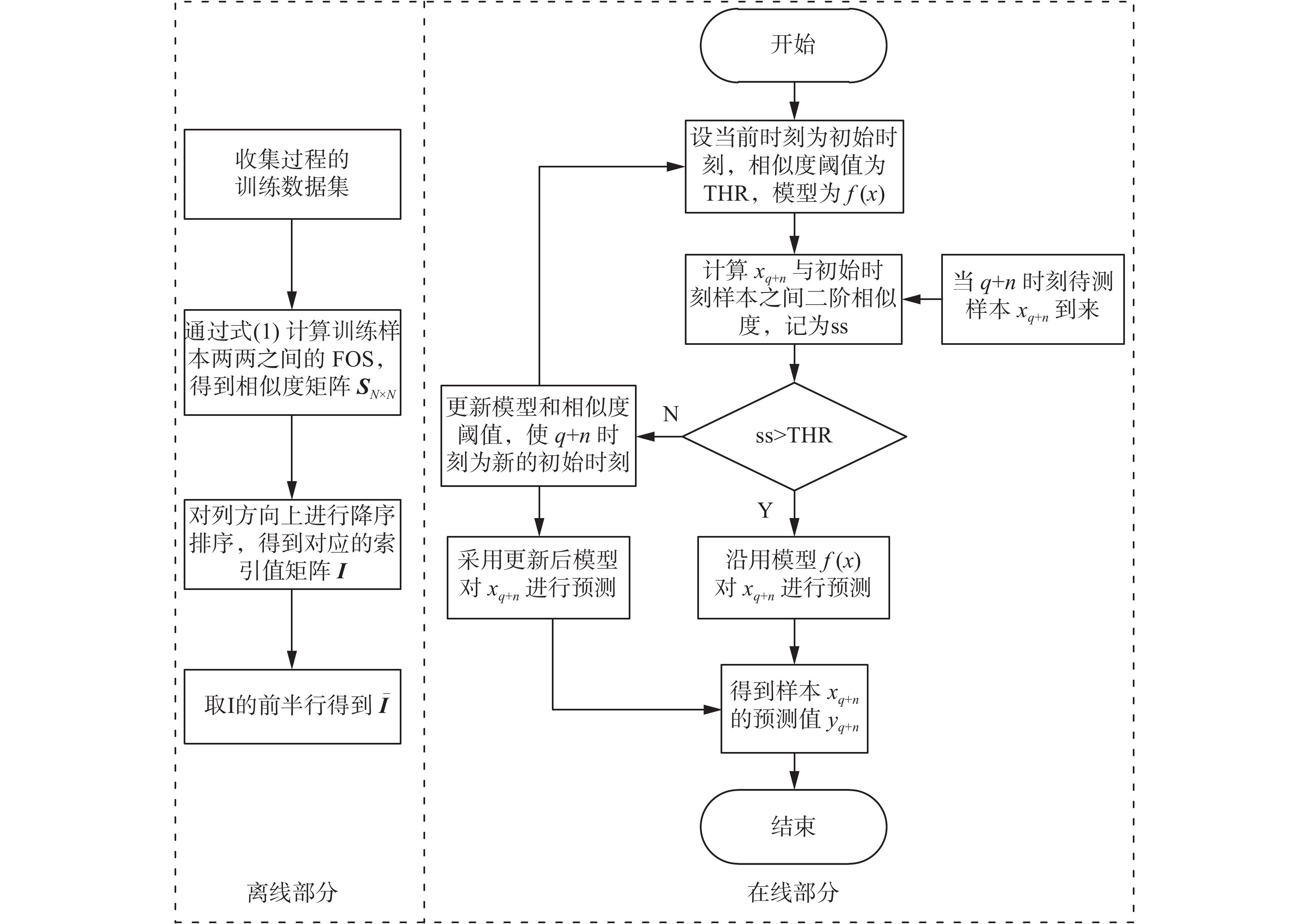
基于SOS-JITL软测量建模流程图如图4，具体建模步骤如下：

1）采用式(1)计算历史数据相互间的FOS，得到相似度矩阵，同时将其降序排序返回索引值矩阵 ${{I}}$ 。

2）假如当前q时刻模型需要更新，针对待测数据x_q，计算其与历史数据之间的FOS，并返回索引值向量 ${{ i}_q}$ 。

3）通过1.2节计算 ${{ \bar{ i}}_q}$ 与 ${{ \bar{ i}}_i}$ 间的SOS，同时采用累积相似度因子自适应选取与 ${{ x}_q}$ 近邻最多的一批数据建立此刻的GPR模型，并估计 ${{ x}_q}$ 同时更新模型的THR。

4）若 $q + 1$ 时刻测试数据 ${{ x}_{q + 1}}$ 到来，计算其和当前模型更新之初时刻数据 ${{ x}_q}$ 间的SOS，并与THR比较，若小于THR，如步骤3）更新模型和THR，并采用新模型估 ${{ x}_{q + 1}} $ ，同时将 $q + 1 $ 时刻设置为模型更新之初时刻；否则，仍采用q时刻模型估计 ${{ x}_{q + 1}} $ 。

5)对于 $q + n$ 时刻的待测数据 ${{ x}_{q + n}}$ ，重复步骤4），可得估计值 ${{ y}_{q + n}}$ 。

4 实验仿真

青霉素产生菌在适当的温度、pH值等外部环境条件下生长与抗生素合成这一过程称为青霉素发酵过程，此过程分为3个阶段，即产生菌生长阶段、青霉素合成阶段与产生菌的自溶阶段^[19]。作为模拟青霉素发酵过程的Pensim仿真平台，其包含了众多的输入变量与输出变量，其中青霉素这一重要产物的浓度在实际发酵过程中难以测得，因此可以采用软测量建模进行在线预测。本文采用通气速率、CO₂浓度和pH值等6个变量作为输入变量，青霉素浓度作为输出变量，建立软测量模型。采用Pensim仿真平台产生400组样本，选取其中200组作为训练数据，剩余的作为测试数据来验证所提方法。

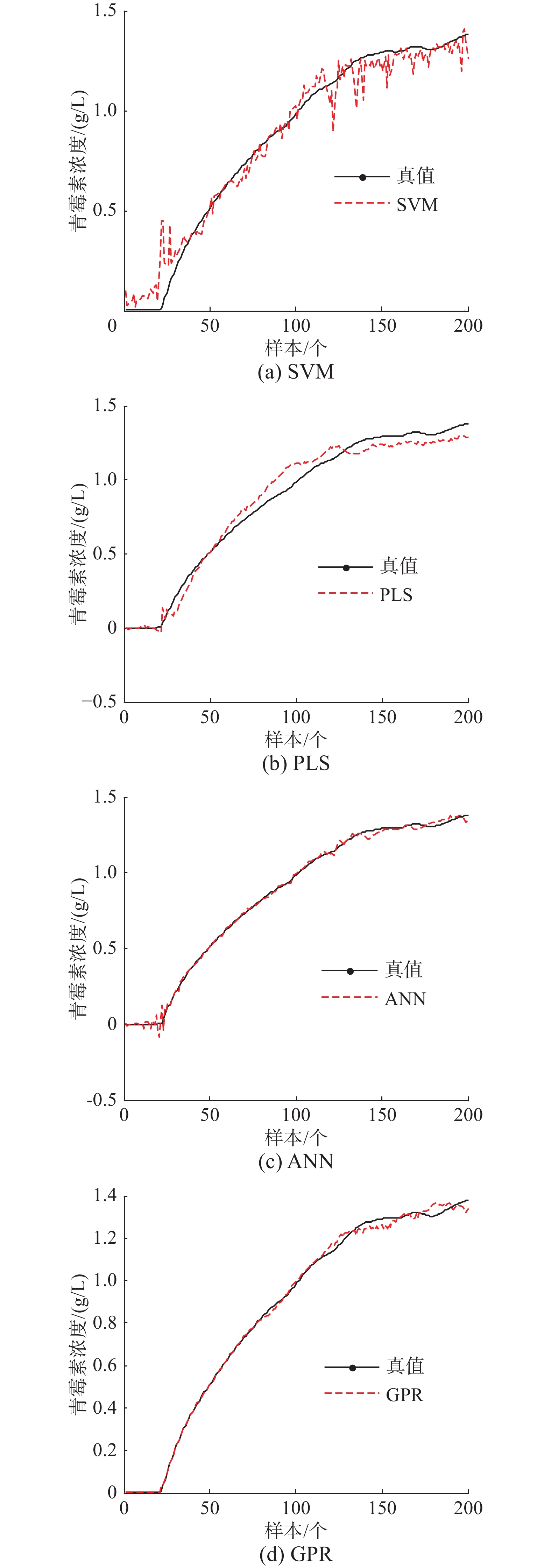
为了对比建模方法的性能，分别采用SVM、PLS、ANN、GPR建模方法预测青霉素浓度。其中定义ANN的网络层为3层、隐藏层节点数为20、步长为0.01、迭代次数为100次、训练目标最小误差为0.001；SVM采用高斯核函数。图5给出了4种方法的预测结果，图中实线表示青霉素浓度的实际值，虚线表示各方法的预测值。从图中可以得到，GPR方法的预测值更逼近于实际真值，表明GPR建模方法的精度更高。

为了进一步分析GPR方法的优势，采用均方根误差^[20](RMSE)这一指标对比各种建模方法，其计算公式为

${\rm{RMSE}}{ = }\sqrt {\frac{{\displaystyle\sum\limits_{j = 1}^M {{{({y_j} - y_j^ * )}^2}} }}{M}} $

(10)

式中： ${y_j}$ 表示第 $j$ 测试样本的真实值； $y_j^ * $ 为测试样本的估计值； $M$ 表示测试样本的数目。

表1给出了4种方法的RMSE，从表中可以清晰地看出本文所采用GPR方法的RMSE最小，进一步表明该方法建立的模型估计精度更高，跟踪能力更强。

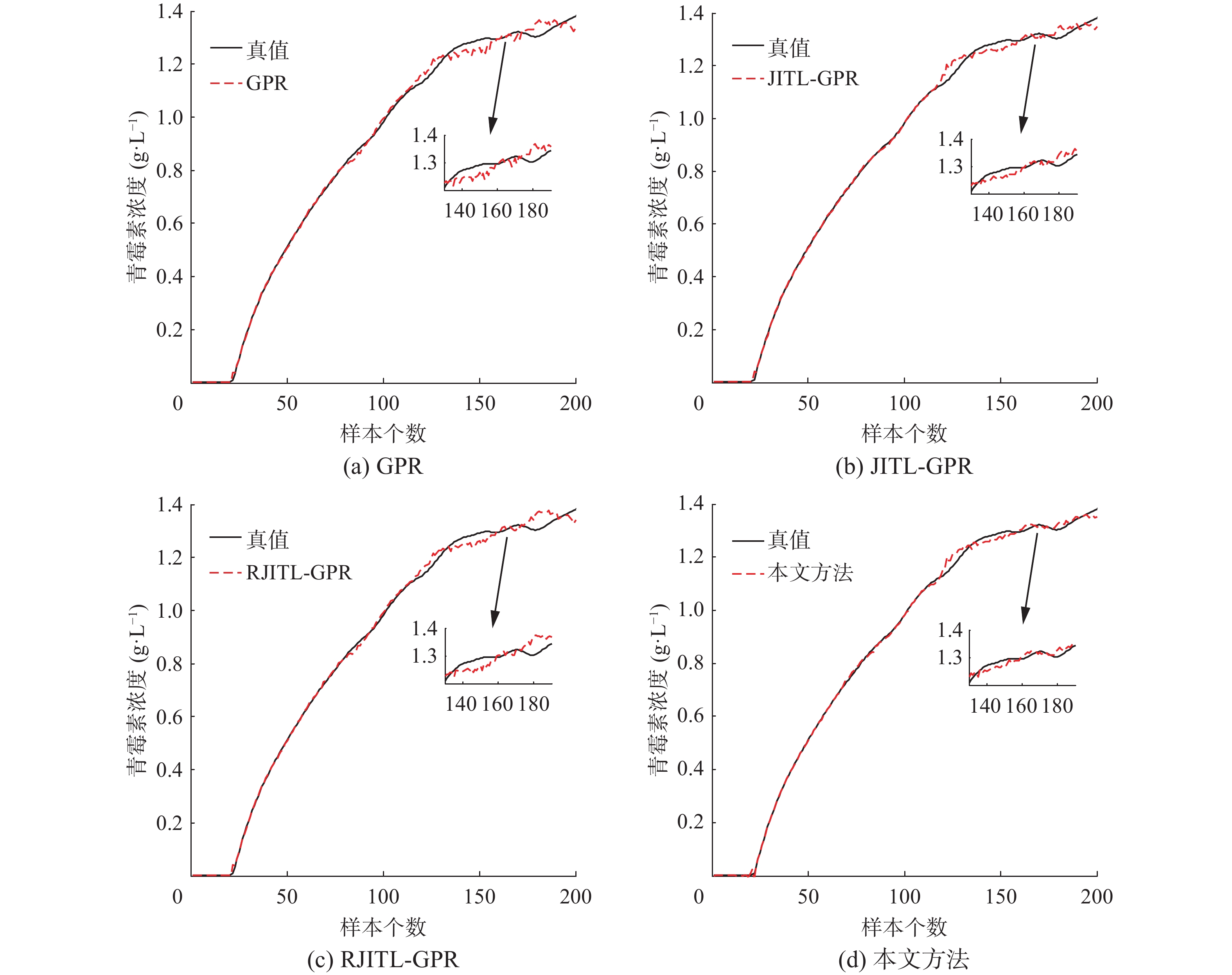
为了验证本文所提方法的预测性能，分别选取GPR方法、一阶相似度的GPR方法（简写为JITL-GPR）、减少模型耗时的一阶相似度GPR方法（简写为RJITL-GPR）3种方法与本文方法(proposed)对比，且JITL在选取局部相似样本数目时均采用累积相似度因子。4种方法预测曲线如图6所示，将样本130~190的预测曲线进行放大，可以直观的看出，与前3种方法相比，所提方法的跟踪性能更好。4种方法的预测误差如图7所示，其中，图7（d）中的误差曲线在0处抖动幅度更小，表明该方的预测精度更高。

为了进一步分析所提方法的优越性，采用RMSE和模型时耗作为评价标准。表2给出了4种方法的RMSE和建模耗时。由表中的信息可以得到，与单一GPR方法相比，JITL-GPR尽管提高了模型的精度，但是建模所花费的时间太长，对于一些实时性要求较高的生产过程，该方法可能无法满足实际要求；RJITL-GPR由于降低了模型的更新频率使得建模时间大大缩短，与此同时降低了模型精度；与前3种方法对比，所提方法不仅降低了模型的时耗，同时提高了模型的精度。这是由于SOS在选择局部相似数据时，可以更合理地选取到相似数据，同时也更准确地判断模型是否更新，使当前选取的二阶相似样本建立的局部模型更适用于模型未更新时刻的数据。

5 结束语

从工业过程实时性角度出发，提出一种基于SOS的JITL-GPR方法，在自适应模型更新机制的框架下，采用SOS方法从历史数据中选取与当前待测数据用于更多邻居的样本建立此时的局部GPR模型，同时引入累计相似度因子优化局部模型的样本数目。与FOS准则相比，SOS准则在选取相似样本时，既关注了两数据单点间的相似度，同时也考虑了单个数据与历史集总体分布特征之间的关系。因此，所提方法在选择相似样本时更合理，同时也可以更为准确地判断模型是否更新。采用青霉素发酵过程中青霉素浓度对所提方法进行验证，结果表明该方法不仅减少模型的时耗，同时提高了模型的精度。