数据分类研究是数据挖掘领域的一个重要分支,它主要通过已知类别的数据集构建出各类别的特征空间,再将未知类别的数据映射到该特征空间中,从而来确定其所属类别[1]。目前,数据分类主要应用于机器学习、模式识别、遗传算法、神经网络、统计学、数据库、专家系统等领域。模糊规则分类系统(fuzzy rule-based classification system, FRBCS)[2-4]广泛地用于求解分类问题。FRBCS能够建立清晰的语义模型,具有良好的可解释性,能够定性定量地处理专家信息。此后,Yang等[5]提出了基于证据推理的置信规则库推理方法,该方法以IF-THEN规则库、模糊理论、D-S证据理论和决策理论等为基础,有效地利用不精确或不完整的信息对复杂决策问题进行建模;Jiao等[6]在置信函数框架上扩展模糊规则库分类系统(FRBCS),提出置信规则库分类系统(belief rule base classification system, BRBCS)。置信规则库分类系统采用数据驱动方式由数据集自动生成置信规则,建立特征空间与类空间之间的不确定关系,利用基于置信函数理论的置信推理方法(belief reasoning method,BRM)对查询模式进行分类推理。但是传统的置信规则库分类系统的推理性能极为依赖于内部参数取值,因此刘莞玲等[7]在BRBCS的基础上提出基于差分的置信规则库分类方法(DEBRM)。该方法能够有效解决BRBCS中参数优化的问题,使分类系统不需要依赖于增加模糊区间划分数量来提高分类准确度。但该方法随着前提属性个数的增加,规则数量呈指数式增长,就会导致置信规则库复杂度增加。因此本文针对Liu等提出的DEBRM分类方法存在无法兼顾准确率和复杂度的问题进行改进,提出置信规则库分类系统的多目标优化模型。
多目标优化问题(multi-criterion optimization problems)涉及多个目标的极大化或极小化,同时这些目标之间往往是互相冲突的[8],一个目标性能的优化可能导致另一个目标性能的下降。多目标的最优解不是一个特定的解,而是一组Pareto最优解,这些解没有优劣之分[9-10]。目前用于解决多目标优化问题的智能优化算法有:传统遗传算法、群集智能算法(粒子群、蚁群)、人工免疫算法、神经网络等[11]。本文拟在DEBRM分类系统中,结合多目标免疫系统算法(MISA),提出利用MISA的置信规则库分类方法,通过特征属性约简来降低复杂度并使得准确率尽可能高;通过对系统的分类准确率和复杂度进行多目标优化,从而得到一组均衡解供决策者选择。在实验中选用Iris、Wine、Cancer、Glass这4个经典的公共测试数据集来验证本文方法的有效性。
1 相关概念 1.1 基于DE的置信规则库分类方法置信规则库分类系统(BRBCS)由模糊规则库分类系统(FRBCS)在置信函数框架上扩展得来,采用数据驱动方式构建规则库,规则库的规则条数即结构复杂度取决于前提属性个数和模糊区间划分数。BRBCS的置信规则结构:
| $\left\{\begin{aligned} & {\rm{If}}\;{x_1}\;{\rm{is}}\;A_1^q \wedge {x_2}\;{\rm{is}}\;A_2^q \wedge \cdots \wedge {x_p}\;{\rm{is}}\;A_p^q,\\ & {\rm{then}}\;\;\;\;{C_q} = \left\{ {\left( {{\omega _1},\beta _1^q} \right),\left( {{\omega _2},\beta _2^q} \right), \cdots ,\left( {{\omega _m},\beta _m^q} \right)} \right\} \end{aligned}\right.$ | (1) |
式中:
传统基于置信规则库参数学习的分类系统(BRBCS)准确率受参数值约束,因此Liu等[7]提出基于DE的置信规则库推理的分类方法(DEBRM),该方法主要包括基于DE的参数训练和置信推理过程。
1.2 多目标优化基本原理一个具有
| $\left\{ \begin{aligned} & \min {{y}} = f\left( {{x}} \right) = \left( {{f_1}\left( {{x}} \right),{f_2}\left( {{x}} \right), \cdots ,{f_m}\left( {{x}} \right)} \right) \\ & {g_j}\left( {{x}} \right) \leqslant 0,\;j = 1,2, \cdots ,l \\ & {h_j}\left( {{x}} \right) \leqslant 0,\;j = l + 1,l + 2, \cdots ,k \end{aligned} \right.$ | (2) |
式中:
定义1 Pareto支配。若
定义2 Pareto最优解。当且仅当
定义3 Pareto最优解集。即包含所有最优解的集合,定义为
在分类系统中,增加前提属性个数可以提高系统推理的准确率,但同时也增加了分类系统的复杂度,所以复杂度和准确率是一组相互冲突的目标。如何从训练数据集中找到使准确率尽可能大、复杂度尽可能小的折中方案具有重要意义,因此本文提出利用MISA多目标优化的置信规则库分类方法。该方法对数据集进行特征属性约减,并采用差分进化方法进行参数学习来获取最优结构参数,同时对经典的MISA算法进行适应性改进,对分类系统的准确率和复杂度进行多目标优化,从而保证分类系统的规则数尽可能少(即系统结构复杂度尽可能低)的同时,又能保证系统分类的准确率尽可能高。
最大化分类准确率即最小化分类错误率,所以本文的两个目标函数为分类错误率
| $\min y = f(\theta ) = (\mathop f\nolimits_1 (\theta ),\mathop f\nolimits_2 (\theta ))$ |
MISA算法是Coello等[12]根据免疫系统中抗体的克隆选择原则提出的。
2.1.1 改进型MISA算法原理改进型MISA算法将群体中的所有个体均视作“抗体”。依据克隆选择原则,选择群体中的非支配解进行克隆,根据它们在解空间的拥挤程度来决定克隆的数目,并对克隆的个体进行高概率变异和交叉操作,生成新的抗体群[12]。本文对Coello等提出的MISA针对基于置信规则库分类问题做适应性改进,并在个体变异中增加接种疫苗的变异操作。改进型MISA与原始型MISA的一个主要区别在于确定待克隆抗体的复制个体数的方法不同,改进型MISA根据待克隆抗体所处网格密度及支配情况确定最大可复制数,再根据抗体群所能容纳的最大个体数确定最终的复制数量,确定待克隆抗体复制个体数的具体方法如下:
1)确定待克隆抗体最大可复制个数
按照个体在外部种群(外部种群中个体互为非支配解)中所处网格的密度及支配关系分配等级,按照等级确定最大的克隆数。分4个等级:所处网格密度小于平均网格密度,等级为4,最多可复制4个个体;所处网格密度等于平均网格密度,等级为3,最多可复制3个个体;所处网格密度大于平均网格密度,等级为2;个体被支配且被选为待克隆抗体则等级为1,最多可复制1个个体。
2)确定待克隆抗体的复制个数
抗体群设置最多可容纳个体数。将抗体群可容纳个体数视为复制名额个数,具体过程如下:
①待克隆抗体按照优先级:被支配数少>所处网格密度小>支配其他个体数多排成一列纵队;
②从队头到队尾依次查看待克隆抗体的等级,当待克隆抗体等级大于0且抗体群可容纳个体数大于0时,待克隆抗体获得1个复制名额,每分配出1个名额,获得名额的待克隆抗体等级减1,抗体群可容纳数减1;当抗体群可容纳个体数等于0时结束分配;
③走到队尾整个抗体群的抗体等级累加和大于0,返回执行②。
除了待克隆抗体的克隆个体数确定方式不同外,改进型MISA采用二进制染色体编码,抗体长度等于最大前提属性个数,取值为0代表删除这个前提属性,取值为1代表选中这一前提属性。确定前提属性后构建规则库,规则库编码采用实数编码,一个规则库作为一个个体;无交叉操作,变异操作包括单点变异和接种疫苗,具体的提取疫苗和接种疫苗方法说明如下。
1)提取疫苗:疫苗群体限制最大个数,抗体被选为疫苗的条件为被支配数为0,支配数大于0。根据Pareto的定义,能够支配其他个体的个体不是属性最少也不是属性最多的个体,而是属性个数居中的个体,如选取的特征属性个数为5,受它支配的解是属性个数大于5且分类错误率大于它的个体,这一定程度上说明这5个属性中可能具有区分性较高的特征属性或特征属性组合。
2)接种疫苗操作:随机从免疫群体中随机选取一个个体,从疫苗染色体中所有值为1的染色体单位中随机选取1个单位,再从所有值为0的染色体单位中随机选取1个单位,将这2个单位植入个体中。植入个体后,有4种可能情况:个体特征属性减少或增加一个;个体特征属性完全不变;个体属性特征个数不变但选取的特征属性改变;有可能使个体具有高区分性的特征属性,或删除不必要的属性。
2.1.2 外部种群及自适应网格算法外部种群用于保存Pareto非劣解,外部种群中的个体两两之间不存在支配与被支配关系。为了使非支配解尽可能均匀地分布于Pareto前沿,外部种群采用Knowles等[13]提出的自适应网格法进行更新,详见算法1。
算法1 自适应网格算法
输入 抗体群中所有非支配解
输出 Pareto最优前沿。
1)输入抗体群中所有非支配解组成的集合
2)循环遍历Q;
3)判断
4)判断
5)判断外部种群个体数是否达到最大值:如果外部种群个体数达到所能容纳的最大值,那么执行6),否则将
6)按照所给划分数构建自适应网格:如果
7)循环结束。
2.1.3 改进型 MISA 算法流程改进型MISA算法的算法流程的主要部分和原始MISA算法相同:生成抗体群,更新自适应网格,选择待克隆抗体,确定待克隆抗体的复制数量。但改进型MISA在变异操作中加入了接种疫苗操作,因此增加了疫苗提取的过程,具体流程如算法2~4所示。
算法2 疫苗提取及更新算法
输入 抗体群;
输出 更新后的疫苗群体。
1)选取出抗体群中被支配数为0,支配数大于0的个体,将选出的个体按照支配个体数降序排列形成群体P;
2)疫苗提取及更新:如果疫苗群体为空,在符合群体P个体数和疫苗群体个体数最大值的约束条件下,按队列先后顺序将群体P中个体复制到疫苗群体中;否则,将群体P中个体和疫苗群体中个体合并起来,并按照支配个体数降序排列形成群体P',在符合群体P'个体数和疫苗群体个体数最大值的约束条件下,按队列先后顺序将群体P'中个体复制到疫苗群体中。
算法3 加入接种疫苗的多目标变异算法
输入 被选中将要进行克隆的个体;
输出 经过变异/接种疫苗生成新抗体群。
1)将待克隆抗体按照可克隆个数进行克隆,生成新的初始抗体群V;
2)循环遍历
3)随机选取[0, 1]的一个值r;
4)如果
5)否则进行疫苗接种:随机选取一个疫苗w;随机选取w中染色体单位值为0的片段
6)循环结束。
利用MISA多目标优化的置信规则库分类算法有机融合了算法1、2、3、MISA和DE参数训练方法。多目标免疫系统算法的选择进化机制是整个算法的核心,使得差分训练规则库参数和特征属性选择组合两个优化过程相互促进,最终获得一组Pareto最优解。DE参数训练方法对根据抗体构建的规则库进行参数优化,得到不同的特征属性选择组合构建的置信规则库的近似最优分类性能,进而采用MISA的选择机制和自适应网格进行抗体选择,将分类性能好的特征属性组合保留在外部种群中,同时也将区分性高的特征属性保留下来,在抗体进化的时候,采用变异增加抗体群的多样性,疫苗提取、更新和接种疫苗算法使得区分性高的特征属性在抗体群中扩散,让抗体能够得到更优的分类性能,迭代更新外部种群,不断优化外部种群中抗体的特征属性选择组合、分类性能。
算法4 利用MISA多目标优化的置信规则库分类算法
输入 无;
输出 Pareto最优前沿。
1)初始化抗体群,初始化外部种群为空;
2)对由每个抗体构建得来的置信规则库采用DE参数训练方法进行参数训练;
3)计算每个抗体的适应值,进而判断每个抗体是否是Pareto解;
4)将得到的非支配个体复制到外部种群(调用算法1);
5)按一定的标准选取待克隆抗体;
6)按一定的标准确定待克隆抗体的复制数量;
7)抽取并更新疫苗(调用算法2);
8)如果达到MISA算法最大迭代次数则end,否则进行9);
9)克隆抗体,并对个体进行变异或疫苗接种(调用算法3);
10)返回到2)。
2.2 MISA-BRM分类模型在MISA-BRM分类方法中,将前提属性的选取编码作为抗体,根据抗体构建出初始的规则库,将置信推理方法BRM作为推理机,结合差分进化算法对待优化参数进行学习矫正,进而计算抗体在复杂度、分类错误率两个目标函数上的适应值,然后采用MISA的选择进化机制,在系统的复杂度、分类错误率两个维度上寻找Pareto解。算法的流程如图1所示。

|
Download:
|
| 图 1 MISA-BRM模型 Fig. 1 MISA-BRM model diagram | |
实验环境的基本信息:Intel(R) Core(TM) i7-6700 CPU @3.40 GHz处理器,8核,16 GB内存,Window10 操作系统。
3.2 数据集参数设置 3.2.1 实验数据集在实验部分本文选用University of Galifornia at Irvine分校网页中获取的公共测试集来验证算法有效性。数据集主要包括鸢尾花特征数据Iris、红酒化学成分特征数据Wine、乳腺癌数据Cancer和玻璃类型数据Glass。表1列举了这4个测试数据集中前提属性数量、类别数量和数据集大小的信息。
其中Cancer原数据集中存在缺失数据,实验中将缺失的16条数据删除,保留683条数据。
| 表 1 测试数据的基本信息 Tab.1 Basic information regarding the test data |
本文置信规则库的模糊区间划分数
| 表 2 DEBRM参数设置信息 Tab.2 The parameter setting information for DEBRM |
| 表 3 MISA参数设置信息 Tab.3 The parameter setting information for MISA |
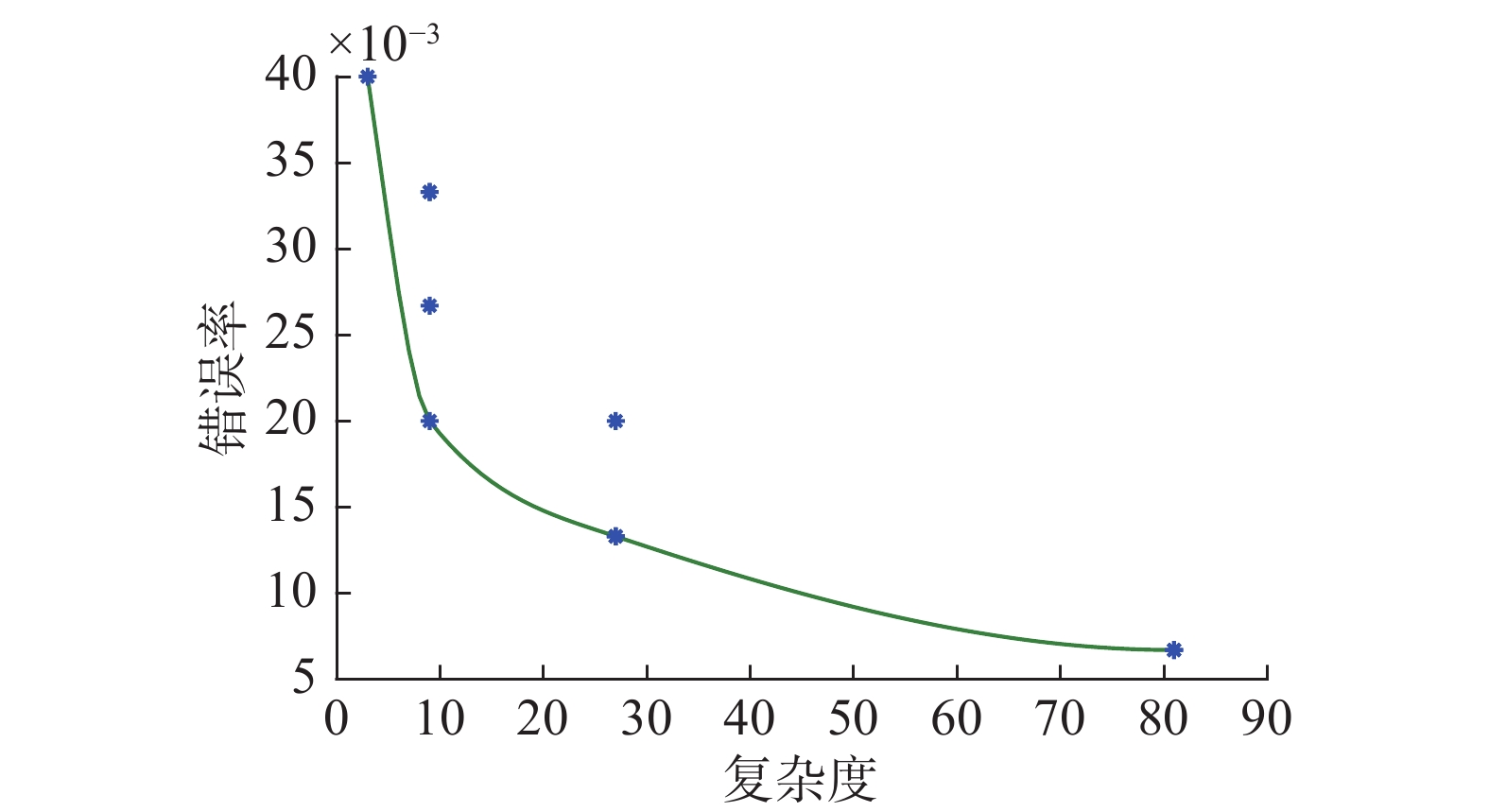
实验中针对每组数据集,采用十折交叉验证方法对提出的算法进行测试,数据集划分方法采用分层抽样方法。实验中用总的数据集(训练集+测试集)的错误率进行Pareto适应值计算。针对每一数据集,取10组实验中在整个数据集上获得的最高准确率值最大的一组的实验结果来展示,采用图表方式展示实验结果。用图2~5分析整个数据集的Pareto最优解集分布情况,图中的点是外部种群中保存的Pareto非劣解,图中的曲线是外部种群中所有Pareto最优解对应的目标向量组成的Pareto最优曲线;用表格数据分析数据集的Pareto最优解集及其对应的训练集和测试集的实验结果。
|
Download:
|
| 图 2 Iris数据集的Pareto最优曲线 Fig. 2 The Pareto optimal curve for the Iris dataset | |

|
Download:
|
| 图 3 Wine数据集的Pareto最优曲线 Fig. 3 The Pareto optimal curve of the entire Wine dataset | |
|
Download:
|
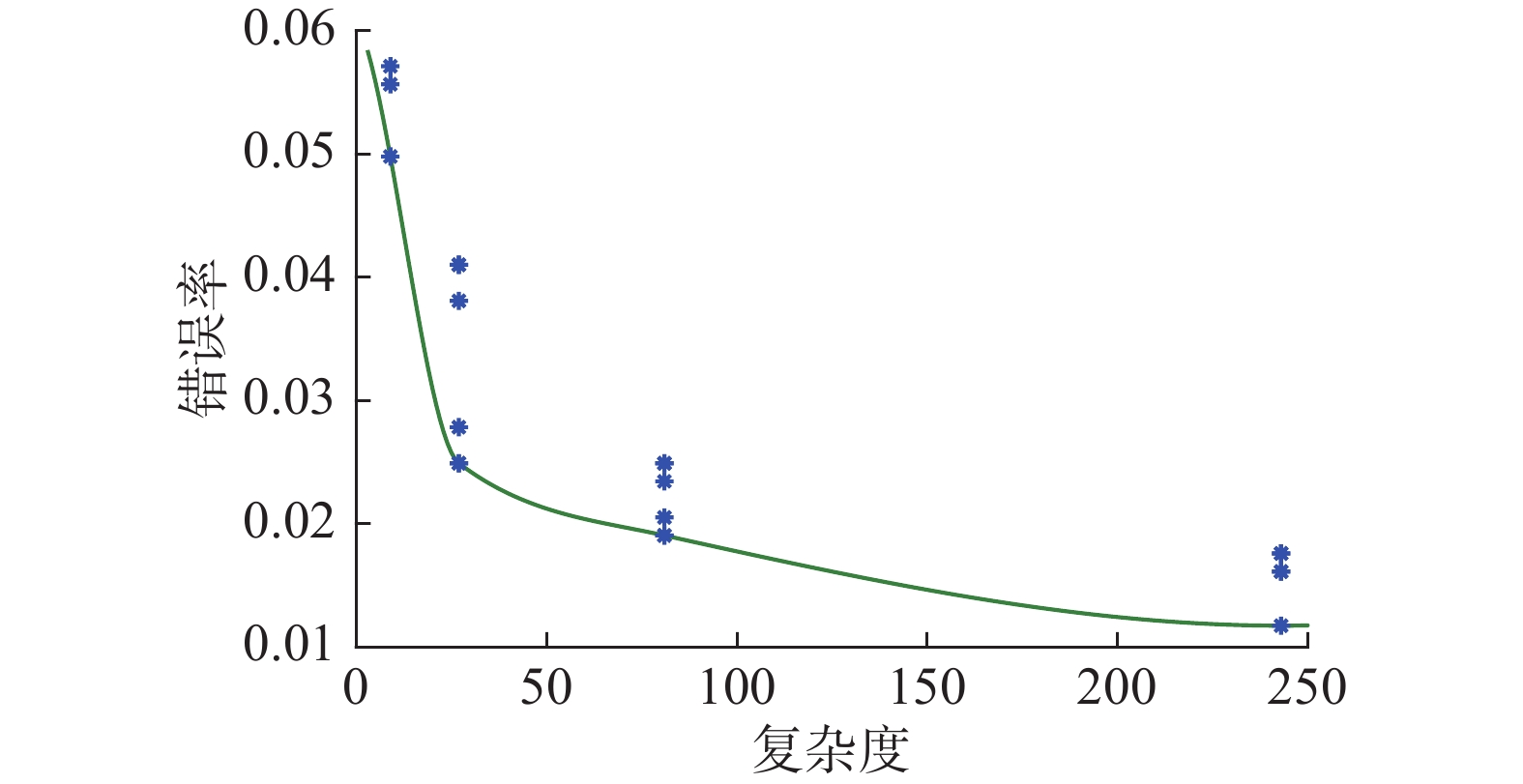
| 图 4 Cancer数据集的Pareto最优曲线 Fig. 4 The Pareto optimal curve of the entire Cancer dataset | |
|
Download:
|
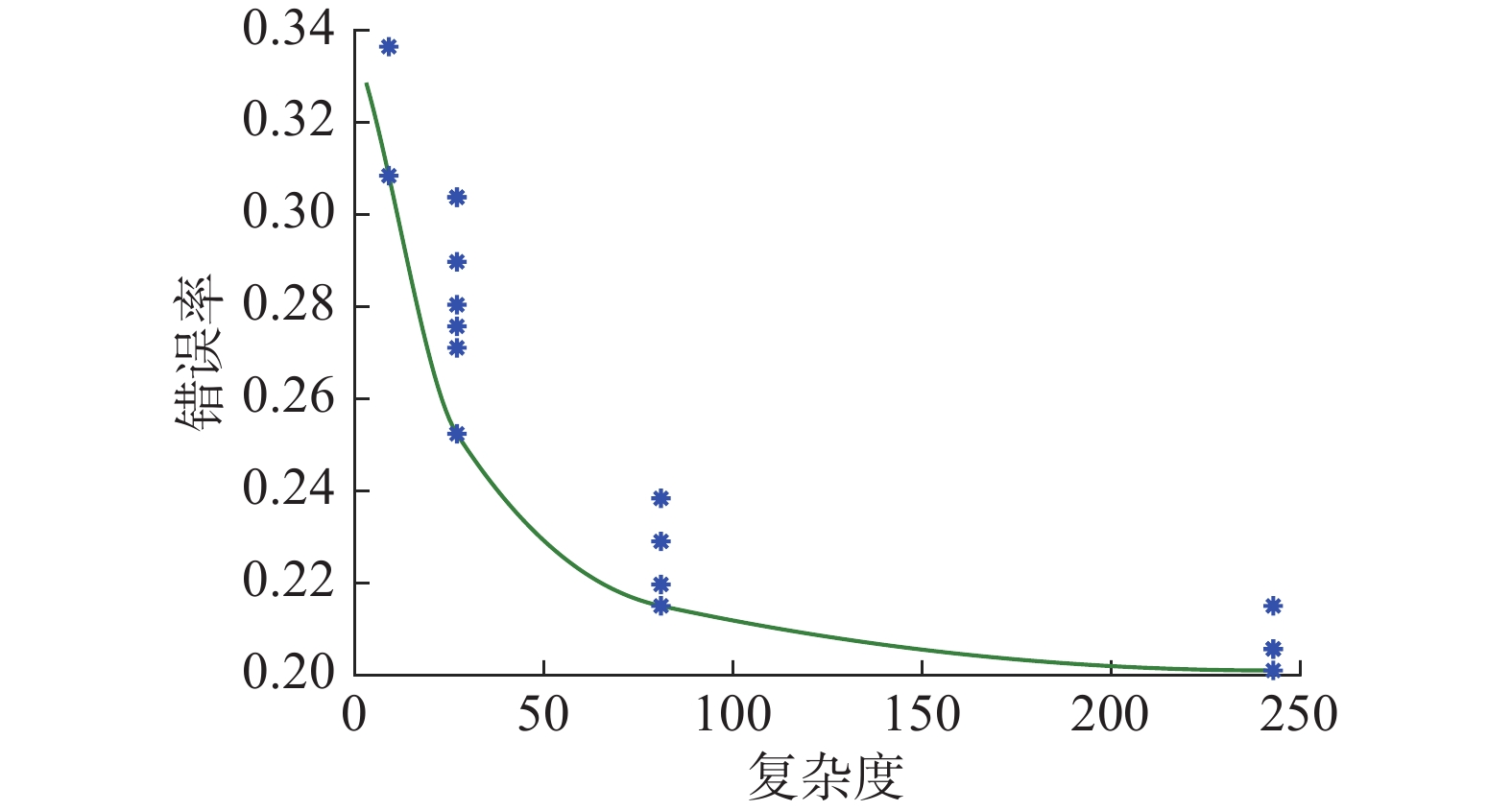
| 图 5 Glass数据集的Pareto最优曲线 Fig. 5 The Pareto optimal curve of the entire Glass dataset | |
在Iris数据集中,每个类别的数据分布均匀。本文方法解决Iris数据集分类问题的Pareto最优曲线如图2所示。对Iris的训练数据集、测试数据集及整个数据集上的分类准确率如表4所示。
| 表 4 Iris数据集上MISA-BRM的Pareto最优解集 Tab.4 The Pareto optimal solution set of MISA–BRM for the Iris dataset |
通过以上实验结果分析可知,在Iris总数据集上,Pareto最优解集中4种不同的前提属性个数的分类准确率差距较小,其中4个前提属性的分类结果与3个前提属性分类的准确率仅相差0.66%。相同的前提属性个数,选取不同的前提属性构建规则库分类系统得到的分类准确率不同。通过实验可知,针对Iris,本文方法通过对分类系统进行多目标优化可以在满足较高准确率情况下构建出复杂性更低的分类模型。
为了进一步说明本文方法的有效性,将本文方法与BRBCS、DEBRM分类方法解决Iris 数据集分类问题时构建的分类系统的复杂度和准确率进行对比,如表5所示。通过表5分析可知,传统的BRBCS规则条数有两千多条,而本文方法将规则条数约简到二十多条,且本文方法在整个数据集的分类准确率比传统的BRBCS高。相比于DEBRM,规则约简了54条,测试数据集的分类准确率与DEBRM持平,训练数据集的分类准确率低了1.48%,总的数据集分类准确率低了1.33%,尽管该方法牺牲了一定的准确率,但其降低了系统复杂度,可以为决策者根据实际需要提供更多的选择。
| 表 5 Iris数据集结构复杂度和分类准确率对比 Tab.5 Comparison of the structural complexity and classification accuracy with respect to the Iris dataset |
在Wine数据集中,各类别的数据量分布较不均匀。本文方法用于解决Wine数据集的Pareto最优,曲线如图3所示。
对Wine的训练数据集、测试数据集及整个数据集上的分类准确率如表6所示。
| 表 6 Wine数据集上MISA-BRM的Pareto最优解集 Tab.6 The Pareto optimal solution set of MISA–BRM with respect to the Wine dataset |
通过图3及表6分析可知,在Wine数据集上,取其中4个前提属性能获得100%的分类准确率,相比于取13个前提属性规则条数由上万条减少为几十条,且分类准确率得到提高;通过实验可知,针对Wine数据集前提属性个数在4~6,系统能够获得较好的分类效果。
为了进一步说明本文方法的有效性,将本文方法与DEBRM分类方法解决Wine数据集分类问题时构建的分类系统的复杂度和准确率进行对比,如表7所示。
| 表 7 Wine数据集结构复杂度和分类准确率对比 Tab.7 Comparison of the structural complexity and classification accuracy with respect to the Wine dataset |
通过表7分析可知,相比于Liu等提出的DEBRM分类系统,基于MISA多目标优化的置信规则库分类系统的规则数量由
Cancer数据集总的数据量较大,同样各类别数据分布较不均匀。本文方法用于解决Cancer数据集的Pareto最优曲线,如图4所示。对Cancer训练数据集、测试数据集及整个数据集上的分类准确率如表8所示。
| 表 8 Cancer数据集上MISA-BRM Pareto 最优解集 Tab.8 The Pareto optimal solution set of MISA–BRM using the Cancer dataset |
通过图4和表8分析可知,Cancer数据集上取4~5个前提属性时在训练数据集上的分类准确率相差0.81%,测试数据集的分类效果相同。可知,针对Cancer 数据集,该模型在保证系统复杂度尽可能低的情况下,还能有效保证系统的分类准确。
为了进一步说明本方法的有效性,将本文方法与BRBCS、DEBRM分类方法解决Cancer 数据集分类问题时构建的分类系统的复杂度和准确率进行对比,如表9所示。
| 表 9 Cancer数据集结构复杂度和分类准确率对比 Tab.9 Comparison of the structural complexity and classification accuracy with respect to the Cancer dataset |
通过表9分析可知,相比于BRBCS、DEBRM,在Cancer总数据集上,MISA-BRM分类方法的准确率分别降低0.37%、0.73%。但系统的规则条数则约简了上万条。因此,当对系统复杂度要求较高时,MISA-BRM在准确率和复杂度两个标准的均衡下有较好的效果。
3.3.4 Glass数据集实验分析Glass数据集有6个类别,各类别数据分布不均匀,且有的类别的数据量占总的数据量的比率小。本文方法用于解决Glass数据集的Pareto最优曲线,如图5所示。
对Glass的训练数据集、测试数据集及整个数据集上的分类准确率如表10所示。
| 表 10 Glass数据集MISA-BRM的Pareto最优解集 Tab.10 The Pareto optimal solution set of MISA−BRM with respect to the Glass dataset |
将本文方法与BRBCS、DEBRM分类方法解决Glass 数据集分类问题时构建的分类系统的复杂度和准确率进行对比,如表11所示。
| 表 11 Glass数据集结构复杂度和分类准确率对比 Tab.11 Comparison of the structural complexity and classification accuracy with respect to the Glass dataset |
分析表10和表11可知:本文方法在前提属性个数为4个或5个时系统能够获得较好的分类效果;本文方法在Glass数据集上的分类准确率比BRBCS和DEBRM分别降低了14.56%、2.83%,但规则条数分别减少了1 952 882条、19 440条,虽然牺牲了一定的分类准确率,但规则数极大降低。对于Glass测试数据集不仅极大约简了规则条数且分类准确率得到提高。
综上,通过Iris数据集、Wine数据集、Cancer数据集、Glass数据集的实验结果分析可知:本文采用属性约简思想、差分参数训练方法,并结合改进型MISA算法对置信规则库分类系统的复杂度和准确度进行多目标优化是有效可行的。
3.4 与其他分类方法的准确率比较为了进一步说明本文方法的有效性,本节对比了MISA-BRM与现有其他分类方法[14]用于解决Iris数据集、Cancer数据集、Wine数据集、Glass数据集分类问题时的准确率,详见表12和表13。
| 表 12 MISA-BRB和其他分类方法的比较 Tab.12 Comparison with other classification methods |
| 表 13 MISA-BRB和其他建模方法的比较 Tab.13 Comparison with other modeling methods |
对比表12中数据,MISA-BRB分类方法在Iris数据集上准确率比Naïve Beyes、C4.5方法高,在Cancer数据集上准确率仅比Fuzzy-Gain Measure方法低;在Wine数据集上,得到100%的最好结果;在Glass数据集上,相比于其他6中分类方法,MISA-BRB的准确率最高。
在表13中,NSGA-II-FRBCS[15]分类方法、基于Pareto混合烟花−差分进化算法[16](表中称混合烟花−差分进化)都是以准确率、解释性为目标,进行多目标优化的模糊规则库分类方法。从表13可得,针对Iris数据集、Wine数据集和Glass数据集,利用MISA多目标优化的置信规则库分类方法比NSGA-II-FRBCS准确率更高;利用MISA多目标优化的置信规则库分类方法和基于Pareto混合烟花−差分进化算法相比,在Cancer数据集上准确率略高,在Wine数据集上准确率较高。
4 结束语本文首次针对提高置信规则库分类系统准确率和降低系统复杂度的多目标优化问题进行建模。算法采用基于特征属性序列编码的方法进行特征搜索,使得在规则数量减少的情况下尽可能提高分类准确率。此外,对经典的MISA算法进行改进,加入基于Pareto支配关系的个体疫苗提取和接种疫苗操作,提出MISA-BRM模型。实验结果表明,该算法能寻找到一组具有不同准确率和复杂度的Pareto最优解集,方便决策者根据实际需要进行选择。
| [1] |
魏茂胜. 数据挖掘中的分类算法综述[J]. 网络安全技术与应用, 2017(6): 65-66. WEI Maosheng. Overview of classification algorithms in data mining[J]. Network security technology and application, 2017(6): 65-66. DOI:10.3969/j.issn.1009-6833.2017.06.039 (  0) 0)
|
| [2] |
TSAKIRIDIS N L, THEOCHARIS J B, ZALIDIS G C. DECO3R: a differential evolution-based algorithm for generating compact fuzzy rule-based classification systems[J]. Knowledge-based systems, 2016, 105: 160-174. DOI:10.1016/j.knosys.2016.05.013 ( 0) 0)
|
| [3] |
PRUSTY M R, JAYANTHI T, CHAKRABORTY J, et al. Performance analysis of fuzzy rule based classification system for transient identification in nuclear power plant[J]. Annals of nuclear energy, 2015, 76: 63-74. DOI:10.1016/j.anucene.2014.09.039 ( 0) 0)
|
| [4] |
LIUBICH L D, KOVALEVSKA L M, LISYANY M I, et al. TGF-β1 expression by glioma C6 cells in vitro[J]. Experimental oncology, 2017, 39(4): 258-263. DOI:10.31768/2312-8852.2017.39(4):258-263 ( 0) 0)
|
| [5] |
YANG Jianbo, LIU Jun, WANG Jin, et al. Belief rule-base inference methodology using the evidential reasoning Approach-RIMER[J]. IEEE transactions on systems, man, and cybernetics-part a: systems and humans, 2006, 36(2): 266-285. DOI:10.1109/TSMCA.2005.851270 ( 0) 0)
|
| [6] |
JIAO Lianmeng, PAN Quan, DENŒUX T, et al. Belief rule-based classification system: Extension of FRBCS in belief functions framework[J]. Information sciences, 2015, 309: 26-49. DOI:10.1016/j.ins.2015.03.005 ( 0) 0)
|
| [7] |
刘莞玲, 王韩杰, 傅仰耿, 等. 基于差分进化算法的置信规则库推理的分类方法[J]. 中国科学技术大学学报, 2016, 46(9): 764-773. LIU Wanling, WANG Hanjie, FU Yanggeng, et al. Belief rule based inference methodology for classification based on differential evolution algorithm[J]. Journal of University of Science and Technology of China, 2016, 46(9): 764-773. (  0) 0)
|
| [8] |
MIRJALILI S, SAREMI S, MIRJALILI S M, et al. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization[J]. Expert systems with applications, 2016, 47: 106-119. DOI:10.1016/j.eswa.2015.10.039 ( 0) 0)
|
| [9] |
HOU Yan, WU Naiqi, ZHOU Mengchu, et al. Pareto-optimization for scheduling of crude oil operations in refinery via genetic algorithm[J]. IEEE transactions on systems, man, and cybernetics: systems, 2017, 47(3): 517-530. DOI:10.1109/TSMC.2015.2507161 ( 0) 0)
|
| [10] |
范立云, 周伟, 刘鹏, 等. 高速电磁阀动态响应的多目标优化[J]. 哈尔滨工程大学学报, 2018, 39(1): 53-59. FAN Liyun, ZHOU Wei, LIU Peng, et al. Multi objective optimization of dynamic response of high speed solenoid valve[J]. Journal of Harbin Engineering University, 2018, 39(1): 53-59. (  0) 0)
|
| [11] |
童晶. 多目标优化的Pareto解的表达与求取[D]. 武汉: 武汉科技大学, 2009. TONG Jing. Expressing and obtaining Pareto solutions in multi-objective optimization problem[D]. Wuhan: Wuhan University of Science and Technology, 2009. (  0) 0)
|
| [12] |
COELLO C A, CORTÉS N C. Solving multiobjective optimization problems using an artificial immune system[J]. Genetic programming and evolvable machines, 2005, 6(2): 163-190. DOI:10.1007/s10710-005-6164-x ( 0) 0)
|
| [13] |
KNOWLES J, OATES M, CORNE D. Advanced multi-objective evolutionary algorithms applied to two problems in telecommunications[J]. BT technology journal, 2000, 18(4): 51-65. DOI:10.1023/A:1026754608572 ( 0) 0)
|
| [14] |
FALLAHNEZHAD M, MORADI M H, ZAFERANLOUEI S. A hybrid higher order neural classifier for handling classification problems[J]. Expert systems with applications, 2011, 38(1): 386-393. DOI:10.1016/j.eswa.2010.06.077 ( 0) 0)
|
| [15] |
李继东. 遗传模糊分类系统构建中规则获取和解释性优化的关键技术研究[D]. 昆明: 云南大学, 2011. LI Jidong. Research on key techniques of rule acquisition and interpretive optimization in the construction of genetic fuzzy classification system[D]. Kunming: Yunnan University, 2011. (  0) 0)
|
| [16] |
刘冲. 基于烟花算法的模糊建模方法研究[D]. 郑州: 郑州大学, 2016. Liu Chong. Research on fuzzy modeling method based on fireworks algorithm [D]. Zhengzhou: Zhengzhou University, 2016. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


