受到自然界中动物集体运动(或者集群、编队运动)行为的启发，人们发现由多个具有自主“计算”能力的个体组成的分布式多自主体系统通常能够完成相对复杂的任务，且具有单个个体所不具有的能力。一致性作为分布式多自主体协同控制的基础^[1-4]，现在已经成为人工智能控制方向的一个研究热点问题。

近年来，对于分布式多自主体的研究热度不断增长，并涌现出了大量的研究成果。文献[5-6]研究了在固定和变换拓扑下二阶多自主体系统协同控制信息的一致性算法。文献[7]针对有向拓扑结构研究了时变的二阶多自主体网络的一致性问题。在多自主体系统中如果减少自主体之间的通信次数，就可以减少网络中的节点之间数据的传递次数和频率，提高系统的收敛速度。文献[8]研究了具有交换拓扑和存在噪声的多自主体系统模型，提出了一种基于自主体自身以及邻居状态的一致性采样控制协议。文献[9]研究了在采样数据集中的情况下具有领导者的多自主体收敛问题。文献[10]研究了在时变拓扑下通过采样数据实现多自主体系统一致性的问题。尽管采样控制容易实现，且在一定程度上能够减少自主体之间信息交互次数，但在采样数据差值微小或当系统趋近于稳定的时候系统仍然采样还会存在资源浪费的现象。所以Dimarogonas等^[11-13]提出了仅需要自主体自己的状态与其邻居自主体状态的事件触发机制，并且给出了可以使多自主体网络实现一致性的集中式、自触发式和分布式的一阶系统的事件触发函数。文献[14]研究并给出了非线性多自主体系统的基于Lyapunov方法和驻留时间方法两种事件触发机制的设计方法。文献[15-16]通过引入合理的状态误差研究了基于事件触发机制的多自主体系统有限时间快速收敛问题，得到了系统实现一致性的事件触发条件。文献[17]针对强连通图提出一种自适应事件触发控制方案，该方案根据采样数据动态改变系统参数可以实现触发间隔的动态调节。文献[18]研究了线性结构下异构多自主体系统的输出收敛问题，设计了一个事件触发下的输出控制机制。文献[19-21]综述了多自主体系统分布式事件触发控制的研究现状，分析了当前几种主要的多自主体系统事件触发一致性算法。在以上的文献中主要研究了一阶系统的分布式事件触发算法，或者二阶系统的集中式触发算法。

本文给出了一种分布式事件触发机制下的二阶多自主体系统的控制协议和触发函数，设计的事件触发函数的触发时刻仅依赖自主体自身状态和其邻居状态的误差值。应用矩阵论和现代控制理论等工具对分布式事件触发多自主体领导跟随一致性进行了分析，得到了二阶系统协同运动的收敛条件。

1 预备知识

一个自主体可以利用图中的一个节点来表示，利用边来表示自主体之间的信息传递。带有领导者的网络中的通信拓扑可以由含有 $N + 1$ 个自主体的有向图 ${\bar{ G}} = \{ {\bar{ V}},{{E}},{\bar{ A}}\} $ 来表示，其中 ${\bar{ V}} = $ $\{ 0,1, \cdots ,N\} $ 表示自主体的集合。 ${{E}} = {\bar{ V}} \times {\bar{ V}}$ 代表有向边的集合，自主体 $i$ 的邻接矩阵为 ${{{N}}_i} = \{ j \in $ $ {{V}}|(j,i) \in {{E}}\} $ ， ${\bar{ A}} = {({a_{ij}})_{N \times N}}$ 表示邻接矩阵，其中 ${a_{ij}}$ 表示边 $(i,j)$ 的权重。如果有向边 $(i,j)$ 存在，即 $(i,j) \in {{E}}$ ，则与之对应的边的权值 ${a_{ij}} > 0$ ，否则 ${a_{ij}} = 0$ 。

邻接矩阵 ${\bar{ A}}$ 所有的对角元素为0。在图 ${\bar{ G}}$ 中分别令 ${d_{{\rm{in}}}} = \displaystyle\sum\limits_{i = 1}^N {{a_{ij}}} $ 和 ${d_{{\rm{out}}}} = \displaystyle\sum\limits_{i = 1}^N {{a_{ji}}} $ 为第 $i$ 个节点的入度和出度。特别地，若 ${d_{{\rm{in}}}}(i) = {d_{{\rm{out}}}}(i)$ ，则称图 ${\bar{ G}}$ 为平衡图。若定义 ${{D}} = {\rm{diag}}\{ {d_{{\rm{in}}}}(i)\} $ 为图的度矩阵，则图 ${\bar{ G}}$ 的 ${\rm{Laplacian}}$ 矩阵 ${{L}}$ 定义为 ${{L}} = {{D}} - {\bar{ A}}$ 。定义矩阵 ${{H}} = {\rm{diag}}\{ {a_{10}}\;\;{a_{20}}\;\; \cdots \;\;{a_{N0}}\} $ 为跟随者与领导者的邻接矩阵，其中 ${a_{i0}}$ 不全为0。

引理1　 L为连通图 G 的 ${\rm{Laplacian}}$ 矩阵

1) ${{\textit{λ}} _1}=0$ 是 L 中的一个特征值，且其对应的特征向量为 ${{{1}}_N}$ ，即满足 ${{L}}{{{1}}_N} = {{{0}}_N}$ 。

2) 令 ${\bar{ L}} = {{L}} + {{H}}$ ，那么其特征值 ${{\textit{λ}} _i}({\bar{ L}}) > 0$ 。

引理2　对于对称矩阵 ${{S}} = \left[ {\begin{array}{*{20}{c}} {{{{S}}_{11}}}&{{{{S}}_{12}}} \\ {{{{S}}_{21}}}&{{{{S}}_{22}}} \end{array}} \right]$ ，其中 ${{{S}}_{11}}$ 、 ${{{S}}_{22}}$ 均为方阵。如果 ${{S}} > {{0}}$ ，下面的两个条件等价：

1) $ {{{S}}_{11}} > 0,{{{S}}_{22}} - {{{S}}_{12}}^{\rm{T}}{{{S}}_{11}}^{ - 1}{{{S}}_{12}} > 0 $ ；

2) $ {{{S}}_{22}} > 0,{{{S}}_{11}} - {{{S}}_{12}}^{\rm{T}}{{{S}}_{22}}^{ - 1}{{{S}}_{12}} > 0 $ 。

引理3　对于任意维度的矩阵 ${{M}}$ 、 ${{N}}$ 、 ${{P}}$ 和 ${{Q}}$ ，并且 ${{M}}$ 和 ${{N}}$ 是可逆矩阵， ${\rm{Kronecker}}$ 积具有以下性质：

1) $ ({{P}} + {{Q}}) \otimes {{M}} = {{P}} \otimes {{M}} + {{Q}} \otimes {{M}} $ ；

2) $ {({{M}} \otimes {{N}})^{\rm{T}}} = {{{M}}^{\rm{T}}} \otimes {{{N}}^{\rm{T}}} $ ；

3) $ {{\textit{λ}} _{\min }}({{M}}) = {{\textit{λ}} _{\min }}({{M}} \otimes {{{I}}_{m \times m}}) $ ；

4) $ ({{M}} \otimes {{N}})({{P}} \otimes {{Q}}) = ({{MP}}) \otimes ({{NQ}}) $ 。

引理4　若 ${{A}}$ 、 ${{B}}$ 是 ${\rm{Hermite}}$ 矩阵，则下式成立：

1) $ {{\textit{λ}} _{\min }}({{A}}) + {{\textit{λ}}_{\min }}({{B}}) \leqslant {{\textit{λ}}_{\min }}({{A}} + {{B}}) $ ；

2) $ {{\textit{λ}} _{\max }}({{A}}) + {{\textit{λ}}_{\max }}({{B}}) \geqslant {{\textit{λ}}_{\max }}({{A}} + {{B}}) $ 。

2 基于分布式事件触发机制的多自主体系统的一致性 2.1 问题描述

针对一个二阶多自主体系统中有 $N$ 个可以相互通信的个体，其动力学方程可以描述为

$\left\{ {\begin{array}{*{20}{c}} {{{\dot x}_i}(t) = {v_i}(t)} \\ {{{\dot v}_i}(t) = {u_i}(t)} \end{array}} \right.$

(1)

式中： ${x_i}(t) \in {{\bf{R}}^m}$ ，为第 $i$ 个跟随者在 $t$ 时刻的位置； ${v_i}(t) \in {{\bf{R}}^m}$ ，为第 $i$ 个跟随者在 $t$ 时刻的速度； ${u_i}(t) \in {{\bf{R}}^m}$ ，为第 $i$ 个跟随者在 $t$ 时刻的控制协议； $i = 1,2, \cdots ,N$ 。对于领导者0，其动力学方程可以描述为

$\left\{ {\begin{array}{*{20}{c}} {{{\dot x}_0}(t) = {v_0}(t)} \\ {{{\dot v}_0}(t) = {u_0}(t)} \end{array}} \right.$

(2)

式中： ${x_0}(t) \in {{\bf{R}}^m}$ ，为领导者在 $t$ 时刻的位置； ${v_0}(t) \in {{\bf{R}}^m}$ ，为领导者在 $t$ 时刻的速度； ${u_0}(t) \in {{\bf{R}}^m}$ ，为领导者在 $t$ 时刻的控制协议，并且这里假设领导者 $0$ 的加速度保持不变，即 ${u_0}(t)=0$ 。

定义1　称跟随者自主体 $i$ 与领导者 $0$ 实现一致性，当且仅当存在控制协议 ${u_i}(t)$ 使得系统在任意的初始条件下满足：

$ \begin{aligned} & \mathop {\lim }\limits_{t \to \infty } \left| {{x_i}(t) - {x_0}(t)} \right| = 0\\ & \mathop {\lim }\limits_{t \to \infty } \left| {{v_i}(t) - {v_0}(t)} \right| = 0 \end{aligned} $

式中 $ i = 1,2, \cdots ,N $ 。

2.2 事件触发控制器的设计

假设连续时间下的控制协议为

$\begin{split} {u_i}(t) = & - \alpha \sum\limits_{j \in {N_i}} {({x_i}(t) - {x_j}(t))} - \beta \sum\limits_{j \in {N_i}} {({v_i}(t) - {v_j}(t))} - \\ & \alpha {a_{i0}}({x_i}(t) - {x_0}(t)) - \beta {a_{i0}}({v_i}(t) - {v_0}(t)) \\ \end{split} $

设基于事件触发机制的控制协议为

$ \begin{split} {u_i}(t) = & - \alpha \sum\limits_{j \in {N_i}} {({x_i}(t_k^{i}) - {x_j}(t_k^{i}))} - \beta \sum\limits_{j \in {N_i}} {({v_i}(t_k^{i}) - {v_j}(t_k^{i}))} - \\ & \alpha {a_{i0}}({x_i}(t_k^{i}) - {x_0}(t)) - \beta {a_{i0}}({v_i}(t_k^{i}) - {v_0}(t)) \end{split} $

(3)

式中： $\alpha > 0$ ， $\beta > 0$ 为系统控制协议的可调增益系数； $t \in \left[ {t_k^{i},t_{k + 1}^{i}} \right)$ ， $t_k^{i}=\inf \{ t > t_{k - 1}^{i}:{f_i}(t) \geqslant 0\} (k = 1,2, \cdots )$ 为触发器的第 $k$ 次事件触发时刻，其中 ${f_i}(t)$ 为事件触发函数。

定义误差函数为 $\left\{ {\begin{array}{*{20}{c}} {e_x^{i}(t) = {x_i}(t_k^{i}) - {x_i}(t)} \\ {e_v^{i}(t) = {v_i}(t_k^{i}) - {v_i}(t)} \end{array}} \right.$ ，所以

$ \begin{split} {u_i}(t) = & - \alpha \sum\limits_{j \in {N_i}} {({x_i}(t) - {x_j}(t){\rm{ + }}e_x^{i}(t) - e_x^{j}(t))}- \\ & \beta \sum\limits_{j \in {N_i}} {({v_i}(t) - {v_j}(t){\rm{ + }}e_v^{i}(t) - e_v^{j}(t))} -\\ & \alpha {a_{i0}}({x_i}(t){\rm{ + }}e_x^{i}(t) - {x_0}(t))- \beta {a_{i0}}({v_i}(t){\rm{ + }}e_v^{i}(t) - {v_0}(t)) \end{split}$

(4)

因此式(1)可以变为

$ \begin{array}{l} \left\{ \begin{array}{l} {{\dot x}_i}(t) = {v_i}(t)\\ {{\dot v}_i}(t) = - \alpha \sum\limits_{j \in {N_i}} {({x_i}(t) - {x_j}(t){\rm{ + }}e_x^i(t) - e_x^j(t))} - \end{array} \right.\\ \quad \quad \quad \;\beta \sum\limits_{j \in {N_i}} {({v_i}(t) - {v_j}(t){\rm{ + }}e_v^i(t) - e_v^j(t))} - \\ \quad \quad \quad \;\alpha {a_{i0}}({x_i}(t){\rm{ + }}e_x^i(t) - {x_0}(t)) - \beta {a_{i0}}({v_i}(t){\rm{ + }}e_v^i(t) - {v_0}(t)) \end{array} $

(5)

为了简化书写，令

$ \begin{split} & {{x}}(t)={\left[ {{x_1}(t)\;\;{x_2}(t)\;\; \cdot \cdot \cdot \;\;{x_N}(t)} \right]^{\rm{T}}} \in {{\bf{R}}^N} \\ & {{v}}(t)={\left[ {{v_1}(t)\;\;{v_2}(t)\;\; \cdot \cdot \cdot \;\;{v_N}(t)} \right]^{\rm{T}}} \in {{\bf{R}}^N} \end{split} $

$ \begin{split} & {{{e}}_x}(t)={\left[ {e_x^1(t)\;\;e_x^2(t)\;\; \cdot \cdot \cdot \;\;e_x^N(t)} \right]^{\rm{T}}} \in {{\bf{R}}^N}\\ & {{{e}}_v}(t)={\left[ {e_v^1(t)\;\;e_v^2(t)\;\; \cdot \cdot \cdot \;\;e_v^N(t)} \right]^{\rm{T}}} \in {{\bf{R}}^N} \end{split} $

则式(5)可以改写为

$\begin{gathered} \left[ {\begin{array}{*{20}{c}} {{{\dot x}}(t)} \\ {{{\dot v}}(t)} \end{array}} \right] = - {{A}} \otimes {{{I}}_{m \times m}}\left[ {\begin{array}{*{20}{c}} {{{x}}(t)} \\ {{{v}}(t)} \end{array}} \right] - {{B}} \otimes {{{I}}_{m \times m}}\left[ {\begin{array}{*{20}{c}} {{{{e}}_x}(t)} \\ {{{{e}}_v}(t)} \end{array}} \right] + \\ \;\;{\left[ {\begin{array}{*{20}{c}} \alpha \\ \beta \end{array}} \right]^{\rm{T}}} \otimes ({{H}} \otimes {{{I}}_{m \times m}})\left[ {\begin{array}{*{20}{c}} {{{1}}{x_0}(t)} \\ {{{1}}{v_0}(t)} \end{array}} \right] \\ \end{gathered} $

(6)

式中： ${{A}} = \left[ {\begin{array}{*{20}{c}} {{{{\bf{0}}}_{N \times N}}}&{ - {{{I}}_{N \times N}}} \\ {\alpha {\bar{ L}}}&{\beta {\bar{ L}}} \end{array}} \right],$ ${{B}} = \left[ {\begin{array}{*{20}{c}} {{{{\bf{0}}}_{N \times N}}}&{{{{\bf{0}}}_{N \times N}}} \\ {\alpha {\bar{ L}}}&{\beta {\bar{ L}}} \end{array}} \right],$ ${\bar{ L}} = {{L}} + $ H； ${{H}} = {\rm{diag}}\{ {a_{10}}\;\;{a_{20}}\;\; \cdots \;\;{a_{N0}}\} $ ； ${{\bf{1}}}$ 表示全为1的列向量； ${{L}}$ 为图 ${\bar{ G}}$ 中跟随者的 ${\rm{Laplacian}}$ 矩阵。令 ${\hat x_i}(t) = $ ${x_i}(t) - {x_0}(t) $ ， ${\hat v_i}(t) = {v_i}(t) - {v_0}(t)$ ，那么 ${x_i}(t) = {\hat x_i}(t){\rm{ + }}{x_0}(t)$ ， ${v_i}(t) = {\hat v_i}(t){\rm{ + }}{v_0}(t)$ ，所以式(6)整理后得

$\left[ {\begin{array}{*{20}{c}} {\mathop {{{\hat x}}}\limits^ \cdot (t)}\\ {\mathop {{{\hat v}}}\limits^ \cdot (t)} \end{array}} \right] = - {{A}} \otimes {{{I}}_{m \times m}}\left[ {\begin{array}{*{20}{c}} {{{\hat x}}(t)}\\ {{{\hat v}}(t)} \end{array}} \right] - {{B}} \otimes {{{I}}_{m \times m}}\left[ {\begin{array}{*{20}{c}} {{{{e}}_x}(t)}\\ {{{{e}}_v}(t)} \end{array}} \right]$

(7)

由式(7)可以看出，通过模型变换将研究系统式(1)、(2)的领导跟随一致性问题，变为研究式(7)的稳定性问题。下面针对式(7)设计分布式事件触发函数。

定理1　考虑带有一个领导者的多自主体系统式(1)、(2)，如果连通图 ${\bar{ G}}$ 至少含有一个全局可达点，领导者为根节点，即图 ${\bar{ G}}$ 中至少有一个自主体可以接收到领导者发送的位置和速度状态，对于多自主体系统，那么设计分布式事件触发函数为

$\begin{array}{c} {f_i}({{\hat x}_i}(t),{{\hat v}_i}(t),{e_{xi}}(t),{e_{xj}}(t),{e_{vi}}(t),{e_{vj}}(t))= \\ \sqrt m \cdot \displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}}[\alpha ({{\left\| {{e_{xi}}(t)} \right\|}^2} + {{\left\| {{e_{xj}}(t)} \right\|}^2})} + \\ \beta ({\left\| {{e_{vi}}(t)} \right\|^2} + {\left\| {{e_{vj}}(t)} \right\|^2}) + {a_{i0}}(\alpha {\left\| {{e_{xi}}(t)} \right\|^2} + \beta {\left\| {{e_{vi}}(t)} \right\|^2})] - \\ {\theta _i}(\delta - 1)({\left\| {{{\hat x}_i}(t)} \right\|^2} + {\left\| {{{\hat v}_i}(t)} \right\|^2}) \end{array} $

(8)

式中： $\alpha > 0$ ， $\beta > 0$ 为系统控制增益； ${\theta _i} \in (0,1)$ ， $\delta {\rm{ = max\{ inf}}\{ {{\textit{λ}}_{\min }}(2\alpha {\bar{ L}}) - 1,({{\textit{λ}}_{\min }}(2\beta {\bar{ L}}) - 2) - 1\} ,1{\rm{\} }}$ 。在控制协议式(3)的作用下，当 ${f_i}(t) \geqslant 0$ 时，多自主体系统式(1)、(2)可以实现领导跟随一致。

证明　令 ${{\xi }}(t) = {[{{\hat x}}{(t)^{\rm{T}}}\;\;{{\hat v}}{(t)^{\rm{T}}}]^{\rm{T}}}$ ，构造 ${\rm{Lyapunov}}$ 函数 $V(t) = {{\xi }}{(t)^{\rm{T}}}({{P}} \otimes {{{I}}_{m \times m}}){{\xi }}(t)$ ，其中

${{P}} = \left[ {\begin{array}{*{20}{c}} {(\alpha + \beta ){\bar{ L}} + {{{I}}_{N \times N}}}&{{{{I}}_{N \times N}}} \\ {{{{I}}_{N \times N}}}&{{{{I}}_{N \times N}}} \end{array}} \right]$

对 $V(t)$ 求导可得

$\begin{array}{c} \dot V(t) = {{\dot \xi }}{(t)^{\rm{T}}}{{P}} \otimes {{{I}}_{m \times m}}{{\xi }}(t) + {{\xi }}{(t)^{\rm{T}}}{{P}} \otimes {{{I}}_{m \times m}}{{\dot \xi }}(t) = \\ ( - {{\xi }}{(t)^{\rm{T}}}({{{A}}^{\rm{T}}}{{P}} + {{PA}}) \otimes {{{I}}_{m \times m}}{{\xi }}(t)) + \\ ( - {{e}}{(t)^{\rm{T}}}{{{B}}^{\rm{T}}}{{P}} \otimes {{{I}}_{m \times m}}{{\xi }}(t) - {{\xi }}{(t)^{\rm{T}}}{{P}} \otimes {{{I}}_{m \times m}}{{Be}}(t)) \end{array} $

其中 ${{e}}(t) = {[{{{e}}_x}{(t)^{\rm{T}}}\;\;{{{e}}_v}{(t)^{\rm{T}}}]^{\rm{T}}} $ ，计算得

$\begin{array}{c} \dot V(t)= - {{\hat x}}{(t)^{\rm{T}}}(2\alpha {\bar{ L}}) \otimes {{{I}}_{m \times m}}{{\hat x}}(t) + {{\hat x}}{(t)^{\rm{T}}}{{{I}}_{n \times n}} \otimes {{{I}}_{m \times m}}{{\hat v}}(t) + \\ {{\hat v}}{(t)^{\rm{T}}}{{{I}}_{N \times N}} \otimes {{{I}}_{m \times m}}{{\hat x}}(t) - {{\hat v}}{(t)^{\rm{T}}}(2\beta {\bar{ L}} - 2{{{I}}_{N \times N}}) \otimes {{{I}}_{m \times m}}{{\hat v}}(t) + \\ ( - {{e}}{(t)^{\rm{T}}}{{{B}}^{\rm{T}}}{{P}} \otimes {{{I}}_{m \times m}}{{\xi }}(t) - {{\xi }}{(t)^{\rm{T}}}{{P}} \otimes {{{I}}_{m \times m}}{{Be}}(t)) \end{array} $

根据引理3和引理4可以得到：

$\begin{array}{c} {{\hat v}}{(t)^{\rm{T}}}\left[ {2\beta {\bar{ L}} - 2{{{I}}_{N \times N}}} \right] \otimes {{{I}}_{m \times m}}{{\hat v}}(t) =\\ {{\hat v}}{(t)^{\rm{T}}}\left[ {2\beta {\bar{ L}}} \right] \otimes {{{I}}_{m \times m}}{{\hat v}}(t) - 2{{\hat v}}{(t)^{\rm{T}}}{{{I}}_{N \times N}} \otimes {{{I}}_{m \times m}}{{\hat v}}(t) \geqslant \\ ({{\textit{λ}}_{\min }}(2\beta {\bar{ L}}) - 2){\left\| {{{\hat v}}(t)} \right\|^2} \end{array} $

所以

$\begin{array}{c} \dot V(t) \leqslant - {{\textit{λ}}_{\min }}(2\alpha {\bar{ L}}){\left\| {{{\hat x}}(t)} \right\|^2} + ({\left\| {{{\hat x}}(t)} \right\|^2} + {\left\| {{{\hat v}}(t)} \right\|^2}) -\\ ({{\textit{λ}}_{\min }}(2\beta {\bar{ L}}) - 2){\left\| {{{\hat v}}(t)} \right\|^2}- [{{\hat x}}{(t)^{\rm{T}}}\alpha ({{L}} + {{H}}) \otimes {{{I}}_{m \times m}}({{{e}}_x}(t)+ \\ {{{e}}_v}(t))+ {{\hat v}}{(t)^{\rm{T}}}\alpha ({{L}} + {{H}}) \otimes {{{I}}_{m \times m}}({{{e}}_x}(t) + {{{e}}_v}(t))] \end{array} $

那么

$\begin{array}{c} \dot V(t) \leqslant - {{\textit{λ}} _{\min }}(2\alpha {\bar{ L}}){\left\| {{{\hat x}}(t)} \right\|^2} + ({\left\| {{{\hat x}}(t)} \right\|^2} + {\left\| {{{\hat v}}(t)} \right\|^2}) - \\ ({{\textit{λ}}_{\min }}(2\beta {\bar{ L}}) - 2){\left\| {{{\hat v}}(t)} \right\|^2} - 2g({{\hat x}}(t),{{\hat v}}(t),{{{e}}_x}(t),{{{e}}_v}(t)) \\ \end{array} $

其中

$\begin{array}{c} g({{\hat x}}(t),{{\hat v}}(t),{{{e}}_x}(t),{{{e}}_v}(t)) = \\ \displaystyle\sum\limits_{i = 1}^n {{{\hat x}_i}(t)\left[\alpha \left(\displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}} \otimes {{{I}}_{m \times m}}({e_{xi}}(t) - {e_{xj}}(t))} + {a_{i0}} \otimes {{{I}}_{m \times m}}{e_{xi}}(t)\right)\right]} + \\ \displaystyle\sum\limits_{i = 1}^n {{{\hat x}_i}(t)\left[\beta \left(\displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}} \otimes {{{I}}_{m \times m}}({e_{vi}}(t) - {e_{vj}}(t))} + {a_{i0}} \otimes {{{I}}_{m \times m}}{e_{vi}}(t)\right)\right]} + \\ \displaystyle\sum\limits_{i = 1}^n {{{\hat v}_i}(t)\left[\alpha \left(\displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}} \otimes {{{I}}_{m \times m}}({e_{xi}}(t) - {e_{xj}}(t))} + {a_{i0}} \otimes {{{I}}_{m \times m}}{e_{xi}}(t)\right)\right]} + \\ \displaystyle\sum\limits_{i = 1}^n {{{\hat v}_i}(t)\left[\beta \left(\displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}} \otimes {{{I}}_{m \times m}}({e_{vi}}(t) - {e_{vj}}(t))} + {a_{i0}} \otimes {{{I}}_{m \times m}}{e_{vi}}(t)\right)\right]} \end{array} $

令

$\delta {\rm{ = max\{ inf}}\{ {{\textit{λ}}_{\min }}(2\alpha {\bar{ L}}) - 1,({{\textit{λ}}_{\min }}(2\beta {\bar{ L}}) - 2) - 1\} ,1{\rm{\} }}$

又因为

$\begin{array}{c} \;\; - 2g({{\hat x}}(t),{{\hat v}}(t),{{{e}}_x}(t),{{{e}}_v}(t)) =\\ - {\rm{2}}\displaystyle\sum\limits_{i = 1}^N {({{\hat x}_i}(t) + {{\hat v}_i}(t))\displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}} \otimes {{{I}}_{m \times m}}[\alpha ({e_{xi}}(t) - {e_{xj}}(t))} }+ \\ \beta ({e_{vi}}(t) - {e_{vj}}(t)) + {a_{i0}} \otimes {{{I}}_{m \times m}}(\alpha {e_{xi}}(t) + \beta {e_{vi}}(t))] \leqslant \\ \displaystyle\sum\limits_{i = 1}^N {[({{\left\| {{{\hat x}_i}(t)} \right\|}^2} + {{\left\| {{{\hat v}_i}(t)} \right\|}^2})} + \\ \sqrt m \cdot \displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}}[\alpha ({{\left\| {{e_{xi}}(t)} \right\|}^2} + {{\left\| {{e_{xj}}(t)} \right\|}^2})}+ \\ \beta ({\left\| {{e_{vi}}(t)} \right\|^2} + {\left\| {{e_{vj}}(t)} \right\|^2}) + {a_{i0}}(\alpha {\left\| {{e_{xi}}(t)} \right\|^2} + \beta {\left\| {{e_{vi}}(t)} \right\|^2})]] \end{array} $

所以

$\begin{array}{c} \dot V(t) \leqslant \displaystyle\sum\limits_{i = 1}^N {[ - \delta ({{\left\| {{{\hat x}_i}(t)} \right\|}^2} + {{\left\| {{{\hat v}_i}(t)} \right\|}^2}) + ({{\left\| {{{\hat x}_i}(t)} \right\|}^2} + {{\left\| {{{\hat v}_i}(t)} \right\|}^2})} + \\ \sqrt m \cdot \displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}}[\alpha ({{\left\| {{e_{xi}}(t)} \right\|}^2} + {{\left\| {{e_{xj}}(t)} \right\|}^2})} + \\ \beta ({\left\| {{e_{vi}}(t)} \right\|^2} + {\left\| {{e_{vj}}(t)} \right\|^2}) + {a_{i0}}(\alpha {\left\| {{e_{xi}}(t)} \right\|^2} + \beta {\left\| {{e_{vi}}(t)} \right\|^2})]] \\ \end{array} $

取 $0 < {\theta _i} < 1$ ，使得：

$\begin{array}{c} - {\theta _i}(\delta - 1)({\left\| {{{\hat x}_i}(t)} \right\|^2} + {\left\| {{{\hat v}_i}(t)} \right\|^2}) + \sqrt m \cdot \displaystyle\sum\limits_{j \in {N_i}} {{a_{ij}}[\alpha ({{\left\| {{e_{xi}}(t)} \right\|}^2}} + \\ {\left\| {{e_{xj}}(t)} \right\|^2}) + \beta ({\left\| {{e_{vi}}(t)} \right\|^2} + {\left\| {{e_{vj}}(t)} \right\|^2}) + {a_{i0}}(\alpha {\left\| {{e_{xi}}(t)} \right\|^2} + \\ \beta {\left\| {{e_{vi}}(t)} \right\|^2})] \leqslant 0 \\ \end{array} $

所以将触发函数 ${f_i}(t)$ 设计为如下形式：

$\begin{aligned} & \qquad\,\, {f_i}({{\hat x}_i}(t),{{\hat v}_i}(t),{e_{xi}}(t),{e_{xj}}(t),{e_{vi}}(t),{e_{vj}}(t))= \\ & \qquad \quad \sqrt m \cdot \sum\limits_{j \in {N_i}} {{a_{ij}}[\alpha ({{\left\| {{e_{xi}}(t)} \right\|}^2} + {{\left\| {{e_{xj}}(t)} \right\|}^2})} + \\ & \beta ({\left\| {{e_{vi}}(t)} \right\|^2} + {\left\| {{e_{vj}}(t)} \right\|^2}) + {a_{i0}}(\alpha {\left\| {{e_{xi}}(t)} \right\|^2} + \beta {\left\| {{e_{vi}}(t)} \right\|^2})]- \\ & \qquad \qquad \quad {\theta _i}(\delta - 1)({\left\| {{{\hat x}_i}(t)} \right\|^2} + {\left\| {{{\hat v}_i}(t)} \right\|^2}) \end{aligned} $

对于第 $i$ 个跟随者自主体，如果有 ${f_i}({\hat x_i}(t),{\hat v_i}(t),$ ${e_{xi}}(t),{e_{xj}}(t),{e_{vi}}(t),{e_{vj}}(t)) \geqslant {\rm{0}} $ ，那么第 $k = 0,1,2, \cdots ,n$ 个条件触发，此时获取系统的位置和速度状态。

由 ${\rm{Lyapunov}}$ 稳定性理论可知，当事件触发条件式(8)满足时对于任意的初始位置状态 ${\hat x_i}(t){|_{t = {t_0}}}$ 和速度状态 ${\hat v_i}(t){|_{t = {t_0}}}$ ， $\dot V(t) \leqslant 0$ ，二阶微分方程式(7)的解都可以满足 $\mathop {\lim }\limits_{t \to \infty } \left| {{{\hat x}_i}(t)} \right| = 0$ ， $\mathop {\lim }\limits_{t \to \infty } \left| {{{\hat v}_i}(t)} \right| = 0$ 那么表明 $\mathop {\lim }\limits_{t \to \infty } \left| {{x_i}(t) - {x_0}(t)} \right| = 0$ ， $\mathop {\lim }\limits_{t \to \infty } \left| {{v_i}(t) - {v_0}(t)} \right| = 0$ 。因此，根据定义1可以知道系统式(1)、(2)达成了领导跟随一致性。

于事件触发条件式(8)是分布式的，任意的两个自主体的事件触发时刻可以是不相同的。如果 ${f_i}(t) < 0$ 事件触发，系统提取自身及其邻居的状态来更新控制器。

如果芝诺现象产生则认为我们设计的事件触发函数是不可行的。为了证明系统在运行过程中不会被触发无数次，下面计算任意两次事件触发的最小间隔。

定理2　考虑带有一个领导者的多自主体系统式 (1)、(2)，如果领导者作为图 ${\bar{ G}}$ 中的一个全局可达点，应用一致性协议式(3)和分布式事件触发函数式(7)，则系统式 (1)、(2)中的任意一个自主体 $q$ ，得到的所有的触发时刻为 ${\tau _0},{\tau _1}, \cdots ,{\tau _k},{\tau _{k + 1}}$ ，它的触发时刻的间隔 $t_{s + 1}^q - t_s^q$ ，( $s = 0,1, \cdots ,k$ )≥ ${\tau _q}$ ， $ {\tau _q}$ 为

${\tau _q} = \frac{{\sqrt {{\theta _q}(\delta - 1)} \cdot \sup {{\{ \left\| {{A}} \right\|,\left\| {{B}} \right\|\} }^{ - 1}}}}{{\sqrt {\alpha + \beta } (\left\| {{\varGamma }} \right\| + \left\| {{{HD}}} \right\|) + \sqrt {{\theta _q}(\delta - 1)} }}$

(9)

式中： ${{\varGamma }}{\rm{ = diag}}\{ {\varGamma _i}\} $ ， ${\varGamma _i}$ 为矩阵 ${{D}} + {{A}}$ 的第 $i$ 行元素绝对值的和； $\delta {\rm{ = max\{ inf}}\{ {{\textit{λ}} _{\min }}(2\alpha {\bar{ L}}) - 1,({{\textit{λ}} _{\min }}(2\beta {\bar{ L}}) - 2)-1\} , $ $ 1{\rm{\} }} $ ； $0 < {\theta _i} < 1$ ， $i = 1,2, \cdots ,N$ 。

证明　构造 $\dfrac{{\left\| {{{e}}(t)} \right\|}}{{\left\| {{{\xi }}(t)} \right\|}}$ 的动态方程：

$\begin{aligned} & \frac{{\rm{d}}}{{{\rm{d}}t}}\left(\frac{{\left\| {{{e}}(t)} \right\|}}{{\left\| {{{\xi }}(t)} \right\|}}\right) = \frac{{\rm{d}}}{{{\rm{d}}t}}\frac{{{{({{e}}{{(t)}^{\rm{T}}}{{e}}(t))}^{\frac{1}{2}}}}}{{{{({{\xi }}{{(t)}^{\rm{T}}}{{\xi }}(t))}^{\frac{1}{2}}}}}= \\ & \frac{{{{e}}{{(t)}^{\rm{T}}}{{\dot e}}(t)}}{{\left\| {{{\xi }}(t)} \right\|\left\| {{{e}}(t)} \right\|}} - \frac{{\left\| {{{e}}(t)} \right\|{{\xi }}{{(t)}^{\rm{T}}}{{\dot \xi }}(t)}}{{{{\left\| {{{\xi }}(t)} \right\|}^3}}} \end{aligned} $

当 $t \in \left[ {{t_k},{t_{k + 1}}} \right)$ 时， ${{e}}(t) = {{\xi }}({t_k}) + {{\xi }}(t)$ ，所以 ${{\dot e}}(t) = {{\bf{0}}} - $ ${{\dot \xi }}(t) $ 。又因为 ${{\dot \xi }}(t) = {{A\xi }}(t) + {{Be}}(t)$ ，令 $\varphi (t)=\dfrac{{\left\| {{{e}}(t)} \right\|}}{{\left\| {{{\xi }}(t)} \right\|}}$ ，可以得到不等式： $\dot \varphi (t) \leqslant {(1 + \varphi (t))^2} \cdot \sup \{ \left\| {{A}} \right\|,\left\| {{B}} \right\|\} ,$ 如果 $\varphi (t)$ 满足 $\varphi (t) \leqslant \phi (t,{\phi _{{t_0}}})$ ，当且仅当 $\phi (t,{\phi _{{t_0}}})$ 是 $\dot \varphi (t) \leqslant {(1 + \varphi (t))^2} \cdot \sup \{ \left\| {{A}} \right\|,\left\| {{B}} \right\|\} $ ， $\phi (0,{\phi _{{t_0}}})$ 的解。当 $ t \in$ $ [t_s^q,t_{s + 1}^q)$ 时，解微分方程 ${\rm{d}}\varphi(t)={{(1 + \varphi (t))^2} \cdot \sup }\{ \left\| {{A}} \right\|,$ $\left\| {{B}} \right\|\} ){\rm{d}}t $ 可得：

$\varphi (t) \leqslant \frac{{\sup \{ \left\| {{A}} \right\|,\left\| {{B}} \right\|\} \cdot t - {C_1} + 1}}{{ - \sup \{ \left\| {{A}} \right\|,\left\| {{B}} \right\|\} \cdot t + {C_1}}}$

当 $t = 0$ 时触发时间将取得最小值，代入式(10)， ${C_1} = 1$ 。令 ${{\varGamma }}={\rm{diag}}\{ {\varGamma _i}\} (i = 1,2, \cdots ,n)$ ，其中 ${\varGamma _i}$ 为矩阵 ${{D}} + {{A}}$ 的第 $i$ 行元素绝对值的行和。所以

$\begin{aligned} & \sum\limits_i^n {\sum\limits_{j \in {N_i}} {{a_{ij}}[\alpha ({{\big|\big| {{e_{xi}}(t)} \big|\big|}^2} + {{\left\| {{e_{xj}}(t)} \right\|}^2}) + \beta ({{\big|\big| {{e_{vi}}(t)} \big|\big|}^2} + {{\left\| {{e_{vj}}(t)} \right\|}^2})} } + \\ & \qquad\qquad\qquad{a_{i0}}(\alpha {\left\| {{e_{xi}}(t)} \right\|^2} + \beta {\left\| {{e_{vi}}(t)} \right\|^2})] \leqslant \\ & \qquad\qquad{\left\| {\left[ {\alpha {{\varGamma }},\beta {{\varGamma }}} \right]e(t) + {{HD}}[\alpha ,\beta ] \otimes {{{I}}_{N \times N}}e(t)} \right\|^2} \leqslant \\ & \qquad\qquad\,\,\,\,\,\,{\left\| {\left[ {\alpha {{\varGamma }},\beta {{\varGamma }}} \right] + {{HD}}[\alpha ,\beta ] \otimes {{{I}}_{N \times N}}} \right\|^2} \cdot {\left\| {e(t)} \right\|^2} \end{aligned} $

令

$q = \arg \mathop {\max }\limits_{i \in N} {\rm{(}}{\left\| {{{\hat x}_i}(t)} \right\|^2}{\rm{ + }}{\left\| {{{\hat v}_i}(t)} \right\|^2}{\rm{)}}$

则

$\begin{aligned} & N\sum\limits_{j \in Nq} {{a_{ij}}\Big[\alpha ({{\left\| {{e_{xq}}(t)} \right\|}^2} + {{\left\| {{e_{xj}}(t)} \right\|}^2}) + \beta ({{\left\| {{e_{vq}}(t)} \right\|}^2} + {{\left\| {{e_{vj}}(t)} \right\|}^2})} + \\ & \,\,\,\,{a_{i0}}(\alpha {\left\| {{e_{xq}}(t)} \right\|^2} + \beta {\left\| {{e_{vq}}(t)} \right\|^2})\Big] \cdot {(N{\rm{(}}{\left\| {{{\hat x}_q}(t)} \right\|^2}{\rm{ + }}{\left\| {{{\hat v}_q}(t)} \right\|^2}{\rm{)}})^{ - 1}} \leqslant \\ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{{{\left\| {\left[ {\alpha {{\varGamma }},\beta {{\varGamma }}} \right] + {{HD}}[\alpha ,\beta ] \otimes {{{I}}_{N \times N}}} \right\|}^2} \cdot {{\left\| {{{e}}(t)} \right\|}^2}}}{{{{\left\| {{{\xi }}(t)} \right\|}^2}}} \end{aligned} $

因此

$\sqrt {\alpha + \beta } (\left\| {{\varGamma }} \right\| + \left\| {{{HD}}} \right\|)\phi ({\tau _q},0)=\sqrt {{\theta _q}(\delta - 1)} $

解得触发间隔的最小值为

${\tau _q} = \frac{{\sqrt {{\theta _q}(\delta - 1)} \cdot \sup {{\{ \left\| {{A}} \right\|,\left\| {{B}} \right\|\} }^{ - 1}}}}{{\sqrt {\alpha + \beta } (\left\| {{\varGamma }} \right\| + \left\| {{{HD}}} \right\|) + \sqrt {{\theta _q}(\delta - 1)} }}$

证毕。

3 计算机仿真

在这一部分，将利用计算机仿真来验证控制算法和事件触发函数。仿真实验中共有6个 ${\rm{Follower}}$ 和1个 ${\rm{Leader}}$ ，该系统如图1所示的拓扑结构，那么相应的 ${\rm{Laplacian}}$ 矩阵如下：

${{L}} = \left[ {\begin{array}{*{20}{c}} 1&0&{ - 1}&0&0&0 \\[0.5pt] 0&1&{ - 1}&0&0&0 \\[0.5pt] { - 1}&{ - 1}&3&{ - 1}&0&0 \\[0.5pt] 0&0&{ - 1}&2&{ - 1}&0 \\[0.5pt] 0&0&0&{ - 1}&0&{ - 1} \\[0.5pt] 0&0&0&0&{ - 1}&1 \end{array}} \right]$

领导跟随矩阵为

${{H}}{\rm{ = diag\{ 1\,\,\,\, 0\,\,\,\, 0\,\,\,\, 1\,\,\,\, 1\,\,\,\, 0\} }}$

本文考虑多自主体系统在二维平面内的运动的情况。根据在定理1中给出的限制条件，选取 $\alpha =1.500$ ， $\beta {\rm{ = 2}}{\rm{.000}}$ ， ${\theta _i}=0.0{\rm{15\,\,18}} \in {\rm{(0,1)}}$ ，所以在 $\alpha $ 、 $\beta $ 给定的情况下 $\delta $ 取1.591 2。在仿真过程中时长为20 s，采样间隔为 $2.5 \times {10^{ - 3}}$ s，共有 $8 \times {10^3}$ 个采样点。给出自主体的初始状态分别为：

${{{x}}_1}({t_0}) = {[{\rm{0}}\,\,\,\, {\rm{6}}{\rm{.002]}}^{\rm{T}}}$ ， ${{{x}}_2}({t_0}) = {[{\rm{0}}\,\,\,\, {\rm{2}}{\rm{.123]}}^{\rm{T}}}$ ，

${{{x}}_3}({t_0}) = {[{\rm{0}}\,\,\,\, {\rm{12}}{\rm{.915]}}^{\rm{T}}}$ ， ${{{x}}_4}({t_0}) = {[{\rm{0}}{\rm{.204}} \,\,\,\,0{\rm{]}}^{\rm{T}}}$ ，

${{{x}}_5}({t_0}) = {[{\rm{12}}{\rm{.978}}\,\,\,\, {\rm{0]}}^{\rm{T}}}$ ， ${{{x}}_6}({t_0}) = {[{\rm{8}}{\rm{.293}} \,\,\,\,0{\rm{]}}^{\rm{T}}}$ 。

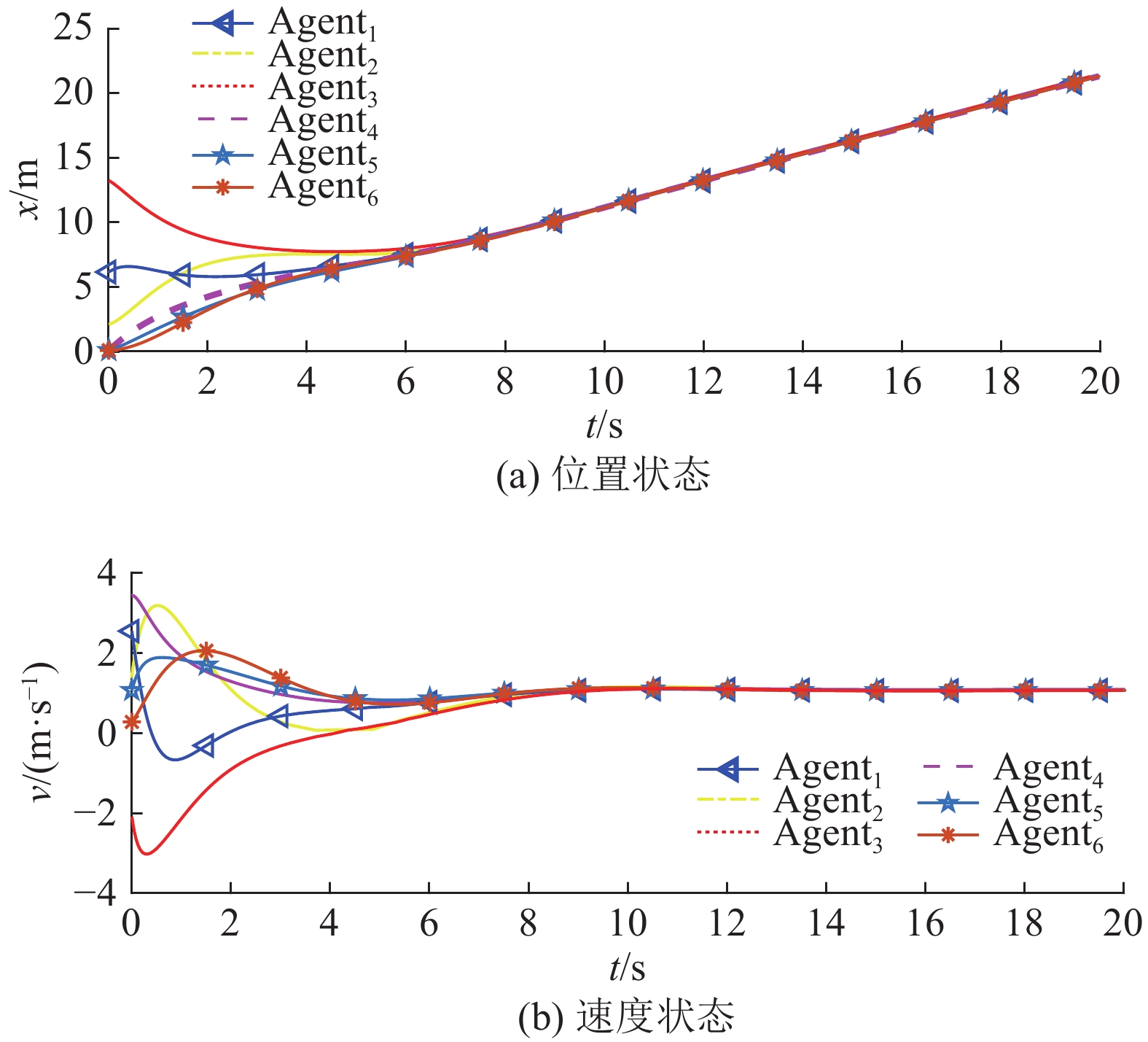
按照给出的控制器来调控系统得到如图2和图3所示的在两个方向上的位置和速度状态，可见多自主体系统逐渐达到一致。

表1分别给出了在分布式事件触发机制下，多自主体系统在20 s内触发器的触发次数，由表中数据可以看出采用本文的控制协议可以极大降低自主体的采样次数。

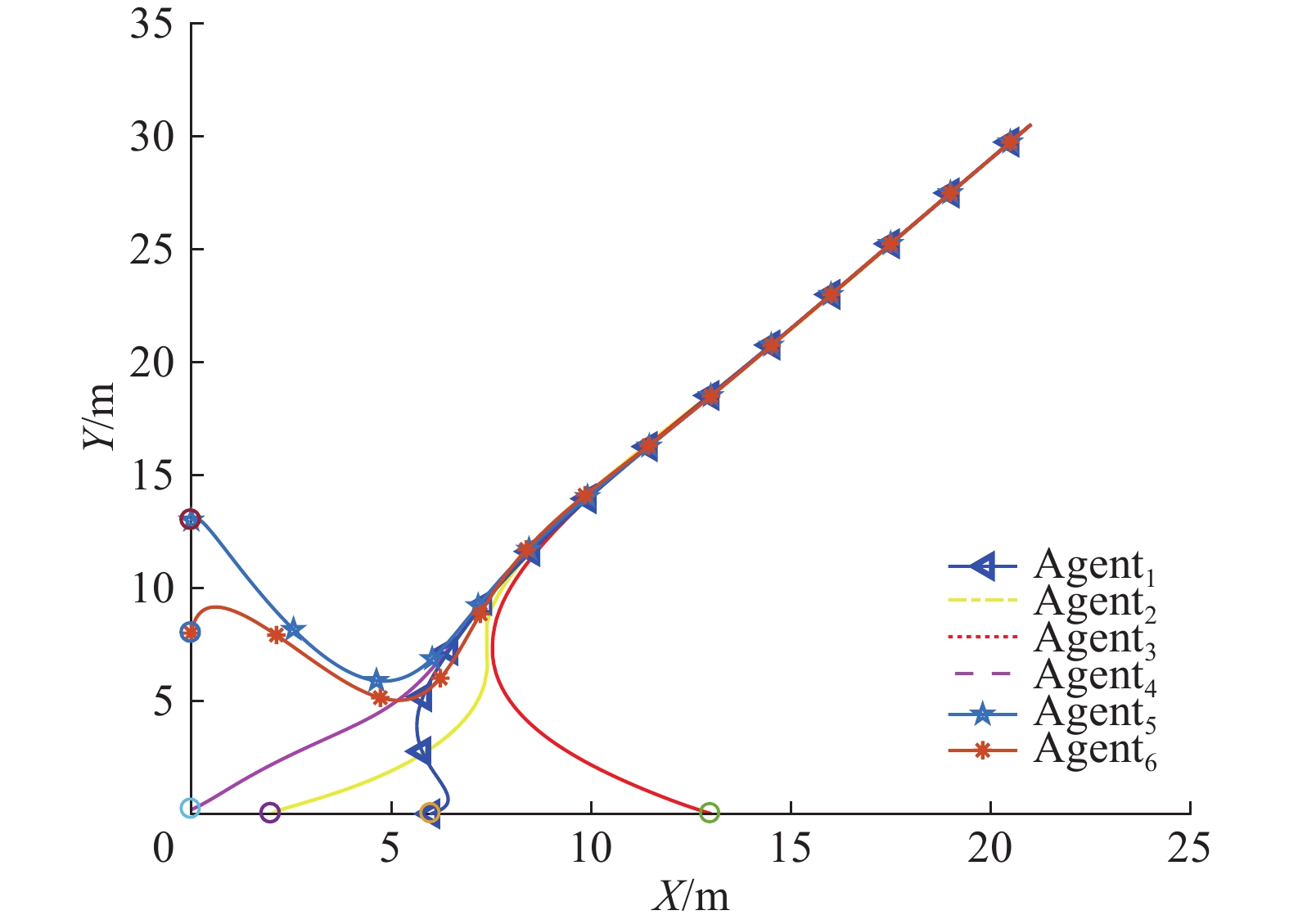
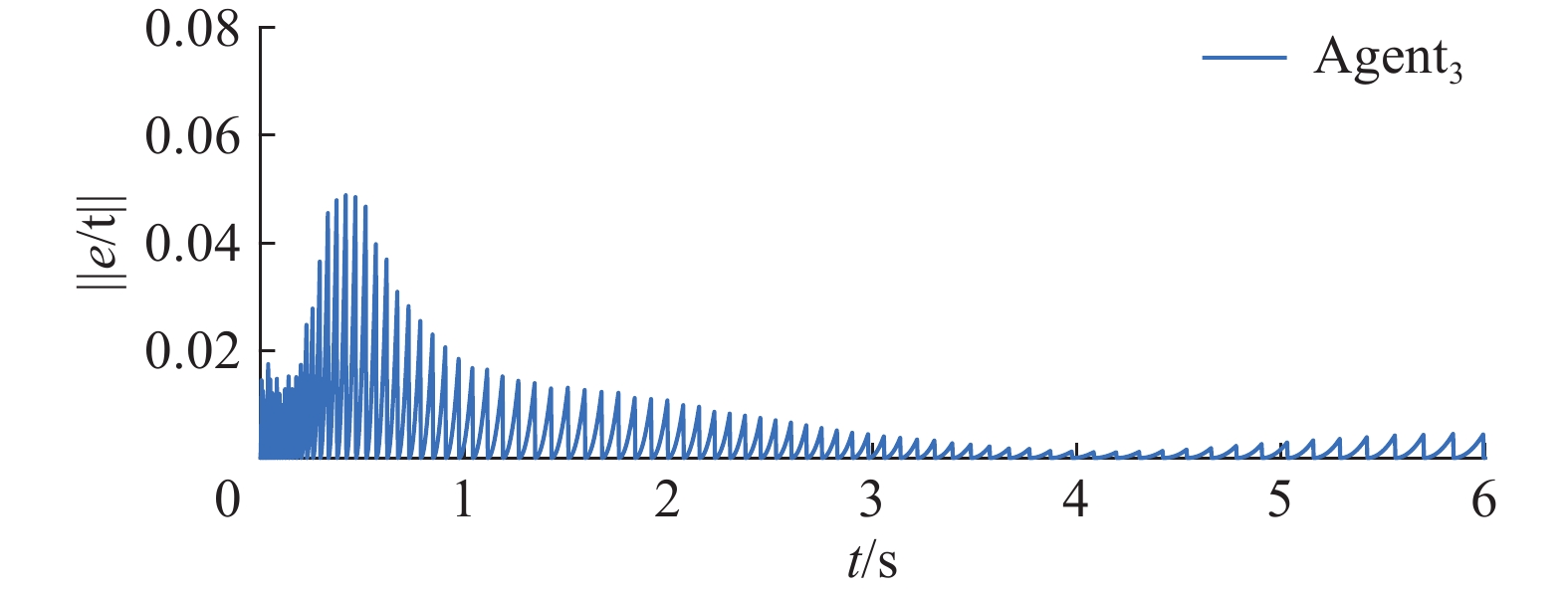
图4描述了6个自主体在平面内的位置信息，从图中可以看到随着时间的推移，最后自主体的运动轨迹实现了一致。图5显示了其中一个自主体每个触发时刻的系统误差，从图中可以看出在初始阶段触发间隔小且误差范数的值相当大，且触发时刻密集，直到整个系统渐渐稳定触发器的触发间隔才会变大，幅值不断减小且触发间隔变得稀疏。

基于以上的仿真结果，本文给出一致性控制算法和分布式事件触发函数可以确保在固定拓扑下多自主体系统实现领导跟随一致性。

4 结束语

本文针对二阶多自主体系统设计了一种分布式事件触发机制的控制算法。通过定义跟随者与领导者之间的偏差向量将二阶微分系统转化为二阶闭环系统的稳定性问题，并运用图论、矩阵论和 ${\rm{Lyapunov}}$ 稳定性理论等对其进行了分析，并给予了仿真验证。下一步工作将研究带有外部扰动的动态多自主体系统的事件触发机制的一致性。