特征提取(或降维)[1-3]在计算机视觉和模式识别领域起着非常重要的作用,它通过把原始数据投影到低维空间而得到最具代表性的特征,其中主成分分析(PCA)[4]和线性判别分析(LDA)[5]是两个最著名的算法,但是它们很难确定数据的流形结构。
为获得数据的局部结构,出现了许多基于图的降维算法[6-12],包括局部保持投影(LPP)[6]、边缘判别分析(MFA)[7]和局部判别嵌入(LDE)[8]等。LPP是一种无监督学习算法,它忽视了数据的判别结构;而MFA和LDE则是有监督学习,它们试图找到一个投影子空间,在该子空间中同类样本点相互靠近,而不同类样本点相互分离,因此它们不仅考虑了数据的邻域结构同时也考虑了数据的判别结构。在基于图的流形学习中,关键是如何通过构造图来获得数据的本质结构。图的构造通常包括两步:第一步是决定样本间的近邻关系,第二步是为每对样本设置权重。通常,可通过
基于协同表示的分类(CRC)[13]近年来得到了广泛而深入的研究,它使用所有的训练样本来协同表示测试样本,其表示系数描述了相应训练样本对测试样本的贡献,再依据残差对样本进行分类。Yuan等[14]提出了基于分类的协同竞争表示(CCRC),在计算各训练样本表示系数的同时确定每类训练样本的竞争能力,从而实现对样本的分类,该算法能很好地权衡训练样本的协同表示和竞争表示之间的关系。Huang等[15]提出了基于协同表示的局部判别投影(CRLDP),它利用协同表示获得表示系数构造样本的关系图,克服了近邻参数设置难的问题。Yang等[16]给出的基于协同表示的投影(CRP)是通过L2范数最小化问题求表示系数,但是CRP是无监督的。为了充分地利用标签信息来提高分类性能,Hua等[17]又提出了基于协同表示重构的投影(CRRP),虽然该算法是有监督的,但是它仅使用了全局信息而忽略了各类别之间的竞争性。
在以上基于CRC的学习算法中,表示系数有正有负,其中正表示系数描述了训练样本对测试样本的正面作用,对重构样本呈正相关性,而负系数则起着负面作用,对重构样本呈负相关性。由于正表示系数可以提取样本的主要特征,且具有一定的判别能力,故本文利用正表示系数来构造类间图和类内图,然后在考虑每类样本的竞争性以及样本标签信息的基础上,给出一种基于竞争性协同表示的局部判别投影特征提取(CCRLDP)。该算法不仅考虑了样本间的协同能力和每类样本的竞争性,还利用了样本的类别信息,因此可在一定程度上提高识别效率。
1 协同分类与局部判别算法给定一组样本
CRC(collaborative representation based classification)的目标是使用所有的训练样本来协同地表示测试样本,其表示系数可通过以下优化问题求得:
| $\mathop {\min }\limits_{\rm{\alpha}} ||{{y}} - {{X\alpha }}||_2^2 + {\textit{λ}} ||{{\alpha }}||_2^2$ | (1) |
式中:
在LDE(local discriminant embedding)中,
| $ {{{W}}_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\exp [ - ||{{{x}}_i} - {{{x}}_j}|{|^2}/t]},\;\;{{l_i} = {l_j},{{{x}}_i} \in {{{N}}_w}({{{x}}_j}){\text{或}}}\\ \qquad\qquad\qquad\qquad{{{{x}}_j} \in {{{N}}_w}({{{x}}_i})}\\ 0,\;\;{{\text{其他}}} \end{array}} \right. $ | (2) |
式中:
| $ {{W'}}_{ij}= \left\{ {\begin{array}{*{20}{l}} {\exp [ - ||{{{x}}_i} - {{{x}}_j}|{|^2}/t]},\;\;{{l_i} \ne {l_j},{{{x}}_i} \in {{{N}}_b}({{{x}}_j}){\text{或}}}\\ \qquad\qquad\qquad\qquad{{{{x}}_j} \in {{{N}}_b}({{{x}}_i})}\\ 0,\;\;{{\text{其他}}} \end{array}} \right. $ | (3) |
式中
| $ {S_w} = \sum\limits_{ij} {||{{{P}}^{\rm{T}}}{{{x}}_i} - {{{P}}^{\rm{T}}}{{{x}}_j}|{|^2}} {W_{ij}} = 2{\rm{tr}}\{ {{{P}}^{\rm{T}}}{{X}}({{D}} - {{W}}){{{X}}^{\rm{T}}}{{P}}\} $ | (4) |
| ${S_b} = \sum\limits_{ij} {||{{{P}}^{\rm{T}}}{{{x}}_i}} - {{{P}}^{\rm{T}}}{{{x}}_j}|{|^2}{W'_{ij}} = 2{\rm{tr}}\{ {{{P}}^{\rm{T}}}{{X}}({{D}}' - {{W}}'){{{X}}^{\rm{T}}}{{P}}\} $ | (5) |
式中:
| $\mathop {\max }\limits_{{P}} \frac{{{S_b}}}{{{S_w}}} = \frac{{{\rm{tr}}\{ {{{P}}^{\rm{T}}}{{X}}({{{D}}^{}}' - {{{W}}^{}}'){{{X}}^{\rm{T}}}{{P}}\} }}{{{\rm{tr}}\{ {{{P}}^{\rm{T}}}{{X}}({{D}} - {{W}}){{{X}}^{\rm{T}}}{{P}}\} }}$ | (6) |
在LDEP算法中,其近邻参数
为了能充分反映样本重构时不同类样本的差异性,对每个训练样本
| $ \mathop {\min }\limits_{{{{w}}_i}} \{ ||{{{x}}_i} - {{X}}{{{w}}_i}||_2^2 + {\textit{λ}}{\rm{||}}{{{w}}_i}||_2^2 + {{\textit{λ}}_1}\sum\limits_{c = 1}^C {||{{{x}}_i} - {{{X}}_c}{{w}}_i^c||_2^2} \} $ | (7) |
式中:
| ${{w}}_i^* = (1 + {{\textit{λ}} _1}){({{{X}}^{\rm{T}}}{{X}} + {\textit{λ}} {{I}} + {{\textit{λ}}_1}{{M}})^{ - 1}}{{{X}}^{\rm{T}}}{{{x}}_i}$ | (8) |
其中
| ${{M}} = \left[ {\begin{array}{*{20}{c}} {{{X}}_1^{\rm{T}}{{{X}}_1}}&0&{\cdots }&0 \\ 0&{{{X}}_2^{\rm{T}}{{{X}}_2}}&{\cdots }&0 \\ \vdots & \vdots &{}& \vdots \\ 0&0& \cdots &{{{X}}_c^{\rm{T}}{{{X}}_c}} \end{array}} \right]$ | (9) |
令系数矩阵
| $ {U_{ij}} = \left\{ {\begin{array}{*{20}{l}} {w_{ij}^*},\;{{l_i} = {l_j}{\text{且}}w_{ij}^* > 0}\\ 0,\;{{\text{其他}}} \end{array}} \right. $ | (10) |
| $ U_{ij}^{'} = \left\{ {\begin{array}{*{20}{l}} {w_{ij}^*},\;{{l_i} \ne {l_j}{\text{且}}w_{ij}^* > 0}\\ 0,\;{{\text{其他}}} \end{array}} \right. $ | (11) |
式(10)和式(11)表示保留样本间具有正相关性的系数,以此来得到两个稀疏矩阵
根据类内紧致图和类间分离图的权矩阵,定义类内紧致性和类间分离性:
| $\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {||{{{P}}^{\rm T}}{{{x}}_i} - {{{P}}^{\rm T}}{{{x}}_j}|{|^2}{U_{ij}}} } = {\rm{tr}}({{{P}}^{\rm T}}{\overline {{S}} _w}{{P}})$ | (12) |
| $\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {||{{{P}}^{\rm T}}{{{x}}_i} - {{{P}}^{\rm T}}{{{x}}_j}|{|^2}{{U'}_{ij}}} } = {\rm{tr}}({{{P}}^{\rm T}}{\overline {{S}} _b}{{P}})$ | (13) |
式中
| $ {\overline {{S}} _w} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {({{{x}}_i} - {{{x}}_j}){{({{{x}}_i} - {{{x}}_j})}^{\rm T}}{U_{ij}}} } = {{X}}({{D}} - {{H}}){{{X}}^{\rm T}} $ | (14) |
| $ {\overline {{S}} _b} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {({{{x}}_i} - {{{x}}_j}){{({{{x}}_i} - {{{x}}_j})}^{\rm T}}{{U'}_{ij}}} } = {{X}}({{D}}' - {{H}}'){{{X}}^{\rm T}} $ | (15) |
式中:
基于竞争性协同表示的局部判别投影法的目标就是找到一个最优投影矩阵,使得投影后样本的类间分离性极大而类内紧致性极小,即优化模型为
| $\mathop {\max }\limits_P \frac{{{\rm{tr}}({{{P}}^{\rm T}}{{\overline {{S}} }_b}{{P}})}}{{{\rm{tr}}({{{P}}^{\rm T}}{{\overline {{S}} }_w}{{P}})}}$ | (16) |
令
假设训练样本
1)使用PCA降维;
2)求解式(7)或由式(8)得第
3)由式(10)和式(11)得权矩阵
4)由式(14)和式(15)计算类内紧致性矩阵
5)求广义特征方程
在本文算法中,步骤2)求解
为了验证算法的性能,本节选择数据集FERET、AR和Binalpha进行实验,并将本文CCRLDP算法与LPP、CRP、CRRP、CCRC和CRLDP等算法做对比,说明该算法的有效性和优越性。
3.1 数据集FERET人脸数据集包含200个人的1 400幅人脸图像(每人有7幅图像),分别在不同光照、姿态和表情变化下采集的,每幅图像的大小为32×32。实验中,对图像加入密度为0.03的椒盐噪声。图1为样本集中部分人脸图像。

|
Download:
|
| 图 1 加椒盐噪声FERET数据集部分样本 Fig. 1 Partial sample of the FERET data set with salt and pepper noise | |
AR人脸数据集包含126人的4 000多幅人脸图像,它们分别是在不同光照、表情和部分遮挡情况下采集的。实验时随机选取40人,每人20幅图像,每幅图像的大小为32×32,并对图像分别加入大小为5×5、10×10和15×15的遮挡。图2为样本集中部分人脸图像。

|
Download:
|
| 图 2 有不同大小遮挡的AR数据集部分样本 Fig. 2 Partial sample of the AR data set with different size occlusions | |
Binalpha数据集包含10个手写数字和26个手写英文字母,总共1 404个图像,每幅图像的大小为20×16,图像中的像素值为1或0。图3为样本集的部分人脸图像。

|
Download:
|
| 图 3 Binalpha数据集部分样本 Fig. 3 Partial sample of the Binalpha data set | |
本节讨论模型中参数
| 表 1 FERET数据集参数比较 Tab.1 Comparison of the FERET data set parameters |
| 表 2 AR数据集参数比较 Tab.2 Comparison of the AR data set parameters |
| 表 3 Binalpha数据集参数比较 Tab.3 Comparison of the Binalpha data set parameters % |
由表1得,在FERET数据集上,对于不同的
另外,由表1和表3可知,随着
从上述数据集中每类随机选取L张图像作为训练样本,剩下的作为测试样本。对FERET数据集,L取5;对AR数据集,L分别取5、8、10及12;对Binalpha数据集,L分别取20、23及25。在LPP算法中近邻值取
| 表 4 加噪FERET数据集上6种算法识别率及标准差 Tab.4 Recognition rate and standard deviation of six algorithms on the noisy FERET data set |
| 表 5 Binalpha数据集上不同训练样本数时6种算法识别率及标准差 Tab.5 Recognition rate and standard deviation of six algorithms on the Binalpha data set |
由表6可见,在遮挡和训练样本数不同的情况下,CCRLDP算法的识别率均优于所有其他4种算法。在同一种遮挡之下,CRRP、CRLDP和CCRLDP这3种算法的识别率均随着训练样本数L的增大而增大;而对不同尺寸的遮挡,随着遮挡尺寸的增大,各算法的识别率在一定程度上均有所降低。CCRC是一种分类算法,直接通过测试样本求其系数,但是当输入图片的尺寸比较大时,算法的复杂度将会特别高,而且由表6可知CCRC的鲁棒性比较弱。表7给出各算法在不同数据集上的计算时间,在大多数情况下,本文算法的计算速度高于其他算法,个别算法的计算时间虽然少,但是其识别率远低于本文算法。综上考虑,本文算法优于其他对比算法。
| 表 6 AR数据集上不同大小遮挡和不同训练样本数时6种算法识别率及标准差 Tab.6 Six algorithms for recognition rate and standard deviation of different size occlusions and training samples on the AR data set % |
| 表 7 各算法在不同数据集上的计算时间 Tab.7 Calculation time of each algorithm on different data sets |
图4中描述了除CCRC算法之外其他5种不同算法在各数据集上的平均识别率随特征子空间维数变化而变化的曲线(因为CCRC直接对测试集原数据进行分类,没有涉及特征的提取,即不存在维度变化问题)。随着特征维数的增加,各算法的识别率也在逐渐上升,对于大多数数据集来说,在第20维之后,CCRLDP趋于平稳,性能比较稳定;虽然CRLDP和CRRP均使用协同表示重构来表示类间分离性和类内紧致性的有监督学习算法,但CRLDP考虑了相同标签样本的局部紧致性和不同标签样本的局部分离性,具有一定的判别结构,因此其性能高于CRRP;CRP和LPP均为无监督学习算法,但LPP需要手动构造图,不能有效选择数据的本质结构,所以LPP算法性能次于CRP;另外,CRRP能充分地利用样本的标签信息,故其性能优于LPP。
总之,CCRLDP既考虑了数据的局部结构,又充分地利用了样本的标签信息,因此在构造局部结构图时不需要手动选取k值。由于CCRLDP得到的是具有稀疏性的类间图和类内图,所以对噪声具有一定的鲁棒性,因此它具有较高的识别率。以上结果表明,该算法能提取更多具有区分能力的特征,从而能提升其识别性能。
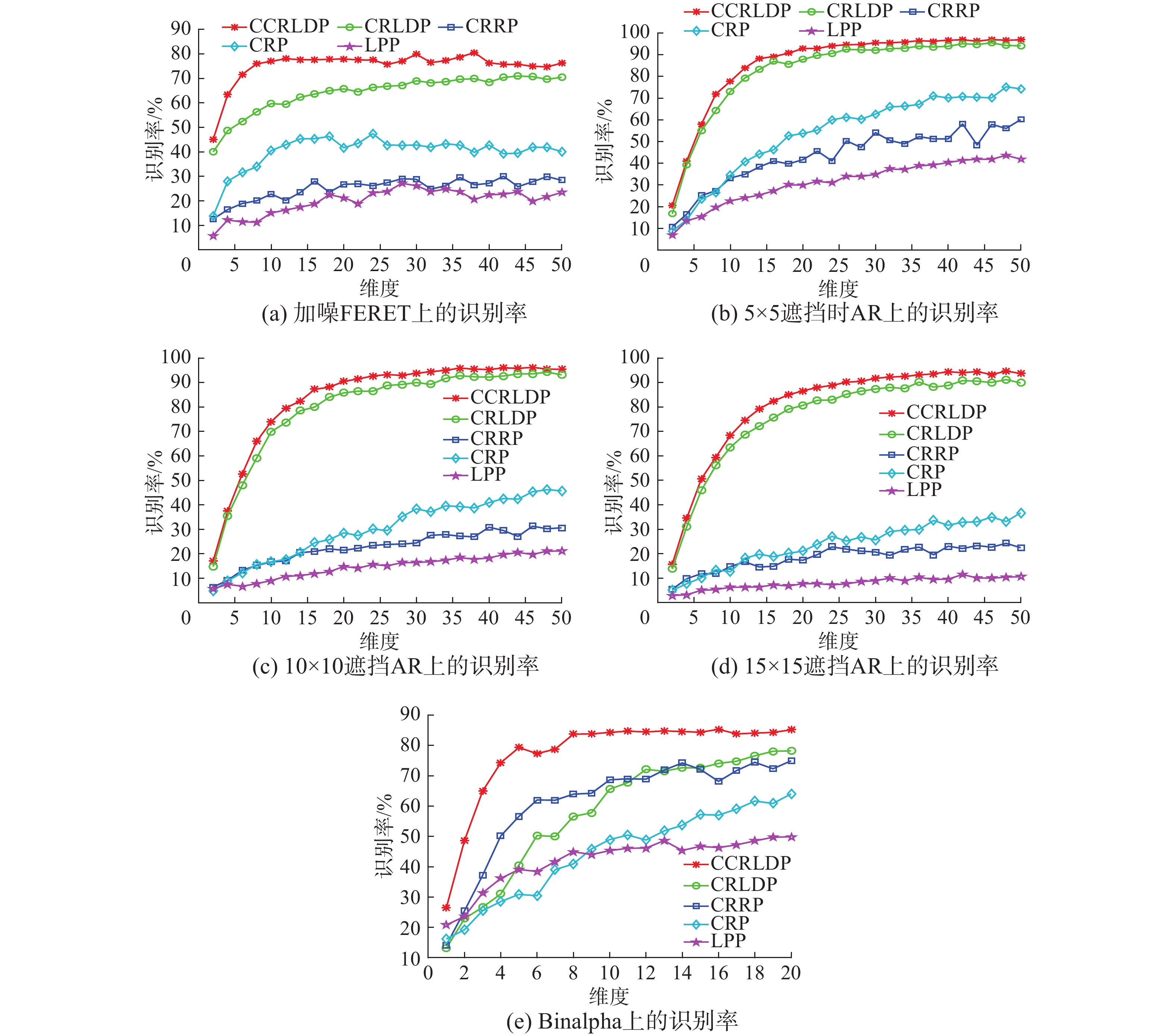
|
Download:
|
| 图 4 不同数据集上5种算法的识别率 Fig. 4 Recognition rate of five algorithms on different data sets | |
本文通过考虑不同系数在对样本重构时的表现,采用竞争性协同表示的思想来构造类间分离图和类内紧致图,提出一种有监督的特征提取算法。该算法通过计算类内紧致矩阵和类间分离矩阵来刻画图像的局部结构并得其最优投影矩阵。与经典的基于流行学习的算法相比,以上算法不仅考虑了样本间的协同表示能力和每类样本的竞争性,还强调了正系数的作用,因此可大大提高其识别效率。
| [1] |
XU Chang, TAO Dacheng, XU Chao, et al. Large-margin weakly supervised dimensionality reduction[C]//Proceedings of the 31st International Conference on Machine Learning. Beijing, China, 2014: II-865–II-873.
( 0) 0)
|
| [2] |
LI Jun, XU Chang, GONG Mingming, et al. SERVE: soft and equalized residual vectors for image retrieval[J]. Neurocomputing, 2016, 207: 202-212. DOI:10.1016/j.neucom.2016.04.047 ( 0) 0)
|
| [3] |
XIE Liping, TAO Dacheng, WEI Haikun. Joint structured sparsity regularized multiview dimension reduction for video-based facial expression recognition[J]. ACM transactions on Intelligent systems and technology, 2017, 8(2): 28. ( 0) 0)
|
| [4] |
TURK M, PENTLAND A. Eigenfaces for recognition[J]. Journal of cognitive neuroscience, 1991, 3(1): 71-86. DOI:10.1162/jocn.1991.3.1.71 ( 0) 0)
|
| [5] |
BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]. IEEE transactions on pattern analysis and machine intelligence, 1997, 19(7): 711-720. DOI:10.1109/34.598228 ( 0) 0)
|
| [6] |
HE Xiaofei, YAN Shuicheng, HU Yuxiao, et al. Face recognition using Laplacian faces[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(3): 328-340. DOI:10.1109/TPAMI.2005.55 ( 0) 0)
|
| [7] |
YAN Shuicheng, XU Dong, ZHANG Benyu, et al. Graph embedding and extensions: a general framework for dimensionality reduction[J]. IEEE transactions on pattern analysis and machine intelligence, 2007, 29(1): 40-51. DOI:10.1109/TPAMI.2007.250598 ( 0) 0)
|
| [8] |
CHEN H T, CHANG Huangwei, LIU T L. Local discriminant embedding and its variants[C]//Proceedings of IEEE computer society conference on computer vision and pattern recognition. San Diego, USA, 2005: 846−l853.
( 0) 0)
|
| [9] |
YANG Jian, ZHANG D, YANG Jingyu. Globally maximizing, locally minimizing: unsupervised discriminant projection with applications to face and palm biometrics[J]. IEEE transactions on pattern analysis and machine intelligence, 2007, 29(4): 650-664. DOI:10.1109/TPAMI.2007.1008 ( 0) 0)
|
| [10] |
HUANG Pu, CHEN Caikou, TANG Zhenmin, et al. Discriminant similarity and variance preserving projection for feature extraction[J]. Neurocomputing, 2014, 139: 180-188. DOI:10.1016/j.neucom.2014.02.047 ( 0) 0)
|
| [11] |
HUANG Pu, CHEN Caikou, ZHANG Zhenmin, et al. Feature extraction using local structure preserving discriminant analysis[J]. Neurocomputing, 2014, 140: 104-113. DOI:10.1016/j.neucom.2014.03.031 ( 0) 0)
|
| [12] |
YU Weiwei, TENG Xiaolong, LIU Chongqing. Face recognition using discriminant locality preserving projections[J]. Image and vision computing, 2006, 24(3): 239-248. DOI:10.1016/j.imavis.2005.11.006 ( 0) 0)
|
| [13] |
ZHANG Lei, YANG Meng, FENG Xiangchu. Sparse representation or collaborative representation: which helps face recognition[C]//Proceedings of International Conference on Computer Vision. Barcelona, Spain, 2012: 471−478.
( 0) 0)
|
| [14] |
YUAN Haoliang, LI Xuecong, XU Fangyuan, et al. A collaborative-competitive representation based classifier model[J]. Neurocomputing, 2018, 275(1): 627-635. ( 0) 0)
|
| [15] |
HUANG Pu, LI Tao, GAO Guangwei, et al. Collaborative representation based local discriminant projection for feature extraction[J]. Digital signal processing, 2018, 76: 84-93. DOI:10.1016/j.dsp.2018.02.009 ( 0) 0)
|
| [16] |
YANG Wankou, WANG Zhenyu, SUN Changyin. A collaborative representation based projections method for feature extraction[J]. Pattern recognition, 2015, 48(1): 20-27. DOI:10.1016/j.patcog.2014.07.009 ( 0) 0)
|
| [17] |
HUA Juliang, WANG Huan, REN Mingwu, et al. Dimension reduction using collaborative representation reconstruction based projections[J]. Neurocomputing, 2016, 193: 1-6. DOI:10.1016/j.neucom.2016.01.060 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


