标记多义性学习作为机器学习领域中一个热门方向，目前单标记学习与多标记学习已经较为成熟^[1-2]。其中多标记学习是单标记学习的拓展，许多已有的研究成果也证实了多标记学习是一种有效的学习范式^[3]。传统的多标记学习虽然可以有效地处理实例和标记之间的关系，但却将标记进行了简单的定义，即存在为“1”不存在为“−1”，忽略了标记对实例的描述有着不同重要程度这一问题，因此并不适用于真实世界中某些实例，例如人的情感分析。人的情感可以通过面部表情来表达，而面部表情往往是一种混合了多种基本情绪的综合表情，例如：惊讶和恐惧可能会同时出现，高兴和感动可能会在同一时刻表现出来；这些基本情绪共同组成了一种情绪分布，在表达的情感中各自占有不同的比重。针对这类实例，Geng等^[4]提出了一种标记分布学习范式(label distribution learning, LDL)。

基于此，为了更好地研究标记分布学习，研究者们提出了许多预测标记分布的算法。目前已有的算法主要分为3类：1)为了使用现有学习范式的相关公式定义，提出了将标记分布学习退化成单标记学习的PT-Bayes(problem transformation bayes)算法和PT-SVM(problem transformation support vector machine)算法^[5]；2)将机器学习领域相关算法引入到标记分布学习中，以提高预测精度，如AA-KNN算法(algorithm adaptation k nearest neighbors)和AA-BP算法 (algorithm adaptation back propagation)^[6]；3)为了切合标记分布学习自身的特性，而专门设计的CPNN(conditional probability neural network)算法^[7]、SA-IIS(specialized algorithms improved iterative scaling)和SA-BFGS算法(specialized algorithms broyden fletcher goldfarb shanno)^[8]。然而上述算法均未考虑样本之间联系，导致样本数目过多，计算时间过长，甚至受异常样本数据的影响使得预测精度下降。为了解决这种问题，本文考虑引入聚类方法处理。

聚类是一种无监督的处理数据并寻找内部关联的分类方式^[9]。目前聚类算法以及改进算法很多，如K-means和模糊聚类等^[10-11]。聚类对简化训练模型效果优秀，其中，张敏灵^[12]在多标记学习中对输入空间进行K-means聚类，构建类属属性，然后训练对应的分类模型；邵东恒等^[13]将K-means引入标记分布学习，取得了较好的效果。但是这些传统聚类算法依托于凸球形样本空间，并且由于采取迭代更新，算法容易陷入局部最优，同时对数据适应性也不够^[14]。为了避免传统聚类这些弊端导致算法可能不具备一般性^[15]，故而引入谱聚类方法。谱聚类近年被引入了机器学习领域，并迅速成为热点之一^[16]。谱聚类算法中最经典的算法是Ng等^[17]提出的NJW (Ng Jordan Weiss) 算法，NJW算法聚类效果也较为理想。

因此，为了解决以上传统聚类的问题，将谱聚类中NJW算法引入到标记分布学习中，提出了一种结合谱聚类的标记分布学习算法(label distribution learning with spectral clustering，SC-LDL)。特征相似的样本对应的标记分布理论上也是相似的，将这些聚类中心作为新的输入空间，可以得到新的预测标记分布。相比于已有算法，本算法考虑了样本之间的联系，并且通过谱聚类预处理后的样本数据有效减少了相似数据和异常数据对模型复杂度及预测精度的影响，相比于其他聚类算法既不限定样本空间，也不需要迭代更新，同时本文通过在12个数据集上和5个经典算法进行对比实验，证明了本文所提算法的有效性。

1 相关知识 1.1 谱聚类算法

谱聚类(spectral clustering)^[18]是一种基于谱图理论的算法，该算法是将数据聚类问题转换成寻求图的最优分割，它是一种点对聚类算法，并且适用于非凸数据^[19]。谱聚类基本步骤可以描述为：通过高斯核函数计算原始数据集对应的相似矩阵W，进而得到一个度矩阵D，之后进行拉普拉斯变换，对转换后的拉普拉斯矩阵L进行特征值分解，找出前m个特征值对应的特征向量，并将特征向量按列存储得到新的特征矩阵，对新的特征矩阵进行K-means聚类处理^[20]。谱聚类算法一经提出，其在数据降维、不规则数据聚类、图像分割等方面获得了广泛的应用。

定义1　高斯核函数。定义一个d维的欧式空间P，其中有一点 $p \in {{X}}$ ，p到某一中心点p₀之间欧氏距离的单调函数记作 $k(\left\| {p - {p_0}} \right\|)$ ，称之为核函数。高斯核函数是一种常用的核函数，定义为

${k_G}(\left\| {p - {p_{\rm{o}}}} \right\|) = \exp ( - \frac{{{{\left\| {p - {p_o}} \right\|}^2}}}{{2{\sigma ^2}}})$

(1)

式中：p属于欧式空间P；p_o为核函数中心； $\sigma $ 为函数的宽度参数。

定义2　相似矩阵。相似矩阵又称亲和矩阵，其与原矩阵特征值和特征向量相同，本文用W来表示，矩阵定义为

${{{W}}_{ij}} = \exp \left( { - \frac{{d({s_i},{s_j})}}{{2{\mu ^2}}}} \right)$

(2)

式中： ${s_i}$ 和 ${s_j}$ 表示样本数据点； $d({s_i},{s_j})$ 通常取 ${\left\| {{s_i} - {s_j}} \right\|^2}$ ；μ是预先设定的尺度因子，用来控制样本点 ${s_i}$ 和 ${s_j}$ 之间距离对 ${{{W}}_{ij}}$ 的影响。

定义3　度矩阵。将W的每行元素相加，将相加后的数值用作对角元素构建对角矩阵，称之为度矩阵，其中非对角元素取值为0。本文用D来表示度矩阵，其定义为

${{{D}}_{ij}} = \sum\limits_{i,j = 1}^n {{{{W}}_{ij}}} $

(3)

定义4　拉普拉斯矩阵。拉普拉斯矩阵主要应用在图论中，是一种用来表示图的矩阵，用L来表示，本文选取不规范拉普拉斯矩阵，其定义为

${{L}} = {{{D}}^{ - 1/2}}{{W}}{{{D}}^{ - 1/2}}$

(4)

1.2 标记分布学习

标记分布学习是一种更加贴近真实世界的分布学习范式^[21]。在传统的多标记学习中，每一个实例对应一个标记集合，其中每一个标记的描述度为“1”或“−1”。当将这种描述度用一种类似于概率分布的形式来表示，即为标记分布。一个实例对应一个标记分布的学习过程，称为标记分布学习^[22]。真实世界中的实例所对应的标记多是有重要程度之分的，标记分布学习考虑这些重要程度，并且结合概率分布理论，将标记集合通过一种概率分布的形式来表达。

定义5　在标记分布学习中，每一个用来描述实例x的标记y用 $d_x^y$ 来标注重要程度，不失一般性，可知 $d_x^y \in [0,1]$ ，且 $\sum\limits_y {d_x^y} = 1$ 。

定义6　给定标记分布学习中的训练集 ${{S}} = \left\{ {({{{x}}_1},{{{D}}_1}),({{{x}}_2},{{{D}}_2}),({{{x}}_3},{{{D}}_3}), \cdots ,({{{x}}_n},{{{D}}_n})} \right\}$ ，其中实例矩阵 ${{X}} = \left[\!\!\! {\begin{array}{*{20}{c}}{{{{x}}_1}}\;{{{{x}}_2}}\; \cdots \;{{{{x}}_n}}\end{array}}\!\!\! \right]$ ， ${{{x}}_i} \in {{\bf{R}}^d}$ 表示X中第i个实例， $i = 1,2,\cdots,n$ 。标记矩阵 ${{Y}} = \left[\!\!\! {\begin{array}{*{20}{c}}{{{{y}}_1}}\;{{{{y}}_2}}\; \cdots \;{{{{y}}_c}}\end{array}} \!\!\! \right]$ ，y_j是第j个标记， $j = 1,2, \cdots ,c$ 。训练集对应的标记分布为 ${{D}} = \left[\!\!\! {\begin{array}{*{20}{c}}{{{{D}}_1}}\;{{{{D}}_2}}\; \cdots \;{{{{D}}_n}}\end{array}} \!\!\!\right]$ ,实例x_i的标记分布为 ${{{D}}_i} = \left[ \!\!\! {\begin{array}{*{20}{c}}{d_{{x_i}}^{{y_1}}}\;{d_{{x_i}}^{{y_2}}}\; \cdots \;{d_{{x_i}}^{{y_c}}}\end{array}} \!\!\! \right]$ 。 $d_{{x_i}}^{{y_j}}$ 为标记y_j对实例x_i的描述程度。

目前的标记分布学习通过训练集S 得到条件概率 $P\left( {y|x} \right)$ ，进而得到预测标记分布。

2 结合谱聚类算法的标记分布学习算法的构造 2.1 谱聚类NJW算法

给定训练集S，将这些数据点看作图节点，相似度矩阵为 $W = \{ {W_{ij}}|1 \leqslant i \leqslant n,1 \leqslant j \leqslant n\} $ ,相似性按照式(2)来计算。根据式(3)得到一个归一化的对角矩阵D,对D进行拉普拉斯变换，根据式(4)得到归一化拉普拉斯图矩阵L。计算L的特征向量，按照从小到大排列，将前m个特征向量按列排序得到新的矩阵 ${{X'}} = \left[ {{{{x'}}_1}\;{{{x'}}_2}\; \cdots\;{{{x'}}_m}} \right] $ ，将该矩阵X′作为新的输入再进行K-means聚类，得到簇类中心C。

算法1　NJW算法

输入　预设参数σ、k，其中k值选择样本数的20%(k为聚类数目)，标记分布训练集S = $\left\{ {({{{x}}_1},{{{D}}_1}),({{{x}}_2},{{{D}}_2}),\cdots ,({{{x}}_n},{{{D}}_n})} \right\}$ ；

输出　簇类中心C。

1)利用式(1)和式(2)计算相似矩阵W；

2)通过式(3)计算度矩阵D，度矩阵主对角线上的元素 ${D_{ij}}$ 为相似矩阵W的第i行元素之和，其余元素均为0；

3)通过式(4)对度矩阵D进行拉普拉斯变换，得到变换后的矩阵L；

4)对矩阵L进行特征值分解；

5)升序排列；

6)得出前m个特征值对应的特征向量，按列存储得到新的特征矩阵 ${{X}}'$ ；

7)对矩阵 ${{X}}'$ 进行K-means聚类得到新的聚类中心；

8)初始样本点S_i划分为j个聚类，当且仅当样本矩阵的第i行被划分为第j聚类；

9)输出聚类中心C ;

10)结束。

通过NJW算法，将原有标记分布集合划分成q个不相关的簇类，其中簇类中心 ${{C}} = \left\{ {{{{c}}_1},{{{c}}_2}, \cdots ,{{{c}}_q}} \right\},$ $q = 1,2,\; \cdots ,k $ 。

2.2 结合谱聚类算法的构造过程

当使用NJW算法对样本数据聚类得到簇类中心C后，对应的标记分布划分为相应簇类，对应新的分布矩阵，命名为 ${{S}}'$ 。使用KNN分类器对 ${{S}}'$ 中的样本 $x'$ 进行分类，通过式(5)计算，得到最终预测标记分布。

$P\left( {{y_j}'|x'} \right) = \frac{1}{k}\sum\limits_{i \in {N_k}\left( x \right)} {d_{{x_i}}^{{y_j}}} $

(5)

式中： ${y_j}'$ 为 ${{S}}'$ 中标记；k为示例 $x'$ 的最近邻居数； ${{N_k}{\left( x \right)}}$ 表示S′中 $x'$ 的索引集。

算法2　结合谱聚类NJW的标记分布学习算法

输入　簇类中心 ${{C}} = \left\{ {{{{c}}_1},{{{c}}_2},\cdots,{{{c}}_q}} \right\}$ ，k值；

输出　 $P\left( {{y_j}'|x'} \right)$ 。

1)计算当前数据点和各个数据点的距离；

2)将该距离升序排列；

3)选择和当前数据点最近的k个数据点；

4)判断这k个数据点对应类别的出现频率；

5)将最高出现频率的这k个数据点对应类别作为当前数据点的预测分类；

6)结束。

3 实验与结果分析

为了验证本文SC-LDL算法有效性，选取5种经典算法在12个标准数据集上进行对比实验。相关实验结果还使用统计分析中Nemenyi检验来进一步表明算法有效性。其中Nemenyi检验是统计学中一种针对成组数据的有效检验方法。

3.1 标记分布学习评价指标

标记分布学习输出的是一个标记分布，评价算法并不能简单地用标记准确度多少来建立。根据Geng等在文献[4]中提出的对标记分布学习评价算法的建议，本实验采用了6种代表性的标记分布评价指标，分别为Chebyshev距离、Clark距离、Canberra距离、Kullback-Leibler(KL-div)散度、余弦相关系数(Cosine)和交叉相似度(Intersection)。其中，前4个指标是衡量距离的指标，后两个是相似度指标。假设有c个标记的实例，真实标记分布为 ${{D}} = [{d_1}\;{d_2}\; \cdots\;{d_c}]$ ，预测标记分布为 $\hat {{D}} = [{\hat d_1}\;$ $ {\hat d_2}\; \cdots\;{\hat d_c}]$ ，各个指标的计算公式见表1，其中↓表示该指标越低越好，而↑表示该指标越高越好。

3.2 实验数据与环境描述

实验数据：本文SC-LDL算法与5种常用经典算法进行对比，使用的12个数据集相关信息如表2。Yeast类都是在酵母菌上做实验收集到的真实数据，每个数据集中含有2 465个酵母菌基因，每个基因由24个特征表达，标记对应不同的时间点，标记分布是不同的时间点上基因表达水平。s-JAFFE和SDU_3DFE数据集是两个常用的表情数据集的拓展，其中s-JAFFE数据集中包含213张对10名日本女性模特进行人脸采集得到表情灰度图，特征向量是由Local Binary Patterns方法抽取图像特征获得的，实例中的标记分布包含了开心、难过、惊讶、害怕、生气和厌恶6种情感。SDU_3DFE数据集与s-JAFFE不同的是，它包含了2 500张表情灰度图。Movie是用户对电影评级的数据集。所有数据来自于Netflix，电影评级分5级，作为标记，用户在各个级别上的评价比例作为标记分布存在，该数据集所有特征均来自于电影相关属性的提取。

本文所有实验均在Matlab2016a中运行，硬件环境Intel® Core^TMi5-7500 3.40 GHz CPU，操作系统为Windows 10。

本文SC-LDL为了加强说服力，使用十折交叉验证来进行实验，即每次进行实验时将数据集随机分为10个部分，其中1份数据集用来测试，剩余9份作为训练数据集，总计进行10次实验，综合10次实验得到的评价指标结果求出平均值(mean)和标准差(std)。

3.3 实验结果与分析

表3~8给出了本文算法与5种对比算法在12个数据集上的实验对比结果，其中在每一个数据集上运行的最优结果用黑体表示；表格最后一行给出了6种算法的算法排位。算法排位越小，表示算法总体性能越好。

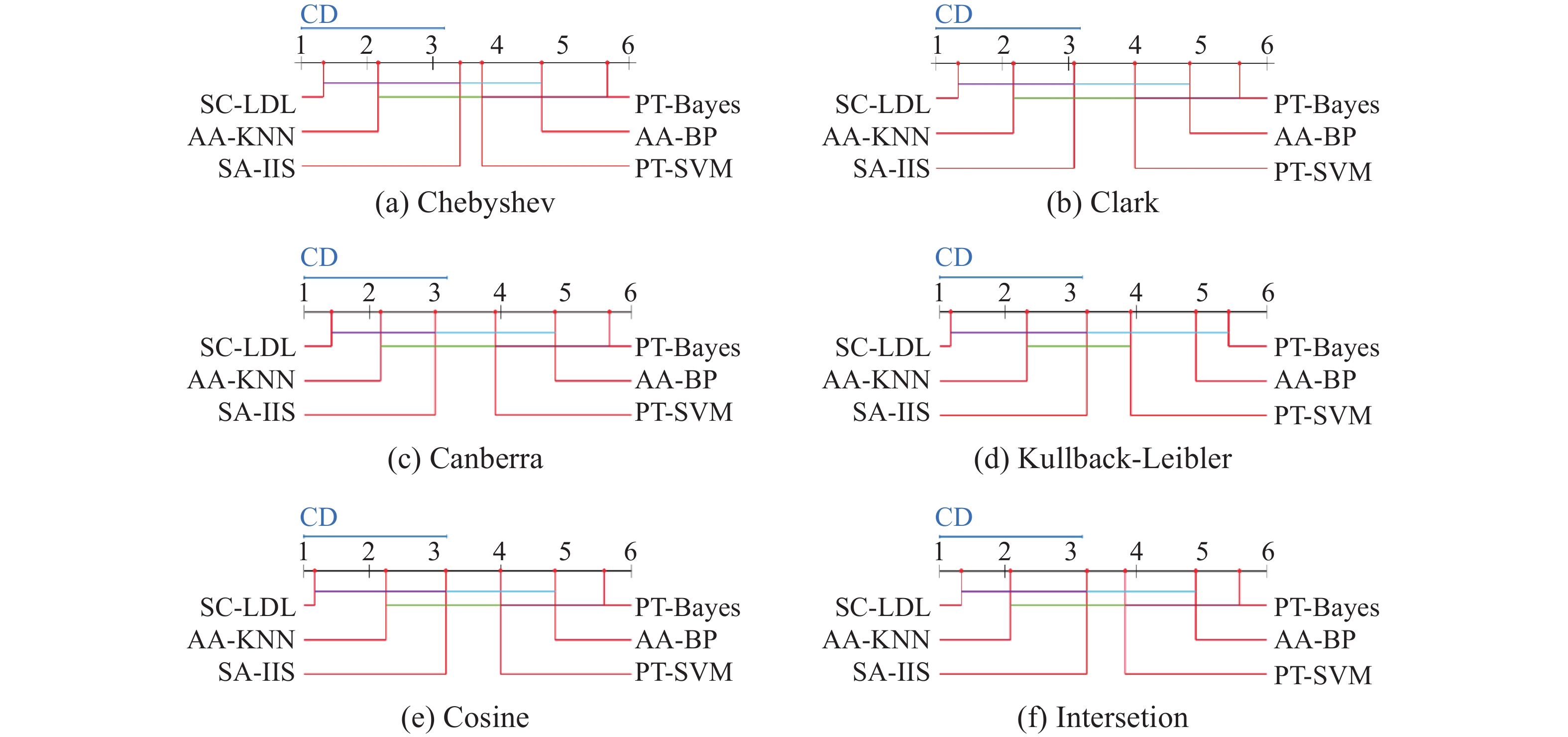
对以上6项评价指标结果进行统计检验，结果如图1所示。

实验结果分析：表2~8给出了6种算法在12个标准数据集上的6项评价指标结果，图1是实验结果的统计分析图。由表2~8分析可以得到：

1)在6项指标中，SC-LDL至少4项占优，其它2项相差也很小；

2)本实验选择的数据集中，9个数据集为酵母菌基因，2个表情数据集，1个影评，其中在酵母菌基因数据集中，SC-LDL效果均最优；

3)在样本数少，特征数多的数据集(例如s-JAFFE)中，少部分结果略优；

4)在样本数多，特征数很多的数据集(Movie)中，算法效果偏低；

5) 通过综合算法排位分析，SC-LDL总是总体最优。

图1统计分析Nemenyi检验结果均在显著性水平为5%下得出。Nemenyi检验是当两个算法的评价指标结果在平均排序中差值不大于临界值(critical difference，CD)，则说明二者无显著性差异，反之则有显著性差异。该统计分析中有5个对比算法，12个数据集，其中CD=2.176 7。在图1中，线段相连的算法表示二者的平均排序差值低于CD值，即无显著性差异，各子图中无显著性差异的算法用线段连接，可以看出，SC-LDL与大部分算法有显著性差异。这进一步说明SC-LDL具有更好的效果。

综上所述，在考虑样本相似性的前提下，将原始样本转化为图模型进行降维，在大多数据集下提升了算法精度。这说明使用谱聚类是一种有效的方式。在大样本高维特征下，由于相似度计算的复杂性及Movie数据集的稀疏性，导致算法精度偏低，这也说明了进一步研究降低相似度矩阵构造复杂性的必要性。

4 结束语

谱聚类在图像分割领域取得了较大成就，将 谱聚类引入标记分布学习是一个大胆的尝试。实验结果表明是有效的。本文提出的结合谱聚类的标记分布学习算法SC-LDL，继承了标记分布学习和谱聚类的优点，考虑数据样本之间的联系，对原始数据降维处理，减少了原有标记分布学习计算复杂度。对比现有主流算法，实验结果表明，经过约简的数据建立概率分布模型预测未知样本的标记分布精度更高，假设统计检验也证明了算法的有效性。

虽然谱聚类效果理想，但是在高维样本下计算却变得复杂，如何解决谱聚类在高维下计算复杂问题，将是未来研究重点方向。