维数约简是帮助我们理解数据特征结构的有效工具,被广泛地应用于人脸识别[1-3]、图像检索[4-5]、指纹认证[6-7]、生物信息学[8-9]、数据挖掘[10-11]等。维数约简的目标是减少冗余、不相关的信息和噪声,同时保留数据的潜在结构和本征信息。文献[12]显示,虽然随着样本维数的增加,分类器的性能会逐步上升,但是过高的维数却会使分类器的性能急剧下降,甚至造成“维数灾难”问题。因此,维数约简对于分类具有重要的意义。在过去的几十年中,针对维数约简问题出现了各种不同的解决方案和算法,其中主成分分析[13](principal component analysis,PCA)和线性判别分析[14](linear discriminant analysis,LDA)是最具代表性的两个线性降维算法。PCA的思想是最大化投影空间中样本之间的差异。LDA的目标是找到一组投影轴,使得在投影空间中同类样本尽可能靠近,而不同类样本尽可能分开。LDA是一种监督算法,充分利用了样本的类别信息来发现数据的特征结构,因此在维数约简方面通常比PCA更加有效,但是LDA不能很好地处理非线性分类问题。流形学习[15](manifold learning)是一种非线性的维数约简方法。流形算法的主要思想是学习高维空间中样本的局部邻域结构,并寻找能够保留这种流形结构的子空间,使得样本投影到子空间后有着较好的局部近邻关系。其中局部保持投影[15](locality preserving projections,LPP)就是最常见的流形学习算法之一。LPP方法得到的投影矩阵,可以使样本在投影之后保留邻域结构。
近年来,基于表示的分类方法引起了人们的广泛关注,稀疏表示分类器[16](sparse representation based classification,SRC)是最具代表性的基于表示的分类方法之一。SRC中测试样本用训练样本的稀疏线性组合来表示,然后计算测试样本与每类样本之间的重构误差,最终将测试样本分类到重构误差最小的类别。SRC表现出了良好的分类性能,但是由于SRC计算稀疏表示系数需要求解
为了防止过高的维数影响LLRC的分类性能并且保留数据的潜在结构,所以在使用原始数据时先进行降维处理。大多数的降维方法独立于分类器的决策准则,因此分类器往往不能有效地利用学习到的特征子空间。为了更好地将维数约简与特定的分类器相联系,根据分类器的决策准则来设计维数约简算法是很有必要的。于是,Huang等[19]根据LLRC的决策准则提出了局部线性回归判别分析(locality-regularized linear regression discriminant analysis,LLRDA)。LLRDA根据LLRC的决策准则分别定义了类内局部重构误差和类间局部重构误差,然后使用最大特征值分解方法求解一个迹比问题以得到最优解。然而,在LLRDA算法中,线性回归系数在原始空间进行计算并且假定系数恒定,但是实际上回归系数与投影矩阵是相关的,不是独立的,在求解目标函数的过程中投影矩阵的改变会对回归系数产生影响,所以不能假定系数恒定。另外,LLRDA的目标函数是一个迹比问题,但是为了便于处理,LLRDA将迹比问题隐式地转换成了比迹问题,并用最大特征值分解方法进行求解,因而得到的结果会与原来的目标函数存在偏差。
为了克服LLRDA的缺点,本文提出了面向局部线性回归分类器的判别分析方法(locality-regularized linear regression classification based discriminant analysis,LLRC-DA)。LLRC-DA根据LLRC的决策准则设计目标函数,通过最大化类间局部重构误差并最小化类内局部重构误差来寻找最优的特征子空间。在求解目标函数的过程中,本文利用投影矩阵与线性回归系数之间的关系,使用解析解表示线性回归系数,从而消除了回归系数对求解投影矩阵产生的影响。另外,在求解目标函数过程中使用了一种新的迹比优化方法,直接解决迹比问题而不是使用广义特征值分解的方法近似求解。文献[20]的研究显示,直接解决迹比问题是可行的并且比使用广义特征值分解效果更好。在本文提出的方法中,使用了正交投影来消除冗余信息,提高性能。本文在FERET、ORL人脸库上进行了实验,实验结果验证了算法的有效性。
1 局部线性回归分类器假设有
| ${{y}} = {{\tilde { X}}_i}{{\tilde { \beta }}_i}$ | (1) |
式中:
| ${{\tilde { \beta }}_i} = {\left( {{\tilde { X}}_i^{\rm T}{{{\tilde { X}}}_i}} \right)^{ - 1}}{\tilde { X}}_i^{\rm T}{{y}}$ | (2) |
根据线性回归系数
| ${{{\hat y}}_i} = {{\tilde { X}}_i}{\left( {{\tilde { X}}_i^{\rm T}{{{\tilde { X}}}_i}} \right)^{ - 1}}{\tilde { X}}_i^{\rm T}{{y}}$ | (3) |
根据LLRC的假设,如果重构样本
| $l\left( {{y}} \right) = \mathop {\min }\limits_i \left\| {{{y}} - {{{\tilde { X}}}_i}{{\left( {{\tilde { X}}_i^{\rm T}{{{\tilde { X}}}_i}} \right)}^{ - 1}}{\tilde { X}}_i^{\rm T}{{y}}} \right\|_2^2$ | (4) |
LLRC-DA的目标是将样本投影到一个特征子空间,使得类内局部重构误差最小,同时类间局部重构误差最大。用
从式(4)可以看出,如果
| $\begin{aligned} & \qquad \qquad \quad \frac{1}{n}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\left\| {{{y}}_i^j - {\tilde { Y}}_i^j{\tilde { \beta }}_i^j} \right\|_2^2} } {\rm{ = }} \\ & \quad \qquad {\rm{tr}}\left( {\frac{1}{n}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\left( {{{y}}_i^j - {\tilde { Y}}_i^j{\tilde { \beta }}_i^j} \right){{\left( {{{y}}_i^j - {\tilde { Y}}_i^j{\tilde { \beta }}_i^j} \right)}^{\rm T}}} } } \right){\rm{ = }} \\ & \quad {\rm{tr}}\left( {\frac{1}{n}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\left( {{{{A}}^{\rm T}}{{x}}_i^j - {{{A}}^{\rm T}}{\tilde { X}}_i^j{\tilde { \beta }}_i^j} \right){{\left( {{{{A}}^{\rm T}}{{x}}_i^j - {{{A}}^{\rm T}}{\tilde { X}}_i^j{\tilde { \beta }}_i^j} \right)}^{\rm T}}} } } \right){\rm{ = }} \\ & {\rm{tr}}\left( {\frac{1}{n}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {{{{A}}^{\rm T}}\left( {{{x}}_i^j - {\tilde { X}}_i^j{\tilde { \beta }}_i^j} \right){{\left( {{{x}}_i^j - {\tilde { X}}_i^j{\tilde { \beta }}_i^j} \right)}^{\rm T}}{{A}}} } } \right) = {\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_w}{{A}}} \right) \\ \end{aligned} $ | (5) |
式中:
同样地,在特征子空间中,可以计算类间局部重构误差,即
| $ \begin{aligned} & \qquad\qquad \frac{1}{{nK}}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{m \in l\left( {{{x}}_i^j} \right)} {\left\| {{{y}}_i^j - {\tilde{ Y}}_{im}^j{\tilde{ \beta }}_{im}^j} \right\|_2^2} } } {\rm{ = }}\\ & \quad{\rm{tr}}\left( {\frac{1}{{nK}}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{m \in l\left( {{{x}}_i^j} \right)} {\left( {{{y}}_i^j - {\tilde{ Y}}_{im}^j{\tilde{ \beta }}_{im}^j} \right){{\left( {{{y}}_i^j - {\tilde{ Y}}_{im}^j{\tilde{ \beta }}_{im}^j} \right)}^{\rm T}}} } } } \right) = \\ & {\rm{tr}}\left( {\frac{1}{{nK}}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{m \in l\left( {{{x}}_i^j} \right)} {{{{A}}^{\rm T}}\left( {{{x}}_i^j - {\tilde{ X}}_{im}^j{\tilde{ \beta }}_{im}^j} \right){{\left( {{{x}}_i^j - {\tilde{ X}}_{im}^j{\tilde{ \beta }}_{im}^j} \right)}^{\rm T}}{{A}}} } } } \right) = \\ & \qquad\qquad\qquad\qquad\quad{\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_b}{{A}}} \right) \end{aligned} $ | (6) |
式中:
为了使LLRC-DA表现出更好的性能,本文使用正交投影,即
| ${{{A}}^ * } = \arg \mathop {\rm min}\limits_{{A}} \frac{{{\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_w}{{A}}} \right)}}{{{\rm{tr}}({{{A}}^{\rm T}}{{{S}}_b}{{A}})}}\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\begin{array}{*{20}{c}} {} \end{array}{{{A}}^{\rm T}}{{A}} = {{I}}$ | (7) |
LLRC-DA是一个迹比最小化问题,通常此类问题可以使用广义特征值分解的方法近似求解。最近的研究显示[20],直接解决迹比问题是可行的并且比使用广义特征值分解效果更好。
假设目标函数存在一个最小值
| $\frac{{{\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_w}{{A}}} \right)}}{{{\rm{tr}}({{{A}}^{\rm T}}{{{S}}_b}{{A}})}} \geqslant {\rho ^ * }$ | (8) |
因此可以得到
| ${\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_w}{{A}}} \right) - {\rho ^ * }{\rm{tr}}({{{A}}^{\rm T}}{{{S}}_b}{{A}}) \geqslant 0$ | (9) |
为了优化目标函数,本文定义以下函数:
| $f(\rho ) = \mathop {\min }\limits_{{A}} {\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_w}{{A}} - \rho {{{A}}^{\rm T}}{{{S}}_b}{{A}}} \right)$ | (10) |
式中
引理1 1)
由上述
首先保持
| ${\tilde { \beta }} = {\left( {{\tilde { X}}_i^{\rm T}{{A}}{{{A}}^{\rm T}}{{{\tilde { X}}}_i}} \right)^{ - 1}}{\tilde { X}}_i^{\rm T}{{A}}{{{A}}^{\rm T}}{{y}}$ | (11) |
来消除
1)固定
对于一个给定的
| ${f^{'}}(\,\rho ) = - {\rm{tr}}\left( {{{A}}{{(\,\rho )}^{\rm T}}{{{S}}_b}{{A}}(\rho )} \right)$ | (12) |
已知
2)固定
存在约束条件
| $ \begin{aligned} & \qquad\mathop {\min }\limits_{{A}} J({{A}}) = \mathop {\min }\limits_{{A}} {\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_w}{{A}} - \rho {{{A}}^{\rm T}}{{{S}}_b}{{A}}} \right) = \\ & \qquad \quad \mathop {\min }\limits_{{A}} \left( {{\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_w}{{A}}} \right) - \rho {\rm{tr}}\left( {{{{A}}^{\rm T}}{{{S}}_b}{{A}}} \right)} \right) = \\ & \mathop {\min }\limits_{{A}} \left( {\frac{1}{n}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {J_i^{{j^{({\rm{w}})}}}({{A}})} } - \frac{\rho }{{nK}}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{m \in l\left( {{{x}}_i^j} \right)} {J_{im}^{{j^{({\rm{b}})}}}({{A}})} } } } \right)\\ & {\rm{s}}{\rm{.t}}{\rm{.}}\begin{array}{*{20}{l}} {} \end{array}{{{A}}^{\rm T}}{{A}} = {{I}} \end{aligned} $ | (13) |
其中:
| $ \begin{aligned} & J_i^{{j^{({\rm{w}})}}}({{A}}) = {\rm{tr}}\left( {{{{A}}^{\rm T}}\left( {{{x}}_i^j - {\tilde { X}}_i^j{\tilde { \beta }}_i^j} \right){{\left( {{{x}}_i^j - {\tilde { X}}_i^j{\tilde { \beta }}_i^j} \right)}^{\rm T}}{{A}}} \right)\\ & J_{im}^{{j^{({\rm{b}})}}}({{A}}) = {\rm{tr}}\left( {{{{A}}^{\rm T}}\left( {{{x}}_i^j - {\tilde { X}}_{im}^j{\tilde { \beta }}_{im}^j} \right){{\left( {{{x}}_i^j - {\tilde { X}}_{im}^j{\tilde { \beta }}_{im}^j} \right)}^{\rm T}}{{A}}} \right) \end{aligned} $ |
因为目标函数要在正交约束条件下进行求解,所以首先要对其进行求导。
| $ \frac{{{\rm d}J({{A}})}}{{{\rm d}{{A}}}} = \frac{1}{n}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\frac{{{\rm d}J_i^{{j^{({\rm w})}}}({{A}})}}{{{\rm d}{{A}}}}} } - \frac{\rho }{{nK}}\sum\limits_{i = 1}^C {\sum\limits_{j = 1}^{{n_i}} {\sum\limits_{m \in l\left( {{{x}}_i^j} \right)} {\frac{{{\rm d}J_{im}^{{j^{({\rm b})}}}({{A}})}}{{{\rm d}{{A}}}}} } } $ | (14) |
对于每一个
| $ \frac{{{\rm{d}}J_i^{{j^{({\rm{w}})}}}({{A}})}}{{\rm{d}}{{A}}} = (2{{x}}{{{x}}^{\rm T}} + 6{{G}}{{{G}}^{\rm T}}{\rm{ + }}{{R}} + {{{R}}^{\rm T}} - {{H}} - {{{H}}^{\rm T}}){{A}} $ | (15) |
式中:
同样地,可以计算
| $\frac{{{\rm d}J_{im}^{{j^{({\rm{b}})}}}({{A}})}}{{\rm{d}}{{A}}} = (2{{x}}{{{x}}^{\rm T}} + 6{{G}}{{{G}}^{\rm T}}{\rm{ + }}{{R}} + {{{R}}^{\rm T}} - {{H}} - {{{H}}^{\rm T}}){{A}}$ | (16) |
式中:
求完导数之后,定义一个斜对称矩阵
| ${{M}} = \frac{{{\rm{d}}J({{A}})}}{{\rm{d}}{{A}}}{{{A}}^{\rm T}} - {{A}}{(\frac{{{\rm{d}}J({{A}})}}{{\rm{d}}{{A}}})^{\rm T}}$ | (17) |
然后,可以通过Crank-Nicolson-like方法,得到更新后的投影矩阵
| ${{{A}}_{{\rm{new}}}} = {{A}} - \frac{\tau }{2}{{M}}\left( {{{A}} + {{{A}}_{{\rm{new}}}}} \right)$ | (18) |
式中:
通过前面对LLRC-DA的描述,可以得到LLRC-DA的算法:
输入 训练样本矩阵
输出 投影矩阵
1)如果原始样本的维数大于样本总数,先使用PCA方法将原始样本投影到低维子空间,其中
2)固定
3)固定
4)重复2)、3),直到
5)最终的投影矩阵为
为了验证LLRC-DA的有效性,本文分别在FERET和ORL人脸库上进行实验,并与PCA[13]、LDA[14]、LPP[15]、RDA[24]和LLRDA[19]等先进的维数约简算法进行比较。在维数约简之后,分别使用NNC[25]、MDC[26]、LRC[17]和LLRC[18]分类器来比较每种维数约简方法在不同分类器下的分类性能。本文中的实验通过MATLAB编程实现,硬件环境为酷睿i7处理器、主频2.6 GHz、内存8 GB。
3.1 FERET人脸库上的实验FERET人脸库包含1 400幅人脸图像,共计200类,其中每类7幅图像,包括两张面部表情图,两张左侧图,两张右侧图和一张光照图,图1所示为一个人的7幅图像。实验中所有的图像均被裁剪为 80像素

|
Download:
|
| 图 1 FERET库中一个人的7幅图像 Fig. 1 Seven images of a person from the FERET database | |
| 表 1 FERET库上的识别率 Tab.1 Recognition accuracy when using the FERET database |
通过表1可以看出:1)与PCA、LPP等非监督学习方法相比,监督学习的降维方法明显具有更好的性能,因为监督学习方法利用了类别信息,使识别率显著提高;2)同一种降维方法,在不同的分类器上的实验结果不同,甚至会有很大差异,例如LLRC-DA在MDC与LLRC这两种分类器上的识别率相差很大,这也说明选择合适的分类器对于识别性能至关重要;3)在所有的降维方法与分类器的组合中,LLRC-DA与LLRC的组合具有最高的识别率,由于使用了LLRC的决策准则,因此和其他降维方法相比,LLRC-DA学习的特征子空间与LLRC更加契合;4)LLRC-DA在LRC、LLRC上的识别率均明显高于LLRDA,证明本文提出的方法对于提高分类率是有效的。
3.2 ORL人脸库上的实验ORL人脸库的400幅图像来自40个人,其中每人10幅图像,图像在不同条件下进行采集,如光照、面部表情、面部细节等,图2所示为一个人的10幅图像。实验中所有的图像均压缩成 56像素

|
Download:
|
| 图 2 ORL库中一个人的10幅图像 Fig. 2 Ten images of a person from the ORL database | |
在ORL人脸库上,本文对LLRC-DA在不同参数下的性能进行评估。首先,对每类中的最近邻参数
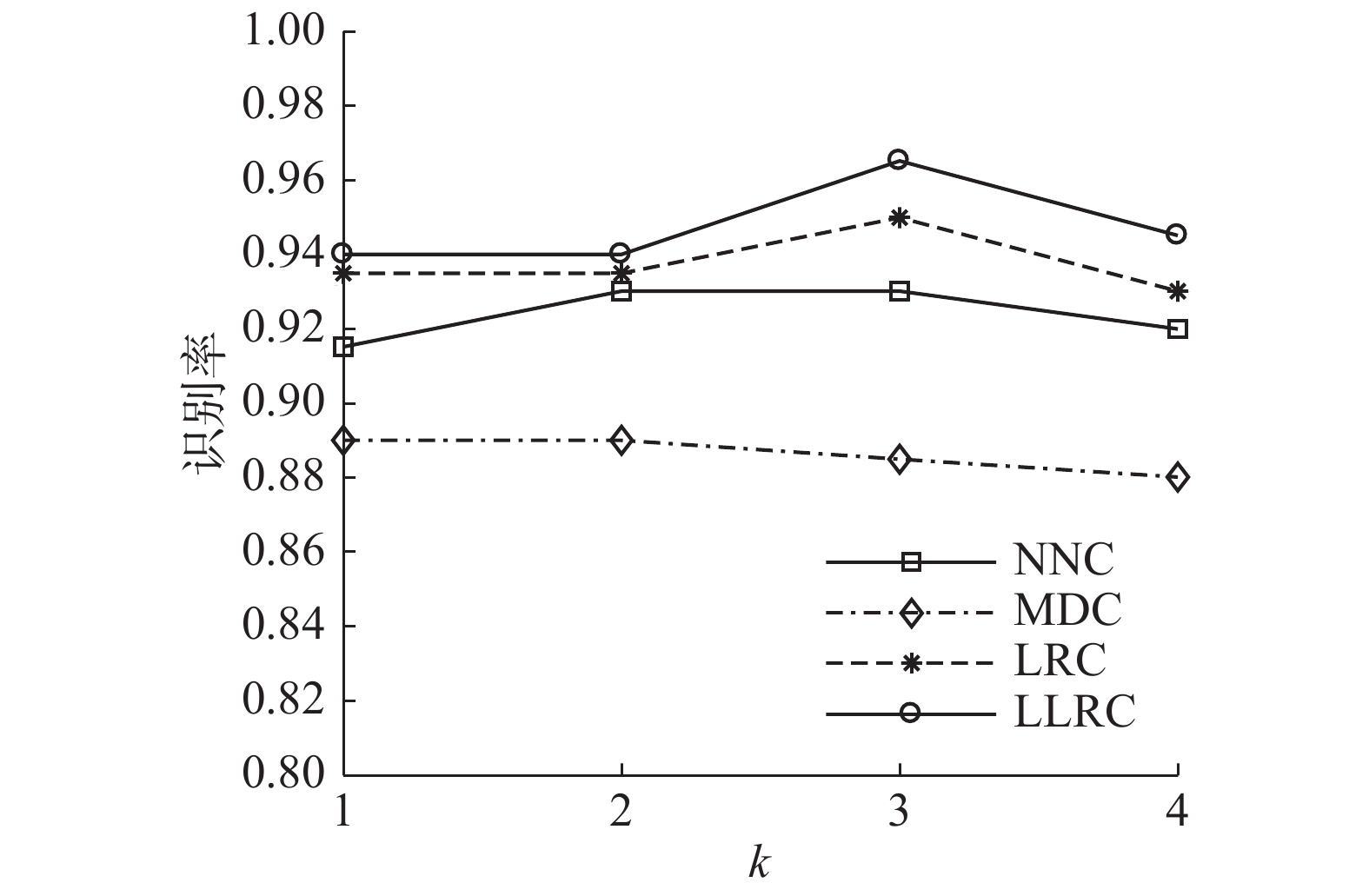
|
Download:
|
| 图 3 LLRC-DA在不同k下的识别率 Fig. 3 Recognition rate of LLRC-DA with varied k | |
接着,对近邻类参数

|
Download:
|
| 图 4 LLRC-DA在不同K下的识别率 Fig. 4 Recognition rate of LLRC-DA with varied K | |
最后,比较在不同分类器下LLRC-DA的性能,设置
| 表 2 ORL库上的识别率 Tab.2 Recognition accuracy when using the ORL database |
本文提出了面向局部线性回归分类器的判别分析方法LLRC-DA,根据LLRC的决策准则设计目标函数,通过最大化类间局部重构误差并最小化类内局部重构误差来寻找最优的特征子空间。本文利用了投影矩阵与线性回归系数之间的关系,消除了线性回归系数的影响,使得目标函数只和投影矩阵相关。LLRC-DA通过对投影矩阵添加正交约束来消除冗余信息,并得到更好的特征子空间。相比于传统算法使用最大特征值分解来求解迹比问题,本文利用了一种新的迹比优化算法来有效地求解投影矩阵。本文在FERET、ORL人脸库上进行了实验,与先进的维数约简算法进行了比较,实验结果表明,本文提出的方法具有更好的性能。对于LLRC-DA中的最近邻参数
| [1] |
HARANDI M, SALZMANN M, HARTLEY R. Dimensionality reduction on SPD manifolds: the emergence of geometry-aware methods[J]. IEEE transactions on pattern analysis and machine intelligence, 2018, 40(1): 48-62. DOI:10.1109/TPAMI.2017.2655048 ( 0) 0)
|
| [2] |
CHOI S, SHIN J H, LEE J, et al. Experimental demonstration of feature extraction and dimensionality reduction using memristor networks[J]. Nano letters, 2017, 17(5): 3113-3118. DOI:10.1021/acs.nanolett.7b00552 ( 0) 0)
|
| [3] |
YIN Jun, WEI Lai, SONG Miao, et al. Optimized projection for collaborative representation based classification and its applications to face recognition[J]. Pattern recognition letters, 2016, 73: 83-90. DOI:10.1016/j.patrec.2016.01.012 ( 0) 0)
|
| [4] |
XIA Zhihua, WANG Xinhui, ZHANG Liangao, et al. A privacy-preserving and copy-deterrence content-based image retrieval scheme in cloud computing[J]. IEEE transactions on information forensics and security, 2016, 11(11): 2594-2608. DOI:10.1109/TIFS.2016.2590944 ( 0) 0)
|
| [5] |
GONG Yunchao, LAZEBNIK S, GORDO A, et al. Iterative quantization: a procrustean approach to learning binary codes for large-scale image retrieval[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(12): 2916-2929. DOI:10.1109/TPAMI.2012.193 ( 0) 0)
|
| [6] |
YUAN Chengsheng, SUN Xingming, LV Rui. Fingerprint liveness detection based on multi-scale LPQ and PCA[J]. China communications, 2016, 13(7): 60-65. DOI:10.1109/CC.2016.7559076 ( 0) 0)
|
| [7] |
DUBEY R K, GOH J, THING V L L. Fingerprint liveness detection from single image using low-level features and shape analysis[J]. IEEE transactions on information forensics and security, 2016, 11(7): 1461-1475. DOI:10.1109/TIFS.2016.2535899 ( 0) 0)
|
| [8] |
YE Jieping, LI Tao, XIONG Tao, et al. Using uncorrelated discriminant analysis for tissue classification with gene expression data[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2004, 1(4): 181-190. DOI:10.1109/TCBB.2004.45 ( 0) 0)
|
| [9] |
ZOU Quan, ZENG Jiancang, CAO Liujuan, et al. A novel features ranking metric with application to scalable visual and bioinformatics data classification[J]. Neurocomputing, 2016, 173: 346-354. DOI:10.1016/j.neucom.2014.12.123 ( 0) 0)
|
| [10] |
LI Tao, ZHU Shenghuo, OGIHARA M. Using discriminant analysis for multi-class classification: an experimental investigation[J]. Knowledge and information systems, 2006, 10(4): 453-472. DOI:10.1007/s10115-006-0013-y ( 0) 0)
|
| [11] |
AMATRIAIN X, PUJOL J M. Data mining methods for recommender systems[M]//RICCI F, ROKACH L, SHAPIRA B. Recommender Systems Handbook. Boston, MA: Springer, 2015: 227–262.
( 0) 0)
|
| [12] |
RAUDYS S J, JAIN A K. Small sample size effects in statistical pattern recognition: recommendations for practitioners[J]. IEEE transactions on pattern analysis and machine intelligence, 1991, 13(3): 252-264. DOI:10.1109/34.75512 ( 0) 0)
|
| [13] |
TURK M, PENTLAND A. Eigenfaces for recognition[J]. Journal of cognitive neuroscience, 1991, 3(1): 71-86. DOI:10.1162/jocn.1991.3.1.71 ( 0) 0)
|
| [14] |
BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. Fisherfaces: recognition using class specific linear projection[J]. IEEE transactions on pattern analysis and machine intelligence, 1997, 19(7): 711-720. DOI:10.1109/34.598228 ( 0) 0)
|
| [15] |
HE Xiaofei, YAN Shuicheng, HU Yuxiao, et al. Face recognition using laplacianfaces[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(3): 328-340. DOI:10.1109/TPAMI.2005.55 ( 0) 0)
|
| [16] |
ZHANG Lei, YANG Meng, FENG Xiangchu. Sparse representation or collaborative representation: which helps face recognition?[C]//Proceedings of 2011 International Conference on Computer Vision. Barcelona, Spain, 2011: 471–478.
( 0) 0)
|
| [17] |
NASEEM I, TOGNERI R, BENNAMOUN M. Linear regression for face recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(11): 2106-2112. DOI:10.1109/TPAMI.2010.128 ( 0) 0)
|
| [18] |
BROWN D, LI Hanxi, GAO Yongsheng. Locality-regularized linear regression for face recognition[C]//Proceedings of the 21st International Conference on Pattern Recognition. Tsukuba, Japan, 2012: 1586–1589.
( 0) 0)
|
| [19] |
HUANG Pu, LI Tao, SHU Zhenqiu, et al. Locality-regularized linear regression discriminant analysis for feature extraction[J]. Information sciences, 2018, 429: 164-176. DOI:10.1016/j.ins.2017.11.001 ( 0) 0)
|
| [20] |
WANG Huan, YAN Shuisheng, XU Dong, et al. Trace ratio vs. Ratio trace for dimensionality reduction[C]//Proceedings of 2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, USA, 2007: 1–8.
( 0) 0)
|
| [21] |
NGO T T, BELLALIJ M, SAAD Y. The trace ratio optimization problem[J]. SIAM review, 2012, 54(3): 545-569. DOI:10.1137/120864799 ( 0) 0)
|
| [22] |
JIANG Wenhao, CHUNG Fulai. A trace ratio maximization approach to multiple kernel-based dimensionality reduction[J]. Neural networks, 2014, 49: 96-106. DOI:10.1016/j.neunet.2013.09.004 ( 0) 0)
|
| [23] |
WEN Zaiwen, YIN Wotao. A feasible method for optimization with orthogonality constraints[J]. Mathematical programming, 2013, 142(1/2): 397-434. ( 0) 0)
|
| [24] |
CHEN Yi, JIN Zhong. Reconstructive discriminant analysis: a feature extraction method induced from linear regression classification[J]. Neurocomputing, 2012, 87: 41-50. DOI:10.1016/j.neucom.2012.02.001 ( 0) 0)
|
| [25] |
COVER T, HART P. Nearest neighbor pattern classification[J]. IEEE transactions on information theory, 1967, 13(1): 21-27. DOI:10.1109/TIT.1967.1053964 ( 0) 0)
|
| [26] |
ZHANG Daoqiang, CHEN Songcan, ZHOU Zhihua. Learning the kernel parameters in kernel minimum distance classifier[J]. Pattern recognition, 2006, 39(1): 133-135. DOI:10.1016/j.patcog.2005.08.001 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


