近几年，卷积神经网络^[1](convolutional neural networks，CNN)在目标检测、图像分类和语义分割^[2]等视觉领域取得了巨大的突破，从而引起许多研究者的关注。卷积神经网络是一种利用共享参数和局部连接的神经网络框架，通过梯度反向传播的方式，能够有效拟合模型输出。

为了达到理想学习情况，深度学习通常需要大量的标注数据，并且各个标签之间的分布要能够尽量均衡。然而在实际情况中，很难保证这种标签的均衡，往往面对的是类别不平衡情况。类别不平衡问题^[3-4](class imbalance problem)指数据集中各类别样本总数存在明显差异。极端情况下二者不平衡比率甚至高达1 000倍。这类情况在计算机视觉^[5]和医疗诊断^[6]领域尤为凸显。这种类别不平衡问题极大地影响着模型的拟合和泛化能力，导致模型产生过拟合情况，而往往忽视对小类别样本的学习^[7]。典型问题，如实际生活中癌症患者数量远远少于健康者数量。如果模型采用标准算法以最大化正确率为目标，则会偏好正常人类别，易将病患错误预测为正常人，从而严重影响患者的治疗时机。因此对类别不平衡问题的研究尤其重要。

基于数据层面的平衡算法主要通过对样本重采样，来改善原始数据集类别分布平衡。过采样(oversampling，OS)^[8]是目前机器学习中针对类别不平衡问题最广泛使用的方法之一。该方法的简单做法是直接随机从小类别中重复选取样本。但重复的样本可能会导致模型的过拟合问题^[9]。一种比较有效的方法是SMOTE采样^[10]，其思想是通过邻近样本点人工生成相似的样本。但该方法可能存在生成的样本处于类别边界处，反而降低了模型的决策能力。欠采样^[8](under-sampling)的思想是将大类别中的样本剔除一部分，从而保持类别平衡。由于除去了部分样本，可能会导致数据集缺少部分信息。为解决该问题，一些改善的方式是更为谨慎地选择剔除的样本。如除去处于类别边界处的冗余样本^[11]或通过聚类方式生成样本权重来对大类别样本进行欠采样。一种新近方法是结合过采样和欠采样优点，对大类别样本欠采样，小类别样本过采样，从而使数据集达到一个较好的平衡点^[12]。

而模型层面的算法主要通过修改模型损失函数或调整模型结构来降低数据集的不平衡性。阈值移动^[13](thresholding)是一种通过改变后验概率的决策阈值来调整模型分类的算法。其根据类别信息对模型输出概率使用先验信息对其做补偿，从而调整分类器的决策阈值，更好地适应不平衡分类问题。代价敏感学习^[14](cost sensitive learning)认为模型将样本错分成其他类别时的错分代价是不同的，因此对不同类别错分代价赋予不同权重。一种方法是在算法梯度反向传播阶段调整模型损失。模型将一个类别错分成另一个类别时，对该样本损失乘以相应错分代价。但目前对于错分代价的量化仍属于一个问题。而Focal Loss方法^[15]试图根据预测样本的概率高低动态地给样本损失赋予不同的权重，从而引导模型更多地学习较难样本。

采样方法需要人工分析样本特性去生成或剔除样本，处理繁杂。而调整模型类算法一般需要引入额外参数来控制平衡性，增加了模型的学习复杂度。且随机打乱的样本序列和类别间的不平衡性，使得在每个小批量内类别间不平衡率动态变化。在本文中，针对图像不平衡多分类问题，设计了一种在小批量内动态调整样本损失比例的期望损失函数。该方法相较于交叉熵损失函数和目前在类别不平衡问题上常见的过采样方法，其在测试集上的正确率和调和平均F₁都取得一定程度的提高。

1 损失平衡函数 1.1 交叉熵损失函数

在图像多分类任务中，传统损失函数通常采用交叉熵^[16]的形式(cross entropy loss function，CE)，其表达式为

${\rm{CE}}(\theta ) = - \sum\limits_{i = 1}^n {\mathop y\nolimits_i } \log \overline {\mathop y\nolimits_i } $

(1)

式中：θ表示模型参数；n表示样本总数；i表示样本编号；y_i代表样本i的真实标记； $\overline {\mathop y\nolimits_i } $ 表示模型对样本i的预测结果。交叉熵损失函数主要考虑每个样本对应于其正确类别的概率，如果该概率较低，说明当前模型对该样本的学习程度不够，给予较大损失；反之，则赋予该样本较小损失。但交叉熵损失函数前提是类别间分布平衡，因此在面对类别不平衡问题时，交叉熵损失函数将不再适用。

1.2 改进的损失平衡函数

类别不平衡问题导致模型效果不佳的根本原因在于训练集中部分类别样本数量过少，模型对这些类别的样本学习程度不够，模型泛化能力不佳。由于该问题在实际情况中普遍存在，解决该问题只能尽可能增加数据规模，对小类别样本多采样。但由类别不平衡问题引起的模型对大类别样本的过拟合问题可采用一些方法来降低其影响，如过采样方法。

在前期实验中发现，模型在训练过程中，每个小批量内各类别样本总数都是不平衡的。而且由于各类别样本数量差异性，在对所有样本序列随机打乱后，每个小批量内包含的各类别样本总数比例更是动态变化，难以确定。这种类别间的不平衡性导致大类别样本损失占据比例较大，从而控制了整个梯度传播方向，而使模型忽略对小类别样本的学习。

过采样方法虽然在数据层面重采样以达到类别分布平衡，但从模型训练角度，其实质上同样是调整每个类别在总损失中的占据比例。结合前文观察到的小批量内类别损失动态不平衡问题，本文试图在模型层面利用过采样方法的思维解决该问题，提出了在小批量内对每个样本产生的损失进行自适应调整，利用样本的标签信息，使各个类别损失在总损失中占据比例相等。据此提出两种函数：一种是对模型输出的样本概率进行均衡化的概率期望损失函数(probability expectation loss function，PE)，另一种是对模型输出的样本损失进行均衡化的损失期望损失函数(loss expectation loss function，LE)，其公式分别为

${\rm{PE}}(\theta ) = - \sum\limits_{i = 1}^n {\mathop y\nolimits_i } \log \frac{1}{{\left| t \right|}}\overline {\mathop y\nolimits_i } $

(2)

${\rm{LE}}(\theta ) = - \sum\limits_{i = 1}^n {\mathop y\nolimits_i } \frac{1}{{\left| t \right|}}\log \overline {\mathop y\nolimits_i } $

(3)

式中： $\dfrac{1}{{\left| t \right|}}$ 用来控制类别间平衡性； $\left| t \right|$ 表示属于当前类别的样本在小批量内的总数。该损失函数将模型输出的样本概率或损失进行动态调整，根据在当前小批量内各类别样本数量信息，控制每个样本在总损失中占据的比例，从而使每个样本的损失不仅与样本本身有关，还与当前小批量内同类样本的总数量有关。如图1所示，交叉熵损失函数中每个样本损失在总损失中比重为一个单位，由于大类别样本数量多，该类别在总损失中比重大。如果小类别样本极少，那由小类别样本产生的梯度方向将会被大类别样本覆盖。这种现象在不平衡数据集上使用小批量算法训练时更为严重。而本文提出的方法在对每个样本进行损失控制后，每个类别产生的损失比重相等，不会出现类别梯度覆盖现象。另一种理解可以认为模型不再以单个样本损失为基准，而是以每个类别的概率期望或损失期望作为学习程度的评判标准。该方法在一定程度上消除了类别不平衡问题的影响，实现了更好的性能。

2 实验过程与结果分析 2.1 数据集及预处理

本次实验数据集来源于caltech101^[17]和ILSVRC2014^[18]。数据集caltech101是一个图像物体识别数据集，总共包含101类物体，每个类别最少包含30张图像。ILSVRC2014数据集为Large Scale Visual Recognition Challenge 2014年比赛的训练数据，包含200类物体图像。相比于caltech101数据集，ILSVRC2014数据集物体变化尺度较大，分类难度更具有挑战性。为研究该方法在不平衡数据集上效果，对caltech101和ILSVRC2014数据集中部分类别样本进行采样，生成3个类别比例差异较大的数据集。分别为caltech PART、ILSVRC PART1和ILSVRC PART2。数据集样本数量信息如表1所示。

实验主要采用不同深度的ResNet^[19]预训练网络，固定底层模型参数，修改模型顶层的全连接层进行训练。为了实验公平，使用同样在模型层面的交叉熵损失函数作为对比基准，为比较模型的提升程度，使用数据层面的过采样方法作为对比。为表述方便，将分别使用CE^[16]、OS^[8]、PE、LE代表交叉熵损失函数、过采样方法以及本文提出的概率期望损失函数和损失期望损失函数。实验选择0.1作为所有模型的初始学习率。整个实验选用随机梯度下降法作为优化方法，每次实验进行100次迭代，每30次迭代学习率缩放到0.4倍。所有模型都采用基本的数据增强手段，在训练集上对图像随机裁剪至224×224，并随机水平翻转。在测试集上只有中心裁剪至224×224。

2.2 实验结果分析

为准确清晰地观察每个算法的分类效果，尽量减小随机初始化带来的影响，各进行5次实验，取正确率和调和平均F₁^[20]作为评判标准，结果如表2所示。

由表2可知，相比于交叉熵损失函数，本文提出的两种期望损失函数，在测试集上每个类别的调和平均F₁都有所提高，这是因为交叉熵损失函数没有考虑到类别不平衡情况。因此每次梯度反向传播时数量多的大类别样本控制了梯度传播的方向，模型会过度向大类别样本拟合。而对于在数据层面的过采样方法，本文的概率期望损失函数获得了与其几乎同等的性能，本文的LE损失函数效果仍然优于过采样方法。其原因在于，过采样方法虽然使得数据集各类别数量几乎均衡，但忽略了在训练过程中样本序列的随机性，使得仍然存在小批量内各类别样本数量不均衡问题。而且由于过采集相同样本，数据集中存在大量重复样本，可能会导致模型的过拟合问题^[10]。

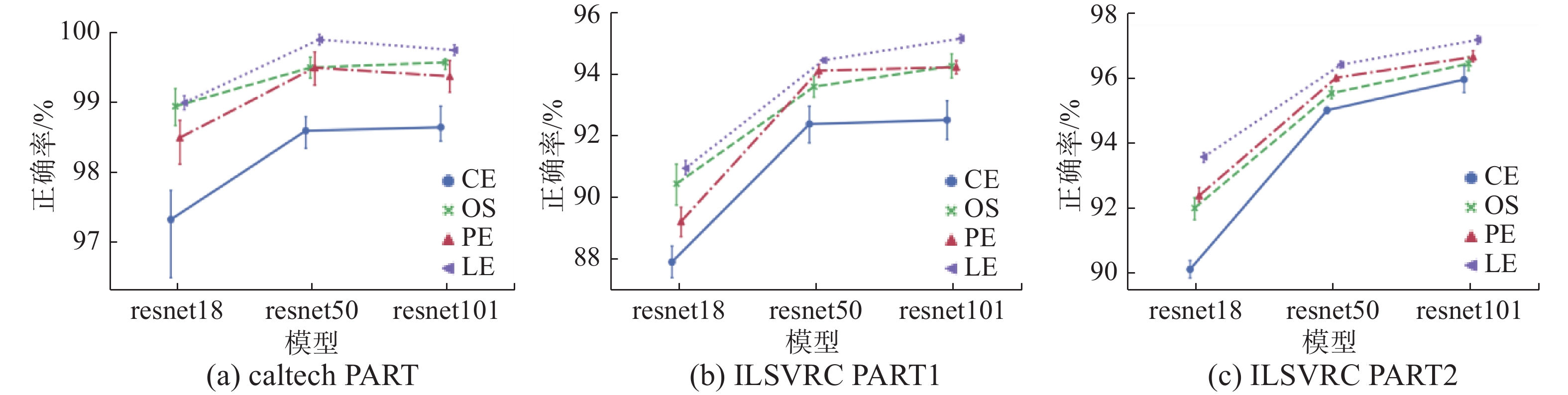
模型的正确率可以作为衡量模型整体能力的度量标准之一。从图2可以发现，本文的两种方法都能提高模型的整体判别能力，提出的损失期望损失函数在较优学习率情况下对模型的增幅相较于交叉熵损失函数最高可提高3.5%，而对比过采样方法最高可提高1.5%。模型深度越浅，提升效果越明显。在试探选择初始学习率时，发现在选择较差学习率情况下提升效果更为明显。由于该方法在每次更新参数时各类别占据总损失的比例相同，不会出现某个类别主导梯度传播方向的问题，这使得在训练过程中模型表现得更为稳定，正确率的波动范围远远小于交叉熵损失函数。

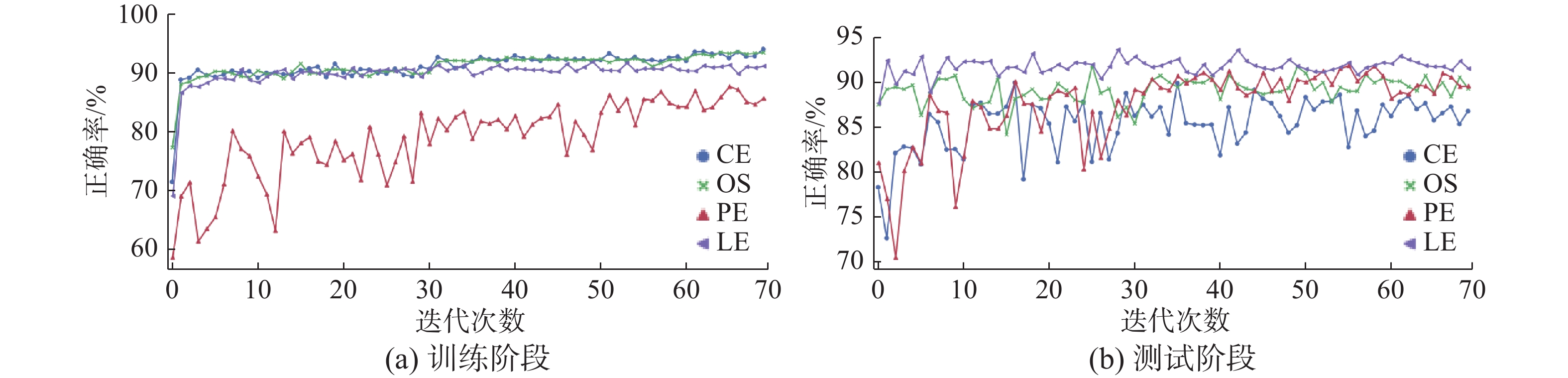
由图3可知，在训练集上交叉熵损失函数和过采样方法模型正确率曲线处于几乎完全一致状态，但在测试集上，过采样方法的正确率要比交叉熵损失函数方法高，说明过采样方法能够提高模型的泛化能力。而基于PE方法的结果在训练集出现较大的波动，表明其在寻找最优参数过程中搜索的范围更为广泛，同时也不够稳定，容易陷入局部极小点。LE损失函数在训练集上正确率低于交叉熵损失函数和过采样方法，在测试集上却高于其他算法。这证明该方法一定程度上避免了模型的过拟合问题，实现了更好泛化能力。这是该方法能够优于与其思想类似的过采样方法的主要原因。

3 结束语

本文基于传统处理类别不平衡问题的手段，结合过采样和代价敏感学习的优点，利用模型在小批量训练过程中动态产生的类别信息，实现了在小批量内样本的损失平衡。在提高算法便利性的同时，进一步提高了模型在不平衡数据集上的分类精度。将该方法应用于3个不平衡图像数据集分类实验中，结果证明该方法的可行性。在视觉领域一阶段的目标检测模型中，背景和目标的不平衡性严重影响了模型的分类效果。因此将该算法应用于目标检测领域，以验证该算法的有效性是接下来的工作之一。