鉴于缺失数据重建的重要性，研究人员已经就缺失数据重建问题提出了多种解决方法。粒子群优化(particle swarm optimization，PSO)在1995年由Kennedy和Eberhart提出^[1-2]。PSO通过群体内个体之间的信息共享来对问题的解进行协同搜索^[3]，即初始化一群随机粒子，并通过迭代找到最优解。在每一次迭代中，粒子通过跟踪局部最优值和全局最优值来更新自己的速度与位置^[4]。文献[5]通过调整惯性权重的取值，提出了自适应混沌粒子群优化算法，该算法避免了粒子早熟收敛情况。文献[6]中Krishna和Ravi提出了一种基于粒子群优化和矩阵协方差结构的数据重建方法，他们使用PSO重建缺失值。

进化聚类算法(evolving clustering method，ECM)是一步到位的快速聚类算法，在ECM中，由用户定义的阈值参数 $\tau $ 会影响群集合数量的估计， $\tau $ 值太大或太小都不利于找出群集合数量^[7-8]。Ravi等^[9-10]提出了4种用于重建的混合方法。在线重建中使用了具有广义回归神经网络的ECM(ECM+GRNN)，在离线重建中使用了K-means+GRNN和K-medoids+GRNN以及具有多层感知机的K-medoids(K-medoids+MLP)。他们虽然提出了基于ECM的数据重建，但 $\tau $ 值选择涉及了试错法，结果都不同程度地受到 $\tau $ 值的影响。

极限学习机(extreme learning machine，ELM)是由Huang等^[11-12]提出的，它是一种新颖的前馈神经网络，不需要权重更新。目前ELM的理论与算法研究主要集中在随机生成参数的优化、最优外权的求解、最优隐藏层节点个数的选取、ELM 核函数、在线极限学习机算法等方面^[13]。文献[14]发现自联想的极限学习机(auto associative extreme learning machine，AAELM)在同一个数据集合中的不同运行产生了不同的结果。有时，连接输入层和隐藏层的随机加权会使结果出现很大的波动。在文献[15]中Ravi和Krishna为重建提出了多种在线和离线方法，即粒子群优化训练后的自动关联神经网络(PSOAANN)、粒子群优化训练后的自动关联子波神经网络(PSOAAWNN)、径向基函数自动关联神经网络(RBFAANN)、广义回归自动关联神经网络(GRAANN)，这些算法仍有待于进一步改进。

鉴于以上研究中存在的PSO重建缺失值效率低、 $\tau $ 值的选取会影响基于ECM的数据重建、AAELM结构中连接输入层和隐藏层的随机加权导致重建结果波动较大以及文献[15]中所提的神经网络的重建效率低等问题，本文根据协方差矩阵具有旋转不变性的特征^[16]，在PSO适应度函数中用到了协方差矩阵及协方差矩阵的行列式，选取了最佳 $\tau $ 值，使用具有最佳 $\tau $ 值的ECM进行缺失数据重建，我们称之为PSOECM方法，PSOECM方法解决了 $\tau $ 值的选取困难及其对基于ECM重建结果的影响问题。随后，在AAELM中调用具有最佳 $\tau $ 值的ECM，去除了AAELM的随机性，我们称之为改进型的AAELM(MAAELM)。

1 基础理论 1.1 PSO算法

在D维搜索空间中，由 $n$ 个粒子组成的群体中粒子 $i$ ( $i=1,2, \cdots ,n$ )的位置表示为D维位置矢量 ${{{z}}_i} = \left( {{z_{i1}},{z_{i2}}, \cdots ,{z_{id}}, \cdots ,{z_{iD}}} \right)$ ,每次迭代中粒子 $i$ 移动的距离为速度矢量或飞行速度 ${{{v}}_i} = ( {{v_{i1}},{v_{i2}}, \cdots ,{v_{id}},\cdots , } $ ${v_{iD}})$ ，粒子迄今为止搜索到的最优位置 ${{{p}}_i} = \left( {{p_{i1}},{p_{i2}}, \cdots ,{p_{id}}, \cdots ,{p_{iD}}} \right)$ ，整个粒子群迄今为止搜索到的最优位置为 ${{{p}}_g} = \left( {{p_{g1}},{p_{g2}}, \cdots ,{p_{gd}}, \cdots ,{p_{gD}}} \right)$ ，每次迭代中任一粒子根据式(1)、式(2)来更新自己的速度和位置：

$v_{id}^{k + 1} = \omega v_{id}^k + {a_1}{r_1}\left( {{p_{id}} - z_{id}^k} \right) + {a_2}{r_2}\left( {{p_{gd}} - z_{id}^k} \right)$

(1)

$z_{id}^{k + 1} = z_{id}^k + v_{id}^{k + 1}$

(2)

式中： $i=1,2, \cdots ,n$ ； $\omega $ 是惯性权重； $k$ 是迭代次数； ${a_1}$ 、 ${a_2}$ 是加速系数； ${r_1}$ 、 ${r_2}$ 是[0,1]范围内的随机数。PSO算法的描述如下：

1)随机初始化群体，设定粒子的位置和速度；

2)根据适应度函数计算粒子的适应度值，选取具有最优适应度值的粒子位置作为 ${{{p}}_g}$ ，每个粒子当前位置为 ${{{p}}_i}$ ；

3)根据式(1)、式(2)更新粒子的速度和位置；

4)把每个粒子的适应度值与 ${{{p}}_i}$ 的适应度值进行比较，若优于 ${{{p}}_i}$ 的值，则将其值设为 ${{{p}}_i}$ ；

5)把每个粒子的适应度值与 ${{{p}}_g}$ 的适应度值进行比较，若优于 ${{{p}}_g}$ 的值，则将其值设置为 ${{{p}}_g}$ ；

6)检查是否满足终止条件，如果满足则终止迭代，否则返回2)。

1.2 ECM算法

创建新群集 $C$ 时，定义群集中心 $C'$ ，并将群集半径 $R$ 初始为零。随着样本的相继出现，已经创建的群集可以通过改变群集中心 $C'$ 位置和增加群集半径 $R$ 来更新。当群集半径 $R$ 达到阈值 $\tau $ 值时，将不再更新群集。ECM算法过程如下：

1)创建第一个群集 ${C_1}$ ，并将输入数据中的第一个样本作为群集中心 $C'{_1}$ ，设置群集半径 ${R_1}=0$ 。

2)如果输入数据流的所有样本都已处理完毕，则算法结束。否则，取当前样本 ${x_i}$ ，计算 ${x_i}$ 与已经创建的所有 $n$ 个集群中心 $C{'_j}$ 之间的距离， ${D_{ij}} = \left\| {{x_i} - C{'_j}} \right\|$ ，其中 $j = 1,2, \cdots ,n$ 。

3)如果存在群集中心 $C{'_j}$ ，其中 $j = 1,2, \cdots ,n$ ，使得 ${D_{ij}} = \left\| {{x_i} - C{'_j}} \right\| \leqslant R$ ，则假定当前样本 ${x_i}$ 属于最近群集 ${C_m}$ ， ${D_{im}} = \left\| {{x_i} - C{'_m}} \right\| = \min \left( {\left\| {{x_i} - C{'_j}} \right\|} \right)$ 。在这种情况下，既不创建新群集，也不更新现有群集，并返回到2)，否则进入4)。

4)从已经创建的所有 $n$ 个集群的中心中，通过计算 ${S_{ij}} = {D_{ij}} + {R_j},j = 1,2, \cdots ,n$ ，找出一个群集 ${C_a}$ 。再通过计算算出最小的 ${S_{ia}}$ 值， ${S_{ia}} = {D_{ia}} + {R_a} = $ $\min \left\{ {{S_{ij}}} \right\}$ ， $j = 1,2, \cdots ,n$ ，来找出 ${C_a}$ 的群集中心 $C{'_a}$ 。

5)如果 ${S_{ia}} > 2 \tau $ ，则样本 ${x_i}$ 不属于任何现有群集，那么以与1)的相同方式创建新集群，执行2)。

6)如果 ${S_{ia}} \leqslant 2 \tau $ ，则通过移动群集中心 $C{'_a}$ 和增加群集半径 ${R_a}$ 来更新群集 ${C_a}$ ，返回2)。

ECM算法不保持已传递样本的任何信息，但任一群集 ${C_i}$ 的群集中心 $C{'_i}$ 到该群集的最远样本之间距离都小于阈值 $\tau $ ，即 $\max \left( {{R_i}} \right) < \tau $ 。

在ECM算法中，向量 ${{x}}$ 和 ${{y}}$ 之间的距离计算使用归一化欧几里德距离，即

$\left\| {{{x}} - {{y}}} \right\| = {{{{\left( {\sum\limits_{i = 1}^q {{{\left| {{{{x}}_i} - {{{y}}_i}} \right|}^2}} } \right)}^{1/2}}}/ {{q^{1/2}}}}\begin{array}{*{20}{c}} ,\;{{{x}},{{y}} \in {{\bf{R}}^q}} \end{array}$

(3)

在5)、6)中 $\tau $ 值的大小影响到群集合数量，所以 $\tau $ 值的选取影响到了基于ECM的数据重建结果。

1.3 ELM算法

输入层的节点个数为 $n$ ，隐藏层节点个数为 $L$ ，输出层节点个数为 $m$ ， ${a_{ij}}$ 代表第 $i$ 个输入层节点与第 $j$ 个隐藏层节点间的权值， ${b_j}$ 代表隐藏层中第 $j$ 个节点的偏置。 ${\beta _{jk}}$ 是需要计算的值, 代表第 $j$ 个隐藏层节点与第 $k$ 个输出层节点间的权值。训练集实例个数为 $N$ 的输入矩阵 ${{X}}$ 以及输出矩阵 ${{T}}$ 分别为

${{X}}=\left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1N}}} \\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2N}}} \\ \vdots & \vdots &{}& \vdots \\ {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{nN}}} \end{array}} \right]$

(4)

${{T}}=\left[ {\begin{array}{*{20}{c}} {{t_{11}}}&{{t_{12}}}& \cdots &{{t_{1N}}} \\ {{t_{21}}}&{{t_{22}}}& \cdots &{{t_{2N}}} \\ \vdots & \vdots &{}& \vdots \\ {{t_{n1}}}&{{t_{n2}}}& \cdots &{{t_{nN}}} \end{array}} \right]$

(5)

第 $i$ 个实例在第 $j$ 个隐藏层神经元上的输出为 $G\left( {{a_j},{b_j},{x_i}} \right)$ ，整个的输出层值为

$\sum\limits_{j = 1}^L {{\beta _j}G\left( {{a_j},{b_j},{x_i}} \right)} = {t_i},\quad i= 1,2, \cdots ,N$

(6)

式(6)也可以表示为

${{H\beta }} = {{T}}$

(7)

式中H表示隐藏层的矩阵。H矩阵第i行代表输入层中第i个实例在隐藏层所有神经元上的输出，H矩阵的第j列代表所有训练样本在第j个隐藏层神经元上的输出，即

$\begin{gathered} {{H}}\left( {{a_1}, \cdots ,{a_L},{b_1}, \cdots ,{b_l},{x_1}, \cdots ,{x_n}} \right) = \\ {\left[ {\begin{array}{*{20}{c}} {G\left( {{a_1},{b_1},{x_1}} \right)}&{...}&{G\left( {{a_L},{b_L},{x_1}} \right)} \\ \vdots &{}& \vdots \\ {G\left( {{a_1},{b_1},{x_N}} \right)}&{...}&{G\left( {{a_L},{b_L},{x_N}} \right)} \end{array}} \right]_{N \times L}} \\ \end{gathered} $

(8)

$ {{\beta }} = {\left[ {\begin{array}{*{20}{c}} {{{\beta}} _1^{\rm{T}}} \\ {{{\beta}} _2^{\rm{T}}} \\ \vdots \\ {{{\beta}} _L^{\rm{T}}} \end{array}} \right]_{L \times m}}\;\;{{T}} = {\left[ {\begin{array}{*{20}{c}} {{{t}}_1^{\rm{T}}} \\ {{{t}}_2^{\rm{T}}} \\ \vdots \\ {{{t}}_N^{\rm{T}}} \end{array}} \right]_{N \times m}} $

(9)

在已知权值和偏置的情况下，上面问题的求解就转化为求解线性系统 ${{H}}{{\beta}} = {{T}}$ 的最小范数最小二乘解：

$\hat {{\beta}} ={{{H}}^{{{\dagger } }}}{{T}}$

(10)

式中： ${{{H}}^{{{\dagger} }}}$ 是 ${{H}}$ 的Moore-penrose广义逆矩阵； $\hat {{\beta}} $ 的范数是最小且唯一的。

2 提出的混合式重建方法 2.1 PSOECM方法

全部数据记录 ${{{X}}_{{t}}}$ 可以分为两个部分：用于训练模型的完整记录集 ${{{X}}_{{c}}}$ 和用于检验模型的不完整记录集 ${{{X}}_{{{ic}}}}$ 。

PSOECM方法步骤：

1)计算出 ${{{X}}_{{c}}}$ 的协方差矩阵。

2)在具有PSO随机初始化 $\tau $ 值的 ${{{X}}_{{c}}}$ 上应用ECM。

3)对 ${{{X}}_{{{ic}}}}$ 执行基于ECM的重建：通过测量除去缺失值的不完整记录与除去相同位置上值的群集中心 $C'$ 之间的欧几里德距离确定最近群集中心，由最近群集中心的对应属性值重建不完整记录的属性值( ${x_k}$ )。欧几里德距离的测定公式为

${D_j} = \sum\limits_{i = 1;i \ne k}^n {{{\left| {{x_i} - C{'_j}} \right|}^2}} $

(11)

式中： $j$ 为群集中心的数量； $n$ 为每条记录中完整成分的数量。

4)数据重建后计算 ${{{X}}_{{t}}}$ 的协方差矩阵。如果 ${{{X}}_{{t}}}$ 为 $\left( {m \times n} \right)$ 秩序的矩阵，则它的协方差矩阵 ${{T}}_{\rm{COV}}$ 就是一个 $n \times n$ 矩阵。如果 ${\rm{MSE}} \left( {{{X}}_{\rm{COV}},{{T}}_{\rm{COV}}} \right) < \varepsilon $ 且 $\left( {\left| {{\rm{Det}}\left( {{{X}}_{\rm{COV}}} \right) - {\rm{Det}}\left( {{{T}}_{\rm{COV}}} \right)} \right|} \right) < \varepsilon $ ，则退出计算。否则，调用PSO选出改善后的 $\tau $ 值。其中 $\varepsilon $ 为预先设定的小正值， ${\rm{MSE}} \left( {{{X}}_{\rm{COV}},{{T}}_{\rm{COV}}} \right)$ 为 ${{X}}_{\rm{COV}}$ 和 ${{T}}_{\rm{COV}}$ 元素之间的均方差， ${\rm{Det}}\left( {{{X}}_{\rm{COV}}} \right)$ 是 ${{X}}_{\rm{COV}}$ 的行列式， ${\rm{Det}}\left( {{{T}}_{\rm{COV}}} \right)$ 是 ${{T}}_{\rm{COV}}$ 的行列式。

5) 重复1)～4)直至收敛。

计算平均绝对百分比误差(mean absolute percentage error，MAPE)值：

${\rm{MAPE}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\frac{{{x_i} - {{\hat x}_i}}}{{{x_i}}}} \right|} \times 100{\rm{\% }}$

(12)

式中： ${x_i}$ 为实际值； ${\hat x_i}$ 为预测值； $n$ 为缺失值的全部样本数量。

PSOECM方法采用与文献[6]相同的适应度函数 ${\rm{MSE}} \left( {{{X}}_{\rm{COV}},{{T}}_{\rm{COV}}} \right)$ 和 $\left( {\left| {{\rm{Det}}\left( {{{X}}_{\rm{COV}}} \right) - {\rm{Det}}\left( {{{T}}_{\rm{COV}}} \right)} \right|} \right)$ ，但文献[6]使用PSO重建缺失值，而PSOECM方法使用PSO以迭代的方式完成了上述两个适应度函数的最小化工作，只有两个适应度函数在两个连续迭代中都小于预先设定 $\varepsilon $ 值才停止运算，并计算出最佳 $\tau $ 值，再在ECM中使用PSO选择最佳 $\tau $ 值进行缺失数据重建。这样不仅可以得出最佳的数据重建，还可以保存数据的协方差结构。

2.2 MAAELM方法

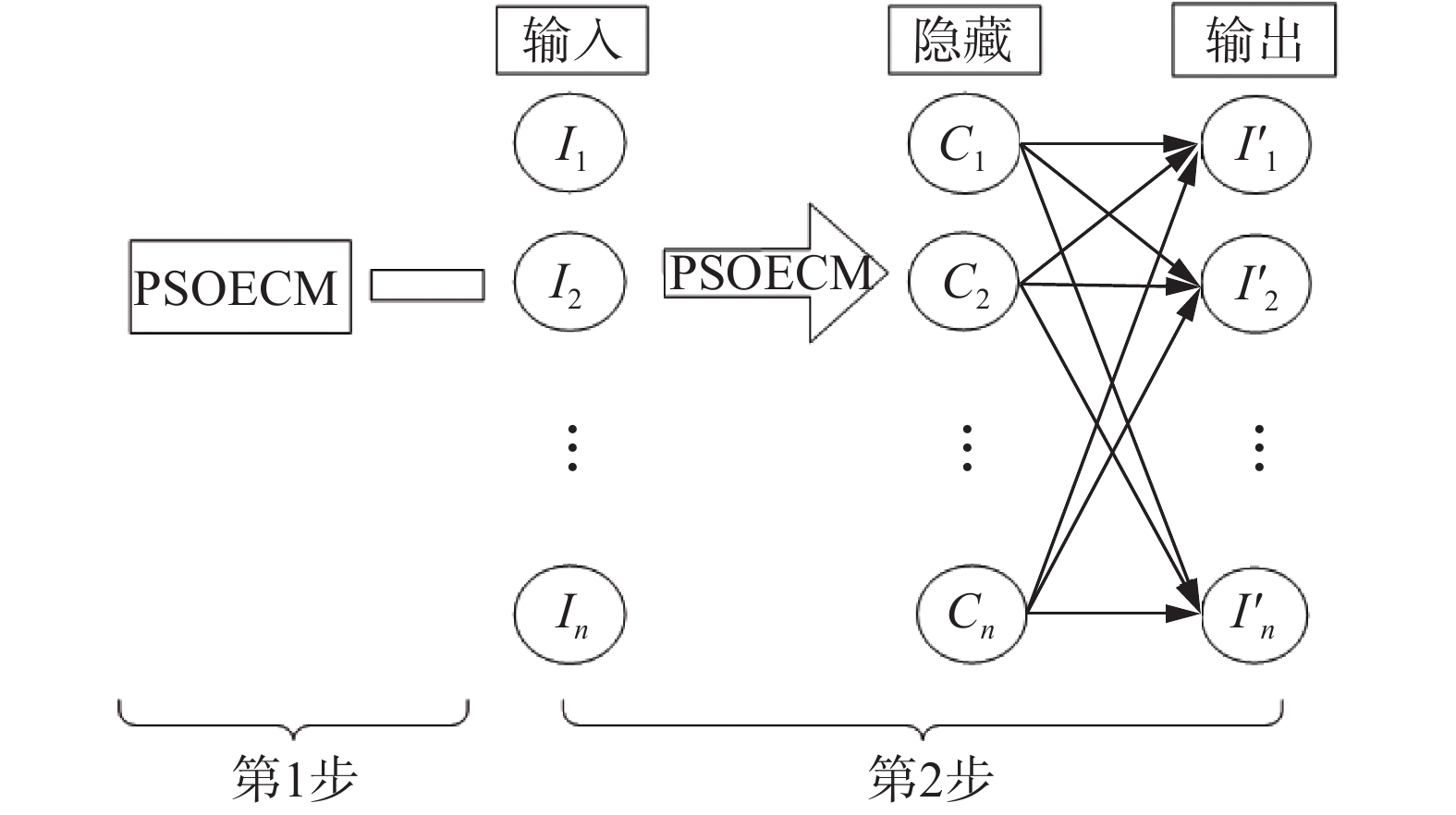
MAAELM方法采用PSOECM与AAELM混合重建缺失数据。MAAELM结构如图1所示。

MAAELM方法步骤：

1)将数据归一化至[0,1]范围内。

2)将数据集合分为完整记录集合和不完整记录集合。

3)在1)中执行基于PSOECM的重建，确定群集中心。

4)在2)中使用1)中得出的最佳 $\tau $ 值在完整记录集合中应用ECM。这相当于使用1)中得到的群集中心作为MAAELM结构中的隐藏节点。

5)执行PSOECM方法的3)。

6)计算得到各个群集中心之间的归一化欧几里德距离。

为了估算出隐藏层和输出层之间的权重，在6)得到的距离中应用激活函数并进行非线性转换，再应用Moore-Penrose广义逆矩阵得出 ${{{H}}^{{{†} }}}$ 。

最后，根据文献[12]使用Moore-Penrose广义逆矩阵求解 ${{{H}}^{{{†} }}}{{\beta}} ={{T}}$ 估算出隐藏层和输出层之间的权重，其中 ${{\beta}} $ 为权向量， ${{T}}$ 为目标向量。利用式(12)计算平均绝对百分误差(MAPE)值。

3 选取实验数据集与激活函数

实验选取UCI机器学习数据库中的6个标准数据集来进行验证，实验数据集如表1所示。同时，在选取的实验数据集上使用9个激活函数来研究它们对文章所提方法的影响。实验选取激活函数如表2所示。所选数据集中除Auto-mpg中的马力属性值存在缺失，其他5个数据集均不存在属性缺失值，所以通过随机删除原始数据集的一些值来进行实验，并创建了除目标变量以外的所有变量中的缺失值。每一个数据集被分成10个相等的小集合，其中9个小集合经过聚类处理，剩下的1个留下为缺失值备用。

为了在每一个小集合中创建缺失值，随机删除了近10%的值(单元)，并确保从每个记录中删除至少一个单元。因此，在10倍交叉验证中，有不同缺失记录的10个小集合。

对于完整记录集合中的各个小集合，将它们从全部记录中分理并用于聚类。在完整记录集合中应用ECM算法，并通过最近群集中心属性的对应值重建出不完整记录集合中的属性缺失值。

使用PSO优化算法和文献[6]提及的两个适应度函数为PSOECM选出最佳 $\tau $ 值，并将相同的 $\tau $ 值提供给MAAELM。对于所有数据集合，对比了本文所提方法与文献[6, 9-10, 15, 17]所提多种混合方法的MAPE平均值。

4 实验结果和分析

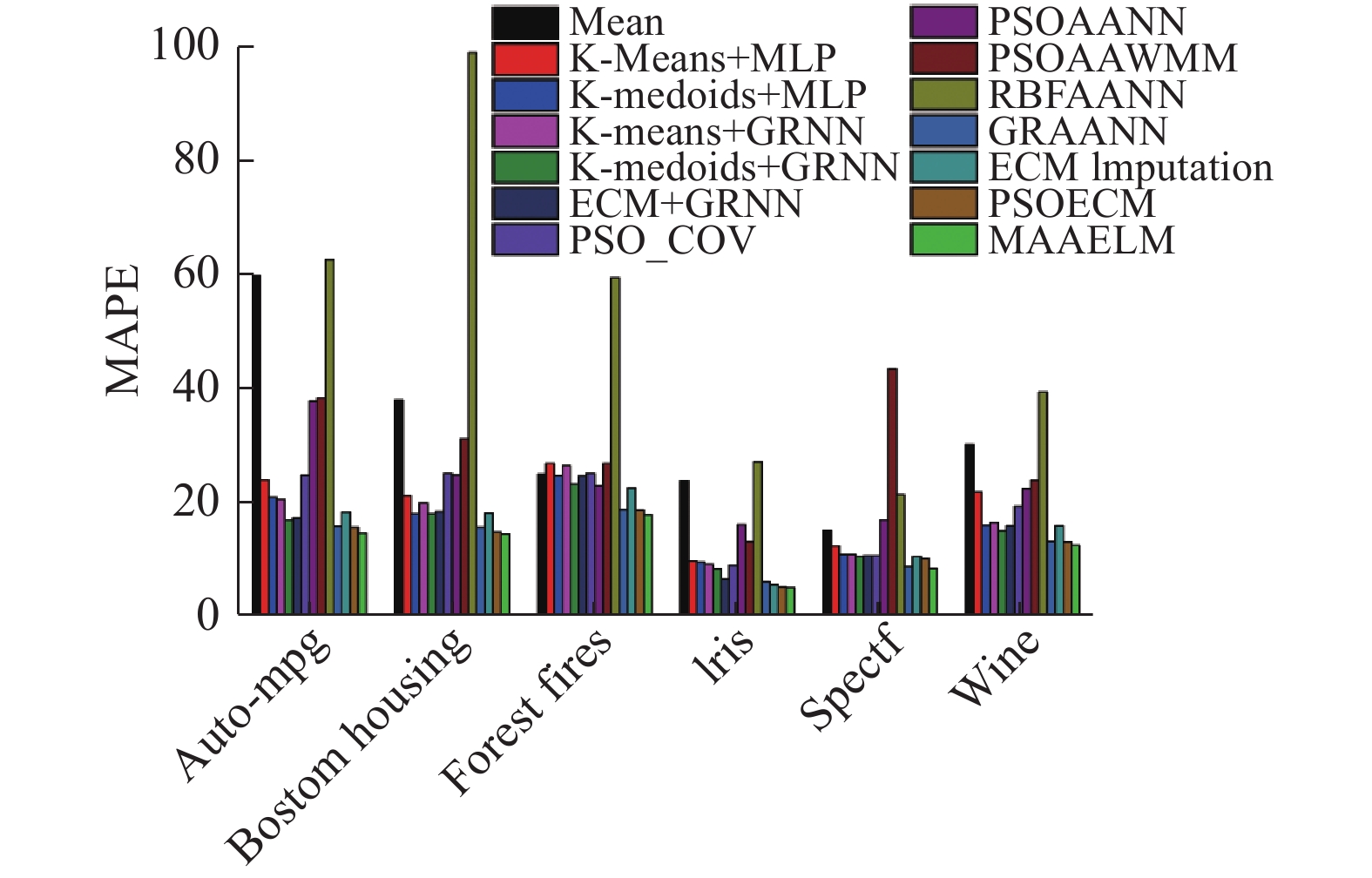
不同激活函数作用于MAAELM所得的MAPE值以及PSOECM、MAAELM与其他算法比较的结果如图2和图3所示。

根据图2所展示的不同激活函数作用于MAAELM所得的MAPE值可以发现：Sigmoid在所有激活函数中的表现最佳，Hardlim激活函数表现最差，而其他激活函数对于MAAELM的MAPE值影响基本相同。Hardlim激活函数表现最差是因为它将一个输入空间只分割为0和1两个类别。

图3中将本文所提算法与Krishna M和Ravi V^[6]的PSO_COV算法，Nishanth和Ravi^[9]的K-means+GRNN、K-medoids+MLP、K-medoids+GRNN、ECM+GRNN等算法，Gautam和Ravi^[10]的ECM Imputation算法，Ravi和Krishna^[15]的PSOAANN、PSOAAWNN、RBFAANN、GRAANN等算法，Ankaiah和 Ravi^[17]的K-Means+MLP算法的结果进行对比，对比结果显示了最佳 $\tau $ 值在所提方法中可以更有效地进行基于ECM的重建，以及在大部分数据集合上局部学习和整体学习混合使用优于文献[6, 9-10, 15, 17]所提方法。

在Auto-mpg 数据集合方面，只有K-medoids+GRNN、ECM+GRNN和GRAANN这3种混合法的结果与PSOECM方法接近，分别落后1.31%、1.65%和0.19%。PSOECM 通过选择最佳 $\tau $ 值，在Auto-mpg数据集合中的表现优于ECM重建。将PSOECM得出的相同 $\tau $ 值带入MAAELM时，误差又降低了0.96%。

在Boston Housing数据集合方面，除了GRAANN方法与PSOECM方法相差0.88%之外，其他方法的MAPE值至少比PSOECM高3%。PSOECM 通过选择最佳 $\tau $ 值，在Boston Housing数据集合中的表现同样优于ECM重建。在MAAELM中应用PSOECM得出的最佳 $\tau $ 值之后，MAPE值便可以进一步降低0.32%。

在Forest fires数据集合方面，可以观察到与Boston Housing数据集合相似的性能。除了GRAANN落后PSOECM的结果0.13%之外，其他方法的MAPE值比PSOECM至少高4%。PSOECM 通过选择最佳 $\tau $ 值，MAPE同样有所下降。在MAAELM中应用PSOECM得出最佳 $\tau $ 值之后，误差又降低了0.68%。

除了在Spectf 数据集合中，PSOECM略逊于GRAANN之外，在Iris、Spectf 和Wine recognition数据集合中，PSOECM与MAAELM同样表现出了类似在Auto-mpg、Boston Housing、Forest fires数据集合中的优势。

经上述实验结果的分析得出：1)PSOECM 通过选择最佳 $\tau $ 值，在各个数据集合中的表现优于ECM重建；2)将PSOECM得出的相同 $\tau $ 值代入MAAELM时，所得MAPE值均有所降低。

5 结束语

本文提出了2种新颖的缺失数据的混合式重建方法，并使用6个数据集验证了所提方法的有效性。发现由PSO为ECM选出的最佳 $\tau $ 值在 PSOECM和MAAELM的优异性能方面起到了重要作用，解决了 $\tau $ 值的选取困难和 $\tau $ 值对ECM重建结果的影响问题，同时去除了AAELM的随机性。下一步研究将增大实验数据集，验证本文所提方法在原始数据缺失不同百分比时的结果，以及使用更多的激活函数来进一步验证所提方法的有效性，并对所提方法与现有方法进行威尔克森符号秩检验，验证所提方法的显著性。