四轴飞行器凭借着其机械构造简单、方向控制灵活、抗干扰能力强、飞行稳定、可远距离遥控等特点，在科研与工程领域得到了广泛的应用。例如，在发生地震、台风等重大灾害的野外救援过程中，在安保、军事侦察中，在对电线进行巡线过程中，在对陌生空域进行地图构建过程中，这些应用场景都需要进行避障，因此对障碍物的准确识别非常重要。

在四轴飞行器的众多研究方向中，其在飞行过程中对障碍物的辨识是一个研究热点和难点。目前，国内外有许多研究机构和大学在四轴飞行器和无人机避障领域开展研究。文献[1]针对障碍物建立了障碍物威胁分级模型，提出了一种速度障碍圆弧法，该方法通过速度障碍圆弧参数对威胁障碍进行了量化。文献[2]在此基础上将动态不确定性通过威胁障碍速度矢量方向角的偏差进行表示，并且建立了动态不确定性速度障碍模型。文献[3]研究了一种基于Dubins路径的无人机的避障规划算法，通过采用遗传算法，结合无人机的飞行性能和最小转弯半径，提出了一种在已知障碍空间位置前提下的无人机路径算法。文献[4]针对路径规划中存在的快速移动威胁，提出基于威胁状态预测模型预测控制(MPC)算法，进行无人机动态路径规划。文献[5]设计微型UAV的避障导引律且能够满足避障不等式约束条件。文献[6]提出了一种解决多UAV避障的选择速度障碍法，设定了飞行器避障的优权准则、转弯速率，解决了多UAV之间的飞行冲突问题。文献[7]将光流传感器应用于避障中，结合改进的势场法，提高障碍辨识精度。文献[8-12]将人工势场法应用到三维空间中增加一个势场函数，以改善在狭小空间飞行器抖动问题。文献[13-14]提出了一种新的基于金字塔LK光流与平移光流融合的单目视觉避障算法。目前，已有的方法存在对障碍物辨识精度低，实时性差等不足。为了提高四轴飞行器在执行飞行任务过程中安全飞行能力，四轴飞行器需借助传感器对障碍物进行高精度的辨识。障碍物辨识主要通过各种传感器进行感知，其中大致分为2类，一类为被动传感器，主要是各种摄像头通过获取障碍物图像并进行相应处理，进而得到障碍物的各种信息，但是，视觉传感器容易受到环境影响，获取的信息可靠性差；另一类是主动传感器，即超声波、红外、激光测距等一些常见传感器，他们受环境影响小，感知信息准确度高。采用单一传感器获取环境障碍物信息能力较弱、误差大、精度低。为了进一步提高四轴飞行器障碍物检测准确度，提出采用超声波传感器、激光雷达传感器和红外传感器等几种传感器得到的信息通过改进的D-S证据理论算法进行融合。

1 D-S证据理论

D-S证据理论^[15]是由Dempster在1967年提出，并由Shafer进一步发展起来的一种具有不确定推理模型理论。被广泛地应用于处理各种不确定信息的数据融合算法。其优点是可以将大量的不同性质的主观不确定信息，通过D-S证据理论转变为确定性的决策信息。在四轴飞行器进行障碍物辨识的过程中，由于存在大量的干扰因素，以至于传感器得到的数据不准确，主观不确定性比较高，采用多种传感器对障碍物数据进行获取可以有效提高其准确性，而D-S证据理论是融合这类数据信息的有效途径之一^[16-18]。

1.1 基本概念

D-S证据理论使用集合的方式表示命题，把问题涉及到的所有可能取值定义为N个详细和具有排他性非空假设的一个非空集合 $\theta $ ，称为样本空间或者识别框架。 ${{\rm{2}}^\theta }$ 是 $\theta $ 所有子集组成的集合。

定义　在识别框架 $\theta $ 下，定义 $m\left( A \right)$ 是一个m： ${{\rm{2}}^\theta } \to {\rm{[0,1]}}$ 的函数。

1)基本概率赋值函数(BPA)

若满足下列条件：

$\left\{ {\begin{array}{*{20}{c}} {m\left( \text{Ø} \right) = {\rm{0}}\;\;\;\;} \\ {\displaystyle\sum\limits_{A \in \theta } {m\left( A \right) = {\rm{1}}} } \end{array}} \right.$

(1)

则 $m\left( A \right)$ 为基本赋值函数，其中， $\text{Ø}$ 为空集，如果 $m\left( A \right) > {\rm{0}}$ ， $A $ 称之为焦元， $m\left( A \right)$ 的作用是对命题的可信度进行分配， $m\left( A \right)$ 反映了证据对集合 $\theta $ 中命题 $A $ 支持程度。

2)信任函数(BEL)

${\rm{BEL}}\left( A \right) = \sum\limits_{B \subseteq A} {m\left( B \right)} ,\forall A \in {{\rm{2}}^\theta }$

(2)

式中： $\overline A = \varOmega - A;{\rm{BEL}}$ 是A的可信度。

3)似真函数(PL)

${\rm{PL}}\left( {{A}} \right) = {\rm{1}} - {\rm{BEL}}\left( {\overline A } \right) = \sum\limits_{B \cap A\phi } {m\left( B \right)} $

(3)

如图1所示，在有关于命题 $A $ 的证据中，有3种证据，即支持证据、中性证据、拒绝证据。

1.2 D-S证据理论组合规则

假设识别框架 $\theta $ 中用于障碍辨识的证据为 ${E_{\rm{1}}}$ 、 ${E_{\rm{2}}}$ ， ${E_{\rm{1}}}$ 、 ${E_{\rm{2}}}$ 的基本概率分配函数和焦元分别为 ${E_1}{\text{、}}{A_i}$ 和 ${E_2}{\text{、}}{B_j}$ 。定义函数m： ${{\rm{2}}^\theta } \to {\rm{[0,1]}}$ 是进行信息融合的信度函数分配，则有：

$m\left( A \right) = \left\{ {\begin{array}{*{20}{l}} {{\rm{0}},} \quad {A = \text{Ø} } \\ {\dfrac{{\rm{1}}}{{{\rm{1}} - K}},} \quad {A \ne \text{Ø} } \end{array}} \right.$

(4)

式中 $K = \displaystyle\sum\limits_{{A_i} \cap {B_j} = \phi } {{m_{{\rm{1}}}\left( {{A_i}} \right)}{m_{\rm{2}}}\left( {{B_j}} \right)} < {\rm{1}}$ 是不确定因子。

1.3 D-S证据理论证据冲突问题

由于面对复杂环境各种传感器在工作的时候会产生噪声、杂波等干扰信号，或者在工作中由于人为操作出现干扰信息等都有可能导致证据冲突^[19-21]。

设m₁、m₂是相同识别框架 ${{\rm{2}}^\theta }$ 上的2个相互独立的基本概率赋值，焦元分别是 ${A_{\rm{1}}}, {A_{\rm{2}}},\cdots ,{A_k}$ 和 ${B_{\rm{1}}},{B_{\rm{2}}} ,\cdots, {B_k}$ ，又设：

$K = \sum\limits_{{A_i} \cap {B_j} = \phi } {{m_{{\rm{1}}}\left( {{A_i}} \right)}{m_{\rm{2}}}\left( {{B_j}} \right)} < {\rm{1}}$

(5)

则其在融合之后的概率赋值函数m： ${{\rm{2}}^\theta }$ → $\left[ {0,1} \right]$ 对于所有的基本概率赋值函数的非空集合 $A $ 有：

$m\left( C \right) = \left\{{\begin{array}{{l}} {\displaystyle\sum\limits_{{A_i} \cap {B_j} = C} {{m_{\rm{1}}}\left( {{A_i}} \right){m_{\rm{2}}}\left( {{B_j}} \right)} ,\quad}{\forall C \in \theta {\text{且}}C \ne \text{Ø} } \\ {{\rm{0}},\quad}{C = \text{Ø} } \end{array} } \right.$

(6)

在式(6)中，若 $K \ne {\rm{1}}$ ，则m可以按照组合规则确定一个基本概率赋值，若 $K = {\rm{1}}$ 或者无限接近于1，则可以认为m₁、m₂证据矛盾，不能按照规则对基本概率赋值进行组合。

在解决证据冲突主要有2种途径，一种是改进D-S证据理论的Dempster组合规则，另一种就是认为这种原因是由于证据源的不确定性导致的，需要在融合之前处理传感器得到的信息源，修正证据。

1.4 证据权

当 $K \to {\rm{1}}$ ，即证据高度冲突时，利用原组合原则就会导致与实际常理相违背的结果，可以利用文献[22]提出的证据权对基本分配函数进行修正来解决此类问题。 ${m_i}{\text{、}}{m_j}$ 的距离定义为

$\begin{array}{c} d\left( {{m_{i,}}{m_j}} \right) = \\ \sqrt {\dfrac{{\rm{1}}}{{\rm{2}}}\left( {\left\langle {{M_i},{M_j}} \right\rangle + \left\langle {{M_j},{M_i}} \right\rangle - {\rm{2}}\left\langle {{M_i},{M_j}} \right\rangle } \right)} \end{array}$

(7)

其中

$\left\langle {{M_i},{M_j}} \right\rangle = \sum\limits_{{A_i}} {\sum\limits_{{A_j}} {{m_i}\left( {{A_i}} \right){m_j}\left( {{A_j}} \right)\frac{{\left| {{A_i} \cap {A_j}} \right|}}{{\left| {\left| {{A_i} \cup {A_j}} \right|} \right|}}} } $

(8)

${m_i}{\text{、}}{m_j}$ 的近似度定义为

$s\left( {{m_{\rm{1}}},{m_{\rm{2}}}} \right) = {\rm{1}} - d\left( {{m_{\rm{1}}},{m_{\rm{2}}}} \right)$

(9)

证据 ${e_i}$ 的基本概率分配函数与系统中其他的基本概率分配函数相似度之和为

$\alpha \left( {{m_i}} \right) = \sum\limits_{j = {\rm{1}},j \ne {\rm{1}}}^n {s\left( {{m_i},{m_j}} \right)} $

(10)

关键证据 ${e_f}$ 定义为

$\alpha \left( {{m_f}} \right) = \mathop {\rm max }\limits_{{\rm{1}} \leqslant i \leqslant n} \left\{ {\alpha \left( {{m_i}} \right)} \right\}$

(11)

各证据 ${e_i}$ 相对于关键证据的证据权定义为

${\beta _i} = \frac{{\alpha \left( {{m_i}} \right)}}{{\alpha \left( {{m_f}} \right)}}$

(12)

对证据 ${e_i}$ 的基本概率分配函数修正为

$m_i'\left( A \right) = {\beta _i}{m_i}\left( A \right),\forall A \in {{\rm{2}}^\theta },A \ne \theta $

(13)

$m_i'\left( \theta \right) = {\beta _i}{m_i}\left( \theta \right) + \left( {{\rm{1}} - {\beta _i}} \right)$

(14)

式(13)的作用是使证据权小的证据的元素A所提供的确定性信息减小。式(14)使得证据权小的证据的不确定性元素 $\theta $ 所提供的不确定性信息增加。

2 D-S证据最优权值优化算法

由于各传感器提供的数据证据源不同，所以需要对各种证据进行加权处理，在加权证据合成过程中，权值的确定是基础也是核心关键。如果不能获取优化的权值将严重影响融合结果。果蝇算法实现简单，全程只有进化代数与种群规模2个参数需要调节，而且有强大的全局寻优能力。对权值优化有很好的效果。

2.1 果蝇算法

果蝇优化算法^[23-24](fruit fly optimization algorithm, FOA)是基于果蝇觅食行为的仿生学原理而提出的一种新兴群体智能优化算法。首先果蝇利用其灵敏的嗅觉迅速定位出食物的大概方位，并快速飞近食物源；其次在靠近食物一定距离时，利用其敏锐视觉系统找到同伴及食物的准确位置，并飞向此位置。果蝇优化算法基本原理可以概括为：1)嗅觉搜索阶段：利用嗅觉感知空气中各种气味，并判断出食物的大致距离，靠近食物；2)视觉定位阶段：在靠近食物后，达到可视距离后，准确判断食物的确切位置，飞向食物。

2.2 果蝇算法优化权值

传统多传感器信息融合过程中通常采用专家打分赋值或者用的是专家经验对其赋值的方法，这种方法主观性比较强，很大程度上对融合效果产生影响。

本文根据实际情况，给出传感器提供的证据源F₁，F₂， $ \cdots, {{F}_{t}} $ 。以及对应的目标 ${G_0}$ ，根据传感器本身工作性能，以及对其长期测试或者多周期循环测量，通过统计试验将传感器识别结果与真实目标对比，结合专家经验给出这些证据权值的上限值 $\;\beta _i^{\;{\rm{max}} }$ 和下限值 $\;\beta _i^{\;{\rm{min}} }$ 。证据融合的最终目标就是准确的识别出正确的目标，也就是被识别目标的合成的基本概率赋值与其他目标的差值最大，所以果蝇算法权值寻优就是寻找一个使得 ${G_0}$ 合成的基本概率赋值 $m\left( {{G_0}} \right)$ ，且与其他目标的差值绝对值最大，这个权值就是优化权值。本文介绍的这种权值优化方法既考虑了专家的主观作用，又部分消除了专家的主观误差，提升证据融合精度。

果蝇算法寻找最优权值步骤如下：

Step1　参数初始化

包括最大迭代次数、群体规模、随机初始化果蝇群体位置范围(LR)以及果蝇随机方向和随机距离(FR)。

Step2　生成潜在解

1)把每个权值作为果蝇个体，对果蝇位置进行初始化：

${x_{ - \rm axis}} = {\rm random}\left( {\rm LR} \right)$

${y_{ -\rm axis}} = {\rm random}\left( {\rm LR} \right)$

2)根据已知嗅觉给出觅食果蝇飞行的随机方向和随机距离：

${x_i} = {x_{ - \rm axis}} + {\rm random}\left( {\rm FR} \right)$

${y_i} = {y_{ - \rm axis}} + {\rm random}\left( {\rm FR} \right)$

3)计算觅食果蝇与原点的距离：

${D_i} = \sqrt {x_i^{\rm{2}} + y_i^{\rm{2}}} $

4)计算气味浓度判定值 ${S_i}$ ：

${S_i} = \frac{{\rm{1}}}{{{D_i}}}$

$\frac{{\rm{1}}}{{{D_i}}} = \sqrt {\begin{array}{*{20}{l}} {{{\left( {{x_{ -\rm axis}} + {\rm random}\left( {\rm FR} \right)} \right)}^{\rm{2}}}}+\\ { {{\left( {{y_{ - \rm axis}} + {\rm random}\left( {\rm FR} \right)} \right)}^{\rm{2}}}} \end{array}} $

Step3　将气味浓度判定值 ${S_i}$ 代入目标函数(function)中计算个体果蝇所处位置的气味浓度 $\left( {{\rm{Smel}}{{\rm{l}}_i}} \right)$

${\rm{Smel}}{{\rm{l}}_i} = {\rm{function}}\left( {{S_i}} \right)$

其中，function目标函数为

$F = {\rm max} \left\{ {{\rm min} \left[ {m\left( {{C_{\rm{0}}}} \right) - m\left( {{C_i}} \right)\left| {i = {\rm{1}},2, \cdots ,N - {\rm{1}}} \right.} \right]} \right\}$

Step4　寻到群体中最优的气味浓度和个体位置，本文取最大值

$\left[ {\rm bestSmell\;bestindex} \right] = ｛\rm max｝ \left( {\rm Smell} \right)$

Step5　果蝇群体飞向气味浓度最大值的果蝇个体，形成新的果蝇群体位置，记录此时的权值

$\begin{array}{*{20}{c}} {\rm Smell\;best = best\;smell}\\ {{X_{{\rm{ - }}\rm axis}} = X\left( {\rm bestindex} \right)}\\ {{Y_{{\rm{ - }}\rm axis}} = Y\left( {\rm bestindex} \right)} \end{array}$

Step6　开始迭代优化，重复执行step2~step5，当气味浓度值在约束条件下不再优于先前的迭代气味浓度或者迭代数达到最大时，循环停止，并将此时的权值代入D-S证据理论中进行多传感器信息融合。

约束条件为

$m\left( c \right) = \left\{ {\begin{array}{l} {\begin{array}{l} \!\!\! \!\!\! \!\!\! {\rm{0}},\;\;{C = \text{Ø} } \end{array}} \\ {\begin{array}{*{20}{c}} \!\!\! \!\!\! \!\!\! {\displaystyle\sum\limits_{{A_i} \cap {B_j}} {\frac{{m_{\rm{1}}^{{\beta _{\rm{1}}}}\left( {{A_{\rm{1}}}} \right)m_{\rm{2}}^{{\beta _{\rm{2}}}}\left( {{B_j}} \right)}}{{{\rm{1}} - {K_{\rm{1}}}}}} },\;\;{\forall C \subset \theta ,}{C \ne \text{Ø} } \end{array}} \end{array}} \right.$

$\begin{array}{*{20}{c}} {{K_{\rm{1}}} = \displaystyle\sum\limits_{{A_i} \cap {B_j} = C} {\frac{{m_1^{{\beta _1}}\left( {{A_i}} \right)m_{\rm{2}}^{{\beta _{\rm{2}}}}\left( {{B_j}} \right)}}{{\left( {{\rm{1}} - {K_{\rm{1}}}} \right)}} < {\rm{1}}}}\\ {m\left( {{C_{\rm{0}}}} \right) - m\left( {{C_i}} \right) > {\rm{0}}} \end{array} $

(15)

${\rm{0}} \leqslant {\beta _i} \leqslant {\rm{1}},\sum\limits_{i = 1}^N {{\beta _i}} = {\rm{1}},\beta _i^{{\rm{min}} } \leqslant {\beta _i} \leqslant \beta _i^{{\rm{max}} }$

式中：N为命题个数； $m\left( {{C_i}} \right)\; \left( {i = {\rm{1}}, 2,\cdots, N - {\rm{1}}} \right)$ 为其他命题的合成基本概率赋值； $\;\beta _i^{\;{\rm{min}} }{\text{、}}\;\beta _i^{\;{\rm{max}} }$ 分别为专家经验给出的加权值上限和下限。

3 四轴飞行器信息检测系统

四轴飞行器多传感器信息融合^[25-26]中使用的传感器由超声波传感器、红外测距传感器、激光雷达传感器构成。3种测距传感器同时对障碍物进行距离测量获取环境信息。

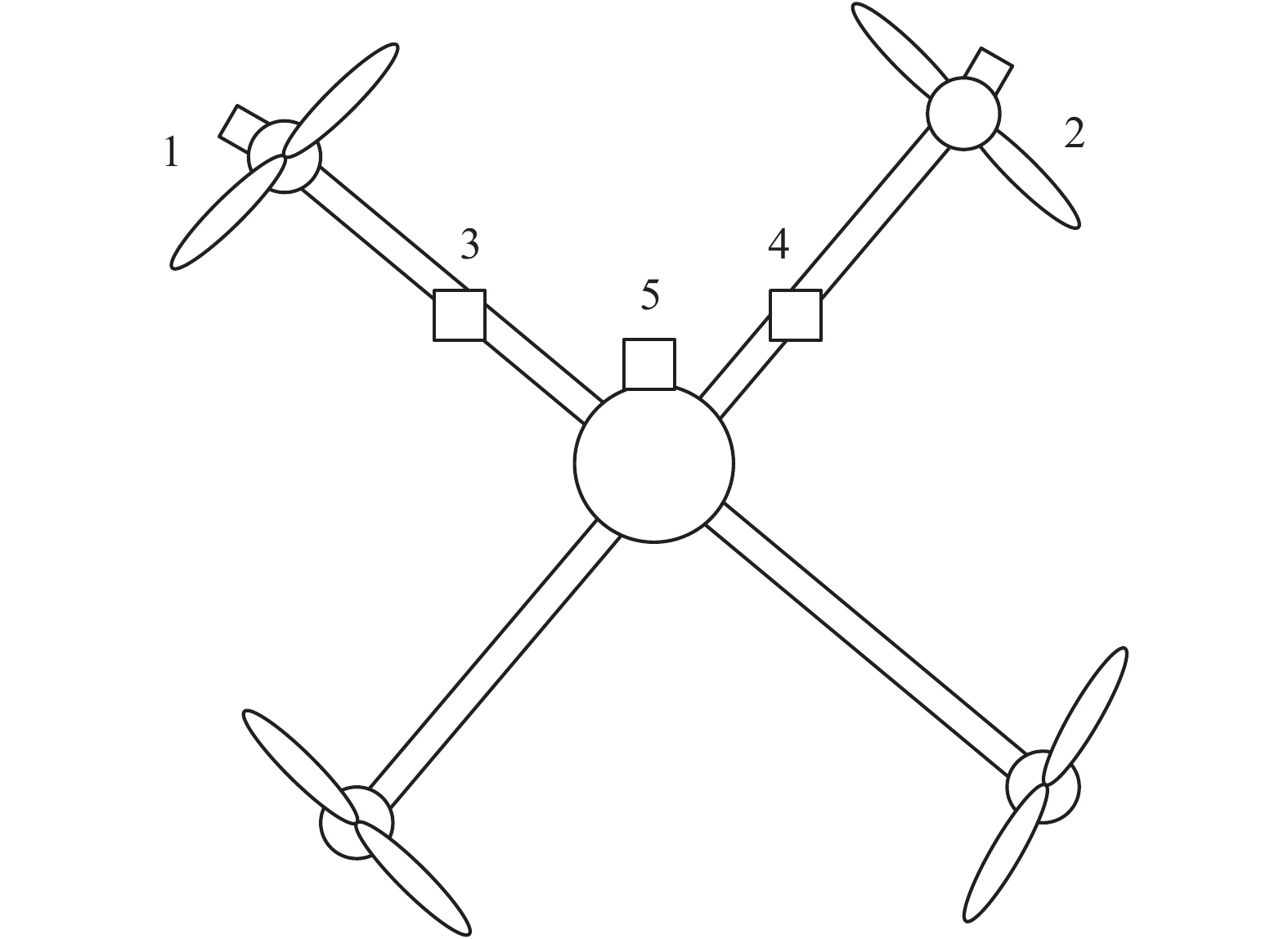
超声波传感器使用的是超声波信号，所以其几乎不受灰尘、烟雾，以及复杂的电磁场干扰等恶劣环境的影响。激光传感器具有量程范围广、测量精度高、检测实时性好、重量轻等特点。红外传感器具有角分辨率高、功耗低，不会出现镜面反射的等特点。图2为传感器安装示意图，分别标记为1、2、3、4、5。其中，1、2为超声波传感器，3和4是激光雷达传感器，5是红外传感器。

4 基于FOA-DS的多传感器信息融合技术在四轴飞行器障碍辨识中的应用

本文采用果蝇算法对证据源各组证据的证据权进行优化，寻找最优权值，进而进行信息融合，步骤如下：

1)获取证据源，参考专家经验给出的权值上下限，确定范围。

2)由果蝇算法在范围内按照2.2节寻找最优权值。

3)将最优权值按照式(7)~(14)进行基本概率重分配，以满足D-S证据理论组合规则对各证据的权重要求相同的条件。

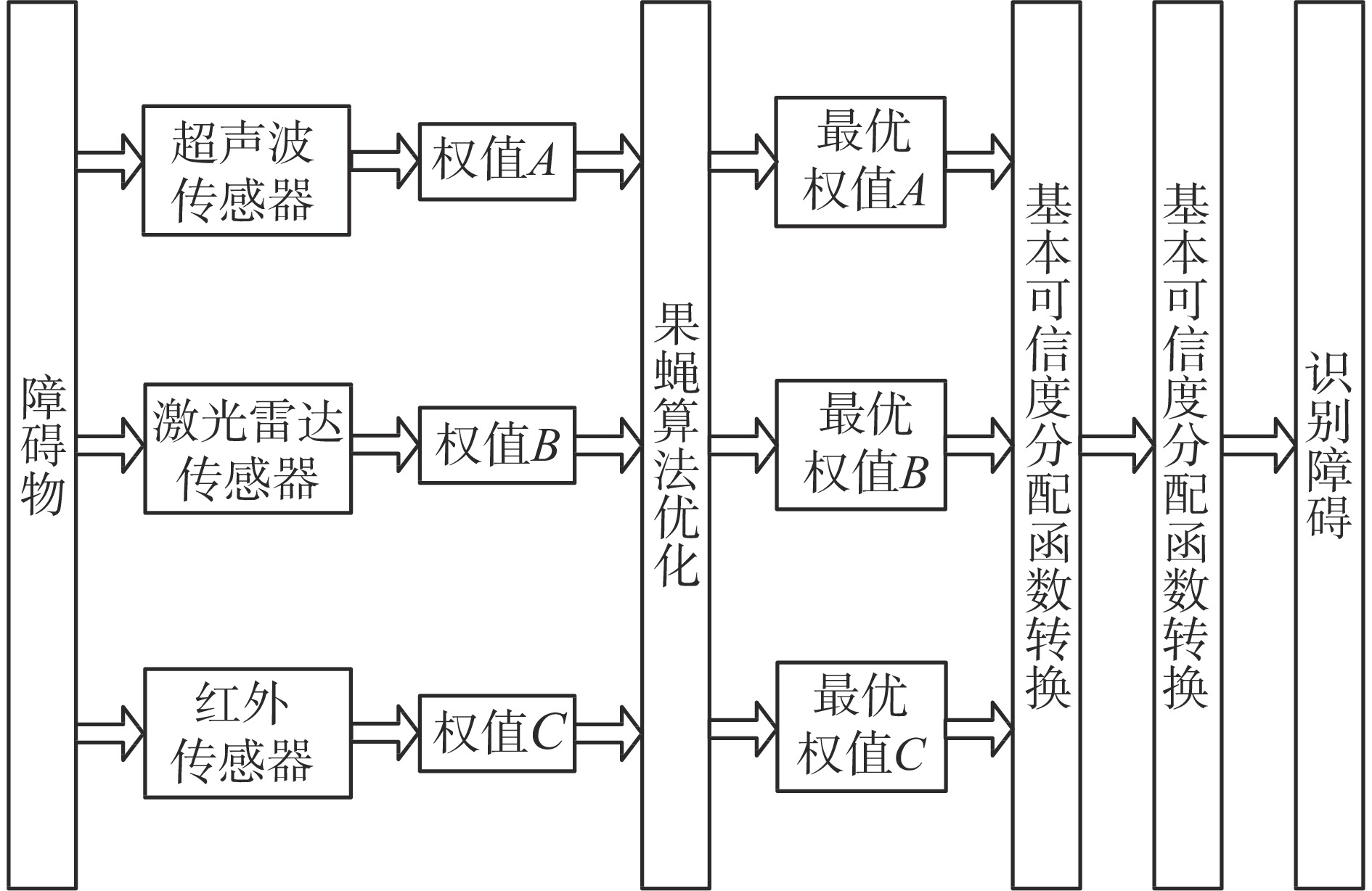
4)按照组合规则进行数据融合输出结果。FOA−DS证据理论障碍辨识流程如图3所示。

将搭载超声波传感器、激光雷达传感器、红外传感器的四轴飞行器对一块陌生空域进行障碍辨识，识别框架为：{有障碍(A)，无障碍(B)，不确定因素(C)}。由经验给出一定权值范围分别为(0.4，0.65)、(0.25，0.45)、(0.08，0.20)，由果蝇算法在范围内利用式(23)~(28)寻找最优权值，分别为0.55、0.3、0.15。然后，利用式(15)求取证据的融合结果。

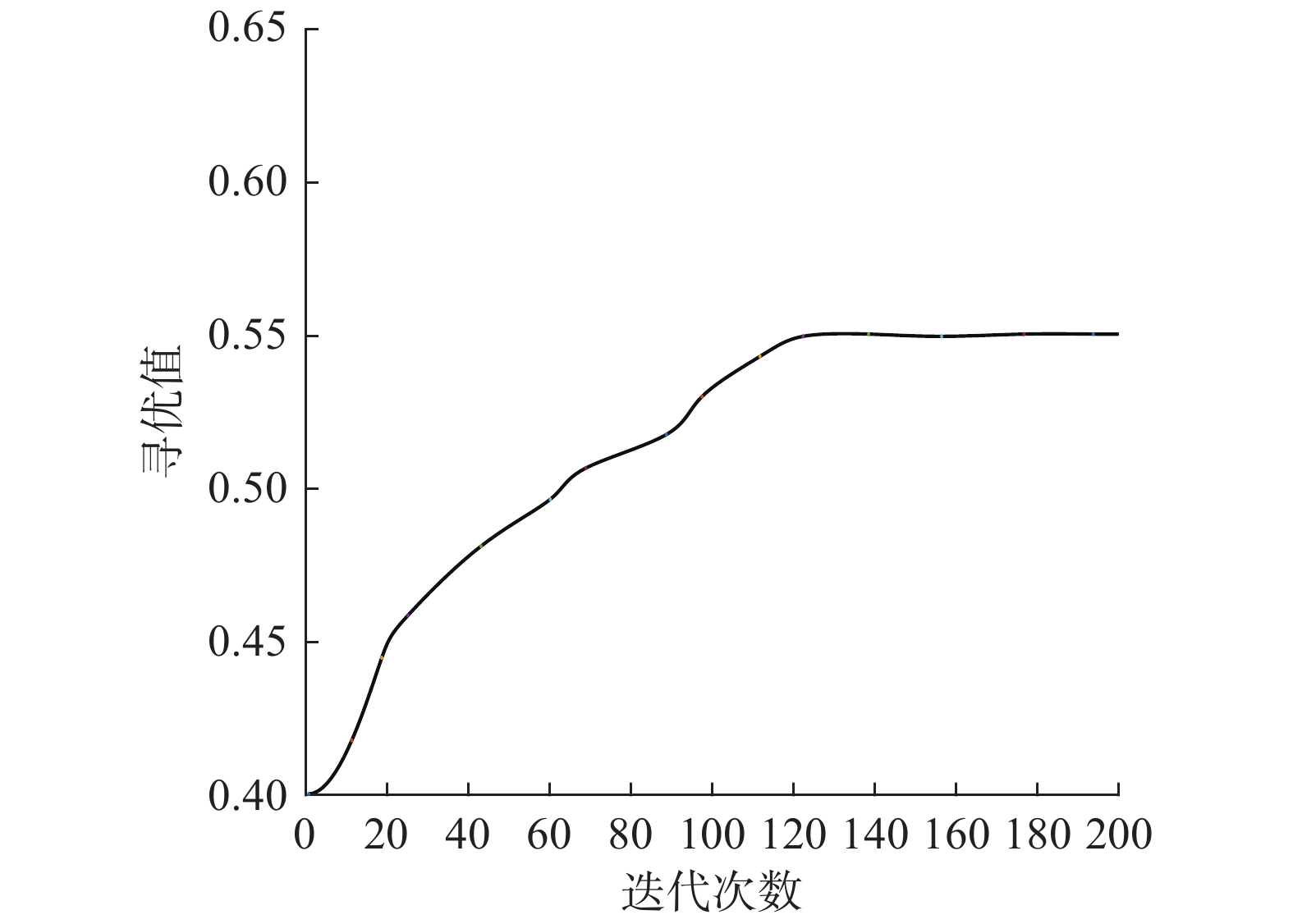
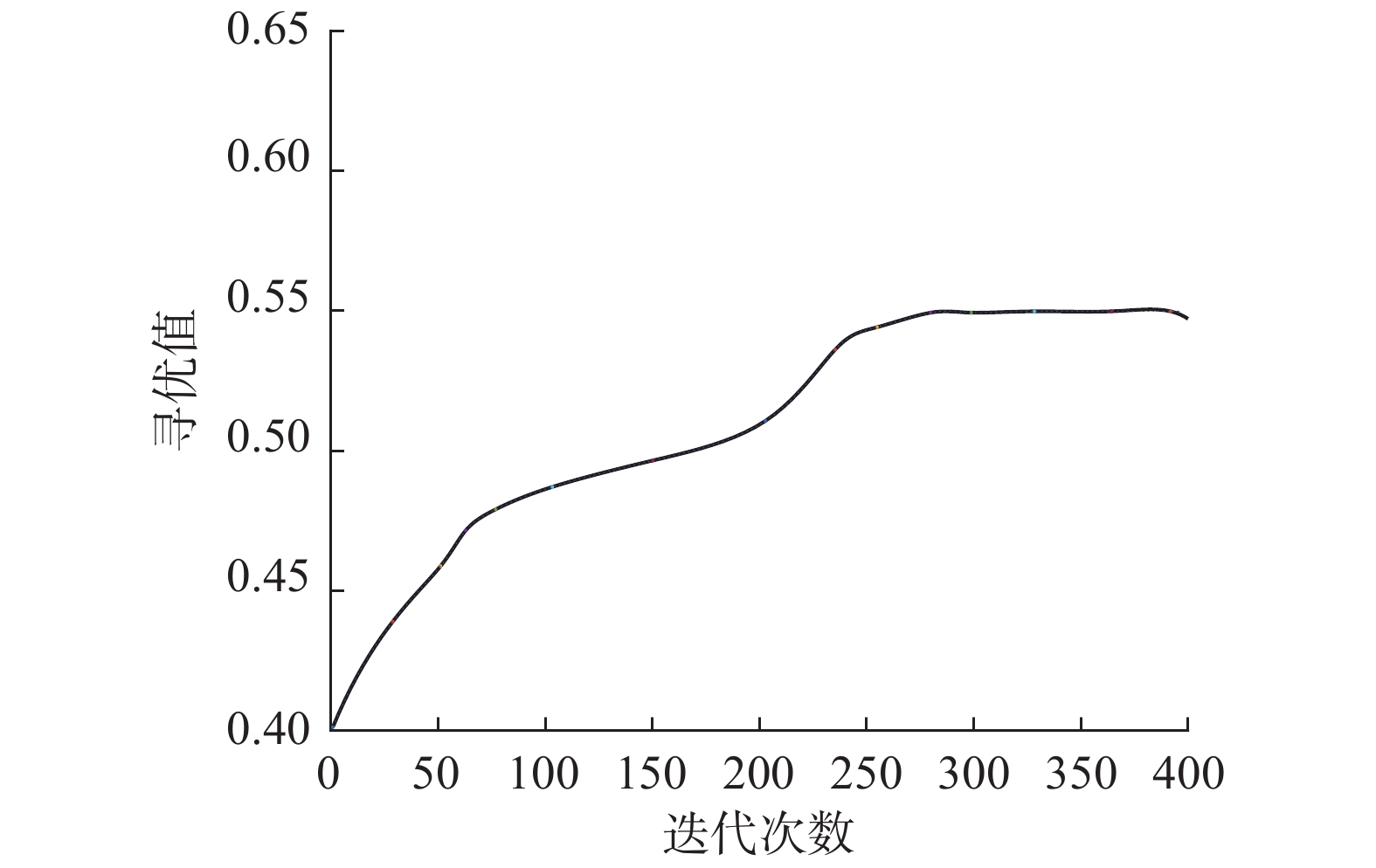
在寻找最优权值的过程中，使用果蝇算法和PSO粒子群寻优算法比较二者寻优性能。图4、5是超声波传感器最优权值寻找迭代次数。

由图4、5可知，果蝇算法在迭代了120次左右就寻得了最优权值，而PSO粒子群算法则是在进行了250多次迭代后才确定最优权值，由此可以得出果蝇算法寻找最优权值更加迅速，符合本文需求。

实验场地选在50 m×50 m的开放空域，设置不同形状的气模模拟障碍物。表1是3次实验中各传感器提供的基本可信度分配函数以及融合结果。表2是加权转换后的基本可信度分配函数及融合结果。

由表2可知，识别框架中各个基本命题的信任函数为

$ \begin{array}{*{20}{c}} {{\rm{BEL}}\left( {{A}} \right) = 0.629}\\ {{\rm{BEL}}\left( {{B}} \right) = 0.135}\\ {{\rm{BEL}}\left( {{C}} \right) = 0.112} \end{array} $

由判决结果可以得出有障碍。

为了突出算法的优越性，在实验中其余条件相同的情况下，只保留超声波传感器工作，以用来验证单一传感器与多传感器障碍识别效果对比。

此时识别框架中各个基本命题的信任函数为

$ \begin{array}{*{20}{c}} {{\rm{BEL}}\left( {{A}} \right) = 0.362}\\ {{\rm{BEL}}\left( {{B}} \right) = 0.253}\\ {{\rm{BEL}}\left( {{C}} \right) = 0.385} \end{array} $

无法准确识别出障碍物。

同理，验证其余传感器，结果显示均无法准确识别出障碍物。

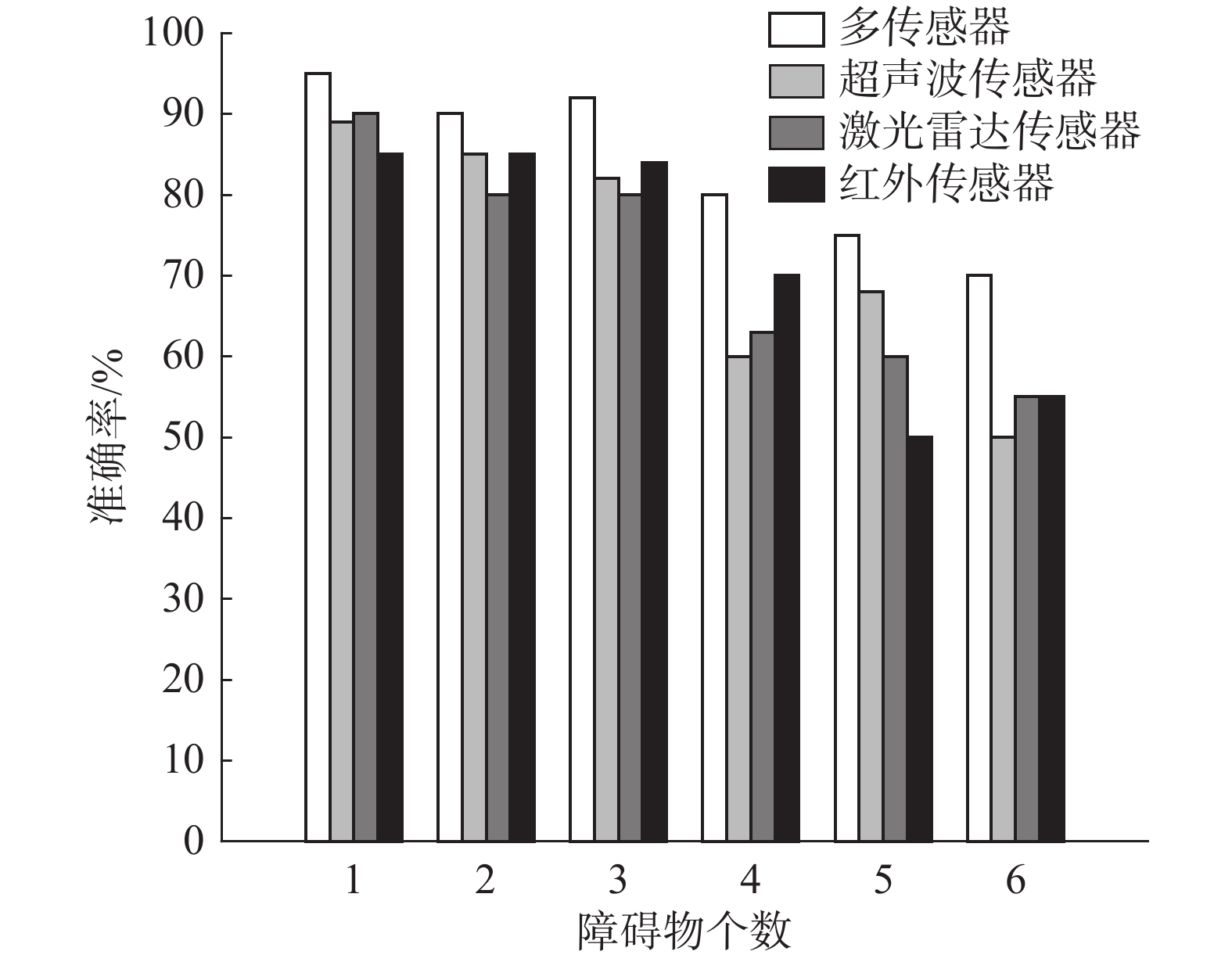
在飞行速度为0.5 m/s的情况下对不同数量的障碍物分别进行20次试验，试验结果如图6所示。横轴为障碍物个数，纵轴为判断准确率，即飞行过程中识别出障碍物个数占障碍物总个数的百分比多次试验取均值。例如，障碍物个数为5时，每次试验识别出障碍物个数占5个障碍物个数的百分比，然后求取20次试验的平均值。图6中黑色条形代表多传感器对障碍物的识别准确率，白色的代表超声波传感器的准确率，浅灰色的代表激光雷达传感器的准确率，深灰色的代表红外传感器的准确率。从图6中可以看出，本文提出的多传感器信息融合障碍识别方法的准确率随着障碍物个数的逐渐增加而提高，其余单一传感器虽然识别准确率差别不大，但是整体来看其识别准确率远远低于本文提出的方法。

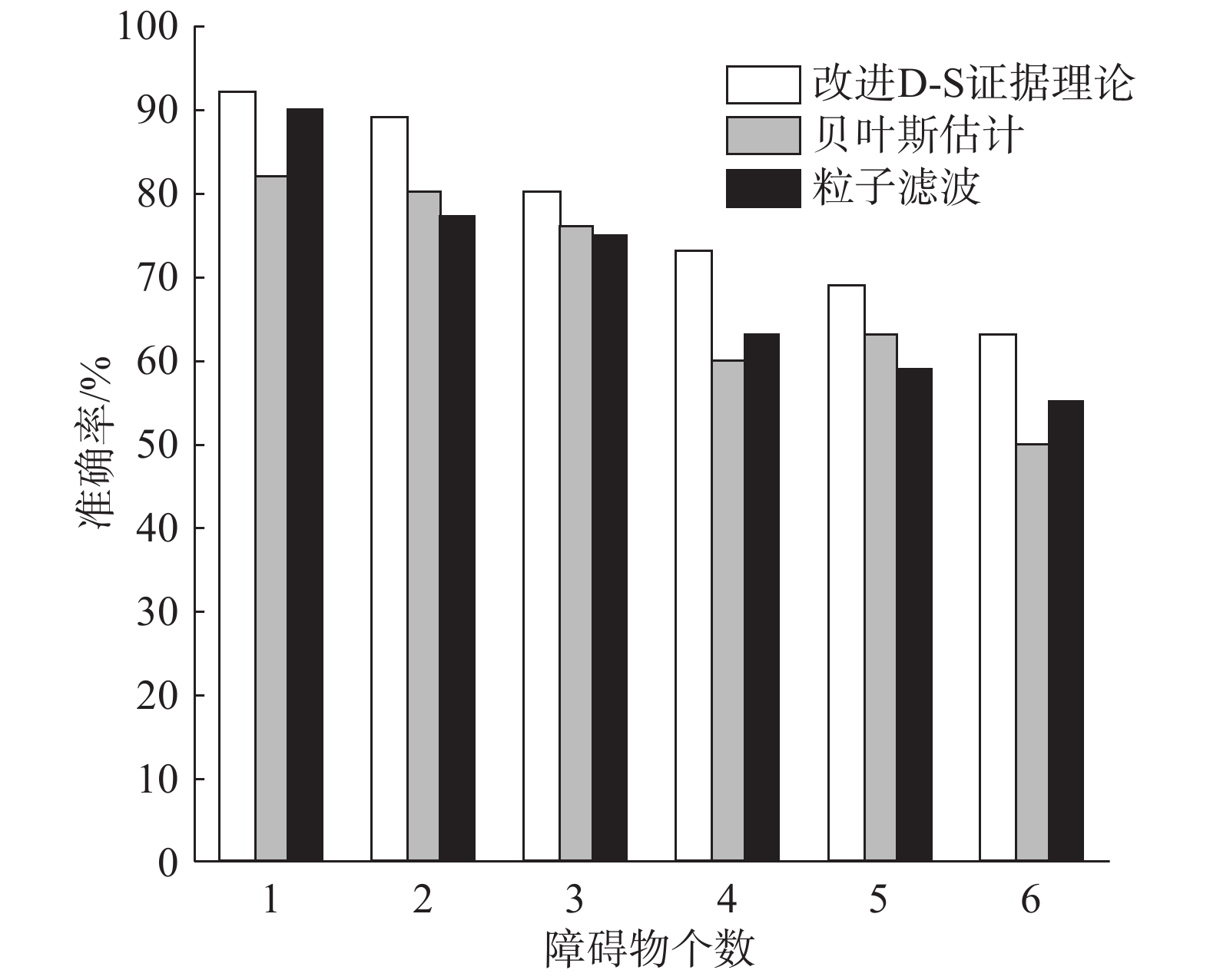
同时本文也将改进的D-S证据理论与贝叶斯估计以及粒子滤波数据融合算法进行了实验对比结果如图7所示，由图7中可以看出，贝叶斯估计与粒子滤波算法相比，于本文提出的方法精度存在一定差距。这是因为贝叶斯估计主观性较强，即贝叶斯估计用来判断的先验概率密度标准不一，由于不同的人对于先验概率的理解不同，故得出的结果也不尽相同，由于贝叶斯估计核心原理就是利用旧资料先验概率进行更精确的估计，故结果精度相差较大。粒子滤波算法在进行数据融合的时候容易出现粒子贫化问题，滤波精度不稳定，并且需要大量粒子才能对非线性系统进行准确估计，大大降低了算法的综合性以及辨识精度。

通过上述实验可知，本文提出的基于改进D-S证据理论的多传感器信息融合技术在实际应用中可以对障碍物进行高精度的识别，也验证了本问提出的方法的可行性。除此之外通过对算法执行时间和准确性的测试也反映出了算法的实时性和准确性。

5 结束语

为了提高四轴飞行器的避障效果，本文提出了利用超声波传感器、红外传感器和激光雷达传感器基于D-S证据理论的数据融合四轴飞行器障碍辨识方法。该方法利用果蝇优化算法对传感器原始数据的权值进行优化获取最优权值，其次通过D-S证据理论方法对信息进行融合。通过飞行试验验证，相比于单一传感器该方法能够更加有效地检测和定位障碍物的位置信息，对比同类数据融合算法，本文提出的方法对障碍物的识别率更高，能够使得四轴飞行器适应复杂的飞行环境。