云模型是李德毅院士创立的定性与定量相互转换的不确定性模型[1-2]。云模型在空间数据挖掘[3]、粒度计算[4]、图像分割[5]、控制[6]等领域有着广泛的深入应用。集合论是现代数学的基础,创立至今已有百年之久[7]。集合论的观点和方法渗透在现代数学的各个分支以及科学技术的许多领域之中,也是目前对系统进行数学描述的主要工具[8],集合论在电力系统[9]、指挥信息系统[10]和计算机科学[11]等领域均有应用。1965年Zadeh[12]提出了模糊集合理论,集合与模糊集合均是人工智能的基础理论。模糊数学在金融[13]、故障分析[14]、物资需求分析[15]、控制优化[16-17]、聚类算法[18]等方面均有应用。模糊集合中给出了交、并、补等基本运算,研究了截集及其运算,给出了分解定理,这些基本运算和定理是模糊数学进一步应用的基础。云模型表示的半定性半定量概念的运算,有赖于云模型的集合视角的理论扩展。如果能够从集合论的角度建立云模型的集合基础理论与方法,即云集合理论,并建立云集合与模糊集合、经典集合的转换桥梁,则可以进一步应用集合理论与方法拓展云模型的应用范围和领域,将来的进一步研究则有可能将云模型扩展到函数、关系、基数、有序集和序数等方面。因此构建云模型的集合论基础理论和方法具有十分重要的理论和实际意义。参照模糊集合,本文对云集合定义及其集合基础运算方法、云集合的截集与分解定理进行了研究。
1 云集合及其组成元素 1.1 云集合定义1 云集合。设
云集合和模糊集的关系:一个云集合对应多个模糊集,理论上对应无限个模糊集,因此云集合是一个无限集合;同时由于元素隶属度的随机性,云集合可看作包含多个模糊集的随机集合,所以云集合又是一个随机隶属度集合。模糊集可以看作是云集合的一次具体实现。云集合与模糊集之间的转化关系:设
| $\mathop A\limits_\wp = \Bigg\{ \mathop x\limits^\wp \left| {{u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )} \right. = {{\rm{e}}^{ - \frac{{{{(\mathop x\limits^\wp - {\rm{E}}x)}^2}}}{{2{\rm{E}}n{{_j'}^2}}}}}{\rm{, }}{\rm{E}}n_j' = {\rm{Nor}}({\rm{E}}n,He)\Bigg\} $ |
式中:
对集合内的所有
| $\mathop A\limits_{\sim} = \Bigg\{ \left. {\mathop x\limits^{\sim} } \right|{u_{\mathop A\limits_{\sim} }}(\mathop x\limits^{\sim} ) = {{\rm{e}}^{ - \frac{{{{(\mathop x\limits^{\sim} - {\rm{E}}x)}^2}}}{{2{{({\rm{Cer}}({\rm{E}}n_j'))}^2}}}}}\Bigg\} $ |
式中
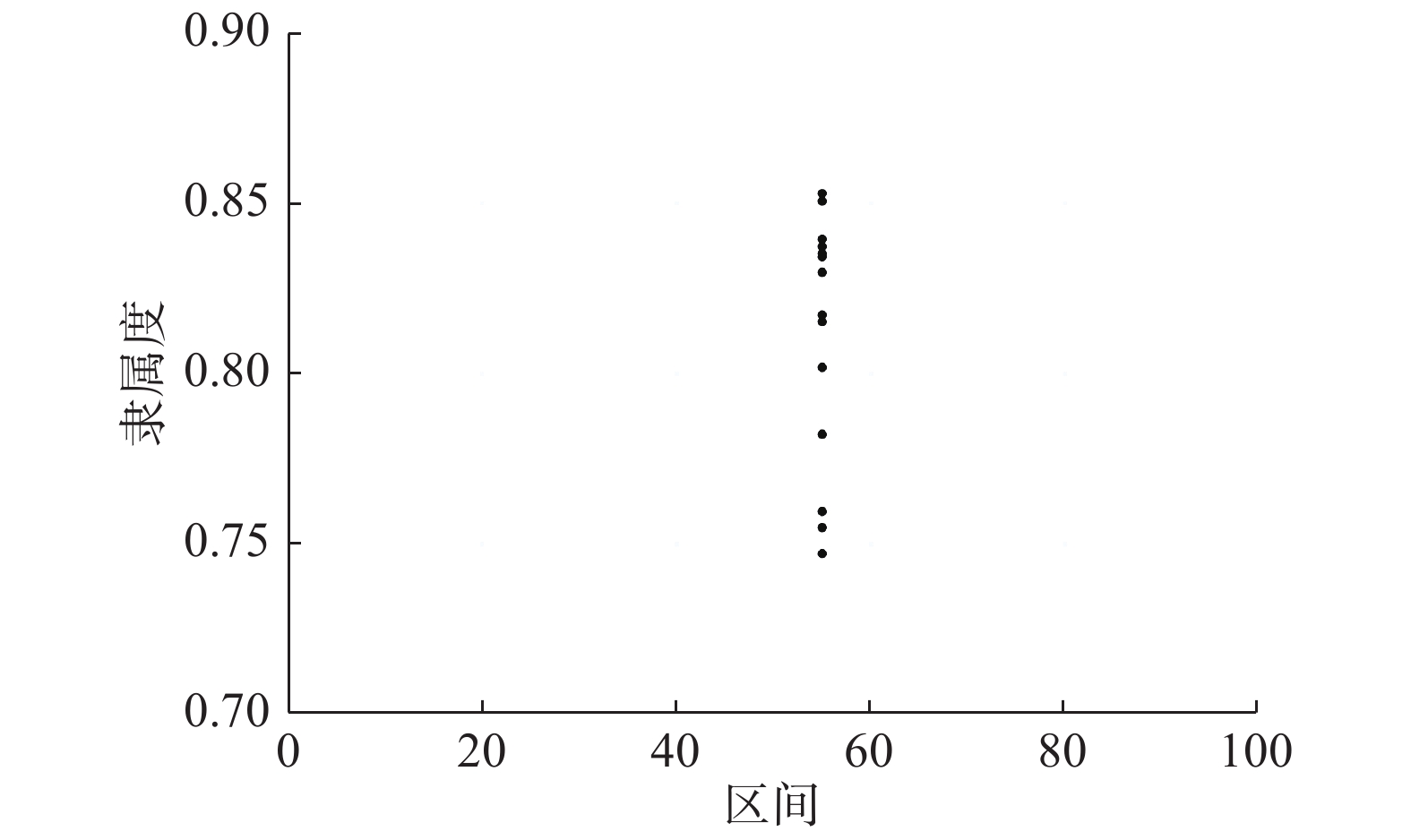
定义2 云集合元素。云集合元素定义为云集合中具有随机隶属度的数(元素)。当
1)首先生成以
2)令
因为在1)中生成的随机数有多种可能的值,所以2)中
|
Download:
|
| 图 1 具有随机隶属度的云集合元素 Fig. 1 Element of cloud set with random subjection degree | |
| $I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) = \left[ {{{\rm{e}}^{ - \frac{{{{(\mathop x\limits^\wp - {\rm{E}}{x_A})}^2}}}{{2{{({\rm{E}}{n_A}{\rm{ - }}3H{{\rm{e}}_A})}^2}}}}},\;{{\rm{e}}^{ - \frac{{{{(\mathop x\limits^\wp - {\rm{E}}{x_A})}^2}}}{{2{{({\rm{E}}{n_A} + 3H{{\rm{e}}_A})}^2}}}}}} \right],\quad \forall \mathop x\limits^\wp \in \mathop A\limits_\wp $ | (1) |
式(1)主要依据正态分布的
| $I({\rm{E}}n_j') = [{\rm{E}}n - 3He,{\rm{E}}n + 3He]$ |
| $\begin{array}{l} P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) \geqslant I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp ))) = P([{a^l},{b^r}] \geqslant [{a^l},{b^r}]) = \\ \left\{ {\begin{array}{*{20}{l}} 1,\quad{{a^l} \geqslant {b^r}} \\ {\dfrac{{{a^r} - {b^r}}}{{{a^r} - {b^l}}} + \dfrac{{{b^r} - {a^l}}}{{2({a^r} - {b^l})}}},\quad{{b^l} < {a^l} < {b^r} < {a^r}} \\ {\dfrac{1}{2}},\quad{{a^l} = {b^l},{a^r} = {b^r}} \\ {\dfrac{{{a^r} - {b^l}}}{{2({b^r} - {a^l})}}},\quad{{a^l} < {b^l} < {a^r} < {b^r}} \\ {\dfrac{{{a^r} - {b^r}}}{{{a^r} - {a^l}}} + \dfrac{{{b^r} - {b^l}}}{{2({a^r} - {a^l})}}},\quad{{a^l} < {b^l} < {b^r} < {a^r}} \\ {\dfrac{{{a^r} - {a^l}}}{{2({b^r} - {b^l})}}},\quad{{b^l} < {a^l} < {a^r} < {b^r}} \\ 0,\quad{{b^l} \geqslant {a^r}} \end{array}} \right. \\ \end{array} $ |
设
云集合
| $\begin{array}{l} \mathop A\limits_\wp = \mathop B\limits_\wp \Leftrightarrow {C_A}({\rm{E}}{x_A},{\rm{E}}{n_A},H{e_A}) = \\ {C_B}({\rm{E}}{x_B},{\rm{E}}{n_B},H{e_B}) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{\rm{E}}{x_A} = {\rm{E}}{x_B}} \\ {{\rm{E}}{n_{\rm{A}}} = {\rm{E}}{n_{\rm{B}}}} \\ {H{e_A} = H{e_B}} \end{array}} \right. \end{array} $ |
从集合运算的角度,对于
| $\left\{ {\begin{array}{*{20}{l}} {\mathop A\limits_\wp = \mathop B\limits_\wp \Leftrightarrow P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp ))) = \dfrac{1}{2}} \\ {{a^l} = {b^l},{a^r} = {b^r}} \end{array}} \right.$ |
云集合
|
Download:
|
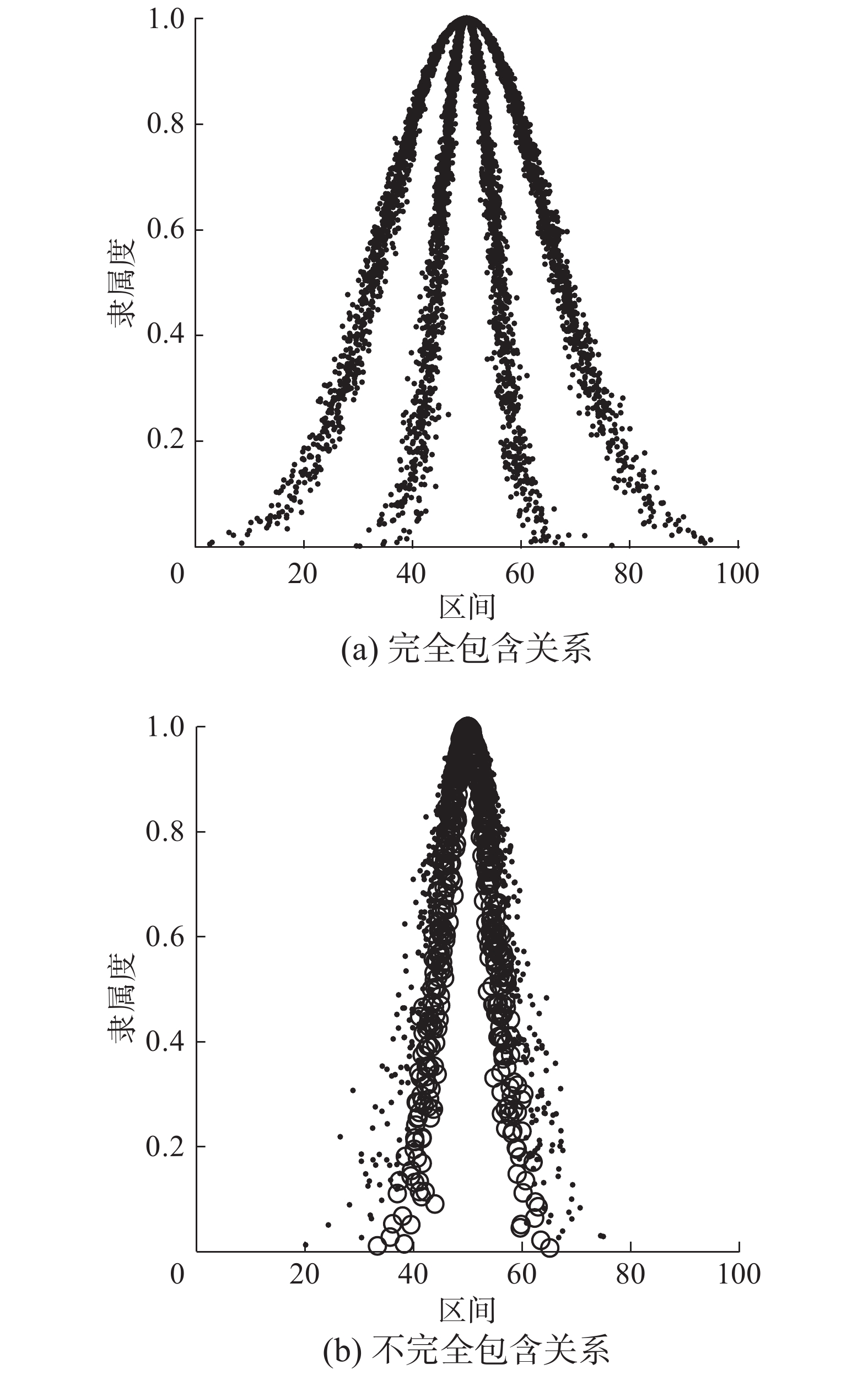
| 图 2 完全包含与不完全包含关系 Fig. 2 Relations between complete and incomplete inclusion | |
对于
| $\begin{array}{c} \mathop A\limits_\wp \supset \mathop B\limits_\wp \Leftrightarrow P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp ))) = 1 \Leftrightarrow \\ P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) >I( {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} $ |
对于论域内
| $\mathop A\limits_\wp \mathop \supseteq \limits^p \mathop B\limits_\wp \Leftrightarrow \frac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )))}}{{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1$ |
云集合
| ${u_{\mathop A\limits_\wp \cup \mathop B\limits_\wp }}\left( {\mathop x\limits^\wp } \right) = {u_{\mathop A\limits_\wp }}\left( {\mathop x\limits^\wp } \right) \vee {u_{\mathop B\limits_\wp }}\left( {\mathop x\limits^\wp } \right)$ |
符号“
| $\begin{array}{c} {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ) \vee {u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp ) = \\ \left\{ {\begin{array}{*{20}{l}} {{u_{\mathop A\limits_\wp }}\left( {\mathop x\limits^\wp } \right)},\quad{\dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )))}}{{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} > 1}\\ {{u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),{u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )},\quad{\dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )))}}{{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} = 1}\\ {{u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )},\quad{\dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )))}}{{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} <1}\\ {{u_{\mathop A\limits_\wp }}\left( {\mathop x\limits^\wp } \right)},\quad{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0} \end{array}} \right. \end{array}$ | (2) |
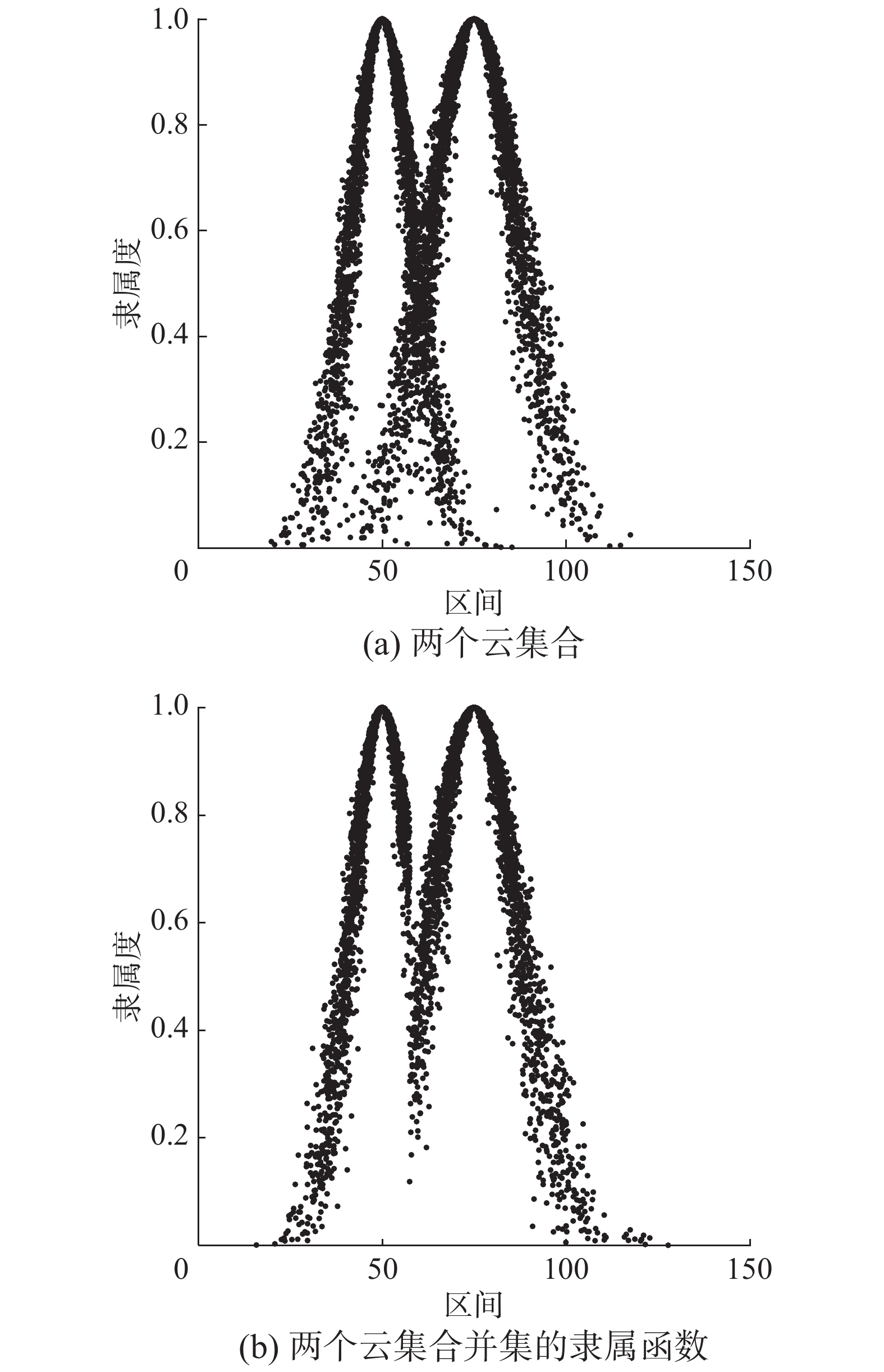
对于在论域
|
Download:
|
| 图 3 两个云集合及其并集隶属函数 Fig. 3 Two cloud sets and the subjection degree function of their union | |
云集合
| ${u_{\mathop A\limits_\wp \cap \mathop B\limits_\wp }}(\mathop x\limits^\wp ) = {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ) \wedge {u_{\mathop B\limits_\wp }}\left( {\mathop x\limits^\wp } \right)$ |
符号“
| $\begin{array}{c} {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ) \wedge {u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp ) = \\ \left\{ {\begin{array}{*{20}{l}} {{u_{\mathop A\limits_\wp }}\left( {\mathop x\limits^\wp } \right)},\quad{\dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )))}}{{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} <1}\\ {{u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),{u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )},\quad{\dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )))}}{{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} = 1}\\ {{u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )},\quad{\dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )))}}{{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} > 1}\\ {{u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )},\quad{P(I({u_{\mathop B\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0} \end{array}} \right. \end{array}$ | (3) |
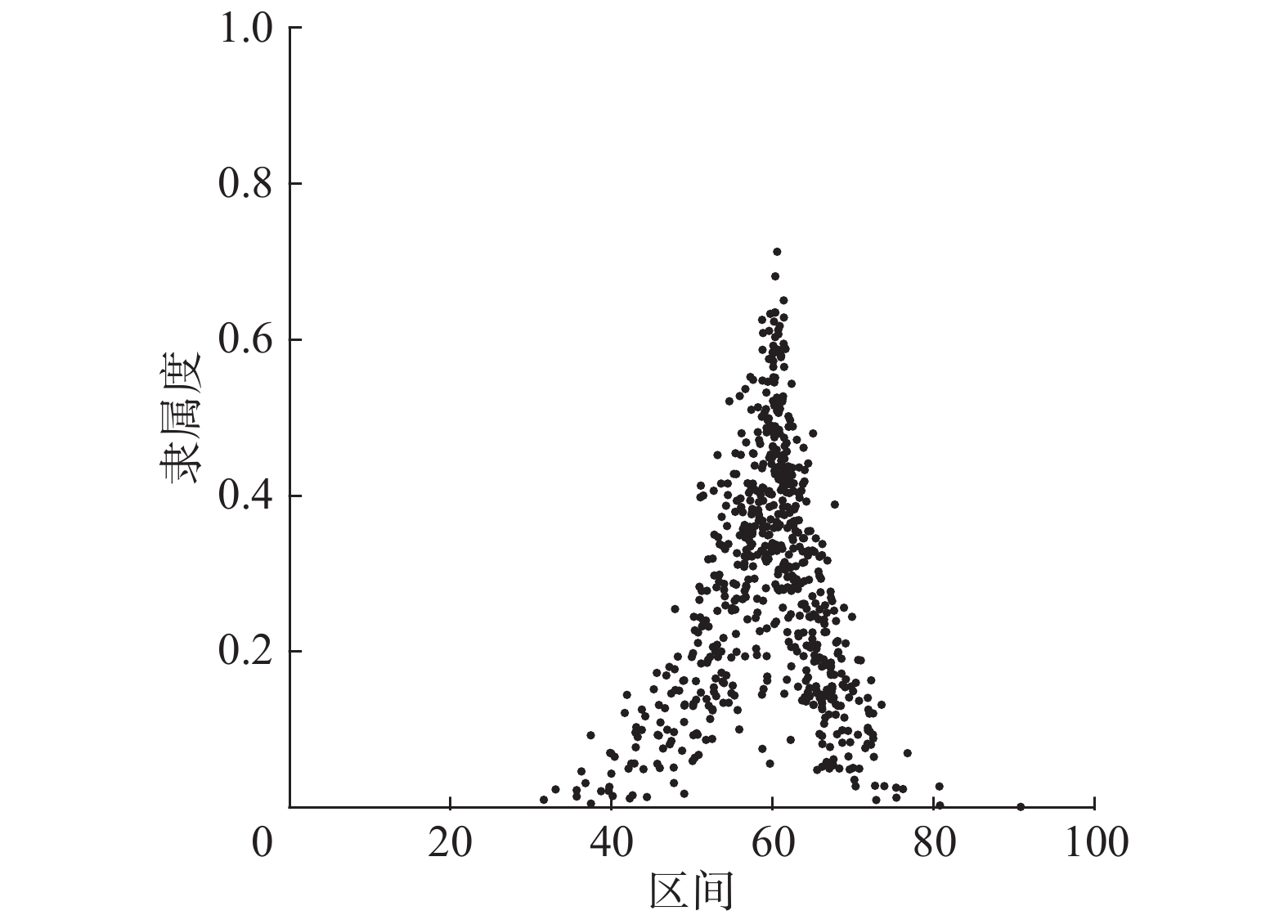
对于在论域
|
Download:
|
| 图 4 两个云集合的交集隶属函数 Fig. 4 Subjection degree function of the intersection of two cloud sets | |
云集合
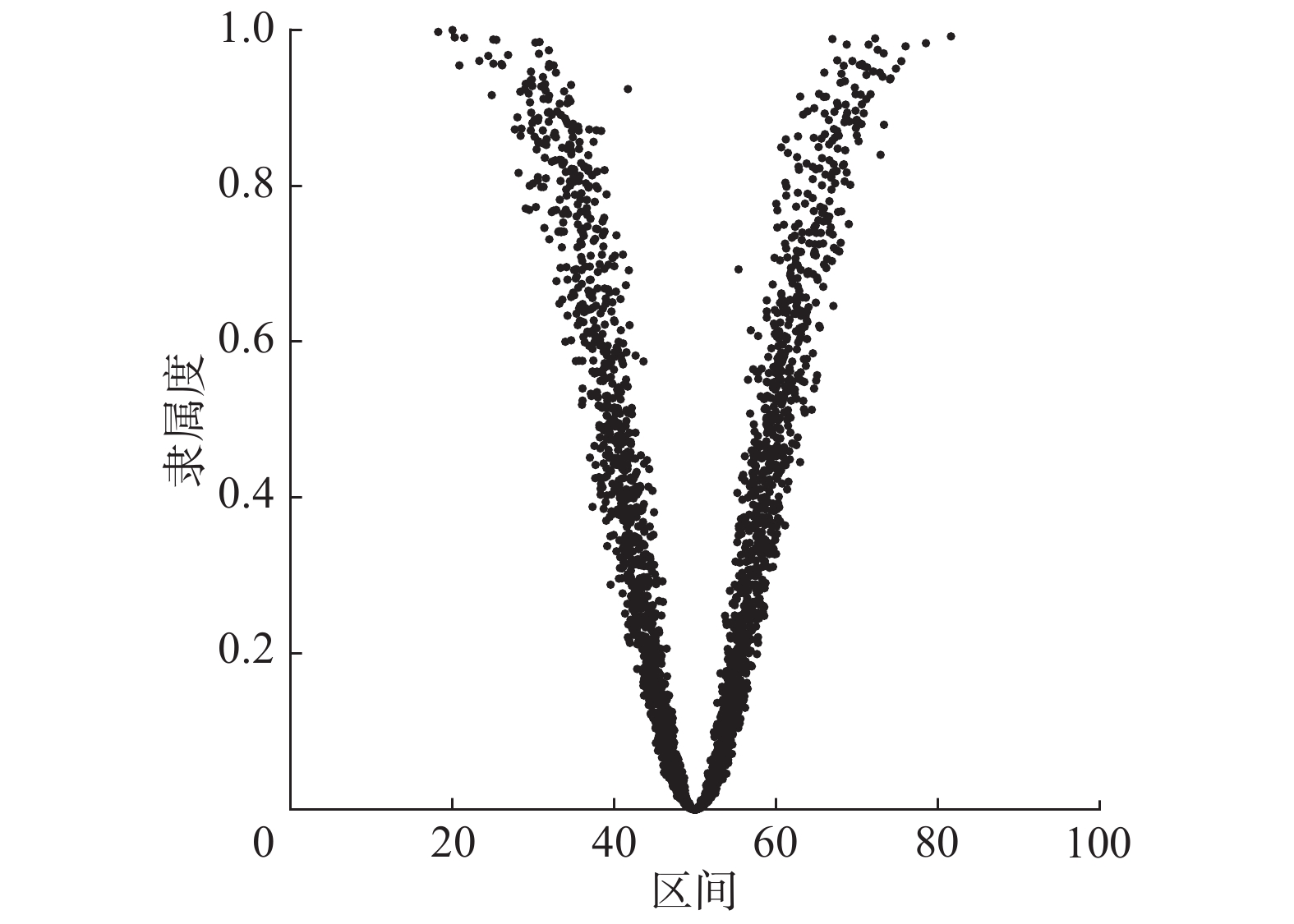
| ${u_{{{\mathop A\limits_\wp }^c}}}(\mathop x\limits^\wp ) = 1 - {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )$ |
云集合的余(补)集隶属函数如图5所示。
|
Download:
|
| 图 5 云集合的补集 Fig. 5 Complement set of cloud set | |
参照经典集合与模糊集合中直积的定义[20],设云集合
| ${u_{\mathop A\limits_\wp {\rm{(}}X{\rm{)}} \times \mathop B\limits_\wp {\rm{(}}Y{\rm{)}}}} = {u_{\mathop A\limits_\wp {\rm{(}}X{\rm{)}}}} \wedge {u_{\mathop B\limits_\wp {\rm{(}}Y{\rm{)}}}}$ |
设
| $({{\mathop A\limits_\wp} _\lambda })(\mathop x\limits^\wp ) = \left\{ {\begin{array}{*{20}{l}} {{u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),\quad I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))\mathop \geqslant \limits^{\rm{L}} \lambda } \\ {0,\quad I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))\neg {\mathop \geqslant \limits^{\rm{L}}} \lambda } \end{array}} \right.$ |
云集合的
| $({A_\lambda })(\mathop x\limits^\wp ) = \left\{ {\begin{array}{*{20}{l}} {1,\quad I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))\mathop \geqslant \limits^{\rm{L}} \lambda } \\ {0,\quad I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))\neg \mathop \geqslant \limits^{\rm{L}} \lambda } \end{array}} \right.$ |
云集合的
| $({{\mathop A\limits_{\sim}} _\lambda })(\mathop x\limits^{\sim} ) = \left\{ {\begin{array}{*{20}{l}} {{u_{\mathop A\limits_{\sim} }}(\mathop x\limits^{\sim} ),\quad I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))\mathop \geqslant \limits^{\rm{L}} \lambda } \\ {0,\quad I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))\neg \mathop \geqslant \limits^{\rm{L}} \lambda } \end{array}} \right.$ |
定义区间I “左大于”
对于正态云集合,根据隶属度函数有
| ${{\rm{e}}^{ - \frac{{{{\left( {x - {\rm{E}}x} \right)}^2}}}{{2{{({\rm{E}}n')}^2}}}}} \geqslant \lambda $ |
因此,对于正态云模型,云集合
| ${A_\lambda } = \left\{ {\left. x \right|{\rm{E}}x{\rm{ - }}\sqrt {{\rm{ - 2}}{\rm{E}}{{n'}^2}\ln \lambda } \leqslant x \leqslant {\rm{E}}x + \sqrt {{\rm{ - 2}}{\rm{E}}{{n'}^2}\ln \lambda } } \right\}$ |
式中:
设
| $ ({{\mathop A\limits_\wp} _{{{\mathop x\limits^\wp }_i}}})(\mathop x\limits^\wp ) = \left\{ {\begin{array}{*{20}{c}} {{u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop {{x_i}}\limits^\wp )))}}{{P(I({u_{\mathop A\limits_\wp }}(\mathop {{x_i}}\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1} \\ \begin{array}{l} 0,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop A\limits_\wp }}({x_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))}} < 1 \\ {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),\quad P(I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp} _i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} \end{array}} \right. $ |
| $ ({A_{{{\mathop {\rm{x}}\limits^\wp }_i}}})(x) = \left\{ {\begin{array}{*{20}{l}} {1,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1} \\ \begin{array}{l} 0,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} < 1 \\ 1,\quad P(I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp} _i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} \end{array}} \right. $ | (4) |
称集合
设
| ${{\mathop A\limits_\wp} _{[a,b]}}\left( {\mathop x\limits^\wp } \right) = \left\{ {\begin{array}{*{20}{c}} {{u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I([a,b]))}}{{P(I([a,b])) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1}\\ \begin{array}{l} 0,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I([a,b]))}}{{P(I([a,b])) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} < 1\\ {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),\quad P(I([a,b]) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} \end{array}} \right.$ |
| ${A_{[a,b]}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I([a,b]))}}{{P(I([a,b])) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1}\\ \begin{array}{l} 0,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I([a,b])}}{{P(I([a,b])) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} < 1\\ 1,\quad P(I([a,b]) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} \end{array}} \right.$ |
称集合
设
| $ {{\mathop A\limits_\wp} _{{u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_{\rm{i}}})}}\left( {\mathop x\limits^\wp } \right) = \left\{ {\begin{array}{*{20}{l}} {{u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1}\\ \begin{array}{l} 0,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} < 1\\ {u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ),\quad P(I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp} _i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} \end{array}} \right. $ |
| $ {{\mathop A\limits_{}} _{{u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1}\\ \begin{array}{l} 0,\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp }_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} < 1\\ 1,\quad P(I({u_{\mathop B\limits_\wp }}({{\mathop x\limits^\wp} _i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} \end{array}} \right. $ | (5) |
称
定理1 设
| $\mathop A\limits_\wp = \bigcup\limits_{x \in U}^{} {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}){A_{{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})}}} \left( x \right)$ | (6) |
式中:
| ${u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp} _i})A = \left\{ {\begin{array}{*{20}{c}} {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}),\quad x \in A} \\ {0,\quad x \notin A} \end{array}} \right.$ |
证明 根据随机隶属度
| $\begin{array}{c} \left( {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}){A_{_{\mathop A\limits_\wp }({{\mathop x\limits^\wp }_i})}}\left( x \right)} \right)\left( {\mathop x\limits^\wp } \right) = \\ \left\{ {\begin{array}{*{20}{c}} {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}),\quad\mathop x\limits^\wp \in {A_{{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_{\rm{i}}})}},\quad \dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} \geqslant 1}\\ \begin{array}{l} 0,\quad \mathop x\limits^\wp \notin {A_{{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_{\rm{i}}})}},\dfrac{{P(I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )) > I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})))}}{{P(I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp )))}} < 1\\ {u_{\mathop A\limits_\wp }}({\mathop x\limits^\wp _i}),\quad \mathop x\limits^\wp \in {A_{{u_{\mathop A\limits_\wp }}\left( {{{\mathop x\limits^\wp }_i}} \right)}},P(I({u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp} _i})) > I({u_{\mathop A\limits_\wp }}(\mathop x\limits^\wp ))) = 0 \end{array} \end{array}} \right. \end{array}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ | (7) |
由式(7)可进一步得
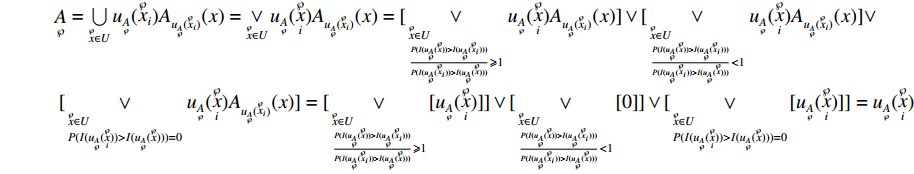
|
定理2 设
| $\mathop A\limits_\wp = \bigcup\limits_{{{\mathop x\limits^\wp }_i} \in U} {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}){A_{{{\mathop x\limits^\wp }_i}}}} (x)$ | (8) |
证明 根据式(4)和式(5),易知:
| ${A_{{{\mathop x\limits^\wp }_i}}}(x){\rm{ = }}{A_{{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})}}\left( x \right)$ |
于是有
| $\bigcup\limits_{{{\mathop x\limits^\wp }_i} \in U} {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}){A_{{{\mathop x\limits^\wp }_i}}}} (x){\rm{ = }}\bigcup\limits_{{{\mathop x\limits^\wp }_i} \in U} {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}){A_{{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i})}}\left( x \right)} $ |
根据云分定理1得到:
| $\bigcup\limits_{{{\mathop x\limits^\wp }_i} \in U} {{u_{\mathop A\limits_\wp }}({{\mathop x\limits^\wp }_i}){A_{{{\mathop x\limits^\wp }_i}}}} (x) = \mathop A\limits_\wp $ |
本文参照模糊集,提出一种云模型的集合理论与方法。提出
| [1] |
李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995, 32(6): 15-20. LI Deyi, MENG Haijun, SHI Xuemei. Membership clouds and Membership cloud generators[J]. Computer R&D, 1995, 32(6): 15-20. (  0) 0)
|
| [2] |
LI Deyi, LIU Changyu, GAN Wenyan. A new cognitive model: cloud model[J]. International journal of intelligent systems, 2009, 24(3): 357-375. DOI:10.1002/int.20340 ( 0) 0)
|
| [3] |
WANG Shuliang, LI Deren, SHI Wenzhong, et al. Cloud model-based spatial data mining[J]. Geographic information sciences, 2003, 9(1/2): 60-70. ( 0) 0)
|
| [4] |
LIU Yuchao, LI Deyi, HE Wen, et al. Granular computing based on Gaussian cloud transformation[J]. Fundamenta informaticae, 2013, 127(1/2/3/4): 385-398. ( 0) 0)
|
| [5] |
QIN Kun, XU Kai, LIU Feilong, et al. Image segmentation based on histogram analysis utilizing the cloud model[J]. Computers & mathematics with applications, 2011, 62(7): 2824-2833. ( 0) 0)
|
| [6] |
GAO Hongbo, ZHANG Xinyu, LIU Yuchao, et al. Longitudinal control for mengshi autonomous vehicle via Gauss cloud model[J]. Sustainability, 2017, 9(12): 2259. DOI:10.3390/su9122259 ( 0) 0)
|
| [7] |
孙文植, 王元元. 集合论——简史与近况[J]. 自然杂志, 1983(03): 184-190, 240. SUN Wenzhi,WANG Yuanyuan. Set theory: a brief history and current situation[J]. Journal of nature, 1983(03): 184-190, 240. (  0) 0)
|
| [8] |
李维岳. 系统论与集合论[J]. 系统辩证学学报, 1996, 4(1): 49-52. LI Weiyue. System theory and set theory[J]. Journal of system dialectics, 1996, 4(1): 49-52. (  0) 0)
|
| [9] |
马爽, 徐震, 王利明. 基于集合论的电网信息物理系统模型构建方法[J]. 电力系统自动化, 2017, 41(6): 1-5. MA Shuang, XU Zhen, WANG Liming. Set theory based modeling method of cyber physical system for power grid[J]. Automation of electric power system, 2017, 41(6): 1-5. DOI:10.7500/AEPS20160804007 (  0) 0)
|
| [10] |
周文君, 张远华, 徐帆, 等. 基于集合论的战术通信网络重构[J]. 指挥信息系统与技术, 2014, 5(4): 26-30. ZHOU Wenjun, ZHANG Yuanhua, XU Fan, et al. Tactical communication network reconstruction based on set theory[J]. Command information system and technology, 2014, 5(4): 26-30. DOI:10.3969/j.issn.1674-909X.2014.04.006 (  0) 0)
|
| [11] |
苗夺谦, 徐菲菲, 姚一豫, 等. 粒计算的集合论描述[J]. 计算机学报, 2012, 35(2): 351-363. MIAO Duoqian, XU Feifei, YAO Yiyu, et al. Set-theoretic formulation of granular computing[J]. Chinese journal of computers, 2012, 35(2): 351-363. DOI:10.3724/SP.J.1016.2012.00351 (  0) 0)
|
| [12] |
ZADEH L A. Fuzzy sets[J]. Information and control, 1965, 8(3): 338-353. DOI:10.1016/S0019-9958(65)90241-X ( 0) 0)
|
| [13] |
许金兰, 刘娟, 淡志强. 模糊集合论在信贷融资风险评价中的应用[J]. 中国注册会计师, 2018(04): 105-109. XU Jinlan, LIU Juan, DAN Zhiqiang. Application of fuzzy set theory in credit financing risk assessment[J]. Chinese certified public accountant, 2018(04): 105-109. (  0) 0)
|
| [14] |
赵海鸣, 熊志宏, 曾雷, 等. 基于模糊集合理论的液压缸故障树分析方法研究[J]. 合肥工业大学学报(自然科学版), 2016, 39(2): 150-155. ZHAO Haiming, XIONG Zhihong, ZENG Lei, et al. Research on fault tree analysis method for hydraulic cylinder based on fuzzy set theory[J]. Journal of Hefei University of Technology (nature science edition), 2016, 39(2): 150-155. (  0) 0)
|
| [15] |
蔡玫, 曹杰. 应急物资需求量的二型模糊集合预测方法[J]. 中国安全科学学报, 2015, 25(9): 165-170. CAI Mei, CAO Jie. A type-2 fuzzy set based approach to predicting emergency material demand[J]. China safety science journal, 2015, 25(9): 165-170. (  0) 0)
|
| [16] |
唐小涛, 陶建峰, 李志腾, 等. 自动导航插秧机路径跟踪系统稳定性模糊控制优化方法[J]. 农业机械学报, 2018, 49(1): 29-34. TANG Xiaotao, TAO Jianfeng, LI Zhiteng, et al. Fuzzy control optimization method for stability of path tracking system of automatic transplanter[J]. Transactions of the Chinese society for agricultural machinery, 2018, 49(1): 29-34. DOI:10.6041/j.issn.1000-1298.2018.01.003 (  0) 0)
|
| [17] |
朱丽燕, 李铁山, 单麒赫. 船舶航向非线性离散系统自适应模糊最优控制[J]. 哈尔滨工程大学学报, 2019, 40(9): 1576-1581. ZHU Liyan, LI Tieshan, SHAN Qihe. Optimal adaptive fuzzy control for ship course discrete-time systems[J]. Journal of Harbin Engineering University, 2019, 40(9): 1576-1581. (  0) 0)
|
| [18] |
李凯, 高岩, 曹喆. 自动调整样本和特征权值的模糊聚类算法[J]. 哈尔滨工程大学学报, 2018, 39(9): 1554-1560. LI Kai, GAO Yan, CAO Zhe. Fuzzy clustering algorithm based on the automatic variable weights of samples and features[J]. Journal of Harbin Engineering University, 2018, 39(9): 1554-1560. (  0) 0)
|
| [19] |
许修国, 乔君辉, 王文龙, 等. 基于3σ法整车制动距离试验方法研究
[J]. 汽车零部件, 2017(7): 54-56. XU Xiuguo, QIAO Junhui, WANG Wenlong, et al. Braking distance test based on 3σ method [J]. Automobile parts, 2017(7): 54-56. (  0) 0)
|
| [20] |
谢季坚, 刘承平. 模糊数学方法及其应用[M]. 3版. 武汉: 华中科技大学出版社, 2006: 16−17.
( 0) 0)
|
 2020, Vol. 15
2020, Vol. 15


