由于步态容易受到物体遮挡、衣着、视角和携带物等协变量因素的影响，提取到的步态特征呈现很强的类内变化^[1-3]。为了解决这一问题，需要设计出更好的步态表征方法，使其更完备地表达有利于识别的步态特征^[4-6]。近年来，基于类能量图的方法是步态识别领域中的初级特征提取技术之一。Han等^[7]将归一化的一个周期步态图像叠加，提出步态能量图(gait energy image, GEI)，像素的浓度代表在该像素位置人体运动的频率。Zhang^[8]提出主动能量图(active energy image, AEI)，前后帧间信息得到保留，可有效避免背包衣着等的影响，但丢失了步态图像的静态特征。为了克服衣着变化的影响，Bashir等^[9]提出步态熵图(gait entropy image, GenI)，GEI的动态及静态信息得到有效分割。Lamthw等^[10]提出步态流图(gait flow image, GFI)，即将光流场引入到步态类能量图中提取步态特征。Lee等^[11]计算像素的均值和方差，累积周期中的每帧提出步态概率图(gait probability image, GPI)，该方法表征步态帧间时序信息不完备。Deng等^[12]计算周期步态轨迹参数提出步态动态图(gait dynamics graph, GDG)，但是三维参数的提取过程较复杂。

一些研究人员通过融合不同的类能量图实现特征完备表达。陈实等^[13]提出彩色步态运动历史图(color gait history image, CGHI)表征时空步态序列信息。CGHI^[13]将3种灰度图像通过分配到RGB通道实现像素级融：单足站立为起点的前向单步运动历史图、对侧足站立为起点的前向单步运动历史图和GEI。Hofmann等^[14]通过决策级融合实现步态表征：GEI和深梯度直方能量图(depth gradient histogram energy image, DGHEI)，该方法仍存在步态信息丢失的问题。CCA及其改进方法在生物特征融合领域也有较多应用^[15-17]。采用串行和并行的方式融合CCA可以得到两组步态特征。但是，串行和并行融合方式的先天不足，使得这种融合方式应用的普适性不是很好。

针对步态特征表达不完备问题，本文提出一种基于加权CCA的多信息融合的步态表征方法。在GFI基础上，首先，将行走的步宽时序信息编码到RGB颜色空间，提升GFI的时序表征能力，得到多通道彩色类能量图；然后，将R、G通道的步态特征进行CCA，对得到的两个新特征加权融合，融合结果与B通道特征重复上述融合过程。保留了初始特征关系属性，得到的新特征融合了更有益识别的步态信息。本文采用彩色类能量图保存步态特征，借助CCA去除特征间的冗余信息，同时将多通道信息融合成单通道，最后采用最近邻分类器识别。

1 三通道彩色类能量图

步态流图(gait flow image, GFI)^[15]提取的动、静态信息更具区分度，将步态的非正面步宽特征编码到RGB空间，增强了GFI的时序信息，得到三通道彩色类能量图，克服了GFI蕴含的弱时序信息的缺点，包含更多的步态信息。

1.1 生成三通道彩色类能量图

对非正面周期步态序列，步宽信息被编码到RGB三通道，即投影到每帧图像的GFI中，生成三通道彩色类能量图，公式为

$E^{\prime}(x, \mathrm{y})=\sum^{p}\left|F_{i}(x, y) \times G\left(P_{i}\right)\right|$

式中：p是四分之一周期的总帧数；F_i(x, y)是第i帧的GFI；P_i是第i帧的步宽；RGB的3个通道分别用 $B( \cdot )$ 、 $G( \cdot )$ 和 $R( \cdot )$ 表示。

一个步态周期的彩色类能量图定义为

$E(x,y) = \frac{1}{4}\sum\limits_{i = 1}^4 {E_{}^i(x,y)} $

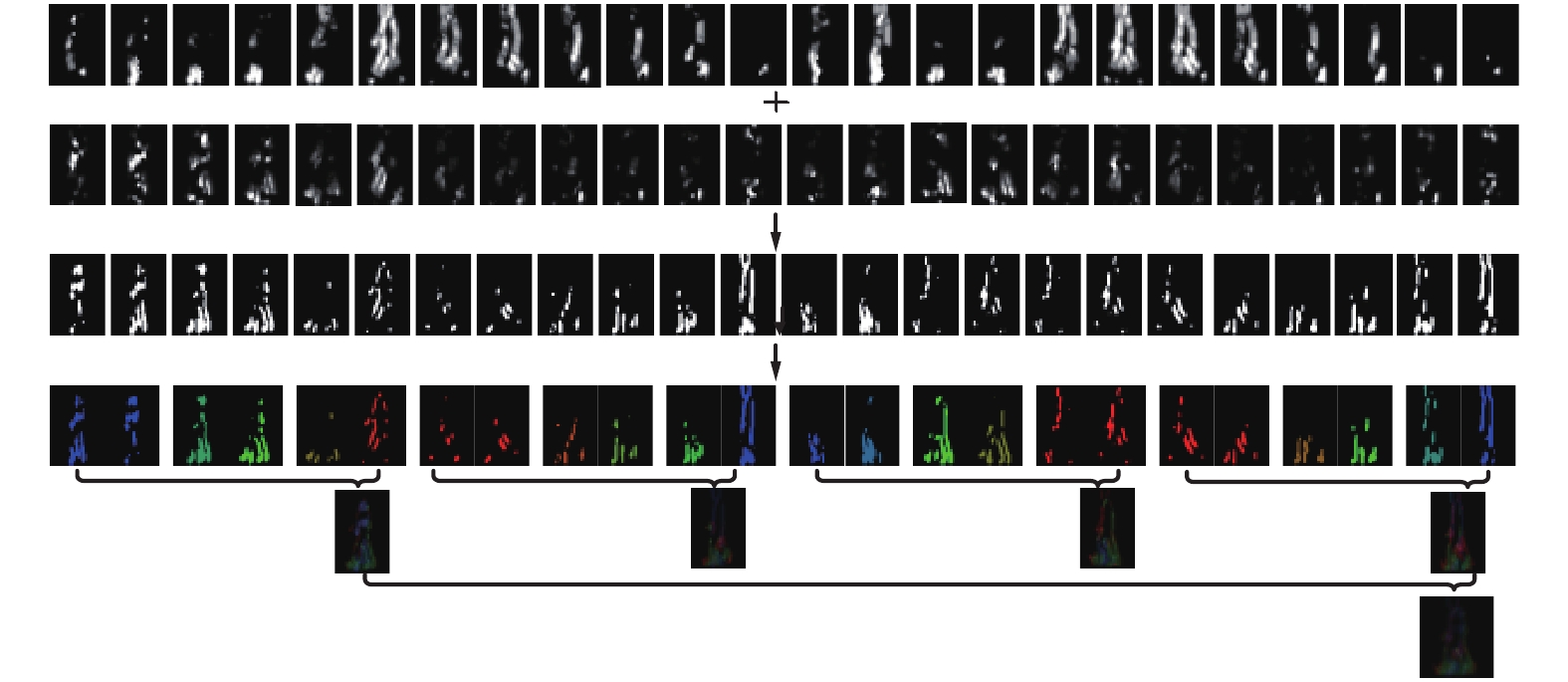
生成过程如图1所示：第1行是水平方向的GFI；第2行是垂直方向的GFI；第3行是水平和垂直方向合成的GFI；第4行是增强时序信息后的彩色类能量图；第5行是前一行生成的彩色类能量图，包含四幅四分之一周期的彩色类能量图；第六行是单周期的彩色类能量图。

1.2 基于步宽的时序信息

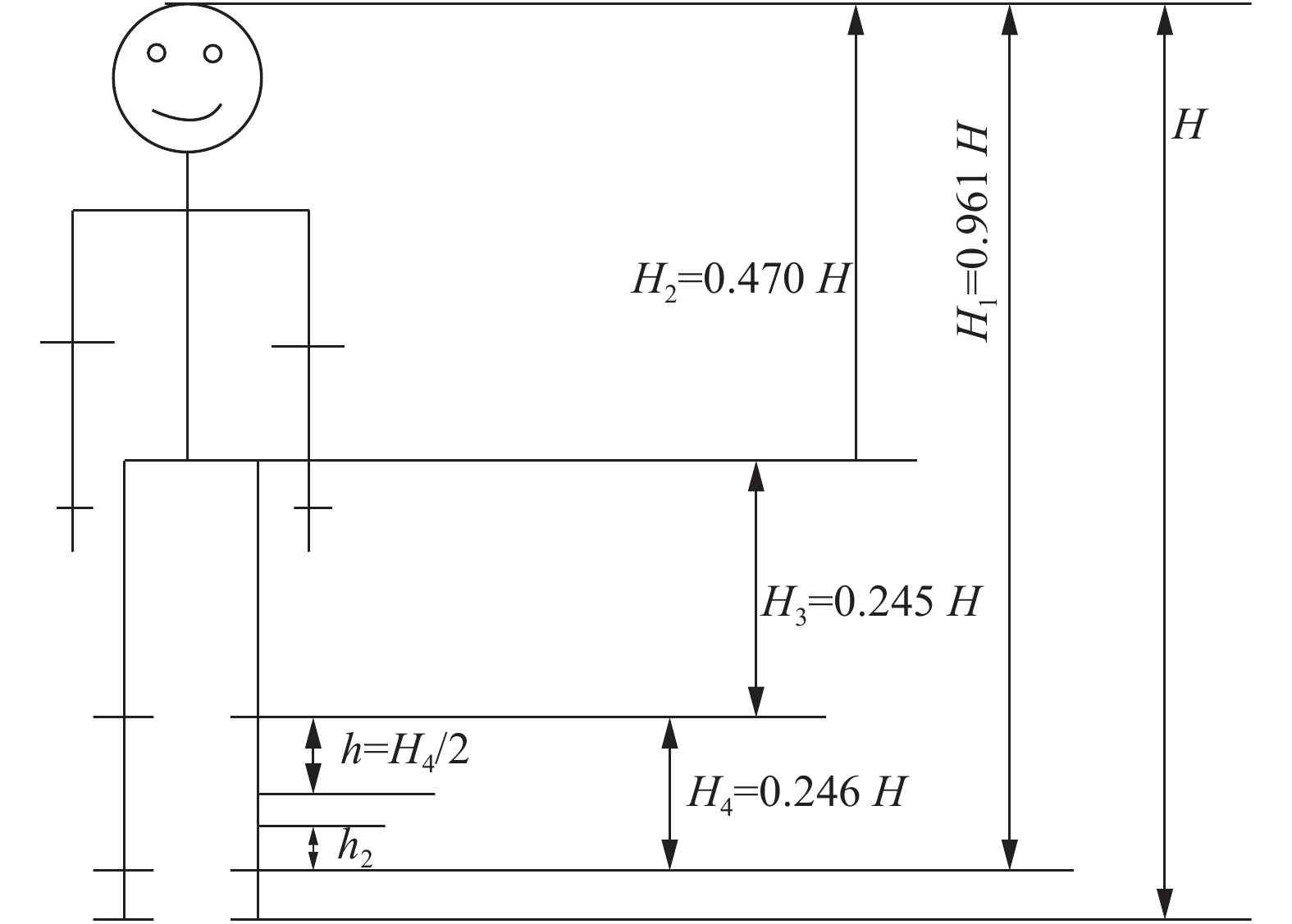
采用一种基于步宽信息的线性插值函数关系，将周期步态的时序信息编码到三通道RGB空间，不仅能够提升步态时序特征表达能力，还实现了时序特征的可视化。以四分之一步态周期为例，定义步宽信息P_i：

${P_i} = \frac{{{G_i} - {G_{\min }}}}{{{G_{\max }} - {G_{\min }}}}$

${G_i} = \frac{1}{{({h_2} - {h_1} + 1)}}\sum\limits_{j = {h_1}}^{{h_2}} {({\varDelta _j}} )$

式中： ${\varDelta _j}$ 是每帧图像前景第j行的左右像素点位置之差；图2标识了h₁和h₂；G_i表示第i帧腿部区域宽度的平均值；G_max和G_min为G_i的两个最值。

可视化技术能够表示某些随时序变化的数据特征^[18]，将人体步态的宽度投影到RGB通道进行可视化，I是图像像素的最大值，比如1或255，公式为

$\begin{array}{l} B\left( {{P_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {\left( {1 - 2{P_i}} \right){{I}},}&{0 \leqslant {P_i} \leqslant \dfrac{1}{2}}\\ {0,}&{\dfrac{1}{2} \leqslant {P_i} \leqslant 1} \end{array}} \right.\\ G\left( {{P_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {2{P_i}{{I}},}&{0 \leqslant {P_i} \leqslant \dfrac{1}{2}}\\ {\left( {2 - 2{P_i}} \right){{I}},}&{\dfrac{1}{2} \leqslant {P_i} \leqslant 1} \end{array}} \right.\\ R\left( {{P_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {0,}&{0 \leqslant {P_i} \leqslant \dfrac{1}{2}}\\ {\left( {2{P_i} - 1} \right){{I}},}&{\dfrac{1}{2} \leqslant {P_i} \leqslant 1} \end{array}} \right. \end{array}$

2 加权CCA融合多通道信息

彩色类能量图是多通道图像，采用最近邻分类器进行分类识别时需要先将其变为一维向量，如像素级融合方法，即将彩色图像灰度化：

${E_{\rm{T}}}(x,y) = wE_{\rm{T}}^{\rm{B}}(x,y,1) + \nu E_{\rm{T}}^{\rm{G}}(x,y,2) + uE_{\rm{T}}^{\rm{R}}(x,y,3)$

(1)

式中 $E_{\rm{T}}^{\rm{B}}(x,y,1)$ 、 $E_{\rm{T}}^{\rm{G}}(x,y,2)$ 和 $E_{{\rm{CEI}}}^{\rm{R}}(x,y,3)$ 分别表示三通道类能量图的B、G和R分量。当u = 0.299、v = 0.587、w = 0.114时，式(1)是彩色图像灰度化公式。

像素级融合能够使一部分信息增强，与此同时，也使得一些对识别有益信息削弱。CCA及其改进的算法将具有相关关系的特征接近，与其他特征远离，可分性较好，能够应用到多通道特征融合。

2.1 CCA理论基础

CCA^[19]是常用的多元统计分析方法之一，旨在研究变量间的相关关系。CCA旨在寻找两组随机变量各自的线性变换，使得投影后的两组随机向量中对应元素之间的相关性最大。

定义均值是0的两组随机矩阵分别为X和Y，矩阵中样本数均为n，即 ${{{x}}_{{1}}}{{,}}{{{x}}_{{2}}}{{,}}...{{,}}{{{x}}_{{n}}}$ 是X中的样本， ${{{y}}_{{1}}}{{,}}{{{y}}_{{2}}}{{,}}...{{,}}{{{y}}_{{n}}}$ 是Y中的样本。CCA算法目的是求得两个映射 ${{{p}}_{{x}}}$ 和 ${{{p}}_{{y}}}$ ，使得样本 ${{{x}}_{{i}}}$ 和 ${{{y}}_{{i}}}$ 映射后在新的空间相关度最大，公式为

$\rho = \frac{{{\rm{E}}[{{{p}}_x}^{\rm T}{{X}}{{{Y}}^{\rm T}}{{{p}}_y}]}}{{\sqrt {{\rm{E}}[{{p}}_x^{\rm{{\rm T}}}{{X}}{{{X}}^{\rm T}}{{{p}}_x}] {\rm{E}}[{{p}}_y^{\rm{{\rm T}}}{{Y}}{{{Y}}^{\rm T}}{{{p}}_y}]} }}$

(2)

式中 $\rm{E} ( \cdot )$ 为期望。 ${{{p}}_{{x}}}$ 和 ${{{p}}_{{y}}}$ 的尺度对式(2)值没有影响，可以约束 ${{p}}_x^{\rm T}{{X}}{{{X}}^{\rm T}}{{{p}}_x} = {{p}}_y^{\rm T}{{Y}}{{{Y}}^{\rm T}}{{{p}}_y} = 1$ 。式(2)改写为

$\begin{gathered} \mathop {\max }\limits_{{{{p}}_x},{{{p}}_y}} r = \mathop {\max }\limits_{{{{p}}_x},{{{p}}_y}} {{p}}_x^{\rm T}{{X}}{{{Y}}^{\rm T}}{{{p}}_y} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\; {{p}}_x^{\rm T}{{X}}{{{X}}^{\rm T}}{{{p}}_x} = 1,\quad{{p}}_y^{\rm T}{{Y}}{{{Y}}^{\rm T}}{{{p}}_y} = 1 \\ \end{gathered} $

(3)

利用拉格朗日乘子法可以解决式(3)的优化问题：

$L = {{p}}_x^{\rm T}{{X}}{{{Y}}^{\rm T}}{{{p}}_y} + {{\textit{λ}}_x}(1 - {{p}}_x^{\rm T}{{X}}{{{X}}^{\rm T}}{{{p}}_x}) + {{\textit{λ}} _y}(1 - {{p}}_y^{\rm T}{{Y}}{{{Y}}^{\rm T}}{{{p}}_y})$

得 ${{\textit{λ}} _x} - {{\textit{λ}} _y} = 0$ 。令 ${\textit{λ}} = {{\textit{λ}}_x} = {{\textit{λ}}_y}$ ， ${{p}_y} = ({({Y}{{Y}^{\rm T}})^{ - 1}}{Y}{{X}^{\rm T}}{{p}_x})/{\textit{λ}} $ ， ${{{p}}_x}$ 可由求解广义特征值分解问题得到：

${{X}}{{{Y}}^{\rm T}}{({{Y}}{{{Y}}^{\rm T}})^{ - 1}}{{Y}}{{{X}}^{\rm T}}{{{p}}_x} = {{\textit{λ}}^2}{{X}}{{{X}}^{\rm T}}{{{p}}_x}$

(4)

求解式(4)，选取前 $d(d \leqslant n)$ 对映射向量组成投影矩阵 ${{{W}}_x}$ 和 ${{{W}}_y}$ ，提取X和Y之间的典型相关特征 ${{u}} = {{{W}}_x}{{X}}$ 和 ${{v}} = {{W}}_y^{}{{Y}}$ 。

2.2 加权CCA融合彩色类能量图

彩色类能量图的3个通道特征分别为X_R、X_G、X_B，特征维数m×n，其中 $m \gg n$ ，m是特征向量包含元素个数，n表示训练样本数。

加权CCA融合彩色类能量图算法步骤如下：

1) 对X_R和X_G执行CCA，得到 ${{X}}{'_{\rm{R}}} = {{W}}_{\rm{R}}{{X}}_{\rm{R}}$ 和 ${{X}}{'_{\rm{G}}}= {{{W}}_{\rm{G}}}{{{X}}_{\rm{G}}}$ 。

2) $\psi $ 为融合算子，对执行CCA得到的 ${{X}}{'_{\rm{R}}}$ 和 ${{X}}{'_{\rm{G}}}$ 融合：

${{{X}}_{{\rm{RG}}}} = \psi ({{X}}{'_{\rm{R}}},{{X}}{'_{\rm{G}}}) = \alpha {{X}}{'_{\rm{R}}} + \beta {{X}}{'_G}$

(11)

式中： $\alpha $ 、 $\beta $ 是加权系数，满足 $\alpha + \beta = 1$ 。

3)对X_RG和X_B执行CCA，对得到的 ${{X}}{'_{\rm{RG}}}$ 和 ${{X}}{'_{\rm{B}}}$ 加权融合：

${{{X}}_{{\rm{RGB}}}} = \psi ({{X}}{'_{{\rm{RG}}}},{{X}}{'_{\rm{B}}}) = \delta {{X}}{'_{{\rm{RG}}}} + \gamma {{X}}{'_{\rm{B}}}$

(12)

式中： $\delta $ 、 $\gamma $ 是加权系数，满足 $\delta + \gamma = 1$ 。

这种融合方法的优点在于：可分性较好，初始特征关系得到保留，加权融合得到的新特征具有更多有益于识别的信息。另外，若X_RGB的维数较大，可对X_RGB降维。在运算速度上，与其他融合方式相比，如串行或并行融合，特征维数没有增加且在实数域运算，显然具有最低的运算量。

2.3 计算复杂度分析

对于分辨率为xy，包含步态图像帧数为 $\eta $ 的步态序列，训练样本的数目是n；生成三通道彩色类能量图的计算复杂度为 $O(n \cdot \eta \cdot {(x \cdot y)^2})$ ；加权CCA融合后得到的X_RGB计算复杂度为 $O({(x \cdot y)^6})$ 。采用像素级融合后得到步态特征的计算复杂度为 $O(n \cdot \eta \cdot {(x \cdot y)^6})$ 。其他类能量图方法(如GEI)，计算复杂度为 $O(\eta \cdot x \cdot y)$ ，GFI计算复杂度为 $O(\eta \cdot {(x \cdot y)^2})$ 。

3 实验结果与分析

本文所提算法的有效性实验在USF HumanID^[20]步态数据集上进行。实验的测试平台为IntelCore 2.5 GHz的CPU、4 GB内存、Windows 7操作系统，测试代码在MATLAB2016a上编译运行。

以双脚支撑为计算步态周期的起始点，一个步态序列可得到几幅单周期的类能量图，然后将这几幅平均成一幅进行分析。采用最近邻分类器进行识别。本文进行了3组实验：第1组，与其他类能量图相比，本文提出算法的识别率；第2组，权值 $\alpha $ 、 $\beta $ 、 $\delta $ 、 $\gamma $ 取不同值时，本文提出算法的识别性能；第3组，生成各类能量图时间对比。

在执行CCA时，广义特征值分解会遇到“维数灾难”，为了避免这一问题，先对彩色类能量图降维，采用奇异值分解(SVD)算法，选取特征值之和的99.9%对应的向量，然后再进行CCA。本文采用奇异值分解(SVD)实现PCA。

3.1 多通道彩色类能量图有效性实验

将本文提出的CCA融合三通道表征标记为CFR，采用像素级加权融合三通道特征得到的步态表征标记为PFR，并对比了其他常用的步态表征方法，如步态能量图GEI、步态流图GFI。表1中CFR对应参数取值为 $\alpha = 0.4$ ， $\beta = 0.6$ ， $\gamma = 0.9$ ， $\delta = $ 0.1；PFR对应参数取值为u = 0.7，v= 0.1，w = 0.2。

表1中，与GEI、GFI相比，Rank1指标下，CFR将平均识别率提高了15.72%、14.22%，PFR将平均识别率提高了5.5%、4%；CFR较PFR识别率提高了10.22%；Rank5指标也得到了大幅度提升。分析表1中数据可知，本文提出的三通道彩色类能量图作为步态表征是有效的，描述了更多有利于识别的动态、静态和时序信息；提出的基于加权CCA融合多通道信息的步态表征包含较多有益于识别的信息，取得最优识别性能。

3.2 参数对本文提出的表征方法性能的影响

权值参数α、β、δ、γ影响本文提出算法的识别性能。为了分析参数取值对识别性能的影响，进行了81组实验，参数取值范围为0.1~0.9，表2给出了10组参数的实验结果。

将测试的对象A~L分为3类：第Ⅰ类，要依靠静态信息进行识别；第Ⅲ类，主要依靠动态信息和时序信息进行识别；第Ⅱ类介于上述两类之间，静态、动态及时序信息在识别时占有的地位相同。由表2、表3可知：R、G通道加权系数α、β一定时，随着B通道加权系数γ减小，第Ⅰ、Ⅱ、Ⅲ类及总的平均识别率均呈上升趋势，当γ进一步减小，识别率会略微下降。以α=0.5为例，γ = 0.3相较γ = 0.9的情况下平均识别率提高了6.41%；第I类平均识别率提高了10.4%，第Ⅱ类平均识别率提高了6%，第Ⅲ类平均识别率提高了4.4%。

3.3 生成类能量图时间对比

2.3节从理论上分析了生成表4各类能量图的计算复杂度，进一步，本文在USF数据库上做了生成类能量图的时间对比实验。在多数情况下，单幅类能量图生成时间很短，为便于记录及对比分析，表4中的时间为Gallery组(即训练组)生成类能量图时间的总和，通过表4中数据可知，实验结果与计算复杂度的理论分析一致。生成CFR 、PFR时间相对较长，但在本实验平台下，每秒仍能处理90帧以上数据图像，可以满足实时步态识别系统的需求。

4 结束语

本文提出了一种新的步态表征方法。该方法增强了GFI时序信息的表达，采用CCA去除特征间的冗余信息的同时将多通道信息融合成单通道，使得新特征具有更丰富有益识别的信息，在协变量变化较大的USF数据集进行实验，由实验数据可知，本文提出的方法使得识别率得到了显著的提升。

下一步打算对本文算法直接选取已有的类能量图分配到RGB通道；为了降低计算复杂度，可将融合算法CCA方法扩展到非线性耦合度量学习空间。