2. 郑州轻工业大学 电气信息工程学院,河南 郑州 450002
2. School of Electrical and Information Engineering, Zhengzhou University of Light Industry, Zhengzhou 450002, China
在现实生活中经常会遇到各种各样的分配问题,比如资源分配[1]、收入分配[2]、资产分配[3]、功率分配[4]、任务分配[5]等,因此关于分配问题的研究得到广泛关注。以任务分配为例,从静态任务分配到动态任务分配,从集中式任务分配到分布式任务分配,不同的应用背景和实际需求,推动着任务分配问题研究的不断发展[6]。
时间分配是一类重要的分配问题,旨在提高可重复使用资源的利用率。例如:在生产调度中,单机调度问题研究如何将一台机器按时间顺序分配给等待加工的工件,以提高生产效率[7-8];在交通管理中,交通信号配时研究如何在时间上将互相冲突的交通流予以分类,使其在不同时间通过交叉口[9-10]。如果将机器和交叉口看成有限资源,将工件和交通流视为主体,则时间分配问题可以界定为:将有限的资源在时间维度上进行分割,并安排各主体在不同时间段内轮流使用该资源。
作为一种典型的颇具代表性的时间分配问题,交通信号配时是缓解城市交通拥堵的关键环节之一[11]。在交通信号配时中,来自不同方向的交通流均可通过交叉口,而在任一时刻只能有一股或几股互不冲突的交通流通过交叉口。因此,时间分配问题的一个显著特点就是不同的主体按分时方式共享资源。简而言之,时间分配问题就是将一个时间周期划分为若干时间段,然后把时间段分配给不同的主体。任务分配问题一般指将一个总任务划分为若干子任务,然后把子任务分配给不同的主体去执行。基于这种相似性,任务分配方法同样可以用来求解时间分配问题,而群智能劳动分工是实现任务分配的一种重要方式。
群智能指众多简单的主体通过交互作用所表现出来的宏观智能行为[12],它是那些具有社会性特征的群居生物个体合作进行某些活动时才会产生的涌现现象。在社会性昆虫中,不同的个体执行不同的任务,这种现象叫做劳动分工[13]。群智能劳动分工是一种自下而上的任务分配方式,无需全局信息和中心控制即可实现有效的任务分配,而且能够适应动态变化的环境。群智能劳动分工的这一特点吸引了众多学者的关注,并被用于解决一些任务分配问题,比如供应链中的任务分配[14]、群机器人系统中的任务分配[15]、无线传感网络中的任务分配[16]、无人机群中的任务分配[17]等。此外,群智能劳动分工也被用于求解其他分配问题,比如布局问题的空间分配[18]和社会群体间的利益分配[19]。本文以交通信号配时为代表,将群智能劳动分工用于求解时间分配问题。先从时间分配的视角对交通信号配时问题进行分析,然后提出一种求解交通信号配时问题的群智能劳动分工方法,并通过实例分析与讨论,阐述了面向时间分配问题的群智能劳动分工方法的优越性。
1 时间分配视角下的交通信号配时问题分析 1.1 问题描述交通信号配时指的是利用交通信号灯对道路上的车辆和行人进行指挥,其作用在于保障交叉口的交通安全和充分发挥交叉口的通行效率[20]。交通信号配时问题主要涉及信号相位的确定、配时参数的选择以及运行效率的衡量3个方面。
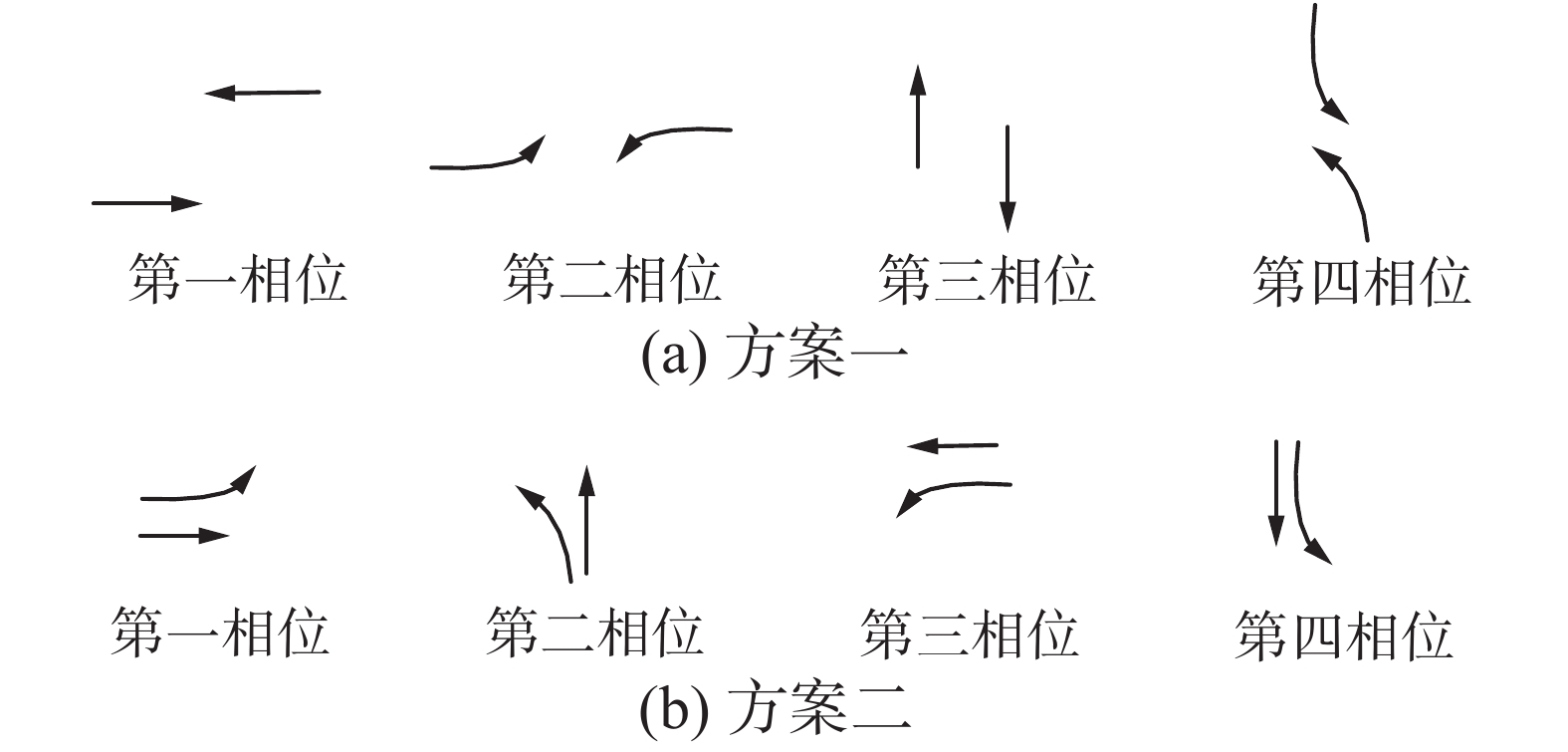
首先,信号相位指在某个或者某几个方向上的交通流同时得到通行权的时间带,信号相位及其组合顺序构成相位方案[21]。以普遍存在的十字交叉口为例(见图1),其在东、西、南、北4个方向上都有左行、直行和右行3个方向的车流,图2描述了2种常用的四相位方案。

|
Download:
|
| 图 1 十字交叉口 Fig. 1 A sketch of the intersection | |
|
Download:
|
| 图 2 四相位方案 Fig. 2 Four phases scheme | |
其次,交通信号配时的主要设计参数有信号周期和绿信比[22]。信号周期指从起始相位到终止相位所经历的时间,用C表示,单位为s。绿信比指在一个信号周期内,某一相位的有效绿灯时长x与信号周期时长C之比,一般用λ表示,
最后,配时参数下交通效益的评价指标包括延误时间、停车次数和通行能力等,其中延误时间和停车次数体现了道路使用者的利益,通行能力体现了道路的使用效率[23]。以第i相位为例,车辆延误时间[24](单位为s)为
| ${D_i} = \frac{{C{{(1 - {{\textit{λ}} _i})}^2}}}{{2(1 - {y_i})}} + \frac{{1 - {{\textit{λ}}_i}}}{{2{q_i}}} + \frac{{{q_i}}}{{2{S_i}{{\textit{λ}}_i}({S_i}{{\textit{λ}}_i} - {q_i})}}$ |
车辆停车次数[24] (单位为次)为
| ${H_i} = \frac{{0.9(1 - {{\textit{λ}}_i})}}{{1 - {y_i}}}$ |
通行能力[24] (单位为pcu/h)为
| ${Q_i} = {S_i}{{\textit{λ}} _i}$ |
式中Si、yi、qi、λi分别为第i相位的饱和流量(pcu/h)、流量比、车流量(pcu/h)和绿信比。
一个周期内交叉口的车辆平均延误时间为
| $D=\sum_{i=1}^{n} D_{i} q_{i} / \sum_{i=1}^{n} q_{i}$ |
车辆平均停车次数为
| $H=\sum_{i=1}^{n} H_{i} q_{i} / \sum_{i=1}^{n} q_{i}$ |
通行能力为
| $Q=\sum_{i=1}^{n} Q$ |
式中n为相位总数。
1.2 时间分配特性以图1所示的交叉口和图2所示的相位方案为例,交通信号配时问题就是分别给4个相位的车辆分配通行权,使其在通过交叉口时保持有序状态,以减少交通拥堵、避免交通事故等。在一个信号周期内,车辆在交叉口处的通行权体现在绿灯时间上。因此,交通信号配时问题可以看成给各相位的车辆分配绿灯时间,是一个典型的时间分配问题。时间分配问题的显著特点是分时使用,该特点在交通信号配时问题上表现为共享性和独占性。共享性指来自不同相位的车辆均可通过交叉口,独占性指任一时刻只能有一个相位的车辆通过交叉口。
由上述分析可知,交通信号配时问题的时间分配特性表现为来自不同相位的车辆分时通过交叉口。一般而言,通过交叉口的车流量是在动态变化的,既有规律性的变化(如潮汐交通),也有非规律性的变化(如汽车保有量的增加)。动态变化的车流量要求配时参数(如信号周期时长、绿灯时长等)能做出适应性的动态调整。
2 求解交通信号配时问题的群智能劳动分工方法对于交通信号配时问题,一般以延误时间最短、停车次数最少和通行能力最大为目标函数。常用的求解方法以智能优化方法为主,包括遗传算法[24]、粒子群算法[25]、蚁群算法[21]、模拟退火算法[26]等。这些算法在求解交通信号配时问题时存在收敛速度慢、效率低等问题[27],而且在不同交通场景下的求解效果差异大,说明算法的适应性较差。群智能劳动分工可以弥补这一欠缺,其显著特点就是在动态环境下仍能实现有效的任务分配。据此本文从分配的视角出发,利用群智能劳动分工方法来求解交通信号配时问题。下面首先引入群智能劳动分工中的激发–抑制原理,然后建立蜂群劳动分工与交通信号配时之间的映射关系,进而提出一种面向交通信号配时问题的蜂群劳动分工算法。
2.1 群智能劳动分工中的激发–抑制原理以蜂群为代表的时间行为多型是群智能劳动分工的一种主要模式,其中个体所执行的任务与其生理年龄有关[13]。具体的,蜜蜂在其生命周期内一般会经历从哺育蜂到储存蜂以及觅食蜂的一个行为发育过程,分别对应哺育、储存食物、觅食等任务。根据蜂群的需要,蜜蜂能够延迟、加速、甚至逆转其行为发育过程[28]。蜜蜂在柔性发育的作用下,能够适应动态变化的环境,从而始终实现有效的任务分配。
Huang等[29]在研究蜂群的时间行为多型的时候,提出了一种激发–抑制原理。该原理认为,蜜蜂的行为发育是由激发剂和抑制剂共同决定的,且二者具有耦合关系,即年长蜜蜂体内激发剂和抑制剂的含量比年幼蜜蜂多。保幼激素被认为是蜜蜂的激发剂,促进其行为发育,该发育过程伴随着蜜蜂从巢内工作向巢外工作的转移。蜜蜂之间进行交互时会传递抑制剂,对其行为发育起阻碍作用。激发剂和抑制剂共同维持着蜜蜂在不同任务上的动态分配平衡。比如:当觅食者减少时,抑制剂会减弱,巢穴内的蜜蜂会加速发育成觅食者;当觅食者较多时,抑制剂会变强,巢穴内蜜蜂的发育会被延迟,甚至觅食者会返回巢穴内工作。
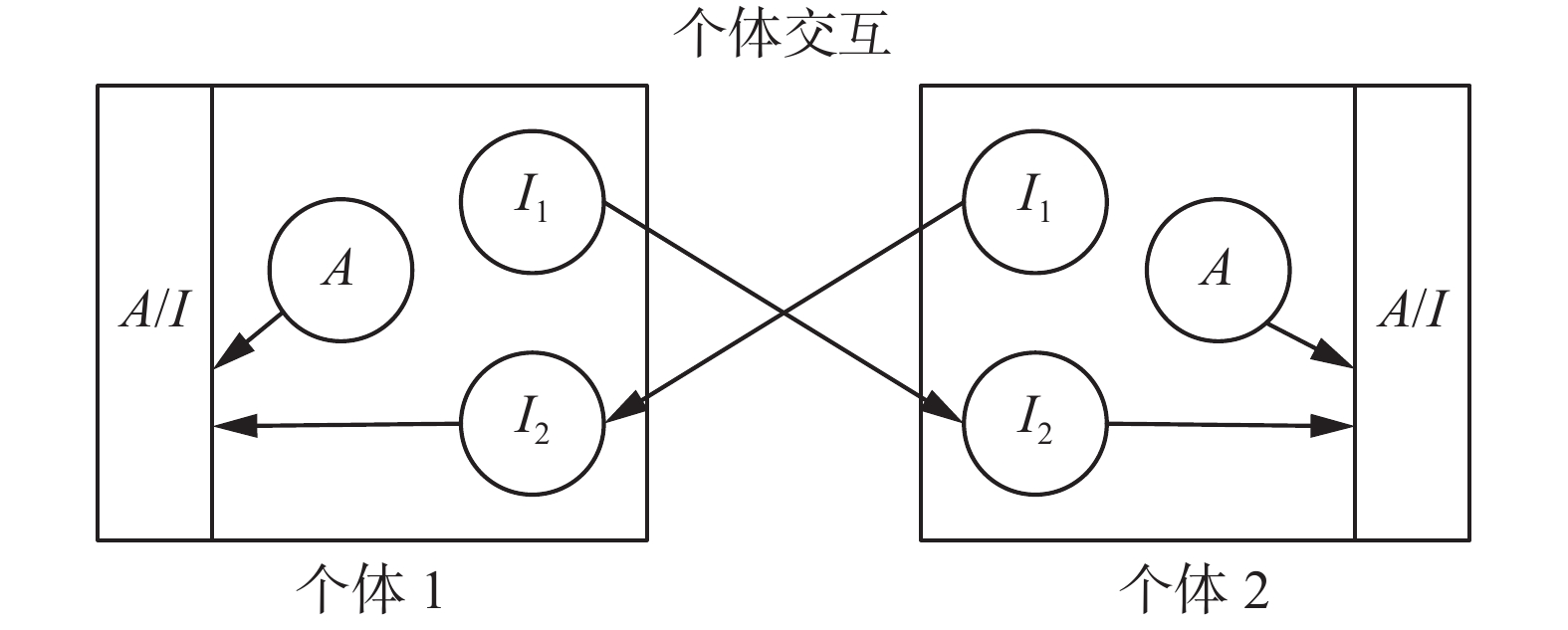
激发–抑制原理以个体–个体交互的方式完成任务分配,Naug等[30]进一步描述了激发–抑制原理中个体间的交互方式,如图3所示。蜂群中每只蜜蜂都包含1个激发剂A(Activator)和2个抑制剂I1和I2(Inhibitor)。A是蜜蜂内在的激发剂,对蜜蜂自身的行为发育起促进作用。I1是蜜蜂内在的抑制剂,不会阻碍自身的行为发育,但在个体交互过程中会对其他蜜蜂的行为发育产生抑制作用。I2是蜜蜂在交互作用中得到的外在抑制剂,会阻碍自身的行为发育。最终,激发剂A和抑制剂I2的相对水平(A/I)决定蜜蜂的行为发育是按照正常速度还是被加速、延迟或逆转。
|
Download:
|
| 图 3 激发–抑制原理中个体间的交互方式 Fig. 3 The interaction between individuals in activator-inhibitor mechanism | |
激发–抑制原理可以简述为:激发剂促进蜜蜂生理年龄的增长,抑制剂阻碍蜜蜂生理年龄的增长,激发剂和抑制剂共同影响蜜蜂的生理年龄,从而决定蜜蜂所执行的任务。此外,在蜂群中激发剂和抑制剂还具有耦合关系,表现为年长蜜蜂体内激发剂和抑制剂的含量比年幼蜜蜂多。在利用激发–抑制原理解决实际分配问题时,这种耦合关系可根据具体情况进行适当放宽。比如,文献[31-32]利用激发–抑制原理分别设计了3种方法来解决机器人间的任务分配问题,这些方法均没有考虑激发剂和抑制剂的耦合关系。
在蜂群劳动分工中,不同的蜜蜂执行不同的任务完成任务分配。在交通信号配时中,不同的信号相位占据不同的绿灯时间完成时间分配。一般而言,某一信号相位的车辆延迟时间长(或者停车次数多),说明该信号相位的绿灯时间短,此时应该增加其绿灯时间。同时,在信号周期固定或有限的情况下,还应减小其他信号相位的绿灯时间。
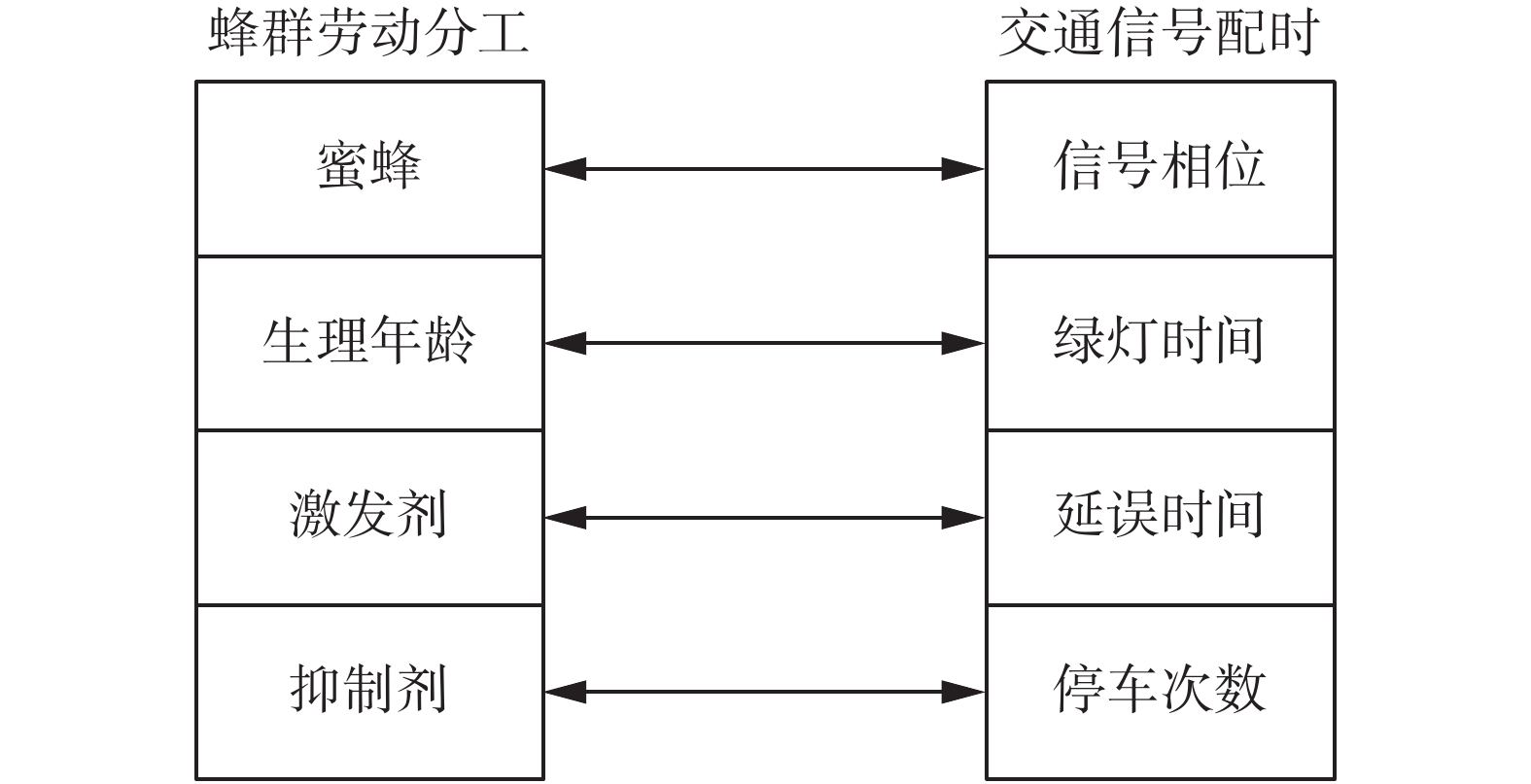
基于上述分析,为了借鉴蜂群劳动分工的任务分配来实现交通信号配时的时间分配,图4给出了劳动分工与交通信号配时之间的映射关系。该映射主要包括:1)将交叉口交通信号灯的每一个信号相位看作一只蜜蜂;2)将信号相位的绿灯时间看作蜜蜂的生理年龄;3)将信号相位的延误时间看作蜜蜂的激发剂;4)将信号相位的停车次数看作蜜蜂的抑制剂。由于本文直接将生理年龄与分配变量时间对应起来,在激发剂和抑制剂的耦合关系中应释放对年龄的约束,即耦合关系变为激发剂含量多的个体产生的抑制剂也多。同时,延误时间和停车次数之间呈指数关联趋势[21],恰好满足这种耦合关系。
|
Download:
|
| 图 4 蜂群劳动分工与交通信号配时之间的映射关系 Fig. 4 The mapping relation between bee swarm’s labor division and traffic signal timing | |
基于图4描述的映射关系,本节提出一种面向交通信号配时问题的蜂群劳动分工算法(bee swarm labor division algorithm, BSLDA)。BSLDA的核心要点是:某一信号相位的延误时间越长,则其激发剂越大,在激发–抑制原理作用下,其绿灯时间将会增加;延误时间越长,相应的停车次数也越大,则抑制剂越大,在激发–抑制原理作用下,其他相位的绿灯时间将会减小。BSLDA通过激发剂和抑制剂调整各信号相位的绿灯时间完成时间分配,具有原理简要明晰、便于实现的特点。
激发–抑制原理需要对激发剂和抑制剂进行比较,而延误时间和停车次数的量纲和量级都不同,难以直接比较。这里以经典F-B配时法的控制方案(TRRL)对应的延误时间和停车次数为标准数,建立相对性能指标。
第i相位车辆延误时间的相对指标为
| $R D_{i}=D_{i} / D_{i}^{\rm TTRL}$ | (1) |
第i相位车辆停车次数的相对指标为
| $R H_{i}=H_{i} / H_{i}^{\rm TTRL}$ | (2) |
第i相位的激发剂为
| $A_{i}=R D_{i}$ | (3) |
第i相位的抑制剂为
| $I_{i}=R H_{i}$ | (4) |
第i相位的激发抑制比为
| $f_{i}=A_{i} / \sum_{j=1 \atop j \neq i}^{n} I_{j}$ | (5) |
式中:n为信号相位的个数,这里假设蜜蜂与其他所有蜜蜂都进行交互。
激发–抑制原理是通过激发–抑制比来控制蜜蜂的生理年龄。相应地,在BSLDA中,通过激发–抑制比来决定信号相位的绿灯时间,具体如下:
1)当
| $\varDelta _{i}^ - = \psi ({f_i})$ | (6) |
式中
2)当
| $\varDelta _i^{\rm{ + }} = \phi ({f_i})$ | (7) |
式中
3)当
为进一步提高算法效率,在每一次时间分配过程中,对各相位绿灯时间的变化量进行修正:当所有相位都选择减少绿灯时间时,以最大减少量作为总的减少量,并按照减少比例分给各相位,此时信号周期变短;当所有相位都选择增加绿灯时间时,以最大增加量作为总的增加量,并按照增加比例分给各相位,此时信号周期变长;当一部分相位选择增加绿灯时间,而另一部分相位选择减少绿灯时间时,通过归一化处理,使得时间的增加量等于时间的减少量,此时信号周期保持不变;当所有相位都选择保持绿灯时间不变时,达到一个时间分配平衡。
BSLDA在解决交通信号配时问题时,每个信号相位都有增加绿灯时间、减少绿灯时间和保持绿灯时间不变3种行为选择。具体选择哪一种行为,是由信号相位的激发–抑制比决定的,激发剂与信号相位自身的延误时间有关,抑制剂与其他信号相位的停车次数有关。信号相位的激发剂、抑制剂和激发抑制比会随着绿灯时间、交通流量以及信号周期等变化,使得同一信号相位在不同交通场景下的行为选择不同,进而能够适应环境的变化。
图5描述了BSLDA的 实现流程,具体步骤为:
1)初始化相位方案、配时参数以及算法参数,包括相位总数n、信号周期C、绿灯时间x、最大迭代次数N、上限阈值α、下限阈值β、负相关函数
2)根据式(3)和式(4)分别计算各相位的激发剂和抑制剂;
3)根据式(5)计算各相位的激发抑制比;
4)若所有相位的激发抑制比都落在上限阈值α和下限阈值β之间,转至8),否则转至5);
5)根据式(6)或式(7)计算各相位的绿灯时间变化量;
6)根据绿灯时间的修正方法确定各信号相位的绿灯时间及信号周期;
7)若达到最大迭代次数,转至8),否则转至2);
8)输出结果。

|
Download:
|
| 图 5 蜂群劳动分工算法的实现流程 Fig. 5 The implementation process of BSLDA | |
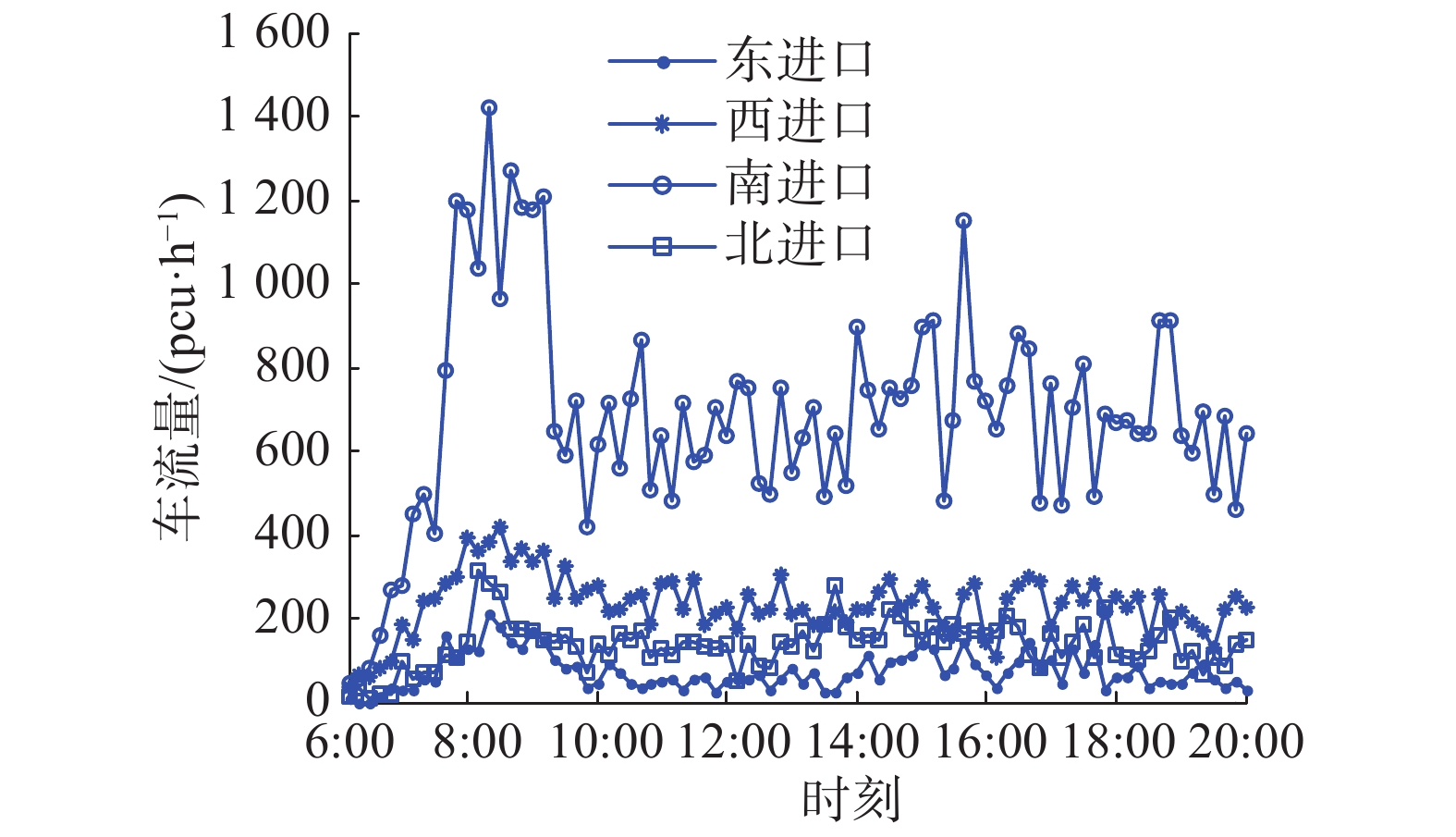
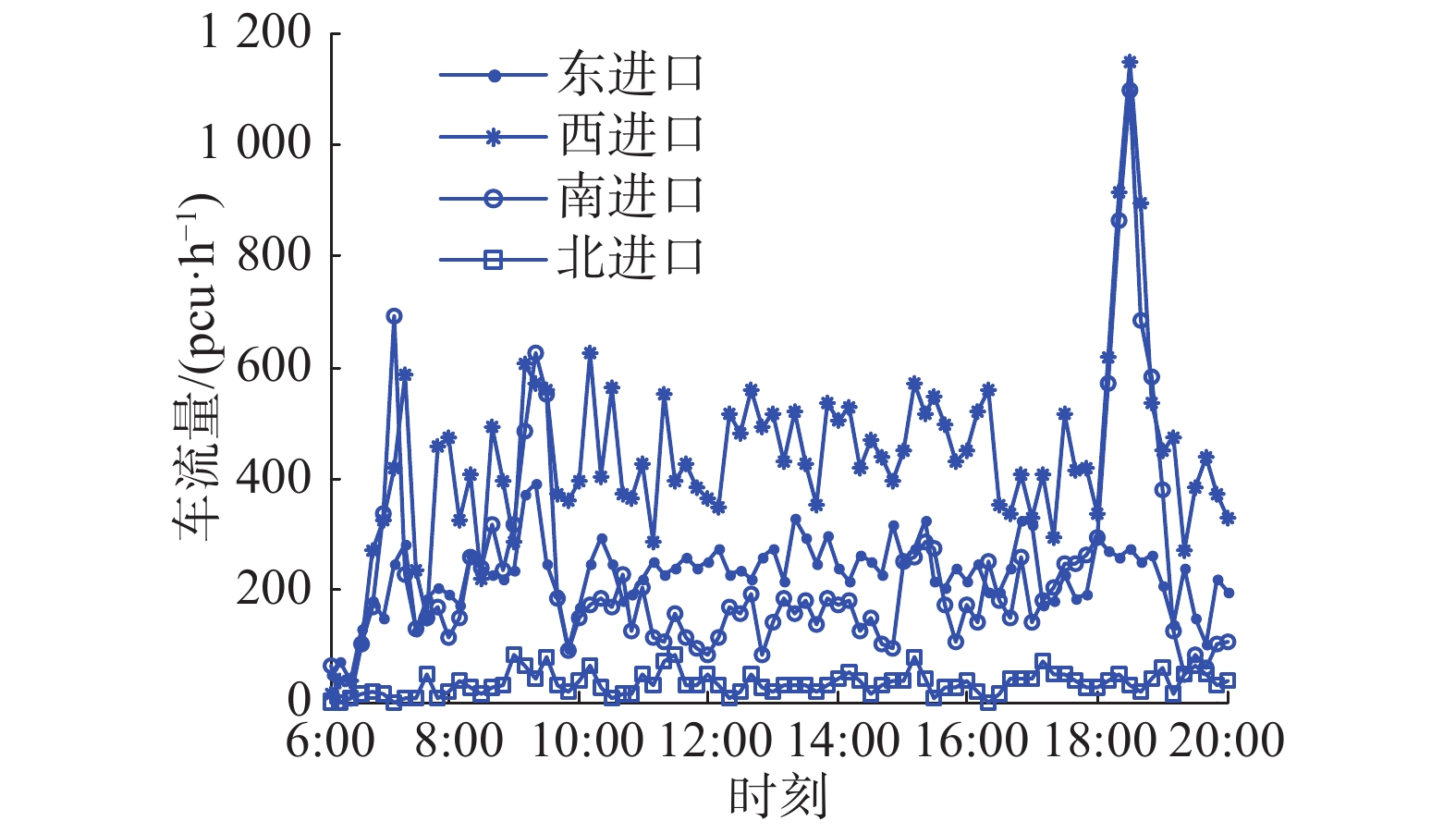
本文使用的交通数据来自于2014年中国“云上贵州”大数据商业模式大赛—智能交通算法大挑战。该数据描述了贵阳市南明区的主干路段在6:00~20:00时间段内通过各交叉路口的车流量情况。图6是贵阳市南明区部分区域的简化道路与红绿灯位置图,其中红绿灯用 tli 来表示。本文选取交通数据文件“flow0901”中红绿灯ID为“tl26”和“tl30”的交通数据,通过处理得到红绿灯“tl26”和“tl30”的车流量情况,如图7和8所示。图7中从南进口驶入的车流整体上处于较高的车流量水平,图8中从西进口驶入的车流整体上处于较高的车流量水平,即不同路口、不同方向的车流存在较大差异。图7和图8中的交通数据反映出了车流的高度动态性,对于评估信号配时方法的效果具有较强的说服力。

|
Download:
|
| 图 6 贵阳市南明区部分区域路口简化示意图 Fig. 6 A simplified diagram of some intersections in nanming district of GuiYang city | |
|
Download:
|
| 图 7 红绿灯“tl26”车流量 Fig. 7 Traffic flow at the traffic light “tl26” | |
|
Download:
|
| 图 8 红绿灯“tl30”车流量 Fig. 8 Traffic flow at the traffic light “tl30” | |
为了体现信号配时方法在不同交通场景下的效果,本文选取图7和图8中的两种车流量,并使用图2中的两种相位方案,通过组合得到4种不同的交通场景。为了方便进行相关描述,本文记图7和图2(a)形成的交通场景为TS1_1,图7和图2(b)形成的交通场景为TS1_2,图8和图2(a)形成的交通场景为TS2_1,图8和图2(b)形成的交通场景为TS2_2。
3.2 参数设置假设车辆在交叉口处直行、左转和右转的比例分别为60%、20%和20%;对于红绿灯“tl26”,东西进口道上直行车道、左转车道和右转车道的饱和流量分别为1 000 pcu/h、500 pcu/h和500 pcu/h,南北进口道上直行车道、左转车道和右转车道的饱和流量分别为2 400 pcu/h、1 200 pcu/h和1 200 pcu/h;对于红绿灯“tl30”,东西进口道上直行车道、左转车道和右转车道的饱和流量分别为2 000 pcu/h、1 000 pcu/h和1 000 pcu/h;南北进口道上直行车道、左转车道和右转车道的饱和流量分别为1 200 pcu/h、600 pcu/h和600 pcu/h;绿灯间隔时间为4 s,黄灯时间为2 s,启动损失时间为2 s,最短绿灯时间为5 s,最长绿灯时间为60 s。负相关函数ψ(fi)取e为底数,α-fi为自变量的指数函数;正相关函数ϕ(fi)取e为底数,fi-β为自变量的指数函数。则α和β是BSLDA中影响绿灯时间分配的2个关键因素。
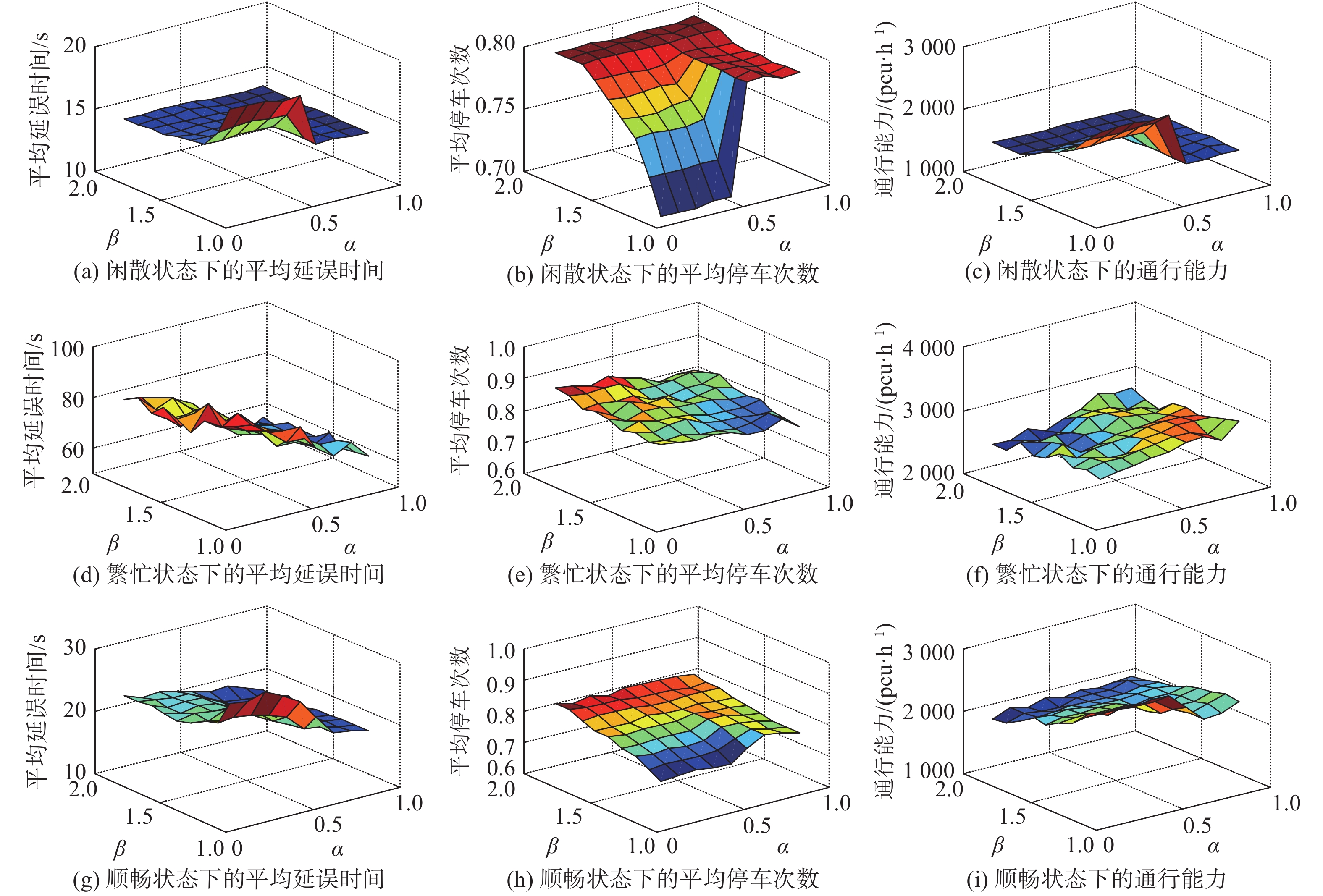
本节主要研究上限阈值α和下限阈值β对平均延误时间、平均停车次数和通行能力3个信号配时评价指标的影响,并以此为依据设置α和β的取值。这里选取图8中6:00~7:00、8:00~9:00和11:00~12:00三个时间段的数据,它们分别代表了闲散、顺畅和繁忙3种交通状态。在图2(a)的相位方案下,得到α和β对各项指标的影响(见图9)。
|
Download:
|
| 图 9 上限阈值α和下限阈值β对各项指标的影响 Fig. 9 The effects of upper threshold α and lower threshold β on evaluation indicators | |
从图9中可以看出,在不同的交通状态下,上限阈值α和下限阈值β对同一指标的影响大致相同。比如,平均延误时间随着α的增大呈减小趋势,随着β的减小呈增大趋势。这是因为平均延误时间受信号周期的影响较大,随着α的增大,更多的相位选择减少绿灯时间,并且绿灯时间的减少量变大,从而使得信号周期变短,延误时间变短;随着β的减小,更多的相位选择增加绿灯时间,并且绿灯时间的增加量变大,从而使得信号周期变长,延误时间变长。平均停车次数随着β的增大呈增大趋势,随着α的增大呈减小趋势,但是在β较小时又呈增大趋势。这是因为平均停车次数只受绿信比影响,β增大以后,更多停车次数多的相位难以通过增加绿灯时间来增加绿信比,减少停车次数;α增大以后,更多停车次数少的相位会让出绿灯时间,从而使停车次数多的相位的绿信比变大,停车次数减小;当β较小、α较大时,在每一次的分配过程中都存在增加绿灯时间和减少绿灯时间的相位,信号周期保持不变,此时的平均停车次数变大,说明当前的信号周期不是最佳信号周期。通行能力与绿信比成正比,其变化趋势与平均停车次数相反。在本文实验中,α选取为0.8,β选取为1.3。
3.3 对比实验为了验证本文算法(BSLDA)的有效性,本节选择与经典的Webster配时方法、人工蜂群算法(ABC)和蚁群算法(ACO)等群智能优化方法进行对比实验。求解时,先用Webster方法估计初始周期,然后利用等饱和比的方法计算各相位的大致信号配时,再用BSLDA进行分配求解。
在4种交通场景下,分别得到4种配时方法在每个小时的性能对比情况,如图10和图11所示。从图10可以看出,在交叉口和交通流量相同的情况下,同一种配时方法在不同的相位方案下得到了不同的控制效果。同样的,在图11中也观察到了类似的情形。这进一步说明了,TS1_1、TS1_2、TS2_1和TS2_2是4种不同的交通场景,对于评估交通信号配时方法的效果具有较强的说服力。从图10和图11中可以看出,BSLAD得到的计算结果比其他算法延误时间和停车次数均有减小,并且通行能力得到了提高。

|
Download:
|
| 图 10 TS1_1和TS1_2交通场景下各项指标的比较 Fig. 10 Comparison of evaluation indicators in traffic scenes TS1_1 and TS1_2 | |

|
Download:
|
| 图 11 TS2_1和TS2_2交通场景下各项指标的比较 Fig. 11 Comparison of evaluation indicators in traffic scenes TS2_1 and TS2_2 | |
表1~3统计了4种配时方法在不同交通场景下的整体效果。从表1中可以看出,与Webster、ABC和ACO相比,本文所提方法分别减少平均延误时间11.7%~20.3%、7.6%~17.2%、6.7%~14.7%。从表2可以看出,与Webster、ABC和ACO相比,本文所提方法分别减少平均停车次数4.5%~8.2%、6.2%~10.0%、2.2%~5.3%。从表3可以看出,与Webster、ABC和ACO相比,本文所提方法分别提高通行量4.3%~19.6%、9.8%~24.6%、4.5%~12.8%。
| 表 1 平均延误时间对比情况 Tab.1 Comparison of average time delay |
| 表 2 平均停车次数对比情况 Tab.2 Comparison of average stops |
| 表 3 通行能力对比情况 Tab.3 Comparison of traffic capacity |
交通信号配时问题可以看成给各相位的车辆分配绿灯时间,使其分时通过交叉口。对于不同相位的车辆,既有因早中晚高峰等原因造成的规律性变化,也有因汽车保有量增加等原因造成的非规律性变化。也就是说,各相位的车辆是动态变化的。这就要求分配给各相位车辆的绿灯时间不应一成不变,而应随着车流动态变化。因此,交通信号配时问题属于动态时间分配问题。
群智能劳动分工的显著特点是:由于个体行为柔性产生群体分工的可塑性,在行为柔性的作用下,个体能够根据环境变化调整所执行的任务,从而使得族群在变动环境下仍能实现有效的任务分配。群智能劳动分工在动态环境下的分配柔性是蜂群等社会性昆虫生态成功的首要原因,分配柔性这一特点也被众多学者用于求解动态环境下的分配问题,并取得了很好的效果。
在蜂群劳动分工中,个体的行为柔性是通过激发–抑制原理实现的,本文所提出的方法继承了这种行为柔性的特点。在本文方法中,每个信号相位都有增加绿灯时间、减少绿灯时间和保持绿灯时间不变3种行为选择,信号相位的具体行为选择是由其激发–抑制比来决定的,而激发–抑制比会随着环境动态变化。行为柔性使得本文方法在不同的交通情况下都能实现有效的时间分配,图10和图11的比较实验恰好证明了这一点。
约束条件下的分配问题都是在寻求一种最优的资源配置方式,传统的求解以优化方法为主。参照文献[6]对任务分配问题的分类,可将一般的分配问题分为确定环境下的静态分配问题和不确定环境下的动态分配问题两类。确定环境下的静态分配问题或者近似静态分配问题(比如将m个任务分配给n个主体的任务分配问题),适于采用蚁群、蜂群、粒子群等算法,这类方法求解高效。不确定环境下的动态分配问题(比如交通信号配时中的动态时间分配问题),适于采用群智能劳动分工方法,这类方法适应性强。
4 结束语本文通过分析蜂群劳动分工和交通信号配时的特点,给出了劳动分工与信号配时之间的映射关系;在BSLDA中设计了3种行为方式,并利用激发剂和抑制剂的相互作用指导信号相位选择恰当的行为完成时间分配,BSLDA在激发–抑制原理下具有柔性特点;不同交通情景下的实验结果表明,与其他方法相比,BSLDA展现出明显的有效性,适于求解不确定环境下的动态分配问题。
后续工作将从机理分析和扩展研究两个方面展开:1)在BSLDA中,激发剂体现了一种正反馈作用,抑制剂体现了一种负反馈作用,当正反馈和负反馈达到平衡时,就实现了有效的时间分配,分析其反馈机理;2)将研究对象由单交叉口交通信号配时进一步扩展到干线交通信号配时和区域交通信号配时。
| [1] |
王喆, 王红卫, 唐攀, 等. 考虑资源分配的HTN规划方法及其应用[J]. 管理科学学报, 2013, 16(3): 53-60. WANG Zhe, WANG Hongwei, TANG Pan, et al. HTN Planning method with resource allocation and its application[J]. Journal of management sciences in China, 2013, 16(3): 53-60. DOI:10.3969/j.issn.1007-9807.2013.03.006 (  0) 0)
|
| [2] |
吕冰洋, 郭庆旺. 中国要素收入分配的测算[J]. 经济研究, 2012, 47(10): 27-40. LÜ Bingyang, GUO Qingwang. Calculation on China’s functional income distribution and redistribution[J]. Economic research journal, 2012, 47(10): 27-40. DOI:10.3969/j.issn.1004-7778.2012.10.009 (  0) 0)
|
| [3] |
甘敏, 彭辉, 陈晓红. 基于市场微结构模型和进化算法的资产分配[J]. 系统工程学报, 2011, 26(3): 314-321. GAN Min, PENG Hui, CHEN Xiaohong. Asset allocation based on a market microstructure model and evolutionary algorithms[J]. Journal of systems engineering, 2011, 26(3): 314-321. (  0) 0)
|
| [4] |
万晓榆, 冯小龙, 王正强, 等. 基于能量采集异构蜂窝网络的功率分配算法研究[J]. 电子学报, 2017, 45(9): 2308-2312. WAN Xiaoyu, FENG Xiaolong, WANG Zhengqiang, et al. Power allocation algorithm for heterogeneous cellular networks based on energy harvesting[J]. Acta electronica sinica, 2017, 45(9): 2308-2312. DOI:10.3969/j.issn.0372-2112.2017.09.036 (  0) 0)
|
| [5] |
张嵛, 刘淑华. 多机器人任务分配的研究与进展[J]. 智能系统学报, 2008, 3(2): 115-120. ZHANG Yu, LIU Shuhua. Survey of multi-robot task allocation[J]. CAAI transactions on intelligent systems, 2008, 3(2): 115-120. (  0) 0)
|
| [6] |
唐苏妍, 朱一凡, 李群, 等. 多Agent系统任务分配方法综述[J]. 系统工程与电子技术, 2010, 32(10): 2155-2161. TANG Suyan, ZHU Yifan, LI Qun, et al. Survey of task allocation in multi agent systems[J]. Systems engineering and electronics, 2010, 32(10): 2155-2161. DOI:10.3969/j.issn.1001-506X.2010.10.30 (  0) 0)
|
| [7] |
王长军, 徐琪, 贾永基. 单机下异构任务调度的解性质研究[J]. 管理科学学报, 2015, 18(7): 70-81. WANG Changjun, XU Qi, JIA Yongji. Properties of solution for heterogeneous tasks scheduling on single machine[J]. Journal of management sciences in China, 2015, 18(7): 70-81. DOI:10.3969/j.issn.1007-9807.2015.07.007 (  0) 0)
|
| [8] |
吴花平, 黄敏, 王兴伟. 考虑多个RMAs的单机调度问题[J]. 控制与决策, 2014, 29(12): 2253-2258. WU Huaping, HUANG Min, WANG Xingwei. Single-machine scheduling problem with multi-RMAs[J]. Control and decision, 2014, 29(12): 2253-2258. (  0) 0)
|
| [9] |
姚荣涵, 王筱雨, 赵胜川, 等. 基于机动车比功率的单点信号配时优化模型[J]. 交通运输系统工程与信息, 2015, 15(5): 89-95. YAO Ronghan, WANG Xiaoyu, ZHAO Shengchuan, et al. An optimization model of signal timing for isolated intersections based on vehicle specific power[J]. Journal of transportation systems engineering and information technology, 2015, 15(5): 89-95. DOI:10.3969/j.issn.1009-6744.2015.05.013 (  0) 0)
|
| [10] |
孙棣华, 杨陈成, 廖孝勇, 等. 基于公交GPS数据的交叉口信号配时参数估计[J]. 控制与决策, 2018, 33(4): 724-730. SUN Dihua, YANG Chencheng, LIAO Xiaoyong, et al. Signal timing estimation for intersections using bus GPS data[J]. Control and decision, 2018, 33(4): 724-730. (  0) 0)
|
| [11] |
ZHAO Dongbin, DAI Yujie, ZHANG Zhen. Computational intelligence in urban traffic signal control: a survey[J]. IEEE transactions on systems, man, and cybernetics, part C: applications and reviews, 2012, 42(4): 485-494. DOI:10.1109/TSMCC.2011.2161577 ( 0) 0)
|
| [12] |
肖人彬, 陶振武. 群集智能研究进展[J]. 管理科学学报, 2007, 10(3): 80-96. XIAO Renbin, TAO Zhenwu. Research progress of swarm intelligence[J]. Journal of management sciences in China, 2007, 10(3): 80-96. DOI:10.3321/j.issn:1007-9807.2007.03.011 (  0) 0)
|
| [13] |
ROBINSON G E. Regulation of division of labor in insect societies[J]. Annual review of entomology, 1992, 37: 637-665. DOI:10.1146/annurev.en.37.010192.003225 ( 0) 0)
|
| [14] |
XIAO Renbin, YU Tongyang, GONG Xiaoguang. Modeling and simulation of ant colony’s labor division with constraints for task allocation of resilient supply chains[J]. International journal on artificial intelligence tools, 2012, 21(3): 1240014. DOI:10.1142/S0218213012400143 ( 0) 0)
|
| [15] |
DE LOPE J, MARAVALL D, QUIÑONEZ Y. Response threshold models and stochastic learning automata for self-coordination of heterogeneous multi-task distribution in multi-robot systems[J]. Robotics and autonomous systems, 2013, 61(7): 714-720. DOI:10.1016/j.robot.2012.07.008 ( 0) 0)
|
| [16] |
LOW K H, LEOW W K, ANG M H JR. Autonomic mobile sensor network with self-coordinated task allocation and execution[J]. IEEE transactions on systems, man, and cybernetics, part C: applications and reviews, 2006, 36(3): 315-327. DOI:10.1109/TSMCC.2006.871590 ( 0) 0)
|
| [17] |
KIM M H, BAIK H, LEE S. Response threshold model based UAV search planning and task allocation[J]. Journal of intelligent and robotic systems, 2014, 75(3-4): 625-640. DOI:10.1007/s10846-013-9887-6 ( 0) 0)
|
| [18] |
WANG Yingcong, XIAO Renbin, WANG Huimin. A flexible labour division approach to the polygon packing problem based on space allocation[J]. International journal of production research, 2017, 55(11): 3025-3045. DOI:10.1080/00207543.2016.1229070 ( 0) 0)
|
| [19] |
肖人彬, 王英聪. 面向群体利益分配的蚁群劳动分工建模与仿真[J]. 管理科学学报, 2016, 19(10): 1-15. XIAO Renbin, WANG Yingcong. Modeling and simulation of ant colony’s labor division for interest allocation of social groups[J]. Journal of management sciences in China, 2016, 19(10): 1-15. DOI:10.3969/j.issn.1007-9807.2016.10.001 (  0) 0)
|
| [20] |
杨佩昆, 吴兵. 交通管理与控制[M]. 北京: 人民交通出版社, 2004.
( 0) 0)
|
| [21] |
HE Jiajia, HOU Zaien. Ant colony algorithm for traffic signal timing optimization[J]. Advances in engineering software, 2012, 43(1): 14-18. DOI:10.1016/j.advengsoft.2011.09.002 ( 0) 0)
|
| [22] |
刘爽, 岳芳, 郭彦东, 等. 基于模式搜索算法的交叉口信号配时优化研究[J]. 交通运输系统工程与信息, 2011, 11(S1): 29-35. LIU Shuang, YUE Fang, GUO Yandong, et al. Optimization research on signal timing for urban intersections based on pattern search algorithm[J]. Journal of transportation systems engineering and information technology, 2011, 11(S1): 29-35. (  0) 0)
|
| [23] |
徐勋倩, 黄卫. 单路口交通信号多相位实时控制模型及其算法[J]. 控制理论与应用, 2005, 22(3): 413-416, 422. XU Xunqian, HUANG Wei. Multiphase traffic signal real-time controlling model of isolated intersection and its algorithm[J]. Control theory and applications, 2005, 22(3): 413-416, 422. DOI:10.3969/j.issn.1000-8152.2005.03.014 (  0) 0)
|
| [24] |
杨文臣, 张轮, 饶倩, 等. 基于黄金分割点遗传算法的交通信号多目标优化[J]. 交通运输系统工程与信息, 2013, 13(5): 48-55. YANG Wenchen, ZHANG Lun, RAO Qian, et al. Multi-objective optimization for traffic signals with golden ratio based genetic algorithm[J]. Journal of transportation systems engineering and information technology, 2013, 13(5): 48-55. DOI:10.3969/j.issn.1009-6744.2013.05.008 (  0) 0)
|
| [25] |
PANG Hao, CHEN Feng. An optimization approach for intersection signal timing based on multi-objective particle swarm optimization[C]//Proceedings of 2008 IEEE Conference on Cybernetics and Intelligent Systems. Chengdu, China, 2008: 771-775.
( 0) 0)
|
| [26] |
顾怀中, 王炜. 交叉口交通信号配时模拟退火全局优化算法[J]. 东南大学学报, 1998, 28(3): 68-72. GU Huaizhong, WAGN Wei. A global optimization simulated annealing algorithm for intersection signal timing[J]. Journal of Southeast University, 1998, 28(3): 68-72. (  0) 0)
|
| [27] |
陈小红, 钱大琳, 秦雪梅, 等. 基于互补问题的混合交通信号配时优化模型[J]. 系统工程理论与实践, 2010, 30(1): 184-191. CHEN Xiaohong, QIAN Dalin, QIN Xuemei, et al. Complementarity problems-based optimization model for the signal timing under mixed traffic conditions[J]. Systems engineering-theory and practice, 2010, 30(1): 184-191. (  0) 0)
|
| [28] |
HUANG Zhiyong, ROBINSON G E. Regulation of honey bee division of labor by colony age demography[J]. Behavioral ecology and sociobiology, 1996, 39(3): 147-158. DOI:10.1007/s002650050276 ( 0) 0)
|
| [29] |
HUANG Zhiyong, ROBINSON G E. Honeybee colony integration: worker-worker interactions mediate hormonally regulated plasticity in division of labor[J]. Proceedings of the national academy of sciences of the United States of America, 1992, 89(24): 11726-11729. DOI:10.1073/pnas.89.24.11726 ( 0) 0)
|
| [30] |
NAUG D, GADAGKAR R. Flexible division of labor mediated by social interactions in an insect colony—a simulation model[J]. Journal of theoretical biology, 1999, 197(1): 123-133. DOI:10.1006/jtbi.1998.0862 ( 0) 0)
|
| [31] |
ZAHADAT P, HAHSHOLD S, THENIUS R, et al. From honeybees to robots and back: division of labour based on partitioning social inhibition[J]. Bioinspiration & biomimetics, 2015, 10(6): 066005. ( 0) 0)
|
| [32] |
ZAHADAT P, SCHMICKL T. Division of labor in a swarm of autonomous underwater robots by improved partitioning social inhibition[J]. Adaptive behavior, 2016, 24(2): 87-101. DOI:10.1177/1059712316633028 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


