作为计算机视觉和模式识别中最具挑战性的研究课题之一,人脸识别(FR)[1-8]在近几年一直是研究的热点课题。在实际生活中,人脸识别也被广泛应用,比如视频监控、安全相关访问和人机交互技术等。随着研究的深入,目前无污损情况下的人脸识别已经达到理想的效果。但在面部有遮挡和伪装的情况下进行人脸识别和分类仍然是一个具有挑战性的难题。
1 低秩稀疏表示理论近年来,基于稀疏表示的方法在人脸识别领域内被广泛使用。Wright等[5]提出基于稀疏表示分类(SRC)。稀疏表示分类的主要思想是将一个测试样本看成一个过完备字典中少量原子的线性表示,并计算出测试样本关于字典矩阵的编码系数,最后利用最小重构误差法分类。近年来,很多基于SRC的算法被相继提出。Zhang等[9]提出了基于协同表示的分类(CRC),将SRC中的l1-norm换为l2-norm,在保证分类结果理想的同时加快了分类速度。针对小样本问题,Deng等[10]提出ESRC,使用辅助的类内变化字典表示训练样本和测试样本之间可能存在的变化。RRC[8](regularized robust coding)算法和JRPL[11](joint representation and pattern learning)算法进一步增强了SRC算法在存在污染情况下的鲁棒性。虽然SRC及其改进算法达到了较高的识别率,但是当测试样本和训练样本中都存在遮挡或像素污损的时候,算法的分类效果依然会受到影响。而直接忽略被遮挡的训练样本,隐藏在原始训练样本中的判别信息就不能被充分地利用,从而导致性能变差。因此,SRC在实际的应用中受到了限制。
最近的研究表明,视觉数据具有低秩结构,低秩矩阵恢复技术成为研究的热点题。Candès等[12]提出的鲁棒主成分分析(robust principal component analysis, RPCA)可以从被污染的数据中恢复出原始数据的低秩矩阵,随后Liu等[13]提出了低秩表示(low-rank representation,LRR)方法。基于RPCA和LRR,研究者提出了很多方法来处理训练样本中存在的遮挡和污损。Chen等[7]使用RPCA把原始的训练数据分解为低秩矩阵和误差矩阵,同时让不同类的低秩部分结构不相关,在一定程度上增加了鉴别信息。Ma等[14]提出的DLRD_SR(discriminative low-rank dictionary for sparse representation)在字典学习的过程中加入了低秩和稀疏约束,在样本存在污染时取得了较好的分类效果。Zhang等[15]提出LSLR(learning structured low-rank representations),通过在训练过程中加入结构化约束,构造出了一个结构化的字典,使得系数更加趋近于块对角结构,并通过优化后的系数对测试样本进行分类,但是LSLR并没有着重加强每类子字典对同类训练样本的表示能力。Nguyen[16]在LRR的基础上增加了标签约束项和重构误差约束项,让类内的重构误差减小而类间的重构误差增大,进一步加强了每一类子字典的判别性。Chang[17]在算法中加入权重约束项,使得在块对角上的低秩系数值更大,非块对角上的值更加趋于0,同时提高了表示系数和字典的判别性。Zhang等[18]提出BDLRR (block-diagonal low-rank representation),将对表示系数的块对角约束和权重约束相结合,得到了更加理想的表示系数。而上述这些基于低秩矩阵恢复的方法的主要思想都是构造一个干净的具有判别性的字典,消除训练样本中的遮挡带来的影响,但是并没有考虑到测试样本中存在遮挡的情况。如果测试样本中也存在遮挡且没有通过算法被有效地移除,也将导致测试样本无法正确分类,会对实验结果产生很大的影响。
针对样本中存在污染的问题,本文提出一种结构化加权稀疏低秩恢复算法。该算法在原始低秩表示的基础上对低秩系数进行了加权和结构化稀疏约束,可以得到一个结构化的判别低秩系数,而且同类样本的表示系数会有更强的相关性。跟上述方法不同的是,受到Chen等[19]提出的DLRR(discriminative low-rank representation)的启发,本文在得到训练样本的恢复样本后,根据原始训练样本和恢复后的干净训练样本学习到一个低秩投影矩阵,并对存在遮挡的测试样本进行投影,有效地消除了测试样本中存在的遮挡,解决了测试样本中存在遮挡从而影响最终分类结果的问题。最后使用SRC方法对恢复后的测试样本进行分类识别。在几个标准数据上的实验结果验证了所提出方法的有效性和鲁棒性。
2 相关工作 2.1 稀疏表示分类稀疏表示分类方法的主要思想是将测试样本表示为训练样本的稀疏线性组合,并计算测试样本和每个类别的重构误差,最后将测试样本分在最小重构误差对应的类别中。假设
| $\mathop {\min }\limits_\alpha \left\| {y - {{X}}\alpha } \right\|_2^2 + {\textit{λ}} {\left\| \alpha \right\|_1}$ | (1) |
式中:
| ${\rm{identity}}(y) = \arg \mathop {\min }\limits_i \left\| {y - {{{X}}_i}{\alpha _i}} \right\|_2^2$ | (2) |
式中
要从有遮挡的训练样本中恢复出干净的训练样本,需要借助于低秩矩阵恢复技术。有遮挡的训练样本可以表示为低秩矩阵
因此,Candès等[14]提出使用鲁棒PCA方法来对
| $ \mathop {\min }\limits_{{{D}},{{E}}} {\rm{rank}}({{D}}) + \lambda {\left\| {{E}} \right\|_0},\; \ \ \ {\rm{s}}{\rm{.t}}{\rm{.}} \ {{X}} = {{D}} + {{E}} $ | (3) |
由于式(3)是非凸的,常用的做法是把
| $ \mathop {\min }\limits_{{{D}},{{E}}} {\left\| {{D}} \right\|_*} + {\textit{λ}} {\left\| {{E}} \right\|_1},\; \ \ \ \ {\rm{s}}{\rm{.t}}{\rm{.}} \ {{X}} = {{D}} + {{E}} $ | (4) |
RPCA假设数据来自一个单独的子空间,但是实际中的数据通常来自多个子空间[20],基于此,Liu等[15]推广了RPCA的概念并提出了更一般的秩最小化问题,即低秩表示,目标函数为
| $ \mathop {\min }\limits_{{{Z}},{{E}}} {\left\| {{Z}} \right\|_*} +{\textit{λ}} {\left\| {{E}} \right\|_1},\; \ \ \ \ {\rm{s}}{\rm{.t}}{\rm{.}} \ {{X}} = {{A}}Z + {{E}} $ | (5) |
式中:
通过结构化加权稀疏低秩表示SWLRR(structured and weighted low-rank represen -tation)将污染的样本恢复成干净的样本,同时学习一个原始训练样本到恢复训练样本的投影矩阵。SWLRR利用了原始训练样本的标签信息,并对低秩表示系数进行加权稀疏约束,使得相似的样本尽可能有相似的表示,也增强了恢复矩阵的判别能力。
3.1 结构化的加权稀疏低秩表示(SWLRR)为了提高SRC的性能,可以利用低秩矩阵恢复技术来解决上面提到的几个影响分类效果的问题。把原始的训练样本分解为干净的训练样本和对应的稀疏误差。受Zhang等[15]和Zhang等[18]的启发,本文在原始式(5)的基础上增加了两个对低秩表示系数的约束项,提出了用SWLRR来恢复污染的样本,同时增强恢复矩阵的判别性。
将
| $\begin{array}{*{20}{c}} {\mathop {\min }\limits_{Z,E} {{\left\| {{Z}} \right\|}_*} + \alpha {{\left\| {{{D}} \odot {{Z}}} \right\|}_0} + \beta \left\| {{{Z}} - {{Q}}} \right\|_F^2 + \lambda {{\left\| {{E}} \right\|}_1}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;{{X}} = {{AZ}} + {{E}}} \end{array}$ |
式中:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{{Z}},{{E}}} {{\left\| {{Z}} \right\|}_*} + \alpha {{\left\| {{{D}} \odot {{Z}}} \right\|}_1} + \beta \left\| {{{Z}} - { Q}} \right\|_F^2 + {\textit{λ}} {{\left\|{{E}} \right\|}_1}}\\ {{\rm{s.t}}.\;{{X}} = {{AZ}} + {{E}}} \end{array} $ | (7) |
| ${{{Z}}^*} = \left( {\begin{array}{*{20}{c}} {{{Z}}_1^*}&\rm{ }&\rm{ }&\rm{ } \\ \rm{ }&{{{Z}}_2^*}&\rm{ }&\rm{ } \\ \rm{ }&\rm{ }&{ \ddots }&\rm{ } \\ \rm{ }&\rm{ }&\rm{ }&{{{Z}}_C^*} \end{array}} \right)$ |
其中
基于LRR中原始训练数据
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{{Z}},{{E}}} {{\left\| {{Z}} \right\|}_*} + \alpha {{\left\| {{{D}} \odot {{Z}}} \right\|}_1} + \beta \left\| {{{Z}} - {{Q}}} \right\|_F^2 + \lambda {{\left\| {{E}} \right\|}_1}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;{{X}} = {{XZ}} + {{E}}} \end{array} $ | (8) |
为了将变量分离,引入辅助变量
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{{Z}},{{P}},{{J}},{{E}}} {{\left\| {{P}} \right\|}_*} + \alpha {{\left\| {{{D}} \odot {{J}}} \right\|}_1} + \beta \left\| {{{Z}} - {{Q}}} \right\|_F^2 + \lambda {{\left\| {{E}} \right\|}_1}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;{{X}} = {{XZ}} + {{E}},\;{{Z}}{\rm{ = }}{{P}},\;{{Z}}{\rm{ = }}{{J}}} \end{array} $ | (9) |
式(9)可以用ALM求解,它对应的增广拉格朗日函数为
| $ \begin{array}{*{20}{c}} {L({{Z}},{{P}},{{J}},{{E}},{{{Y}}_1},{{{Y}}_2},{{{Y}}_3},\mu ) = }\\ {{{\left\| {{P}} \right\|}_*} + \alpha {{\left\| {{{D}} \odot {{J}}} \right\|}_1} + \beta \left\| {{{Z}} - {{Q}}} \right\|_F^2 + \lambda {{\left\| {{E}} \right\|}_1} + }\\ { < {{{Y}}_1},{{X}} - {{XZ}} - {{E}} > + < {{{Y}}_2},{{Z}} - {{P}} > + < {{{Y}}_3},{{Z}} - {{J}} > + }\\ {\displaystyle\frac{\mu }{2}(\left\| {{{X}} - {{XZ}} - {{E}}} \right\|_F^2 + \left\| {{{Z}} - {{P}}} \right\|_F^2 + \left\| {{{Z}} - {{J}}} \right\|_F^2){\rm{ }}} \end{array} $ | (10) |
式中:
| $ \begin{array}{*{20}{c}} {L({{Z}},{{P}},{{J}},{{E}},{{{Y}}_1},{{{Y}}_2},{{{Y}}_3},\mu )}=\\ { {{\left\| {{P}} \right\|}_*} + \alpha {{\left\| {{{D}} \odot {{J}}} \right\|}_1} + \beta \left\| {{{Z}} - {{Q}}} \right\|_F^2 + \lambda {{\left\| {{E}} \right\|}_1} + }\\ {q({{Z}},{{P}},{{J}},{{E}},{{{Y}}_1},{{{Y}}_2},{{{Y}}_3},\mu ) - \displaystyle\frac{1}{{2\mu }}(\left\| {{{{Y}}_1}} \right\|_F^2 + \left\| {{{{Y}}_2}} \right\|_F^2 + \left\| {{{{Y}}_3}} \right\|_F^2){\rm{ }}} \end{array} $ | (11) |
式中
可以交替优化变量Z、P、J、E,即优化其中一个时,固定另外3个变量。每次迭代时变量的更新情况如下。
1)固定 Z、J、E,更新
式(11)可转化为
| ${{{P}}_{k + 1}} = \arg \min \varepsilon {\left\| {{{{P}}}} \right\|_*} + \frac{1}{2}\left\| {{{{P}}} - {{A}}} \right\|_F^2$ | (12) |
式中:
| ${{{P}}} = {{U}}{{{S}} }{{{V}}^{\rm{T}}} = {{U}}{T_\varepsilon }[{{S}}]{{{V}}^{\rm{T}}}$ | (13) |
式中:
| ${T_\varepsilon }[{{S}}] = \left\{ {\begin{array}{*{20}{l}} {{{{S}}_{i,j}} - \varepsilon ,\begin{array}{*{20}{c}} {} \end{array}{S_{i,j}} > \varepsilon } \\ {{{{S}}_{i,j}} + \varepsilon ,\begin{array}{*{20}{c}} {} \end{array}{S_{i,j}} < - \varepsilon } \\ {{\rm{ }}0,\;\;{\text{其他}}} \end{array}} \right.$ | (14) |
2)固定J、E、P,更新Z
将J、E、P这3个变量看成常数后,式(11)可以写成式(15)只关于变量
| $ \begin{array}{l} L({{Z}}) = \mathop {\min }\limits_{{Z}} \beta \left\| {{{Z}} - {{Q}}} \right\|_F^2 + \displaystyle\frac{\mu }{2}(\left\| {{{X}} - {{XZ}} - {{E}} + \displaystyle\frac{{{{{Y}}_1}}}{\mu }} \right\|_F^2 + \\ \left\| {{{Z}} - {{P}} + \displaystyle\frac{{{{{Y}}_2}}}{\mu }} \right\|_F^2 + \left\| {{{Z}} - {{J}} + \displaystyle\frac{{{{{Y}}_3}}}{\mu }} \right\|_F^2) \end{array} $ | (15) |
为了求出使式(15)最小的Z值,将对
| $ \begin{array}{*{20}{c}} {{{{Z}}} = {{(2\beta + {\mu }{{{X}}^{\rm{T}}}{ X} + 2{\mu })}^{ - 1}}(2\beta {{Q}} + {\mu }{{{X}}^{\rm{T}}}{{X}} - {\mu }{{{X}}^{\rm{T}}}{{{E}}} + }\\ {{{{X}}^{\rm{T}}}{{{Y}}_{1}} + \mu {{{P}}} + \mu {{ J}} - {{{Y}}_{2}} - {{{Y}}_{3}})} \end{array} $ | (16) |
3)固定
| $ {{{J}}_{k + 1}} = {{{T}}}({{{Z}}_{k + 1}} + \frac{{{{{Y}}_{3,k}}}}{{{\mu _k}}}) $ | (17) |
4)固定
| ${{{E}}_{k + 1}} = {{{T}}}({{X}} - {{X}}{{{Z}}_{k + 1}} + \frac{{{{{Y}}_{1,k}}}}{{{\mu _k}}})$ | (18) |
式(16)、(17)中的
|
Download:
|
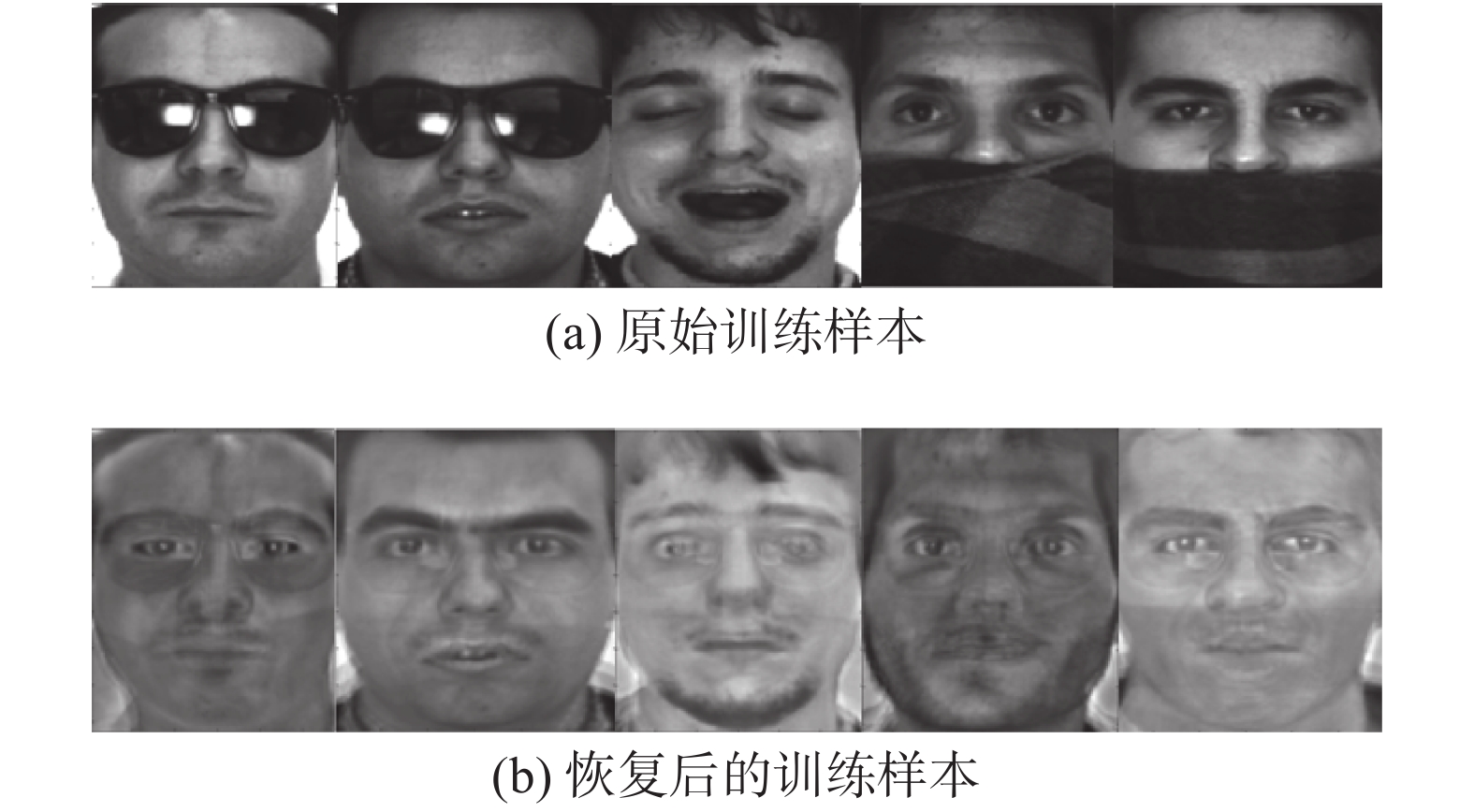
| 图 1 SWLRR算法得到的恢复结果 Fig. 1 Recovery results obtained using SWLRR method | |
算法1 用LADMAP求解问题 (即式(8))
输入 训练数据样本
输出
初始化
若不满足式(7)中的收敛条件,则循环下列更新步骤:
1)根据式(13)更新
2)根据式(16)更新
3)根据式(17)更新
4)根据式(18)更新
5)更新拉格朗日乘子:
6)更新参数
7)检查收敛条件:
8)更新
在对样本进行分类时,训练样本和测试样本中存在的遮挡都会对分类结果产生影响。所以将训练样本恢复成干净样本后,接下来要考虑的问题就是如何移除测试样本中可能存在的遮挡。受Bao等[24]启发,可以通过学习一个低秩投影矩阵,将受污染的测试样本投影到相应的低秩子空间。
根据算法1求出低秩表示系数
| $ \mathop {{\rm{min}}}\limits_{{A}} {\left\| {{A}} \right\|_*},\;\;\;{\rm{s}}.{\rm{t}}.\;\;{{Y}} = {{AX}} $ | (19) |
假设
图2是AR数据库中部分测试样本图像经过低秩投影矩阵恢复后的图像,可以看到通过将测试样本投影到低秩投影矩阵,测试图像中的遮挡区域得到一定程度的消除,接下来就可以开始进一步地降维和分类操作,SWLRR的整体流程如算法2所示。

|
Download:
|
|
图 2 测试样本经过矩阵
|
|
算法2 结构约束的低秩投影稀疏算法
输入
输出
1)通过算法1得到所有训练样本的结构化判别秩
2)得到训练样本的恢复数据
3)计算低秩投影矩阵
4)测试样本
5)计算
6)训练样本恢复后的数据
7)求解
8)计算每个类别对应的残差:
为了验证SWLRR的有效性,本文将SWLRR和一些已经提出的经典算法如DLRR、SRC、LRMR、RRC[8]、SVM[25-27]进行了对比。所有算法均使用SRC算法进行分类。实验中SWLRR和DLRR算法引入了低秩投影思想。实验分别在CMU PIE、AR和Extended Yale B人脸数据库上进行。
我们使用有光照、表情变化以及饰物遮挡的人脸图像对SWLRR算法进行测试,实验中所有训练样本和测试样本的污损类型都是相同的,且每一次样本选择都是随机的。实验涉及4个重要参数,包括3个SWLRR的权重参数
实验在CPU为Intel core i5-6500 @3.20 GHz,内存为12.0 GB,操作系统为Windows 7,MATLAB版本为MATLAB R2015a的环境下进行。
4.1 无遮挡的人脸识别实验 4.1.1 Extended Yale B数据库Extended Yale B数据库由38个人的2 414张人脸图片组成,每个人大约有59~64张不同的光照环境下的图片。在实验中,每张人脸图片大小为192像素
|
Download:
|
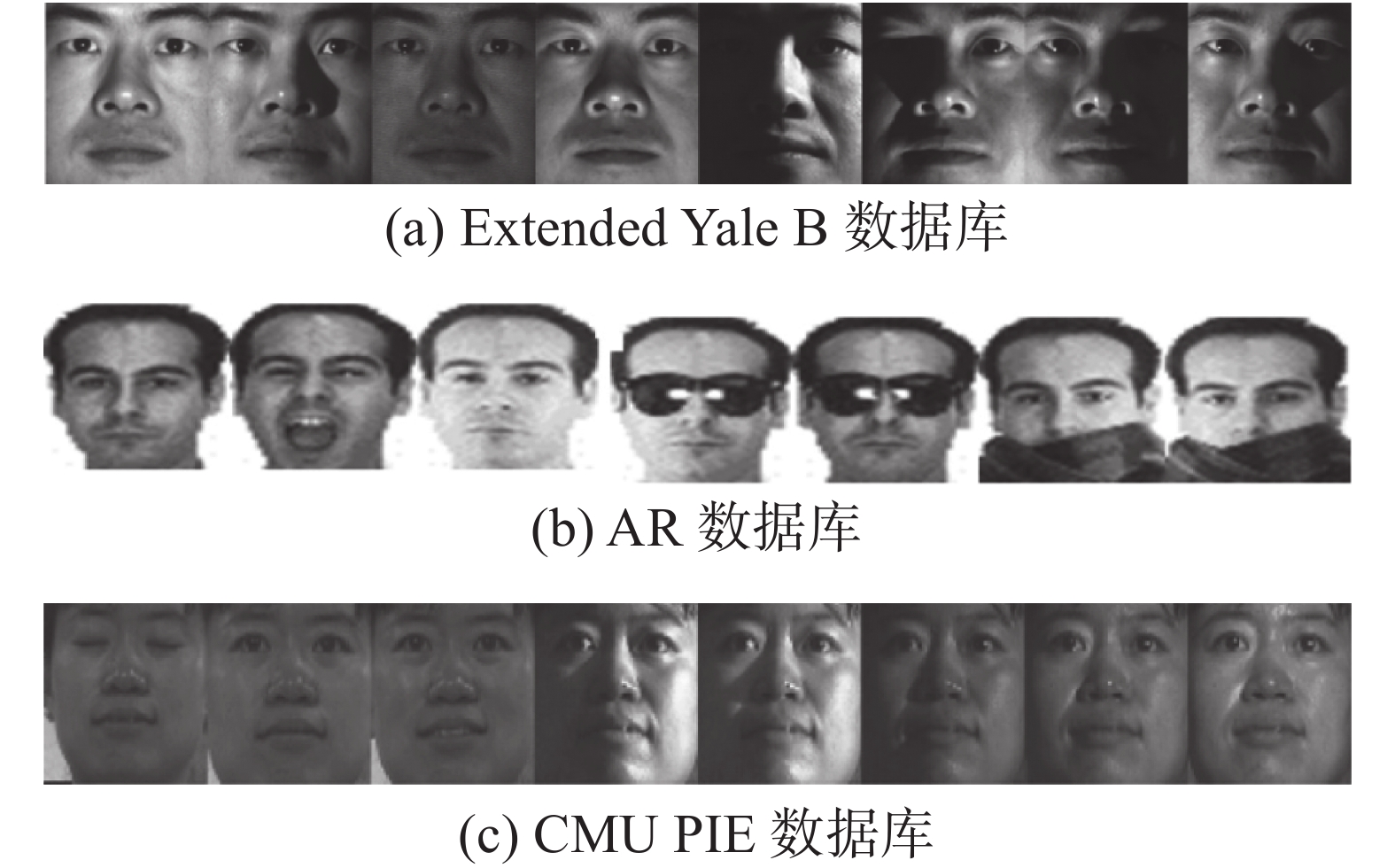
| 图 3 实验中用到的样本图像 Fig. 3 Images used in our experiments | |
| 表 1 Extended Yale B数据库在无遮挡条件下不同维度的算法识别率(16训练样本) Tab.1 The recognition rate of different dimensions in Extended Yale B database without occlusion(16 training samples) % |
| 表 2 Extended Yale B数据库上在无遮挡条件下不同维度的算法识别率(32训练样本) Tab.2 The recognition rate of different dimensions in Extended Yale B database without occlusion(32 training samples) % |
两组实验结果显示以上所有算法的识别率都随着图像特征维度的增加而增加,这是因为相对较高的维度提供了更多的图像信息,从而提高了识别性能。而且在维度相同时,SWLRR的识别率远高于其他算法,尤其是在特征维度较低时,本文提出的方法更加有优势。例如:特征维度为25时,以上的2组实验中SWLRR的识别率高达92.41%和97.75%,远远高于其他算法。实验结果可以证实,SWLRR可以较好地解决样本中存在不同的光照和表情的问题。
4.1.2 AR数据库实验AR数据库包含126个人的4 000多张人脸图片,每个人有26张,被分为两部分,每部分由含有表情光照变化的7幅无遮挡图片、3幅戴墨镜图片和3幅戴围巾图片组成,每幅图片大小被裁剪成165像素
| 表 3 AR数据库在无遮挡条件下不同维度的算法识别率 Tab.3 The recognition rate of different dimensions in AR database without occlusion % |
CMU PIE数据库由68个人的41 368张图片组成,所有图片在不同姿势、光照和表情条件下采集。本文选用编号为C07的子数据库用来实验,其包含68个人的1 629张图片,每人大约24张,每张图片大小为64
| 表 4 CMU PIE数据库上不同算法在无遮挡条件下的识别率 Tab.4 The recognition rate of different dimensions in CMU PIE database without occlusion % |
从表4可以看出,在CMU PIE数据库上SWLRR算法在不同维度下识别率同样远高于其他算法。在维度为25时,SWLRR算法识别率为93.39%,高于DLRR算法将近11%。但是,随着维度的增加,各种算法识别率的差异变得越来越小,主要是因为在低维度情况下,DLRR算法缺乏结构化特征,数据的线性特征不足以分离不同子空间的样本,SWLRR增强了不同类样本的结构性,进一步提高了样本的判别能力,从而提高了识别率。
4.2 有噪声的人脸识别实验 4.2.1 加入人工噪声的人脸识别为了验证SWLRR算法的鲁棒性,首先在Extended Yale B数据库上进行添加随机高斯噪声的实验。实验中,每张图片大小为192
| 表 5 Extended Yale B 数据库上不同算法在两种比例噪声污染下的识别率 Tab.5 The recognition rate of different methods on the Extended Yale B database with two kinds of pixel corruptions % |
表5中,前3行和后3行分别是随机选择数据库中10%和20%比例的样本进行污染后,SWLRR算法在该数据库上的识别库(不同特征维度下)。
4.2.2 有真实遮挡的人脸识别本节进一步研究SWLRR算法在不同类型的面部遮挡情况下的性能,实验选用了难度较大的AR数据库,因为AR数据库中的图像会存在多种类型的遮挡。主要通过选取以下2种类型的遮挡来评估算法的鲁棒性。
1)太阳镜:验证SWLRR在选取的训练样本和测试样本中均含有太阳镜遮挡时的性能,太阳镜大概遮挡了人脸的20%。选择每一类前半部分中的7张中性图片(表情光照)加上随机选取的一个有太阳镜遮挡图片作为训练样本,则后半部分的7张中性图片和所有剩下的5张太阳镜图片作为测试样本(8个训练样本,12个测试样本)。
2)太阳镜围巾混合情形:验证SWLRR在选取的训练样本和测试样本中均含有太阳镜和围巾遮挡时的性能。每一类前半部分中的7张中性图片(表情光照)和随机选取的一个有太阳镜遮挡图片、一个有围巾遮挡图片作为训练样本,则后半部分的所有图片和前半部分剩下的的2张含有太阳镜和2张含有围巾的图片作为测试样本(9个训练样本,17个测试样本)。
实验中,对类型1)进行3次实验,每次选择不同的遮挡图片作为训练样本,最后取3次分类结果的均值;对类型2),进行9次实验,每次选择不同组合的太阳镜样本和墨镜样本作为训练样本,最后取9次结果的均值。特征维度选择为25、50、100、200和300。以下列举了各种算法在类型1)和2)时的识别率,如表6、表7所示。
| 表 6 AR数据库上不同算法在太阳镜遮挡条件下的识别率 Tab.6 The recognition rate of different methods on the AR database with the occlusion of sunglasses % |
| 表 7 AR数据库上不同算法在混合遮挡条件下的识别率 Tab.7 The recognition rate of different methods on the AR database with mix occlusion % |
从表6、表7可以看出,在样本存在真实遮挡的情形下,SWLRR算法在不同维度时,性能仍然优于其余所有算法,这表明SWLRR算法在样本存在真实遮挡时有着较好的鲁棒性。
5 结束语本文提出了用于人脸识别的结构化加权稀疏低秩恢复算法(SWLRR),主要解决了训练样本和测试样本同时存在污染导致无法正确分类的问题。SWLRR首先对低秩系数进行权重和结构化约束,继而通过移除训练样本和测试样本中的污染,有效减少了样本中的污染对实验结果造成的负面影响。因此SWLRR算法样本在有无遮挡的情况下都有着较为突出的性能。在AR、Extended Yale B、CMU PIE数据库上的实验验证了SWLRR算法在不同情况下的有效性和对噪声的鲁棒性。下一步将尝试将本文思想与其他解决样本中存在污染的算法结合,进一步提升算法性能。
| [1] |
TURK M, PENTLAND A. Eigenfaces for recognition[J]. Journal of cognitive neuroscience, 1991, 3(1): 71-86. DOI:10.1162/jocn.1991.3.1.71 ( 0) 0)
|
| [2] |
BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. fisherfaces: recognition using class specific linear projection[J]. IEEE transactions on pattern analysis and machine intelligence, 997, 19(7): 711-720. ( 0) 0)
|
| [3] |
LIU Chengjun, WECHSLER H. Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition[J]. IEEE transactions on image processing, 2002, 11(4): 467-476. DOI:10.1109/TIP.2002.999679 ( 0) 0)
|
| [4] |
HE Xiaofei, YAN Shuicheng, HU Yuxiao, et al. Face recognition using Laplacianfaces[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(3): 328-340. DOI:10.1109/TPAMI.2005.55 ( 0) 0)
|
| [5] |
WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 ( 0) 0)
|
| [6] |
MIN R, DUGELAY J L. Improved combination of LBP and sparse representation based classification (SRC) for face recognition[C]//Proceedings of 2011 IEEE ICME. Barcelona, Spain, 2011: 1–6.
( 0) 0)
|
| [7] |
CHEN C F, WEI C P, WANG Y C F. Low-rank matrix recovery with structural incoherence for robust face recognition[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA, 2012: 2618–2625.
( 0) 0)
|
| [8] |
YANG Meng, ZHANG Lei, YANG Jian, et al. Regularized robust coding for face recognition[J]. IEEE transactions on image processing, 2013, 22(5): 1753-1766. DOI:10.1109/TIP.2012.2235849 ( 0) 0)
|
| [9] |
ZHANG Lei, YANG Meng, FENG Xiangchu. Sparse representation or collaborative representation: which helps face recognition?[C]//Proceedings of 2011 ICCV. Barcelona, Spain, 2011: 471–478.
( 0) 0)
|
| [10] |
DENG Weihong, HU Jiani, GUO Jun. Extended SRC: undersampled face recognition via intraclass variant dictionary[J]. IEEE transactions on pattern analysis and machine intelligence, 2012, 34(9): 1864-1870. DOI:10.1109/TPAMI.2012.30 ( 0) 0)
|
| [11] |
YANG Meng, ZHU Pengfei, LIU Feng, et al. Joint representation and pattern learning for robust face recognition[J]. Neurocomputing, 2015, 168: 70-80. DOI:10.1016/j.neucom.2015.06.013 ( 0) 0)
|
| [12] |
CANDÈS E J, LI Xiaodong, MA Yi, et al. Robust principal component analysis[J]. Journal of the ACM, 2011, 58(3): 11. ( 0) 0)
|
| [13] |
LIU Guangcan, LIN Zhouchen, YAN Shuicheng, et al. Robust recovery of subspace structures by low-rank representation[J]. IEEE transactions on pattern analysis and machine intelligence, 2013, 35(1): 171-184. DOI:10.1109/TPAMI.2012.88 ( 0) 0)
|
| [14] |
MA Long, WANG Chunheng, XIAO Baihua, et al. Sparse representation for face recognition based on discriminative low-rank dictionary learning[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA, 2012: 2586–2593.
( 0) 0)
|
| [15] |
ZHANG Yangmuzi, JIANG Zhuolin, DAVIS L S. Learning structured low-rank representations for image classification[C]//Proceeding of 2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, USA, 2013: 676–683.
( 0) 0)
|
| [16] |
NGUYEN H, YANG Wankou, SHENG Biyun, et al. Discriminative low-rank dictionary learning for face recognition[J]. Neurocomputing, 2016, 173(3): 541-551. ( 0) 0)
|
| [17] |
CHANG Heyou, ZHENG Hao. Weighted discriminative dictionary learning based on lowrank representation[J]. Journal of physics: conference series, 2017, 90: 012009. ( 0) 0)
|
| [18] |
ZHANG Zheng, XU Yong, SHAO Ling, et al. Discriminative block-diagonal representation learning for image recognition[J]. IEEE transactions on neural networks and learning systems, 2018, 29(7): 3111-3125. DOI:10.1109/TNNLS.2017.2712801 ( 0) 0)
|
| [19] |
CHEN Jie, YI Zhang. Sparse representation for face recognition by discriminative low-rank matrix recovery[J]. Journal of visual communication and image representation, 2014, 25(5): 763-773. DOI:10.1016/j.jvcir.2014.01.015 ( 0) 0)
|
| [20] |
COSTEIRA J P, KANADE T. A multibody factorization method for independently moving objects[J]. International journal of computer vision, 1998, 29(3): 159-179. DOI:10.1023/A:1008000628999 ( 0) 0)
|
| [21] |
ZHUANG Liansheng, GAO Haoyuan, LIN Zhouchen, et al. Non-negative low rank and sparse graph for semi-supervised learning[C]//Proceedings of 2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence, USA, 2012: 2328–2335.
( 0) 0)
|
| [22] |
LIN Zhouchen, LIU Risheng, SU Zhixun. Linearized alternating direction method with adaptive penalty for low-rank representation[J]. Advance in neural information processing systems, 2011: 612-620.
( 0) 0)
|
| [23] |
LIN Zhouchen, CHEN Minming, MA Yi. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[R]. Urbana-Champaign: University of Illinois at Urbana-Champaign, 2009.
( 0) 0)
|
| [24] |
BAO Bingkun, LIU Guangcan, XU Changsheng, et al. Inductive robust principal component analysis[J]. IEEE transactions on image processing, 2012, 21(8): 3794-3800. DOI:10.1109/TIP.2012.2192742 ( 0) 0)
|
| [25] |
CORTES C, VAPNIK V. Support-vector networks[J]. Machine learning, 1995, 20(3): 273-297. ( 0) 0)
|
| [26] |
HEISELE B, HO P, POGGIO T. Face recognition with support vector machine: global versus component-based approach[C]//Proceedings Eighth IEEE International Conference on Computer Vision. Vancouver, BC, Canada, 2001: 688–694.
( 0) 0)
|
| [27] |
CHANG C C, LIN C J. Libsvm: a library for support vector machines[J]. ACM transactions on intelligent systems and technology, 2011, 2(3): 1-27. ( 0) 0)
|
| [28] |
MARTINEZ A, BENAVENTE R. The AR face database[R]. CVC Technical Report No.24. Barcelona : Universitat Autonoma de Barcelona, 1998.
( 0) 0)
|
| [29] |
GEORGHIADES A S, BELHUMEUR P N, KRIEGMAN D J. From few to many: illumination cone models for face recognition under variable lighting and pose[J]. IEEE transactions on pattern analysis and machine intelligence, 2001, 23(6): 643-660. DOI:10.1109/34.927464 ( 0) 0)
|
| [30] |
LEE K C, HO J, KRIEGMAN D J. Acquiring linear subspaces for face recognition under variable lighting[J]. IEEE transactions on pattern analysis and machine intelligence, 2005, 27(5): 684-698. DOI:10.1109/TPAMI.2005.92 ( 0) 0)
|
| [31] |
SIM T, BAKER S, BSAT M. The CMU pose, illumination, and expression database[J]. IEEE transactions on pattern analysis and machine intelligence, 2003, 25(12): 1615-1618. DOI:10.1109/TPAMI.2003.1251154 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


