2. 江南大学 物联网工程学院,江苏 无锡 214122;
3. 江南大学 信息化建设与管理中心,江苏 无锡 214122
2. School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China;
3. Information Construction and Management Center, Jiangnan University, Wuxi 214122, China
粒子群算法自1995年被Kennedy和Eberhart提出后[1],由于其简单高效,收敛速度快,逐渐在优化算法中脱颖而出。随之粒子群算法被Coelloran应用到多目标优化问题上[2-3],得到了各界的广泛认可。后来更多学者对多目标粒子群算法(MOPSO)进行了更深入的研究:Raquel等[4]使用了拥挤距离作为适应值对粒子进行排序;Li等[5]通过整合粒子的GMR(global margin ranking)和粒子密度信息的方法来对粒子进行排序,能高效快速地选择出pbest和gbest粒子;除了对排序选择的方法进行优化外,有的利用聚合函数来对多个目标函数进行处理[6];有的使用了目标空间分解的方法来保障粒子最优解的多样性[7];以及将MOPSO和其他优化算法进行交叉使用,如教与学方法[8]、差分方法[9]等, 通过一定的比例调用MOPSO。
上述的这些方法不断地对MOPSO的多样性和全局收敛进行改进和优化,虽然取得了较好的研究成果,但是这些方法的改进策略只对MOPSO某一性能效果进行改进,其他的性能指标并没有同时得到很好的改进。例如:文献[7]中,多样性方面得到很大的提升,但是其收敛性方面仍有很大不足。所以,本文借鉴Pareto支配强度[10]和连续变异的方法[11]对基于目标空间分解方法的多目标粒子群算法[7]进行优化,在给每个子区域分配粒子时,删除没有归属的粒子,给没分到粒子的区域初始化新的粒子,增加获得较优粒子的可能性。这样既从整体和局部两方面提升了粒子的收敛性,同时多样性也得到了一定的优化提升,这种新的算法被称为基于目标空间分解和连续变异的多目标粒子群优化算法(multi-objective particle swarm optimization based on decomposition and continuous mutation ,MOPSO/DC)。
1 多目标优化问题 1.1 基本概念| $\left\{ {\begin{array}{*{20}{l}} {\min y = F(x) = ({f_1}(x),{f_2}(x),\cdots,{f_m}(x))} \\ {{\rm{s.t}}.{g_i}(x) \leqslant 0,\;i = 0,1,2,\cdots,q} \\ {{h_j}(x) = 0,\;j = 1,2,\cdots,p} \end{array}} \right.$ | (1) |
式中:
定义1 Pareto支配。解
| $\left\{ {\begin{array}{*{20}{c}} {\forall i \in \{ 1,2,\cdots,m\},\,\,\, {f_i}(d) \leqslant {f_i}(e)} \\ {\exists i \in \{ 1,2,\cdots,m\},\,\,\, {f_i}(d) < {f_i}(e)} \end{array}} \right.$ | (2) |
定义2 Pareto最优。如果
定义3 Pareto最优解集(
| ${\rm PS} = \{ x \in \varOmega |\neg \exists z \in \varOmega ;z \succ x\} $ | (3) |
定义4 Pareto前沿(
| ${\rm{PF}} = \{ F(x)|x \in {\rm{PS}}\} $ | (4) |
粒子群算法中的粒子由速度信息和位置信息组成,更新公式为
| $V_k^{t + 1} = WK_k^t + {C_1}{R_1}(P - X_k^t) + {C_2}{R_2}(G - X_k^t)$ | (5) |
| $X_k^{t + 1} = V_k^{t + 1} + X_k^t$ | (6) |
式中:k指粒子群中第k个粒子;t为当前迭代次数;W为权衡局部搜索和全局搜索的参数,
把目标空间Y分成M个子区域Y1,Y2,···,YM。令
| $ \begin{split} u = & \displaystyle\sum\limits_{{k_1} = 0}^h {\displaystyle\sum\limits_{{k_2} = 0}^{h - {k_1}}\cdots}\\ & \displaystyle\sum\limits_{{k_i} = 0}^{h - {k_1} - \cdots - {k_{i - 1}}} \cdots\displaystyle\sum\limits_{{k_{m - 3}} = 0}^{h - {k_1} - \cdots - {k_{m - 4}}} {{{\left[\displaystyle\sum\limits_{{k_{m - 2}} = 1}^{h - {k_1} - \cdots - {k_{m - 3}}} {(h + 2 - \displaystyle\sum\limits_{l = 1}^{m - 2} {{k_l}} ) + {k_{m - 1}} + 1} \right]} } } \end{split} $ |
其中参数h、m和子区数M满足关系:h取满足
在对粒子进行分配时,通过参考点确定每个粒子的方向向量[7]。令参考点为
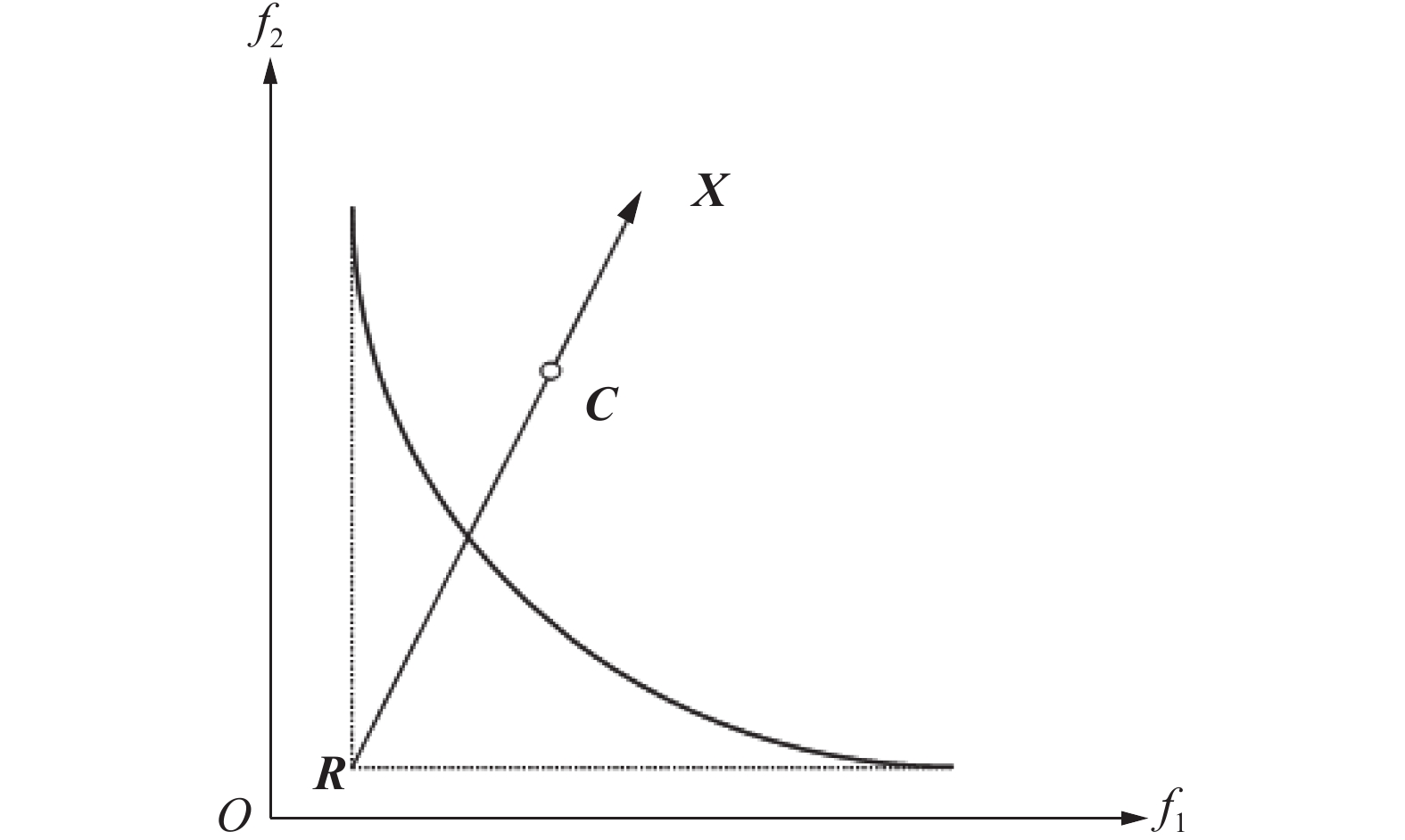
|
Download:
|
| 图 1 粒子的方向向量 Fig. 1 Direction vector of the particle | |
在对粒子进行分配时会有以下两种特殊情况:
1)有的子区域粒子数大于子区域的容量Vol时,通过适应值进行取舍,适应值公式为
| $f = aT + {\rm{CD}}$ | (7) |
式中:T是Pareto支配强度,其数值为当前粒子支配的粒子数,在适应值计算中加入了Pareto支配强度T,增强每个子区域中的粒子趋向真实PF的能力;参数a表示支配强度对适应值的影响程度,
计算该子区域包含的粒子的适应值,从大到小排序,选择序列中前30%的粒子,再从这些粒子中选择离所在子区域中心向量最近的Vol个粒子,多余的劣质粒子删除。
2)当子区域粒子数少于该子区域容量Vol时,由于情况1)中已经对劣质的粒子进行删除,为了尽可能保证整体的优越性,所以重新初始化该子区域所缺数目的粒子作为该区域的粒子,增加获得较优粒子的可能性,增加粒子多样性。然后计算新粒子的目标函数值。
2.3 连续变异操作当只采用一种方法进行变异时,不能兼顾全局粒子和局部粒子的特性。在MOPSO/DC中提出差分+柯西[12]+高斯[13]连续的变异策略,公式为
| $\left\{ \begin{gathered} {X_{{\rm{diff}}}} = X + 0.5({X_1} - {X_2}) \hfill \\ {X_{{\rm{Cauchy}}}} = \frac{{c{{(t)}^2}}}{{\text{π} ({X^2} + c{{(t)}^2})}} \hfill \\ {X_{{\rm{Gauss}}}} = \frac{1}{{g(t)\sqrt {2\text{π} } }}\exp (\frac{{ - {X^2}}}{2}) \hfill \\ \end{gathered} \right.$ | (8) |
式中:X为当前引导粒子gbest的位置;X1和X2是从EPOP中随机选出的两个不同粒子的位置。这样在变异时可保留全局粒子的一部分性质,起到一定信息交流的作用,增加了多样性。t为当前迭代的次数,gmax为最大迭代次数,
高斯变异步长较短,能很好地吸取局部粒子性质,柯西变异具有相对大的步长,能进行较大范围的变异,具有全局范围变异的特性,这样能很好地产生全新的粒子。
下面对标准柯西分布

|
Download:
|
| 图 2 标准高斯和分布柯西分布对比 Fig. 2 Comparison of standard Gaussian and Cauchy distributions | |
用这3种方法进行变异操作,既增强了gbest的引导能力,同时gbest吸取局部或全局粒子的性质,促进了粒子之间信息交流共享,增加了多样性。
2.4 MOSPO/DC步骤1)初始化2N个粒子的位置,这些粒子的位置集合记为POP,初始化N个速度,这些速度集合记为V,设目标函数的个数为m,当前迭代次数为t,初始化最大迭代次数gmax、每个子区域容量
2)进行目标空间分解操作。
3)计算粒子群POP目标函数值,选出每个目标函数的最小值作为参考点R用于计算每个粒子的方向向量,方向向量的计算参考图1。
4)进行粒子的分类与更新操作,接着将当前所有子区域粒子的位置信息存入集合EPOP中,最后更新参考点R,并重新计算每个粒子的方向向量,清空POP备用。
5)gbest的选择:产生[0,1]之间的随机数r1,当r1>0.8时,随机从EPOP集合中选择一个粒子作为当前粒子的gbest;否则,在该粒子所在区域的邻域内操作。首先计算该粒子邻域中每个子区域的中心向量和该子区域中粒子方向向量的余弦值,然后选出余弦值最大的子区域中的粒子作为当前粒子的gbest。过多地使用变异会让算法变得更加随机,降低了算法的效率,所以产生[0,1]之间的随机数r2,当r2<0.6时,对选出的引导粒子位置进行连续变异操作,确定最终的引导粒子gbest。否则,不对gbest进行变异操作。
6)pbest的选择:产生[0,1]之间的随机数r3,当r3>0.8时,随机从EPOP中选择一个粒子;否则,从该粒子的所在区域的邻域中随机选择一个粒子。让当前粒子和这个随机选出的粒子进行比较,选出支配权优先的作为当前粒子的pbest。
7)通过上述选出的gbest和pbest,以及粒子速度更新式(5)和位置更新式(6)产生下一代新的粒子群体,这些新粒子位置集合记为NPOP,下一代新的速度集合重新覆盖集合V。
8)如果当前迭代次数t大于最大迭代次数gmax,则循环结束,输出EPOP作为最优解集,否则把NPOP和EPOP合并放入POP中,然后跳转至3),继续循环。
3 实验分析为了测试所提出的MOPSO/DC算法的性能,将其与目前较流行的MOPSO/D[7]、MOPSOTL[8]、MOPSODE[9]和NNIA[14]算法进行对比,实验中同样选择了文献[7]中的6个测试函数,依次为F1,F2···F6。为了定量比较5种算法的性能,采用以下3种广泛使用的性能指标:HV[15],测量了粒子收敛于真实PF的效果以及最优解集的多样性,所获得值越大越好;GD[16],指算法获得的PF到真实PF的距离,数值越小越接近真实PF,效果越好;IGD[15],显示真实PF到算法所得到PF的距离,值越小越能说明算法得到的PF上的点可以分散地均匀地收敛于真实PF上。
MOPSO/DC参数设置:当目标函数个数
MOPSO/DC与其他算法关于这6个测试函数的3种性能指标对比结果见表1,表中给出了通过MOPSO/DC和其他4个算法获得关于这6个问题的IGD、GD和HV的平均值和标准差。从表1中可以看出:1)MOPSO/DC获得的IGD平均值远小于其他4种算法;2)MOPSO/DC获得的GD平均值都是最佳的,除F3函数外,不过关于F3的GD均值,本算法也优于MOPSO/D算法[7];3)通过MOPSO/DC获得的HV值总体来说比其他算法获得的HV值好(除F1函数),说明MOPSO/DC的收敛性以及解的多样性也相当好。整体来说,MOPSO/DC的这3个性能指标优于其他4个算法,对MOPSO/D算法进行了很好的改进。
| 表 1 各算法效果指标对比 Tab.1 Comparison of the effect of each algorithm |
MOPSO/DC算法的仿真图如图3,结果显示该算法得到的PF和真实PF完全重合。
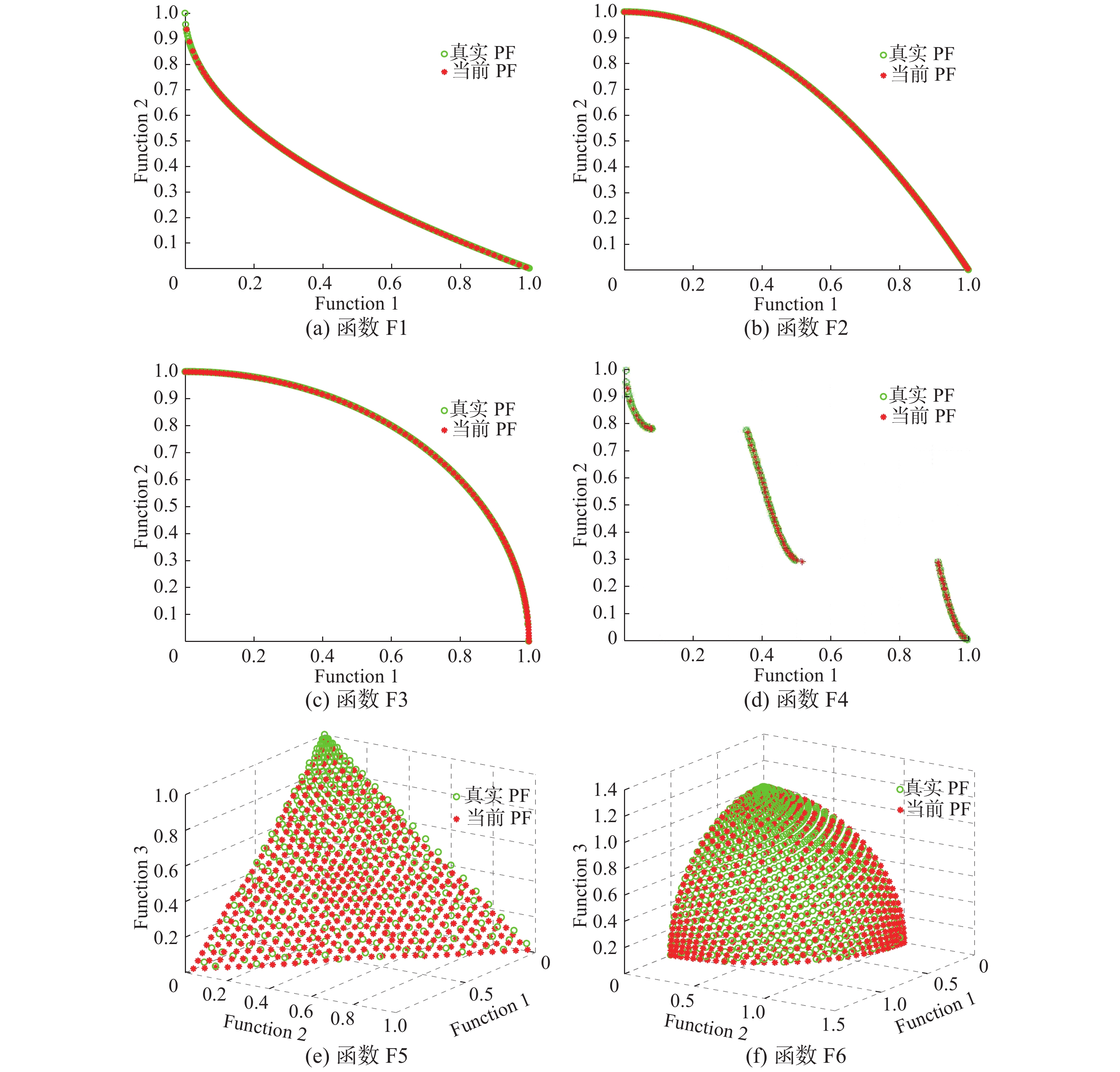
|
Download:
|
| 图 3 测试函数的仿真图 Fig. 3 Test function’s simulations | |
通过这些对比实验得出结论:MOPSO/DC对原算法[7]的收敛性和多样性进行了很好地优化,增强了粒子趋向真实PF的效果,并且具有很好的稳定性。
4 结束语本文提出的算法采用目标空间分解与子区域粒子更新和对引导粒子gbest的位置进行连续变异的方法来提高粒子多样性和收敛性,对原算法的不足之处进行了很好地弥补和优化。通过和4个不同种类的优化算法对不同种测试函数进行多种性能的测试对比实验证明,MOPSO/DC整体效果最好,具有很高收敛性,多样性方面也有提升。总之,MOPSO/DC对多目标优化问题的多个性能指标同时进行了很好的优化。未来的研究重点是,将该算法更好地适应更多目标的优化问题,增强其通用性,用于解决实际问题。
| [1] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of ICNN’95-International Conference on Neural Networks. Perth, WA, Australia, Australia: IEEE, 1995: 1942–1948.
( 0) 0)
|
| [2] |
COELLO C A C, LECHUGA M S. MOPSO: a proposal for multiple objective particle swarm optimization[C]//Proceedings of the 2002 Congress on Evolutionary Computation. Honolulu, HI, USA: IEEE, 2002: 1051–1056.
( 0) 0)
|
| [3] |
COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE transactions on evolutionary computation, 2004, 8(3): 256-279. ( 0) 0)
|
| [4] |
RAQUEL C R, NAVAL P C JR. An effective use of crowding distance in multiobjective particle swarm optimization[C]//Proceedings of the 7th Annual Conference Genetic and Evolutionary Computation Washington, DC, USA: ACM, 2005: 257–264.
( 0) 0)
|
| [5] |
LI Li, WANG Wanliang, XU Xinli. Multi-objective Particle swarm optimization based on global margin ranking[J]. Information sciences, 2017, 375: 30-47. DOI:10.1016/j.ins.2016.08.043 ( 0) 0)
|
| [6] |
LIN Qiuzhen, LI Jiangqiang, DU Zhihua, et al. A novel multi-objective particle swarm optimization with multiple search strategies[J]. European journal of operational research, 2015, 247(3): 732-744. DOI:10.1016/j.ejor.2015.06.071 ( 0) 0)
|
| [7] |
DAI Cai, WANG Yuping, YE Miao. A new multi-objective particle swarm optimization algorithm based on decomposition[J]. Information sciences, 2015, 325: 541-557. DOI:10.1016/j.ins.2015.07.018 ( 0) 0)
|
| [8] |
CHENG Tingli, CHEN Minyou, FLEMING P J, et al. A novel hybrid teaching learning based multi-objective particle swarm optimization[J]. Neurocomputing, 2017, 222: 11-25. DOI:10.1016/j.neucom.2016.10.001 ( 0) 0)
|
| [9] |
SU Yixin, CHI Rui. Multi-objective particle swarm-differential evolution algorithm[J]. Neural Computing and applications, 2017, 28(2): 407-418. DOI:10.1007/s00521-015-2073-y ( 0) 0)
|
| [10] |
ZITZLER E, LAUMANNS M, THIELE L. SPEA2: Improving the strength Pareto evolutionary algorithm for multiobjective optimization[M]//GIANNAKOGLOU K C, TSAHALIS D T, PÉRIAUX J, et al. Evolutionary Methods for Design, Optimisation and Control with Applications to Industrial Problems. Athens, Greece: International Center for Numerical Methods in Engineering, 2002: 95–100.
( 0) 0)
|
| [11] |
JORDEHI A R. Enhanced leader PSO (ELPSO): a new PSO variant for solving global optimisation problems[J]. Applied Soft Computing, 2015, 26: 401-417. DOI:10.1016/j.asoc.2014.10.026 ( 0) 0)
|
| [12] |
陈明杰, 黄佰川, 张旻. 混合改进蚁群算法的函数优化[J]. 智能系统学报, 2012, 7(4): 370-376. CHEN Mingjie, HUANG Baichuan, ZHANG Min. Function optimization based on an improved hybrid ACO[J]. CAAI transactions on intelligent systems, 2012, 7(4): 370-376. DOI:10.3969/j.issn.1673-4785.201111004 (  0) 0)
|
| [13] |
CHELLAPILLA K, FOGEL D B. Two new mutation operators for enhanced search and optimization in evolutionary programming[C]//Proceedings Volume 3165, Applications of Soft Computing. San Diego, CA, United States: SPIE, 1997: 260–269.
( 0) 0)
|
| [14] |
GONG Maoguo, JIAO Licheng, DU Haifeng, et al. Multiobjective immune algorithm with nondominated neighbor-based selection[J]. Evolutionary computation, 2008, 16(2): 225-255. DOI:10.1162/evco.2008.16.2.225 ( 0) 0)
|
| [15] |
STORN R, PRICE K. Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 ( 0) 0)
|
| [16] |
ZITZLER E, THIELE L, LAUMANNS M, et al. Performance assessment of multiobjective optimizers: an analysis and review[J]. IEEE transactions on evolutionary computation, 2003, 7(2): 117-132. ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


