随着物联网及信息技术的发展，数据资源呈海量特征。在数据量不断增大的同时，数据标注结构的复杂度也在增加，传统的单标记学习已不能满足现实应用的需求，因此多标记学习的重要性逐渐突显。在多标记学习中，每个样本在一个特征向量下，可能同时隶属于多个类别标记。近年来，多标记学习问题已成为机器学习、数据挖掘和模式识别等领域的研究热点之一^[1-4]。

波兰数学家Pawlak教授于1982年提出的粗糙集理论是一种用于处理不精确、不完全和不相容知识的数学工具^[5]，近年来，该理论在机器学习和数据挖掘领域得到了广泛的应用^[6-7]。属性约简，又称特征选择，是粗糙集理论的核心内容之一，其目的是在保持分类能力不变的条件下，删除不相关或冗余特征。与单标记学习一样，多标记学习也面临着“维数灾难”的挑战。高维数据不仅影响算法的执行效率，也降低了分类器的分类性能，而特征降维技术是解决维数灾难的有效方法。目前，针对单标记数据特征降维技术的研究较为广泛，而针对多标记数据特征降维技术的研究相对较少。因此，基于多标记学习特征选择的研究具有重要的理论和应用意义。另外，在现实应用领域中，数据特征的获取往往需要花费一定的代价，为此从代价敏感的视角研究多标记特征选择问题显得尤为重要。

1 相关工作

近年来，在多标记特征提取方面已经取得一些有意义的研究成果。如Sun等^[8]提出的多标记降维方法(LDA)，其直接将单标记特征降维的方法应用于多标记特征降维中，忽略了标记之间的相关性。Zhang等^[9]采用核矩阵进行映射降维，设计了一种最大化依赖度的多标记特征降维方法(MDDM)。Yu等^[10]提出了一种有监督的多标记潜在语义索引降维方法(MLSI)。多标记特征提取能够实现特征降维的效果，但由于其忽略了标记之间的关联以及损失了原始特征的物理含义，这对多标记学习问题的研究造成了较大的困难。

多标记特征选择通过设计特征度量准则从原始特征中剔除冗余或不相关特征，得到一组相对最优的特征子集，从而可有效降低特征空间的维数，提升算法的分类性能。特征选择的结果能够保持原始特征的物理含义，使得多标记学习的研究更容易理解。目前许多研究人员针对多标记特征选择开展研究，段洁等^[11]重新定义了多标记邻域粗糙集的下近似和依赖度的计算方法，在此基础上，设计了一种基于邻域粗糙集的特征选择算法(ARMLNRS)。王晨曦等^[12]从每个标记对样本不同分组的角度出发，提出了基于信息粒化的多标记特征选择算法(MFIG)。Lin等^[13]在乐观、中立和悲观这3种不同的视角下，通过3种基于邻域互信息准则进行特征选择。刘景华等^[14]通过引入局部子空间模型，构建了一种基于局部子空间的多标记特征选择算法(MFSLS)。上述算法的计算复杂度相对较大。后来Lee等^[15]通过特征信息熵之差最大化和正向搜索的方法选择特征子集，设计时间复杂度较低的特征选择算法，但其没有给出和分析的信息熵阈值对特征子集的影响。张振海等^[16]利用信息增益下的阈值选择设计了一种多标记特征选择算法(MLFSIE)。综上所述，这些多标记特征选择算法并未考虑到特征的代价敏感问题。

在许多实际应用领域中，获取和采集数据是需要花费代价的，因此从代价敏感的视角研究多标记学习具有重要的意义。针对当前多标记特征选择算法的计算复杂度较大且未考虑特征代价的问题，提出了一种面向代价敏感数据的多标记特征选择算法。首先，该方法计算出特征与标记集合之间的信息增益，在此基础上重新定义了特征重要度的计算方法，并根据服从正态分布的特征重要度与特征代价的标准差之间的差值，提出了一种合理的阈值选择方法，从而实现对冗余或不相关特征的剔除，同时能得到总代价较低的特征子集。为了验证算法的有效性，利用Mulan平台上的真实多标记数据集进行实验比较和分析，通过实验结果进一步验证算法的有效性和可行性。

2 基本知识 2.1 多标记学习

在粒计算理论中，多标记数据可表示成一个多标记决策表 ${\rm{MDT}} = (U,A \cup D,V,f)$ ，其中： $U$ 为样本集 ${\rm{\{ }}{x_1},{x_2}, \cdots ,{x_n}{\rm{\} }}$ ，也称为论域； $A$ 为条件特征集 ${\rm{\{ }}{a_1},{a_2}, \cdots ,{a_m}{\rm{\} }}$ ； $D$ 为多标记决策特征 ${\rm{\{ }}{l_1},{l_2}, \cdots ,{l_k}{\rm{\} }}$ ，且 $A \cap D = \text{Ø} $ ； $V$ 为全特征集的值域，其中 $V = \cup {V_a}$ ， $a \in A \cup D$ ， ${V_a}$ 表示特征 $a$ 的值域； $f$ 是 $U \times \left( {A \cup D} \right) \to V$ 的信息函数。

定义1　给定多标记决策表 ${\rm{MDT}} = (U,A \cup $ $D,$ $V,f)$ ，对于 $\forall a \in A$ ，特征 $a$ 的等价关系 ${R_a}$ 为

${R_a} = \{ ({x_i},{x_j}) \in U \times U,f({x_i},a) = f({x_j},a)\} $

定义2　给定多标记决策表 ${\rm{MDT}} = (U,A \cup $ $D,$ $V,f)$ ，对于 $\forall {l_t} \in D$ ，标记 ${l_t}$ 的等价关系 ${R_{{l_t}}}$ 为

$ {R_{{l_t}}} = \{ ({x_i},{x_j}) \in U \times U,f({x_i},{l_t}) = f({x_j},{l_t})\} $

2.2 信息熵

基于条件信息熵下的特征选择是研究者从信息观视角对高维数据进行特征选择，该方法可有效地度量信息的不确定性程度。

定义3　给定多标记决策表 ${\rm{MDT}} = (U,A \cup D,$ $V,f)$ ，对于任意特征子集 $B \subseteq A$ ，根据特征子集 $B$ 的等价关系 ${R_B}$ 可得 $U/B = \{ {X_1},{X_2}, \cdots ,{X_q}\} $ ，则特征子集 $B$ 的信息熵为

$H(B) = - \sum\limits_{i = 1}^q {p({X_i})} \log p({X_i})$

当信息熵 $H(B)$ 的值越大，说明特征子集 $B$ 的不确定性越大。

定义4　给定多标记决策表 ${\rm{MDT}} = (U,A \cup D,$ $V,f)$ ，对于任意标记子集 $L \subseteq D$ ，根据标记子集 $L$ 的等价关系 ${R_L}$ 可得 $U/L = \{ {Y_1},{Y_2}, \cdots ,{Y_p}\} $ ，则在特征子集 $B$ 下标记子集 $L$ 的条件熵为

$H(L{\rm{|}}B) = - \sum\limits_{i = 1}^q {p({X_i})} \sum\limits_{j = 1}^p {p({Y_j}|{X_i})} \log \; p({Y_j}|{X_i})$

由定义4可知，当 $H(L{\rm{|}}B){\rm{ = }}0$ 时，说明标记子集 L 完全依赖于特征子集 B，当 $H(L{\rm{|}}B){\rm{ = }}H(L)$ 时，表明标记子集 L 独立于特征子集 B。

定义5　给定多标记决策表 ${\rm{MDT}} = (U,A \cup D,$ $V,f)$ ，对于任意特征子集 $B \subseteq A$ ，则标记子集 $L$ 在特征子集 $B$ 上的信息增益为

${\rm {IG}}(L{\rm{|}}B) = H(L) - H(L{\rm{|}}B)$

信息增益 ${\rm {IG}}(L{\rm{|}}B)$ 值用于衡量特征子集 B 与标记子集 L 的相关程度， ${\rm {IG}}(L{\rm{|}}B)$ 值越大，说明其特征子集 B 与标记子集 L 的相关程度越大。

为了使得各个特征与标记之间的信息增益值在同一量纲下比较，需先对信息增益的值进行归一化处理：

${\rm{NIG}}(L{\rm{|}}B) = \frac{{{\rm {IG}}(L{\rm{|}}B)}}{{H(B) + H(L)}}$

3 代价敏感下的多标记学习 3.1 基于特征代价的信息熵模型

在机器学习和数据挖掘领域，代价敏感学习是十大最具有挑战性问题之一^[17]。因此，将特征代价引入到多标记特征选择具有重要的意义。

定义6　给定基于测试代价的多标记决策表 ${\rm{CMDT}} = (U,A \cup D,V,f,c)$ ，其中 $c:A \to {R^ + } \cup \{ 0\} $ 为测试代价函数，对于任意特征 $\forall {a_i},{a_j} \subseteq A$ ，标记集合 $D$ 在特征 ${a_i}$ 上的特征重要度为

${\rm{CSIG}}(D{\rm{|}}{a_i}) = {\rm{NIGS}}(D{\rm{|}}{a_i})^{\rm{*}} - {\mathop{\rm Cos}\nolimits} {\rm{t}}({a_i})^*$

由定义5可得，标记集合 $D$ 在特征 ${a_i}$ 上的信息增益为

${\rm{NIGS}}(D{\rm{|}}{a_i}) = \sum\limits_{t = 1}^k {{\rm{NIG}}({l_t}{\rm{|}}{a_i})} $

为了获取合理的阈值，使得信息增益的值服从正态分布：

${\rm{NIGS}}(D{\rm{|}}{\rm{ }}{a_i})^{\rm{*}} = \frac{{{\rm{NIGS}}(D{\rm{|}}{\rm{|}}{a_i}) - \mu }}{\sigma }$

式中： $\mu $ 表示特征与标记集合的信息增益均值； $\sigma $ 表示特征与标记集合的信息增益标准差，其公式分别为

$\mu {\rm{ = }}\frac{1}{k}\left(\sum\limits_{t = 1}^k {{\rm{NIG}}({l_t}{\rm{|}}{a_i}} )\right)$

$\sigma = \sqrt {\frac{1}{k}\sum\limits_{t = 1}^k {{{\left[{\rm{NIG}}({l_t}|{a_i}) - \mu \right]}^2}} } $

在计算测试代价下的标记集合下特征重要度之前，需先将特征代价进行归一化处理：

${\mathop{\rm Cos}\nolimits} {\rm{t(}}{{{a}}_i}{{\rm{)}}^*} = \frac{{{\mathop{\rm Cos}\nolimits} {\rm{t(}}{a_i}{\rm{) - min(Cost(}}{a_j}{\rm{))}}}}{{{\rm{max(Cost(}}{a_j}{\rm{)) - min(Cost(}}{a_j}{\rm{))}}}}$

式中： $\max (\operatorname{Cos} {\rm{t}}({a_j}))$ 表示特征的测试代价最大值； $\min (\operatorname{Cos} {\rm{t}}({a_j}))$ 表示特征的测试代价最小值。

定义7　给定基于测试代价的多标记决策表 ${\rm{CMDT}} = (U,A \cup D,V,f,c)$ ，其阈值 $\delta $ 定义为

$\delta {\rm{ = }}\frac{1}{m}\sum\limits_{i = 1}^m {\left| {{\rm{CSIG}}(D{\rm{|}}{a_i})} \right|} - {\mathop{\rm Cos}\nolimits} {\rm{t}}.\sigma $

式中： $\operatorname{Cos}\!{\rm{t}}.\sigma $ 表示所有特征的测试代价标准差，其公式为

${\mathop{\rm Cos}\nolimits} {\rm{t}}.\sigma = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m \left[{{\mathop{\rm Cos}\nolimits} {\rm{t}}({a_i})} - {\mathop{\rm Cos}\nolimits} {\rm{t}}.\mu \right]^2} $

${\mathop{\rm Cos}\nolimits} {\rm{t}}.\mu {\rm{ = }}\frac{1}{m}\left(\sum\limits_{i = 1}^m {{\mathop{\rm Cos}\nolimits} {\rm{t}}({a_i})} \right)$

式中： $\operatorname{Cos} \!{\rm{t}}.\mu $ 表示所有特征的测试代价均值。

3.2 基于特征代价的信息熵模型可行性分析

性质1　若特征 $a$ 与标记 ${l_t}$ 相互独立，则特征 $a$ 与标记 ${l_t}$ 之间的信息增益取最小值；若标记 ${l_t}$ 完全依赖于特征 $a$ ，则特征 $a$ 与标记 ${l_t}$ 的信息增益取最大值。

证明　由信息论理论结合定义4和定义5可推导出， $H(L{\rm{|}}B) \geqslant 0$ ，且 ${\rm {IG}}(L{\rm{|}}B) \leqslant H(L)$ 。当 $H(L{\rm{|}}B){\rm{ = }}0$ 时， ${\rm {IG}}(L{\rm{|}}B){\rm{ = }}H(L)$ ，信息增益的值最大；当 $H(L{\rm{|}}B){\rm{ = }}$ $H(L) $ 时， ${\rm {IG}}(L{\rm{|}}B){\rm{ = }}0$ ，此时信息增益的值最小，同时可知，信息增益 ${\rm {IG}}(L{\rm{|}}B)$ 值具有非负性。

对于任意特征 $a \in A$ ， ${l_t} \in D$ ，由定义5可知， ${\rm {IG}}({l_t}{\rm{|}}a) = H({l_t}) - H({l_t}{\rm{|}}a)$ ，由定义3和定义4可推导出， ${\rm {IG}}({l_t}{\rm{|}}a) =$ $\displaystyle \sum\limits_{i = 1}^q {p({X_i})} \log p({X_i}) - \displaystyle\sum\limits_{i = 1}^q {p({X_i})} \displaystyle\sum\limits_{j = 1}^p {p({Y_j}} |{X_i})\log p({Y_j}|$ ${X_i})$ ，且由上述推导可知，当 $H({l_t}{\rm{|}}a){\rm{ = }}H({l_t})$ 时， ${\rm {IG}}({l_t}{\rm{|}}a) \;=\; 0$ ，信息增益的值最小，此时 $\log p({X_i}) \;= \;$ $\displaystyle\sum\limits_{j = 1}^p{p({Y_j}|{X_i})} \log p({Y_j}|{X_i})$ ，表明标记 ${l_t}$ 独立于特征 $a$ 。同理，当 $H({l_t}{\rm{|}}a) = 0$ 时，此时 ${\rm {IG}}({l_t}{\rm{|}}a){\rm{ = }}H({l_t})$ ，信息增益 ${\rm {IG}}({l_t}{\rm{|}}a)$ 最大，即 $\log p({X_i}) - \displaystyle\sum\limits_{j = 1}^p {p({Y_j}|{X_i})} $ $\log p({Y_j}|{X_i})$ 最大，当 $\displaystyle\sum\limits_{j = 1}^p {p({Y_j}|{X_i})} |$ $\log p({Y_j} {X_i}){\rm{ = }}0$ 时，表明标记 ${l_t}$ 完全依赖于特征 $a$ 。

性质2　标记集合D 在特征 ${a_i}$ 上的特征重要度具有单调性，即标记 D 在特征 ${a_i}$ 上的信息增益随单个标记在特征 ${a_i}$ 上的信息增益的增大而增大，且标记与特征之间的相关程度越大。

证明　由性质1可得，若单个标记与特征 ${a_i}$ 的相关性越大，则信息增益值越大，即 ${\rm {IG}}({l_t}|{a})$ 越大。由定义6可知， ${\rm{NIGS}}(D{\rm{|}}a){\rm{ = }}\displaystyle\sum\limits_{t = 1}^k {{\rm{NIG}}({l_t}|{a_i})} $ ，因此 ${\rm{NIG}}({l_t}|{a_i})$ 越大，则 ${\rm{NIGS}}(D{\rm{|}}a)$ 的值越大，而特征代价的值 $\operatorname{Cos} \!{\rm{t}}({a_i})^*$ 是固定的，此时可得 ${\rm{CSIG}}(D{\rm{|}}{{{a}}_i})=$ ${\rm{ NIGS}}(D{\rm{|}}{a_i}){\rm{^*\!- Cost}}({a_i})^* $ 越大，即标记 $D$ 在特征 ${a_i}$ 上的信息增益随单个标记在特征 ${a_i}$ 上的信息增益的增大而增大。由性质1可知，标记与特征之间信息增益越大，则其相关程度也越大。由此可得，标记集合 $D$ 在特征 ${a_i}$ 上的信息增益具有单调性。

性质3　阈值 $\delta $ 具有单调性，即阈值随标记集合 $D$ 在特征 ${a_i}$ 上的信息增益值的增大而增大。

证明　由性质2和定义7可知，特征代价的标准差 $\operatorname{Cos}\!{\rm t}.\sigma $ 的值是固定的， ${\rm{CSIG}}(D{\rm{|}}{{\rm{a}}_i})$ 的值越大，则 $\dfrac{1}{m}\displaystyle\sum\limits_{i = 1}^m {\left| {{\rm{CSIG}}(D{\rm{|}}{a_i})} \right|} - \operatorname{Cos}\! {\rm{t}}.\sigma $ 越大，即阈值 $\delta $ 的值越大。

4 多标记特征选择算法 4.1 算法描述

根据上述分析可知，在多标记学习算法中，一个特征不仅与某一标记具有相关性，也可能同时与多个标记具有相关性，因此需要计算单个特征与标记集合之间的相关性。在此基础上，从代价敏感学习的视角，提出了一种基于测试代价的特征重要度；然后根据服从正态分布的特征重要度以及特征代价的标准差设计出一种合理的阈值选择方法；最后，通过计算的阈值删除冗余或不相关的特征。

本文提出的代价敏感数据的多标记特征选择算法(CSMLFSIE)具体步骤如下：

算法　代价敏感数据的多标记特征选择算法(CSMLFSIE)

输入　多标记决策表 $ < U,A \cup D,V,f > $ ；

输出　特征子集 Red。

1)初始化 ${\rm Red} \leftarrow \varnothing $ ；

2)对于 $\forall a \in A$ ， $\forall {l_t} \in D$ ，执行操作：

①计算在特征集 A 下每个特征的信息增益 $H(a)$ ；

②每个特征相对于每个标记的条件信息熵 $H({l_t}|a)$ ；

3)对于 $\forall a \in A$ ， $\forall {l_t} \in D$ 分别计算每个特征相对于每个标记的信息增益 ${\rm {IG}}({l_t}|a)$ ；

4)对于 $\forall a \in A$ ，执行操作:

①计算标记集合下每个特征的重要度 ${\rm {CSIG}}(D{\rm{|}}a)$ ；

②计算阈值 $\delta $ ；

5)对于 $\forall a \in A$ ，执行操作：

若 ${\rm{CSIG}}(D{\rm{|}}a) > \delta $ ，则 ${\rm {Red}} \leftarrow {\rm {Red}} \cup \left\{ a \right\}$

6)输出特征子集 Red，算法结束。

4.2 时间复杂度分析

代价敏感数据的多标记特征选择算法中：步骤1)初始化一个变量存放特征选择后的特征子集，其时间复杂度为 $O(1)$ ；步骤2)中①需利用基数排序^[18]计算等价类, 则整个条件特征集每个特征的信息熵的时间复杂度为 $O(|A||U|)$ ，步骤2)中②计算每个特征的条件信息熵的时间复杂度为 $O(|U/A||U||D|)$ ，可知步骤2)的时间复杂度最坏为 $O(|A||U||D|)$ ；步骤3)分别计算每个标记与每个特征之间的信息增益，其时间复杂度为 $O(|A||U||D|)$ ；步骤4)中①计算标记集合下每个特征重要度，其时间复杂度为 $O(|A||U||D|)$ ，步骤4)中②计算阈值的时间复杂度为 $O(|A||U|)$ ，因此步骤4)的时间复杂度最坏为 $O(|A||U||D|)$ ；步骤5)根据阈值进行特征选择其时间复杂度为 $O(|A|)$ 。因此本文算法的时间复杂度为 $O(|A||U||D|)$ 。

为了分析本文算法在计算复杂度上的优越性，将本文算法分别与CSMLPA^[19]算法和MLDM算法进行比较。CSMLPA算法是基于文献[20]的正区域模型设计的，并且考虑了测试代价的多标记特征选择算法，算法采用的是向前启发式搜索策略，其计算复杂度主要消耗在计算加入单个特征到特征子集后的正域大小，时间复杂度为 $O(|A{|^2}|U||D|)$ 。MLDM算法是基于文献[21]的差别矩阵方法改进的多标记特征选择算法，该算法主要耗时在对实例进行两两比较，其时间复杂度为 $O(|A||U{|^2}|D|)$ 。本文算法与CSMLPA算法和MLDM算法相比，时间复杂度由非线性 $O(|A{|^2}|U||D|)$ 和 $O(|A||U{|^2}|D|)$ 降低至线性 $O(|A||U||D|)$ 。由此可知，本文算法在计算复杂度上具有显著的优越性。

5 实验结果与分析

为了验证本文的CSMLFSIE算法的性能，从Mulan数据集中选取了Emotions、Birds和Yeast 这3个真实数据集进行实验测试和分析。实验将算法CSMLFSIE与MLFSIE、CSMLPA、MLPA和MLDM进行对比分析，其中，MLFSIE^[16]是一类基于信息熵的多标记特征选择算法，CSMLPA算法是基于文献[20]的正区域模型设计的考虑了测试代价的多标记特征选择算法，MLPA是一种利用文献[20]中的正区域模型改进的多标记特征选择算法，MLDM算法是基于文献[21]的差别矩阵方法改进的多标记特征选择算法。最后通过IBLR-ML多标记分类器验证上述算法特征选择结果的分类性能。

实验过程中首先采用以上5种特征选择算法分别对3个数据集进行特征降维，然后使用分类算法对降维后的数据集采用10倍交叉验证法验证算法的有效性。本实验的测试环境：CPU为Inter(R) Core(TM) i5-4590s (3.0 GHz)，内存8.0 GB，算法编程语言为Python和Java，使用的开发工具分别是记事本和Eclipse 4.7。

5.1 数据集

实验中选取的3个真实数据集的相关信息如表1所示，表中Yeast^[22]数据集描述的是酵母菌的基因功能分类，Emotions^[23]数据集是来自于某音乐学院的音频剪辑，Birds^[24]数据集通过鸟叫声的记录来区分鸟的种类。其中，Yeast数据集涉及的是生物信息领域，而Emotions和Birds数据集涉及的是音频信息领域。表1中对数据集中的实例个数、特征数、标记数、标记基数和总代价进行了描述，其中，标记基数用于统计训练集中实例的平均标记个数，总代价是指利用正态分布函数为数据集中的所有特征生成的代价总和。

5.2 评价指标

文中选用了代价约简率以及平均分类精度(average precision，AP)、汉明损失(Hamming loss，HL)、覆盖率(Coverage)、1错误率(one error，OE)、排序损失(ranking loss，RL)这5种多标记评价性能指标来评价算法性能。给定一组多标记对象集合 $({x_i},{Y_i})$ ， $i = 1,2, \cdots ,m$ ， $m$ 表示对象大小， ${Y_i}$ 表示多标记分类器预测测试对象 ${x_i}$ 具有的标记集合， ${Y_i}$ 表示多标记分类器预测测试对象 ${x_i} $ 具有的标记集合， ${Y_i} \subseteq L$ ， $L{\rm{ = }}\left\{ {{\lambda _j}:j = 1,2 ,\cdots, q} \right\}$ ， $L$ 表示所有标记集合， ${Z_i}$ 表示测试对象 ${x_i}$ 实际的标记集合， $\overline {{Y_i}} $ 表示 ${Y_i}$ 的补集， ${r_i}(\lambda )$ 为标记 $\lambda $ 的排序。

1) 代价约简率是考虑特征代价的特征子集 $B$ 的代价占全特征集 $A$ 总代价的比率：

${\rm{PC}} = \frac{{{\mathop{\rm Cos}\nolimits} {{\rm t}_B}(D)}}{{{\mathop{\rm Cos}\nolimits} {{\rm t}_A}\left( D \right)}}$

2) 平均分类精度(AP)是指在标记预测序列中，排在相关标记之前的标记仍是相关标记的比率：

${\rm{AP}}{\rm{ = }}\frac{1}{m}\sum\limits_{i = 1}^m {\frac{1}{{{\rm{|}}{Y_i}{\rm{|}}}}} \sum\limits_{\lambda \in {Y_i}} {\frac{{|\left\{ {{\lambda{\text{′}}} \in {Y_i}:{r_i}({\lambda {\text{′}}}) \leqslant {r_i}(\lambda )} \right\}|}}{{{r_i}(\lambda )}}} $

3) 汉明损失(HL)是指预测出的标记与实际标记的平均差异值：

${\rm{HL}} = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{|{Y_i}\varDelta {Z_i}|}}{M}} $

其中 $\varDelta $ 为 ${Y_i}$ 、 ${Z_i}$ 两个集合之间的对称差。

4) 覆盖率(Coverage)是指所有对象实际包含的所有标记所需最大的排序距离：

${\rm{Coverage}}{\rm{ = }}\frac{1}{m}\sum\limits_{i = 1}^m {\mathop {\max }\limits_{{\textit{λ}} \in {Y_i}} } \,{r_i}({\textit{λ}}) - 1$

5) 1错误率(OE)是指预测出的标记排序最靠前的标记不在实际对象中的比率：

${\rm{OE}}{\rm{ = }}\frac{1}{m}\sum\limits_{i = 1}^m {\delta (\mathop {\arg \min }\limits_{{\textit{λ}}\in {Y_i}} {r_i}({\textit{λ}}))} $

若 $\mathop {\arg }\limits_{\lambda \in {Y_i}}\min {r_i} ({\textit{λ}}) \notin {Y_i}$ 条件满足时，则 $\delta (\mathop {\arg \min }\limits_{{\textit{λ}} \in {Y_i}} {r_i}({\textit{λ}} ))$ =1，否则为0。

6) 排序损失(RL)是指预测出的标记中实际不包含的标记比实际包含的标记排序高的比率：

$ \begin{split} {\rm{RL}} = & \frac{1}{m}\sum\limits_{i = 1}^m {\dfrac{1}{{\left\| {{Y_i}} \right\|\left\| {{{\overline Y}_i}} \right\|}}} \times\\ & |\left\{ {\left( {{{\textit{λ}}_a},{{\textit{λ}}_b}} \right):{r_i}\left( {{{\textit{λ}}_a}} \right) > {r_i}\left( {{{\textit{λ}}_b}} \right)} \right.\left( {{{\textit{λ}}_a},{\lambda _b}} \right) \in {Y_i} \times {{\overline Y}_i}\} | \end{split} $

平均分类精度越大说明分类性能越好，代价约简率、汉明损失、覆盖率、1错误率、排序损失越小说明分类性能越好。

5.3 实验结果及比较 5.3.1 离散参数 $k$ 的选择

由于本文所选择的3个多标记数据集的特征值都包含连续型数据，但CSMLFSIE算法处理的是离散型特征变量，因此对于多标记数据集的处理需要对特征值进行离散化处理。在实验过程中发现， $k$ 的步长取值为5时，降维后的特征子集的分类性能差别较为明显。因此，本文将 $k$ 以步长5从5增加到50进行实验分析与比较。下面以Emotions数据集为例，讨论离散化参数 $k$ 的选择对多标记分类性能的影响，图1～5给出了Emotions数据集的5项评价指标随着离散化参数 $k$ 的值增加的变化曲线。CSMLFSIE曲线、MLFSIE曲线、CSMLPA曲线、MLPA曲线和MLDM曲线分别为这几种多标记特征选择算法的性能。

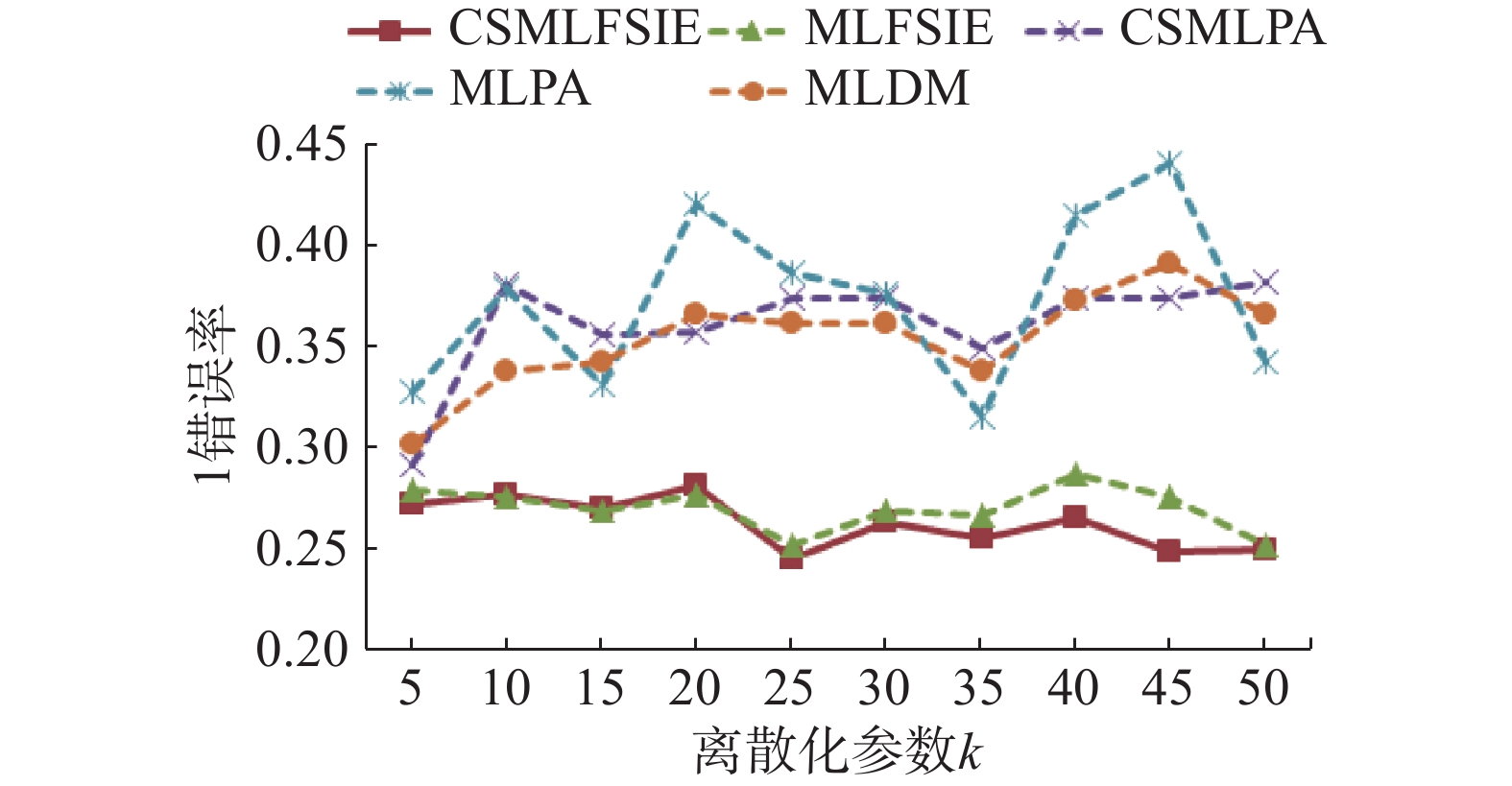
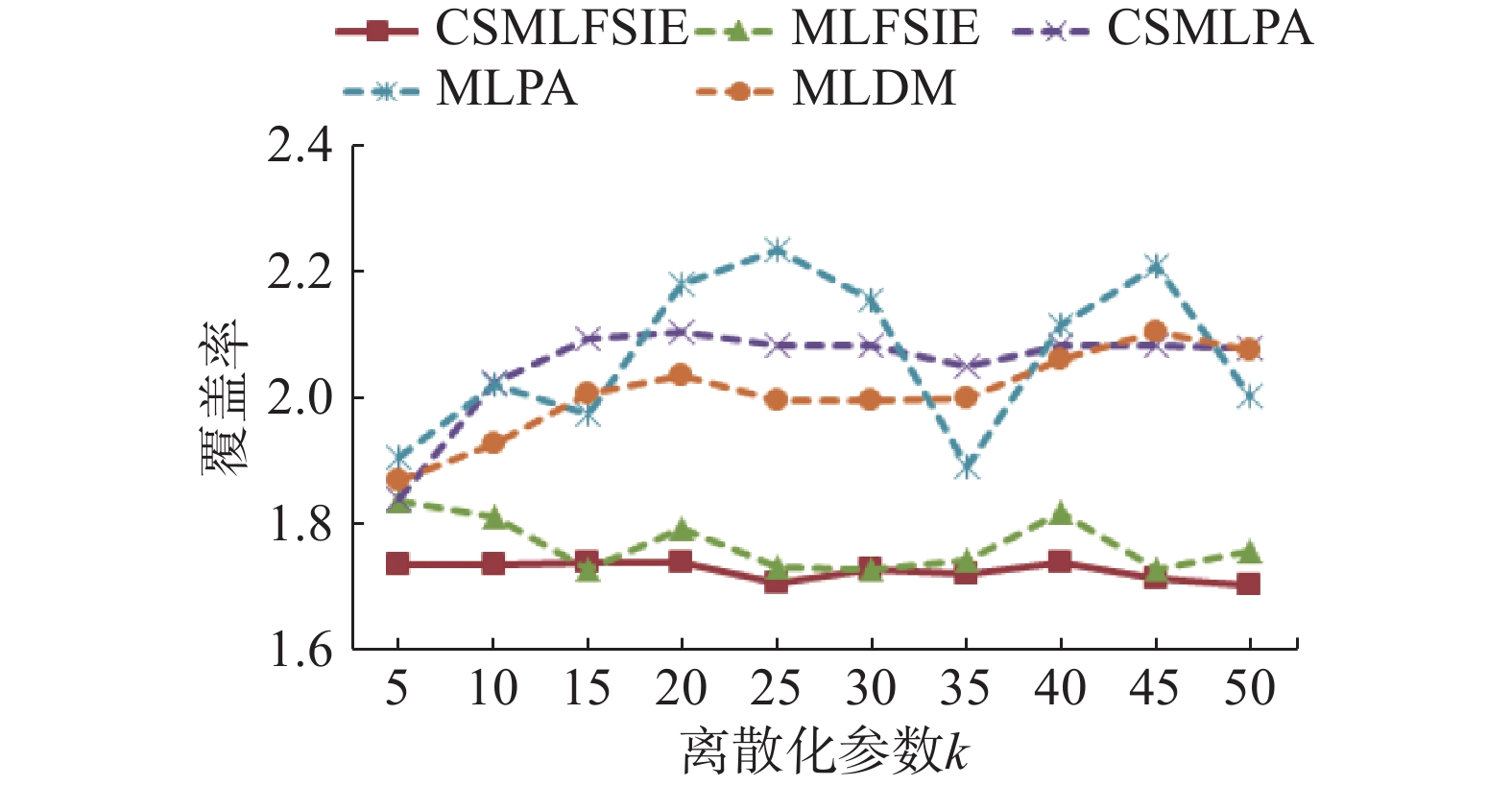
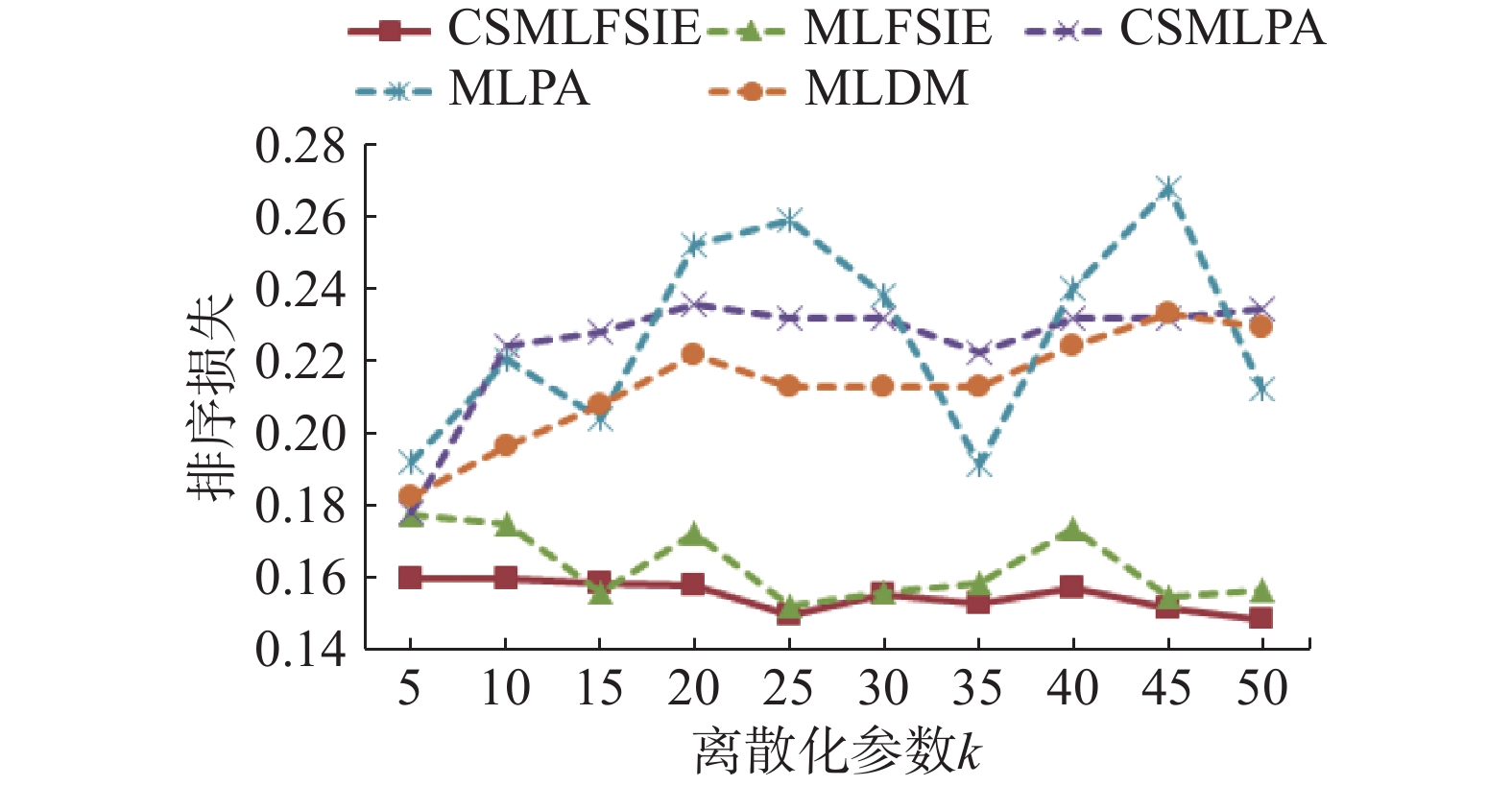
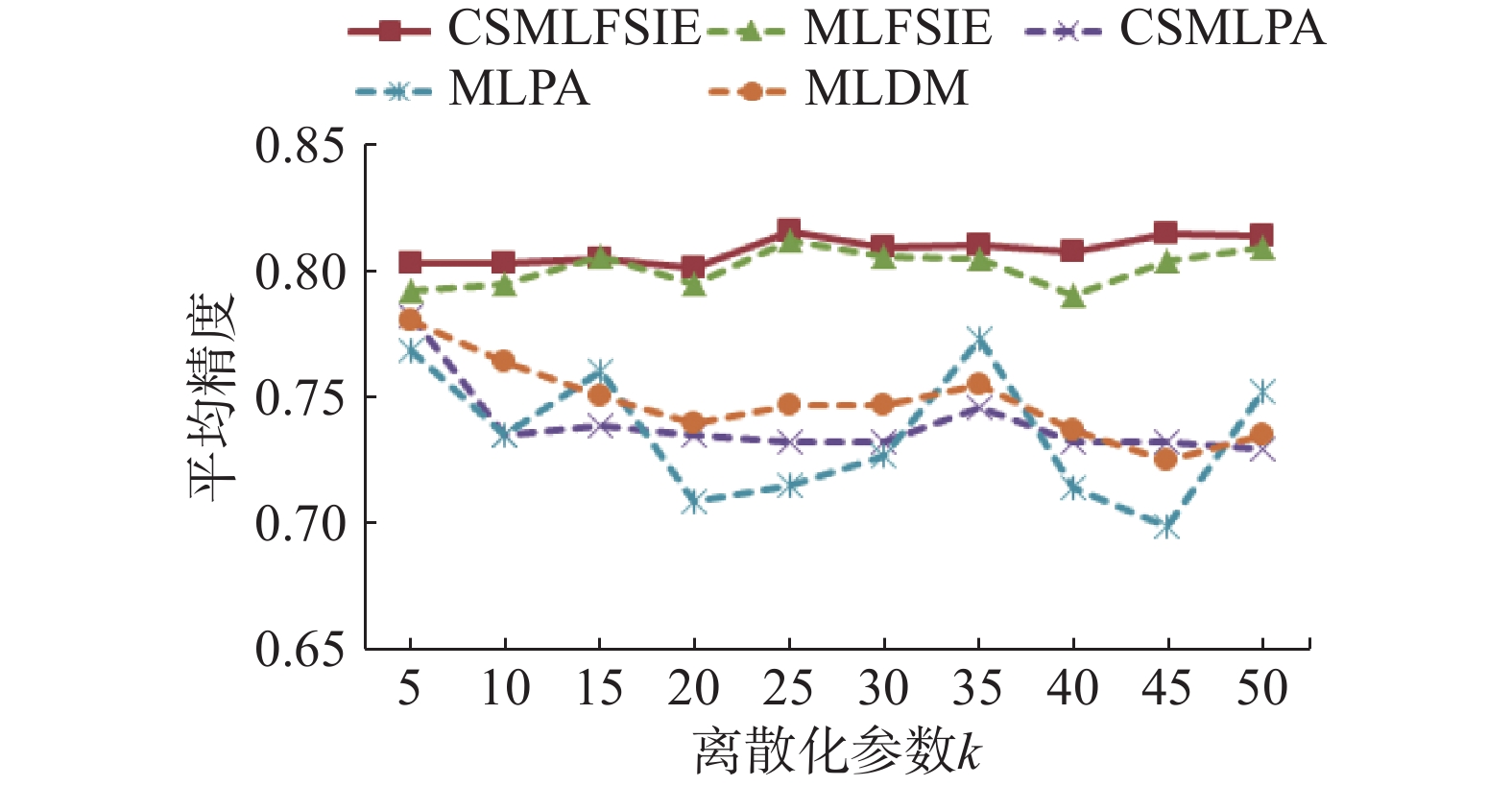
由图1～5可知，CSMLFSIE和MLFSIE算法的5项分类性能随离散化参数增加变化较为平缓，CSMLPA、MLPA和MLDM算法的5项分类性能随离散化参数增加变化较为显著，其中，变化较显著的是MLPA算法，5项分类性能随离散化参数 $k$ 取值的增加变化趋势较明显。针对CSMLPA算法，当 $k$ 的取值在[5，10]这个区间时，HL、OE、Coverage和RL的值随离散化参数 $k$ 的取值增加而增大，同时，AP的值随离散化参数 $k$ 的取值增加而减小，5项多标记性能指标的值变化较为明显。当 $k$ 的取值在[40，50]区间时，HL、OE、Coverage、RL和AP这5项多标记分类性能指标的值变化较小。针对MLDM算法，当离散化参数值从5变化至20时，HL、OE、Coverage和RL的值呈上升趋势，AP的值呈下降趋势，降维后的特征子集的分类性能变化较显著。当离散化参数取值从25变化至35时，HL、OE、Coverage、RL和AP的5项性能指标的值变化较为平缓，由此可知，降维后的特征子集的分类性能在这个区间的稳定性较强。另外，通过实验结果可知，当离散化参数 $k$ 的值为25时，CSMLFSIE和MLFSIE算法所取得的特征子集的分类性能最优；CSMLPA和MLDM算法在离散化参数 $k$ 为5时，其降维后的特征子集分类性能最优；当 $k=35$ 时，MLPA算法得到的特征子集的分类性能最优。

综上所述，与其他4种算法相比，随离散化参数增加，CSMLFSIE算法的5项分类性能变化最为平缓，即离散化参数的变化对CSMLFSIE算法影响最小，因此CSMLFSIE算法的稳定性和健壮性更优。

5.3.2 实验对比

实验过程中将训练数据集和测试数据集相结合，采用10倍交叉验证法来验证算法的有效性，实验结果采用评价指标的平均值和标准差表示。另外，由于Mulan数据集自身并不含测试代价，因此本文采用正态分布函数为每个特征生成测试代价，其中，正态分布函数的取值以100为期望，以30为标准差。

表2～4中表示在正态分布函数下，用5种多标记特征选择算法分别对Yeast、Emotions和Birds这3个数据集进行特征降维，并用IBLR-ML分类算法验证降维后的特征子集的分类性能，同时，与原始数据集的分类性能进行对比。表2～4中给出的数据是AP取最优值时，所对应的PC、HL、OE、Coverage、RL和k的值。另外，各项评价指标的最优值用黑体标注，↓表示该项指标值越小算法的分类性能越好，↑表示该项指标的值越大算法的分类性能越好。

由表2～4中的5种多标记分类性能评价指标的结果可以看出，CSMLFSIE算法总体优于其他4种算法，较为明显的有Coverage、HL和AP这3项性能指标。同时，通过CSMLFSIE算法进行特征降维后，特征子集的分类性能优于原始数据集，其中，最为突出的是在PC这项指标上。另外，由表2～4可知，各个算法分类性能最优时，所对应的离散化参数k的取值也存在差异。由表2中的Yeast数据集可知，由本文CSMLFSIE算法降维后的特征子集的分类性能较优，其降维后的特征子集PC的值与MLFSIE、CSMLPA、MLPA和MLDM算法相比，分别减少了0.92%、14%、13.47%和12.68%；同时，AP分别提高了0.13%、2.54%、2.54%和3.26%，且OE、Coverage和RL值相对较优。另一方面，CSMLFSIE算法降维之后的特征子集与原始数据集相比，PC的值为2.34%，比原始数据集减少了97.66%，且其他5项分类性能评价指标的值更优，其中，AP的值提高了0.37%，HL、OE、Coverage、RL值分别降低了0.02%、0.66%、3.6%和0.16%。

针对Emotions数据集，由本文CSMLFSIE算法选择的特征子集的分类性能总体较优，根据表3中各项性能指标的结果可知，除HL和OE性能指标之外，其他3项多标记分类性能指标的值最优，且总测试代价PC的值最小。CSMLFSIE 算法与MLPA算法相比，PC的值同为6.47%，但AP的值却提高了6.26%，同时，HL、OE、Coverage和RL的值都显著降低。由此可知，CSMLFSIE算法要优于MLPA算法。CSMLFSIE算法与MLFSIE算法相比，PC的值减少了12.49%，另外，Coverage、RL和AP这3项性能指标相对更优，因此CSMLFSIE算法总体优于MLFSIE算法。此外，CSMLFSIE算法与CSMLPA和MLDM算法相比，PC的值分别减少了15.36%和10.61%，其HL、OE、Coverage、RL和AP这5项性能指标的值更优。

从表4中的Birds数据集可以看出，CSMLFSIE算法选择后的特征子集的分类性能与Raw Data相比，除HL这项性能指标之外，其他4项性能指标的值都更优，PC的值也减少了88.65%，因此CSMLFSIE算法选择后的特征子集的分类性能总体优于Raw Data。CSMLFSIE算法与MLFSIE算法相比，Coverage、RL和AP的值较优，PC的值减少了35.89%。CSMLFSIE算法与CSMLPA算法相比，PC的值减少了10.18%，AP的值由59.05%提高至61.71%，HL、OE、Coverage和RL的值分别降低了0.08%、2.18%、21.21%和0.79%。CSMLFSIE算法与MLPA算法和MLDM算法相比，AP的值分别提高了4.25%、4.37%，HL、OE、Coverage和RL的值有所下降，但PC的值分别增加了8.88%、8.7%。由此可知，由CSMLFSIE算法选择的特征子集的分类性能总体较优。

另外，由表2～4可知，针对CSMLPA算法，3个数据集的离散化参数k取值为5时，其降维后特征子集的分类性能最优；针对CSMLFSIE算法进行离散化处理时，参数值为45时，Yeast数据集和Birds数据集降维后的特征子集的分类效果较佳，而对于Emotions数据集来说，离散化参数取25较优；针对MLFSIE算法和MLPA算法，在3个数据集降维后的特征子集的分类性能最优时，所对应的离散化参数的取值也不同；针对MLDM算法，对于Yeast数据集和Emotions数据集，离散化参数取5时，降维后的特征子集的分类性能较优，在Birds数据集中，离散化参数取值为25较好。由此可知，各个算法的分类性能与离散化参数k的取值相关，降维后的特征子集影响着分类器的分类性能。

综上所述，原始数据集中存在大量冗余和不相关特征，且这些特征直接影响了分类器的分类性能，综合各项性能评价指标可知，CSMLFSIE算法总体优于其他4种算法，达到了较好的特征降维的效果。

6 结束语

传统的基于多标记的特征选择算法往往忽略了每个特征获取和采集所需花费的代价问题，为此，本文提出了一种代价敏感数据的多标记特征选择算法，该算法利用信息熵分析特征与标记之间的相关性，利用均匀分布函数和正态分布函数为特征生成测试代价，从代价敏感的研究视角，构建一种新特征重要度准则。然后，根据服从正态分布的特征重要度和特征代价的标准差设置阈值，通过阈值剔除冗余和不相关特征。通过对3个真实数据集实验结果的分析与比较，验证了本文算法的有效性和高效性。但是，该算法并未充分考虑标记之间的相关性以及误分类代价的问题，这也是我们下一步的研究工作。