图像融合技术是将两幅或者多幅图像中感兴趣的信息提取出来,得到一幅信息更加丰富适合于人眼视觉感官和更利于计算机处理的图像处理技术。传统相机的光学镜头经常遭受有限景深的问题,难以在不使用专用光学器件和传感器的情况下获得所拍摄场景的全聚焦图像。对于人类视觉感知和计算机处理而言,多聚焦图像更为可取,对于同一场景,多聚焦图像的融合可以将两幅以上的图像选取各自聚焦区域融合到一幅图像中,从而获得比各自源图像更多的信息。目前,多聚焦图像融合在军事监视、医学成像、遥感图像和机器视觉等领域具有广泛应用[1]。
图像融合方法主要分为空间域融合和频率域融合[2]两类。空间域融合方法直接对源图像像素进行融合,未进行任何的分解运算,融合的效果不理想,无法清晰地提取源图像的边缘轮廓信息。由于多尺度变换的多尺度分解过程适合于人类视觉分析,并且易于计算机处理,目前,多数图像融合技术都是基于频率域的多尺度变换方法。其主要有离散小波变换(discrete wavelet transformation,DWT)[3]、脊波(ridgelet)变换[4]、曲线波(curvelet)变换[5]、轮廓波(contourlet)变换[6]、非下采样轮廓波变换(nonsubsampled contourlet transform,NSCT)和剪切波(shearlet)变换[7]以及非下采样剪切波变换(NSST)等。NSCT运算十分耗时,且在图像方向分解上受到限制,因此无法达到对图像的实时处理。而剪切波变换以小波理论为基础,运算简单,并且对于图像分解方向没有要求。在此基础上的NSST不仅具有剪切波变换的多尺度、多方向特性,而且具有各向异性和平移不变性,极大地消除了伪吉布斯现象,因此NSST逐渐较多地运用在图像处理领域。
稀疏表示是近年来提出的一种在信号处理中的新的研究模型[8],其在信号和图像处理的各个领域都有着广泛的应用,包括盲源分离、图像去噪、图像融合、人脸识别等领域。稀疏表示能够以稀疏的方式来表示图像信息,给图像处理带来了极大的便利。
脉冲神经网络(pulse coupled neural networks,PCNN)是Eckhorn于20世纪90年代提出的一种基于猫的视觉原理构建的简化神经网络模型,其信号形式和处理机制更符合人类视觉神经系统的生理学基础,在图像融合、图像分割、图像识别以及边缘检测等领域起着重要作用。1999年Broussard等在图像融合中利用PCNN提高融合图像的准确度,证明了PCNN在图像融合中具有很好的应用价值[9]。
稀疏表示的融合方法通常会导致融合图像比较光滑,不利于对源图像边缘信息的保留,目前很多稀疏表示的图像融合方法都是基于多尺度变换的[10-11]。PCNN具有耦合特性以及脉冲同步特性,在图像融合中可以有效利用局部信息。但PCNN参数较多且难以确定,因此现有的一些融合算法都采用了PCNN的自适应参数模型[12-14]。近年来,基于多尺度变换和PCNN结合的图像融合算法相继被提出。文献[15]提出了将非下采样轮廓波(NSCT)与PCNN相结合的图像融合算法;文献[16]提出了基于非下采样剪切波(NSST)和PCNN相结合的医学图像融合算法;文献[17]提出了一种稀疏表示和PCNN相结合的红外与可见光图像融合算法。这些算法可以取得较好的融合效果,但在边缘处会有虚影产生。在上述理论的基础上,本文提出了一种基于改进的稀疏表示和脉冲耦合神经网络的图像融合算法。首先,将待融合的源图像进行NSST分解,分别得到低频和高频子带系数。对低频子带由稀疏表示方式进行融合,即利用K奇异值分解(K-SVD)算法从源图像中得到学习字典,然后将两个源图像得到的子字典结合生成联合字典,再采用正交匹配追踪(orthogonal matching pursuit,OMP)算法得到稀疏系数,完成低频子带的融合。对于高频子带,本文则采用PCNN算法进行融合,将高频子带改进的空间频率(modified spatial frequency,MSF)作为PCNN的激励,以总的点火幅度取最大值为高频子带的融合规则。实验结果表明,本文所提出的算法在视觉效果和客观评价上都取得了较好的效果。
1 基本原理 1.1 图像的NSST变换剪切波变换是由Easley等在传统仿射系统的基础上,将几何与多尺度变换结合起来而提出的合成小波理论,当维数n为2时,具有合成膨胀的仿射系统为
| $ {M_{{{{AB}}}}}\left( {\psi } \right){\rm{ = \{ }}{{\psi }_{{j},{l},{k}}}\left( {x} \right){\rm{ = }}{\left| {{\rm{det}}\left( {{{A}}} \right)} \right|^{\frac{{\rm{j}}}{{\rm{2}}}}}{\psi }\left( {{{{B}}^{{l}}}{{{A}}^{j}}{x}{\rm{ - }}{k}} \right):{j},{l} \in {{\bf{R}}}{\rm{;}}{k} \in {{{\bf{R}}}^{\rm{2}}}{\rm{\} }} $ | (1) |
式中:
| ${{{A}}_0} = \left[ {\begin{array}{*{20}{l}} 4&0\\ 0&2 \end{array}} \right],\quad {{{B}}_0} = \left[ {\begin{array}{*{20}{l}} 1&1\\ 0&1 \end{array}} \right] $ |
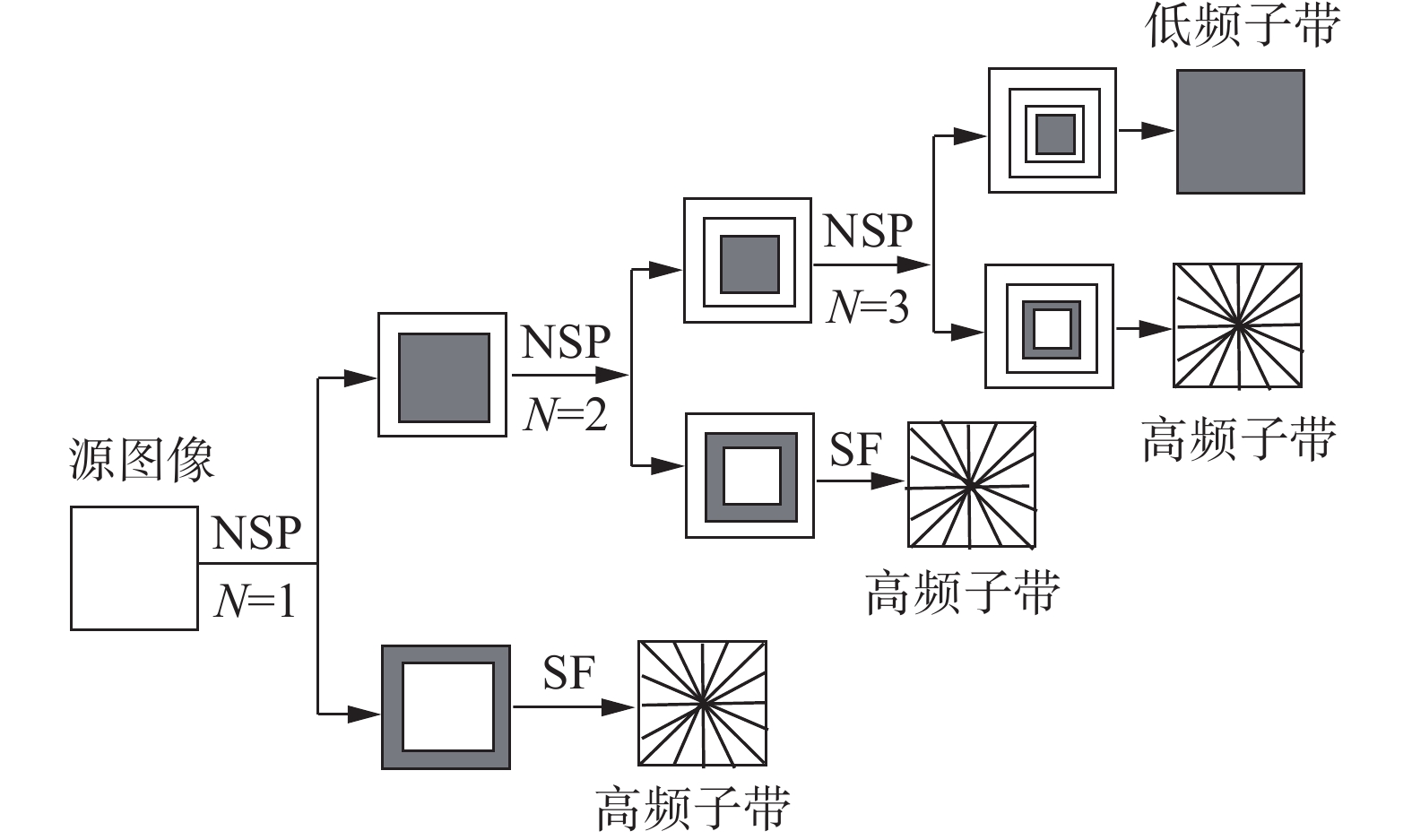
NSST由非下采样金字塔分解(non-subsample pyramid,NSP)和剪切滤波器组成,图像经过k级NSP分解之后,会分解成由k个高频子带和1个低频子带组成的子图像。分解后的k+1个子带与源图像大小相同,但是尺度不同。3级NSST分解过程如图1所示。
|
Download:
|
| 图 1 3级NSST分解过程示意 Fig. 1 Diagram of three-level NSST decomposition process | |
向量信号x可以表示为x=[
| $ {{X}} = \sum\limits_{i = 1}^k {{a}} (i){{\phi}} (j) $ | (2) |
式中:α为完备字典;ϕ为信号x基于α字典下的稀疏系数。在稀疏模型中,过完备字典起着关键作用。获得过完备字典的主要方法有两种:1)基于DCT、小波和曲线波等分析方法的分析字典;2)学习字典,对大量的数据样本进行训练得到具有针对性的过完备字典。通常情况下,分析字典一般比较简单,但是表达形式单一,适应性不够,而学习字典的适应性强,可以适应不同的数据图像。常用的字典学习求解方法有最优方向法(method of optimal directions,MOD)、FOCUSS字典学习算法、广义PCA(generalized PCA)算法以及K-SVD算法等。稀疏表示问题的求解等同于优化问题,常用的稀疏系数基本算法有匹配追踪(MP)、正交匹配追踪(OMP)和基追踪(BP)等。本文采用K-SVD[18]算法来构建学习字典,用OMP算法来求解稀疏系数,以得到更好的收敛性。
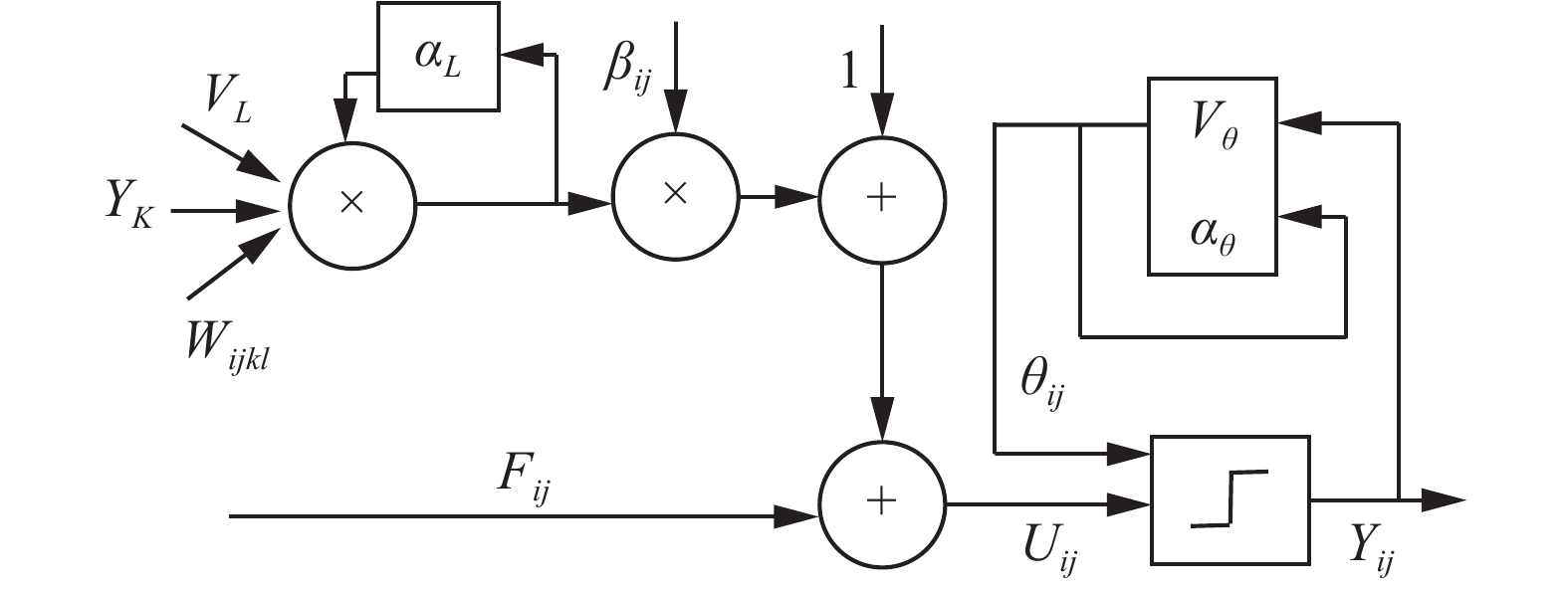
1.3 PCNN模型PCNN由多个神经元构成,每个神经元由3个部分组成,分别是连接域、调制域和脉冲产生器。PCNN神经元对应着源图像中的每个像素,每个神经元的点火输出有点火和不点火2种状态。PCNN简化模型如图2所示。
|
Download:
|
| 图 2 PCNN单个神经元简化模型 Fig. 2 Simple model of single neuron in PCNN | |
为了提高PCNN的效率,本文采用简化的PCNN模型:
| $ \left\{ \begin{aligned} & {{F}_{{ij}}}{\rm{(}}{n}{\rm{) = }}{{I}_{{ij}}}\\ & {{L}_{{ij}}}{\rm{(}}{n}{\rm{) = exp}}\left( {{\rm{ - }}{{\alpha }_{L}}} \right){{L}_{{ij}}}{{(n - 1) + }}{{V}_{L}}\mathop \sum \limits_{{kl}} {{W}_{{ijkl}}}{{Y}_{{ij}}}{\rm{(}}{n}{\rm{ - 1)}}\\ & {{U}_{{ij}}}{\rm{(}}{n}{\rm{) = }}{{F}_{{ij}}}{\rm{(}}{n}{\rm{)}}\left( {{\rm{1 + }}{\beta }{{L}_{{ij}}}{\rm{(}}{n}{\rm{)}}} \right)\\ & {{\theta }_{{ij}}}{\rm{(}}{n}{\rm{) = exp}}\left( {{\rm{ - }}{{\alpha }_{\theta }}} \right){{\theta }_{{ij}}}{{(n - 1)}}{{V}_{\theta }}{{Y}_{{ij}}}{\rm{(}}{n}{\rm{ - 1)}}\\ & {{Y}_{{ij}}}{\rm{(}}{n}{\rm{) = }}\left\{ \begin{array}{l} \begin{array}{*{20}{c}} \!\!\!\!\! {\rm{1}},&{{{U}_{{ij}}}{\rm{(}}{n}{\rm{)> }}{{\theta }_{{ij}}}{\rm{(}}{n}{\rm{)}}} \end{array}\\ \begin{array}{*{20}{c}} \!\!\!\!\! {\rm{0}},&\text{其他} \end{array} \end{array} \right. \end{aligned} \right. $ | (3) |
式中:Iij为外部输入激励;Fij为反馈输入;Lij为链接输入项;Wijkl为神经元与其他神经元的连接权值;k、l为神经元与周围连接的范围;αL、αθ为衰减时间常数;β为神经元连接强度;VL为连接输入放大系数;Vθ为阈值放大系数;Yij为神经元脉冲输出。
2 改进的融合算法本文选用NSST对已配准的源图像A和B进行4级分解,得到1个低频子带和4个高频子带。针对分解后得到的低频子带和高频子带的特点,分别采用改进的稀疏表示和PCNN进行融合。最后对融合后的低频子带和高频子带进行NSST逆变换,从而获得融合图像。本文的融合算法原理如图3所示。

|
Download:
|
| 图 3 基于改进的稀疏表示和PCNN融合流程图 Fig. 3 Flowchart of fusion based on the improved sparse presentation and PCNN | |
低频子带通常包含图像的大部分信息,反映了图像的整体面貌,对于低频子带的处理,本文对稀疏表示加以改进,得到新的融合规则。假定两个源图像低频子带大小为M×N,,一般来说,自然图像包含复杂和非稳定信息,而局部块形式相对简单且结构一致。因此,采用滑动窗口技术在获取局部特征方面能取得更好的性能。具体处理过程:首先,利用一个大小为n×n,以步长为1的滑动窗口,对低频子带LA和LB进行窗口滑动,将低频子带分成若干个子图像块;将每个子块转换成一个列向量,所有的列向量构成LA和LB的样本训练矩阵VA和VB,样本矩阵大小为J×L(J=n×n, L=(M−n+1)×(N−n+1));其次,对样本训练矩阵VA、VB的列向量分别求平均,得到平均矩阵
| $ \begin{array}{l} {{\widetilde {{V}}}_{\rm{A}}} = {{{V}}_{\rm{A}}} - {{\overline {{V}}}_{\rm{A}}}\\ {{\widetilde {{V}}}_{\rm{B}}} = {{{V}}_{\rm{B}}} - {{\overline {{V}}}_{\rm{B}}} \end{array} $ |
本文提出的新算法是:先采用K-SVD算法分别对去平均的样本矩阵
| $ {{D}}= \left[ {{{{D}}_{A}}\;\;{{{D}}_B}} \right] $ |
然后利用OMP算法求出样本矩阵
| $ {{M}}_{\rm{A}}^i = {\left( {{{\left\| {{{a}}_{\rm{A}}^i} \right\|}_1}} \right)^{{\omega _t}}} \times {\left( {{{\left\| {{{a}}_{\rm{A}}^i} \right\|}_0}} \right)^{{\omega _O}}} $ | (4) |
| $ {{M}}_{\rm{B}}^i = {\left( {{{\left\| {{{a}}_{\rm{B}}^i} \right\|}_1}} \right)^{{\omega _t}}} \times {\left( {{{\left\| {{{a}}_{\rm{B}}^i} \right\|}_0}} \right)^{{\omega _O}}} $ | (5) |
式中:ω1=ω0=0;
| $ {\alpha }_{F}^{i}{\rm{ = }}\left\{ \begin{array}{l} \begin{array}{*{20}{c}} \!\!\!\! {{\alpha }_{{\rm{A}}}^{i}},&{{{{M}}}_{{\rm{A}}}^{i} > {{{M}}}_{{\rm{B}}}^{i}} \end{array}\\ \begin{array}{*{20}{c}} \!\!\!\! {{{\alpha}_{{\rm{B}}}^{i}}},&\text{其他} \end{array} \end{array} \right. $ |
则融合结果
| $ {{V}}_F^i = Da_F^i $ |
融合平均矩阵取值为
| $ {{\overline V}_F}{\rm{ = }}\left\{ \begin{array}{l} {{\overline V}_A},\;\;\;\;{M_A} > {M_B}\\ {{\overline V}_B},\;\;\;\;\text{其他} \end{array} \right. $ |
样本训练矩阵的融合结果为
| $ {V_F} = V_F^i + {{\overline V}_F} $ |
最后,将样本的融合矩阵转换为数据子块,再对数据子块进行重构即可得到低频子带的融合系数。
2.2 高频子带的融合规则高频子带通常对应着图像的边缘信息和纹理细节,直接关系到图像的清晰程度和视觉效果。对于高频子带的融合,本文提出一种改进的空间频率(MSF)作为神经元的反馈输入。对于窗口大小为(2M+1)×(2N+1)的图像块,MSF定义公式为
| $ {M_{{\rm{SF}}}} = \sqrt {{R_F}^2 + {C_F}^2 + {D_F}^2} $ | (6) |
式中:
| $ {{R}_{F}} = \sqrt {\frac{{\rm{1}}}{{\left( {2M{\rm{ + 1}}} \right)\left( {2N{\rm{ + 1}}} \right)}}\mathop \sum \limits_{{m} = - M}^M \mathop \sum \limits_{{n} = - N}^N {{{\rm{[}}{X}\left( {{i} + {m},{j} + {n}} \right) - {X}\left( {{i} + {m},{j} + {n}{\rm{ - 1}}} \right){\rm{]}}}^{\rm{2}}}} $ | (7) |
| ${C_F} = \sqrt {\frac{{\rm{1}}}{{\left( {2M + 1} \right)\left( {2N + 1} \right)}}\mathop \sum \limits_{m = - M}^M \sum\limits_{n = - N}^N {{{[X\left( {i + m,j + n} \right) - X\left( {i + m,j + n} \right)]}^{\rm{2}}}} } $ | (8) |
| $ \begin{split} {D_F}{\rm{ = }} & \sqrt {\frac{{\rm{1}}}{{\left( {2M} \right)\left( {2N} \right)}}\mathop \sum \limits_{m = - M + 1}^M \mathop \sum \limits_{n = - N + 1}^N {{{\rm{[}}X\left( {i + m,j + n} \right) - X\left( {i + m - 1,j + n - 1} \right){\rm{]}}}^{\rm{2}}}} + \\ & \sqrt {\frac{{\rm{1}}}{{\left( {2M} \right)\left( {2N} \right)}}\mathop \sum \limits_{m = - M}^{M - 1} \mathop \sum \limits_{n = - N }^{N-1} {{{\rm{[}}X\left( {i + m - 1,j + n} \right) - X\left( {i + m,j + n - 1} \right){\rm{]}}}^{\rm{2}}}} \end{split} $ | (9) |
式中:X(i,j)为源图像对应位置像素;RF为行频率;CF为列频率;DF为对角线频率。
在经典的PCNN模型中,通常以相同迭代次数内的点火次数作为融合规则,点火输出值只有1和0两种状态,则其不能准确地反映点火幅度的差异。本文加以改进,以神经元输出总幅度值作为高频子带的融合规则,其定义为
| $ {{X}_{{ij}}}{\rm{(}}{n}{\rm{) = }}\frac{{\rm{1}}}{{{\rm{1 + exp[}}{{\theta }_{{ij}}}\left( {n} \right){\rm{ - }}{{U}_{{ij}}}{\rm{(}}{n}{\rm{)]}}}} $ | (10) |
| $ M_{i j}(n)=M_{i j}(n-1)+X_{i j}(n) $ | (11) |
式中Mij(n)为神经元输出的总幅度值。在n次迭代运算内,选择输出总幅度值最大的系数作为融合系数,有
| $ {{I}_{{F}{\rm{,}}{ij}}}{\rm{ = }}\left\{ \begin{array}{l} \begin{array}{*{20}{c}} \!\!\!\! {{{I}_{{\rm{1,}}{ij}}}},&{{{M}_{{\rm{1,}}{ij}}}{\rm{ > }}{{M}_{{\rm{2,}}{ij}}}} \end{array}\\ \begin{array}{*{20}{c}} \!\!\!\! {{{I}_{{\rm{2,}}{ij}}}},&\text{其他} \end{array} \end{array} \right. $ | (12) |
式中I1,ij、I2,ij分别为源图像A、B高频子带系数。
最后,将融合后的低频子带和高频子带进行NSST逆变换,得到最终的融合图像。
3 实验结果与分析为了验证本文融合算法的融合效果,采用的仿真环境为:Intel i5,1.8 GHz双核处理器,500 GB硬盘,4 GB内存,windows10系统,MATLAB2015a仿真平台。采用了两组图像进行实验,实验图像如图4所示,分别为512×512的Pepsi图像和256×256的Clock图像。Pepsi图像融合结果分别与基于NSCT-PCNN、文献[11]、文献[12]算法中的Pepsi图像融合结果进行比较;Clock图像融合结果分别与基于NSCT-PCNN、文献[10]、文献[11]算法中的Clock图像融合结果进行比较。本文采用互信息量(MI)、边缘信息传递因子(QAB/F)、空间频率(SF)、平均梯度(AG)[19]作为融合效果的客观评价指标。各融合算法的融合结果如图5、图6所示,客观评价如表1、表2所示。

|
Download:
|
| 图 4 实验源图像 Fig. 4 Source images | |

|
Download:
|
| 图 5 各种算法Pepsi图像融合结果 Fig. 5 Pepsi image fusion of each algorithm | |

|
Download:
|
| 图 6 各种算法Clock图像融合结果 Fig. 6 Clock image fusion of each algorithm | |
| 表 1 各算法Pepsi图像融合的评价指标值 Tab.1 Evaluation index of Pepsi image fusion for each algorithm |
| 表 2 各算法Clock图像融合的评价指标值 Tab.2 Evaluation index of clock image fusion for each algorithm |
从图5和图6各算法的融合结果中可以看出,本文算法的融合效果要好于其他3种算法,且在边缘和细节纹理等方面都处理得较好,处理后的整体清晰度也高于其他3种算法。
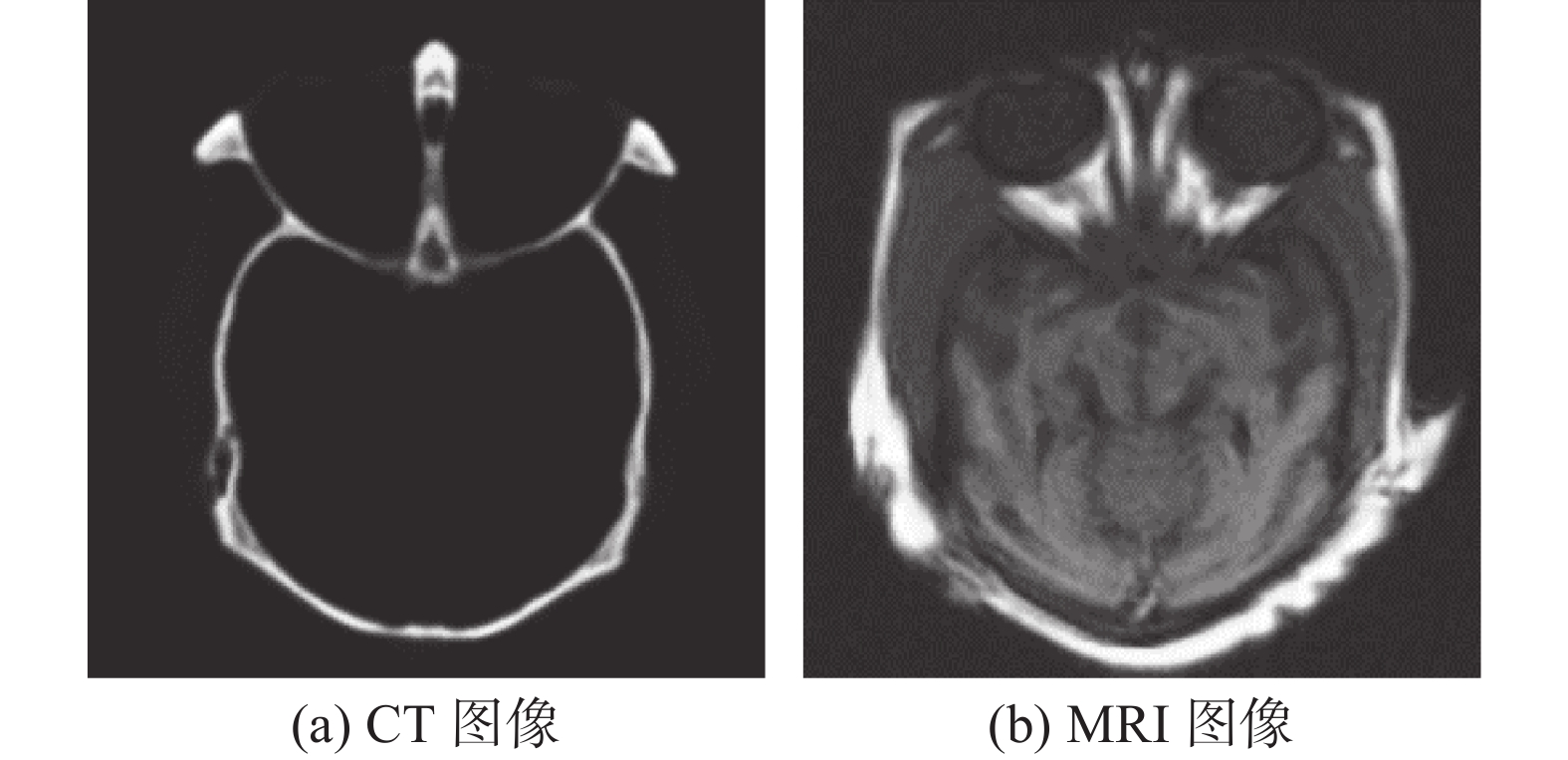
本文提出的算法在医学图像融合方面也具有很好的融合效果,图7分别为CT图像和MRI图像。在实验中,本文所提出的算法融合效果分别与文献[15]中NSCT-PCNN算法、文献[16]中NSST-PCNN算法以及文献[20]中MNLMF-SF算法的融合效果进行比较,融合结果如图8和表3所示。
|
Download:
|
| 图 7 CT图像和MRI图像 Fig. 7 CT and MRI images | |

|
Download:
|
| 图 8 各种算法CT和MRI图像融合结果 Fig. 8 CT and MRI image fusions of different algorithms | |
| 表 3 各算法CT和MRI图像融合的评价指标值 Tab.3 Evaluation index of CT and MRI image fusions for each algorithm |
从图8中各算法的CT和MRI图像的融合结果可以看出:NSCT-PCNN算法的融合结果边缘会有虚影;NSST-PCNN算法和MNLMF-SF算法的融合图像MRI细节部分有细微的缺失;本文算法既保留了原图像的边缘清晰度,又保留了更多的细节信息。
从客观来说,MI、QAB/F、SF和AG等指标都是对融合图像融合效果的客观评价,MI是融合图像从源图像中获得的信息量;QAB/F、SF都与边缘信息有关,AG反映图像清晰度,这4个指标值越大则表明融合效果越好。从表1和表2中可以看出,本文算法处理后的各项指标都相当不错,除Pepsi图像的MI指标比文献[11]算法稍有不足,位列第2外,其他所有指标都位列第1,在医学图像融合上本文算法除边缘信息传递因子指标略低于MNLMF-SF算法外,其他指标都优于对比算法,表明了本文算法的有效性和优势。
4 结束语本文提出了一种基于改进的稀疏表示和脉冲耦合神经网络的融合算法。与相关算法比较,本文算法在融合源图像信息时,既克服了稀疏表示算法造成的平滑问题,又保留了更多的图像边缘、纹理细节等信息,使融合图像更加清晰,可以获得更理想的效果,实验结果也验证了本文算法的有效性。
| [1] |
王卫卫, 水鹏朗, 宋国乡. 小波域多聚焦图像融合算法[J]. 系统工程与电子技术, 2004, 26(5): 668-671. WANG Weiwei, SHUI Penglang, SONG Guoxiang. Multi-focus image fusion in wavelet domain[J]. Systems engineering and electronics, 2004, 26(5): 668-671. DOI:10.3321/j.issn:1001-506X.2004.05.034 (  0) 0)
|
| [2] |
LI Shutao, KANG Xudong, FANG Leyuan, et al. Pixel-level image fusion: A survey of the state of the art[J]. Information fusion, 2017, 33: 100-112. DOI:10.1016/j.inffus.2016.05.004 ( 0) 0)
|
| [3] |
ROCKINGER O, FECHNER T. Pixel-level image fusion: the case of image sequences[C]//Proceedings of SPIE 3374, Signal Processing, Sensor Fusion, and Target Recognition VII. Orlando, USA, 1998: 378–388.
( 0) 0)
|
| [4] |
EHLERS M. Multisensor image fusion techniques in remote sensing[J]. ISPRS journal of photogrammetry and remote sensing, 1991, 46(1): 19-30. DOI:10.1016/0924-2716(91)90003-E ( 0) 0)
|
| [5] |
赵景朝, 曲仕茹. 基于Curvelet变换与自适应PCNN的红外与可见光图像融合[J]. 西北工业大学学报, 2011, 29(6): 849-853. ZHAO Jingchao, QU Shiru. A better algorithm for fusion of infrared and visible image based on Curvelet transform and adaptive pulse coupled neural networks (PCNN)[J]. Journal of Northwestern Polytechnical University, 2011, 29(6): 849-853. DOI:10.3969/j.issn.1000-2758.2011.06.005 (  0) 0)
|
| [6] |
张雄美, 李俊山, 易昭湘, 等. 非抽样轮廓波变换域图像融合方法研究[J]. 电光与控制, 2008, 15(7): 16-19. ZHANG Xiongmei, LI Junshan, YI Zhaoxiang, et al. Image fusion based on nonsubsampled contourlet[J]. Electronics optics and control, 2008, 15(7): 16-19. DOI:10.3969/j.issn.1671-637X.2008.07.005 (  0) 0)
|
| [7] |
EASLEY G R, LABATE D, LIM W Q. Optimally sparse image representations using shearlets[C]//Proceedings of 2006 Fortieth Asilomar Conference on Signals, Systems and Computers. Pacific Grove, USA, 2006: 974–978.
( 0) 0)
|
| [8] |
YANG Bin, LI Shutao. Multifocus image fusion and restoration with sparse representation[J]. IEEE transactions on instrumentation and measurement, 2010, 59(4): 884-892. DOI:10.1109/TIM.2009.2026612 ( 0) 0)
|
| [9] |
BROUSSARD R P, Rogers S K, Oxley M E, et al. Physiologically motivated image fusion for object detection using a pulse coupled neural network[J]. IEEE Transactions on neural networks, 1999, 10(3): 554-563. ( 0) 0)
|
| [10] |
赵春晖, 郭蕴霆. 一种快速的基于稀疏表示和非下采样轮廓波变换的图像融合算法[J]. 电子与信息学报, 2016, 38(7): 1773-1780. ZHAO Chunhui, GUO Yunting. Fast image fusion algorithm based on sparse representation and non-subsampled contourlet transform[J]. Journal of electronics and information technology, 2016, 38(7): 1773-1780. (  0) 0)
|
| [11] |
XIANG Fengtao, JIAN Zhang, LIANG Pan, et al. Robust image fusion with block sparse representation and online dictionary learning[J]. IET image processing, 2018, 12(3): 345-353. DOI:10.1049/iet-ipr.2017.0327 ( 0) 0)
|
| [12] |
谢秋莹, 易本顺, 柯祖福, 等. 基于SML和PCNN的NSCT域多聚焦图像融合[J]. 计算机科学, 2017, 44(6): 266-269, 282. XIE Qiuying, YI Benshun, KE Zufu, et al. Multi-focus image fusion based on SML and PCNN in NSCT domain[J]. Computer science, 2017, 44(6): 266-269, 282. (  0) 0)
|
| [13] |
王红梅, 付浩. 脉冲耦合神经网络自适应图像融合算法研究[J]. 计算机工程与应用, 2017, 53(7): 177-180. WANG Hongmei, FU Hao. Adaptive image fusion algorithm based on pulse coupled neural networks[J]. Computer engineering and applications, 2017, 53(7): 177-180. DOI:10.3778/j.issn.1002-8331.1509-0099 (  0) 0)
|
| [14] |
张宝华, 吕晓琪. 一种复合型PCNN的NSCT域多聚焦图像融合方法[J]. 小型微型计算机系统, 2014, 35(2): 393-396. ZHANG Baohua, LV Xiaoqi. Multi-focus image fusion algorithm based on compound PCNN in NSCT domain[J]. Journal of chinese computer systems, 2014, 35(2): 393-396. DOI:10.3969/j.issn.1000-1220.2014.02.039 (  0) 0)
|
| [15] |
DING Shifei, ZHAO Xingyu, XU Hui, et al. NSCT-PCNN image fusion based on image gradient motivation[J]. IET computer vision, 2018, 12(4): 377-383. DOI:10.1049/iet-cvi.2017.0285 ( 0) 0)
|
| [16] |
田娟秀, 刘国才. 基于NSST变换和PCNN的医学图像融合方法[J]. 中国医学物理学杂志, 2018, 35(8): 914-920. TIAN Juanxiu, LIU Guocai. Medical image fusion method based on non-subsampled shearlet transform and pulse coupled neural network[J]. Chinese journal of medical physics, 2018, 35(8): 914-920. DOI:10.3969/j.issn.1005-202X.2018.08.010 (  0) 0)
|
| [17] |
夏景明, 陈轶鸣, 陈轶才, 等. 基于稀疏表示和NSCT-PCNN的红外与可见光图像融合[J]. 电光与控制, 2018, 25(6): 1-6. XIA Jingming, CHEN Yiming, CHEN Yicai, et al. Fusion of infrared and visible images based on sparse representation and NSCT-PCNN[J]. Electronics optics and control, 2018, 25(6): 1-6. (  0) 0)
|
| [18] |
ZHANG Qiang, LI Baoxin. Discriminative K-SVD for dictionary learning in face recognition[C]//Proceedings of 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, USA, 2010: 2691–2698.
( 0) 0)
|
| [19] |
HONG Richang. Objective image fusion performance measure[J]. Military technical courier, 2000, 56(2): 181-193. ( 0) 0)
|
| [20] |
王峰, 程咏梅. 基于MNLMF和SF方向滤波的图像融合算法[J]. 控制与决策, 2017, 32(12): 2183-2189. WANG Feng, CHENG Yongmei. Image fusion method based on multi-scale non-local mean filter and shear direction filter[J]. Control and decision, 2017, 32(12): 2183-2189. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


