图像分割^[1]的本质是将图像中不同类目标按照要求划分成不同区域，用于解决相似特性像素的分类问题，使同类像素更可能划分为一类，它是图像处理和图像分析的一个重要环节。由于图像从三维目标投影为平面对象时会有信息损失，人眼对相邻灰度级的区分存在不确定性，从而使得模糊聚类^[2]在图像分割领域得到了广泛应用。目前，模糊C-均值(fuzzy c-means, FCM)^[3]聚类是图像分割中最常用的聚类方法之一，但该聚类所对应的划分信息仅采用隶属度表达样本分类程度大小，无法刻画样本归类中存在的不确定性和拒绝程度，导致该算法难以有效聚类复杂的非凸数据。针对这一不足，Chaira等^[4-5]将传统模糊C-均值聚类推广至直觉模糊集，提出直觉模糊聚类算法(intuitionistic fuzzy c-means, IFCM)，该算法不仅考虑了样本聚类的模糊隶属度，而且考虑了其隶属度的不确定性，使分类隶属度尽可能最大化并达到改善聚类性能的目的。但是，无原则地增大样本分类隶属度会导致样本误分的概率偏大，不利于光照不均匀、噪声干扰等复杂图像分割的需要。文献[6]将图形模糊集引入传统模糊C-均值聚类，对聚类过程中的图形模糊隶属度、中立度和拒分度进行规范约束，并得到一种称为图形模糊聚类算法(fuzzy clustering method on picture fuzzy sets, PFCM)^[6]，该聚类中的拒分度计算仅利用隶属度和中立度经Yager补算子获得，导致交替迭代所获得的隶属度、中立度和聚类中心出现负值，使聚类算法失效。Thong等^[7]提出了另一种新的图形模糊聚类算法(fuzzy clustering of picture fuzzy sets, FC-PFS)，该聚类性能相比现有FCM算法有一定程度提升。

图形模糊聚类被广泛应用于医学影像和气象云图的分割^[8-9]，但该聚类仅结合当前像素的的灰度信息，并未考虑当前像素的邻域像素空间信息和灰度信息对聚类的影响，导致该种算法对噪声的抑制能力较差。为此，文献[10]将文献[7]中的中立度和拒分度相结合，构造正则项幂积型表达式，并引入像素邻域灰度信息，提出一种具有鲁棒性的改进图形模糊聚类分割算法(PFCM with spatial constraints, PFCM_S1)，同理，可将此思想引入文献[7]，获得一种改进图形模糊聚类算法(FC-PFS with spatial constraints, FC-PFS_S1)，该算法采用欧氏距离构造聚类目标函数，将样本空间中相近的样本聚在一起，易于陷入局部极小值点且对初始化值较为敏感，主要适合于类样本数相差不悬殊的团状凸数据集，而对于那些非凸数据的聚类，其聚类性能存在显著下降^[11]。而核模糊C-均值(kernel-based fuzzy c-means clustering method, KFCM)聚类算法^[12]，能有效解决非凸数据聚类问题，它将样本数据通过非线性映射至高维特征空间并改善样本的可分性，从而达到改善聚类性能的目的。但是核函数的引入将增加算法时间复杂度，不利于实时性要求较高场合图像分割的需要。为此，Cai等^[13-14]提出了空间信息约束的快速FCM分割算法(fast generalized FCM, FGFCM)，该算法利用原始图像的每个像素邻域窗内的灰度和空间位置信息构造新的线性加权图像，然后在该图像的灰度直方图上进行图像聚类，减少运行时间，并且提高了抑制噪声能力，但无法改善该类分割算法的分割性能，不利于诸如医学和遥感等复杂场合的图像分割需要。

为了提高鲁棒图形模糊聚类分割法的分割性能和噪声抑制能力，并能降低大幅面遥感或医学等影像分割的时间开销，本文将PFCM_S1算法推广至核空间并与FGFCM分割算法相结合，提出一种改进的鲁棒核空间图形模糊聚类分割算法，并将像素与其邻域像素紧密关联的二维直方图引入新的鲁棒分割算法中，获得一种快速鲁棒核空间图形模糊聚类分割算法。测试结果表明，本文提出的算法能有效地提高大幅面图像分割速度；同时，相比现有的图形模糊聚类分割法能有更强的分割性能。

1 鲁棒图形模糊聚类

针对现有PFCM算法中的拒分度存在负值问题，导致隶属度、中立度和聚类中心出现非法值，且缺乏鲁棒抗噪性。文献[10]利用文献[7]有关中立度和拒分度的正则化思想并引入像素邻域均值信息，构造一种PFCM_S1算法，其最优化模型为

$\begin{array}{l} \!\!\min \;{{J}}({{U}},{{V}},{{\eta}} ,{{\xi}} ) \!=\! \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^c {{{(\displaystyle\frac{{{u_{i,k}}}}{{1 \!-\! {\eta _{i,k}} \!-\! {\xi _{i,k}}}})}^m}[{{({x_i} \!-\! {v_k})}^2}} } +\\ \;\;\;\;\;\;\;\; \alpha {({{\bar x}_i} - {v_k})^2}]{\rm{ + }}\displaystyle\sum\limits_{i{\rm{ = 1}}}^n {\displaystyle\sum\limits_{k{\rm{ = 1}}}^c {({\xi _{i,k}}\eta _{i,k}^{\rm{2}}{\rm{ + }}\xi _{i,k}^{\rm{2}}{\eta _{i,k}})} } \end{array}$

(1)

s.t.

1) $0 \leqslant {u_{i, k}} $ 、 ${\eta _{i, k}}$ 、 ${\xi _{i, k}} \leqslant 1,$ $0 \leqslant {u_{i, k}} + {\eta _{i, k}} + {\xi _{i, k}} \leqslant 1$ , $i = 1, 2, $ $\cdots, n, k = 1, 2, \cdots, c$ ；

2) $\displaystyle\sum\limits_{k = 1}^c {\displaystyle\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - {\xi _{i, k}}}}} = 1, i = 1, 2, \cdots, n;$

3) $\displaystyle\sum\limits_{k = 1}^c {({\eta _{i, k}} + \displaystyle\frac{1}{c}{\xi _{i, k}})} = 1, $ $i = 1, 2, \cdots, n$ 。

式中： $n$ 表示聚类样本数； $c$ 表示聚类数； ${u_{i, k}}$ 、 ${\eta _{i, k}}$ 和 ${\xi _{i, k}}$ 分别表示第 $i$ 个样本 ${x_i}$ 属于第 $k$ 类的隶属度、中立度和拒分度； ${x_i}$ 代表第 $i$ 个样本，其中 ${\bar x_i}$ 表示当前样本 ${x_i}$ 所对应的邻域窗内样本的均值； ${v_k}$ 代表第 $k$ 类的聚类中心， ${({x_i} - {v_k})^2}$ 为样本 ${x_i}$ 与聚类中心 ${v_k}$ 之间的欧氏距离平方， ${({\bar x_i} - {v_k})^2}$ 表示均值 ${\bar x_i}$ 和 ${v_k}$ 之间的欧氏距离平方； $m$ 是模糊指数，常取 $m = 2$ ； $\alpha $ 是描述像素邻域信息对当前像素聚类分割的影响参数。

2 鲁棒图形模糊聚类算法的改进 2.1 核空间鲁棒图形模糊聚类

针对最优化模型式(1)，它所对应的迭代聚类算法主要适合呈团状数据分析。为了增强该聚类模型对不同形状数据聚类的适应性，将数据样本通过非线性函数 $\varPhi ( \cdot )$ 映射至高维希尔伯特再生核空间，它与核函数之间具有内积关系 $K(x, y) =$ $ < \varPhi (x), \varPhi (y) > $ ，通过改变样本之间的空间分布结构，促使模糊聚类性能得到改善，相应的核空间鲁棒图形模糊聚类(kernel-based PFCM_S1, PKFCM_S1)最优化模型为：

$\begin{aligned} & \!\!\!\!\! \min \;{{J}}({{U}}, {{V}}, {{\eta}}, {{\xi}} ) = \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^c {{{(\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - {\xi _{i, k}}}})}^m}} } [d_\varPhi ^2({x_i}, {v_k})+\\ & \qquad\quad \alpha d_\varPhi ^2({\bar x_i}, {v_k})] + \sum\limits_{i = 1}^n {\sum\limits_{k = 1}^c {({\xi _{i, k}}\eta _{i, k}^2 + \xi _{i, k}^2{\eta _{i, k}})} } \end{aligned}$

(2)

式中：该模型约束条件与最优化模型式(1)相同， $d_\varPhi ^2({x_i}, {v_k}) = ||\varPhi ({x_i}) - \varPhi ({v_k})|{|^2}$ 表示 $\varPhi ({x_i})$ 和 $\varPhi ({v_k})$ 之间的平方欧氏距离； $d_\varPhi ^2({\bar x_i}, {v_k}) = ||\varPhi ({\bar x_i}) - \varPhi ({v_k})|{|^2}$ 表示均值 $\varPhi ({\bar x_i})$ 和 $\varPhi {v_k}$ 之间的平方欧氏距离； $\varPhi ({{\rm{{x}}}_i})$ 和 $\varPhi ({v_k})$ 分别表示样本 ${x_i}$ 和聚类中心 ${v_k}$ 在高维特征空间中的像。核函数 $K(x, y)$ 常选取高斯核函数 ${K_\sigma }(x, y) = \exp $ $( - {\sigma ^{ - 2}} \cdot ||x - y|{|^2})$ ( $\sigma $ 是核函数参数)，于是有 $d_\varPhi ^2({x_i}, {v_k}) = 2(1 - {K_\sigma }({x_i}, {v_k}))$ 成立，相应的优化求解式(2)所对应的隶属度、中立度和聚类中心迭代表达式分别为：

${u_{i, k}} = \displaystyle\frac{{1 - {\eta _{i, k}} - {\xi _{i, k}}}}{{\displaystyle\sum\limits_{j = 1}^c {{{\left( {\displaystyle\frac{{d_\varPhi ^2({x_i}, {v_k}) + \alpha d_\varPhi ^2({{\bar x}_i}, {v_k})}}{{d_\varPhi ^2({x_i}, {v_j}) + \alpha d_\varPhi ^2({{\bar x}_i}, {v_j})}}} \right)}^{\frac{1}{{m - 1}}}}} }}$

(3)

${\eta _{i,k}} = {\xi _{i,k}}(2{\eta _{i,k}} + {\xi _{i,k}})/(c({\eta _{i,k}} + 2{\xi _{i,k}}))$

(4)

${\xi _{i,k}} = 1 - ({u_{i,k}} + {\eta _{i,k}}) - {(1 - {({u_{i,k}} + {\eta _{i,k}})^\beta })^{1/\beta }}$

(5)

${v_k} = \displaystyle\frac{{\displaystyle\sum\limits_{i = 1}^n {{{\left(\displaystyle\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - \xi {}_{i, k}}}\right)}^m}({K_{{\sigma _1}}}({x_i}, {v_k}){x_i} + \alpha {K_{{\sigma _2}}}({{\bar x}_i}, {v_k}){{\bar x}_i})} }}{{\displaystyle\sum\limits_{i = 1}^n {{{\left(\displaystyle\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - \xi {}_{i, k}}}\right)}^m}({K_{{\sigma _1}}}({x_i}, {v_k}) + \alpha {K_{{\sigma _2}}}({{\bar x}_i}, {v_k}))} }}$

(6)

式中： $\beta \in (0, 1)$ 为调节因子； ${\sigma _1}$ 、 ${\sigma _2}$ 为不同高斯核函数参数。

可将模型式(2)推广至FGFCM算法中，获得一种快速核图形模糊聚类分割算法(fast generalized kernel-based PFCM, FGPKFCM)，从而使得聚类性能远优于FGFCM分割算法。

2.2 改进核空间鲁棒图形模糊聚类

为了进一步提高图形模糊聚类抑制噪声能力，将文献[13]中图像邻域像素平滑滤波信息推广至图形模糊聚类，相应的最优化模型为：

$\begin{array}{l} \min \;{{J}}({{U}}, {{V}}, {{\eta}}, {{\xi}} ) = \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^c {{{\left(\displaystyle\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - {\xi _{i, k}}}}\right)}^m}} } {d^2}({g_i}, {v_k})+\\ \qquad\qquad\qquad\quad \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^c {({\xi _{i, k}}\eta _{i, k}^2 + \xi _{i, k}^2{\eta _{i, k}})} } \end{array}$

(7)

式中 ${g_i}$ 表示当前样本 ${x_i}$ 所对应的邻域窗内所有样本估计所得的加权图像^[13]。

虽然最优化式(7)对噪声具有一定的抑制能力，但难以满足医学、遥感等复杂场合影像分割的需要。为此，将最优化模型式(2)和式(7)相结合，构造一种更强噪声抑制能力的鲁棒核空间图形模糊聚类分割算法，最优化模型表示为：

$\begin{array}{l} \min \;\;{{J}}({{U}}, {{V}}, {{\eta}}, {{\xi}} ) = \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^c {{{\left(\displaystyle\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - {\xi _{i, k}}}}\right)}^m}} } [d_\varPhi ^2({g_i}, {v_k})+\\ \;\;\;\;\;\;\;\;\;\; \alpha d_\varPhi ^2({\bar g_i}, {v_k})] + \displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{k = 1}^c {({\xi _{i, k}}\eta _{i, k}^2 + \xi _{i, k}^2{\eta _{i, k}})} } \end{array}$

(8)

式中： ${\bar g_i}$ 是当前样本 ${x_i}$ 所对应的邻域窗内所有 ${g_r}(r \in {N_i})$ 经均值估计所得。

针对最优化模型式(8)，核函数选取局部逼近能力的高斯核函数 $K{}_\sigma (x, y) = \exp ( - {\sigma ^{ - 2}} \cdot ||x - y|{|^2})$ ，则获得类似式(3)~(6)的迭代表达式，相应分割算法虽然能改善最优化模型式(2)的抑制噪声能力，但二者存在的共同不足是非常耗时，不利于大幅面的医学、遥感等影像快速分割的需要。

2.3 快速核空间图形模糊聚类

为了提高像素邻域信息加权图像分割法的快速性，将直方图模糊聚类^[14-15]引入线性加权图像鲁棒核空间图形模糊聚类，探索一种基于二维直方图的鲁棒核空间图形模糊聚类分割法。

假设大小为 ${M_1} \times {N_1}$ 的灰度图像 ${G}$ $ = {({g_{xy}})_{{M_1} \times {N_1}}}$ ，不同灰度级数为 $L$ ，采用 $3 \times 3$ 或 $5 \times 5$ 大小的邻域模板平滑所得图像为 ${G}'$ $ = {\left( {g_{xy}'} \right)_{{M_1} \times {N_1}}}$ 。图像 ${G}$ 与平滑滤波图像 ${G}'$ 相同位置不同像素对所对应的二维直方图描述如下：

${{H}}(i,j) = \sum\limits_{x = 1}^{{M_1}} {\sum\limits_{y = 1}^{{N_1}} {\delta ({g_{xy}} - i)} } \delta (g_{xy}' - j)$

(9)

它描述了图像 ${G}$ 与其平滑滤波图像 ${G}'$ 相同位置不同灰度级的分布情况，已广泛用于解决噪声干扰图像的鲁棒分割问题^[16-17]；同时，利用它可获得大幅面图像快速分割，对实时性要求高场合的目标跟踪与识别等具有较大实用价值。

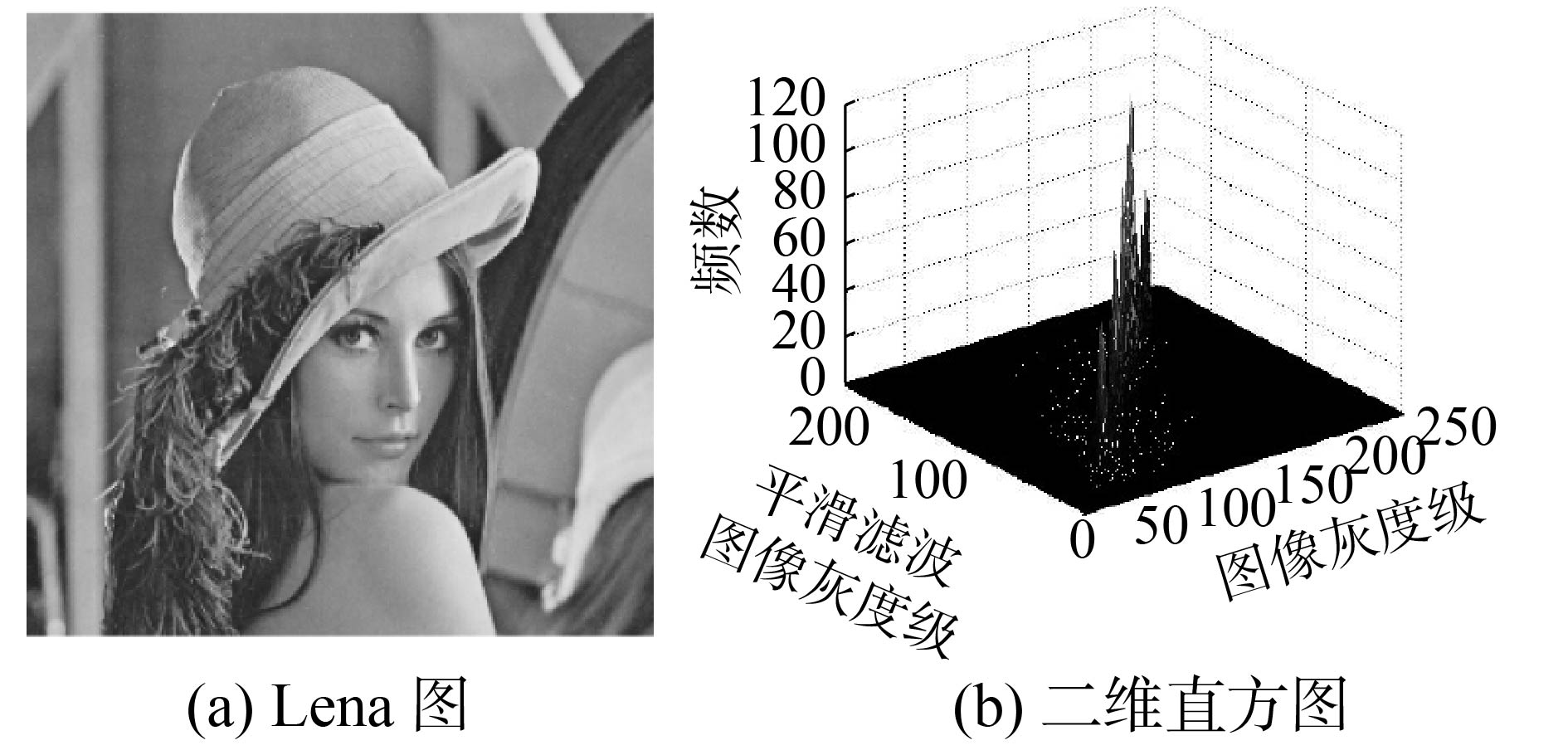
针对灰度Lena图像，与平滑滤波图像联合获得的二维直方图如图1所示。

由图1可见，该二维直方图描述了图像任意像素与其邻域像素滤波信息的空间分布关系，利用它可增强阈值分割或聚类分割等算法对噪声干扰的抑制能力。为此，本文将其应用于鲁棒图形模糊聚类分割算法，改善聚类分割算法的实时性，促使该算法在医学、遥感等领域的广泛应用。

针对鲁棒核空间图形模糊聚类分割最优化模型式(8)，将二维直方图引入并得到等价模型为：

$\begin{aligned} & \quad \min \;\;{{J}}({{U}}, {{V}}, {{\eta}}, {{\xi}} ) = \sum\limits_{i = 1}^{{M_1}} {\sum\limits_{j = 1}^{{N_1}} {\sum\limits_{k = 1}^c {{{\left(\frac{{{u_{{g_{ij}}, k}}}}{{1 - {\eta _{{g_{ij}}, k}} - {\xi _{{g_{ij}}, k}}}}\right)}^m}} } } \times\\ & [d_\varPhi ^2({g_{ij}}, {v_k}) + \alpha d_\varPhi ^2({\bar g_{ij}}, {v_k})] + \sum\limits_{i = 1}^{{M_1}} {\sum\limits_{j = 1}^{{N_1}} {\sum\limits_{k = 1}^c {({\xi _{{g_{ij, k}}}}\eta _{{g_{ij, k}}}^2 + \xi _{{g_{ij, k}}}^2{\eta _{{g_{ij, k}}}})} } }= \\ & \qquad \;\;\;\;\; \sum\limits_{i = 0}^{L - 1} {\sum\limits_{j = 0}^{L - 1} {\sum\limits_{k = 1}^c {{{H}}(i, j)} } } {\left(\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - \xi {}_{i, k}}}\right)^m} \times [d_\varPhi ^2(i, {v_k})+\\ & \qquad \quad \alpha d_\varPhi ^2(j, {v_k})] + \sum\limits_{i = 0}^{L - 1} {\sum\limits_{j = 0}^{L - 1} {\sum\limits_{k = 1}^c {{{H}}(i, j)({\xi _{i, k}}\eta _{i, k}^2 + \xi _{i, k}^2{\eta _{i, k}})} } } \end{aligned}$

(10)

s.t.

1) $0 \leqslant {u_{i, k}}$ 、 ${\eta _{i, k}}$ 、 ${\xi _{i, k}} \leqslant 1$ , $0 \leqslant {u_{i, k}} + {\eta _{i, k}} + {\xi _{i, k}} \leqslant 1, $ $0 \leqslant i \leqslant $ $L - 1$ , $1 \leqslant k \leqslant c$ ；

2) $ \displaystyle\sum\limits_{k = 1}^c {\displaystyle\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - {\xi _{i, k}}}}} = 1, \;\displaystyle\sum\limits_{k = 1}^c {({\eta _{i, k}} + \displaystyle\frac{1}{c}{\xi _{i, k}})} = 1$ , $ 0 \leqslant i \leqslant $ $L - 1$ ；

3) $0 < \displaystyle\sum\limits_{i = 0}^{L - 1} {{u_{i, k}}}, \displaystyle\sum\limits_{i = 0}^{L - 1} {{\eta _{i, k}}}, \displaystyle\sum\limits_{i = 0}^{L - 1} {{\xi _{i, k}}} < L, \;1 \leqslant k \leqslant c $ 。

式中： ${{g}} = {({g_{xy}})_{{M_1} \times {N_1}}}$ 是图像 ${{G}}$ $ = {({g_{xy}})_{{M_1} \times {N_1}}}$ 经式(8)利用像素邻域信息加权所得的； $\bar {{g}} = {({\bar g_{xy}})_{{M_1} \times {N_1}}}$ 是图像 ${{g}} =$ $ {({g_{xy}})_{{M_1} \times {N_1}}}$ 所对应邻域像素均值滤波图像，二维直方图 ${{H}}(i, j) = \displaystyle\sum\limits_{x = 1}^{{M_1}} {\displaystyle\sum\limits_{y = 1}^{{N_1}} {\delta ({g_{xy}} - i){\kern 1pt} } } \delta ({\bar g_{xy}} - j)$ 。

针对最优化模型式(10)，采用高斯核函数所对应的隶属度 ${u_{i, k}}$ 、中立度 ${\eta _{i, k}}$ 和聚类中心 ${v_k}$ 的迭代表达式为：

${u_{i, k}} = \displaystyle\frac{{1 - {\eta _{i, k}} - {\xi _{i, k}}}}{{\displaystyle\sum\limits_{q = 1}^c {{{\left( {\displaystyle\frac{{(1 - {K_{{\sigma _1}}}(i, {v_k})) + \alpha (1 - {K_{{\sigma _2}}}(j, {v_k}))}}{{(1 - {K_{{\sigma _1}}}(i, {v_q})) + \alpha (1 - {K_{{\sigma _2}}}(j, {v_q}))}}} \right)}^{\frac{1}{{m - 1}}}}} }}$

(11)

${\eta _{i,k}} = {\xi _{i,k}}(2{\eta _{i,k}} + {\xi _{i,k}})/c({\eta _{i,k}} + 2{\xi _{i,k}})$

(12)

${\xi _{i,k}} = 1 - ({u_{i,k}} + {\eta _{i,k}}) - {(1 - {({u_{i,k}} + {\eta _{i,k}})^\beta })^{1/\beta }}$

(13)

${v_k} = \displaystyle\frac{{\displaystyle\sum\limits_{i = 0}^{L - 1} {\displaystyle\sum\limits_{r = 0}^{L - 1} {{{H}}(i, r)} {{\left(\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - \xi {}_{i, k}}}\right)}^m}({K_{{\sigma _1}}}(i, {v_k})i + \alpha {K_{{\sigma _2}}}(r, {v_k})r)} }}{{\displaystyle\sum\limits_{i = 1}^{L - 1} {\displaystyle\sum\limits_{r = 0}^{L - 1} {{{H}}(i, r)} {{\left(\frac{{{u_{i, k}}}}{{1 - {\eta _{i, k}} - \xi {}_{i, k}}}\right)}^m}({K_{{\sigma _1}}}(i, {v_k}) + \alpha {K_{{\sigma _2}}}(r, {v_k}))} }}$

(14)

式中 ${\sigma _1}$ 和 ${\sigma _2}$ 利用加权和图像 ${G}$ $ = {({g_{xy}})_{{M_1} \times {N_1}}}$ 及邻域均值平滑图像 $\bar {{G}}$ $ = {({\bar g_{xy}})_{{M_1} \times {N_1}}}$ 的像素均方差进行估计。

利用上述迭代表达式可构造鲁棒核空间图形模糊聚类分割快速算法，其详细过程描述如下：

1)引入文献[13]思想，获取被分割原始图像 ${{G}}$ $ = {({g_{xy}})_{{M_1} \times {N_1}}}$ 所对应的加权图像 ${{g}} = {({g_{xy}})_{{M_1} \times {N_1}}}$ ，以及对加权图像获取局部均值滤波图像 $\bar {{g}} = {({\bar g_{xy}})_{{M_1} \times {N_1}}}$ 。

2)利用加权图像 ${{g}} = {({g_{xy}})_{{M_1} \times {N_1}}}$ 和局部均值滤波图像 $\bar {{g}} = {({\bar g_{xy}})_{{M_1} \times {N_1}}}$ 获取不同位置像素对所对应的二维直方图 ${{H}}(i, j),i, j = 0, 1, \cdots, L - 1$ 。

3)利用二维直方图 ${{H}}(i, j)$ 分别求出加权图像的高斯核函数参数 ${\sigma _1}$ 和局部均值滤波图像的高斯核函数参数 ${\sigma _2}$ 。

4)初始化聚类中心 $v_k^{(0)}$ 、选取聚类数 $c$ 、糊指数 $m$ 和迭代终止误差 $\varepsilon $ ，设置初始迭代次数 $t = 0$ ，最大迭代次数 ${t_{\max }} = 1\;000$ ，参数 $\alpha $ 和 $\beta $ 依经验选取适当值，其中 $\beta \in (0, 1)$ 。

5)利用式(11)、(12)和式(13)所对应的隶属度 ${u_{i, k}}$ 、中立度 ${\eta _{i, k}}$ 、拒分度 ${\xi _{i, k}}$ 迭代表达式，计算相应灰度级聚类模糊隶属度、中立度和拒分度值。

6)采用式(14)所对应的聚类中心 ${v_k}$ 迭代表达式，更新相应的聚类中心。

7)若 $\mathop {\max }\limits_{1 \leqslant k \leqslant c} \left\{ {|v_k^{(t + 1)} - v_k^{(t)}|} \right\} > \varepsilon $ 且 $t + 1 < T$ 时，执行迭代次数增加 $t = t + 1$ ，转5)；否则，聚类分割算法终止。

3 测试结果与分析

为了客观评价不同图形模糊聚类分割算法的聚类性能，将现有的图形复合基(picture composite cardinality，PCC)^[18]作为图形聚类性能好坏的评价指标，将其进行修改并定义为：

${\rm{PCC}} = \frac{1}{n}\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^c {{u_{i, k}}(1 - {\eta _{i, k}} - {\xi _{i, k}})} } $

(15)

一般而言，图形模糊聚类结果所对应的PCC值越小，则相应的模糊聚类性能越好，反之亦然。

将改进的峰值信噪比(peak signal to noise ratio, PSNR)^[19]作为量化指标来评价聚类算法抗噪性能强弱，其定义为：

${\rm{PSNR = 10}} \cdot {\log _{{\rm{10}}}}({\rm{25}}{{\rm{5}}^{\rm{2}}}{\rm{/}}{\rm{MSE}})$

(16)

式中： ${\rm{MSE}} = \displaystyle\frac{1}{{mn}}\displaystyle\sum\limits_{i = 1}^m {\displaystyle\sum\limits_{j = 1}^n {||{I_{ij}} - {K_{ij}}|{|^2}} } $ ， ${\rm{MSE}}$ 表示均方根误差； ${I_{ij}}$ 表示无噪声干扰图像分割结果的像素值； ${K_{ij}}$ 表示噪声干扰图像分割结果的像素值， $m \times n$ 表示图像大小。PSNR的值越大表明聚类分割算法抗噪性能越好，对噪声抑制能力越强。另外，为了定量分析不同聚类分割算法的分割效果，本文将误分率作为不同算法分割效果好坏的定量评定指标，其定义式为：

${\rm{ME}} = \left(1 - \sum\limits_{i = 1}^c {{A_i} \cap {B_i} \cdot {{\left(\sum\limits_{j = 1}^c {{B_j}} \right)^{ - 1}}}} \right) \times 100\text{%} $

(17)

式中： ${A_i}$ 表示分割算法所得图像中属于第 $i$ 类的像素点数； ${B_i}$ 表示无噪声理想分割图像中属于第 $i$ 类的像素点数； $c$ 表示图像分割总类别数。ME值越小表示分割结果与理想分割结果越相近，聚类分割算法结果越好；反之，聚类分割算法越差。

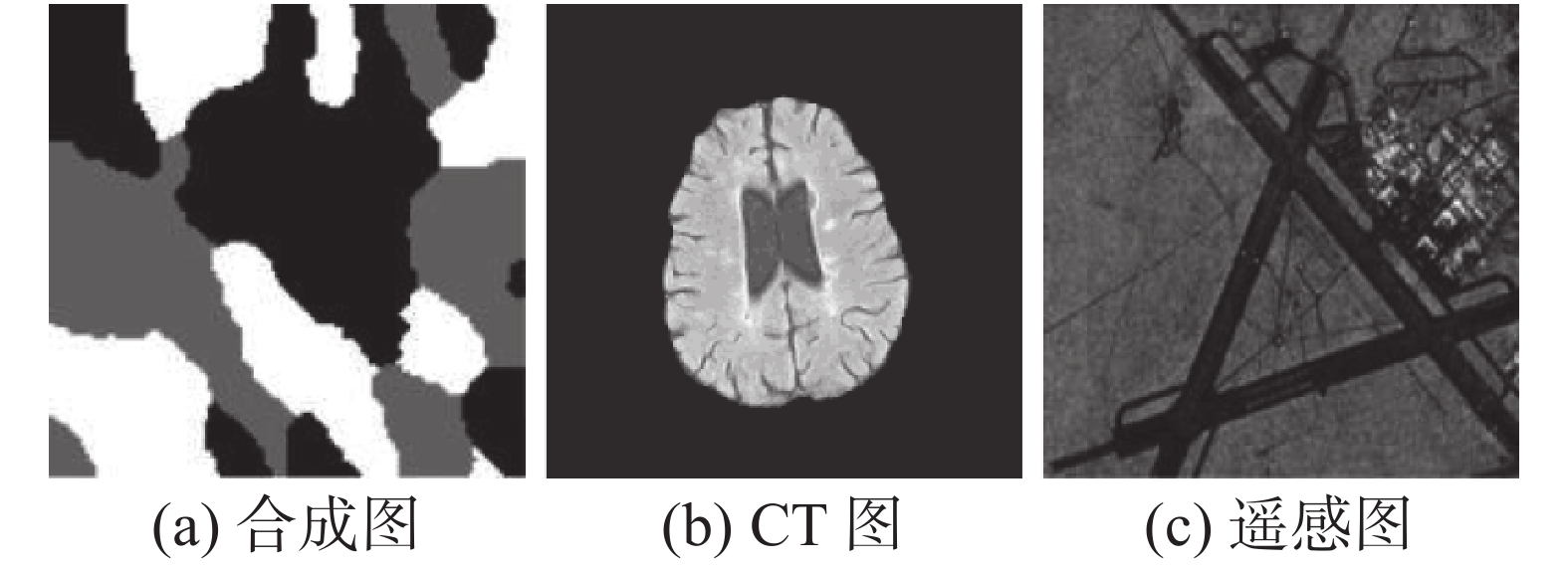
为了比较FC-PFS、PFCM、FC-PFS_S1、PFCM_S1、PKFCM_S1、FGPKFCM算法及本文算法的分割性能、噪声抑制能力、时间开销等差异性，文中选取大小为 $660 \times 660$ 的人工合成图、 $512 \times 510$ 的医学CT图和 $972 \times 804$ 的机场遥感图，如图2所示，对其添加不同强度的高斯和椒盐噪声，采用FC-PFS、PFCM、FC-PFS_S1、PFCM_S1、PKFCM_S1、FGPKFCM算法及本文算法对其分割测试，采用改进的图形复合基、峰值信噪比值和误分率定量评价不同算法的抗噪性能和分割性能，并统计不同算法收敛的时间开销，以便客观评价各算法执行效率。

3.1 高斯噪声干扰图像测试与分析

对图2中3幅标准灰度图像，分别添加均值为0且均方差为98、98和57(归一化方差分别为0.15、0.15、0.05)的高斯噪声，采用FC-PFS、PFCM、FC-PFS_S1、PFCM_S1、PKFCM_S1、FGPKFCM及本文算法对其分割测试，所得结果如图3所示，以及各算法聚类性能的图形复合基评价数值，如表1所示。

从表1的测试结果可知，本文算法的PCC值最小，说明本文算法的聚类性能更为优越。另外，从图3的分割结果可知，FC-PFS和PFCM算法所得分割结果被噪声污染较严重，存在明显噪声颗粒，而其他5种算法比FC-PFS和PFCM抗高斯噪声能力显著增强，其中，嵌入邻域像素灰度信息的图形模糊聚类算法FC-PFS_S1、PFCM_S1、PKFCM_S1及本文算法相比未嵌入邻域像素灰度信息的FC-PFS、PFCM聚类算法具有更强的鲁棒分割能力；同时，相比其他6种算法，文中提出的算法所得结果边缘更为清晰且颗粒噪声点明显减少。

为客观定量评价各算法抗噪声性能强弱，表2给出不同算法抑制高斯噪声的峰值信噪比值和分割误分率。从表2的峰值信噪比值和误分率可以看出，嵌入邻域信息的算法峰值信噪比值更高，而误分率更低，但相比其他6种算法，本文算法的峰值信噪比值(误分率)更高(低)，说明本文算法具有更强的鲁棒抗噪性和分割能力。

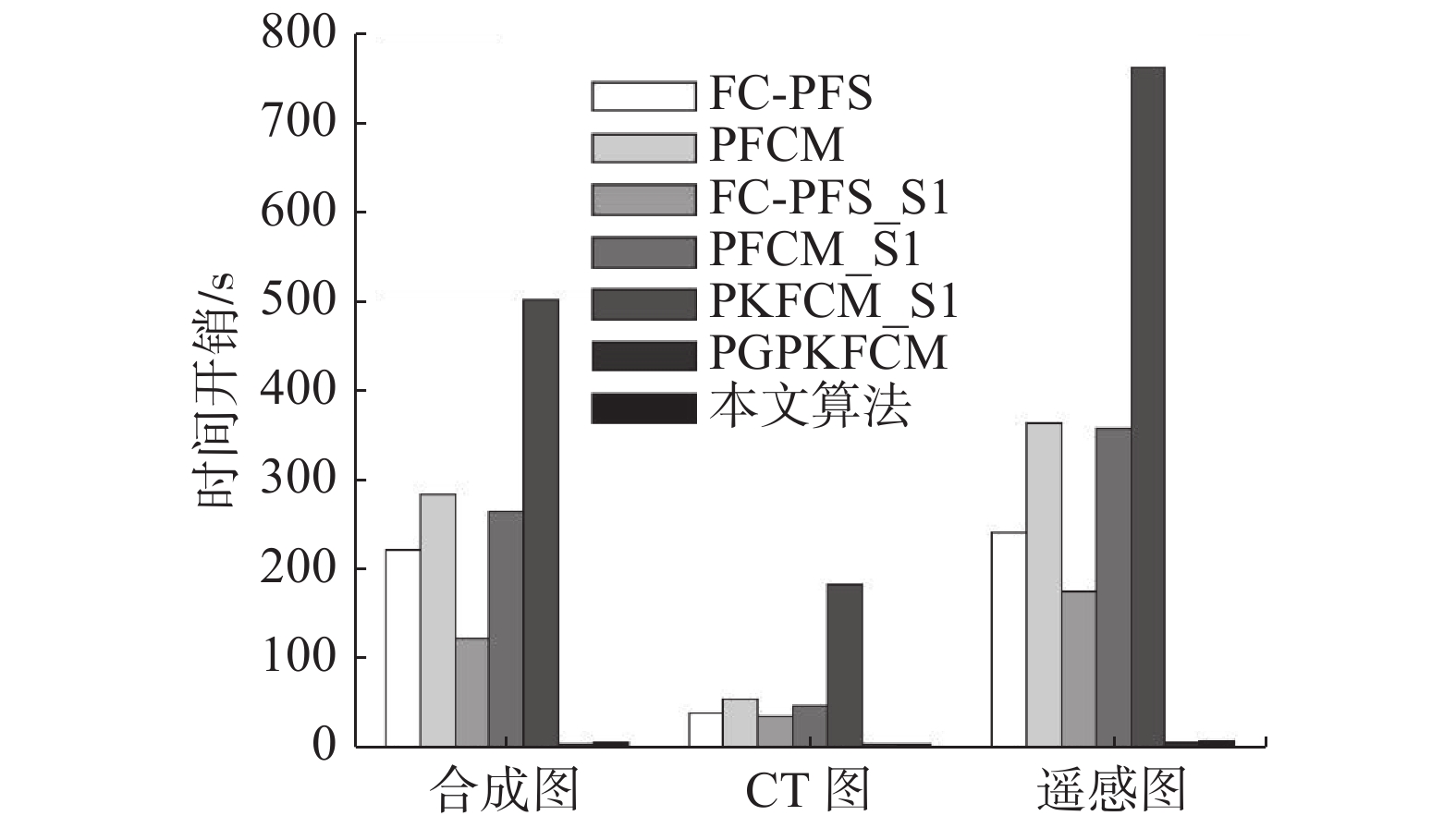
为了证实本文算法耗时少的优势，对图2中的3幅图像分别添加不同均方差的高斯噪声，采用上述7种算法进行分割测试，统计各算法的时间开销，所得结果如图4所示。

从图4可见，本文算法与FGPKFCM算法的时间开销相当，但与其他6种算法相比，本文算法的时间开销明显减少，说明本文算法有较好的执行效率。

3.2 椒盐噪声干扰图像测试与分析

对图2中3幅图像，分别添加30%、20%、30%大小椒盐噪声，采用FC-PFS、PFCM、FC-PFS_S1、PFCM_S1、PKFCM_S1、FGPKFCM算法及本文算法进行图像分割测试，所得结果如图5所示，以及各算法的聚类性能评价指标PCC值，如表3所示。

从图5所示的7种分割算法所得结果可知，含邻域均值信息的FC-PFS_S1、PFCM_S1、PKFCM_S1及本文算法相比FC-PFS和PFCM算法具有更强的抗椒盐噪声能力，分割结果存在的噪声颗粒明显减少，且本文算法相比其他6种算法所获得分割图像轮廓更为清晰并能保持原图像中丰富的细节信息。另外，从表3测试的图形复合基PCC值可以看出，本文算法的PCC值最小，说明它有更好的聚类性能。

为了进一步验证本文算法抗噪性和分割有效性，对图2中的3幅图像加入不同强度的椒盐噪声，采用上述7种算法进行分割测试，对其分割结果用峰值信噪比值和误分率进行评估，如表4所示。

从表4所示的评价结果可以看出，本文算法的峰值信噪比(误分率)明显增大(减小)，更接近理想的分割结果，相比其他6种分割算法，本文算法的抗噪性能和分割能力明显增强。

为客观评价各算法执行的时间效率，对图2中3幅图像，添加不同强度的椒盐噪声，分别采用上述7种算法进行分割测试，并统计各算法的时间开销，结果如图6所示。由图6可见，本文算法的时间开销和FGPKFCM算法相近，但相比其他5种算法，本文算法的时间开销明显减少，提高了运行效率，说明本文算法具有更好的实时性。

4 结束语

为了进一步提升基于核空间的鲁棒图形模糊聚类分割算法的鲁棒性和实时性，提出一种图像邻域像素平滑滤波信息的鲁棒核空间图形模糊聚类分割算法。同时，将当前聚类像素与其邻域像素均值所对应的二维直方图信息嵌入上述算法中，提出一种基于核空间的快速鲁棒图形模糊聚类分割算法。对大幅面图像在不同强度噪声干扰环境下进行分割测试，实验结果表明，本文所提算法在鲁棒性能和实时性能上均有所增强。