在机器学习中，特征选择从原始数据集中提取最具代表性子集，降低数据维度以提高后续分类、聚类处理精度，是当前研究的热点。按已标记数据样本数量划分，特征选择方法可分为监督、无监督和半监督学习。监督特征选择^[1-2]在已知数据集和类别标签上训练学习模型。在已获取大量已知标签时，该类方法能取得较好的识别效果。但在实际应用中获取大量已知标签较困难，且当已知标签数量不足时该类方法性能迅速下降。无监督特征选择方法^[3-4]通过对无标签数据的训练以发现其隐藏的结构性知识，但由于缺乏可区分性的标签信息导致学习性下降。近年来，半监督特征选择将少量已知标签数据与未标记数据结合建立学习模型，受到学者的广泛研究。Doquire等^[5]提出以数据方差为评价准则筛选出重要特征，但其忽略了特征间的相关性，易陷入局部最优。为解决此问题，研究者提出基于谱图理论的半监督方法，依据某准则建立Laplacian矩阵提取数据底层流形结构进行特征选择，如Liu等^[6]提出以迹比准则为评价机制，Ma等^[7]引入流形正则化的稀疏特征选择方法等。

在现实应用中，存在某个数据样本同时隶属于一个或多个不同的类别，如网页分类、自然场景分类等。以图像标注为例，一幅自然图像可包含多种场景，如树、陆地、沙漠，即一个图像样本可属于多种类别。最简单的解决方法将多标签簇问题分解为多个独立单标签分类问题，但其忽略了多标签间的相关性。为此，Ji等^[8]利用多标签的共享子空间建立学习框架，文献[9]使用互信息和交互信息的理论方法寻找最优子集，这些方法均属于监督类方法。但现实应用中大量训练样本中已标记数据极少。如何利用未标记数据及其之间的关系信息提高泛化性能，给多标签特征选择方法带来了巨大的挑战。针对此问题，研究者提出半监督多标签特征学习。Alalga等^[10]提出利用Laplacian得分判断多标签类间关系，但其利用l₂-范数建立Laplacian矩阵易受离群点的影响，从而导致学习稳定性差。Chang等^[11]提出基于全局线性约束的多标签半监督方法，无需构建Laplacian图和特征分解操作，计算量少，速度快，但其忽略了真实数据嵌入在高维空间的底层流形结构。受启于上述研究工作，本文提出基于l₁图的半监督多标签特征选择方法SMFSL (semi-supervised multi-label feature selection method based on L₁-norm graph)，利用全局线性回归函数方法和l_2,1组稀疏约束建立多标签特征选择模型，引用l₁图模型以提高特征选择准确度。

1 范数图模型

在机器学习中，基于图的学习方法通过构建近邻图，利用样本间反映流形分布而建立问题模型，得到广泛的研究应用。其中，基于谱图理论的谱聚类学习方法^[12]，在多种应用场景下取得较好的效果。

谱聚类根据数据样本间的相似关系建立Laplacian矩阵，利用特征值和特征向量获取样本间的内在联系。给定n组数据集X={x₁，x₂，···，x_n}∈R^d×n，其中x_i∈R^d为第i组数据，d为维度。定义G=(V，A)为无向权重图，其中V为向量集，相似矩阵A=[A₁ A₂ ··· A_n]∈R^n×n，A_ji=A_ij≥0。基于高斯核函数σ相似矩阵A定义为

$ {{A}_{ij}} = \left\{ \begin{array}{l} \exp \left( {\displaystyle\frac{{ - {{\left\| {{{x}_i} - {{x}_j}} \right\|}^2}}}{{{\sigma ^2}}}} \right),\;\;\;\;{{x}_i}\text{为}{{x}_j}\text{的近邻}\\ 0,\;\;\;\;\text{其他} \end{array} \right. $

(1)

式中：σ为宽度参数，控制函数的径向作用范围。

基于式(1)构造加权图，谱聚类算法将聚类问题转化为图划分问题，但其最优解为NP问题。传统解决方法以借助松弛方法得到连续的类别标签，进而转换为率切(ratio cut)问题：

$ \mathop {\min }\limits_{{{Q}^{\rm{T}}}{Q} = {I}} {\rm{Tr}}\left( {{{Q}^{\rm{T}}}{LQ}} \right) $

(2)

式中：Q=[q₁ q₂ ··· q_n]^T∈R^n×c为聚类指标矩阵，c为类别标签数，q_k∈R^c为Q矩阵第k列；L为谱图Laplacian矩阵，其定义为L=D-A，D为对角矩阵，其每个i对角元素 ${{D}_{ii}} = \sum\limits_{j = 1}^n {{{A}_{ij}}} $ 。为获取最终的类别标签，必须进一步借助聚类算法将连续值矩阵Q进行离散化，如采用K-means算法等。Nie等^[13]提出基于l₁范数图模型来获取更清晰的流形结构，上述式(2)转换为

$ \mathop {\min }\limits_{{{Q}^{\rm{T}}}{Q} = {I}} \mathop \sum \limits_{i,j = 1}^n {{A}_{ij}}{\left\| {{{q}_i} - {{q}_j}} \right\|_2} $

(3)

2 基于l₁图的半监督多标签特征选择方法 2.1 问题定义

给定数据集X=[x₁ x₂ ··· x_l x_l+1··· x_n]∈R^d×n，x_i∈R^d为第i组数据，d为维度，l为已标记样本数( $l \ll n$ )。设Y_l=[y₁ y₂ ··· y_l]^T∈R^l×c为已标记数据集的标签矩阵，y_i∈{0,1}^c为数据x_i的类别标签。若x_i被标识为j类，则Y_ij=1，否则Y_ij=0。为获取未标签数据的类别标签信息，定义预测标签矩阵 ${F} = {\left[ {{{f}_1}\;{{f}_2}\; \cdot \cdot \;{{f}_n}} \right]^{\rm{T}}} = \left[ \begin{array}{l}{{F}_l}\\{{F}_u}\end{array} \right] \in {{\bf{R}}^{{n} \times {c}}}$ ，其中F_l初始化为Y_l，F_u∈R^(n-l)×c则为未标签数据的标签矩阵，且初始化F_u=Ο，Ο为所有元素为0的矩阵。定义W=[w₁ w₂ ··· w_d]^T∈R^d×c为特征选择分类器，半监督多标签特征选择学习模型定义为

$ \mathop {\min }\limits_{{W},{F},{{F}_l} = {{Y}_l}} \mathop \sum \limits_{i = 1}^n {\rm{loss}}\left( {{W},{{f}_i}} \right) + \gamma {\rm{\Omega }}\left( {W} \right) $

(4)

在式(4)中，Ω(·)为正则化项(可以选择不同的正则化模型，如l₁范数、l_2,1范数等)，参数γ为正则化参数，loss(·)为损失函数。从模型的简单性、高效性角度进行考虑，本文选择最小二乘法作为损失函数，式(4)可表示为

$ \mathop {\min }\limits_{{W},{F},{b},{{F}_l} = {{Y}_l}} \left\| {{{X}^{\rm{T}}}{W} + {{\textit{1}}}{{b}^{\rm{T}}} - {F}} \right\|_F^2 + \gamma {\rm{\Omega }}\left( {W} \right) $

(5)

式中：b∈R^c为偏置量；1∈Rⁿ为元素值全是1的列向量。

从式(5)可以看出，利用线性回归函数逐渐逼近可找出全局最优，但却忽略了其局部数据之间相关性。为提高特征选择准确度，文献[7]提出建立相似矩阵以获取局部流形结构，建立的学习模型如下：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{W},{F},{b},{{F}_l} = {{Y}_l}} \displaystyle\sum \limits_{i,j = 1}^n {{A}_{ij}}\left\| {{{f}_i} - {{f}_j}} \right\|_2^2 + }\\ {\alpha \left\| {{{X}^{\rm{T}}}{W} + {{\textit{1}}}{{b}^{\rm{T}}} - {F}} \right\|_F^2 + \gamma {\rm{\Omega }}\left( {W} \right)} \end{array} $

(6)

式中α为平衡参数。

半监督学习应用中，已标签的数据集往往只占据小部分，无标签数据集非常庞大，而离群点一般存在无标签数据集中。Nie等^[13]研究证明，采用l₁范数有效减少噪音的影响，从而获取更清晰的谱聚类结构，因此本文提出将l₁范数引入半监督学习模型中。同时为减少外界噪声点的干扰，本文提出采用l_2,1范数^[3]来约束最小二乘损失函数。给定任意矩阵M∈R^d×c，其定义为 ${{M}_{2,1}} = \displaystyle\sum\limits_{i = 1}^d {\sqrt {\sum\limits_{j = 1}^c {{M}_{ij}^2} } }$ 。结合式(3)，式(6)转换为

$\begin{array}{*{20}{c}} \begin{array}{l} \mathop {\min }\limits_{{W},{F},{b},{{F}_l}{ = }{{Y}_l}} \displaystyle\sum \limits_{i,j = 1}^n {{A}_{ij}}{\left\| {{{f}_i} - {{f}_j}} \right\|_2} + \alpha {\left\| {{{X}^{\rm{T}}}{W} + {{\textit{1}}}{{b}^{\rm{T}}} - {F}} \right\|_{2,1}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \gamma \varOmega \left( {W} \right) \end{array} \end{array}$

为有效地去除原数据集的冗余特征，本文对特征选择矩阵W引入正则化模型l_2,1范数，最后提出的目标函数定义如下：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{W},{F},{b},{{F}_l} = {{Y}_l}} \displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{{f}_i} - {{f}_j}} \right\|}_2} + } {\alpha {{\left\| {{{X}^{\rm{T}}}{W} +{\textit{1}} {{b}^{\rm{T}}} - {F}} \right\|}_{2,1}} + r{{\left\| {W} \right\|}_{2,1}}} \end{array} $

(7)

2.2 学习模型求解

为获取最终选择特征子集，将对多标签特征选择的目标函数进行模型求解。由于目标函数式(7)引入的l_2,1范数具有非光滑特征，无法直接进行求解，因此本文提出一种迭代优化方法来解决。

首先，将目标函数(7)进行转换。定义对角矩阵S，其元素 ${{S}_{ii}} =\displaystyle \frac{1}{{2{{\left\| {{{X}^{\rm{T}}}{W} + {{\textit{1}}}{{b}^{\rm{T}}} - {F}} \right\|}_2} + \delta }}$ 。其中，为防止S_ii除数为0，δ的值为接近于0的正常量。式(7)转换后形式如下：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{W},{S},{F},{b},{{F}_l} = {{Y}_l}} {\rm{tr}}\left( {{{F}^{\rm{T}}}\tilde{ LF} + \alpha {{\left( {{{X}^{\rm{T}}}{W} + {{\textit{1}}}{{b}^{\rm{T}}} - {F}} \right)}^{\rm{T}}}} \right.}\\ {\left. {{S}\left( {{{X}^{\rm{T}}}{W} + {{\textit{1}}}{{b}^{\rm{T}}} - {F}} \right)} \right) + r{{\left\| {W} \right\|}_{2,1}}} \end{array} $

(8)

式中： $\tilde{ L}$ 为对角矩阵且定义为 ${\tilde{ L}} = {\tilde{ D}} - {\tilde{ A}}$ ；矩阵 $\tilde{ A}$ 元素定义为 ${\tilde{ A}_{ij}} = \displaystyle\frac{{{{A}_{ij}}}}{{2{{\left\| {{{f}_i} - {{f}_j}} \right\|}_2}}}$ ； $\tilde{ D}$ 为对角矩阵，元素值为 ${\tilde{ D}_{ii}} = \sum\nolimits_j {{{\tilde{ A}}_{ij}}} $ 。给定任意矩阵B∈R^n×n，对矩阵B迹函数定义 ${\rm{tr}}\left( {B} \right) = \sum\limits_{i = 1}^n {{{B}_{ii}}} $ ，B_ii为矩阵B的第i个对角元素。

保持W，S，F不变，将式(8)对b求导，令求导结果为0，得到：

$ {b}{\rm{ = }}\frac{1}{{{{{\textit{1}}}^{\rm{T}}}{S}{{\textit{1}}}}}\left( {{{F}^{\rm{T}}}{S} - {{W}^{\rm{T}}}{XS}} \right) $

(9)

将式(9)代入式(8)，为简化公式，令 ${H}{\rm{ = }}$ $\left( {{I} - \displaystyle\frac{1}{{{{{\textit{1}}}^{\rm{T}}}{S}{{\textit{1}}}}}{{\textit{1}}}{{{\textit{1}}}^{\rm{T}}}{S}} \right)$ ，其中H为中心化矩阵，I∈R^n×n为单位矩阵。式(8)将转换为：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{W},{S},{F}} {\rm tr}({{F}^{\rm{T}}}\tilde{ LF} + \alpha ({{\left( {{H}{{X}^{\rm{T}}}{W} - {HF}} \right)}^{\rm{T}}}{S}}\\ {{H}{{X}^{\rm{T}}}{W} - {HF})) + \gamma {{\left\| {W} \right\|}_{2,1}}} \end{array} $

(10)

将式(10)对W求导，并令求导结果为0，得到

$ \alpha {XHSH}{{X}^{\rm{T}}}{W} + \gamma {{D}_{\rm{W}}}{W} = \alpha {XHSHF} $

(11)

式中D_W为对角矩阵，可表示为

$ {{D}_W} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\frac{1}{{2{{\left\| {{{w}_1}} \right\|}_2} + \delta }}}&{}&{}\\ {}& \ddots &{}\\ {}&{}&{\displaystyle\frac{1}{{2{{\left\| {{{w}_d}} \right\|}_2} + \delta }}} \end{array}} \right] $

(12)

由于矩阵D_W与W相关，无法直接求解上式。为解决此问题，将W随机初始化以获取矩阵D_W，转换式(11)，推导出：

$ {W} = {\rm{\alpha }}{\left( {\alpha {XHSH}{{X}^{\rm{T}}} + \gamma {{D}_W}} \right)^{ - 1}}{XHSHF} $

(13)

为求解F，将式(10)进行变换，得到：

$ \begin{array}{l} \mathop {\min }\limits_{{W},{F}} {\rm tr}({{F}^{\rm{T}}}\tilde{ LF}) \!+\! \alpha {\rm tr}\left( {{{F}^{\rm{T}}}{HSHF}} \right) \!+\! \gamma {\rm{tr}}\left( {{{W}^{\rm{T}}}{{D}_{\rm{w}}}{W}} \right)\!+\\ \;\;\;\;\;\;\;\; \alpha {\rm tr}\left( {{{W}^{\rm{T}}}{XHSH}{{X}^{\rm{T}}}{W}} \right) - 2\alpha {\rm{tr}}\left( {{{F}^{\rm{T}}}{HSH}{{X}^{\rm{T}}}{W}} \right) \end{array} $

(14)

转换式(14)，得到：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{W},{F}} {\rm tr}({{F}^{\rm{T}}}\tilde{ LF}) + \alpha {\rm{tr}}\left( {{{F}^{\rm{T}}}{HSHF}} \right)}+\\ { {\rm{tr}}\left( {{{W}^{\rm{T}}}\left( {\alpha {XHSH}{{X}^{\rm{T}}} + \gamma {{D}_{\rm{w}}}} \right){W}} \right)}-\\ { 2\alpha {\rm{tr}}\left( {{{F}^{\rm{T}}}{HSH}{{X}^{\rm{T}}}{W}} \right)} \end{array} $

(14)

将W的求导结果式(13)代入式(15)，得到：

$ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{{F}} {\rm{tr}}({{F}^{\rm{T}}}\tilde{ LF}) + \alpha {\rm{tr}}\left( {{{F}^{\rm{T}}}{HSHF}} \right) - {\alpha ^2}{\rm{tr}}}\\ {\left( {{{F}^{\rm{T}}}{HSH}{{X}^{\rm{T}}}{{\left( {\alpha {XHSH}{{X}^{\rm{T}}} + \gamma {{D}_W}} \right)}^{ - 1}}{XHSHF}} \right)} \end{array} $

(15)

定义M为：

$ \begin{array}{*{20}{c}} {{M} = \tilde{ L} + \alpha {HSH} - }\\ {{{\left( {\alpha {XHSH}{{X}^{\rm{T}}} + \gamma {{D}_W}} \right)}^{ - 1}}{XHSH}} \end{array} $

(16)

将式(16)按分块矩阵形式转换为：

$ \mathop {\min }\limits_{{{F}_u}} {\rm{tr}}\left( {{{\left[ {\begin{array}{*{20}{c}} {{{F}_l}}\\ {{{F}_u}} \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{{M}_{ll}}}\\ {{{M}_{ul}}} \end{array}\begin{array}{*{20}{c}} {{{M}_{lu}}}\\ {{{M}_{uu}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{F}_l}}\\ {{{F}_u}} \end{array}} \right]} \right) $

将上式对F_u求导，并令求导结果为0，得到：

$ {{F}_u} = - {M}_{uu}^{ - 1}{{M}_{ul}}{{F}_l} $

基于以上推导过程求解学习模型，本文方法具体描述如下：

算法1　SMFSL

输入　数据集 ${X} \in {{\bf{R}}^{d \times n}}$ ，类别标签 ${{Y}_{{l}}} \in {{\bf{R}}^{l \times c}}$ ，相似矩阵A，参数 $\alpha ,\gamma $ ；

输出　特征选择矩阵W，预测标签矩阵F。

1) t=0，随机初始化W ^tϵR^d×c，b^tϵR^c，F ^tϵR^n×c

2) repeat

3) 计算 $\tilde{ L} = \tilde{ D} - \tilde{ A}$ ，其中 ${\tilde{ A}_{ij}} = \displaystyle\frac{{{{A}_{ij}}}}{{2{{\left\| {{f_i} - {f_j}} \right\|}_2}}}$ ， $\tilde{ D}$ 为对角矩阵，其元素值为 ${\tilde{ D}_{ii}} = \displaystyle\sum\nolimits_j {{{\tilde{ A}}_{ij}}} $

4) 计算对象矩阵 ${{S}^t}$ ，其第i个元素 ${{S}_{ii}}^t =$ $ \displaystyle\frac{1}{{2{{\left\| {{{X}^{\rm{T}}}{{W}^t} + {\textit{1}}{{({{b}^t})}^{\rm{T}}} - {{F}^t}} \right\|}_2} + \delta }}$

5) 计算H， ${H} = \left( {{I} - \displaystyle\frac{1}{{{{\textit{1}}^{\rm{T}}}{{S}^t}{\textit{1}}}}{{\textit{1}}}{{{\textit{1}}}^{\rm{T}}}{{S}^t}} \right)$

6) 根据式(12)计算对角矩阵 ${D}_w^t$

7) 根据式(17)计算 ${{M}^{t + 1}} = \tilde{ L} + \alpha {H}{{S}^t}{H} -{\alpha ^2}{H}{{S}^t}{H}{{X}^{\rm{T}}}$ $ {\left( {\alpha {XH}{{S}^t}{H}{{X}^{\rm{T}}} + \gamma {D}_w^t} \right)^{ - 1}}{XH}{{S}^t}{H}$

8) 计算 ${F}_u^{t + 1} \!=\! - {\left( {{M}_{uu}^{t + 1}} \right)^{ - 1}}{M}_{ul}^{t + 1}{{F}_l}$ ，并且更新 ${{F}^{t + 1}} =$ $ \left[ \begin{array}{l}{{F}_{\rm{l}}}\\{F}_u^{t + 1}\end{array} \right]$

9) 更新

$ {{W}^{t + 1}} = {\rm{\alpha }}{\left( {\alpha {XH}{{S}^t}{H}{{X}^{\rm{T}}} + \gamma {D}_w^t} \right)^{ - 1}}{XH}{{S}^t}{H}{{F}^{t + 1}} $

10) 更新

$ {{b}^{t + 1}} = \frac{{ 1}}{{{{{\textit{1}}}^{\rm{T}}}{{S}^t}{{\textit{1}}}}}\left( {{{\left( {{{F}^{t + 1}}} \right)}^{\rm{T}}}{{S}^t}{{\textit{1}}} - {{\left( {{{W}^{t + 1}}} \right)}^{\rm{T}}}{X}{{S}^t}{{\textit{1}}}} \right) $

11) t=t+1

12) until 收敛

在得到特征选择矩阵W后，按照 ${\left\| {{w}_i^t} \right\|_2}$ $\left( {i = 1,2, \cdots ,d} \right)$ 的值，对输入数据的特征进行降序排列，其中最前面的p个特征即为所选择的特征。

2.3 收敛性分析

本小节将对上一小节提出的SMFSL算法收敛性进行证明。

引理1　对于任意非零的向量p,q∈R^c，有以下不等式成立：

$ {\left\| {p} \right\|_2} - \frac{{\left\| {p} \right\|_2^2}}{{2{{\left\| {q} \right\|}_2}}} \leqslant {\left\| {q} \right\|_2} - \frac{{\left\| {q} \right\|_2^2}}{{2{{\left\| {q} \right\|}_2}}} $

(17)

根据以上引理，本文提出以下定理：

定理1　算法SMFSL在每次迭代过程中最小化目标函数。

证明　为方便起见，首先定义g(W,F,b^T,S)=αtr((X^TW+1b^T-F)^TS(X^TW+1b^T-F)) 。目标函数可写为：

$ \mathop {\min }\limits_{{W},{F},{b}} \mathop \sum \limits_{i,j = 1}^n {\tilde{ A}_{ij}}\left\| {{{f}_i} - {{f}_j}} \right\|_2^2 + \gamma {\left\| {W} \right\|_{2,1}} + g\left( {{W},{F},{{b}^{\rm{T}}},{S}} \right) $

假设在第t次迭代后获得了W，F,b^T和S。在下一次迭代中，固定W为W ^t、b为b^t、S为S^t来求解F ^t+1，参考文献[14]中的方法可得出：

$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\displaystyle \sum \limits_{i,j = 1}^n {{({{\tilde{ A}}^t})}_{ij}}\left\| {{f}_i^{t + 1} \!- \! {f}_j^{t + 1}} \right\|_2^2}+\!\! { \gamma {{\left\| {{{W}^t}} \right\|}_{2,1}} \!\!+\! g\left( {{{W}^t},{{F}^{t + 1}},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)}\leqslant \end{array}}\\ {\begin{array}{*{20}{c}} { \displaystyle \sum \limits_{i,j = 1}^n {{({{\tilde{ A}}^t})}_{ij}}\left\| {{f}_i^t - {f}_j^t} \right\|_2^2}+ { \gamma {{\left\| {{{W}^t}} \right\|}_{2,1}} + g\left( {{{W}^t},{{F}^t},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)} \end{array}} \end{array} $

(18)

将 ${({\tilde{ A}^t})_{ij}} = \displaystyle\frac{{{{A}_{ij}}}}{{2{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2}}}$ 代入式(19)，得到：

$ \begin{array}{l} \displaystyle\sum \limits_{i,j = 1}^n \displaystyle\frac{{{{A}_{ij}}\left\| {{f}_i^{t + 1} - {f}_j^{t + 1}} \right\|_2^2}}{{2{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2}}} + \gamma {\left\| {{{W}^t}} \right\|_{2,1}}+ g\left( {{{W}^t},{{F}^{t + 1}},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)\leqslant \\ \begin{array}{*{20}{c}} {\displaystyle \sum \limits_{i,j = 1}^n}{ \displaystyle\frac{{{{A}_{ij}}\left\| {{f}_i^t - {f}_j^t} \right\|_2^2}}{{2{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2}}} + \gamma {{\left\| {{{W}^t}} \right\|}_{2,1}}} { + g\left( {{{W}^t},{{F}^t},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)} \end{array} \end{array} $

(19)

结合引理1的式(18)，有以下公式：

$ \begin{array}{*{20}{c}} {\displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}\left( {{{\left\| {{f}_i^{t + 1} - {f}_j^{t + 1}} \right\|}_2} - \displaystyle\frac{{\left\| {{f}_i^{t + 1} - {f}_j^{t + 1}} \right\|_2^2}}{{2{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2}}}} \right)}\leqslant\\ { \displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}\left( {{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2} - \displaystyle\frac{{\left\| {{f}_i^t - {f}_j^t} \right\|_2^2}}{{2{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2}}}} \right)} \end{array} $

(20)

结合式(20)和(21)，得到

$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{f}_i^{t + 1} - {f}_j^{t + 1}} \right\|}_2} + } {\gamma {{\left\| {{{W}^t}} \right\|}_{2,1}} + g\left( {{{W}^t},{{F}^{t + 1}},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)}\leqslant \end{array}}\\ {\begin{array}{*{20}{c}} { \displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2} + } {\gamma {{\left\| {{{W}^t}} \right\|}_{2,1}} + g\left( {{{W}^t},{{F}^t},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)} \end{array}} \end{array} $

(21)

接下来，固定F为F ^t+1、b为b^t、S为S^t来求解W ^t+1，根据算法1可得出：

$ \begin{array}{*{20}{c}} {{{W}^{t + 1}} = {\rm arg}\mathop {\min }\limits_{{W}} \displaystyle \sum \limits_{i,j = 1}^n {{({{\tilde{ A}}^t})}_{ij}}\left\| {{f}_i^{t + 1} - {f}_j^{t + 1}} \right\|_2^2}+\\ { \gamma {{\left\| {{{W}^t}} \right\|}_{2,1}} + g\left( {{{W}^t},{{F}^{t + 1}},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)} \end{array} $

同样，参考文献[14]中的方法，可得出：

$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{f}_i^{t + 1} \!-\! {f}_j^{t + 1}} \right\|}_2} \!+\! \gamma {{\left\| {{{W}^{t + 1}}} \right\|}_{2,1}}} { \!\!+\!\! g\left( {{{W}^{t + 1}},{{F}^{t + 1}},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)}\leqslant \end{array}}\\ {\begin{array}{*{20}{c}} { \displaystyle\sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{f}_i^{t + 1} - {f}_j^{t + 1}} \right\|}_2} + \gamma {{\left\| {{{W}^t}} \right\|}_{2,1}}} { + g\left( {{{W}^t},{{F}^{t + 1}},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)} \end{array}} \end{array} $

(22)

接下来，固定F为F ^t+1、W为W ^t+1求解b^t+1、S ^t+1，同样，参考文献[14]中的方法，可得出：

$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\displaystyle\sum \limits_{i,j \!= 1}^n {{A}_{ij}}{{\left\| {{f}_i^{t \!+\! 1} \!\!-\!\! {f}_j^{t \!+\! 1}} \right\|}_2} \!+\! \gamma {{\left\| {{{W}^{t \!+\! 1}}} \right\|}_{2,1}}} { \!\!+\!\! g\left( {{{W}^{t \!\!+\! 1}},{{F}^{t + 1}},{{({{b}^{t \!+\! 1}})}^{\rm{T}}},{{S}^{t + 1}}}\! \right)}\leqslant \end{array}}\\ {\begin{array}{*{20}{c}} { \displaystyle\sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{f}_i^{t + 1} - {f}_j^{t + 1}} \right\|}_2} + \gamma {{\left\| {{{W}^t}} \right\|}_{2,1}}} { + g\left( {{{W}^t},{{F}^{t + 1}},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)} \end{array}} \end{array} $

(23)

最后，结合式(22)、(23)和(24)，可得出：

$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{f}_i^{t + 1} \!-\! {f}_j^{t + 1}} \right\|}_2} \!\!+\!\! \gamma {{\left\| {{{W}^{t + 1}}} \right\|}_{2,1}}} { \!\!+\! g\left( {{{W}^{t + 1}},{{F}^{t + 1}},{{({{b}^{t + 1}})}^{\rm{T}}},{{S}^{t + 1}}} \right)} \end{array}}\\ {\begin{array}{*{20}{c}} {\leqslant \displaystyle \sum \limits_{i,j = 1}^n {{A}_{ij}}{{\left\| {{f}_i^t - {f}_j^t} \right\|}_2} + \gamma {{\left\| {{{W}^t}} \right\|}_{2,1}}} { + g\left( {{{W}^t},{{F}^t},{{({{b}^t})}^{\rm{T}}},{{S}^t}} \right)} \end{array}} \end{array} $

(24)

从式(25)中可证明出算法1是收敛的。

3 实验分析 3.1 对比方法及实验数据

为验证本文方法的有效性，对相关方法进行描述。

All-feature：其数据未采用特征选择，本次实验以该分类结果作为基准线。

TRCFS(trace ratio criterion for feature selection)^[6]：采用谱图的半监督学习方法，其通过引入具有抗噪声的率切准则提高特征选择的效率。

CSFS(convex semi-supervised multi-label feature selection)^[12]：该将线性回归模型引入特征选择模型中，是一种快速的半监督特征选择方法。

FSNM(feature selection via joint l_2,1-norms minimization)^[1]：监督学习方法，其在损失函数和正则化方面采用l_2,1范数模型进行特征选择。

本次实验将所提出方法应用到各种场景，包括自然场景分类、网页分类和基因功能分类。同时本文将各方法应用到多种开源数据库，包括MIML^[15]、YEAST^[16]、Education^[17]和Entertainment^[17]，数据集的相关属性描述如表1所示。

本文对于每一种方法所有涉及到的参数(如果有的话)的范围设定为{10⁻⁴、10⁻²、10⁰、10²、10⁴}。对于每种数据集，随机选择n个样本作为训练集，其中分别选择10%、20%和40%的数据为已标记数据集，其余为未标记数据。实验独立重复5次，最后取其平均值。本次实验选择MLKNN作为多标签分类器，其中MLKNN的优化参数参照文献[18]。

3.2 性能对比分析

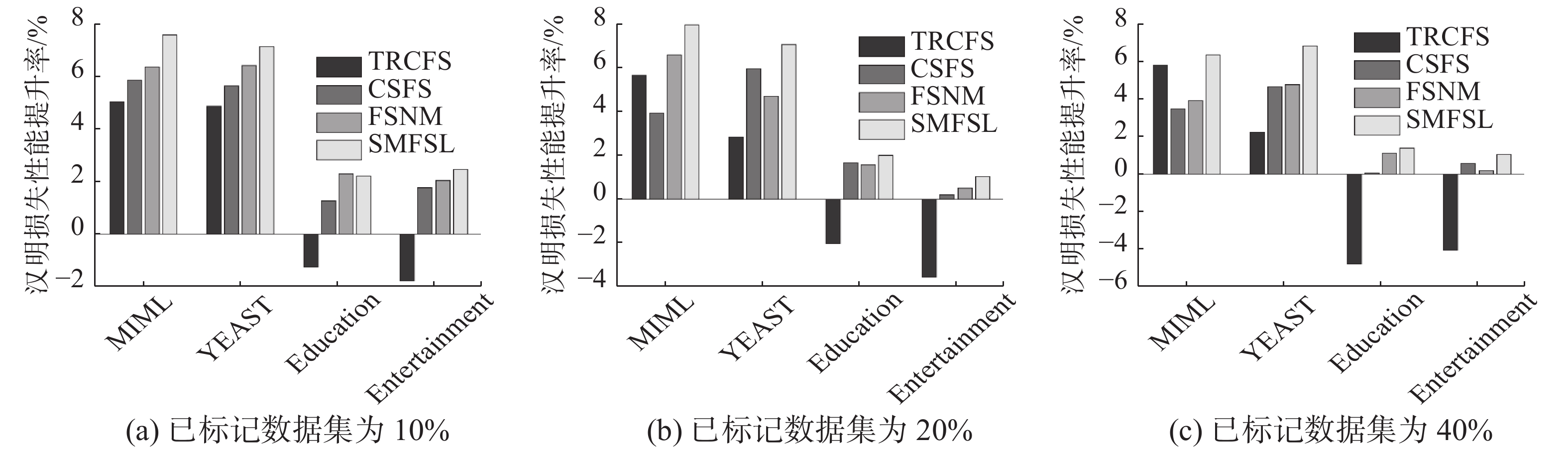
本次实验选择Hamming loss(HL，汉明损失)、One-Error(OE，单错误)作为评价指标^[19]用来评价方法的分类性能。其中，Hamming loss和One Error值越低代表性能越好。图1、2列出了以All-feature方法的分类结果为基准线，TRCFS、CSFS、FSNM以及本文提出的SMFSL方法在各种数据集的性能对比分析。其中图1分别为HL评价标准的性能提升百分比，以及图2分别为OE评价标准的性能提升百分比。从图中可以看出：

1) 大部分特征选择方法要优于未采用特征选择的All-feature，由此可证明特征选择有助于提高多标记学习性能。但在YEAST、Education和Entertainment数据集中，TRCFS学习性能整体略低于All-feature，但该方法经过特征选择后维度会有所降低，从而能有效地节省后续分类时间。

2) CSFS在部分数据集上表现略差于FSNM，这是由于CSFS方法采用l₂范式损失函数，对噪声较敏感。当无标签数据集比例较大时，噪声较多，CSFS的分类性能受噪声影响较大。而当已标记数据集比例增加时，其与FSNM差距越小。

3) 本文提出的SMFSL方法优于其他方法，由此可证明采用l_2,1范式约束全局回归函数能有效减少外界噪声影响，同时结合l₁图建立相似矩阵能有效获取底层局部流形结构，提高分类性能。

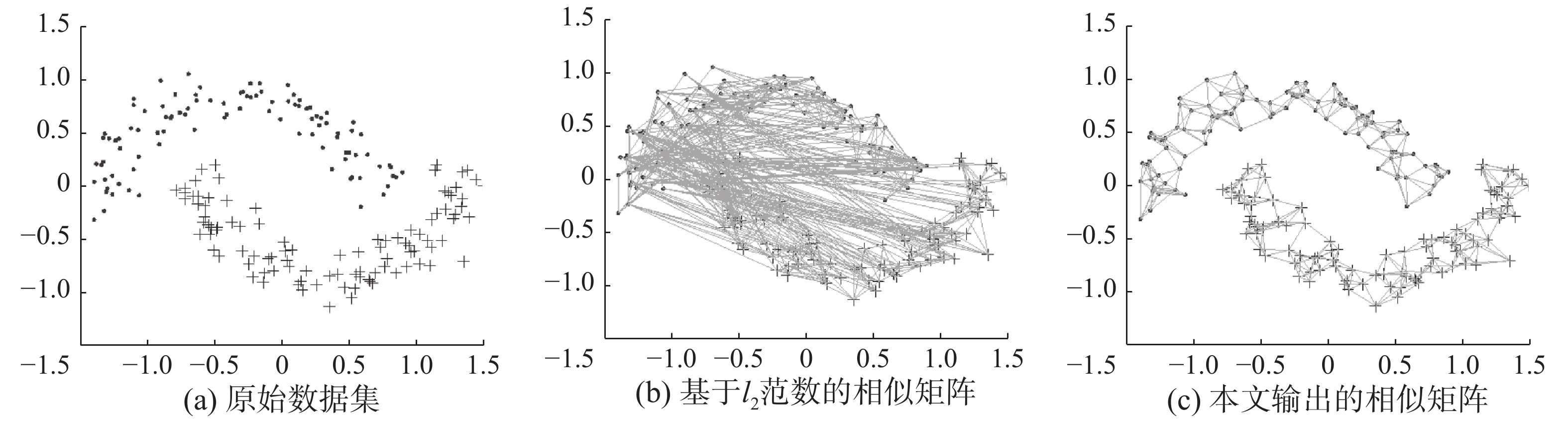
3.3 模型鲁棒性分析

为验证本文所提出模型的鲁棒性，本次实验针对不同类型相似矩阵进行对比分析。实验采用如图3(a)所示的双月(two-moon)数据集。该数据集可分为上半月形和下半月形2个类别数据，具有明显的流形结构。基于l₂范数的相似矩阵如图3(b)所示，其中任意2个数据间的连线代表其具有相似性。从图中可以看出，该相似矩阵存在过多冗余连接，无法提取清晰的流形结构信息，很难直接应用于后续对数据的分类任务。本文模型输出的相似矩阵如图3(c)所示，可明显看出，在l₁范数稀疏性约束下，该相似矩阵可有效剔除数据间的无关连接，提取更加清晰的流形结构信息，进而有助于提高分类模型的准确性和对外界噪声的抗干扰性。

3.4 特征数对分类性能的影响

本次实验挑选了MIML、YEAST和Education数据集在已标记样本集为20%时，选择不同特征数的Average Precision(AP，平均查准率)性能^[19]对比效果，具体如图4所示。据文献[19]得知，AP值越高，表示方法性能越好。从图中可以看出，MIML、YEAST、Education数据集在选择特征数分别为40、80和400时AP值最高。这意味着选择最大特征数并不一定能产生最高的AP值。在给定不同的特征数量时，本文所提方法普遍高于其他方法，尤其是在MIML和Education数据集优势更加明显。另外，从图中看出不同方法的结果曲线出现交叉，这是由于不同方法所选择出的最优特征子集不同，其对应的分类准确度也会有所不同。

3.5 参数敏感性分析

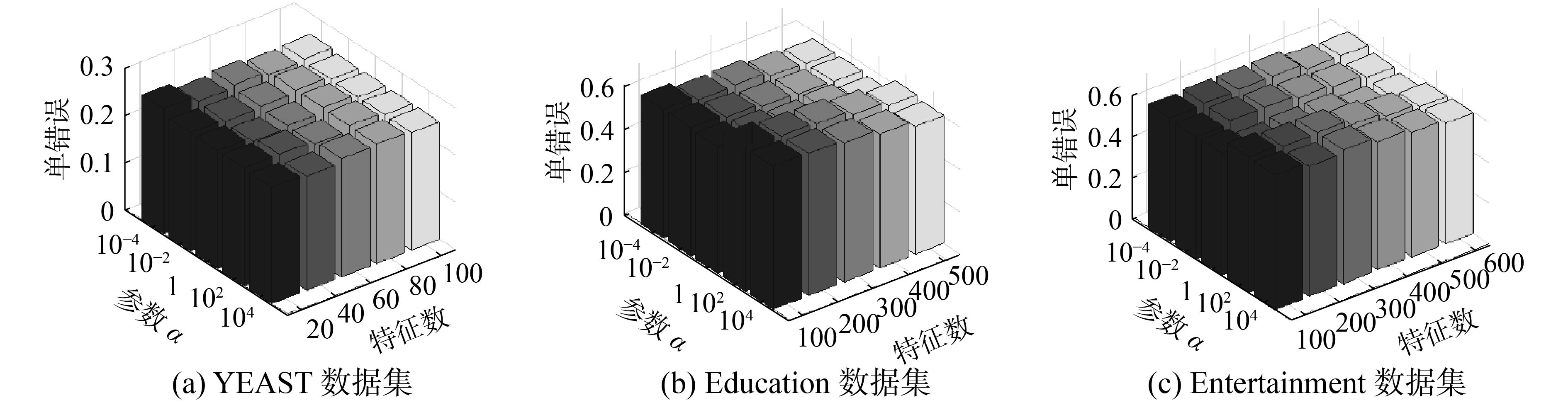
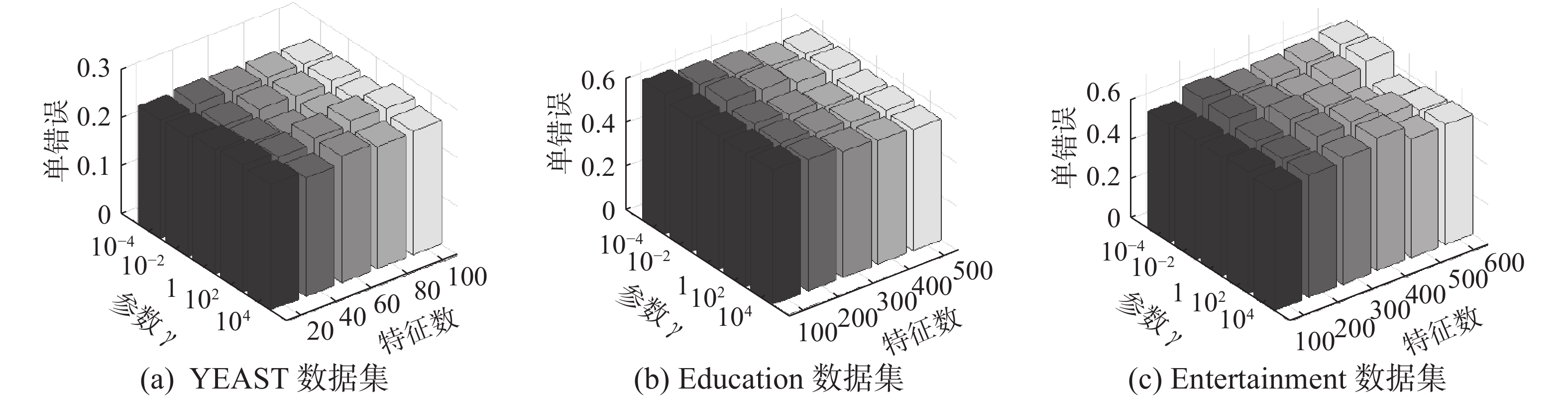
本次实验将对学习模型中涉及的参数进行具体分析。为节省篇幅，本次实验挑选YEAST、Education和Entertainment在已标记数据为40%、评价标准为One Error的性能分析。首先，固定α值为1，即参数调节范围的中位数，调整γ和特征数进行分析，结果如图5所示。同样，固定参数γ的值为1，对α和特征数的变化进行分析，具体如图6所示。从图5、图6可以看出，参数α、γ的选择依赖于所选数据集，如Entertainment数据集在固定α、特征数为600时，选择γ=10⁻⁴时One Error性能最佳，而当γ=1该性能表现最差。因此在实验测试时需对不同的数据集设置不同的参数。

4 结束语

本文提出一种鲁棒的半监督多标签特征选择方法SMFSL。不同于传统基于谱图的特征选择方法，本文方法利用l_2,1范数约束全局线性回归函数，减少外界噪声干扰，还借助l₁图获取更清晰的数据底层流形结构，有效提取局部特征，以提高学习效率。为提高特征选择准确度，本文引入l_2,1范数约束特征选择过程，有效利用特征间相关信息，进而过滤冗余特征。文中所提出的模型涉及l_2,1范数具有非光滑特征，无法直接对其求闭合解，因此提出一套快速有效迭代方法求解学习模型。最后通过多个开源数据集实验证明了本文方法的有效性。结合自适应学习及采用鲁棒性更好的损失函数以进一步提高特征选择的准确度，为本文的下一步研究目标。