轨迹规划是机器人运动控制的核心[1],旨在确定机器人末端执行器在其工作空间的轨迹[2]。轨迹规划分为关节空间轨迹规划和笛卡尔空间轨迹规划。关节空间轨迹规划算法具有约束条件少和计算速度快等优势,但存在空间轨迹不直观和轨迹形状会随速度不同而改变等缺点[3-5]。笛卡尔空间轨迹规划描述路径准确,可以直观地观测到机械手末端的运动轨迹。笛卡尔空间轨迹规划包括位姿规划和速度规划,即通过设计机器人末端位置和姿态的数学表达式,并结合加减速控制模型加以实现[6]。
目前机器人系统中常用的速度规划算法有梯型速度规划算法和S型速度规划算法。后者因其速度曲线形如S状而得名,广泛应用于高速、高精度的加工系统[7]。Hu等[8]通过梯型速度规划方法控制机床,验证加速度的不连续变化会引起振动和冲击。史步海等[9]提出一种等价梯型的新型S型速度规划算法,算法简单,一定程度上降低机械冲击,但实质上仍属于梯型速度规划。Jahanpour等[10]针对加速度的不连续变化,研究一种基于S型的速度曲线的轨迹规划方法,但未考虑路径约束下会对速度规划参数的影响。
本文以机械手笛卡尔空间的轨迹规划为目标,建立空间直线和圆弧插补运动的位姿模型。采用S型加减速控制模型,并根据路径长度和始末速度等约束条件,将S型速度规划分4种类型。将算法集成于自主研发的六自由度机械手实时控制平台中,验证了本文算法的有效性和合理性。
1 S型速度规划常用的七段式S型速度曲线由加加速阶段、匀加速阶段、减加速阶段、匀速阶段、加减速阶段、匀减速阶段、减减速阶段组成。本文根据路径长度和始末速度等约束条件将S型速度曲线分4种类型,如图1所示。

|
Download:
|
| 图 1 S型速度规划 Fig. 1 S-type speed planning | |
图1中,
| ${s_1} = \frac{{Jv_{\max }^2 + v_{\max }^{}a_{\max }^2}}{{2Ja_{\max }^{}}}$ | (1) |
| ${s_2} = \frac{{a_{\max }^3}}{{{J^2}}}$ | (2) |
式中:
类型一 七段式。若
七段式分段用时分别为
| ${T_1} = {T_3} = {T_5} = {T_7} = \frac{{{a_{\max }}}}{J}$ | (3) |
| $ {T_2} = {T_6} = \frac{{{v_{\max }}}}{{{a_{\max }}}} - \frac{{{a_{\max }}}}{J} $ | (4) |
| ${T_4} = \frac{{s - 2{s_1}}}{{{v_{\max }}}}$ | (5) |
七段式速度函数为
| $v(t) = \left\{ \begin{array}{l} \displaystyle\frac{1}{2}J{t^2}, \qquad t < {T_1}\\ \displaystyle\frac{1}{2}JT_1^2 + {a_{\max }}(t - {T_1}), \\ \qquad{T_1} < t < \displaystyle\sum\limits_{i = 1}^2 {{T_i}} \\ {v_{\max }} - \displaystyle\frac{1}{2}J{\left(\displaystyle\sum\limits_{i = 1}^3 {{T_i}} - t\right)^2},\\ \qquad\displaystyle\sum\limits_{i = 1}^2 {{T_i}} < t < \sum\limits_{i = 1}^3 {{T_i}} \\ {v_{\max }}, \qquad \displaystyle\sum\limits_{i = 1}^3 {{T_i}} < t < \displaystyle\sum\limits_{i = 1}^4 {{T_i}} \\ {v_{\max }} - \displaystyle\frac{1}{2}J{\left(t - \displaystyle\sum\limits_{i = 1}^4 {{T_i}} \right)^2}, \\ \qquad \displaystyle\sum\limits_{i = 1}^4 {{T_i}} < t < \displaystyle\sum\limits_{i = 1}^5 {{T_i}} \\ {v_{\max }} - \displaystyle\frac{1}{2}JT_5^2 - {a_{\max }}\left(t - \sum\limits_{i = 1}^5 {{T_i}} \right), \\ \qquad \displaystyle\sum\limits_{i = 1}^5 {{T_i}} < t < \sum\limits_{i = 1}^6 {{T_i}} \\ \displaystyle\frac{1}{2}J{\left(\sum\limits_{i = 1}^7 {{T_i}} - t\right)^2}, \\ \qquad \displaystyle\sum\limits_{i = 1}^6 {{T_i}} < t < \sum\limits_{i = 1}^7 {{T_i}} \end{array} \right.$ | (6) |
七段式位移函数为
| $ d(t) = \left\{ \begin{aligned} & \frac{{J{t^3}}}{6},\quad t < {T_1}\\ & {d_1} + \frac{J}{2}T_1^2(t - {T_1}) + \frac{{a_{\max }^{}}}{2}{(t - {T_1})^2},\quad{T_1} < t < \sum\limits_{i = 1}^2 {{T_i}} \\ & {d_2} + {v_{\max }}\left(t - \sum\limits_{i = 1}^2 {{T_i}} \right) + \frac{J}{6}{\left(\sum\limits_{i = 1}^3 {{T_i}} - t\right)^3} - \frac{{J}}{6}{T_3}^3,\\ & \qquad \sum\limits_{i = 1}^2 {{T_i}} < t < \sum\limits_{i = 1}^3 {{T_i}} \\ & {d_3} + {v_{\max }}\left(t - \sum\limits_{i = 1}^3 {{T_i}}\right),\quad\sum\limits_{i = 1}^3 {{T_i}} < t < \sum\limits_{i = 1}^4 {{T_i}} \\ & {d_4} + {v_{\max }}\left(t - \sum\limits_{i = 1}^4 {{T_i}} \right) - \frac{1}{6}J{\left(t - \sum\limits_{i = 1}^4 {{T_i}} \right)^3},\\ &\qquad \sum\limits_{i = 1}^4 {{T_i}} < t < \sum\limits_{i = 1}^5 {{T_i}} \\ & {d_5} + \left({v_{\max }} - \frac{1}{2}JT_5^2\right)\left(t - \sum\limits_{i = 1}^5 {{T_i}} \right) - \frac{{a_{\max }^{}}}{6}{\left(t - \sum\limits_{i = 1}^5 {{T_i}} \right)^2},\\ & \qquad \sum\limits_{i = 1}^5 {{T_i}} < t < \sum\limits_{i = 1}^6 {{T_i}} \\ & s - \frac{1}{6}J{\left(\sum\limits_{i = 1}^7 {{T_i}} - t\right)^3},\quad\sum\limits_{i = 1}^6 {{T_i}} < t < \sum\limits_{i = 1}^7 {{T_i}} \end{aligned} \right. $ | (7) |
其中,
| $\left\{ \begin{split} & {d_1} = \frac{{a_{\max }^3}}{{6{J^2}}}\\ & {d_2} = {d_1} + \frac{J}{2}T_1^2{T_2} + \frac{{{a_{\max }}T_2^2}}{2}\\ & {d_3} = {d_2} + \frac{{{V_{\max }}{a_{\max }}}}{J} - \frac{{a_{\max }^3}}{{6{J^2}}} = {s_1}\\ & {d_4} = s - {d_3}\\ & {d_5} = s - {d_2}\\ & {d_6} = s - {d_1} \end{split} \right.$ |
式中
类型二 六段式。若
最大速度值修改为
| ${v_{\max }} = \frac{{ - \displaystyle\frac{{a_{\max }^2}}{J} + \sqrt {{{(\displaystyle\frac{{a_{\max }^2}}{J})^2}} + 4{a_{\max }}s} }}{2}$ | (8) |
六段式需要调整的时间段为
| ${T_4} = 0$ | (9) |
类型三 五段式。若
最大加速度值修改为
| ${a_{\max }} = \sqrt {{v_{\max }}J} $ | (10) |
五段式需要调整的时间段为
| ${T_2} = {T_6} = 0$ | (11) |
| ${T_4} = \frac{{s - 2{v_{\max }}\sqrt {\displaystyle\frac{{v_{\max }^{}}}{J}} }}{{{v_{\max }}}} = \frac{s}{{{v_{\max }}}} - 2\sqrt {\frac{{v_{\max }^{}}}{J}} $ | (12) |
类型四 四段式。如果
最大加速度值修改为
| ${a_{\max }} = \sqrt[3]{{\frac{{s{J^2}}}{2}}}$ | (13) |
最大速度值修改为
| ${v_{\max }} = Jt_1^2$ | (14) |
四段式需要调整的时间段为
| ${T_2} = {T_4} = {T_6} = 0$ | (15) |
本文研究的笛卡尔空间的位姿规划主要包括直线插补运动和圆弧插补运动的位置规划和姿态规划。
2.1 位置规划1)直线插补。
给定空间两点
| $s = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} $ | (16) |
| $\left\{ \begin{array}{l} {x_k} = {x_1} + {\lambda _k}({x_2} - {x_1})\\ {y_k} = {y_1} + {\lambda _k}({y_2} - {y_1})\\ {z_k} = {z_1} + {\lambda _k}({z_2} - {z_1}) \end{array} \right.$ | (17) |
式中:
2)圆弧插补。
设三维空间中任意不共线的三点
①确定空间圆弧的圆心坐标
②在局部坐标系
| ${{n}} = {\left[ {\frac{{{x_1} - {x_0}}}{r}{\rm{ }}\;\frac{{{y_1} - {y_0}}}{r}{\rm{ }}\;\frac{{{z_1} - {z_0}}}{r}} \right]^{\rm{T}}}$ | (18) |
令
| ${{a}} = {\left[ {\frac{A}{k}{\rm{ }}\;\frac{B}{k}{\rm{ }}\;\frac{C}{k}} \right]^{\rm{T}}}$ | (19) |
式中
| ${{T}} = \left[ {\begin{array}{*{20}{c}} {{n}}&{{o}}&{{a}}&{{p}}\\ 0&0&0&0 \end{array}} \right]$ | (20) |
令局部坐标系内的任意一点
| ${\left[ {x'\ y'\ z'\ 1} \right]^{\rm{T}}} = {{{T}}^{ - 1}}{\left[ {x'\ y'\ z'\ 1} \right]^{\rm{T}}}$ | (21) |
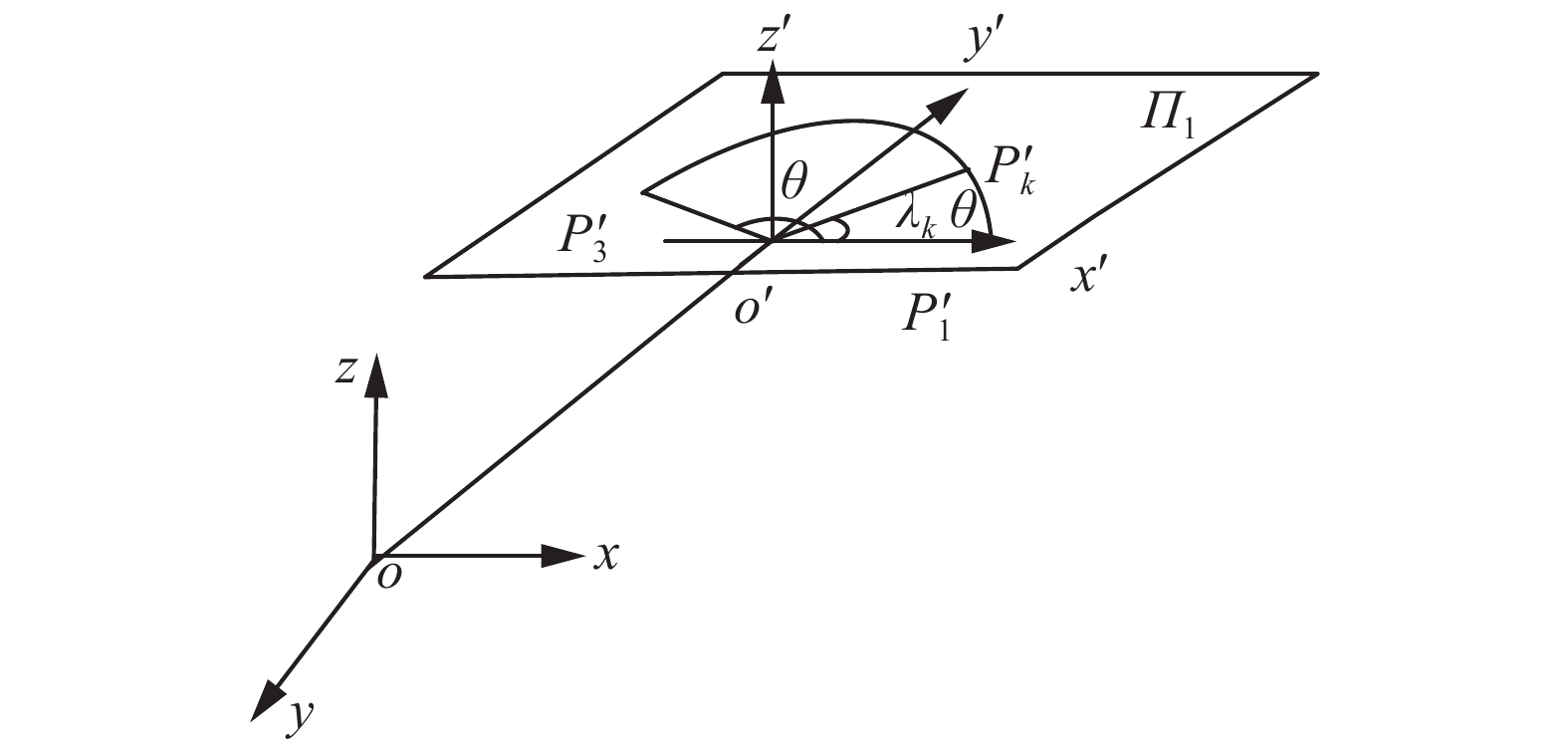
|
Download:
|
| 图 2 基于局部坐标系的圆弧插补 Fig. 2 Arc interpolation based on local coordinate system | |
3)求圆弧的夹角
整个圆弧轨迹插补过程的角度为
| $\theta = \left\{ \begin{array}{l} \arctan 2({y_3}^\prime ,{x_3}^\prime ) + 2{\text{π}},\quad{\rm{ }}{y_3}^\prime < 0;\\ \arctan 2({y_3}^\prime ,{x_3}^\prime ),\quad{y_3}^\prime \geqslant 0.{\rm{ }} \end{array} \right.$ | (22) |
4)在圆弧所在平面上
| $\left\{ \begin{array}{l} {\theta _k} = {\lambda _k} \cdot \theta \\ {{x'}_i} = r \cdot \cos {\theta _k}\\ {{y'}_i} = r \cdot \sin {\theta _k}\\ {{z'}_i} = 0 \end{array} \right.$ | (23) |
对
四元数具有无数据冗余、不存在万向节锁死等优点[13]。设
| $\left\{ \begin{array}{l} s = \pm \sqrt {{n_x} + {o_y} + {a_z} + {1 / 2}} \\ a = {{({o_z} - {a_y})} / {4s}}\\ b = {{({a_x} - {n_z})} / {4s}}\\ c = {{({n_y} - {o_x})} / {4s}} \end{array} \right.$ | (24) |
设工业机器人的初始姿态和目标姿态分别为R1和R2,根据式(24)可求出其对应的四元数q1和q2。由于每个姿态矩阵对应两个互补的四元数,考虑到时间最优,选择与前一姿态夹角较小的一组四元数。定义两个四元数夹角为
| $\cos \;\varOmega = {q_1} \cdot {q_2}$ | (25) |
对于两点间的姿态可由Slerp公式[13]求出:
| ${\rm{Slerp}}({q_1},{q_2},{\lambda _k}) = \frac{{{q_1}\sin (1 - {\lambda _k})\varOmega + {q_2}\sin ({q_2}\varOmega )}}{{\sin \;\varOmega }}$ | (26) |
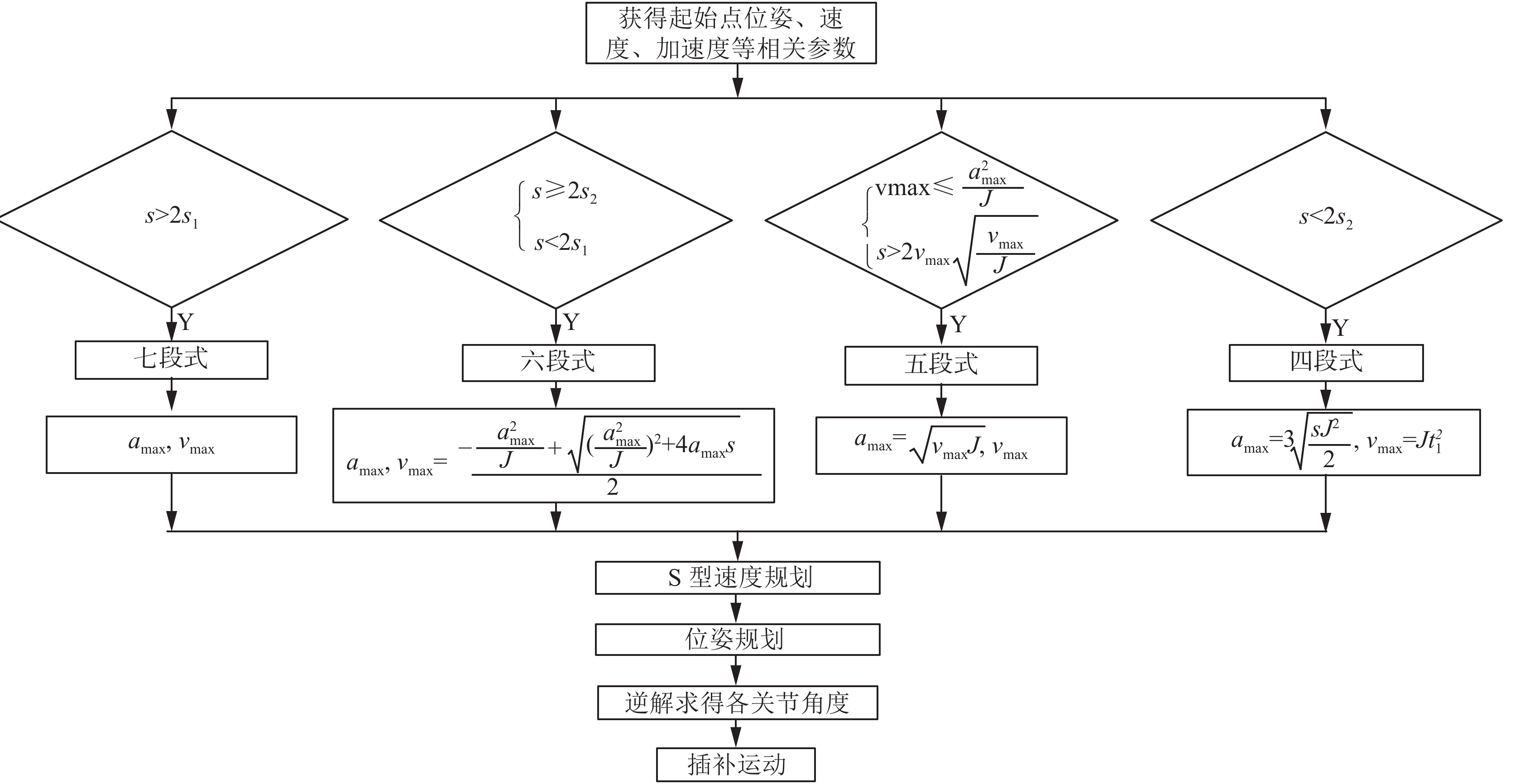
轨迹规划需通过插补算法来实现。本文采用弧长增量法的插补技术,即在每个插补周期内,按照进给速度用微小线段去逼近目标轮廓线[14]。本文设计的插补算法程序流程如图3所示。
|
Download:
|
| 图 3 插补算法程序流程 Fig. 3 Program flow of interpolation algorithm | |
设采样时刻为
| ${\lambda _k} = \frac{{d({t_k})}}{{{d_i}}}{\rm{ }}\;k = 1,2, \cdots, N$ | (27) |
将式(27)代入空间直线或圆弧的位姿表达式中,求解便可得到位置插补点。
3 仿真分析及实验自主开发的六自由度工业机器人控制系统由嵌入式PC(x86架构)、Linux/RTAI实时操作系统和伺服驱动等模块组成。本文在嵌入式PC上利用C++编程实现规划算法。控制器与伺服驱动器之间采用EtherCAT工业实时以太网进行通信[14]。
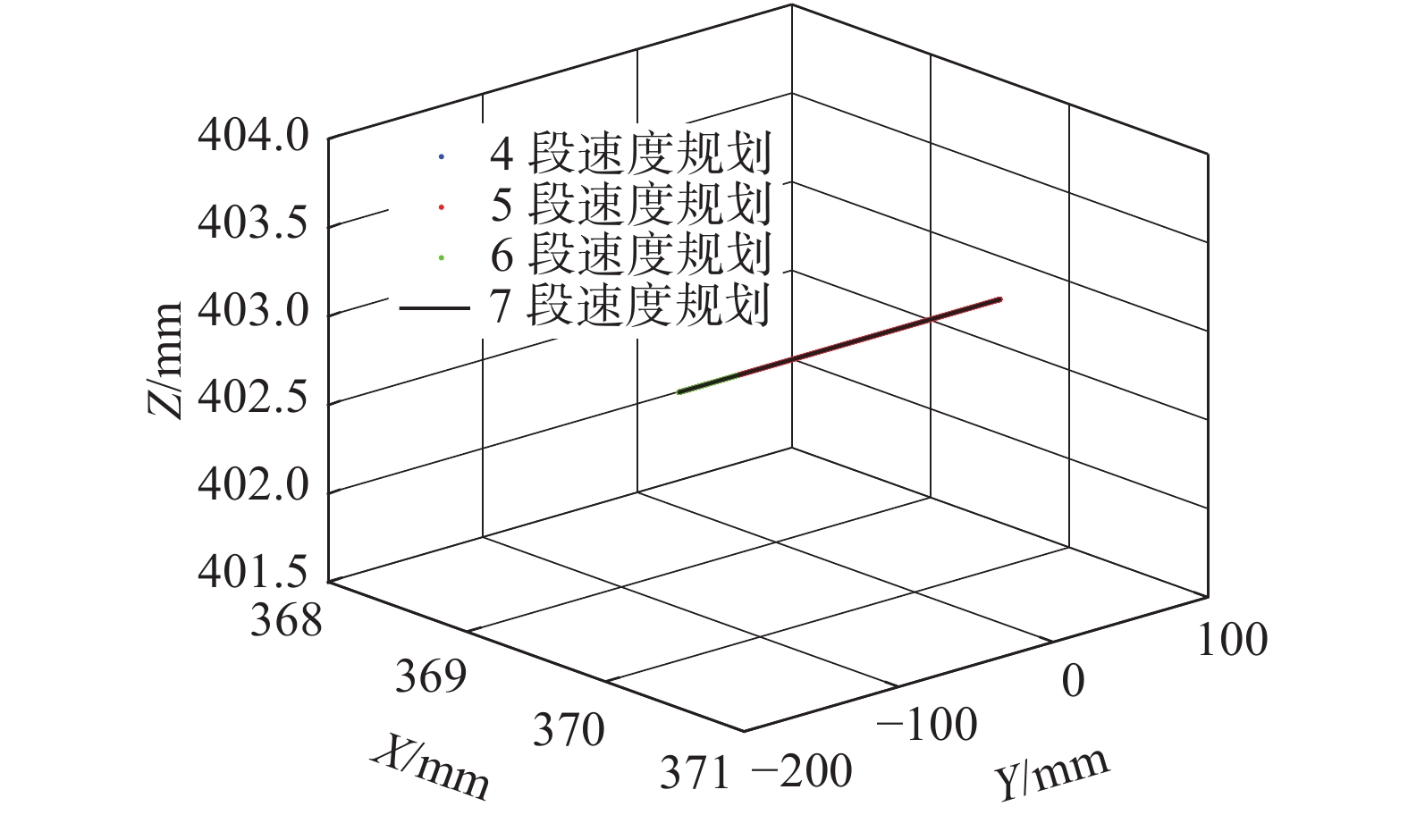
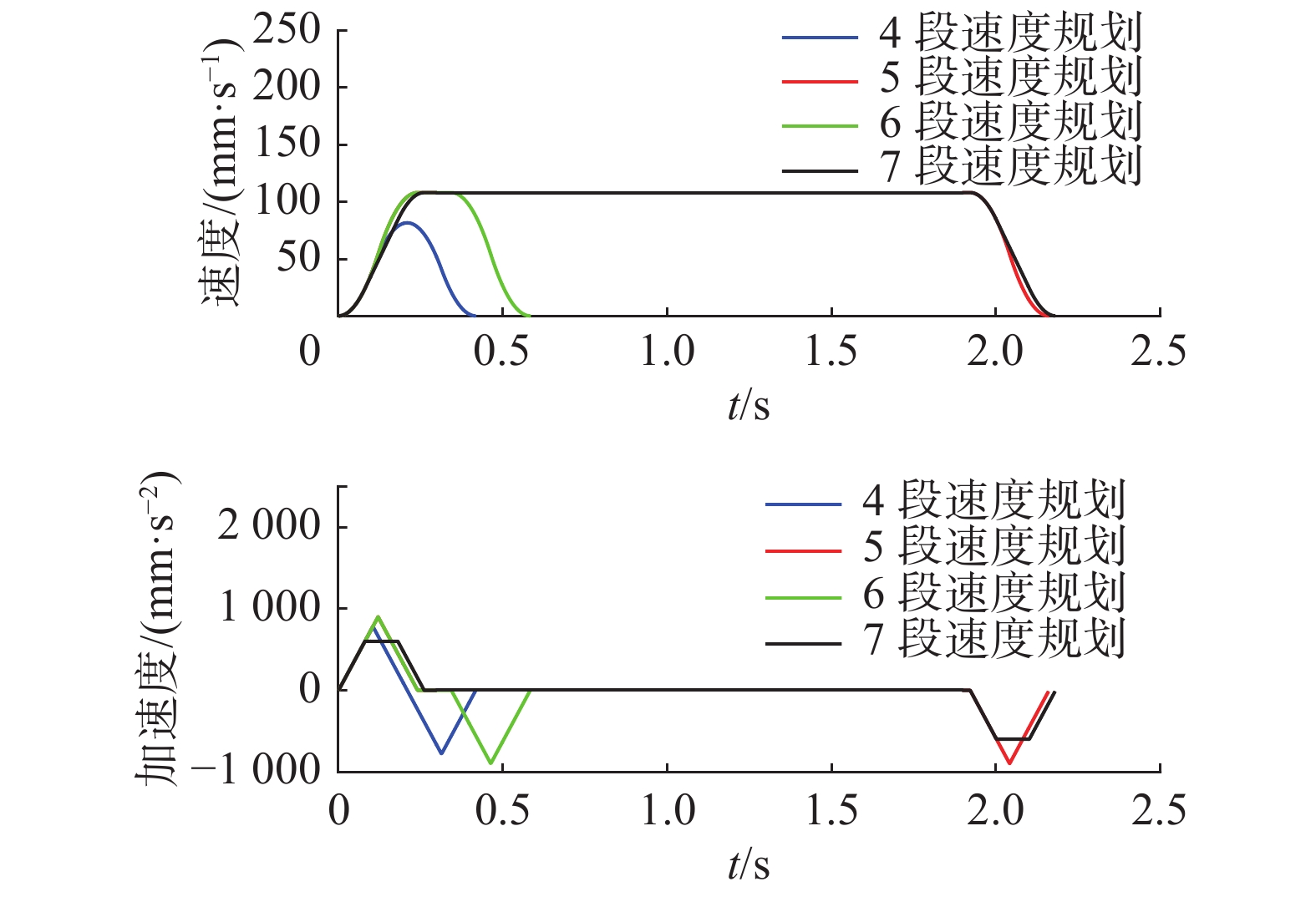
3.1 直线插补实验选取系统允许的最大速度和最大加速度分别为3 600 mm/s和2 800 mm/s2,J=7 500 mm/s3,插补周期为2 ms。选取起始点坐标为(369.7,−127.1,402.8,0.011 81,0.728 92,0.684 36,−0.013 89),目标进给速度为108 mm/s。进行了4组实验,实验参数如表1所示。实验得到的位移、速度、加速度曲线如图4和图5所示。实验得到的直线运动喷绘效果如图6所示。
| 表 1 直线插补运动实验参数 Tab.1 Experimental parameters of linear interpolation motion |
|
Download:
|
| 图 4 直线插补运动的位移曲线 Fig. 4 The displacement curve of line interpolation motion | |
|
Download:
|
| 图 5 直线插补运动的速度与加速度曲线 Fig. 5 The velocity and acceleration curves of line interpolation motion | |

|
Download:
|
| 图 6 直线插补运动喷绘实验效果 Fig. 6 Experimental effect diagram of line interpolation motion spray painting | |
根据4组实验参数可分别得到四段、五段、六段和七段速度规划曲线,验证轨迹规划算法的有效性。此外,由图5可知,S型速度规划可保证加速度连续,减小机械冲击。
3.2 圆弧插补实验与直线插补运算类似,机器人系统运动参数与直线部分相同。选取圆弧起点坐标分别为P0(369.7,−127.1,402.8,0.011 81,0.728 92,0.684 36,−0.013 89),P1(473.6,−23.45,502.8,0.011 81,0.728 92,0.684 36,−0.013 89),P2(369.7,80.2,402.8,0.011 81,0.728 92,0.684 36,−0.013 89)。分别进行加速度为600 mm/s2和2 800 mm/s2两组实验。实验得到的位移、速度、加速度曲线如图7和图8所示。实验得到的圆弧运动喷绘效果如图9所示。
通过对比在加速度为600 mm/s2和2 800 mm/s2两种情况,可分别得到七段式速度规划和五段式速度规划。同理,可通过调整圆弧弧长、速度和加速度等参数获得四段式和六段式速度规划。与直线部分类似,S型速度规划可保证加速度连续。

|
Download:
|
| 图 7 圆弧插补运动的位移曲线 Fig. 7 The displacement curve of arc interpolation motion | |

|
Download:
|
| 图 8 圆弧插补运动的速度与加速度曲线 Fig. 8 Curve of velocity and acceleration of arc interpolation motion | |

|
Download:
|
| 图 9 圆弧插补运动喷绘实验效果 Fig. 9 Experimental effect diagram of arc interpolation motion spray painting | |
1)采用S型速度规划,基于四元数的直线与圆弧运动的位姿模型,可实现笛卡尔空间规划。
2)根据路径长度约束条件,能将速度规划类型分为4种情况,可实现速度和加速度的自动调整。
3)本文设计的S型速度规划算法可保证加速度连续,减小机械冲击。
在下一步工作中,将增加误差等约束条件,提高控制精度;进一步优化机器人控制系统软硬件平台,提高系统实时性。
| [1] |
LIU Huashan, LAI Xiaobo, WU Wenxiang. Time-optimal and jerk-continuous trajectory planning for robot manipulators with kinematic constraints[J]. Robotics and computer-integrated manufacturing, 2013, 29(2): 309-317. DOI:10.1016/j.rcim.2012.08.002 ( 0) 0)
|
| [2] |
GIBERTI H, SBAGLIA L, URGO M. A path planning algorithm for industrial processes under velocity constraints with an application to additive manufacturing[J]. Journal of manufacturing systems, 2017, 43: 160-167. DOI:10.1016/j.jmsy.2017.03.003 ( 0) 0)
|
| [3] |
ABU-DAKKA F J, ASSAD I F, ALKHDOUR R M, et al. Statistical evaluation of an evolutionary algorithm for minimum time trajectory planning problem for industrial robots[J]. The international journal of advanced manufacturing technology, 2017, 89(1/2/3/4): 389-406. ( 0) 0)
|
| [4] |
VULLIEZ M, LAVERNHE S, BRUNEAU O. Dynamic approach of the feedrate interpolation for trajectory planning process in multi-axis machining[J]. The international journal of advanced manufacturing technology, 2016, 88(5/6/7/8): 2085-2096. ( 0) 0)
|
| [5] |
ZHAO Huan, ZHU Limin, DING Han. A real-time look-ahead interpolation methodology with curvature-continuous B-spline transition scheme for CNC machining of short line segments[J]. The international journal of machine tools and manufacture, 2013, 65: 88-98. DOI:10.1016/j.ijmachtools.2012.10.005 ( 0) 0)
|
| [6] |
许健, 梅江平, 段晓斌, 等. 一种工业机器人连续轨迹规划过渡算法[J]. 工程设计学报, 2016, 23(6): 537-543. XU Jian, MEI Jiangping, DUAN Xiaobin, et al. An algorithm for segment transition in continuous trajectory planning of industrial robot[J]. Chinese journal of engineering design, 2016, 23(6): 537-543. (  0) 0)
|
| [7] |
李黎, 尚俊云, 冯艳丽, 等. 关节型工业机器人轨迹规划研究综述[J]. 计算机工程与应用, 2018, 54(5): 36-50. LI Li, SHANG Junyun, FENG Yanli, et al. Research of trajectory planning for articulated industrial robot: a review[J]. Computer engineering and applications, 2018, 54(5): 36-50. (  0) 0)
|
| [8] |
HU Jun, XIAO Liangjian, WANG Yuhan, et al. An optimal feedrate model and solution algorithm for a high-speed machine of small line blocks with look-ahead[J]. The international journal of advanced manufacturing technology, 2006, 28(9/10): 930-935. ( 0) 0)
|
| [9] |
史步海, 孙会会. 基于新S型速度规划的B样条曲线算法研究[J]. 机床与液压, 2016, 2016, 44(15): 72-79. SHI Buhai, SUN Huihui. B-spline curve algorithm research based on new S velocity planning[J]. Machine tool and hydraulics, 2016, 2016, 44(15): 72-79. DOI:10.3969/j.issn.1001-3881.2016.15.018 (  0) 0)
|
| [10] |
JAHANPOUR J, ALIZADEH M R. A novel acc-jerk-limited NURBS interpolation enhanced with an optimized S-shaped quintic feedrate scheduling scheme[J]. The international journal of advanced manufacturing technology, 2015, 77(9/10/11/12): 1889-1905. ( 0) 0)
|
| [11] |
谭民, 徐德, 侯增广, 等. 先进机器人控制[M]. 北京: 高等教育出版社, 2007. TAN Min, XU De, HOU Zengguang, et al. Advanced robot control[M]. Beijing: Higher Education Press, 2007. (  0) 0)
|
| [12] |
SPONG M W, HUTCHINSON S, VIDYASAGAR M. Robot modeling and control[M]. Hoboken, NJ: John Wiley & Sons Inc, 2005.
( 0) 0)
|
| [13] |
李宏胜, 汪允鹤, 黄家才, 等. 工业机器人倍四元数轨迹规划算法的研究[J]. 中国机械工程, 2016, 27(20): 2711-2716. LI Hongsheng, WANG Yunhe, HUANG Jiacai, et al. Research on trajectory planning of industrial robots with double quaternion[J]. China mechanical engineering, 2016, 27(20): 2711-2716. DOI:10.3969/j.issn.1004-132X.2016.20.003 (  0) 0)
|
| [14] |
WINGS E, MÜLLER M, ROCHLER M. Integration of real-time Ethernet in LinuxCNC: using the example of Sercos Ⅲ[J]. The international journal of advanced manufacturing technology, 2015, 78(9/10/11/12): 1837-1846. ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


