近年来，混沌抑制作为生物工程界的关键技术受到了越来越多的关注。将混沌抑制原理应用到生物医学领域取得了很多理论成果。冠状动脉是为心脏提供氧气的肌型血管。血管痉挛是造成心肌梗死、心绞痛等冠状动脉疾病的根本原因^[1-2]。而血管痉挛在数学角度上看就是血管的混沌状态^[3]。血管混沌现象可能会对身体带来致命威胁^[4]。所以，研究冠状动脉系统的混沌特性，实现冠状动脉系统的混沌抑制具有理论意义和实用价值。

混沌抑制控制方法主要有线性法^[5]、非线性方法^[6-8]、局部线性方法^[9]等。其中线性、局部线性方法只适用于线性或线性化的系统。冠状动脉系统是一类非线性生物系统，需要设计非线性控制器来实现混沌抑制。采用非线性方法，已经提出的混沌抑制方法包括高阶自适应滑模控制^[6]、时滞状态反馈控制^[10]、滑模控制^[11]等。

在现实中，冠状动脉系统易受体温、血压等多种不确定性的影响^[1]，这更增大了其混沌抑制的难度。微分积分终端滑模是一种滑模控制设计方法，消除了滑动模态的到达时间，适用于高相对阶系统，这种设计方法不存在奇异现象，能精确估计误差收敛时间^[12]。

虽然滑模控制在滑动模态下对匹配不确定性具有不变性，但是冠状动脉系统的复杂性导致其难以满足滑模控制的匹配条件。已证明，扰动观测器可以有效地克服非匹配不确定性对滑模控制系统的影响，因此本文结合微分积分终端滑模控制方法和扰动观测器来解决不确定性冠状动脉系统的混沌抑制问题。

1 数学模型及问题描述

冠状动脉本质上是一类肌型血管，其动态集总参数模型为：

$ \begin{array}{l} {{\dot x}_1}= - b{x_1} - c{x_2} \\ {{\dot x}_2}= - {\textit{λ}} (1 + b){x_1} - {\textit{λ}} \left( {1 + c} \right){x_2} + {\textit{λ}} x_1^3 + E\cos \omega \tau \\ \end{array} $

(1)

式中：x₁是血管内径变化差；x₂是血管压力差；t是时间变量；b、c、λ为冠状动脉系统的集总参数；Ecosωt表示系统受到周期性刺激。

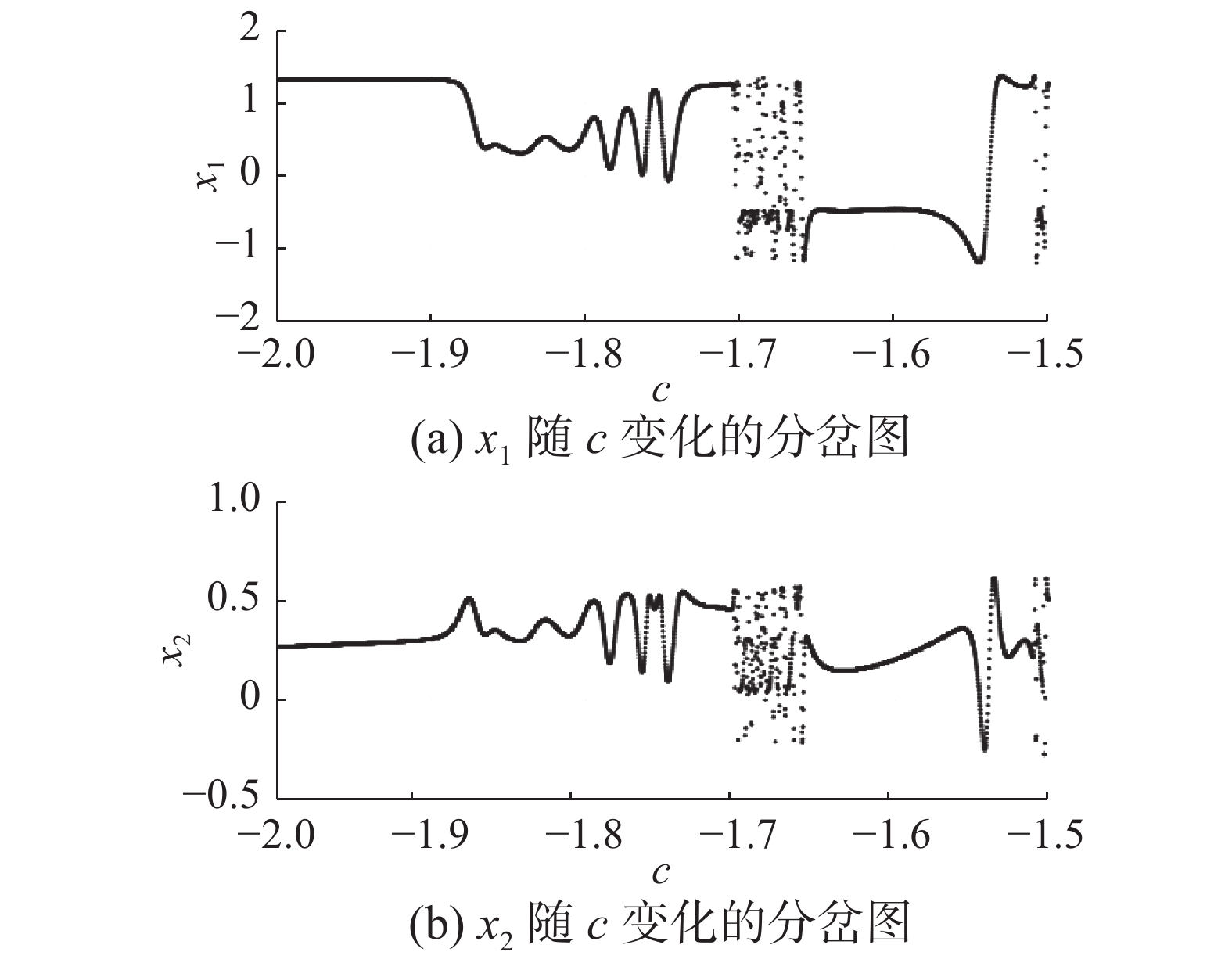
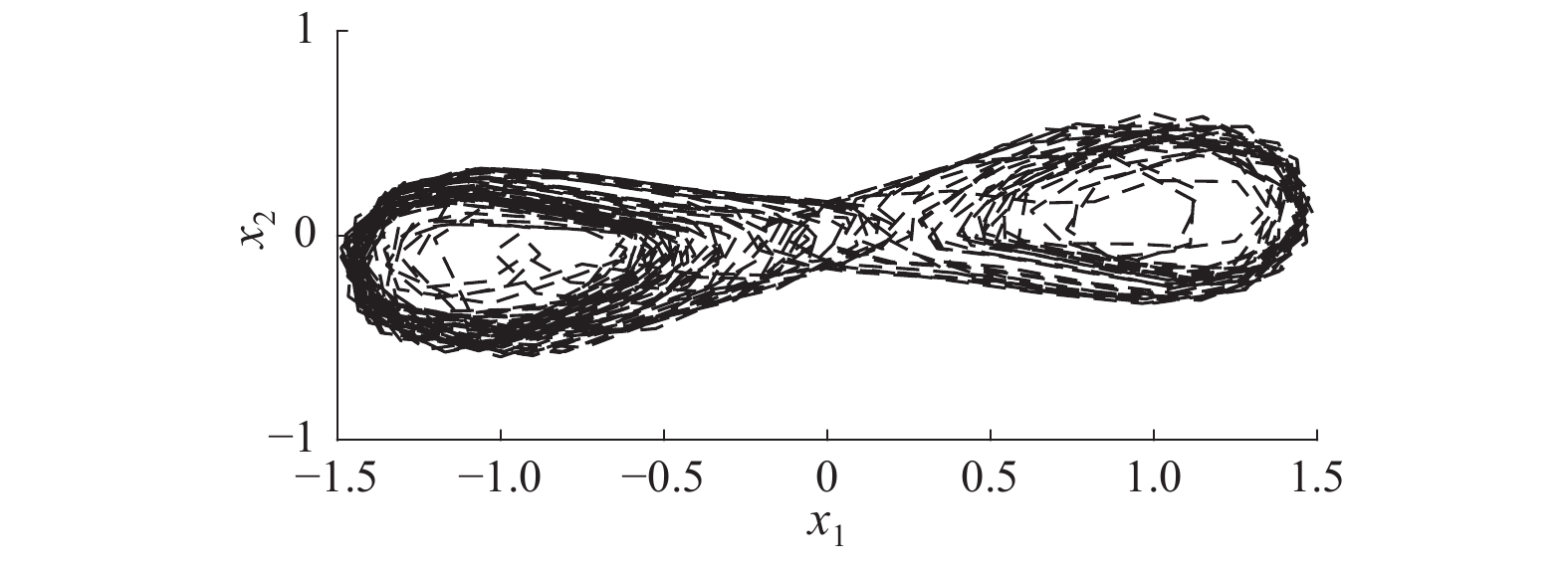
图1表示冠状动脉系统随着参数c变化的分岔图。其中，初始条件为[x₁(0) x₂(0)]^T=[0.2 0.2]^T；其他参数为b=0.15、λ=−0.65、E=0.3和ω=1；时间序列为2π、4π、6π、10π和12π；时间周期为2π。类似地，冠状动脉系统随着λ和b的变化也存在分岔现象。选取参数b=0.15、λ=−0.65、c=−1.7、E=0.3和ω=1，在同样的初始条件下，冠状动脉系统相平面图如图2所示。从图1、图2可见，冠状动脉系统在某些参数下处于混沌状态，其混沌抑制问题具有挑战性。

定义(1)为标称系统，其不确定性系统为

$ \begin{array}{l} {{\dot {\bar x}}_1}= - b{{\bar x}_1} - c{{\bar x}_2} + {d_1} \\ {{\dot {\bar x}}_2}= - {\textit{λ}} (1 + b){{\bar x}_1} - {\textit{λ}} \left( {1 + c} \right){{\bar x}_2} + {\textit{λ}} \bar x_1^3 +\\ \qquad E\cos \omega \tau + u + {d_2} \\ \end{array} $

(2)

式中： $\bar {{x}}=\left[ {{{\bar x}_1}\;{{\bar x}_2}} \right]$ 为状态变量； ${{d}}=\left[ {{d_1}\;{d_2}} \right]$ 代表系统的不确定性； $u$ 表示控制器的控制输入。

假设1　系统不确定性d有界，即 ${\left\| {{d}} \right\|_\infty } \leqslant {d^ {*} }$ ，d^*是未知的正实数。

假设2　 d是慢时变扰动，即 ${\dot {{d}}} \approx {{{\textit{0}}}_{2 \times 1}}$ 。

冠状动脉系统混沌抑制的目的是通过设计控制器使得不确定性系统与标称系统同步，即

$ \mathop {\lim }\limits_{t \to \infty } {{e}}={{\bf{{0}}}_{2 \times 1}} $

(3)

式中：0_2×1=[0 0]^T，e=[e₁ e₂]^T， ${e_1}={\bar x_1} - {x_1}$ 和 ${e_2}={\bar x_2} - {x_2}$ 。

根据式(3)的误差定义，由式(1)、(2)可得

$ \begin{array}{l} {{\dot e}_1}= - b{e_1} - c{e_2} + {d_1} \\ {{\dot e}_2}= - \left( {{\textit{λ}} + b{\textit{λ}} } \right){e_1} - \left( {{\textit{λ}} + c{\textit{λ}} } \right){e_2} +{\textit{λ}} e_1^3 \\ \;\;\;\; + 3{x_1}{{\bar x}_1}{e_1} + u + {d_2} \\ \end{array} $

(4)

定义 ${{\tilde x}_1}={e_1}$ ， ${{\tilde x}_2}={{\dot {e}}_1}$ ，对 ${{\tilde x}_1}$ 和 ${{\tilde x}_2}$ 分别求导，并将式(4)代入 ${\dot {\tilde {x}}_2}$ ，可得

$ \begin{array}{l} {{\dot {\tilde {x}}}_1}={{{\tilde x}}_2} \\ {{\dot {\tilde {x}}}_2}={\textit{λ}} \left( {c - b} \right){{{\tilde x}}_1} - \left( {b +{\textit{λ}} + c{\textit{λ}} } \right){{{\tilde x}}_2} - {\textit{λ}} c{\tilde x}_1^3 -\\ \qquad 3c{x_1}{{\bar x}_1}{{{\tilde x}}_1} - cu - c{d_2} + {{{\dot d}}_1} + {\textit{λ}} \left( {1 + c} \right){d_1} \\ \end{array} $

(5)

根据假设2， ${{\dot d}_1} \approx 0$ ，式(5)可以写成

$ \begin{array}{l} {\dot {\tilde {{{x}}}}}={{F}}\left( {{\tilde {x}},d} \right) + {{B}}u \\ {{y}}={{H}}\left( {{\tilde x}} \right) \\ \end{array} $

(6)

式中：d=−cd₂+λ(1+c)d₁；B=[0 −c]^T； ${\tilde {{x}}}={\left[ {{{{\tilde x}}_1},{{{\tilde x}}_2}} \right]^{\rm{T}}}$ ； $ f\left( {{\tilde x}} \right)={\textit{λ}} \left( {c - b} \right){{\tilde x}_1} - \left( {b + {\textit{λ}} + c{\textit{λ}} } \right){{\tilde x}_2} - {\textit{λ}} c{\tilde x}_1^3 - 3c{x_1}{\bar x_1}{{\tilde x}_1}$ ；F $( {{\tilde {x}}},$ $ { d} )={\left[ {{{{\tilde x}}_2}\;f\left( {{\tilde x}} \right) + d} \right]^{\rm{T}}}$ ； $ {{H}}\left( {{\tilde x}} \right)={{\tilde x}_1}$ 。

假设3　 ${{F}}\left( {{\tilde {x}},d} \right)$ 和 ${{H}}\left( {{\tilde x}} \right)$ 光滑且李导数存在。

根据假设3，可计算如下李导数 ${L_B}{{H}}\left( {{\tilde {x}},d} \right)=0$ ， ${L_B}{L_F}{{H}}\left( {{\tilde {x}},d} \right)= - c \ne 0$ 。可见式(4)的相对阶为2，因此模型(6)适用微分积分终端滑模方法。进一步，该模型的输入输出方程可表示为：

$ \ddot {{y}}=L_F^2{{H}}\left( {{\tilde {x}},d} \right) + {L_B}{L_F}{{H}}\left( {{\tilde {x}},d} \right){{u}} $

(7)

式中： $L_{F}^2{{H}}\left( {{\tilde {x}},d} \right)=\displaystyle\frac{{\partial \left( {{L_{F}}{{H}}\left( {{\tilde {x}},d} \right)} \right)}}{{\partial {\tilde x}}},{{F}}={{f}}\left( {{\tilde x}} \right) + {{d}}$ 。根据式(6)、(7)，该模型的输入输出方程可写为

$ \ddot {{y}}={{f}}\left( {{\tilde x}} \right) + {{d}} - c{{u}} $

(8)

2 控制设计

本文采用微分积分终端滑模控制方法抑制冠状动脉系统的混沌状态，设计微分积分终端滑模面为

$ s={e_{D_1}} + \alpha {e_{I_1}} $

(9)

式中：α是控制器设计参数； $e_{D_0} = e_1$ ， $e_{I_1} = -e_{D_1}$ (0)/α； ${e_{D_1}}={\dot e}_{D_0}^{{P_{11}}/{q_{11}}} + \beta {e_{D_0}}$ ； $\displaystyle{e_{I_1}}=\int_0^t {e_{D_{11}}^{{q_{21}}/{p_{21}}}\left( \tau \right)} {\rm{d\tau}} $ ；β>0；p₁₁>q₁₁>0；p₂₁>q₂₁>0；且p，q均为正奇数。

定理1　若定义式(9)为滑模平面，则状态变量 ${\left[ {\begin{array}{*{20}{c}} {{{{\tilde x}}_1}}&{{{{\tilde x}}_2}} \end{array}} \right]^{\rm{T}}}$ 将在有限时间 $T_{D_1}$ 内收敛至0_2×1，其中 $T_{D_1} $ 为：

$ {T_{D_1}}=\frac{{{{\left| {{e_{{D_1}}}\left( 0 \right)} \right|}^{1 - {q_{21}}/{p_{21}}}}}}{{\alpha \left( {1 - {q_{21}}/{p_{21}}} \right)}} + \frac{{{{\left| {{e_{{D_0}}}\left( {{t_{11}}} \right)} \right|}^{1 - {q_{11}}/{p_{11}}}}}}{{\beta \left( {1 - {q_{11}}/{p_{11}}} \right)}} $

(10)

式中t₁₁是滑模 $e_{D_1}=0 $ 的到达时间。

证明　所设计的滑动模态开始于t=0，所以 $ e_{D_1} = -\alpha e_{I_1}$ 成立。由于 $\displaystyle{e_{I_1}}=\int_0^t {e_{D_{11}}^{{q_{21}}/{p_{21}}}\left( \tau \right)} {\rm{d}}\tau $ ，所以

$ {{\dot {e}}_{I_1}}= - {\alpha ^{{q_{21}}/{p_{21}}}}{e_{I_1}}^{{q_{21}}/{p_{21}}}\left( t \right) $

(11)

式中 $ e_{I_1}(0)=-e_{D_1}(0)/\alpha$ 。解式(11)可得 $ e_{I_1}$ 的收敛时间为

$ {t_{11}}=\frac{{{{\left| {{e_{{D_1}}}\left( 0 \right)} \right|}^{1 - {q_{21}}/{p_{21}}}}}}{{\alpha \left( {1 - {q_{21}}/{p_{21}}} \right)}} $

(12)

在滑模面s=0上 $e_{D_1}$ =–α $e_{I_1} $ ，表明滑模 $e_{D_1} $ 需要花费时间t₁₁收敛至零。当 $e_{D_1} $ =0时， $e_{D_0} $ 也会成功收敛至零。在t=t₁₁时， $e_{D_1}$ 可被描述为

$ {{\dot {e}}_{{D_0}}}\left( {{t_{11}}} \right)= - {\beta ^{{q_{11}}/{p_{11}}}}e_{{D_0}}^{{q_{11}}/{p_{11}}}\left( {{t_{11}}} \right) $

(13)

由式(13)， $e_{D_0}$ (t₁₁)到 $e_{D_0}$ =0时间为

$ {t_{01}}=\frac{{{{\left| {{e_{{D_0}}}\left( {{t_{11}}} \right)} \right|}^{1 - {q_{11}}/{p_{11}}}}}}{{\beta \left( {1 - {q_{11}}/{p_{11}}} \right)}} $

(14)

式(9)的微分项和积分项相互独立，从s=0到 $e_{D_0}$ =0的时间为t₁₁和t₀₁之和，即有限收敛时间为T_D1=t₁₁+t₀₁。

进一步，对式(9)求导并将式(8)代入可得

$ {\dot s}=\frac{{{p_{11}}}}{{{q_{11}}}}{\dot e}_{D_0}^{\left( {{p_{11}}/{q_{11}} - 1} \right)}\left( {f\left( {{\tilde x}} \right) + d - cu} \right) + \psi $

(15)

式中： $ \psi =\beta {{\dot {e}}_{D_0}} + \alpha {\left( {{\dot {e}}_{D_0}^{{p_{11}}/{q_{11}}} + \beta {e_{D_0}}} \right)^{{q_{21}}/{p_{21}}}}$ 。

为了获取微分积分终端滑模控制律，选取李雅普诺夫函数V₀=s²/2，对其求导可得 ${{\dot V}_0}=s{\dot s}$ ，并代入式(15)，令 ${{\dot V}_0} < 0$ 可得微分积分终端滑模控制律

$ u\!=\!\frac{{ - 1}}{c}\left[ \!\!{ - {k_{\rm{e}}}\left| \psi \right|\left(\! {\frac{{{q_{11}}}}{{{p_{11}}}}}\! \right){{{A}}^{ - 1}}\frac{s}{{\left| s \right|}} - f\left( {{\tilde x}} \right) - \left| {k\operatorname{sgn} (s) + \eta s} \right| - d_0^ {*} } \!\right] $

(16)

式中： ${{A}} = \left\{ {\begin{array}{*{20}{l}} {{\dot e}_{_{D_0}}^{\left( {{p_{11}}/{q_{11}} - 1} \right)},\left| {{\dot e}_{_{D_0}}^{\left( {{p_{11}}/{q_{11}} - 1} \right)}} \right| \geqslant \varepsilon }\\ {\varepsilon \quad\text{其他.}} \end{array}} \right.$ ；k>0；η>0；k_e>0。考虑A，参数ϕ>0满足：

$ \left\| {\left( {{{A}} - {\dot e}_{D_0}^{\left( {{p_{11}}/{q_{11}} - 1} \right)}} \right){{{A}}^{ - 1}}} \right\| \leqslant \phi < 1 $

(17)

为了保证 ${{\dot V}_0} < 0$ ，参数k_e应满足k_e>1/(1−ϕ)。

将式(16)代入式(15)，并考虑条件(17)，可得当 $k > d_0^ {*} $ 时， ${{\dot V}_0} < 0$ 。但在假设1中，d^*是未知的，所以 $d_0^ {*} $ 也是未知的，因此通过选取k保证 ${{\dot V}_0} < 0$ 具有保守性，而过于保守的k会恶化抖振现象，降低控制性能。

为解决d^*是未知的问题，本文设计扰动观测器估计系统不确定性，从而同时保证控制系统的稳定性和控制性能。设计扰动观测器如下：

$ \begin{array}{l} {\dot {\textit{z}}}= - {{L}}{{{B}}_2}{{P}} - {{L}}\left( {{{{B}}_2}{{L}}{\tilde x} + {{A}}{\tilde x} + {{{B}}_1}u + {{M}}} \right) \\ {\hat d}={\textit{z}} + {{L}}{\tilde x} \\ \end{array} $

(18)

式中： ${{z}} \in {{\rm{R}}^{1 \times 1}} $ 是观测器的状态变量； ${\hat {{d}}} \in {{\rm{R}}^{1 \times 1}}$ 为不确定性估计值；L∈R^1×2为观测器增益变量。各参数矩阵描述为：

$ \begin{array}{l} {{A}}\!=\!\left[ \!{\begin{array}{*{20}{c}} 0&1 \\ {{\textit{λ}} (c - b)}&{ - (b + {\textit{λ}} + c{\textit{λ}} )} \end{array}}\! \right]; \;{{{B}}_1}=\left[ {\begin{array}{*{20}{c}} 0 \\ { - c} \end{array}} \right];\; {{{B}}_2}=\left[ {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right];\\ {{M}}=\left[ {\begin{array}{*{20}{c}} 0 \\ { - {\textit{λ}} c{\tilde x}_1^3 - 3c{x_1}{{\bar x}_1}{{{\tilde x}}_1}} \end{array}} \right]{\text{。}} \end{array} $

定义估计误差e_d为

$ {e_d}=d - {\hat d} $

(19)

假设4　 e_d有界，即|e_d|≤ $e_d^ {*} $ ，其中 $e_d^ {*} $ 是未知的正实数。

由假设2可知 ${\dot d} \approx 0$ 。对式(19)求导，并将式(18)代入e_d的导数，可得：

$ \begin{array}{c} {{\dot e}_d} \simeq {{L}}{{{B}}_2}P + {{L}}({{{B}}_2}{{L}}{\tilde x} + {{A}}{\tilde x} + {{{B}}_1}u + {{M}}) -\\ \qquad {{L}}({{A}}{\tilde x} + {{{B}}_1}u + {{{B}}_2}d + {{M}})= \\ \qquad {{L}}{{{B}}_2}({\hat d} - {{L}}{\tilde x}) + {{{L}}^2}{{{B}}_2}{\tilde x} - {{L}}{{{B}}_2}d =\\ \qquad {{L}}{{{B}}_2}({\hat d} - d)= - {{L}}{{{B}}_2}{e_d} \\ \end{array} $

(20)

解式(20)可得

$ {e_d}=\exp ( - {{L}}{{{B}}_2}){e_d}(0) $

(21)

可见，通过选取向量L保证LB₂是正常数，可保证估计误差e_d在t→∞时指数收敛。因此，可由扰动观测器输出 ${\hat d}$ 代替式(16)中的 $d_0^ {*} $ 。

定理2　在假设1至4下，针对冠状动脉系统模型(2)，利用输入-输出动态方程(8)，定义微分积分终端滑模面(9)，采用扰动观测器(18)，设计微分积分终端滑模控制律(22)，则闭环混沌抑制系统是渐近稳定的。

$ u= - \frac{1}{c} - {k_{\rm{e}}}\left| \psi \right|\displaystyle\frac{{{q_{11}}}}{{{p_{11}}}}{{{A}}^{ - 1}}s/\left| s \right| - f\left( {{\tilde x}} \right) - [k\operatorname{sgn} (s) + \eta s] - {\hat d} $

(22)

式中 $ k > e_d^ {*}$ 。

证明　采用同样的李雅普诺夫函数V₀=s²/2,对其求导并将式(15)代入，可得

$ {{\dot {{V}}}_0}=s\frac{{{p_{11}}}}{{{q_{11}}}}{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}[f\left( {{\tilde x}} \right) + d - cu] + s\psi $

(23)

将式(22)代入式(23)得

$ \begin{array}{l} {{\dot {{V}}}_0}=s\psi - s{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}{k_{\rm{e}}}\left| \psi \right|{{{A}}^{ - 1}}s/\left| s \right| +\\ \qquad s\displaystyle\frac{{{p_{11}}}}{{{q_{11}}}}{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}[d - {\hat d} - (k\operatorname{sgn} (s) + \eta s)] \\ \end{array} $

(24)

由于p₁₁>0，q₁₁>0，且p₁₁>q₁₁，所以式(24)中所有 ${\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}$ 满足 ${\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)} > 0$ 。式(24)中的第1项和第2项满足不等式(25)：

$ \begin{array}{l} s\psi - s{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}{k_{\rm{e}}}\left| \psi \right|{{{A}}^{ - 1}}s/\left| s \right|= \\ s\psi - {k_{\rm{e}}}\left| \psi \right|s + {k_{\rm{e}}}\left| \psi \right|{{A}}{{{A}}^{ - 1}}s -\\ s{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}{k_{\rm{e}}}\left| \psi \right|{{{A}}^{ - 1}}s/\left| s \right| \leqslant \\ \left| {\psi s} \right| - {k_{\rm{e}}}\left| \psi \right|s + {k_{\rm{e}}}\left| {\psi ({{A}} - {\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}){{{A}}^{ - 1}}s} \right| \leqslant \\ \left| {\psi s} \right| - {k_{\rm{e}}}(1 - \phi )\left| {\psi s} \right| \\ \end{array} $

(25)

选择k_e>(1−ϕ)进而 $s\psi - s{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}$ ${k_{\rm{e}}}\left| \psi \right|{{{A}}^{ - 1}}s/\left| s \right| < 0$ 。

进一步，式(24)中第3项可描述为：

$ \begin{array}{c} s\displaystyle\frac{{{p_{11}}}}{{{q_{11}}}}{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}[d - {\hat d} - (k\operatorname{sgn} (s) + \eta s)] = \\ \displaystyle \frac{{{p_{11}}}}{{{q_{11}}}}{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}[{e_d}s - k\left| s \right| - \eta {s^2}] \leqslant \\ \displaystyle\frac{{{p_{11}}}}{{{q_{11}}}}{\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}[(e_d^ {*} - k)\left| s \right| - \eta {s^2}] \\ \end{array} $

(26)

为使 $s({p_{11}}/{q_{11}}){\dot e}_{D_0}^{({p_{11}}/{q_{11}} - 1)}$ $[d - {\hat d} - (k\operatorname{sgn} (s) + \eta s)] < 0$ 成立，可选择 $k > e_d^ {*} $ 。

由式(25)和式(26)可得 ${{\dot V}_0} < 0$ ，满足滑模动态的可达性条件。

虽然式(22)中同样需要选择k大于未知的 $e_d^ {*} $ 以保证控制系统的稳定性，但是由于e_d是指数收敛的，因此其最大值存在于e_d(0)。较之于式(16)完全依靠经验保守地选择k，采用扰动观测器技术可以在保证系统稳定性的前提下减少滑模控制的抖振现象，提高控制系统的性能。

3 仿真结果

在标称系统(1)和不确定性系统(2)中，系统集总参数取为b=0.1、λ=−0.65、c=−1.7、E=0.3和ω=1。初始状态为[x₁(0) x₂(0)]^T=[0.2 0.2]^T。所设计的微分积分终端滑模器参数为α=2、β=2、p₁₁=p₂₁=11、q₁₁=q₂₁=13、k_e=2、η=0.1、k=2；所设计的扰动观测器参数为L=[0 5]^T。

式(2)、式(5)中，d₁属于非匹配扰动而d₂属于匹配扰动。由于滑模控制在滑动模态下对匹配扰动具有不变性，因此在仿真中仅考虑非匹配扰动的对系统性能的影响，取d₁=2sin(t)和d₂=0。

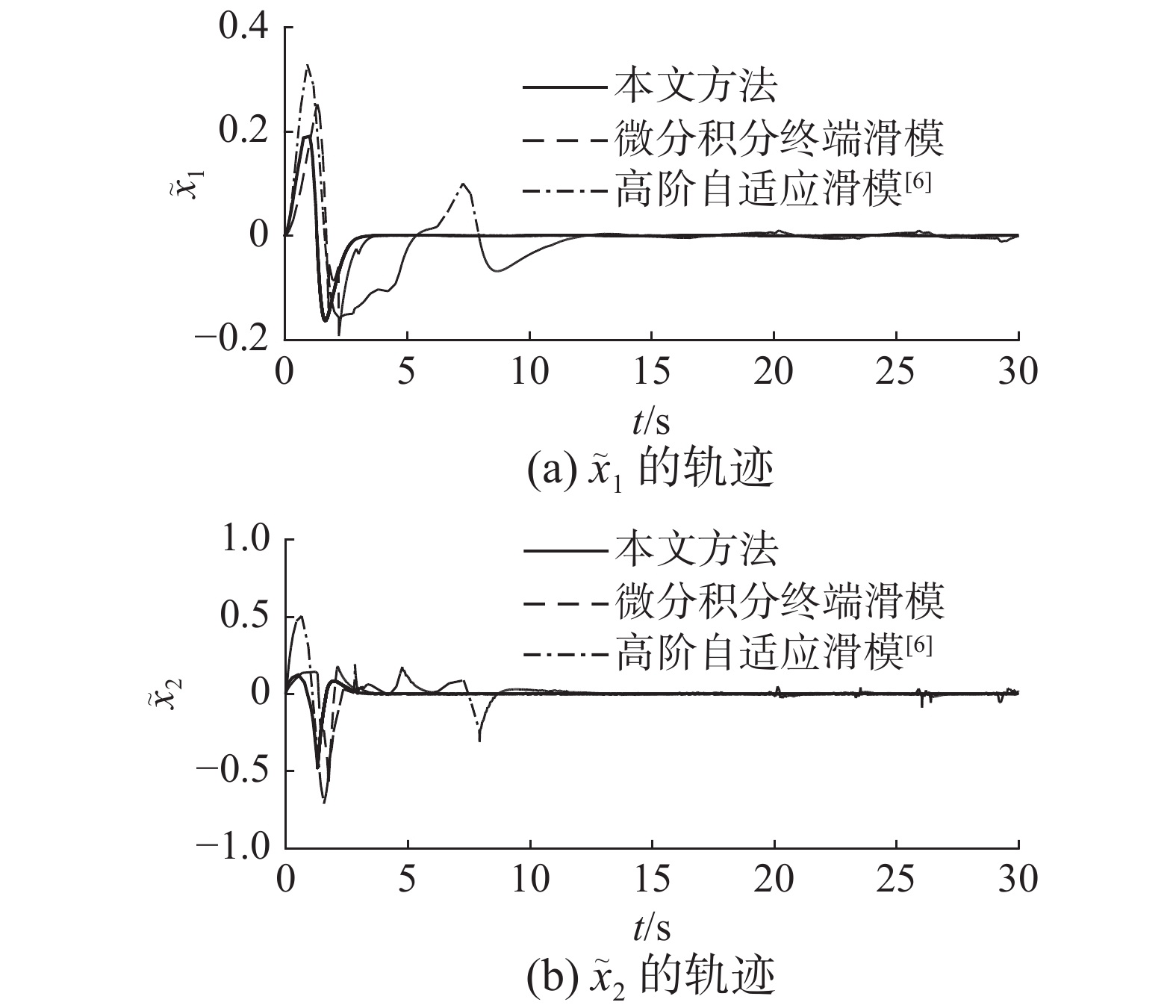
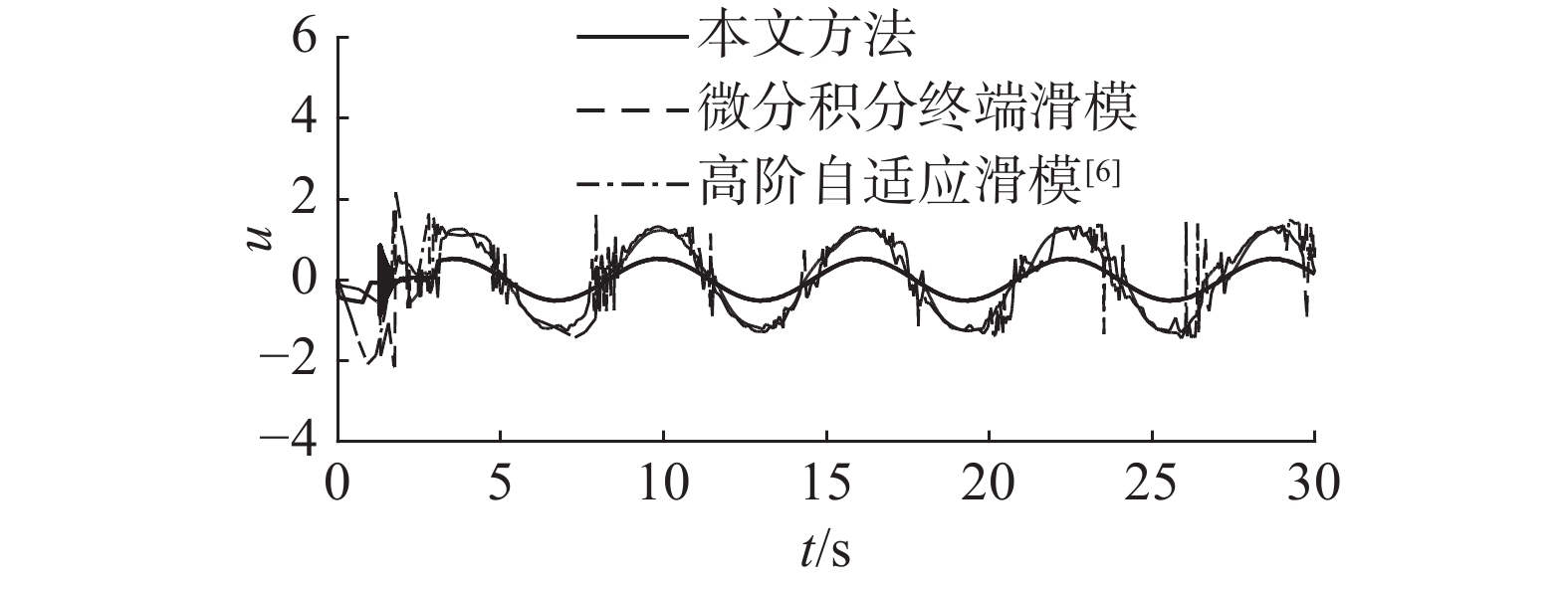
采用文献[6]中的高阶自适应滑模控制方法、微分积分终端滑模控制方法以及本文提出的控制方法进行对比实验，仿真结果如图3 ~ 7所示。如定理2所证，采用所设计的控制策略，冠状动脉系统在非匹配不确定性的影响下能够实现混沌抑制。

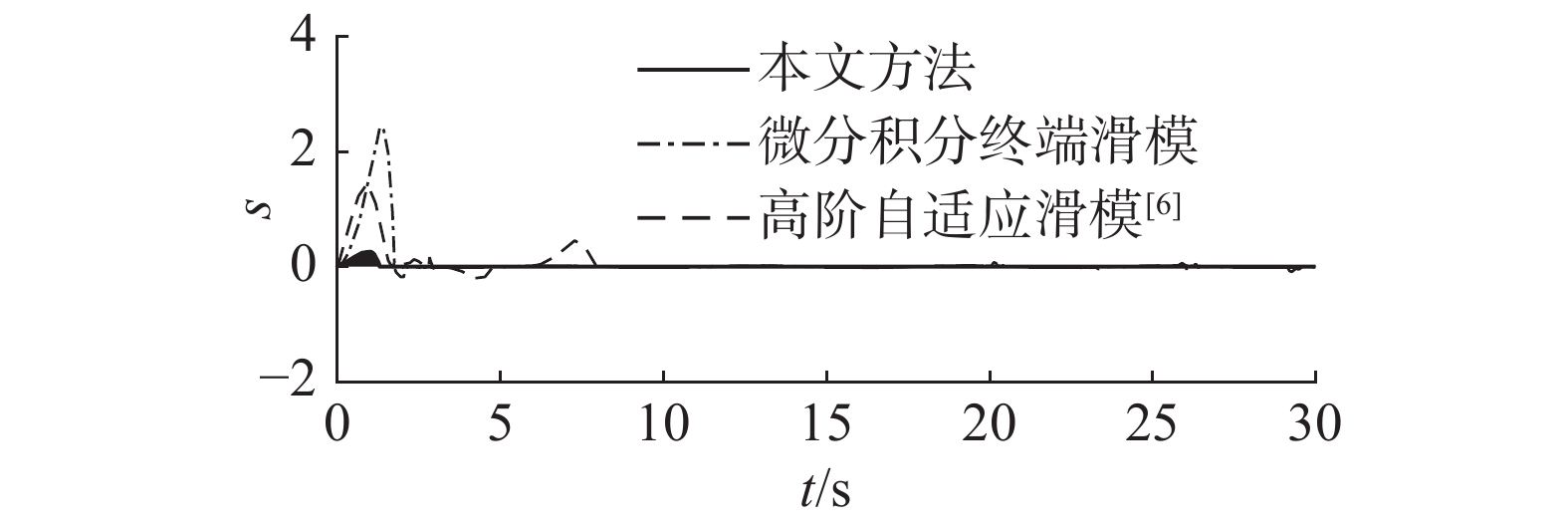
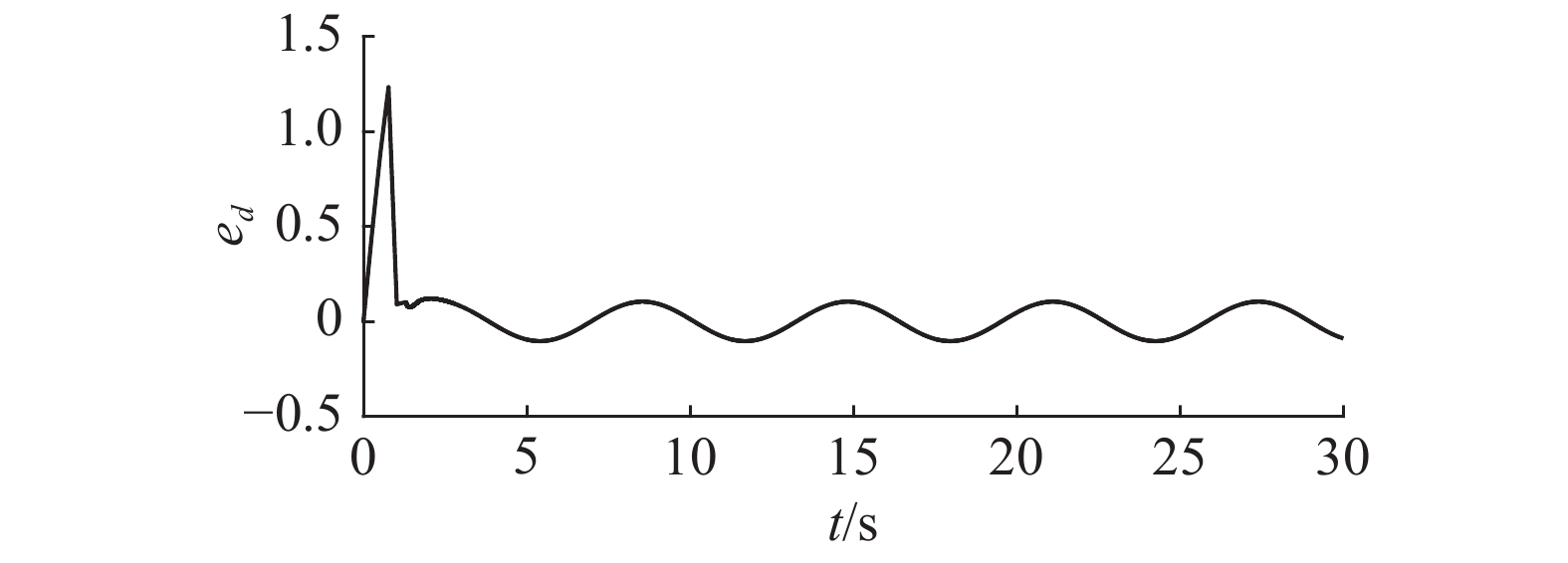
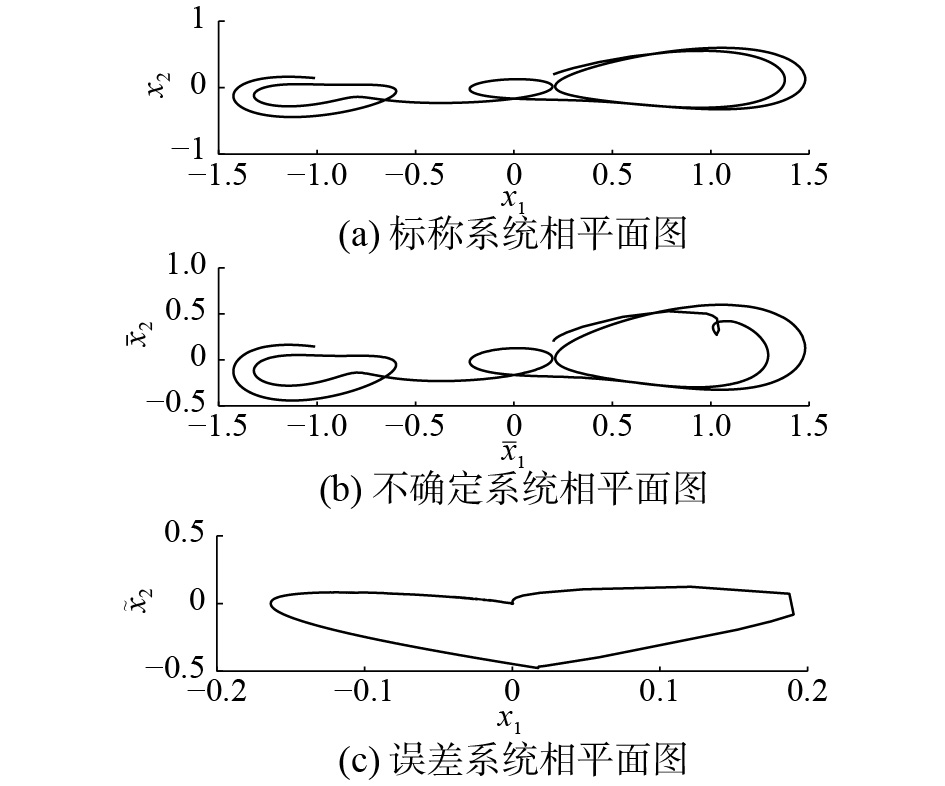
从图3可知，微分积分终端滑模控制方法和扰动观测器可以有效地抑制冠状动脉系统中的混沌现象，具有较高的跟踪精确度。而高阶自适应滑模控制系统受非匹配不确定性的影响较大，动态响应时间较长。图4表示滑模平面变量，如定理1所证，微分积分终端滑模控制方法能够保证系统误差在有限时间内收敛到零。扰动观测器的估计误差示于图5。标称系统(1)、不确定性系统(2)和误差系统(5)的相平面图示于图7。

4 结束语

本文针对冠状动脉系统的混沌抑制问题，提出了微分积分终端滑模控制方法，建立了冠状动脉系统的混沌同步动力学模型，采用扰动观测器克服系统中不确定性的不利影响，利用李雅普诺夫理论分析了所设计混沌抑制控制系统的稳定性，通过与高阶自适应滑模的仿真对比，验证了所提出的控制方法的有效性与可行性。