2. 北京理工大学 自动化学院,北京 100081;
3. 国网山东省电力公司,山东 济南 250000;
4. 昆明北理工产业技术研究院有限公司,云南 昆明 650000
2. School of Automation, Beijing Institute of Technology, Beijing 100081, China;
3. State Grid Shandong Electric Power Company, Ji’nan 250000, China;
4. BIT Industrial Technology Research Institute, Kunming Company Limited, Kunming 650000, China
近年来,多旋翼无人机由于其结构简单、控制灵活、成本低廉以及可扩展性强等优点,成为了人们关注和研究的热点[1-4]。其中自主导航是实现无人机飞行的最重要内容之一,常用的无人机导航方法有:惯性导航、GPS导航、视觉导航、组合导航等[5-6],而对于缺乏GPS信号的无人机室内导航则常采用视觉导航、激光雷达、组合导航等方法[7-8]。随着无人机的室内使用场景日益增多,无人机室内导航已成为众多学者研究的热点问题[9]。路径规划是无人机室内导航的重要环节,通过路径规划可以实现无人机在复杂室内环境中避让障碍物、高效飞行。
Stentz[10-11]首次提出了D*路径规划算法,用于自主机器人在部分已知或完全未知环境中通过局部修正路径,减少计算量,实时获得一条次优路径。Hrabar[12]针对使用立体视觉导航的无人机提出了一种将D*算法与随机路线图法结合的路径规划方法,通过该方法可以实现无人机在未知环境下三维空间避让障碍物的路径规划。郑昌文[13]利用稀疏A*算法实现了离线的三维航迹规划,并通过对稀疏A*算法的动态化实现了无人机遇到未知威胁时的动态轨迹重规划。符小卫等[14]研究了基于Voronoi图和Dijkstra算法的三次样条曲线和序列二次规划的方法。这些研究大多是基于D*算法的无人机三维空间避让障碍物的路径规划,未考虑无人机在轨迹移动时如果距离障碍物较近时会发生与障碍物碰撞或者穿越的情况,不利于无人机室内高精度导航。
本文以通过增加碰撞因子改进D*算法实现了无人机的室内路径规划,并通过布置室内二维码数组图像对改进D*算法进行了试验,验证了改进D*算法对于无人机室内路径规划的适用性。
1 ArUco码的识别和位置求解 1.1 ArUco码的识别本文采用ArUco码作为地面二维标志来设计定位阵列,ArUco系统[15]由Cordoba大学 AVA团队设计并提供面向全平台的SDK,ArUco码(下文简称二维码)由7×7方块阵列,二维码边框为黑色其余方块可以是白色(1)或黑色(0)。
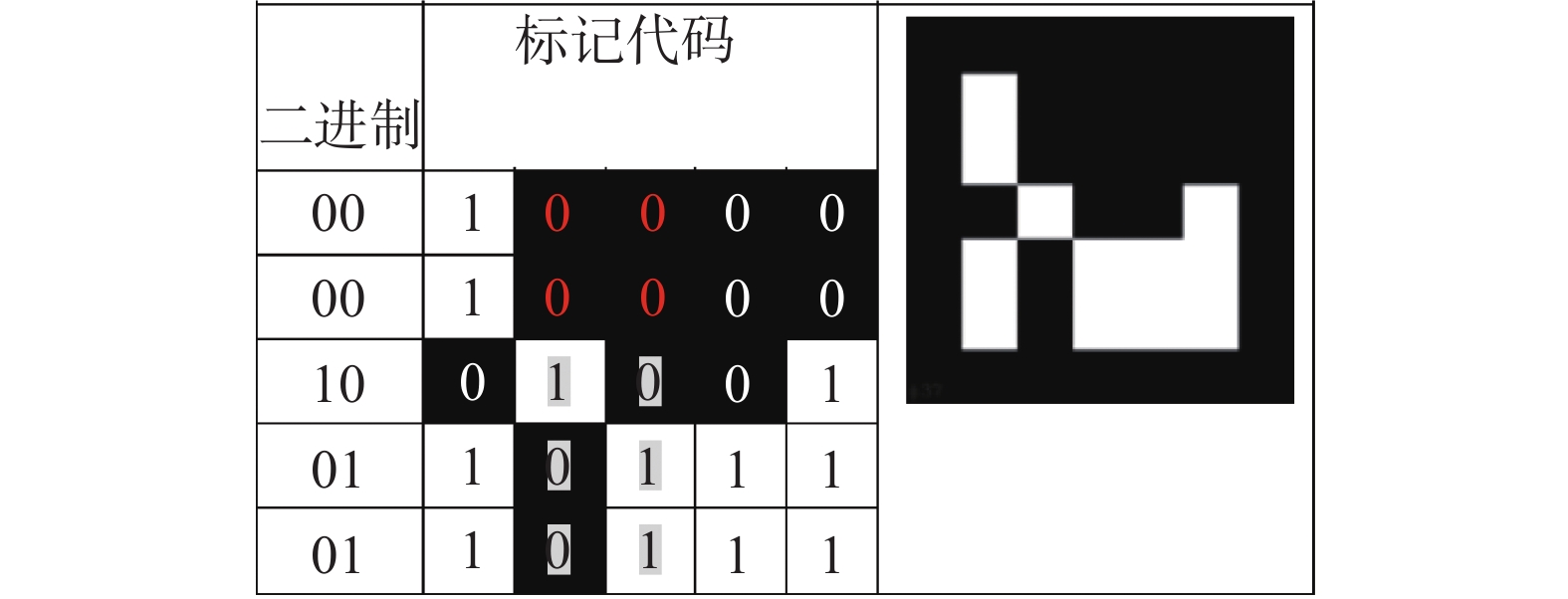
一个ArUco标记是一种合成的方形标记,由一个宽的黑色边框和内部的二进制矩阵构成,这决定了它的标识符(ID)。标记的大小决定了内部矩阵的大小。Aruco码能被当作7×7的布尔居中,外环被黑色充满,能被图像快速检测ArUco码内部数据信息量为(5×5)bit,最大的编码数量为1 024个,每一行使用2bit进行编号,使用另外3bit进行纠错能在任意方向识别出唯一码号,如图1所示解码结果为(00 00 10 01 01)即为37号。
|
Download:
|
| 图 1 No.37 ArUco 二维码 Fig. 1 No.37 ArUco QR code | |
利用OPENCV和ARUCO库可以生成使用的二维码。首先,通过选择aruco模块中一个预定义的字典来创建一个字典对象,具体而言,这个字典是由250个marker组成的,每个marker的大小为(7×7)bit。然而利用语句cv::aruco::drawMarker(dictionary, i, 200, markerImage, 1)生成ID编号为i的二维码。其中,第1个参数为之前创建的字典对象,第3个参数为输出marker的大小,第4个参数为输出图像。
二维码的识别步骤主要有4步:
1)图像分割:提取灰度图像中最突出的轮廓。采用局部自适应阈值的方法来分割marker(图2(b))。
2)轮廓提取和过滤:使用Suzuki等 [16]算法对阈值图像进行轮廓提取。它产生一组图像轮廓,其中大部分与检测目标无关(见图2(c))。然后,使用Douglas-Peucker[17]算法进行多边形近似。由于标记被包围在矩形轮廓中,所以没有近似于4顶点多边形的那些被丢弃。最后,简化了附近的轮廓,只留下外部轮廓。图2(d)显示了从该过程得到的多边形。

|
Download:
|
| 图 2 ArUco码检测步骤 Fig. 2 ArUco code detection steps | |
3)标记代码提取:分析这些轮廓的内部区域以提取其内部代码。首先,通过计算单应性矩阵来消除透视投影(图2(e))。使用Otsu的方法[18]对所得到的图像进行阈值化,其提供了图像分布是双峰的(在这种情况下是正确的)最佳图像阈值。然后,二值化图像被划分为规则网格,并且每个元素根据其中的大多数像素的值被分配值0或1(图5)。第1个测试包括检测黑色边框的存在。如果边界的所有位为0,则使用下述方法分析内部网格。
4)标记识别:在这一点上,有必要确定获得的标记候选哪些属于字典,哪些只是环境的一部分。提取标记的候选码之后,就可获得4个不同的标识符。为了加快这个过程,字典元素使用平衡二叉树排序。为此,标记由通过连接其所有位获得的整数值表示。
1.2 二维码阵列的设计对一幅图像中多个二维码进行识别可以计算出摄像头相对每个二维码的位置和姿态,未被识别的标志不参与位置解算。同时摄像头能在任意方向识别出唯一码号,通过在室内合理布置二维码,综合多个标志解算的信息能够提供较大范围内的无人机全局位置信息。地标阵列除了使用规则排列外,可以通过任意的形式和距离组合,只需要通过人工一次性标定后制表存入机载导航系统存储器中即可。文中以最简单的矩阵规则排列形式为例,所建立的地面定位阵列(后文简称二维码阵列),当确定某二维码为全局坐标系原点后即可以通过几何关系计算出其他二维码在全局坐标中的位置,进而将摄像头解算出相对某二维码的位置转换到全局坐标系下。本文根据ArUco库,生成ID编号为1~100的二维码集,设计如图3所示的二维码地面阵列。其中,单个二维码边长为18 cm,码与码的间距为18 cm,ID编号为1的码的中心为原点,行方向为x方向,列方向为y方向。例如编号为55的二维码位置为(18×8 cm,18×10 cm)。

|
Download:
|
| 图 3 二维码地面阵列 Fig. 3 QR code ground array | |
摄像头经过标定之后,可以解算出二维码相对于摄像头光学中心的旋转向量r和平移向量T以及旋转矩阵R[19],解算过程如下所示:
| $\begin{gathered} \theta = {\rm{norm}}({{r}}) \\ {{r}} = {{r}}/\theta \\ {{R}} = \cos (\theta )I + (1 - \cos \theta ){{rr}}{^{\rm{T}}} + \\ \sin \theta \left[ {\begin{array}{*{20}{c}} 0&{ - {r_z}}&{{r_y}} \\ {{r_z}}&0&{ - {r_x}} \\ { - {r_y}}&{{r_x}}&0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_{11}}}&{{R_{12}}}&{{R_{13}}} \\ {{R_{21}}}&{{R_{22}}}&{R{}_{23}} \\ {{R_{31}}}&{{R_{32}}}&{{R_{33}}} \end{array}} \right] \\ \end{gathered} $ | (1) |
| ${\bf{euler}}{_i} = \left[ \begin{gathered} {\gamma _{{\rm{local}}}} \\ {\theta _{{\rm{local}}}} \\ {\psi _{{\rm{local}}}} \\ \end{gathered} \right] = \left[ \begin{gathered} \arctan (\frac{{{R_{23}}}}{{{R_{33}}}}) \\ - \arcsin ({R_{13}}) \\ \arctan (\frac{{{R_{12}}}}{{{R_{11}}}}) \\ \end{gathered} \right]$ | (2) |
| ${\bf{pos}}{_i} = \left[ \begin{gathered} {x_{{\rm{local}}}} \\ {y_{{\rm{local}}}} \\ {z_{{\rm{local}}}} \\ \end{gathered} \right] = - {{{R}}'}\cdot{{T}}$ | (3) |
根据式(2)可以计算出摄像头当前欧拉角,式(3)可以计算出摄像头当前相对某个二维码的局部位置,然后根据该二维码的全局坐标计算出摄像头当前的全局坐标位置。进一步文中基于扩展卡尔曼滤波器对二维码位置、光流传感器速度测量值和机载IMU数据进行融合得到最优位姿估计。
2 改进D*路径规划算法无人机室内全局路径规划是无人机研究领域的一个重要课题。路径规划的含义为已知无人机运动的起点和终点,通过机载传感器对周围环境进行描述,得到自由区域和障碍区域,从而规划出一条从起点到终点并且避开障碍物的最短路径。本文在对各种主流路径规划算法比较之后,基于室内地面二维码阵列标志,选用D*算法[20],并对D*算法做了改进,实现无人机室内自主飞行。
2.1 D*路径规划为了在室内环境中寻找最短路径,首先需要建立环境模型。D*算法采用栅格表示地图,将地图信息记录在每一个栅格上,定义该栅格的属性为自由或者障碍。无人机的飞行轨迹被栅格离散化之后,每个栅格上的运动信息表征了无人机在这个栅格上的飞行方向。理论上,无人机在每个栅格上的运动有无数种,但考虑到模型建立的复杂性,一般在实际运用中只定义8个方向的运动,分别为:前、后、左、右、右前、右后、左前、左后,如图4所示。

|
Download:
|
| 图 4 栅格地图及无人机可能运动方向 Fig. 4 Raster map and possible direction of movement of the drone | |
地图上的栅格采用矩阵方式储存[21],单个栅格的信息记录在矩阵中的第i行和第j列,记为G(i, j)。采用这种矩阵存储栅格地图的方法,可建立起环境的整幅地图。
在室内无人机飞行空间中,只考虑水平方向,可将飞行空间二维化,其中无人机高度控制由超声波传感器实现。栅格地图模型建立后,需要对每个栅格设置编码信息。编码设置如下:1为含有障碍的栅格,0为自由栅格(无障碍),start为起点,end为终点。本文所建N×N地图如图5所示,其中N=10(可调节)。

|
Download:
|
| 图 5 栅格地图 Fig. 5 raster map | |
D*算法是一种典型的启发式搜索算法,其启发中的代价用代价函数表示为
| $f(n) = g(n) + h(n)$ | (4) |
式中:
| $h(n) = \max (|{x_{{\rm{start}}}} - {x_i}|,|{y_{{\rm{start}}}} - {y_i}|)$ | (5) |
D*算法的实现步骤为从目标节点开始遍历搜索直到找到起始节点。给定起始点s和目标点d,创建2个空链表OpenList和CloseList,计算流程如图6所示。
2.2 改进D*算法当无人机沿着D*算法规划的轨迹在二维码阵列上移动时,距离设定的障碍物比较近,容易发生碰撞,导致无人机事故;而且在同一直线上的路径点,如果无人机沿着设定轨迹飞行会浪费一定的时间,因为从一个二维码飞到一个二维码存在加速、减速、判断等待时间。因此本文对D*算法做了一定的改进。

|
Download:
|
| 图 6 D*算法流程图 Fig. 6 D* algorithm flow chart | |
D*算法中G值为父节点G值与父节点移动到当前节点G值之和,其中父节点移动到当前节点的G值定义为10(直线移动)或者14(斜向移动)。本文通过加入碰撞因子,来改变G值的计算方式。具体操作方式为:在依次扩展周围8个子节点时,加入对每个子节点周围8个节点的判断,如果是子节点的直线方向(前、后、左、右)存在障碍点,加入碰撞因子Ob,则当前节点移动到子节点的路径代价G值为10+Ob(代价增加Ob=8);如果是子节点的斜向方向(右前、右后、左前、左后)存在障碍点,则当前节点移动到子节点的路径代价G值为10+Ob/2(代价增加Ob=4),因为直线方向上存在障碍点的碰撞几率要比斜向方向的大。实验规划的路径结果如图7所示,可以看出在图7(b)中路径避开了一些危险点。

|
Download:
|
| 图 7 改进前后D*路径规划 Fig. 7 Before and after improved D* path planning | |
通过增加碰撞因子规划出的安全路径之后,无人机要沿着路径上二维码的编号依次飞行。对于在同一条直线上的二维码节点,依次沿着码飞行只会降低飞行效率。而且到达某个码附近之后还需要做细微的调整直到满足一定的死区范围才能飞往下一个二维码,这样大大增加了飞行时间。本文对同一直线上的二维码路径信息做出判断,跳过中间点,直接从直线的起点飞往终点,大大节省了无人机的飞行时间。
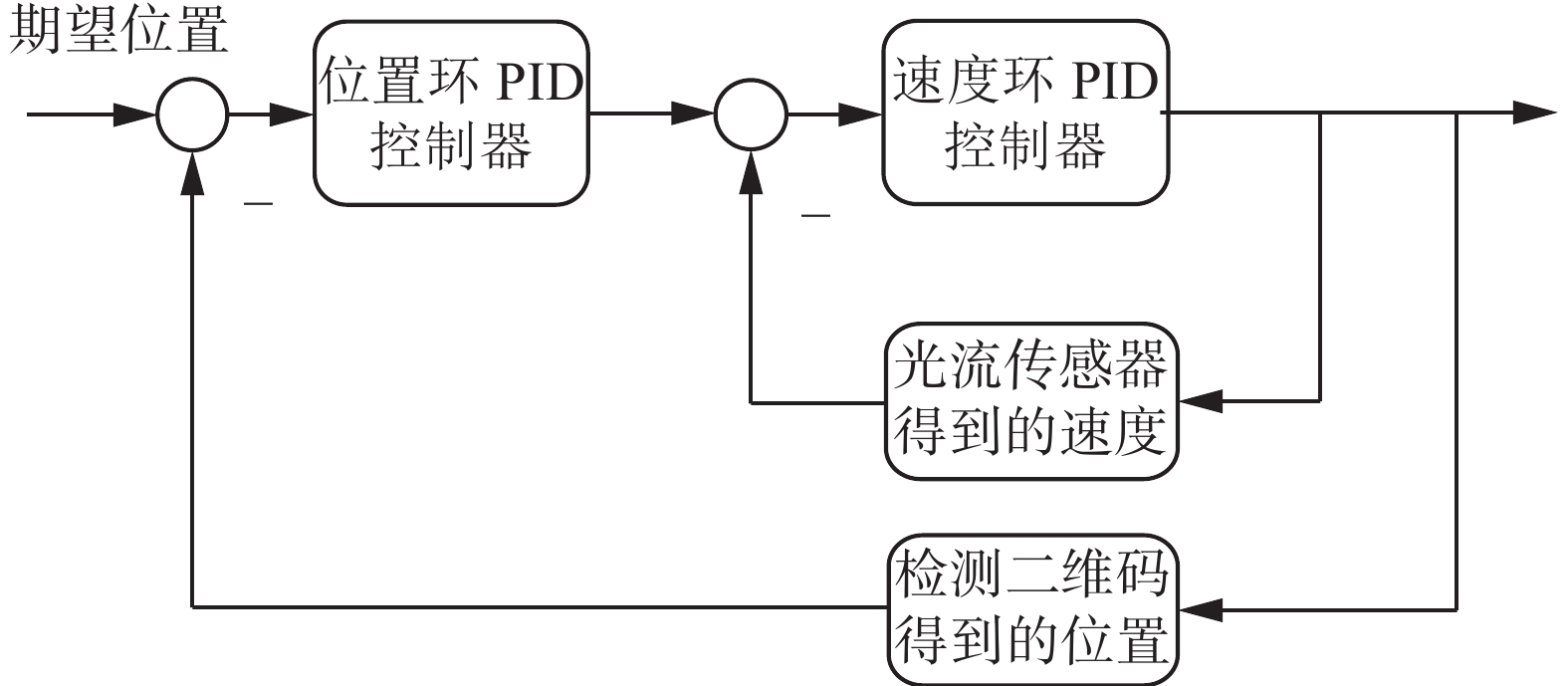
2.3 控制器设计将无人机在二维码阵列中的全局坐标与期望坐标做差,将差值送入串级PID控制器[22],最终计算出飞行时x、y方向控制量,实现无人机在二维码阵列上的自主导航,控制结构如图8所示。
|
Download:
|
| 图 8 串级PID控制器框图 Fig. 8 Cascade PID controller block diagram | |
采用位置环变积分PID控制器。这里采用变积分PID,在系统偏差较大时,减弱积分作用或者消除积分作用,在系统偏差较小时增大积分作用。可以避免因积分作用太大导致系统超调和积分饱和,也可以避免积分作用太小导致难以消除静态误差。因此加入了变积分系数index。
| $\begin{gathered} {e_x} = x - {x_{\exp }} \\ {e_y} = y - {y_{\exp }} \\ {u_x} = {\rm{kp}}_x{e_x} + {\lambda _x}{\rm{ki}}{_x}\int_0^t {{e_x}(\delta )} {\rm{d}}\delta + {\rm{kd}}{_x}\frac{{{\rm{d}}{e_x}(t)}}{{{\rm{d}}t}} \\ {u_y} = {\rm{kp}}{}_y{e_y} + {\lambda _y}{\rm{ki}}{_y}\int_0^t {{e_y}(\delta )} {\rm{d}}\delta + {\rm{kd}}{_y}\frac{{{\rm{d}}{e_y}(t)}}{{{\rm{d}}t}} \\ \end{gathered} $ |
| $ {u_x} = {\rm{kp}}{_x}{e_x} + {\rm{index}} \cdot {\rm{ki}}{_x}\int_0^t {{e_x}} \left( \delta \right){\rm{d}}\delta + {\rm{kd}}{_x}\displaystyle\frac{{{\rm{d}}{e_x}\left( t \right)}}{{{\rm{d}}t}} $ |
式中:x、y为Kalman滤波器位置输出值;xexp和yexp为期望位置;
| ${\rm{index}} = \left\{ {\begin{array}{*{20}{c}} 0,&{\,\, e > 200} \\ {\displaystyle\frac{{200 - e}}{{100}}},&{\text{其他}} \\ 1,&{\,\, e < 100} \end{array}} \right.$ | (6) |
因位置环已经做了变积分,而且位置环的输出为速度环的输入,因此速度环PID控制器设计为一般PID控制形式为
| $\begin{gathered} {e_{vx}} = {v_x} - {v_x}\_\exp \\ {e_{vy}} = {v_y} - {v_y}\_\exp \\ {u_{vx}} = {\rm{kp}}{}_{vx}{e_{vx}} + {\rm{ki}}{_{vx}}\int_0^t {{e_{vx}}(\delta )} {\rm{d}}\delta + {{\rm{kd}}_{vx}}\displaystyle\frac{{{\rm{d}}{e_{vx}}(t)}}{{{\rm{d}}t}} \\ {u_{vy}} = {\rm{kp}}{}_{vy}{e_{vy}} + {\rm{ki}}{_{vy}}\int_0^t {{e_{vy}}(\delta )} {\rm{d}}\delta + {{\rm{kd}}_{vy}}\displaystyle\frac{{{\rm{d}}{e_{vy}}(t)}}{{{\rm{d}}t}} \\ \end{gathered} $ | (7) |
硬件系统包括:330 mm轴距四旋翼无人机平台、自制飞控系统、超声波测距仪、光流传感器、摄像头云台和树莓派,文中实验系统通过2.4 GHz射频信号与地面站通信同时接受遥控信号。实验系统框图如图9所示。

|
Download:
|
| 图 9 实验系统框图 Fig. 9 Experimental system block diagram | |
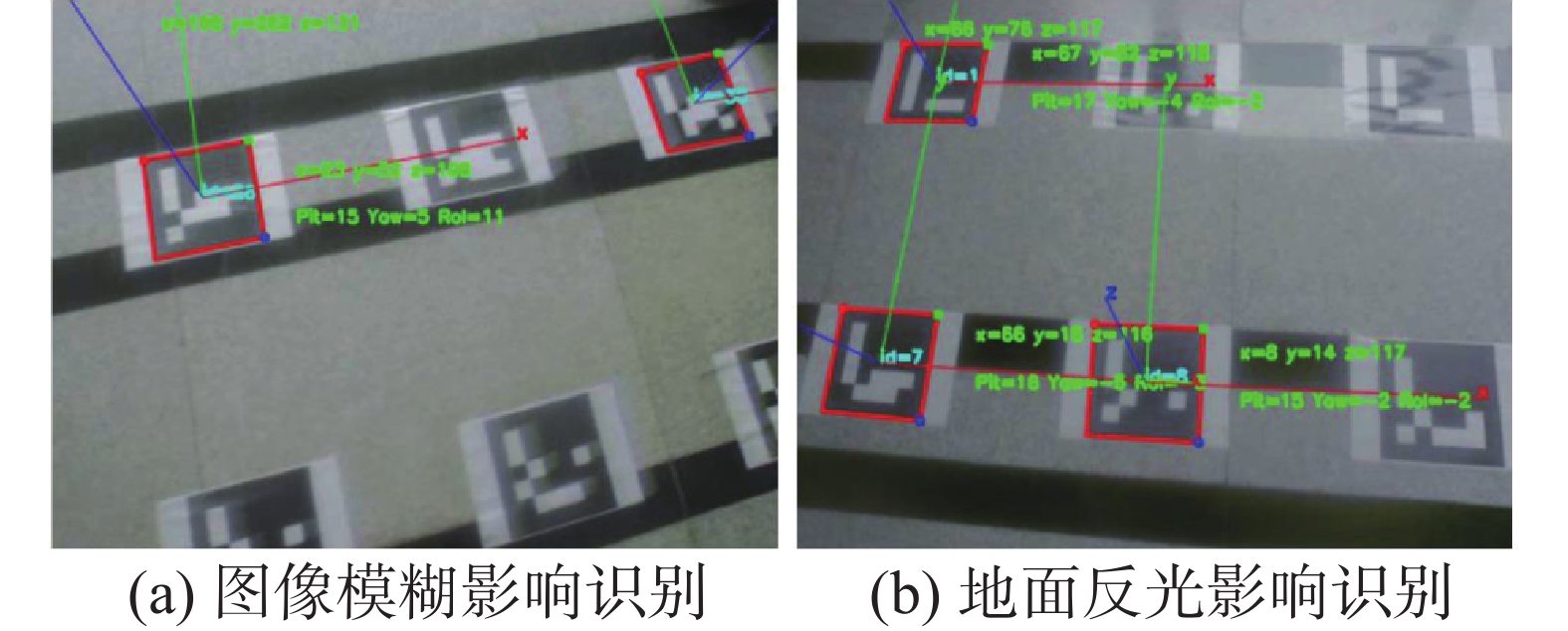
图10为飞行过程中二维码识别效果,可以看出机载摄像头可以同时识别出多个二维码,并可以解算出与单个二维码的局部坐标位置,进而融合得到无人机的全局坐标位置。
|
Download:
|
| 图 10 二维码识别效果 Fig. 10 QR code recognition effect | |
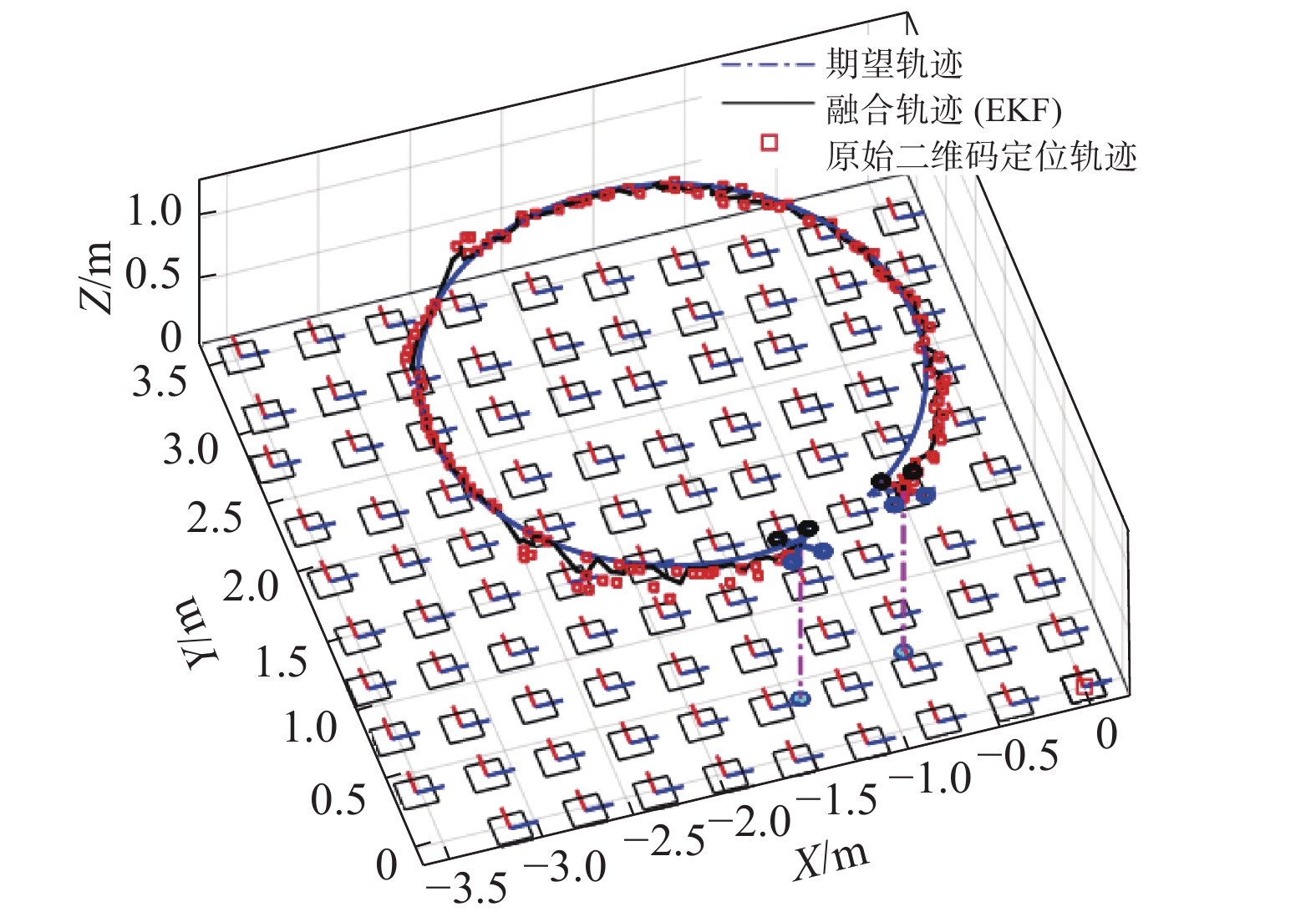
文中采用扩展卡尔曼滤波器(EKF)结合飞行器机载IMU数据,光流传感器速度测量数据和二维码识别位置数据进行融合得到平滑连续的全局定位信息。图11为采用EKF融合得到的无人机位置估计作为反馈实现的圆形轨迹跟踪,可以看到融合后的无人机位置信息光滑连续,所设计控制器能较好地跟踪期望命令。
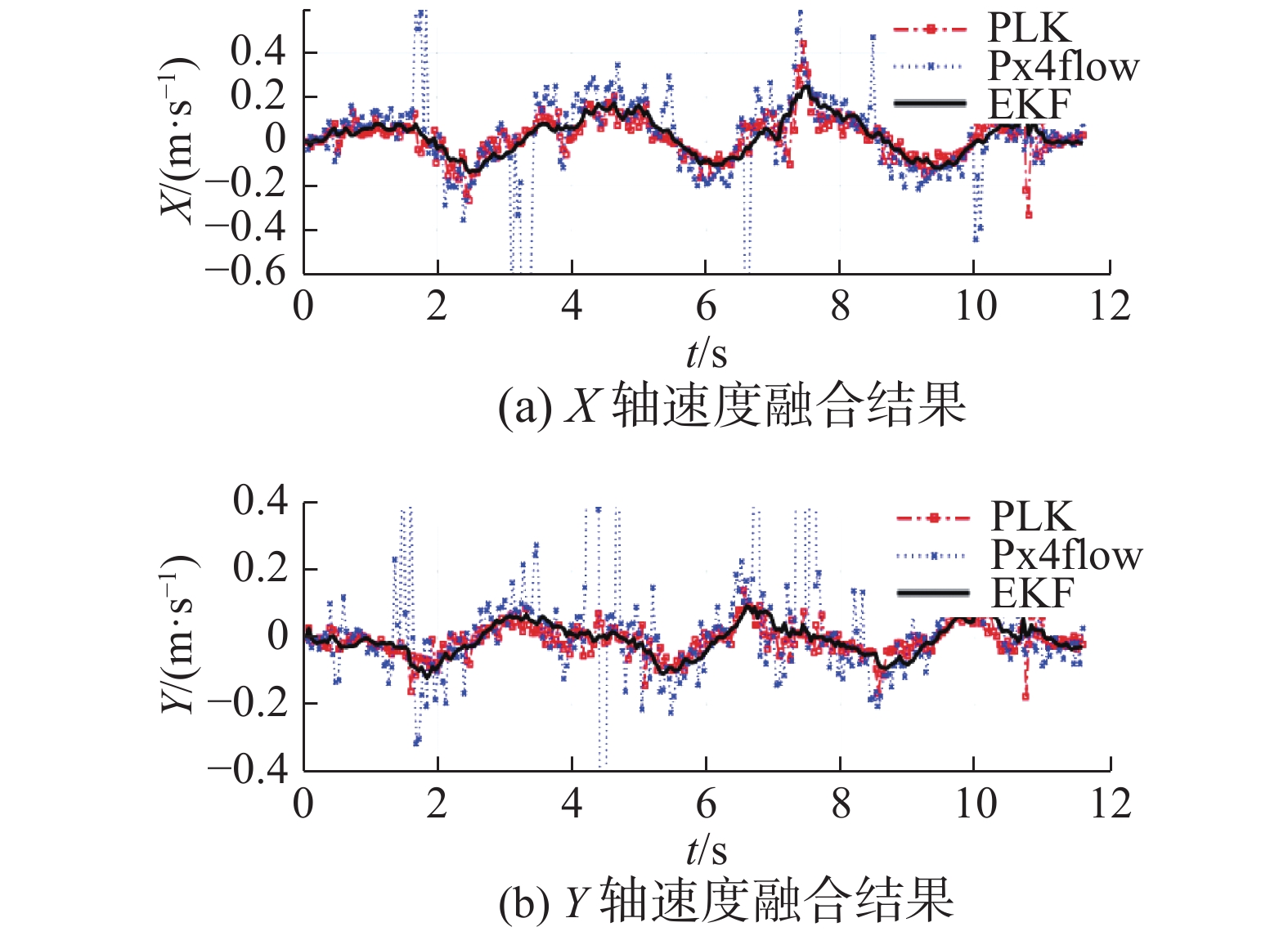
图12为无人机速度估计结果,可以看到EKF估计出的速度相比Pixflow传感器或PLK光流法得到的原始光流测量速度更加平滑,噪声更小。
|
Download:
|
| 图 11 二维的阵列中圆形轨迹跟踪 Fig. 11 Circular trajectory tracking in a two-dimensional array | |
|
Download:
|
| 图 12 无人机速度融合 Fig. 12 UAV speed fusion | |
图13为实验中规划的无人机路径信息,已用实线标出,图中最下方3、4、26、44、54、65、66为无人机运动路径上的二维码编号。

|
Download:
|
| 图 13 仿真路径 Fig. 13 simulation path | |
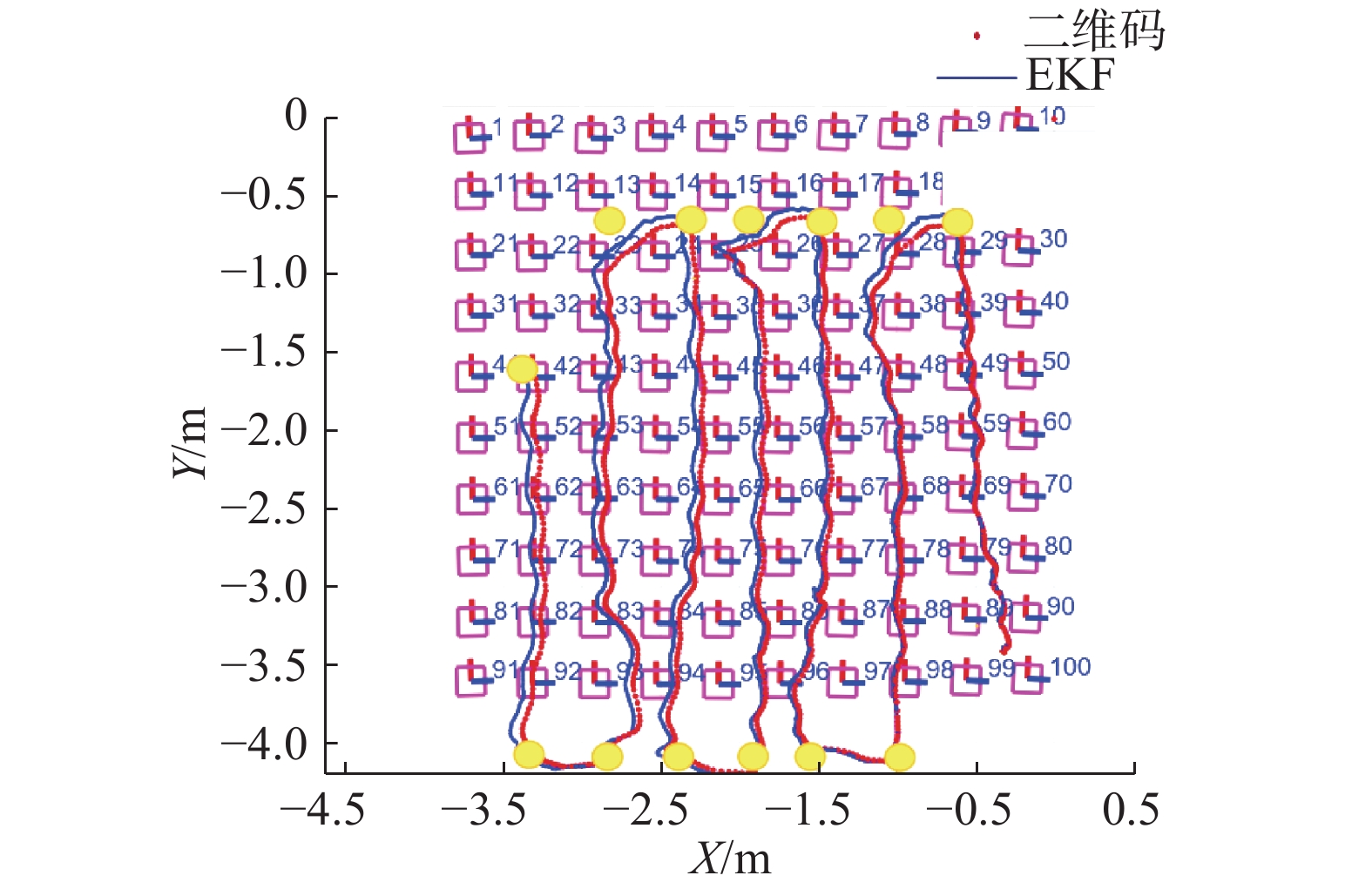
图14为在地面站显示的无人机的实际路径,其中绿色方块位置为起点,蓝色方块为无人机最后停止位置,实线为无人机运动路径。可以看出,无人机实际移动路径与规划路径形状相似。
|
Download:
|
| 图 14 实际飞行实验 Fig. 14 Actual flight experiment | |
图14为采用所提改进D*算法进行的实际飞行实验,实验中给定期望航点,同时设定3个障碍物如图中红色矩形所示,使用所提路径规划算法进行规划并控制飞行器按给定路径飞行,从图中可以看到所提算法成功地规划出了经过各航点所需的期望路径并与障碍物保证一定距离,飞行器能较好地按规划路线进行飞行。
4 结束语文中提出了一种改进D*算法,在传统算法上基于引入障碍因子之后使无人机与障碍物保持一定的安全距离,通过斜率判断只取直线路径的起始点,省略中间点,提高了无人机飞行效率。基于二维码阵列实现了室内低成本高精度的定位系统,进一步使用扩展卡尔曼滤波器对二维码、光流和IMU数据融合得到了无人机精确连续的状态估计,保证了轨迹跟踪反馈控制的可靠性,所设计的控制器能较好地跟踪期望轨迹,文中系统满足室内低成本微小型无人机的导航和定位需求。
| [1] |
LIM H, PARK J, LEE D, et al. Build your own quadrotor: open-source projects on unmanned aerial vehicles[J]. IEEE robotics and automation magazine, 2012, 19(3): 33-45. DOI:10.1109/MRA.2012.2205629 ( 0) 0)
|
| [2] |
RASMUSSEN J, NIELSEN J, GARCIA-RUIZ F, et al. Potential uses of small unmanned aircraft systems (UAS) in weed research[J]. Weed research, 2013, 53(4): 242-248. DOI:10.1111/wre.2013.53.issue-4 ( 0) 0)
|
| [3] |
XIONG Jingjing, ZHENG Enhui. Position and attitude tracking control for a quadrotor UAV[J]. ISA transactions, 2014, 53(3): 725-731. DOI:10.1016/j.isatra.2014.01.004 ( 0) 0)
|
| [4] |
KOTTATH R, NARKHEDE P, KUMAR V, et al. Multiple model adaptive complementary filter for attitude estimation[J]. Aerospace science and technology, 2017, 69: 574-581. DOI:10.1016/j.ast.2017.07.011 ( 0) 0)
|
| [5] |
唐强, 张翔伦, 左玲. 无人机航迹规划算法的初步研究[J]. 航空计算技术, 2003, 33(1): 125-128, 132. TANG Qiang, ZHANG Xianglun, ZUO Ling. Initial study on the path planning's algorithms for unmanned aerial vehicles[J]. Aeronautical computer technique, 2003, 33(1): 125-128, 132. DOI:10.3969/j.issn.1671-654X.2003.01.033 (  0) 0)
|
| [6] |
王俊, 周树道, 朱国涛, 等. 无人机航迹规划常用算法[J]. 火力与指挥控制, 2012, 37(8): 5-8. WANG Jun, ZHOU Shudao, ZHU Guotao, et al. Research of common route planning algorithms for unmanned air vehicle[J]. Fire control and command control, 2012, 37(8): 5-8. DOI:10.3969/j.issn.1002-0640.2012.08.002 (  0) 0)
|
| [7] |
白志君. 四旋翼无人机室内自主导航系统的研究与实现[D]. 厦门: 厦门大学, 2014. BAI Zhijun. Study and realization on indoor autonomous navigation system for quad-copter[D]. Xiamen: Xiamen University, 2014. (  0) 0)
|
| [8] |
何雨枫. 室内微小型无人机路径规划算法研究[D]. 南京: 南京航空航天大学, 2014. HE Yufeng. Research on indoor MUAV path planning[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. (  0) 0)
|
| [9] |
黄媛媛. 基于数据融合的室内无人机导航避障研究[D]. 成都: 成都理工大学, 2017. HUANG Yuanyuan. Research on navigation avoidance of indoor UAV based on data fusion[D]. Chengdu: Chengdu University of Technology, 2017. (  0) 0)
|
| [10] |
STENTZ A. The D* algorithm for real-time planning of optimal traverses[R]. Carnegie: Carnegie Mellon University, 1994.
( 0) 0)
|
| [11] |
STENTZ A. The focussed D* algorithm for real-time replanning[C]//Proceedings of the 14th International Joint Conference on Artificial Intelligence. Montreal, Canada, 1995: 1652–1659.
( 0) 0)
|
| [12] |
HRABAR S. 3D path planning and stereo-based obstacle avoidance for rotorcraft UAVs[C]//Proceedings of 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems. Nice, France, 2008: 807–814.
( 0) 0)
|
| [13] |
郑昌文. 飞行器航迹规划方法研究[D]. 武汉: 华中科技大学, 2003. ZHENG Changwen. Research on route planning for air vehicles[D]. Wuhan: Huazhong University of Science and Technology, 2003. (  0) 0)
|
| [14] |
符小卫, 高晓光. 一种无人机路径规划算法研究[J]. 系统仿真学报, 2004, 16(1): 20-21, 34. FU Xiaowei, GAO Xiaoguang. Study on a kind of path planning algorithm for UAV[J]. Journal of system simulation, 2004, 16(1): 20-21, 34. DOI:10.3969/j.issn.1004-731X.2004.01.007 (  0) 0)
|
| [15] |
GARRIDO-JURADO S, MUÑOZ-SALINAS,R, MADRID-CUEVAS F J, et al. Generation of fiducial marker dictionaries using mixed integer linear programming[J]. Pattern recognition, 2016,3(51): 481-491.
( 0) 0)
|
| [16] |
SUZUKI S, ABE K. Topological structural analysis of digitized binary images by border following[J]. Computer vision, graphics, and image processing, 1985, 30(1): 32-46. DOI:10.1016/0734-189X(85)90016-7 ( 0) 0)
|
| [17] |
DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica: the international journal for geographic information and geovisualization, 1973, 10(2): 112-122. DOI:10.3138/FM57-6770-U75U-7727 ( 0) 0)
|
| [18] |
OTSU N. A threshold selection method from gray-level histograms[J]. IEEE transactions on systems, man, and cybernetics, 1979, 9(1): 62-66. DOI:10.1109/TSMC.1979.4310076 ( 0) 0)
|
| [19] |
KRAJNÍK T, VONÁSEK V, FIŠER D, et al. AR-Drone as a platform for robotic research and education[J]//OBDRŽÁLEK D, GOTTSCHEBER A. Research and Education in Robotics-EUROBOT 2011. Berlin, Heidelberg: Springer, 2011: 172–186.
( 0) 0)
|
| [20] |
FERGUSON D, STENTZ A. Field D*: an interpolation-based path planner and replanner[M]//THRUN S, BROOKS R, DURRANT-WHYTE H. Robotics Research. Berlin, Heidelberg: Springer, 2007: 239–253.
( 0) 0)
|
| [21] |
魏宁, 刘一松. 基于栅格模型的移动机器人全局路径规划研究[J]. 微计算机信息, 2008, 24(11): 229-231. WEI Ning, LIU Yisong. Research on Grid-Base global path planning for mobile robot[J]. Control and automation, 2008, 24(11): 229-231. DOI:10.3969/j.issn.1008-0570.2008.11.094 (  0) 0)
|
| [22] |
NEMRA A, AOUF N. Robust INS/GPS sensor fusion for UAV localization using SDRE nonlinear filtering[J]. IEEE sensors journal, 2010, 10(4): 789-798. DOI:10.1109/JSEN.2009.2034730 ( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


