2. 桂林电子科技大学 广西自动检测重点实验室,广西 桂林 541004
2. Guangxi Key Laboratory of Automatic Detection, Guilin University of Electronic Technology, Guilin 541004, China
交通标志识别[1]是智能汽车的关键技术之一,受到国内外学者和汽车厂商的广泛关注。许多分类器已经开始应用于交通标志的识别,如支持向量机、贝叶斯分类器和随机森林分类器等。这些分类器通常先利用特征描述方法,如加速鲁棒特征(speeded up robust features, SURF)、尺度不变特征变换(scale-invariant feature transform, SIFT)、方向梯度直方图(histogram of oriented gradient, HOG)以及局部二值模式(local binary patterns, LBP)等对训练样本进行局部特征提取,然后对这些特征进行训练,实现对交通标志的识别。例如,Berkaya等[2]提取并整合交通标志图像的LBP、Gabor和HOG等3类特征,利用SVM完成最后的识别。Hoferlin等[3]通过提取SIFT、SURF等特征,结合人工神经网络得到交通标志的识别结果。张卡等[4]基于中心投影特征,利用概率神经网络实现了对交通标志的识别。Lu等[5]采用基于稀疏表示的图嵌入方法也获得了较好的识别效果。宋文杰等[6]采用Hu不变矩和凸壳算法,利用水平和垂直方向直方图特征对待识别区域进行放缩匹配,实现对交通标志的识别。上述特征描述方法通常由人工设计,主要依靠先验知识,人工设计的好坏往往会对实际性能产生很大影响,识别精度和识别效率会有较大起伏,在实际应用中存在着很大的挑战。
2006年加拿大多伦多大学科学家Hinton提出了深度学习[7-8]的概念,它是一种可以通过多层表示来对数据之间的复杂关系进行建模的算法,通过构建具有多个中间层的神经网络模型,将特征和分类器结合到一个框架中,通过组合低层特征形成更为抽象的高层特征,提升分类或识别的准确性。LECUN等[9]已证明深度学习模型相比传统的BP神经网络、SVM等浅层网络具有更强的特征表达和泛化能力,在图像识别、音频信号处理、复杂控制系统建模等领域表现出优越的性能[10-12]。基于深度学习的特征提取方法在交通标志识别中也取得了很好的效果,例如,文献[13]利用深度神经网络对交通标志进行识别,取得了较高的识别率;文献[14]基于图模型与卷积神经网络提出了一种针对限速标志的交通标志识别方法,也取得了较好的效果。采用深度学习的方法首先需要构造出一个多层的神经网络,再通过大量的样本对网络进行训练,得到最终的网络模型。样本集的质量和数量往往会对最终的识别模型造成较大的影响,Chawla等[15]已证明样本质量对于分类的重要性,训练样本过多,会导致训练时间增加,而低质量样本会使训练模型不能充分学习样本特征,无法获得有效的识别模型。
为减少低质量样本对训练的影响,同时避免传统特征描述方法在图像识别领域存在的识别精度低和识别效率差等问题,本文提出了一种基于图像聚类的交通快速CNN快速识别算法,利用图像聚类和图像预处理算法对原始样本进行优化,在此基础上利用深度学习模拟人脑认知的多层结构,通过网络提取和学习交通标志图像特征,最终实现具有深层次的表达特征,实现对交通标志的快速识别。
1 交通标志快速识别算法设计CNN等深度学习方法通过提取数据的低层特征,得到抽象的高层特征,从而实现更为有效的特征表达,低层特征如待识别对象的纹理、边缘信息等,高层特征如语义、结构等信息。样本质量对于网络的训练、特征的提取有着重要的作用,会直接影响最终模型的好坏。
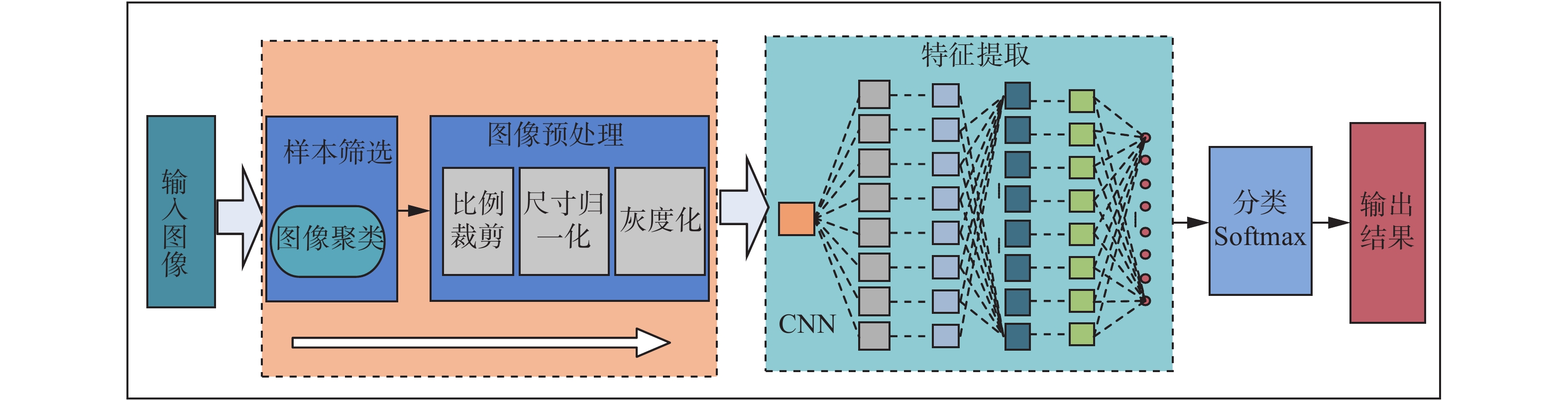
为了优化样本质量,提高识别效果,本文所提出的交通标志识别算法(见图1),主要从3个方面展开:1)采用图像聚类算法,对原始数据进行优化,筛选掉原始样本中的低质量数据,在保证样本数量的前提下,提高样本整体质量;2)通过多种图像预处理方法,如比例裁剪、尺寸归一化、灰度化等,对聚类后的样本进行预处理,样本集整体质量得到进一步提升;3)以LeNet-5网络[16]为基础,通过优化网络结构参数,构造出一个9层CNN结构,并在Caffe平台下利用德国GTSRB数据集设计完成了相关实验,在瑞典BTSD数据集上进行迁移测试,证明了算法的有效性。
|
Download:
|
| 图 1 交通标志识别算法框架 Fig. 1 Traffic sign recognition algorithm framework | |
聚类算法[17]是机器学习中常用的一种算法,一般采用无监督学习的方式进行,它可以根据样本间的关系,优化样本质量,降低训练样本的规模,减少低质量样本数据对训练的影响,提高最终的模型效果。在以深度学习为主的各种图片识别任务中,数据集的质量和数量会对训练结果造成较大的影响,直接影响最终模型的好坏。为了提高CNN训练效果,文中采用了图像聚类算法,通过聚类可以获知数据集的分布特性及分布状况,将数据中的相似数据和异常数据区分开来,从而了解数据集的内在分布结构,简化并提高样本集的整体质量。
相较于划分聚类、密度聚类以及网格聚类等常用的聚类方法,层次聚类算法计算简单快捷,对距离等度量标准的选择敏感性较低,可靠性更高,且不需要事先确定类的数目,更易发现类间的层次关系。根据类间距离计算方式的不同,层次聚类算法可分为Complete-linkage、Single-linkage、Average-linkage 3种,其中Single-linkage聚类算法以样本之间的最小距离,作为相似度的度量,计算简单,在数据量较多的情况下可以有效降低时间复杂度。因此,本文采用Single-linkage聚类算法[18]对原始数据进行聚类处理,筛选掉原始数据中部分低质量数据,从而对样本整体质量进行优化,保证CNN训练效果。Single-linkage聚类算法采用Agglomerative机制,即每次把两个旧类合并为一个新类,最终把所有样本数据合并为一类为止。
Single-linkage算法的实现过程描述如下:
1)将数据集D中的每个数据分别看成一类,共得到N类,每类仅包含一个数据,每两类之间的距离就是它们所包含的数据之间的距离;
2)计算出距离最近的两个类,将它们合并为一类,总类数变成N-1;
3)计算新的类与所有旧类之间的距离;
4)重复步骤2)和步骤3),直到所有数据合并为一类为止。
本文采用欧氏距离来度量原始样本间的相似性,用R、G、B 3个颜色通道作为每幅图像的特征向量,对应的欧式距离可以表示为
| ${d_{{{pq}}}} = \sqrt {{{({{{p}}_x} - {{{q}}_x})}^2} + {{({{{p}}_y} - {{{q}}_y})}^2} + {{({{{p}}_z} - {{{q}}_z})}^2}} $ | (1) |
式中,x、y、z为图中p、q的R、G、B分量。
通过对数据集中的样本进行聚类处理,可以有效筛选出低质量的样本数据,图2是以GTSRB数据集中限速标志20和60进行聚类处理后得到的部分低质量样本数据和高质量样本数据。

|
Download:
|
| 图 2 交通标志聚类效果 Fig. 2 Effect of clustering traffic signs | |
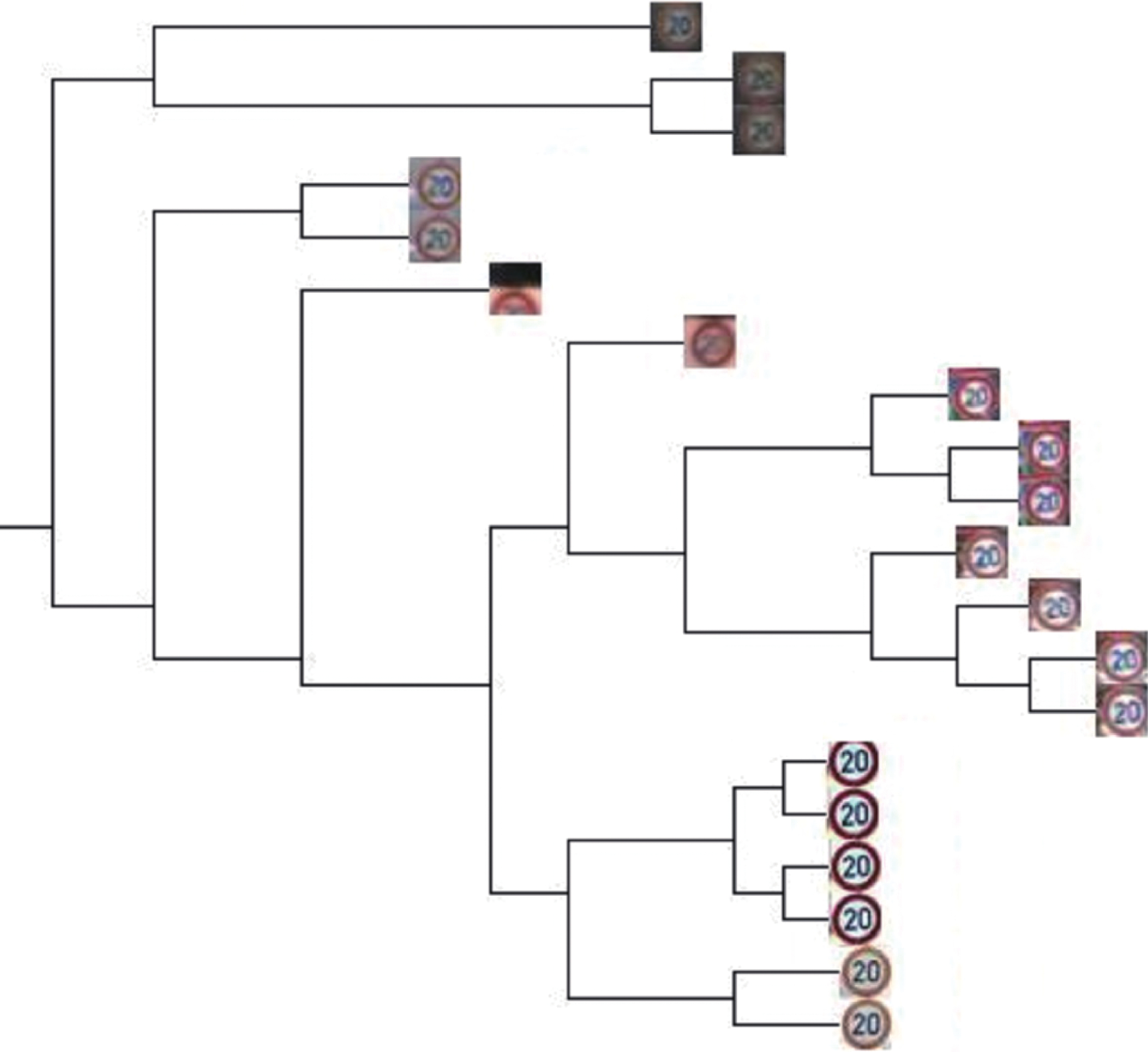
从图2中可以看出,通过对原始样本进行聚类处理,可以有效地筛选出低质量样本,提高数据集的整体质量。为了更为直观的观察聚类效果,以交通标志20为例,从GTSRB中随机选出20张样本图片,绘制出其树状图如图3所示,从图中可以看出,通过聚类,低质量和高质量的样本数据得以区分,有效保证CNN模型训练中样本集的整体质量。
|
Download:
|
| 图 3 交通标志20聚类后得到的树状图 Fig. 3 The dendrogram of traffic sign 20 after clustering | |
通过对训练数据进行图像聚类处理,在优化数据质量的同时保证了训练样本的数量,为算法的进一步展开奠定了基础,保证了CNN的训练效果。
1.2 图像预处理GTSRB数据集中的样本图像尺寸大小存在较大差异,样本数据中除了标志区域外还包含了周围10%的环境区域。为了进一步改善数据集中的图像质量,提高CNN训练速度和识别效果,对聚类得到的训练样本进行了一系列的预处理操作。
1)比例裁剪
通过对数据集进行比例裁剪,获得感兴趣区域,即交通标志的最小包围框,去除交通标志周围10%左右的无关区域,减少环境等背景信息对交通标志识别的影响,提高了识别速度。
2)尺寸归一化
GTSRB原始数据集中交通标志图像的大小分布不均,从15×15到250×250都有分布,统计发现图像尺寸长宽分布的中位数是41×40。综合考虑运算量和图像细节,对交通标志样本数据归一化尺寸大小为48×48。
3)灰度化
形状或图形特征是交通标志识别的关键因素,彩色图像灰度化后可以有效降低计算量,减少光照等因素对数据的干扰,提高CNN训练速度以及识别效果。彩色图像常用的灰度化方法有均值法和加权平均法,为了更好的保留交通标志的细节信息,本文采用加权法对图像进行灰度化处理,式(2)为所用到的灰度化公式,其中R、G、B分别为彩色图像中的红、绿、蓝3个颜色分量,Gray表示计算出的灰度值大小。
| $ {\rm{Gray}} = 0.21R + 0.72G + 0.07B $ | (2) |
对原始样本数据聚类后的数据集按上述方法做预处理后,样本质量和样本特征得到进一步提升,图像预处理操作有效提高了CNN训练速度和识别速度。
1.3 卷积神经网络CNN是深度学习中的一种算法,通常为多层的神经网络结构,其结构模型如图4所示,共分为3个部分:输入层、隐含层以及输出层。输入层通常是输入的二值或彩色图像;隐含层是CNN的关键部分,主要包含卷积层和池化层,每个卷积层由一个滤波器层、一个非线性层、一个空间采样层组成,通常CNN结构越复杂,卷积层和池化层就越多;全连接层通常为一个浅层的分类器,如SVM、SoftMax。交通标志图像输入到CNN后,通过卷积和池化运算对图像进行特征提取,最后通过全连接层完成对交通标志的分类。

|
Download:
|
| 图 4 CNN结构模型 Fig. 4 The architecture of CNN | |
卷积运算可以由式(3)表示:
| ${{y}} = f(({{W}} * {{{X}}_{{s}}}) + {{b}})$ | (3) |
式中:X表示输入图像,X的局部区域定义为
对交通标志图像进行卷积操作以后,就可以利用所提取的特征来训练分类器,但对于图像数据来说,网络训练的数据量很大,且由于交通标志图像包含的特征较多,可能会产生过拟合现象。为了避免这样的问题,本文采用池化操作,池化操作可以有效地降低数据的维度,避免过拟合现象的发生。
在训练过程中,对于单个交通标志样本(x, y),其损失函数可以表示为
| $J({{W}},{{b}};{{x}},{{y}}) = \frac{1}{2}\parallel {h_{{{w}},{{b}}}}({{x}}) - {{y}}{\parallel ^2}$ | (4) |
式中:J是均方差;
文中采用了反向传播算法,它可以计算出训练过程中的偏导数,用于对网络权值的更新,其过程可以表示为:
1)计算前向传播,即图片特征从输入层向前传播,经过隐含层,通过输出层得到网络输出的过程,对于l层i单元和l−1层k个单元,其过程如下:
| ${{z}}_i^{(l)}{\rm{ = }}\sum\limits_k {({{W}}_{ik}^{(l)}{{a}}_k^{(l - 1)} + {{b}}_i^{(l)})} $ | (5) |
| ${{a}}_i^{(l)} = f({{z}}_i^{(l)})$ | (6) |
2)计算残差,残差是某单元对输出值产生多少影响的体现,可以根据式(7)计算出输出层l中单个单元i的残差,其中⊙表示向量乘积运算符:
| $ {{\delta }}_i^{(l)} = \frac{\partial }{{\partial {{z}}_i^{(l)}}}\frac{1}{2}\parallel {{{y}}_i} - {{a}}_i^{(l)}{\parallel ^2} = - ({{{y}}_i} - {{a}}_i^{(l)}) \odot {{{f}}{'}}({{z}}_i^{(l)}) $ | (7) |
3)对
| ${{{\delta }}^{(l)}} = ({({{{w}}^{(l + 1)}})^{\rm{T}}}{{{\delta }}^{(l + 1)}}) \odot {{{f}}{'}}({{{z}}^{(l)}})$ | (8) |
4)计算各层的偏导数:
| $\frac{\partial }{{\partial {{{W}}^{(l)}}}}J({{W}},{{b}};{{x}},{{y}}) = ({{{a}}^{(l)}}){{{\delta }}^{(l + 1)}}$ | (9) |
| $\frac{\partial }{{\partial {{{b}}^{(l)}}}}J({{W}},{{b}};{{x}},{{y}}) = {{{\delta }}^{(l + 1)}}$ | (10) |
计算出偏导数后,就可以对网络权值做进一步的更新,文中选用了随机梯度下降算法(SGD)来对网络参数进行更新,基于SGD的参数更新过程如下所示:
输入 n个训练样本,初始参数θ,学习速率α;
输出 动量参数β,初始速度v。
while没有收敛或达到训练次数do
从训练数据中随机选取n个样本{
计算梯度:
参数更新:
参数更新:
end while
将经过图像聚类和预处理操作得到的交通标志样本集输入到CNN中进行训练,采用前向传播和反向传播算法不断更新网络权值,当达到收敛条件或指定的训练次数时,可以得到网络模型。把实际采集的交通标志送入训练好的网络模型中,经过特征提取可自动得到分类结果。
2 实验结果及分析本实验在Ubuntu 14.04 (64 bit)操作系统搭建的Caffe平台下进行,处理器为Intel® CoreTM i3-2100 CPU @ 3.10 GHz×4,内存为8 GB、1 TB机械硬盘,同时使用NVIDIA GTX1050来实现GPU加速训练。
2.1 数据集准备实验选用GTSRB数据集作为原始数据,该数据集包含43类不同类型的交通标志,共有51 839张RGB类型的交通标志图片,其中训练图片39 209张,测试图片12 630张。
GTSRB原始数据中存在很多分辨率低、运动模糊、局部遮挡、尺寸不一、光照强度不同的低质量数据。通过图像聚类处理,共筛选出8 000多个低质量的训练样本,约占训练训练样本的20%。经过图像预处理操作,最终得到31 000张灰度图像作为训练样本,为了保证训练模型的有效性,对测试集中的12 630张交通标志图像不做处理。
2.2 CNN结构设计实验中以LeNet-5网络为基础,通过优化CNN结构,调整网络参数,构造了一个深度为9的CNN结构(见表1)。
| 表 1 CNN结构参数 Tab.1 CNN structure parameter |
在前两个卷积层采用了5×5的卷积核,第3个卷积层采用了3×3卷积核,而池化层统一采用2×2大小,全连接层的输出改为120,同时优化并改变了每层的输出特征数量,实验中经过多次调参,最终设置学习率大小为0.01。通过上述优化可以有效减少网络训练计算量,提高CNN训练速度和最终的识别效率。
2.3 模型对图像的特征表示及性能分析为测试文中CNN结构对交通标志图像的多尺度特征表示,以限速标志20为例,将其输入到CNN中后,通过可视化方法,得到其在各个卷积层和池化层的特征图谱如图5所示。从图中可以看出,经过一系列的卷积和池化操作后,特征图中限速标志20的边缘信息变得越来越清晰,图像立体感得到有效的提升,整体特征大幅度增强。通过图像聚类和图像预处理操作,训练使用的交通标志数据集整体质量得到优化,图像特征变得更为明显,有利于CNN充分提取图像特征。CNN采用质量较好数据进行训练,可以更充分地提取和学习数据特征,从而获得更好的训练模型,提高最终的识别精度和识别速度。

|
Download:
|
| 图 5 交通标志20的特征图 Fig. 5 The feature maps of Traffic 20 | |
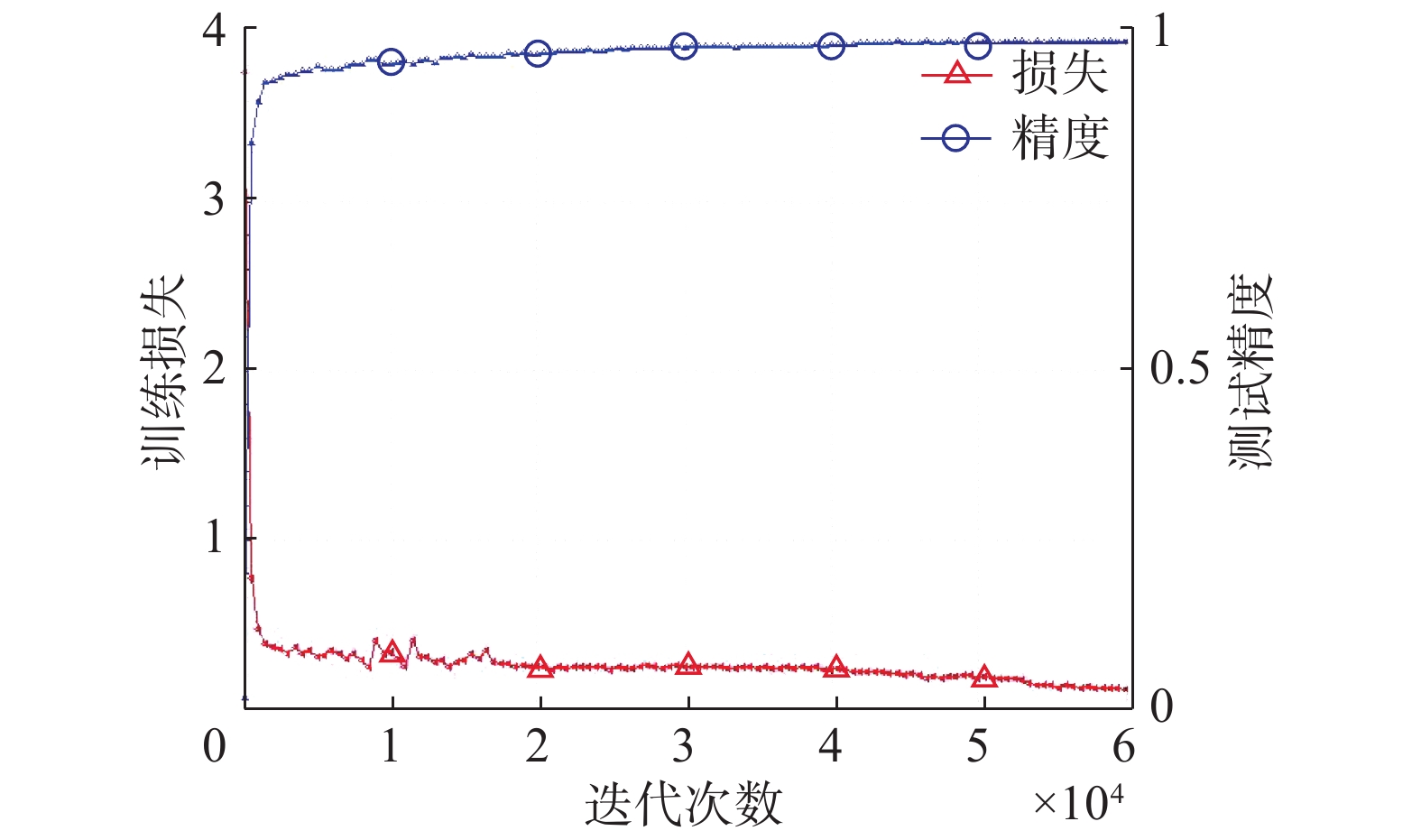
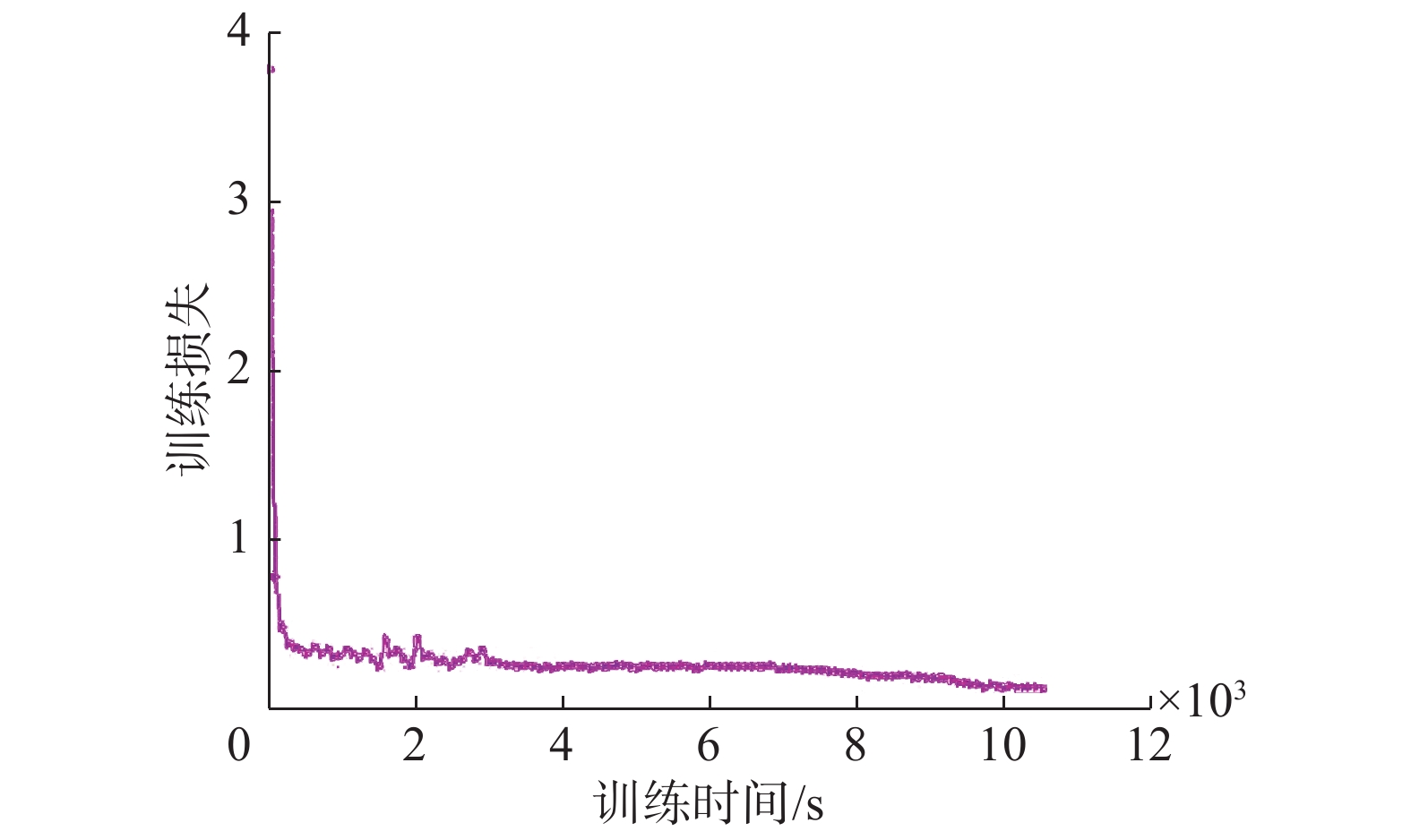
网络训练完成后,绘制出交通标志训练过程中的误差和精度曲线如图6所示,图7是训练误差随时间的变化曲线。从图中可以看出,开始训练后,当迭代次数达到1 000次,训练时间为200 s时,训练整体误差迅速下降到0.5以下,同时测试精度达到93%以上;当迭代次数达到60 000次时,测试精度可以达到98.5%,整体损失下降到0.1左右。以上结果表明,通过对交通标志数据集的优化,CNN训练收敛迅速,可以有效节省训练时间,训练精度可以在短时间内提高到较高水平,同时均方误差下降到较低水平,这说明本算法具有较好的实时性以及较高的识别率。
|
Download:
|
| 图 6 训练误差和测试精度曲线 Fig. 6 Training error and test accuracy curves | |
|
Download:
|
| 图 7 训练误差随时间变化曲线 Fig. 7 Variation curve of training error over time | |
为了进一步检测本文算法的实际性能,同时验证文中图像聚类和图像预处理方法对CNN训练的积极影响,对比了GTSRB数据集在图像聚类以及预处理前后的识别率,实验结果如表2所示。
| 表 2 图像聚类和图像预处理后识别率对比 Tab.2 Comparison of recognition rate after image clustering and image preprocessing |
由实验1和2可以看出,在不进行图像预处理和图像聚类的情况下,交通标志的识别率为94.9%,经过图像预处理操作后,识别率可以达到96.8%,提高了0.9%;对比实验1和4则可以发现,经过图像聚类对原始数据集质量优化后,交通标志的识别率可以达到97.6%,比未经过任何处理的情况下,识别精度提高了1.7%;实验3表明,当同时采用图像聚类和图像预处理的情况下,交通标志的识别率可以达到98.5%。
表2实验表明,采用图像聚类的方法,可以有效优化样本集的整体质量,进而提高交通标志的识别效果,在经过图像预处理操作后,样本集质量得到进一步提升,交通标志的识别率得到提高。
2.5 对比实验和迁移测试表3给出了几种具有代表性的交通标志识别方法的对比结果,从表中可以看出,本文方法的识别率高于文献[2]中的特征描述方法以及文献[19]中的随机森林方法。分析原因,主要是因为相对于上述方法,文中数据经过有效地样本优化和预处理,整体质量得到较大提升,所采用的深度学习方法可以充分学习交通标志图像的高维特征,实现更有效的特征表达,得到更好的识别模型。
| 表 3 本文算法与其他算法识别结果对比 Tab.3 Recognition rate variances of different methods |
将文献[20]中同样采用深度学习的交通标志识别方法与本文方法进行对比,发现文献[20]中的方法略高于本文算法,但文献[20]中选用彩色图像作为训练数据,通过尺寸变化、角度旋转等方式对数据进行了大量的扩充,训练样本接近130 000个,样本庞大且未做有效优化,所采用的CNN结构参数复杂,输入和输出特征较多,因此,尽管其精度高于本文算法,但其训练过程中的计算量非常大,对硬件要求较高,操作复杂,且非常耗时。而本文算法首先通过图像聚类获取高质量训练数据;然后对样本进行多种预处理操作,采用31 209张灰度图像作为训练数据,仅为文献[20]方法数据量的四分之一;在训练网络上,通过优化网络结构,减少网络输出,构造了深度为9的CNN结构,并通过多次训练选择了合适的网络参数,有效地节省了训练时间,提高了训练效果,在较低的硬件条件下得到了较好的识别精度。
为了测试本文算法的实际表现,从比利时BTSD数据集中随机选取的600张真实环境下的交通标志图片进行迁移测试,在新样本下,单张图片的平均识别时间可以保持在0.2 s左右,识别率高达95%,表明训练模型具有良好的鲁棒性和泛化能力,可以满足交通标志识别的实时性和准确性要求。
3 结束语本文基于图像聚类,利用深度学习提出了一种交通标志快速识别算法。在一定程度上解决了传统特征描述方法,在交通标志识别领域鲁棒性和识别精度差等问题。本文将图像聚类算法应用于交通标志数据集的优化,有效地提高了数据整体质量,保证了深度学习训练效果,此方法可泛化到其他图像识别问题。利用公开数据集GTSRB和BTSD,在Caffe平台下,通过仿真实验和对比分析,证明了算法的有效性,可为智能驾驶提供一定的理论依据和技术支持。本文只完成了对交通标志图像的分类,并没有对交通标志进行检测,下一步的工作是研究如何实现自然环境下小目标交通标志的检测,并在此基础上真正实现对交通标志的自动识别。
| [1] |
SAADNA Y, BEHLOUL A. An overview of traffic sign detection and classification methods[J]. International journal of multimedia information retrieval, 2017, 6(3): 193-210. DOI:10.1007/s13735-017-0129-8 ( 0) 0)
|
| [2] |
BERKAYA S K, GUNDUZ H, OZSEN O, et al. On circular traffic sign detection and recognition[J]. Expert systems with applications, 2016, 48: 67-75. DOI:10.1016/j.eswa.2015.11.018 ( 0) 0)
|
| [3] |
HOFERLIN B, ZIMMERMANN K. Towards reliable traffic sign recognition[C]//2009 IEEE Intelligent Vehicles Symposium. Xi'an, China, 2009: 324–329.
( 0) 0)
|
| [4] |
张卡, 盛业华, 叶春, 等. 基于中心投影形状特征的车载移动测量系统交通标志自动识别[J]. 仪器仪表学报, 2010, 31(9): 2101-2108. ZHANG Ka, SHENG Yehua, YE Chun, et al. Automatic recognition of road traffic sign based on central projected shape feature for vehicle-borne mobile mapping system[J]. Chinese journal of scientific instrument, 2010, 31(9): 2101-2108. (  0) 0)
|
| [5] |
LU Ke, DING Zhengming, GE S. Sparse-representation-based graph embedding for traffic sign recognition[J]. IEEE transactions on intelligent transportation systems, 2012, 13(4): 1515-1524. DOI:10.1109/TITS.2012.2220965 ( 0) 0)
|
| [6] |
宋文杰, 付梦印, 杨毅. 一种面向无人驾驶汽车的高效交通标志识别方法[J]. 机器人, 2015, 37(1): 102-111. SONG Wenjie, FU Mengyin, YANG Yi. An efficient traffic signs recognition method for autonomous vehicle[J]. Robot, 2015, 37(1): 102-111. (  0) 0)
|
| [7] |
HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 ( 0) 0)
|
| [8] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 ( 0) 0)
|
| [9] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 ( 0) 0)
|
| [10] |
刘方园, 王水花, 张煜东. 深度置信网络模型及应用研究综述[J]. 计算机工程与应用, 2018, 54(1): 11-18. LIU Fangyuan, WANG Shuihua, ZHANG Yudong. Survey on deep belief network model and its applications[J]. Computer engineering and applications, 2018, 54(1): 11-18. (  0) 0)
|
| [11] |
GOLOVKO V A. Deep learning: an overview and main paradigms[J]. Optical memory and neural networks, 2017, 26(1): 1-17. DOI:10.3103/S1060992X16040081 ( 0) 0)
|
| [12] |
马志强, 李图雅, 杨双涛, 等. 基于深度神经网络的蒙古语声学模型建模研究[J]. 智能系统学报, 2018, 13(3): 486-492. MA Zhiqiang, LI Tuya, YANG Shuangtao, et al. Mongolian acoustic modeling based on deep neural network[J]. CAAI transactions on intelligent systems, 2018, 13(3): 486-492. (  0) 0)
|
| [13] |
CIREŞAN D, MEIER U, MASCI J, et al. Multi-column deep neural network for traffic sign classification[J]. Neural networks, 2012, 32: 333-338. DOI:10.1016/j.neunet.2012.02.023 ( 0) 0)
|
| [14] |
孙伟, 杜宏吉, 张小瑞, 等. 基于CNN多层特征和ELM的交通标志识别[J]. 电子科技大学学报, 2018, 47(3): 343-349. SUN Wei, DU Hongji, ZHANG Xiaorui, et al. Traffic sign recognition method based on multi-layer feature CNN and extreme learning machine[J]. Journal of University of Electronic Science and Technology of China, 2018, 47(3): 343-349. DOI:10.3969/j.issn.1001-0548.2018.03.004 (  0) 0)
|
| [15] |
CHAWLA N V. Data mining for imbalanced datasets: An overview[M]//MAIMON O, ROKACH L. Data Mining and Knowledge Discovery Handbook. Boston, MA: Springer, 2005: 853–867.
( 0) 0)
|
| [16] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 ( 0) 0)
|
| [17] |
MURTAGH F. A survey of recent advances in hierarchical clustering algorithms[J]. The computer journal, 1983, 26(4): 354-359. DOI:10.1093/comjnl/26.4.354 ( 0) 0)
|
| [18] |
PAL N R. A primer on cluster analysis: 4 basic methods that (usually) work[book review][J]. IEEE computational intelligence magazine, 2017, 12(4): 98-100. DOI:10.1109/MCI.2017.2742870 ( 0) 0)
|
| [19] |
ZAKLOUTA F, STANCIULESCU B. Real-time traffic-sign recognition using tree classifiers[J]. IEEE transactions on intelligent transportation systems, 2012, 13(4): 1507-1514. DOI:10.1109/TITS.2012.2225618 ( 0) 0)
|
| [20] |
SERMANET P, LECUN Y. Traffic sign recognition with multi-scale convolutional networks[C]//2011 International Joint Conference on Neural Networks. San Jose, CA, USA, 2011: 2809–2813.
( 0) 0)
|
 2019, Vol. 14
2019, Vol. 14


