椎间孔狭窄症(intervertebral foraminal stenosis, IFS)是指由于椎间孔狭窄压迫脊髓神经根周围神经系统引发的退行性疾病^[1]。脊髓神经根作为感觉输入的传递中枢，受压迫后将会引起疼痛、肌肉无力，甚至身体残疾，并且IFS会随着人的自然衰老过程导致严重的脊柱侧凸和脊椎滑脱，大约80%的老年人深受IFS引起的腰背疼痛折磨^[2]。临床数据表明，治疗计划随着IFS等级的不同而变化，如对于1级狭窄，通常的物理治疗和运动将是治疗的第一选择，而对于更严重的等级，患者可能需要接受手术治疗或者减压治疗等^[3]。因此，有效和精确的分级是椎间孔狭窄症诊断和治疗至关重要的一步。但是现有的临床椎间孔狭窄分级主要存在3个方面的问题：1)医生对IFS图像的目视检查和人工评分，耗时耗力且低效；2)由于IFS的病症多样性，临床医生常更多关注椎间盘突出、椎管狭窄和侧隐窝狭窄的情况，而容易忽略椎间孔的狭窄情况，主观性强；3)特殊的椎间孔解剖结构及复杂的致狭窄因素，易导致临床难以全面准确判定，误诊、漏诊率高。因此，为提高IFS诊断效率、减少医生主观影响以及降低误诊漏诊率，设计自动化的临床辅助诊断系统具有重要的应用价值^[4]。

当前，计算机辅助诊断IFS方面的研究已取得了重要进展，按照感兴趣区域的不同可分为两种类型。第一种类型是基于椎间孔周围结构的自动定位分割研究，主要有Alomari等^[5]使用一种两级模型在核磁共振图像中捕获像素级和对象级特征，以实现对椎间盘的局部异常检测；Zhan等^[6]采用基于CT和MR图像的共同的脊柱几何结构设计分析算法初始化椎骨的标记实现椎体定位；Wang等^[7]采用回归分割的方法分割出M3脊柱图。第二种类型是直接基于椎间孔的自动分割或分级研究，主要有Ghosha等^[8]通过对椎体中心线以及椎间孔主要边界点的检测实现分割；Huang等^[9]采用Adaboost检测算法和迭代归一化分割算法对MRI椎体图像进行检测同时成定位和分割；Klinder等^[10]采用将全局脊柱形状在连续的局部椎体坐标系中表示，并将个体椎骨建模为三角曲面网络的方法，实现了基于双尺度的脊柱和椎间孔建模与分割；He等^[11]采用超像素分割法在对椎间孔狭窄图像定位和良恶性分类问题上精确度达到98.52%。

以上研究均取得不同程度的进展，但仍存在一些问题。此类基于部分形态学解剖结构的定位、分割或者比较简单的二级分类的辅助诊断研究，忽略了全局信息，影响诊断精确度。而临床上基于常规仰卧位MRI图像的椎间孔狭窄诊断是由椎间孔形态、神经根周围脂肪或神经根形态改变情况等多种因素决定的^[3]，如2级狭窄虽然在神经根周围4个方向(垂直和横向)无形态学变化，但椎间盘空间狭窄、韧带黄斑增厚、小关节病变和椎间盘突出等原因同样会导致神经根受压迫，易导致误诊^[12]。因此，研究一种高效的算法提取图像全局“病灶特征”并实现自动分级诊断，就成为辅助IFS诊断亟待解决的重要问题。

在图像处理算法方面，深度学习模型能够很好地提取图像深层特征，且可通过改变模型的网络拓扑结构，如适当增加网络的深度和宽度，降低特征冗余度和提高特征相关性。自1995年Lo等^[13]将卷积神经网络用于医学图像分析起，深度学习模型已经迅速成为研究分析医学图像的重要方法^[14]，且其在辅助脑、乳腺、肺等器官的临床诊断方面已取得重要进展，但在辅助脊椎脊柱疾病诊断的研究基本处于空白。

针对IFS的自动分级问题，本文采用设计基于椎间孔狭窄自动分级的监督式深度卷积神经网络(supervised deep convolutional neural network based on automatic classification of intervertebral foraminal stenosis，IFS-Net)，提取图像纹理特征、颜色特征、形状特征和空间关系特征，并将这些特征融合起来作为不同级别的疾病“症状”特征与IFS之间建立特殊的“病理”联系。另外，由于深度学习算法需要海量的训练数据，而IFS影像数据的数量有限，因此本文选用先进的迁移学习^[15]和微调^[16]方法，来克服和避免因IFS影像数据规模不足导致的过拟合等问题，提高算法对椎间孔狭窄图像的识别率，满足高标准的临床要求。

1 IFS-Net算法 1.1 算法结构

本文设计的IFS-Net是一个端到端的模式识别模型，该模型可实现IFS的高精度自动分级，且具有网络结构简单、高效的特点。端到端的方法使得模型完成提取图像潜在特征的同时，可以自动将loss值前反馈到每一层，经多次迭代调节模型参数，获得最优解。

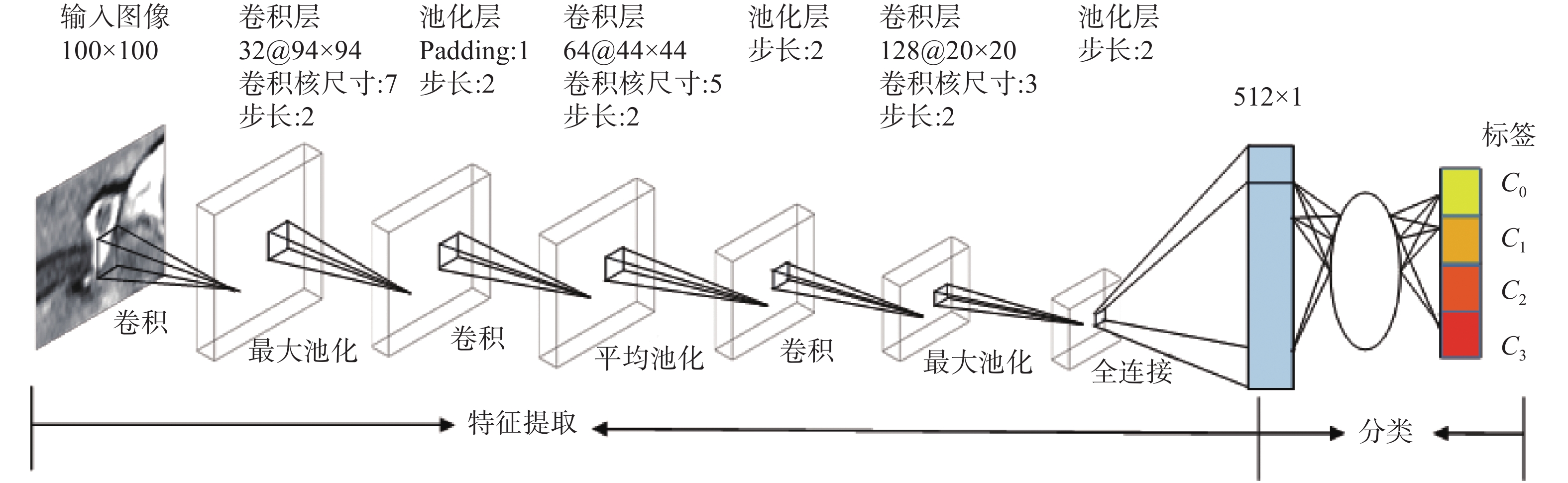
IFS-Net模型结构共包含8层网络结构，分别是3个卷积层、3个池化层、1个全连接层和1个输出层，其中的全连接层和输出层是该模型的优势模块。因椎间孔图像目标区域小而集中(如图1所示，图1为椎间孔结构及狭窄症分级示意图)，故本文采用全连接的方式将所有模型学到的“分布式特征”映射到样本标记空间^[17]，以达到最大化利用模型提取的特征信息，进而实现更有效的分类。IFS-Net模型框架如图2所示，主要结构和功能包括：

1)输入层：该层将整幅椎间孔图像导入IFS-Net结构，并产生第1个卷积层的输入。

2)卷积层：负责特征的学习。该层通过卷积计算连接到输入层或者上一层的局部区域的神经元的输出来提取特征，每个神经元与前一层的区域连接为稀疏连接。其中输入卷积的权重集为卷积核，也称作滤波器。一个可学习的卷积核与前一层若干个Feature Maps作卷积，将所有元素累加后再加上一个偏置，传给一个非线性激活函数，本文结构采用ReLU函数作为非线性激活函数。另外，为了减少计算复杂度，同一层中某些神经元之间的连接权重是共享的，即相同的。每层滤波器的大小依次递减分别为7×7、5×5和3×3，步长设置为2；并由高斯分布初始化，标准差为0.01。3个卷积层分别包含32、64和128个Feature maps。卷积计算公式如(1)所示：

$x_{K_j}^l = f((\sum\limits_{ie{M^{l - 1}}} {x_i^{i - 1}*K_{ij}^l} ) + b_j^l)$

(1)

式中：l表示层数； ${K_{ij}}$ 表示连接第l层的Feature Map $j$ 与l−1层的Feature Map $i$ 的卷积核； ${{M}^{l-1}}$ 表示第l−1层选择的输入Feature Maps；*表示卷积操作； $b_j^l$ 表示l层中Map $j$ 的偏置； $f( \cdot )$ 表示非线性激活函数。

3)池化层：池化层的目的是通过减少相似特征点实现Feature maps的降维，除此之外还可以降低噪声和扩大接受域^[15]。池化层的输出在保持标量不变的基础上减少了参数的数量。本文模型的3个池化层分别采用Max-pooling和Mean-pooling的策略实现特征降维，步长为2。池化层拥有与其前端卷积层相等的Feature map个数，分别为32、64和128个。

4)全连接层：该层有512个神经单元，每个神经单元都与上一层进行全连接，最终得到512维特征向量。

5)输出层：输出层由欧式径向基函数(euclidean radial basis function，E-RNF)单元组成。计算公式为

${y_j} = \sum\limits_j {{{({x_i} - {w_{ij}})}^2}} $

(2)

式中 ${x_i}$ 和 ${w_{ij}}$ 分别为最后一层卷积层的输入和权重。

此外，本文模型学习率为0.000 1，最大迭代次数为25 000次，动量设置为0.9，选取随机梯度下降(stochastic gradient descent，SGD)为优化函数。

1.2 算法训练策略 1.2.1 参数初始化

在IFS-Net模型的参数权重初始化方面，本文采用自训练和迁移学习相融合的参数初始化策略。自训练方法是将网络参数用随机初始化的方式从头开始训练模型；迁移学习方法则是采用预先训练的参数权重来初始化网络，使得模型预先学到最基本特征(比如色彩、边缘特征等)能够有助于目标数据集分类，并提高算法分类性能。随机初始化网络参数是最常用的深度学习训练方法，但考虑到采用深度学习对医学图像进行处理的一个局限是数据集大小不能得到最大满足。因此，为提高分类精确度并解决深度学习算法在小样本数据集上的过拟合问题，本研究借鉴参考文献[18]的方法，将迁移学习应用于本文算法中。

迁移学习主要原理为：存在一个带有任务 ${T_s} = \left\{ {{Y_s},{f_s}( \cdot )} \right\}$ 的源域 ${D_s} = \left\{ {{X_s},{P_s}({X_s})} \right\}$ 和一个带有任务 ${T_t} = \left\{ {{Y_t},{f_t}( \cdot )} \right\}$ 的目标域 ${D_t} = \left\{ {{X_t},{P_t}({X_t})} \right\}$ ，域和任务之间的条件为 ${D_s} \ne {T_t}$ 和/或 ${T_s} \ne {T_t}$ 。在迁移学习中， ${D_s}$ 和 ${T_s}$ 获得的“知识”被用来帮助 ${D_t}$ 中预测函数 ${f_t}( \cdot )$ 的学习。其中一个域由特征空间和边缘概率分布两部分组成， ${T_s}$ 和 ${D_s}$ 为模型训练其他数据集的任务和域， ${T_t}$ 和 ${D_t}$ 为本文训练任务和域。

本文在ImageNet数据集上对模型进行预训练，之后再将获得的网络参数迁移到目标数据集上进行训练，从而获得稳定的网络参数。该数据集包含120余幅自然图像和1 000多种不同的类别。

1.2.2 Softmax分类器

模型采用Softmax分类器对模型提取的“分布式特征”进行概率量化，Softmax是逻辑回归二分类器泛化到多分类的推广。对于训练集 $\left\{ {({x^{(1)}},{y^{(1)}}),({x^{(2)}},{y^{(2)}}),\cdots,({x^{(m)}},{y^{(m)}})} \right\}$ 对应标签为 ${y^{(i)}} \in \left\{ {1,2,} \right.$ $ \left.{\cdots,k} \right\}$ ，本文设定 $k = 4$ 。对于每个输入 $x$ 都有对应的每个类的概率 $p(y = i|x)$ ，即Softmax函数：

$P(j) = \frac{{\exp ({{\theta}} _i^{\rm{T}}x)}}{{\sum\limits_{i = 1}^k {\exp ({{\theta}} _i^{\rm{T}}x)} }}$

(3)

式中： ${{\theta}} _i^{\rm{T}}x$ 为最够一层向输出层的输入， ${{\theta}} $ 为Softmax参数。训练优化实质上是逼近最佳 ${{{\theta}} ^{\rm{T}}}$ 的过程。则Softmax的损失函数为

$J({{\theta}} ) = - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k 1 \left\{ {{y^{(i)}} = j} \right\} \cdot \log (P(j))} } \right]$

(4)

式中： $1({y^{(i)}} = j)$ 为指示性函数，取值规则为：1{值为真的表达式}=1 ，1{值为假的表达式}=0。

2 实验及结果分析 2.1 数据集

为验证和测试IFS-Net模型的性能，实验选用国际通用的脊柱椎间孔图像(intervertebral foraminal stenosis znxtxb-14-4-hongyanfeis, IFSI)数据集作为测试数据集。该数据集包含从110个临床实验对象的脊柱图像中采集的406个椎间孔图像。每一个脊柱图像均使用矢状T₁加权MRI扫描，重复时间(repetition time, TR)为4 000 ms，回波时间(echo time, TE)为85 ms，磁场为1.5 t。平面分辨率为0.5 mm，厚度为1 mm或1.6 mm。在IFSI数据集中，每个IFS图像Ground Truth由拥有7年工作经验的专业医生手工标注，分别是0级(正常)图像108幅、1级(轻微)图像100幅、2级(显著)图像105幅和3级(严重)图像93幅。IFSI数据集分级标注遵循的是Wildermuth椎间孔狭窄分级诊断系统^[19]。

2.2 评价标准

在医学图像数据集中评估机器学习算法的多分类性能，主要有基于患者水平和图像水平的两种评价方法。由于IFSI数据集是基于图像层面的，因此本文从图像层面评估算法的识别率。假设 ${N_{{\rm{all}}}}$ 为图像验证集或测试集的图像总数量，如果 ${N_r}$ 幅图像被正确分类，那么图像层面的准确率RR为

${\rm{RR}}={{N}_{r}}/{{N}_{{\rm{all}}}}$

(5)

由于多分类问题中准确率不再是唯一的评价指标，因此本文引入F-score作为评价本文模型的另一个指标。与F-score密切相关的两个值分别为精确度P_r和召回率R_c:

$P_r ={\rm{TP}}/({\rm{TP}}+{\rm{FP}})$

(6)

$R_c={\rm{TP}}/({\rm{TP}}+{\rm{FN}})$

(7)

式中：TP为真阳性记录数；FN为假阴性记录数；FP为假阳性记录数。

F-score作为调和精确度和召回率的一个综合指标，计算公式如下：

${{F}_{\beta }}=\left( {{\beta }^{2}}+1 \right)/{{\beta }^{2}}P_r +R_c$

(8)

另外， $\;\beta $ 用来调节两部分的比例。当 $\;\beta =1$ 时，式(8)退化成简单的调和平均函数，称为F₁-score：

${{F}_{1}}=\frac{2 P_r R_c}{P_r} +R_c$

(9)

2.3 实验设计

为保证实验的严谨性，尽量避免特殊个例影响最终结果，本文采用交叉验证的方式将IFSI数据集平均分成5份，每次实验训练集和测试集比例为4∶1，且确保用于构建训练集的图像不再用于测试。

本文算法采用Caffe模型编写基本框架^[20]。算法在Lenovo ThinkStation、Intel e3 CPU、NVIDIA Quadro K2200 GPU上训练，平均训练时间为4 min 21 s，单张测试时间平均为0.047 s。

2.4 对比实验

为了验证本文模型的有效性，本文采用传统机器学习算法对IFSI数据集进行分类。传统机器学习算法主要包含两个步骤：特征提取和分类。特征提取部分本文选取5种最先进的纹理表示的全局算法，分别是：局部二值模式 (local binary patterns，LBP)^[21]、局部相位量化 (local phase quantization，LPQ)^[22]、灰度共生矩阵 (gray-level co-occurrence matrix，GLCM)^[23]、方向梯度直方图特征(histogram of oriented gridien，HOG)、ORB (oriented FAST and rotated BRIEF)^[24]。5种特征描述子的特征维度如表1所示。

本文利用4种不同的分类器来评估上述特征集：k近邻算法(k-NN)^[25]、极限学习机 (extreme learning machine，ELM)^[26]、支持向量机 (support vector machine，SVM)^[27]以及随机森林算法(random forest，RF)^[28]。

2.5 实验结果 2.5.1 IFS-Net与传统机器学习算法性能对比结果

为验证本文算法在IFSI数据集上的多分类性能，将其与具有代表性的4种传统机器学习分类器算法(k-NN、ELM、SVM和RF)对比分析，实验结果如表2所示。

在测试集准确度和F₁两个评价指标上，本文设计的IFS-Net算法模型的结果明显优于传统机器学习算法所取得的结果。由图3传统机器学习算法(特征描述子+分类器)分类准确率对比图，可更直观地看出，传统机器学习方法中，选取的特征向量在分类性能上都表现出稳定接近的结果，4种传统分类器对于每个特征描述子的识别率差距都在4%之内。值得一提的是，ORB虽然为关键点描述符且通常用于对象识别，但其在微观图像分类问题上获得了比传统纹理特征更优的结果。

2.5.2 IFS-Net与其他深度学习算法性能对比结果

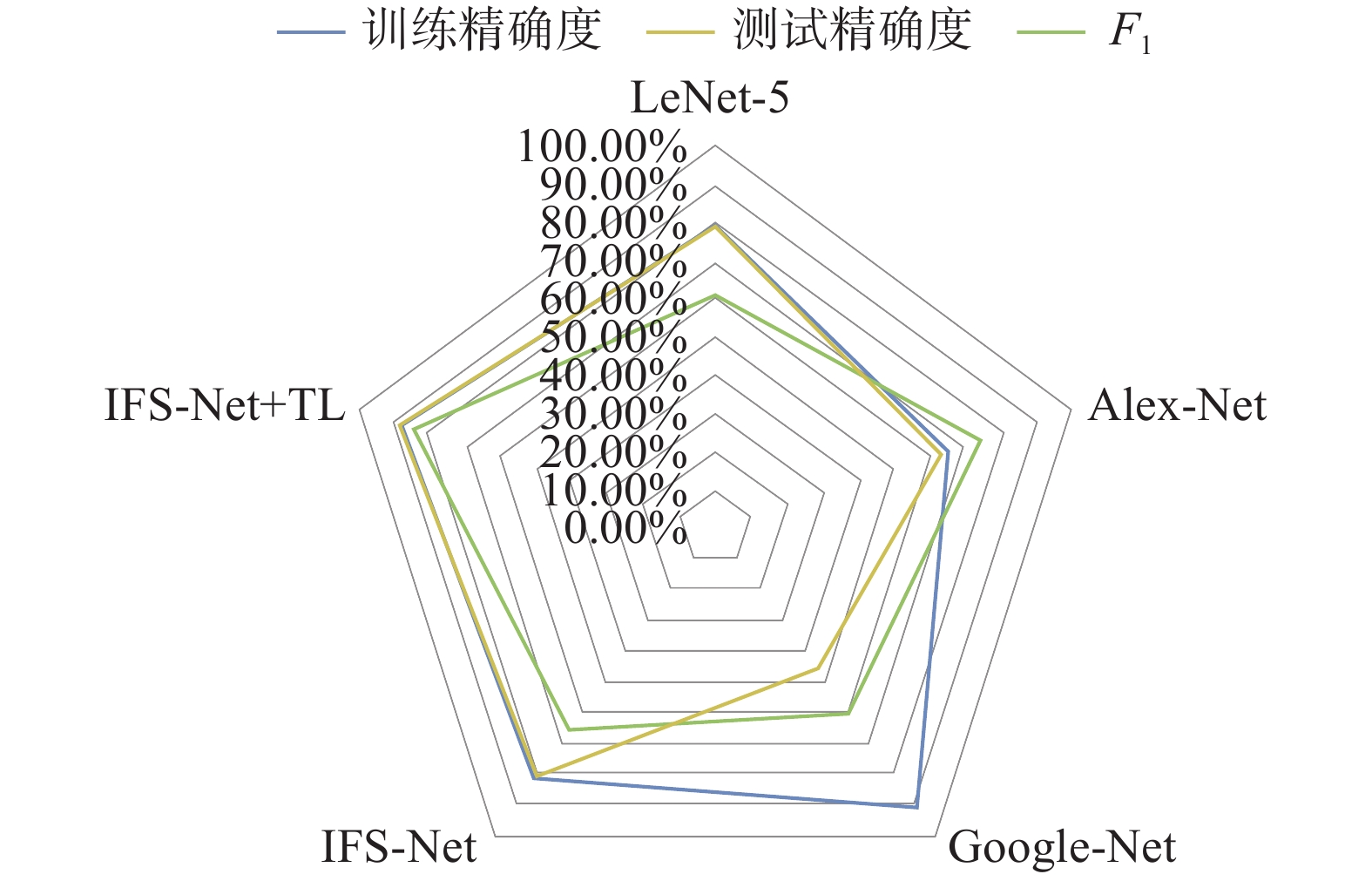
本文算法与其他典型深度学习算法在IFSI数据集上的分类性能对比实验结果，如图4所示。实验中，IFS-Net取得了87.5%的分类精度结果，明显优于其他深度学习算法。该图还直观地显示出本文算法的验证集和测试集几乎具有相同的精确度，这表明IFS-Net模型具有较强的泛化和避免过拟合的能力。而由于数据集的限制，层数过深的卷积神经网络在IFSI数据集上没有表现出层级优势，如GoogLe-Net模型出现的严重的过拟合现象，就是由于其过于复杂的结构造成的，这也是本文采用较为简单网络结构的一个原因。另外，采用迁移学习+微调训练策略的分类精度高于自训练2.5%。如图5不同模型 loss曲线拟合度对比所示，从IFS-Net和IFS-Net + TL两个模型的train-loss和val-loss曲线图可以看出，采用迁移学习方法能够降低模型的过拟合程度。

2.5.3 IFS图像狭窄度识别分析结果

为进一步测试IFS-Net算法在狭窄程度识别分析中的性能，本研究在IFSI数据集上做了不同IFS图像狭窄度识别分析测试实验，实验结果如表3所示。实验结果表明，IFS-Net算法对IFSI数据集中的0级和3级的区分度最高，1级分类结果较差。分析其原因，主要是1级图像中的椎间孔是在两个相对方向(垂直或横向)的脂肪闭塞引起的轻度口部狭窄，没有显示神经根的形态学变化^[19]，因此容易被误分为C₀(正常类)。另外，虽然2级椎间孔也没有表现出形态学上的变化，但其周围结构的变化使得算法可以挖掘出潜在特征并对特征进行相关性建模实现精准分类，说明本文模型具有提取微小病变特征的能力，能够将不同级别的疾病“症状”特征与IFS分级之间建立起特殊的“病理”联系。

3 结束语

为提高计算机辅助椎间孔狭窄症诊断准确率及工作效率，本文提出并设计出一种基于深度学习的椎间孔狭窄图像自动多分级模型。并且在基于设计的IFS-Net模型基础上，采用迁移学习有效提升了网络分类性能。实验结果表明，本文设计的模型不仅结构简单，且分类性能高效，可为临床辅助诊断及分级提供有效的技术支撑。本研究中迁移学习的特定引入方式以及数据联合训练的应用方法，对于医学影像微观数据集分析及多分类任务具有一定的参考价值。在后续的研究工作中，将针对椎间孔狭窄图像多分级工作，融合特定的形态解剖学特征，研究设计性能更优的深度学习模型算法，进一步提高分类识别的性能，给临床提供更有效的辅助诊断技术。