目前针对纺织品瑕疵检测问题的研究方法主要有3类:统计学方法、光谱和基于模型的方法。近几年,Ngan等提出了基于小波预处理的黄金图像相减方法(WGIS)[1]、布林线指标方法(BB)[2]、正则带方法(RB)[3]、Elo评分方法(ER)[4]。其对于纺织品瑕疵检测的研究代表了目前该领域的较高水平。Ngan提出的方法大多都是基于手工模板提取的,然而手工确定模板在实际运用中还有一定的局限性。Jia等[5]提出了一种基于Garbor滤波的自动模板提取瑕疵检测方法(LSG),有效地解决了手工确定模板带来的局限性。但是在光照变化条件下的瑕疵检测还没有很好的效果。实验表明,关照问题是影响纺织品瑕疵检测的重要因素,光照作为外在因素在检测过程中是不受人为控制的,在光照条件不同时,会有不同的二维图像产生,然而对任意光照下的二维图像识别是有一定难度的,因此光照预处理在纺织品瑕疵检测中是关键一步。
目前光照预处理[6-8]方法大致可分为以下几类:基于小波变换的预处理方法[9]、自商图像方法[10]、Retinex方法[11]、各向异性非均质光滑处理[12]、对比度增强[13]等。这些方法中的基于直方图均衡化的增强方法因其实用性和简洁性而受到广泛关注[14],基础理论是根据输入图像的灰度概率分布函数来确定其对应的输出灰度值,通过扩展图像的灰度、动态范围达到提升图像对比度的目的。直方图均衡化分为全局和局部两种,与全局方法相比,局部直方图均衡化可以更好地增强图像的局部信息。本文采用基于完整局部二值模式(CLBP)[15]的特征提取方法,但是传统CLBP算法在提取全面信息的同时增加了时间复杂度,且在图像小部分区域变化幅度剧烈或变化幅度平缓时识别率较低。因此本文提出了一种改进的完整局部二值模式,在一定程度上解决了CLBP存在的局限性。并结合光照预处理解决了受光照影响的纺织品瑕疵检测的问题,在经典纺织品瑕疵检测数据库进行实验,取得较好的检测效果。因此本文针对上述问题所做的工作是:
1)使用局部对比度增强算法处理受光照影响纺织品图像并与一种改进CLBP算子结合,将光滑部分纹理信息考虑进去,提高了纹理识别精细度,解决了受光照影响纺织品瑕疵检测的问题;
2)将上述算法与一种自动格分割方法结合,减少了算法的人工干预,针对本文使用的数据库有出色的检测效果。
1 光照预处理与特征提取 1.1 光照预处理:局部对比度增强(LCE)基于整幅图像的均衡化处理[14]会限制对比拉伸的比率,基于局部的对比增强可以有效地改善细节特征的可视化。局部对比增强变换的公式为:
| $ Y(m,n) = \left\{ \begin{array}{l} \log \left(\dfrac{{L(m,n)}}{{\overline {L(m,n)} }}\right),\quad L(m,n) \!>\! \theta ,\overline {L(m,n)} \!>\! \theta \\ 0,\quad\text{其他} \end{array} \right. $ | (1) |
式中:L(m, n)表示像素(m, n)处的灰度值,
| $ \overline {L(m,n)} = \frac{1}{N}\sum\limits_{i,j \in \varOmega } {L(m + i,n + j)} $ | (2) |
其中,θ为预定义的阈值,Ω是像素(m, n)的邻域。实验采用的5×5邻域,是所选邻域的像素的总和。由于式(2)得到的局部值可正可负,所以有必要进行数据归一化:
| $ f(m,n) = \frac{{Y(m,n) - {Y_{\min }}}}{{{Y_{\max }} - {Y_{\min }}}} \times 255 $ | (3) |
首先由形态学成分分析(MCA)[16]得到图像的卡通层和纹理层,卡通层主要是强调图像边缘和光滑平缓区域,而纹理层主要保留了像素值的细微变化。除去由纹理层中细微变化所带来的干扰,卡通层使背景像素的集中程度更加明显。由于我们的假设条件保证了较高的对比度,纺织品图案的卡通层更加容易区分。如果卡通层是由一个阈值进行二值化处理,那么所得到的结果就能代表纺织品图案,在任意维度上的背景像素总是集中在纺织品图案上。
本文中使用的格分割方法[5]在一定程度上克服了Ngan等方法的缺点,属于一种自动提取模板的格分割方法,在一定程度上减少了人工参与带来的局限性。
1.3 完整局部二值模式CLBP完整局部二值模式提出了3种局部纹理描述算子[17]:窗口灰度差异描述算子S, 梯度窗口差异描述算子M以及中心像素点描述算子C。这3种算子的计算方法为:
| $ \left\{ \begin{aligned} & S = \sum\limits_{p = 0}^{p - 1} {s({g_p} - {g_c}){2^p}} \\ & M = \sum\limits_{p = 0}^{p - 1} {s({D_p} - T){2^p}} \\ & C = s({g_c} - {g_N})\\ & s(x) = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;x \geqslant 0\\ - 1,\;\;\;x < 0 \end{array} \right. \end{aligned} \right. $ | (4) |
其中:
| $ \left\{ \begin{aligned} & {D_p} = {g_p} - {g_c}\\ & T = \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {\frac{1}{P}\sum\limits_{p = 0}^{p - 1} {({g_p} - {g_c})} } \\ & {g_N} = \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {{g_n}} \end{aligned} \right. $ | (5) |
式中:p为邻域数目;s(x)表示算子S, M, C的符号;gc为窗口中心像素点灰度值;gp为中心P邻域各点灰度值;gn为每一个窗口内灰度值均值, N为图像划分子窗口个数。
从上述公式可以看出,S即为传统意义的LBP,M算子是对两像素点的灰度差异幅值与全局灰度差异幅值均值比较,作为S的互补信息,C反映中心像素点的灰度信息。这3种算子构成的联合算子对纹理描述更加精细,大大提高了纹理的识别率。
1.4 KLD散度计算由上述特征提取方法得到的特征值实际上是由直方图的形式呈现的。在这个直方图中,横坐标表示每一类特征,纵坐标表示每一类特征出现的频率。KLD散度又称Kullbac-Leibler_divergence[18],是一种用来衡量两个概率分布距离的方法。传统的KLD计算方法为:
| $ {\rm{KL{D}}_{mc}}(P||Q) = \frac{1}{n}\sum\limits_{i = 1}^n {\log \frac{{P({x_i})}}{{Q({x_i})}}} $ | (6) |
式中P(xi)和Q(xi)分别代表两种概率分布。
2 瑕疵检测算法实现 2.1 算法描述本文算法分为训练和测试两部分实现。
训练部分:
1)用MCA算法得到所有无光照影响无瑕疵图的卡通层与纹理层,且只保留卡通层部分;
2)针对上述卡通层进行分块,并求每一块的特征值与所有块的平均特征值;
3)求每一块的特征值与平均值的KLD散度值并得到阈值T;
测试部分:
4)用LCE算法对所受光照影响有瑕疵图做预处理;
5)用MCA得到上述预处理后图像的卡通层与纹理层,且只保留卡通层部分;
6)计算所有瑕疵图卡通层中每一块特征值并与上述平均值求KLD散度值;
7)将得到的KLD散度值与阈值T比较,并将大于阈值T的部分标记为瑕疵区域。
整体算法流程图如图1所示。
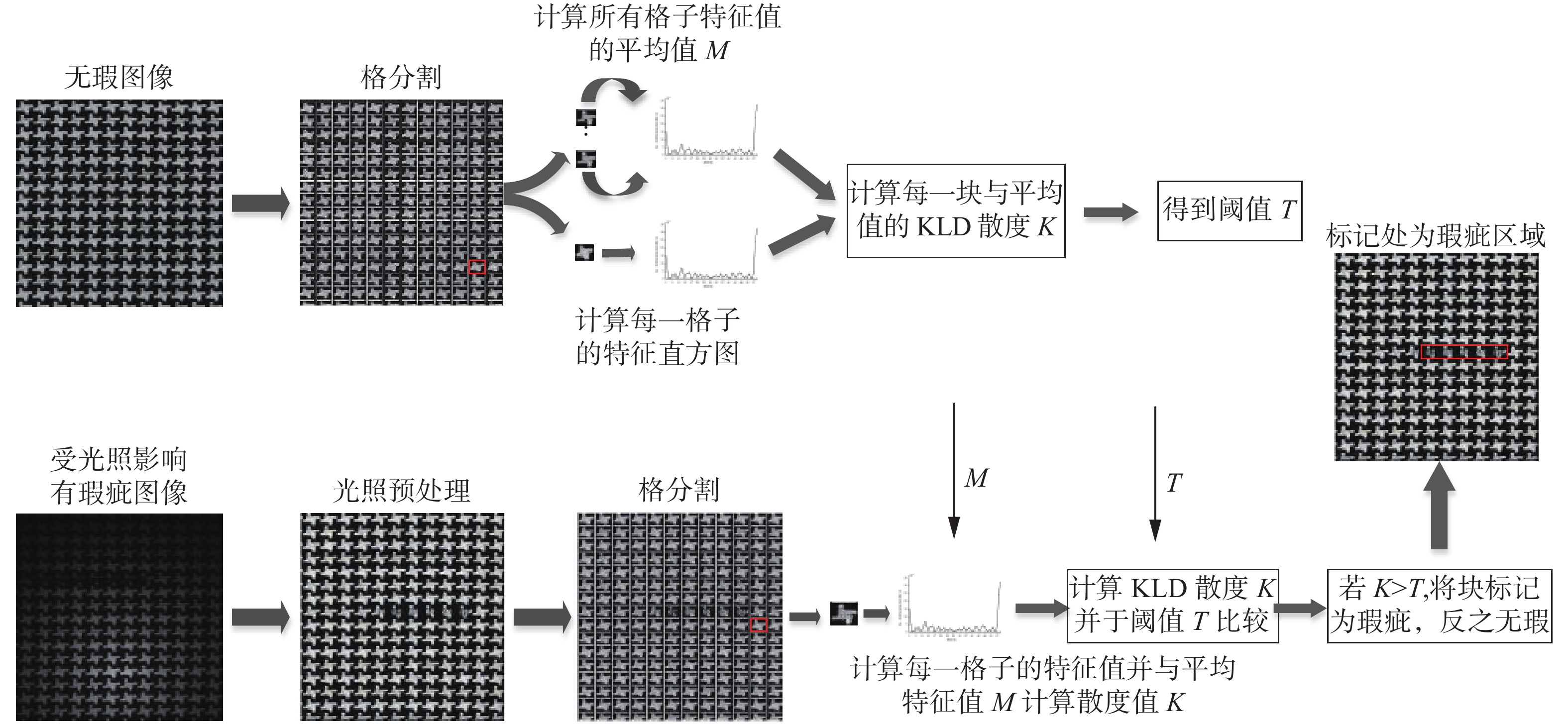
|
Download:
|
| 图 1 算法流程图 Fig. 1 Overall block diagram of the proposed algorithm | |
传统CLBP算法中的M算子仅包含了局部窗口的灰度差异特征[19],若待处理的图像由于基于某种原因导致灰度不平均,则会遗漏掉一部分光滑纹理信息。因此,针对这一问题,改进CLBP的M算子使得其通过对比两像素点的灰度差异幅值与窗口灰度差异幅值的均值大小描述局部窗口内灰度梯度差异特征,改进的M算子可以表示为
| $ M' = \sum\limits_{p = 0}^{p - 1} {s({D_p} - {D_c})} {2^p} $ | (7) |
其中,
| $ {D_c} = \frac{1}{P}\sum\limits_{p = 0}^{p - 1} {({g_p} - {g_c})} $ | (8) |
其余两个算子与传统CLBP相同。格分割与特征提取流程如图2所示。
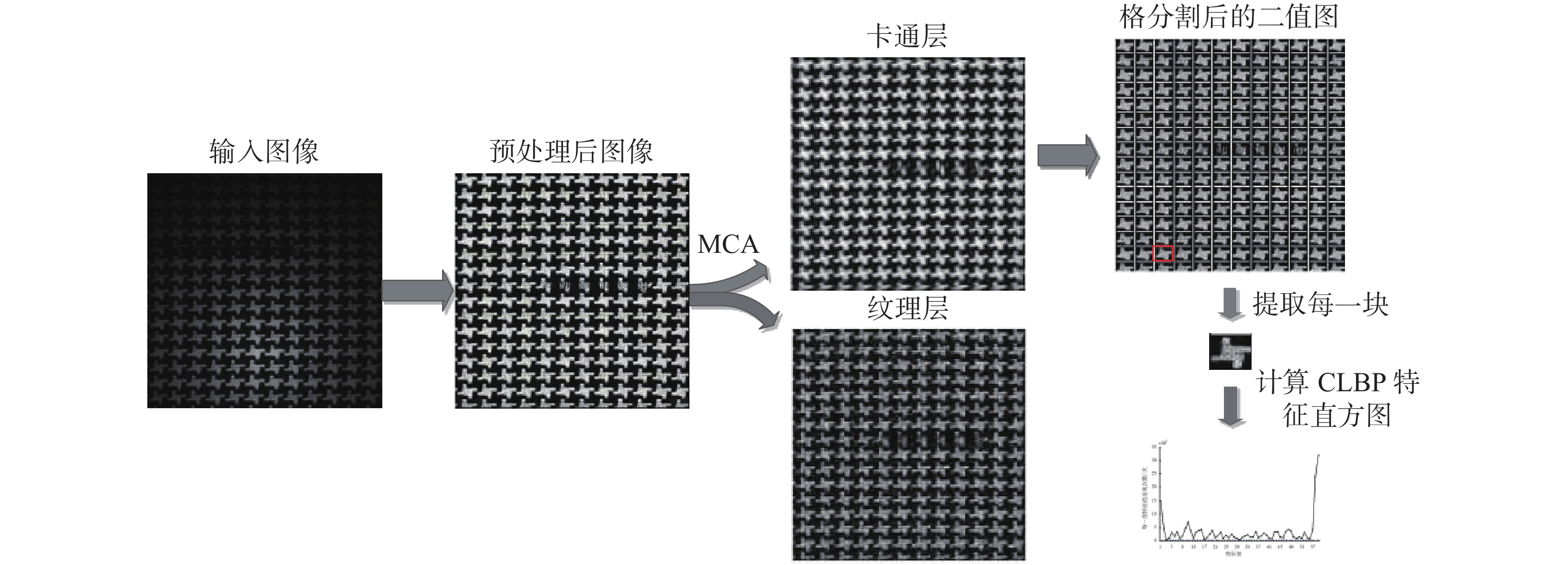
|
Download:
|
| 图 2 预处理与特征提取 Fig. 2 Preprocessing and Feature extraction | |
在阈值选取上,通过计算训练部分中无瑕图的每一块特征值与平均特征值的KLD散度,然后通过这些KLD值进行阈值的筛选,其方法是:
| $ T = \mathop {\max }\limits_k ({T_k}) $ | (9) |
式中:Tk为所有样本中第k个格子计算得到的散度值。
3 实验结果与分析为了验证本文的可行性与正确性,本文在PC机上进行多次仿真实验,处理器为i7-4710HQ,主频为2.5 GHz,内存为8 GB,用MATLAB R2016b软件进行实验。
本文实验的数据库由香港大学电气实验室提供,数据集包含2种类型的纺织品图像且均为彩色图像。在实验中,彩色图像均被转换成灰度图像再进行处理。这2种类型的纺织品图像分别为星形纺织品图像和箱形纺织品图像。其中星形纺织品图像又包含3种瑕疵类型,分别为断端瑕疵类型、网纹瑕疵类型和细条纹瑕疵类型。箱形纺织品瑕疵类型与星形相同。每一种瑕疵图像都有与其对应的Ground-Truth图像,其中1代表瑕疵,0代表背景。本实验采用的评价指标有4种,分别为TPR、FPR、PPV和NPV。其中TPR[19]表示瑕疵处被标记为瑕疵的比例,FPR表示背景处被错误标记为瑕疵的比例,PPV表示输出图像瑕疵区域所占比例,NPV表示输出图像背景所占的比例。
3.1 不同光照预处理方法实验结果分析不同的光照预处理方法对纺织品图像的预处理效果是不同的,本文针对这一问题进行了对比实验,并选择最优预处理算法进行下一步的瑕疵检测,实验结果如图3、图4所示。

|
Download:
|
| 图 3 不同光照预处理算法对星形瑕疵类型瑕疵图处理结果 Fig. 3 Star defect image and preprocessing results with different preprocessing algorithm | |

|
Download:
|
| 图 4 不同光照预处理算法对箱形瑕疵类型瑕疵图处理结果 Fig. 4 Box defect image and preprocessing results with different preprocessing algorithm | |
分析图3、图4的实验结果,局部对比度增强算法针对纺织品图像的预处理效果较其他算法最为出色,LCE可以有效地改善细节特征的可视化。Retinex与同态滤波算法虽然也能还原原图的基本特征,但是仍然有部分区域过暗,无法有效提取细节特征。自商图像处理后的图像亮度过高,影响了局部特征的提取,降低了瑕疵区域与无瑕区域的对比度。下面将对所有算法处理后的纺织品图像进行瑕疵检测。
3.2 不同预处理方法对瑕疵检测结果影响本文使用上述4种光照预处理算法在星形图与箱形图数据集中进行瑕疵检测对比实验,实验结果如表1、表2、图5~10所示。
| 表 1 不同预处理算法对星形图案的检测效果影响 Tab.1 The effect of different pre-algorithm on star pattern % |
| 表 2 不同预处理算法对箱形图案的检测效果影响 Tab.2 The effect of different pre-algorithm on box pattern % |

|
Download:
|
| 图 5 不同光照预处理算法对星形断端瑕疵类型瑕疵图检测结果 Fig. 5 Star broken end defect image and fabric detection results with different preprocessing algorithm | |

|
Download:
|
| 图 6 不同光照预处理算法对星形网纹瑕疵类型瑕疵图检测结果 Fig. 6 Star netting multiple defect image and fabric detection results with different preprocessing algorithm | |

|
Download:
|
| 图 7 不同光照预处理算法对星形细条纹瑕疵类型瑕疵图检测结果 Fig. 7 Star thin bar defect image and fabric detection results with different preprocessing algorithm | |

|
Download:
|
| 图 8 不同光照预处理算法对箱形断端瑕疵类型瑕疵图检测结果 Fig. 8 Box broken end defect image and fabric detection results with different preprocessing algorithm | |

|
Download:
|
| 图 10 不同光照预处理算法对箱形细条纹瑕疵类型瑕疵图检测结果 Fig. 10 Box thin bar defect image and fabric detection results with different preprocessing algorithm | |
分析表1和图5~7检测实验结果,基于LCE预处理算法的疵点检测效果最为出色,针对3种瑕疵类型的TPR值均达到0.99,且不存在误检情况。Retinex算法针对断端和细条纹瑕疵类型的检测结果TPR值虽然达到0.99但是其检测结果存在大面积误检,针对网纹瑕疵类型的检测结果TPR值仅有0.11,且也有大范围的误检。同态滤波算法针对网纹、细条纹和断端瑕疵类型的检测结果TPR值分别为0.91、0.86和0.56且检测结果存在大面积的误检。自商图像算法针对3种瑕疵类型的检测结果TPR值均低于0.3且依然存在大面积的误检。
分析表2、图8~10检测实验结果,基于LCE预处理算法的疵点检测效果最为出色,针对网纹和细条纹瑕疵类型的TPR值均达到0.99,针对网纹类型检测结果存在小范围误检情况。Retinex算法针对断端的TPR值为0.01几乎无法检测出瑕疵区域,针对网纹与细条纹瑕疵类型的检测结果TPR值在0.5左右,但是其检测结果存在大面积误检。同态滤波算法针对网纹、细条纹和断端瑕疵类型的检测结果TPR值分别为0.60、0.56和0.45且检测结果存在大面积的误检。自商图像算法针对3种瑕疵类型的检测结果TPR值均低于0.3且依然存在大面积的误检。

|
Download:
|
| 图 9 不同光照预处理算法对箱形网纹瑕疵类型瑕疵图检测结果 Fig. 9 Box netting multiple defect image and fabric detection results with different preprocessing algorithm | |
综上所述,Retinex算法仅针对星形数据集的实验结果查全率TPR与LCE算法接近,但是前者检测结果误检面积较大,其他两种算法都与LCE算法差距较大,故选择LCE算法作为最优光照预处理算法,并结合本文提出的特征提取算法进行瑕疵检测。
3.3 本文算法与其他算法对比在星形图与箱形图数据集中,本文算法与其他经典算法LSG、WGIS、BB和RB结合LCE光照预处理算法进行对比实验。实验结果如表3、表4、图11~16所示。
分析表3、图11~13检测实验结果,本文算法在所有3种瑕疵类型中的检测结果均为最优。且本方法在所有3种类型的瑕疵中TPR值均达到最优,FPR值保持稳定。
分析表4,图14~16检测实验结果,在3种瑕疵类型的检测结果中本文算法均优于其他3种算法且本方法在所有3种类型的瑕疵中TPR值均达到最优,FPR值保持稳定。
| 表 3 不同算法对星形图案的检测效果影响 Tab.3 The effect of different algorithm on star pattern |
| 表 4 不同算法对箱形图案的检测效果影响 Tab.4 The effect of different algorithm on box pattern |

|
Download:
|
| 图 11 不同算法对星形图断端疵点图像的检测结果 Fig. 11 Star broken end defect image and fabric detection results with different algorithms | |

|
Download:
|
| 图 12 不同算法对星形图网纹疵点图像的检测结果 Fig. 12 Star netting multiple defect image and fabric detection results with different algorithms | |

|
Download:
|
| 图 13 不同算法对星形图细条纹疵点图像的检测结果 Fig. 13 Star thin bar defect image and fabric detection results with different algorithms | |

|
Download:
|
| 图 14 不同算法对箱形图断端疵点图像的检测结果 Fig. 14 Box broken end defect image and fabric detection results with different algorithms | |

|
Download:
|
| 图 15 不同算法对箱形图网纹疵点图像的检测结果 Fig. 15 Box netting multiple defect image and fabric detection results with different algorithms | |

|
Download:
|
| 图 16 不同算法箱形图细条纹疵点图像的检测结果 Fig. 16 Box thin bar defect image and fabric detection results with different algorithms | |
本文提出了一种基于LCE光照预处理算法的改进CLBP纺织品瑕疵检测方法。使用的LCE光照预处理算法可以有效地改善细节特征的可视化,并将LCE光照预处理算法与改进CLBP算法相结合,在一定程度上解决了受光照影响的纺织品瑕疵检测的问题。由实验结果可知,本文算法针对数据集中3种瑕疵类型的纺织品均有不错的检测效果,部分检测结果的TPR可以达到0.99左右。本文方法的局限性在于光照预处理算法仍需要进一步的优化,从而保留更多的图像细节特征,且受限于分块方法的局限性,本算法无法对点形图进行检测。因此克服上述问题是进一步的研究方向。
| [1] |
NGAN H Y T, PANG G K H, YUNG S P, et al. Wavelet based methods on patterned fabric defect detection[J]. Pattern recognition, 2005, 38(4): 559-576. DOI:10.1016/j.patcog.2004.07.009 ( 0) 0)
|
| [2] |
NGAN H Y T, PANG G K H. Novel method for patterned fabric inspection using bollinger bands[J]. Optical engineering, 2006, 45(8): 087202. DOI:10.1117/1.2345189 ( 0) 0)
|
| [3] |
NGAN H Y T, PANG G K H. Regularity analysis for patterned texture inspection[J]. IEEE transactions on automation science and engineering, 2009, 6(1): 131-144. DOI:10.1109/TASE.2008.917140 ( 0) 0)
|
| [4] |
TSANG C S C, NGAN H Y T, PANG G K H. Fabric inspection based on the Elo rating method[J]. Pattern recognition, 2016, 51: 378-394. DOI:10.1016/j.patcog.2015.09.022 ( 0) 0)
|
| [5] |
JIA Liang, CHEN Chen, LIANG Jiuzhen, et al. Fabric defect inspection based on lattice segmentation and Gabor filtering[J]. Neurocomputing, 2017, 238: 84-102. DOI:10.1016/j.neucom.2017.01.039 ( 0) 0)
|
| [6] |
BELHUMEUR P N, KRIEGMAN D J. What is the set of images of an object under all possible illumination conditions[J]. International journal of computer vision, 1998, 28(3): 245-260. DOI:10.1023/A:1008005721484 ( 0) 0)
|
| [7] |
王霞玲, 吕岳, 文颖. 复杂背景和非均匀光照环境下的条码自动定位和识别[J]. 智能系统学报, 2010, 5(1): 35-40. WANG Xialing, LÜ Yue, WEN Ying. Automatic location and recognition of barcodes on objects with complex background and non-uniform lighting[J]. CAAI transactions on intelligent systems, 2010, 5(1): 35-40. (  0) 0)
|
| [8] |
黄腾, 施鹏飞. 非均匀光照下的车牌定位方法[J]. 智能系统学报, 2009, 4(5): 421-426. HUANG Teng, SHI Pengfei. Locating vehicle license plates in a non-uniformly illuminated environment[J]. CAAI transactions on intelligent systems, 2009, 4(5): 421-426. (  0) 0)
|
| [9] |
CANDES E J, DONOHO D L. Curvelets-a surprisingly effective nonadaptive representation for objects with edges[M]. Nashville, TN: Vanderbilt University Press, 1999: 1-10.
( 0) 0)
|
| [10] |
WANG Haitao, LI S Z. WANG Yangsheng, et al. Self quotient image for face recognition[C]//Proceedings of 2004 International Conference on Image Processing. Singapore, Singapore, 2004: 1397-1400.
( 0) 0)
|
| [11] |
LAND E H. Recent advances in Retinex theory[J]. Vision research, 1986, 26(1): 7-21. DOI:10.1016/0042-6989(86)90067-2 ( 0) 0)
|
| [12] |
LANGE C, POLTHIER K. Anisotropic smoothing of point sets[J]. Computer aided geometric design, 2005, 22(7): 680-692. DOI:10.1016/j.cagd.2005.06.010 ( 0) 0)
|
| [13] |
KAO Wenchung, HSU M C, YANG Y Y. Local contrast enhancement and adaptive feature extraction for illumination-invariant face recognition[J]. Pattern recognition, 2010, 43(5): 1736-1747. DOI:10.1016/j.patcog.2009.11.016 ( 0) 0)
|
| [14] |
王美, 梁久祯. 自适应特征提取的光照鲁棒性人脸识别[J]. 计算机工程与应用, 2012, 48(11): 164-169. WANG Mei, LIANG Jiuzhen. Adaptive feature extraction for illumination invariant face recognition[J]. Computer Engineering and Applications, 2012, 48(11): 164-169. DOI:10.3778/j.issn.1002-8331.2012.11.036 (  0) 0)
|
| [15] |
GUO Zhenhua, ZHANG Lei, ZHANG D. A completed modeling of local binary pattern operator for texture classification[J]. IEEE transactions on image processing, 2010, 19(6): 1657-1663. DOI:10.1109/TIP.2010.2044957 ( 0) 0)
|
| [16] |
WEN Jia, ZHAO Junsuo, WANG Cailing. Improved morphological component analysis for interference hyperspectral image decomposition[J]. Computers & electrical engineering, 2015, 46: 394-402. ( 0) 0)
|
| [17] |
周宇旋, 吴秦, 梁久祯. 判别性完全局部二值模式人脸表情识别[J]. 计算机工程与应用, 2017, 53(4): 163-169. ZHOU Yuxuan, WU Qin, LIANG Jiuzhen. Facial expression recognition based on discriminative CLBP[J]. Computer engineering and applications, 2017, 53(4): 163-169. DOI:10.3778/j.issn.1002-8331.1507-0048 (  0) 0)
|
| [18] |
DO M N, VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE transactions on image processing, 2005, 14(12): 2091-2106. DOI:10.1109/TIP.2005.859376 ( 0) 0)
|
| [19] |
赵树志, 狄岚, 何锐波. 基于改进判别性完整局部二值模式与格分割的织物瑕疵检测方法[J]. 纺织学报, 2018, 39(9): 57-64. ZHAO Shuzhi, DI Lan, HE Ruibo. Fabric defect detection based on modified discriminant complete local binary pattern and lattice segmentation[J]. Journal of textile research, 2018, 39(9): 57-64. (  0) 0)
|
 2019, Vol. 14
2019, Vol. 14


